行動網路上身份導向公鑰密碼系統之計算與應用

全文

(1)國立交通大學資訊工程學系博士論文. 行動網路上身份導向公鑰密碼系統之計算與應用 Computation and Application for ID-based Cryptosystems in Mobile Network. 研究生：胡鈞祥指導教授：陳榮傑博士林一平博士. 中華民國九十四年十月.

(2) 行動網路上身份導向公鑰密碼系統之計算與應用 Computation and Application for ID-based Cryptosystems in Mobile Network. 研究生：胡鈞祥指導教授：陳榮傑博士林一平博士. Student: Jing-Shyang Hwu Advisors: Dr. Rong-Jaye Chen Dr. Yi-Bing Lin. 國立交通大學資訊學院資訊工程學系博士論文. A Dissertation Submitted to Department of Computer Science College of Computer Science National Chiao Tung University in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy in. Computer Science. October 2005. Hsinchu, Taiwan, Republic of China. 中華民國九十四年十月.

(3) 行動網路上身份導向公鑰密碼系統之計算與應用. 研究生：胡鈞祥. 指導教授：陳榮傑博士林一平博士. 國立交通大學資訊學院資訊工程學系博士班. 摘. 要. 在下一代的行動通訊系統中，無線資訊服務提供者(例如：行動銀行)必須發展一套安全機制來確保端點對端點之間的安全性(end-to-end security)。目前存在的端點對端點的安全機制主要是建立在公鑰密碼系統上，其中一個非常重要的議題是如何確保公鑰的認證正確性。身份導向公鑰密碼系統利用可以用來確認使用者身份的資訊來產生公鑰，進而確保所取得公鑰的認證正確性。Boneh 和 Franklin 提出一個完整且有效率的身份導向加密系統，他們利用橢圓曲線上的一種雙線性對-威耳對(Weil pairing)來建構加解密系統，其中雙線性對的運算在整個加解密運算過程中佔相當大的份量，因此如何加速雙線性對的運算在身份導向密碼系統中是一個相當重要的議題。本論文主要研究橢圓密碼上雙線性對的特性，並提出在不同有限體上的雙線性對加速演算法，同時也提供行動通訊上有效率的端點對端點安全機制的應用。. i.

(4) Computation and Application for ID-based Cryptosystems in Mobile Network. Student: Jing-Shyang Hwu. Advisors: Dr. Rong-Jaye Chen Dr. Yi-Bing Lin. Department of Computer Science College of Computer Science National Chiao Tung University. ABSTRACT In the next generation mobile telecommunications, any third party that provides wireless data services (e.g., mobile banking) must have its own solution for end-to-end security. cryptosystem.. Existing mobile security mechanisms are based on public-key. The main concern in a public-key setting is the authenticity of the. public key. This issue can be resolved by identity-based (ID-based) cryptography where the public key of a user can be derived from public information that uniquely identifies the user.. The first complete and efficient ID-based encryption scheme was. proposed by Boneh and Franklin. They use a bilinear map (the Weil pairing) over elliptic curves to construct the encryption/decryption scheme.. However, in the. existing ID-based cryptosystem, the pairing computing has significant overhead. Therefore, efficient algorithm for computing bilinear pairing is essential for implementation.. In this dissertation, we will study the bilinear pairings over elliptic ii.

(5) curves and design improved algorithms for the computation of pairing over different finite fields. This will provide efficient implementations for ID-based cryptosystems in mobile devices to construct end-to-end security mechanisms. iii.

(6) 誌. 謝. 能順利畢業，要感謝的人很多；首先要感謝我的指導老師陳榮傑教授以及林一平教授，在論文的研究過程中提供我許多寶貴的意見與費心的指導，使得這份論文能夠順利地完成。也感謝曾文貴教授、葉義雄教授、趙涵捷教授、周勝鄰教授、呂及人教授及陳志成教授，擔任我的論文口試委員，在口試的過程中給予建議與指正，使得論文能更加完整。另外，特別要感謝師母李惠慈女士，不厭其煩地為我指正出英文寫作上的錯誤，並教導我寫作的技巧。此外，也要感謝密碼理論實驗室的學長及學弟們：感謝張仁俊學長在研究及生活上給予的建議和協助。還有實驗室學弟凱群、緯凱、志賢、漢璋、政愷、志彬、韋廷、家瑋，謝謝你們讓我的研究生活更多采多姿。還要感謝世芬在行動運算領域上共同的討論與研究。最後要感謝我的家人們，感謝我的父母從小到大的養育和教誨，讓我能順利地完成學業取得博士學位；也要感謝我的哥哥，謝謝他在生活和學業上對我的關心和支持，更要感謝我的太太冬菊，妳的鼓勵和體諒是我堅持下去的重要動力，僅以這份論文獻給我最親愛的家人們。. iv.

(7) Contents Abstract in Chinese........................................................................................... i Abstract in English .......................................................................................... ii Acknowledgment............................................................................................. iv Contents ............................................................................................................ v List of Figures................................................................................................. vii List of Tables..................................................................................................viii Notation............................................................................................................ ix 1.. 2.. 3.. Introduction............................................................................................... 1 1.1. Research Motivation ......................................................................... 1. 1.2. Organization of the Dissertation ....................................................... 5. Preliminaries ............................................................................................. 7 2.1. Elliptic Curves .................................................................................. 7. 2.2. Divisor Theory ................................................................................ 10. ID-Based Cryptography ......................................................................... 15 3.1. Public-Key Cryptography ............................................................... 15. 3.2. Authentication of Key Distribution ................................................ 18. 3.3. Certificate-Based Public Key Cryptosystem .................................. 20. v.

(8) 4.. 5.. 6.. 3.4. ID-Based Public Key Cryptosystem ............................................... 22. 3.5. ID-Based Cryptography vs. Certificate-Based Cryptography ........ 23. Efficient Computation for Weil Pairing................................................ 32 4.1. Miller’s Algorithm .......................................................................... 32. 4.2. Double-and-Add Method for Weil Pairing ..................................... 34. 4.3. Point Halving .................................................................................. 36. 4.4. Normal Basis Implementation ........................................................ 39. 4.5. Halve-and-Add Method for Weil Pairing........................................ 40. 4.6. Performance Evaluation.................................................................. 44. End-to-End Security for Short Message Service.................................. 49 5.1. Short Message Service Architecture ............................................... 50. 5.2. RSA Mechanism ............................................................................. 51. 5.3. ID-Based Mechanism...................................................................... 53. 5.4. Performance Comparison................................................................ 59. Conclusions and Future Work ............................................................... 66 6.1. Summary ......................................................................................... 66. 6.2. Future Work .................................................................................... 68. Bibliography ................................................................................................... 69. vi.

(9) List of Figures 2.1. Group Law on an Elliptic Curve ........................................................... 9. 3.1. The Man-in-the-middle Attack ............................................................ 19. 3.2. The Certificate-based Public Key Distribution.................................. 21. 3.3. The ID-based Public Key Distribution................................................ 23. 5.1. GSM Short Message Service Network Architecture.......................... 51. 5.2 Procedure of Sending an Encrypted Short Message.......................... 53 5.3. ID-based End-to-end Encryption Mechanism.................................... 58. 5.4. Encrypted Short Message Experimental Environment..................... 59. 5.5. Delivery Delay of Short Message Service............................................ 63. 5.6. Overhead of Ciphered Short Message ................................................ 65. vii.

(10) List of Tables 4.1. Arithmetic Operations for Scalar Multiplication .............................. 45. 4.2. Arithmetic Operations for Rational Function Evaluation ................ 46. 4.3. The Orders of Weil Pairing in the NIST Curves................................ 48. 4.4. Execution Times in ID-based Encryption Schemes ........................... 48. 5.1. Key Size for Equivalent Security Levels ............................................. 60. viii.

(11) Notation The following notation is used throughout this thesis.. K char(K) GF(p) GF(2n) i, j, k, m, n, r, s x, y, a, b, c. finite field characteristic of finite field K finite field of size p, p is a prime larger than 3 finite field of size 2n integer element of finite field. λ α, β. element of finite field indicating the slope of a line. E P, Q, R, S, T, U x P, y P O Div(E) Div0(E) D supp(D) deg(D) f, g, h div(f) e(P, Q) E[m] Um Tr(c). element of finite field GF(2n) group of points on elliptic curve point on elliptic curve coordinate of point P=(xP, yP) point at infinite in elliptic curve group group of divisors on elliptic curve group of divisors on elliptic curve of degree zero divisor on elliptic curve set of supporting points of divisor D degree of divisor D rational function over elliptic curve divisor of rational function f Weil pairing of points P and Q group of m-torsion points on elliptic curve group of mth roots of unity in a finite field trace of element c in a finite field. ix.

(12) Chapter 1 Introduction. 1.1 Research Motivation In the recent years, the third generation (3G) and beyond 3G (B3G) mobile telecommunications networks [21] have been widely deployed or experimented. These networks offer large bandwidths and high transmission speeds to support wireless data services besides traditional voice services. For circuit-switched voice services, mobile operators have provided security protection including authentication and encryption. On the other hand, wireless data services (such as mobile banking) are likely to be offered by the third parties (e.g., banks) who cannot trust the security mechanisms of mobile operators. In this case, the third parties must have their own solution for end-to-end security [22]. End-to-end security mechanisms used in mobile services are typically based on public-key cryptosystem.. 1.

(13) In public-key cryptosystem each user has a key pair (KU, KR), where KU is the public key and KR is the private key. To generate the key pair, one first chooses a private key KR and applies some one-way function to KR to obtain a random and uncontrollable KU.. The main concern in a public-key setting is the. authenticity of the public key. If an attacker convinces a sender that a receiver’s public key is some key of the attacker’s choice instead of the correct public key, he can eavesdrop and decrypt messages intended for the receiver. This is the well known man-in-the-middle attack [32].. This authentication problem is. typically resolved by the use of verifiable information called certificate, which is issued by a trusted third party and consists of the user name and his public key. In 1984, Shamir [30] introduced the concept of identity-based (ID-based) cryptography where the public key of a user can be derived from public information that uniquely identifies the user.. For example, the public key of a. user can be simply his/her email address or telephone number, and hence implicitly known to all other users.. A major advantage of ID-based. cryptosystem is that no certificate is needed to bind user names with their public keys.. The first complete and efficient ID-based encryption scheme was. proposed by Boneh and Franklin in 2001 [8].. 2. They used a bilinear map (the Weil.

(14) pairing) over elliptic curves to construct the encryption/decryption scheme. After that, the bilinear pairings have been used to design numerous ID-based schemes, such as key exchange [18] and short signature [9].. In addition to the Weil pairing, there exists another bilinear map on the group of points on an elliptic curve, which is known as the Tate pairing [13].. From a. computational point of view, the Tate pairing can be done approximately twice as fast as the Weil pairing as it requires half the evaluations of rational functions in Weil pairing.. As our proposed algorithm improves the evaluation of a rational. function, it can be similarly applied to the computation of the Tate pairing theoretically.. A disadvantage of the Tate pairing is that the outcome is not a. unique value, and so cannot be used in many applications. This problem can be solved by performing an exponentiation on the outcome of the Tate pairing [29]. The advantage of the Weil pairing is that its definition is more comprehensible than that of the Tate pairing, which involves equivalence classes of quotient groups.. For the reader to easily follow the derivation of our proposed algorithm,. we introduce the Weil pairing and implement our proposed algorithm on it.. ID-based cryptosystem transparently provides security enhancement to the mobile applications without requiring the users to memorize extra public keys.. 3.

(15) For example, sending an ID-based encrypted short message is exactly the same as sending a normal short message [16] if the mobile phone number of the short message recipient is used as the public key. Therefore, the mobile user (the sender) does not need to memorize the public key of the receiver. This feature is especially desirable for mobile applications such as banking or stock transactions. However, with the existing ID-based cryptosystem, the pairing computing has significant overhead.. Therefore, an efficient algorithm for ID-based. cryptosystem is essential in mobile devices with limited computing power.. The original algorithm for computing Weil pairing was proposed by Miller [26] and most current algorithms are based on it in some way.. It is an efficient. probabilistic polynomial-time algorithm for computing the pairings.. The work. of Barreto, Kim, Lynn and Scott [2] and Galbraith, Harrison and Soldera [14] focus in particular on the Tate pairing and they proposed methods for its fast computation. three.. They also considered a practical case of fields of characteristic. Eisentrager, Lauter and Montgomery developed an algorithm to speed up. point multiplication of an elliptic curve [10].. The most important part of the. Miller’s algorithm is the evaluation of a rational function associated with an m-torsion point of the elliptic curve.. In this dissertation, we extend the idea of. 4.

(16) point halving, which was proposed by Knudsen [19], to speed up the evaluation of a rational function.. We also illustrate an applicable ID-based end-to-end mobile. encryption system for short message service (SMS).. 1.2 Organization of the Dissertation This dissertation is organized as follows.. Chapter 2 states some facts about. elliptic curves and functions on elliptic curves. Then we deal with divisor theory on elliptic curves, which lies at the heart of the definitions of the Weil pairing.. In Chapter 3, we give expositions for certificate-based and ID-based cryptography which provide authentic solutions for public key distribution. After defining ID-based cryptography, we compare ID-based cryptography with conventional certificated-based cryptography in some practical aspects, such as authenticity of system parameters, registration at the authority, key escrow, key revocation, key distribution, master key security, and additional possibilities.. In Chapter 4, we extend the idea of point halving to design an improved evaluation algorithm for a rational function, which is the most important part of Weil pairing computation.. We first describe the original Miller’s algorithm for. 5.

(17) computing Weil pairing and show the double-and-add method. Then we present a new algorithm for computation of Weil pairing using the point halving technique and the normal basis implementation.. We actually implement the ID-based. encryption schemes and compare the performance to show the advantage of our approach over a previously proposed popular solution.. In Chapter 5, we implement two encryption systems for Short Message Service (SMS) and estimate the encryption overheads compared with the original non-ciphered message transmissions.. These two applicable end-to-end. encryption mechanisms for SMS are based on the certificate-based public key cryptosystem and the ID-based public key cryptosystem, respectively. We also evaluate and compare the delivery overheads of these two mechanisms.. Chapter 6 summarizes our results and proposes future work.. 6.

(18) Chapter 2 Preliminaries. In this Chapter, we describe divisor theory on elliptic curves.. First, we. briefly give some facts about elliptic curves in Section 2.1. Next we deal with divisor theory in Section 2.2.. For details on divisor theory, the reader is referred. to [24][31].. 2.1 Elliptic Curves Let p be a prime larger than 3.. An elliptic curve over a finite field of size p. denoted by GF(p) can be given by an equation of the form: y2 = x3 + ax +b, where a, b ∈ GF(p) and 4a3+27b2 ≠ 0 mod p. (The equation over a finite field of size 2n denoted by GF(2n) looks slightly different and will be given later.). The. set of points on the curve is the collection of ordered pairs (x, y) with coordinates. 7.

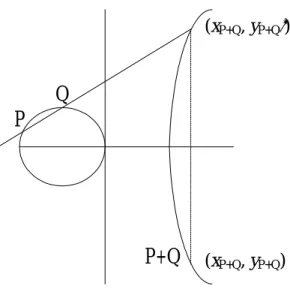
(19) in the field such that x and y satisfy the equation defining the curve, plus an extra point O called the infinity point.. These points form an abelian group E under a. certain addition over GF(p). That is,. E = {(x,y) ∪ O | (x,y) satisfies the equation y2 = x3 + ax +b, x, y∈ GF(p)}.. The group addition operation is defined as follows: to add two points P=(xP, yP) and Q=(xQ, yQ) on the curve, we first pass the straight line through them, find out the third point (xP+Q, yP+Q′) intersected with the curve, and then reflect the point over the x-axis to obtain point P+Q=(xP+Q, yP+Q), i.e., yP+Q= -yP+Q′ (see Fig. 2.1).. Assume that P=(xP, yP) and Q=(xQ, yQ) are on the curve, λ is the slope of the line passing through P and Q, then the coordinates of P+Q = (xP+Q, yP+Q) are ⎧ yQ − y P ⎪ x − x if P ≠ Q x P + Q = λ − x P − xQ P ⎪ Q , where λ = ⎨ 2 . y P + Q = λ ( xP − xP + Q ) − y P ⎪ 3xP + a if P = Q ⎪⎩ 2 y P 2. The infinity point O plays a role as the identity element, that is, P+O = O+P = P for any point P.. Each point P has a unique inverse element -P such that. P+(-P)=O. For P=(xP, yP) in elliptic curve E over GF(p), the unique additive inverse of P is defined by -P=(xP, -yP).. 8.

(20) (xP+Q, yP+Q′). Q P. P+Q. (xP+Q, yP+Q). Figure 2.1 Group law on an elliptic curve. Another category of elliptic curves is defined over the finite field of size 2n denoted by GF(2n).. The equation defining elliptic curves over GF(2n) is of the. form y2 + xy= x3 + ax2 +b , where a, b∈GF(2n) and b≠0.. The addition operation. on points P and Q is the same as before except that yP+Q= xP+Q + yP+Q′. Therefore we can obtain the addition formula as follows. yQ)∈E.. Let P=(xP, yP), Q=(xQ,. Let λ be the slope of the line passing through P and Q, and the. coordinates of P+Q be (xP+Q, yP+Q).. Then. ⎧ yQ + y P ⎪ x + x if P ≠ Q x P + Q = λ + λ + x P + xQ + a ⎪ Q P , where λ = ⎨ . yP + Q = λ ( xP + xP + Q ) + xP + Q + y P ⎪ x + y P if P = Q ⎪⎩ P xP 2. The inverse of P=(xP, yP) is defined by -P=(xP, xP+yP) when P is in elliptic. 9.

(21) curve E over binary field GF(2n).. For elliptic curves, the group operation is written as addition instead of multiplication. Thus the exponentiation in the general multiplicative group can be appropriately referred to as the scalar multiplication in the elliptic curve group. P2 + ... P for an integer r. That is, we denote rP as P 1+4 4 4+ 4 3 r times. 2.2 Divisor Theory A divisor is a useful device for keeping track of the zeros and poles1 of rational functions [24].. A divisor provides a representation to indicate which. points are zeros or poles and their orders for a rational function over the elliptic curve. A divisor D can be defined as a formal sum of points on elliptic curve group E: D =. ∑ n ( P) , where nP is a non-zero integer that specifies the zero/pole. P∈E. P. property of point P and its respective order. Inequality nP > 0 indicates that point P is a zero, and nP < 0 indicates that P is a pole. For example, for P, Q, R∈E, D1 = 2(P) + 3(Q) – 3(R) indicates that divisor D1 has zeros at P and Q with order 2 and 3 respectively, and a pole at R with order 3. And D2= 2(P) + (-2P) – 3(O). 1. Let f be a non-zero rational function, and P∈E. If f(P)=0 then f is said to have a zero at P. is not defined at P then f is said to have a pole at P and we write f(P)=∞.. 10. If f.

(22) indicates that P and -2P are zeros with order 2 and 1, and O is a pole with order 3 for the divisor D2. specific point.. Note that the parenthesis is used to separate the order and the. For example, (2P) indicates that 2P is a zero with order 1, while. 2(P) indicates that P is a zero with order 2.. The group of divisors on E, denoted as Div(E), forms an abelian group with the following addition operation. For D1, D2∈Div(E), if D1 = then D1 + D 2 =. ∑ n ( P) , D P. P∈E. 2. =. ∑ n ( P) + ∑ m ( P) = ∑ ( n. P∈E. For a divisor D =. P. P∈E. ∑ n ( P) ,. P∈E. P. P. P∈E. ∑ m ( P) ,. P∈E. P. P. + mP )( P) .. we define supp(D)={P∈E | nP≠0} as the. support of divisor D, and deg ( D) =. ∑n. P∈E. P. as the degree of divisor D.. For. example, if D1 = 2(P) + 3(Q) – 3(R), D2= 2(P) + (-2P) – 3(O), then supp(D1)={P, Q, R}, supp(D2)={P, -2P, O} and deg(D1)=2+3-3=2, deg(D2)= 2+1-3=0.. From now on, we consider only the set of divisors of degree zero, denoted as Div0(E).. Let f be a rational function from K×K to K, where K is a finite field.. For example, f ( x, y ) =. 3y − 2x − 5 . The evaluation of a rational function f on a 5 y + 3x − 2. point P=(xP, yP) is defined by f(P)=f(xP, yP) and the evaluation of f on a divisor D=. ∑ n (P). P∈E. P. is defined by f(D)=. function f as div (f ) =. ∏ f ( P). nP. . Define the divisor of a rational. P∈supp (D ). ∑n. P∈E. P, f. ( P) , where nP,f is the zero/pole order of point P on f.. 11.

(23) It is well known that the degree of the divisor of a rational function must be zero [24]; that is, div(f)∈Div (E) for any rational function f. 0. For example, let P=(xP,. yP)∈E, f(x,y)= x-xP, then div(f) = div(x-xP) = (P) + (-P) − 2(O). P and -P are the. zeros of f because only they are on both the vertical line x-xP=0 and the elliptic curve E.. The infinity point O is a pole of order 2 because div(f)∈Div0(E).. Then for two rational functions f1 and f2, we have div(f1) + div(f2) = div(f1f2) and div(f1) − div(f2) = div(f1/f2).. As an example, let E be the elliptic curve defined by y2=x3+7x over GF(13). We have P=(4,1), Q=(5,2)∈E, and P+Q=(5,11). Assume that f ( x, y ) =. y−x+3 . x −5. Since P, Q, -(P+Q)=(5,2)=Q are on the line y-x+3=0, div(y-x+3) = (P) + (Q) + (-(P+Q)) − 3(O) = (P) + 2(Q) − 3(O). Also, div(x-5) = (Q) + (-Q) + 2(O) = (Q) + (P+Q) − 2(O) because Q, -Q=(5,11)=P+Q are on the line x-5=0. Therefore, we have div(f) = div(y-x+3) − div(x-5) = (P) + (Q) − (P+Q) − (O).. A divisor D∈Div0(E) is defined to be principal if D=div(f) for some rational function f. The principal divisor D =. ∑ n ( P). P∈E. [24], where. ∑n P. P∈E. P. P. is characterized by. ∑n P = O. P∈E. P. denotes the sum by applying addition operation on the points. in elliptic curve E. For example, let D3 = (P) + (-P) − 2(O), then D3 satisfies deg(D3)=0 and P+(-P)−2O = P−P = O. Therefore D3 is principal. In fact,. 12.

(24) D3=div(x-xP) for the function x-xP.. Two divisors D1, D2∈Div0(E) are said to be equivalent (denoted as D1 ~ D2) if D1−D2 is principal. For any divisor D =. ∑n. R ∈E. point P =. ∑n. R ∈E. R. R. ( R ) ∈Div0(E), there is a unique. R ∈E such that D ~ (P) – (O). In other words, D can be always. written in canonical form: D = (P) – (O) + div(f), where f is a rational function.. Now we introduce a formula for adding two divisors in canonical form, such that the result is still in canonical form. This formula provides a method of finding a rational function f such that div(f) = D for a given divisor D, and is critical for computing Weil pairing.. Let D1, D2 ∈ Div0(E) be given by D1 =. (P1) – (O) + div(f1) and D2 = (P2) – (O) + div(f2). Assume that P1+P2=P3. Let. hP1 , P2 ( x, y ) = ay + bx + c be the equation of the straight line passing through P1 and P2, and hP3 ( x, y ) = x + d be the equation of vertical line passing through P3. (Note that if P1 = P2, hP1 , P2 ( x, y ) is the line tangent to P1. And if P3 = O, we have hP3 ( x, y ) =1, a constant equation.) Then we have div( hP1 , P2 ) = (P1) + (P2) + (-P3) – 3(O) where P1, P2, and -P3 are zeros because they are on line hP1 , P2 , and div( hP3 ) = (P3) + (-P3) – 2(O) where P3, -P3 are zeros because they are on line hP3 (see Fig. 2.1). From the above discussion, the sum of divisors D1 + D2 is written as:. D1 + D2 = (P1) + (P2) – 2(O) + div(f1f2). 13.

(25) = (P3) – (O) + div(f1f2) + div( hP1 , P2 ) – div( hP3 ) = (P3) – (O) + div( f1f2hP1 , P2 /hP3 ).. (2.1). Eq. (2.1) will be used in the computation of Weil pairing in Chapter 4.. 14.

(26) Chapter 3 ID-Based Cryptography. In this chapter, we first introduce the public key cryptography and the authentication of key distribution. Next described are the certificate-based and the ID-based public key cryptosystems which provide authentic solutions for public key distribution. A comparison is also done between the certificate-based and the ID-based systems.. 3.1 Public Key Cryptography All. security. mechanisms. deployed. today. are. based. on. either. symmetric/secret key or asymmetric/public key cryptography, or sometimes a combination of both. Here we introduce the basic aspects of the secret key and public key techniques and compare their main characteristics; a detailed. 15.

(27) description of cryptographic mechanisms and their application can be found in [25].. We will explain the most important elements and procedures that constitute. the public key infrastructure (PKI) on which public key techniques rely.. A. general description of a public key infrastructure can be found in [1].. Secret key techniques are based on the fact that the sender and recipient share a secret, which is used for various cryptographic operations, such as encryption and decryption of messages and the creation and verification of message authentication data. This secret key must be exchanged in a separate procedure prior to the intended communication. For example, in a GSM (Global System for Mobile) cellular radio system the secret key shared between the mobile subscriber and the home operator is installed on a subscriber identity module (SIM) that is owned by the mobile subscriber and administered in the database of the subscriber’s home operator. The need to exchange a secret key prior to the intended communication complicates the provision of security for communications between entities that do not have a pre-established relationship. Authentication is done by proving possession of the pre-shared secret key to each other.. A widely used method for doing this is the challenge-and-response. method. A challenge is sent to the challenged node, which then calculates a. 16.

(28) response using the challenge and the secret key as input for an algorithm. This response is sent to the challenger, which performs the same operation and compares the result with the received response.. The administration and. management of secret keys, including their generation, distribution, renewal and tamper-resistant storage, can become very complicated as the number of keys grows. For each pair of entities a secret key has to be created and distributed, so that for a group of n entities communicating with each other, n(n - 1)/2 keys are required.. Because of the need for pre-shared secret keys, secret key based. solutions have low scalability. A major advantage of secret key techniques is that they are computationally very fast in comparison with public key techniques. This is the main reason why many protocols today still use secret key mechanisms for authentication.. Public key techniques utilize the asymmetric key pairs.. In an asymmetric. key pair, one key is made publicly available, while the other is kept private. Because one of the keys is available publicly, there is no need for a secure key exchange.. However, it is required to distribute the public key authentically.. Because there is no need for pre-shared secrets prior to a communication, public key techniques are ideal for supporting security between previously unknown. 17.

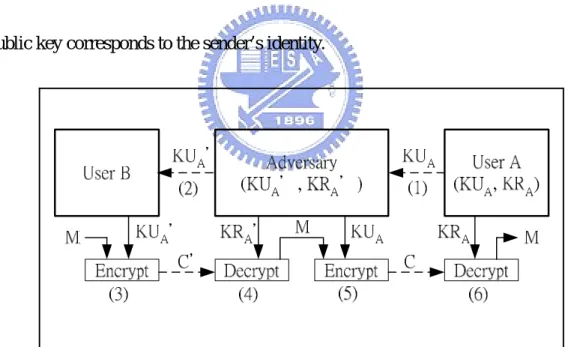
(29) parties. Authentication is achieved by proving possession of the private key. One mechanism for doing this is digital signature, which is generated with the private key and verified using the corresponding public key.. Public key. techniques make it possible to establish secret session keys dynamically.. A. simplified procedure is for one end-entity to calculate a secret session key and send it encrypted with the public key of the entity with which it wants to initiate a session.. That entity then obtains the secret key by decrypting the received. information with its private key. Since the public key of a key pair is usually published in a directory, the overhead associated with distributing keys is reduced significantly in comparison with secret key techniques.. 3.2 Authentication of Key Distribution A main concern in public key distribution is the authenticity of the public key. Fig. 1 illustrates how an adversary between a sender B and a receiver A can impersonate receiver A in the public key encryption scheme. The adversary achieves this by replacing A’s public key KUA with a false public key KUA' which is then received by B (Fig. 3.1 (1) and (2)). User B uses the false public key KUA' to encrypt the message M (Fig. 3.1 (3)). The adversary obtains the secret. 18.

(30) message M (Fig. 3.1 (4)) and delivers the re-encrypted cipher to user A (Fig. 3.1 (5)). In this way, the secret message M is acquired by both user A (Fig. 3.1 (6)) and the adversary. Similar impersonation settings exist between the signer and verifier in the signature schemes. This is the well known man-in-the-middle attack. The following issue arises from the need to prevent these kinds of attacks: how does B know (or authenticate) which particular public key is A’s?. To. answer this question, authentication of public key distribution is required. Authenticating public keys provides assurance to the entity that the received public key corresponds to the sender’s identity.. Figure 3.1 The man-in-the-middle attack. 19.

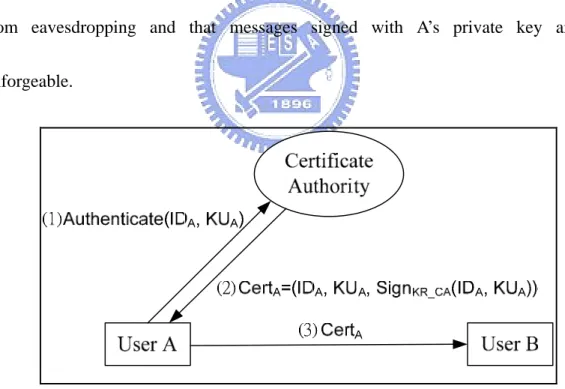
(31) 3.3. Certificate-based Public Key Cryptosystem A typical approach to guarantee the authentication of the public key holder relies on a trusted agent named Certificate Authority (CA). The CA’s digital signature binds entity A’s identity IDA to the corresponding public key KUA. The CA’s signature, when sent along with the identity (e.g., name or telephone number) and public key, forms a digital certificate which can be verified by any entity in possession of the CA’s public key.. This certificate provides a binding between the identity and the public key. Digital certificates can contain extra information, such as cryptographic algorithms to be used in conjunction with the public key in the certificate. The most widely adopted certificate format is based on the X.509 standard [17].. A. basic certificate issued by a CA for entity A is of the form:. CertA = (IDA, KUA, SignKR_CA(IDA, KUA)),. where SignKR_CA(.) denotes the signing algorithm with the CA’s private key as the signing key.. The certificate-based public-key distribution works as follows. User A first chooses a public key cryptosystem, and generates his/her own key pair (KUA,. 20.

(32) KRA), where KUA denotes the public key and KRA is the private key. To attain the authenticity of public-key distribution, user A has to subscribe to the trusted Certificate Authority (CA; see Fig. 3.2 (1)), and requests a certificate CertA for his/her public-key from CA (Fig. 3.2 (2)). The CA signs the certificate with its private key. Then user A can send his/her certificate directly to another user B (Fig. 3.2 (3)) or put it on the public key directory. Once user B is in possession of A’s certificate, B verifies the certificate with the CA’s public key and has confidence that the messages he/she encrypts with A’s public key will be secure from eavesdropping and that messages signed with A’s private key are unforgeable.. Figure 3.2 The certificate-based public key distribution. 21.

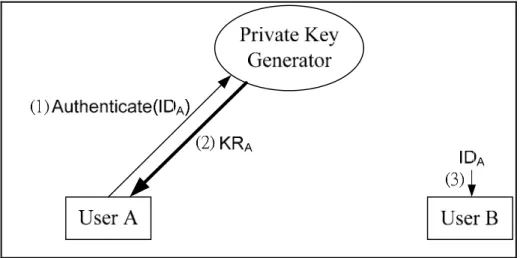
(33) 3.4. ID-based Public Key Cryptosystem Shamir [30] proposed the identity-based (ID-based) public key approach to support public key cryptography without the use of certification. In ID-based public key cryptosystem, user A’s public key KUA is not delivered to user B, and therefore eliminates the attack presented in Fig. 3.1. User B encrypts a message for user A or verifies a signature from user A using a public key which is derived from user A’s identifier IDA (e.g., email address or telephone number; see Fig. 3.3 (3)). The trusted agent has a new role in ID-based public key cryptosystem, and is renamed as the Private Key Generator (PKG). The PKG issues the private key corresponding to the public key (derived from the identifier IDA) to user A over a secure channel (Fig. 3.3 (2)). This issuing action takes place after user A is authenticated by the PKG (Fig. 3.3 (1)). To generate private keys, the PKG makes use of a master key which must be kept secret. The requirement to have an authentic CA’s public key for verifying certificates in certificate-based cryptosystem is replaced by the requirement to have authentic PKG’s system parameters in ID-based cryptosystem. Notice that both the PKG and the user A know the private key KRA.. 22.

(34) Figure 3.3 The ID-based public key distribution. 3.5 ID-based Cryptography vs. Certificate-based Cryptography The conventional public key cryptosystem uses the certificate to solve the authentication problem and is denoted as certificate-based cryptosystems. Both ID-based and certificate-based cryptosystems are asymmetric.. Hence, the. protocols for encryption, decryption, signing and signature verification have similar functionality in both systems.. The main difference, however, is key. management. ID-based cryptography was initially proposed to avoid the need for certificates for public key authentication. In fact, an ideal ID-based system would possess the following properties:. 23.

(35) 1. Users only need to know the identity of the user they want to communicate with.. 2. There is no need for keeping public directories such as files with public keys or certificates.. 3. The services of the Private Key Generator (PKG) are needed only during the system set-up phase.. However, in practice such an ideal scheme seems to be infeasible. Depending on the application, there are several practical issues that stand in the way of the realization of an ideal ID-based system.. We compare ID-based. cryptography with the traditional certificate-based cryptography in the following practical aspects: authenticity of system parameters, registration at the authority, key escrow, key revocation, key distribution, master key security, and additional possibilities.. Authenticity of system parameters. Suppose an attacker in an ID-based system generates his own master key and corresponding system parameters, and fools users into believing that these forged system parameters are correct.. Then for any public key, he can derive the. 24.

(36) corresponding secret key under his master key.. Hence, he can decrypt any. message encrypted under his forged parameters.. Further, he can create. signatures under any name, which will be accepted by users who believe his parameters. The attacker might even impersonate the PKG and issue secret keys to users on request. A similar problem occurs in a traditional situation, where the users need to be sure of the authenticity of the public key of the CA.. Namely, if. an attacker can make users believe that some public key of his choice is the public key of the CA, then he can create certificates containing forged public keys for which he owns the secret key. Consequently, the attacker can read the messages encrypted under the forged public keys and create signatures that appear to be valid under those keys. The only difference with the ID-based setting is that the attacker cannot impersonate the CA, as users would notice that their requested certificate contains an incorrect public key.. Registration at the authority. In both systems, a user who wants to participate needs to register at a Registration Authority (RA), which we often consider part of the PKG or CA. After some authentication procedure, the RA issues a unique digital identity to the user, for instance, in the form of an email address. In a certificate-based system,. 25.

(37) a user can now present his digital identity and public key to the CA, along with a proof of possession of the corresponding secret key.. The CA then issues a. certificate that binds together the digital identity and the public key. Similarly, in an ID-based setting, the user presents his digital identity to the PKG. The PKG then computes the secret key corresponding to the public key derived from the digital identity. ID-based systems have an additional disadvantage that the secret key needs to be transported from the PKG to the user. Thus, a secure channel that guarantees both confidentiality and authenticity is required.. Therefore,. ID-based systems seem to work best in applications where it is easy to achieve a secure channel or where users request secret keys not very often.. Key escrow. ID-based cryptosystems have inherent key escrow. That is, since the PKG owns the master key, he can generate any private key at any moment. Depending on the application, key escrow is not necessarily a bad thing. For instance, key escrow enables recovery of lost keys. For signatures schemes, however, it is often highly undesirable to have key escrow, as it prevents non-repudiation. Note that this escrow capability is also present in traditional public key settings where key pairs are generated by some central authority and. 26.

(38) this authority stores the issued keys. On the other hand, if users generate the key pairs themselves or the central authority does not store the keys, there is no way that keys can be retrieved and there is no key escrow. This is in contrast to an ID-based setting, where the PKG always has the ability to regenerate keys. The ID-based encryption scheme by Boneh and Franklin provides a way to block key escrow by introducing multiple PKGs. In brief, each of these n PKGs has its own master key. A user presents his public key to each KGC and gets from each of them a partial secret key in return. Then the correct secret key is obtained by combining the n partial secret keys. Thus the ability to retrieve any user’s secret key is distributed among n PKGs. In practice, setting up a system with multiple PKGs can be a complex task. Hence, an ID-based system works best in an application where key escrow is not an objection, or where the group of users is small enough to allow multiple PKGs.. Key revocation. When a certificate is revoked in a certificate-based scheme, other users are notified by means of a public Certificate Revocation List (CRL). This occurs when a user leaves the user group or a secret key is compromised. In the latter case, or when a key pair needs to be replaced after expiration of the certificate. 27.

(39) (key rollover), a user can simply generate a new key pair and obtain a certificate for it. However, in an ID-based setting, since a user’s public key is derived from his identity, he cannot simply obtain a new key pair after revocation as in a certificate-based scheme. That is, it can be very inconvenient to change identity every time a new key pair is needed.. A partial solution to this problem could be to derive the public key not only from the identity, but to concatenate the identity with some other general information. For instance, if the current year is added to the identity, users can use their secret key during this year only. Hence, secret keys expire annually and each user has to request a new key every year. Unlike traditional situation, users do not have to obtain new certificates from other users, because the public key is still uniquely determined in a straightforward manner (since the current year is common knowledge). But what if a user’s secret key is compromised during the year? Then the user has to wait until the end of the year. This situation can be improved by concatenating the identity with the current date instead of the current year. But the big disadvantage is that each user has to obtain a new secret key from the PKG every day. This results in a large increase in communications and a computational overhead for the PKG. Hence, the length of the validity period. 28.

(40) is a trade-off between convenience and efficiency.. Key distribution. The great simplification of key distribution (from the users’ point of view) is the main reason to introduce ID-based cryptography. That is, all public keys can be derived from the identity of the users. So obtaining someone’s public key, for encryption or signature verification, becomes a simple and transparent procedure. This is in contrast to certificate-based setting, where one has to look up the corresponding certificate, verify the CA’s signature, and check the expiration date of the certificate.. Master key security. The PKG in an ID-based scheme forms a single point of weakness. An attacker who is able to retrieve the PKG’s master key can derive all secret keys, and is thus able to read all messages and forge signatures under everyone’s name. Therefore, it is very important for a PKG to keep his master key secret. To prevent the master key from being stored in one place, it can be distributed among several KGCs, like the prevention of key escrow.. Similarly, the CA in a. certificate-based setting is a single point of weakness as well. If the CA’s secret. 29.

(41) key is compromised, an attacker can create certificates in the CA’s name for new public keys of his own choice, thereby fooling other users into believing those public keys.. However, the leak of the CA’s secret key does not enable an. attacker to retrieve previously existing secret keys. So the attacker cannot read messages encrypted under previously existing public keys, or forge signature under corresponding secret keys.. Additional possibilities. The fact that any value can be a public key offers some additional possibilities. For instance, we can concatenate the identity with other information to accomplish certain nice properties that do not exist in a certificate-based setting. In fact, in this setting, users can send encrypted messages into the future. This is done by using the public key as the concatenation of the identity with a future date. Now the recipient cannot decrypt the message until the specified date, when the PKG issues the corresponding secret key.. Here we assume that the PKG is. honest and does not issue keys before the specified date.. Furthermore, another application arises from the original idea of ID-based cryptography.. For example, we can combine ID-based cryptography with. traditional public key systems as follows. User U plays the role of PKG and. 30.

(42) generates his own system parameters and master key for an ID-based encryption scheme. U keeps his master key secret and publishes the system parameters. These parameters function as U’s public key in a certificate-based encryption scheme. As in a regular PKI setting, the authenticity of U’s public key (the system parameters) is guaranteed by a certificate from a CA. Now other users can encrypt messages for user U as in an ID-based scheme with system parameters that are given by U’s public key. Since U (and in fact only U) owns the master key for the ID-based system, he can derive the secret key for any identifier key and is thus able to read the messages encrypted under his system parameters.. 31.

(43) Chapter 4 Efficient Computation for Weil Pairing. In this chapter, we propose a halve-and-add method to speed up the evaluation for Weil pairing. We first describe the original Miller’s algorithm for computing Weil pairing.. Then we introduce the point halving operation. proposed by Knudsen in speeding up scalar multiplication on elliptic curve over GF(2n). The advantage of point halving relies on the fast arithmetic operations over GF(2n) in a normal basis. We then propose an efficient halve-and-add evaluation algorithm in Weil pairing computation and compare the performance with original double-and-add method.. 4.1 Miller’s Algorithm Given an elliptic curve E over a finite field K, let m be an integer prime to char(K), the characteristic of K [20]. For example, char(GF(p))=p and. 32.

(44) char(GF(2n))=2. The Weil pairing is a function e : E [m] × E [m ] → U m , where E [m] = {P | mP = O, P ∈ E} is called the m-torsion group, Um is the group of the mth roots of unity in K , the algebraic closure of K [20].. Weil pairing e(P, Q) is defined as follows. Given P, Q∈E[m], there exist divisors DP, DQ∈Div0(E) such that DP ~ (P) – (O) and DQ ~ (Q) – (O). Here we randomly choose points T, U, and assign DP = (P+T) – (T) and DQ = (Q+U) – (U). It is easy to verify that DP ~ (P) – (O) and DQ ~ (Q) – (O). As mP = mQ = O, divisors mDP and mDQ are principal and there exist rational functions fP , fQ such that div(fP) = mDP and div(fQ) = mDQ. Suppose that DP and DQ have disjoint supports, i.e., supp(DP) ∩ supp(DQ) = φ, then the Weil pairing of P and Q is defined as: e( P, Q) =. fP ( D Q ) . fQ ( D P ). The Weil pairing has the bilinearity property: for P, Q, R∈E[m], we have e(P+Q, R) = e(P, R)e(Q, R) and e(P, Q+R) = e(P, Q)e(P, R). for e(P, Q) computation is described as follows.. 33. The first algorithm.

(45) Miller’s Algorithm [26]. INPUT: P, Q∈E[m] OUTPUT: e(P, Q) Step 1. Select random points T, U∈E such that P+T, T, Q+U, U are distinct. Let DP = (P+T) – (T) and DQ = (Q+U) – (U). Step 2. Use an evaluation algorithm to compute fP(Q+U), fP(U), fQ(P+T) and fQ(T), where fP and fQ satisfy that div(fP) = mDP and div(fQ) = mDQ. Step 3. Compute e( P, Q) =. fP ( DQ ) fP (Q + U )fQ (T ) = . fQ ( D P ) fQ ( P + T )fP ( U ). 4.2 Double-and-Add Method for Weil Pairing A crucial part in Miller’s algorithm is the evaluation algorithm in Step 2. The evaluation algorithm for fP(S) produces fP such that div(fP) = mDP, and computes fP(xS, yS) for S=(xS, yS). Recall that DP = (P+T) – (T). For each integer k, there exists a rational function fk such that div (fk ) = k ( P + T ) − k (T ) − ( kP) + (O) . If k = m, then div (fm ) = m( P + T ) − m(T ) − ( mP) + (O) = m( P + T ) − m(T ) , and fP = fm. For any points R, S, let hR,S and hR be linear functions, where hR,S(x, y)= 0 is the straight line passing through R, S, and hR(x, y)= 0 is the vertical line. 34.

(46) passing through R. Then we have div (fk1 + k 2 ) = ( k1 + k 2 )( P + T ) − ( k1 + k 2 )(T ) − (( k1 + k 2 ) P) + (O) = k1 ( P + T ) − k1 (T ) − ( k1P) + (O) + k 2 ( P + T ) − k 2 (T ) − ( k 2 P) + (O). ,. + ( k1P) + ( k2 P) + ( −( k1 + k 2 ) P) − 3(O) − [(( k1 + k2 ) P) + ( −( k1 + k2 ) P) − 2(O)] = div (fk1 ) + div (fk 2 ) + div (hk1 P , k 2 P ) − div (h( k1 + k 2 ) P ). and hence. fk 1 + k 2 =. fk1 fk 2 hk1 P , k 2 P h( k1 + k 2 ) P. .. (4.1). Eq. (4.1) is recursive with initial conditions f0 = 1 and f1 =. hP + T since hP, T. div (f1 ) = ( P + T ) − (T ) − ( P) + (O) = (P + T) + (-(P + T)) − 2(O) − [( P) + (T ) + (-(P + T)) − 3(O)] = div (hP + T ) − div (hP, T ). Based on Eq. (4.1), a conventional double-and-add method was proposed for evaluation of a rational function fP on a given point S, where fP satisfies div(fP) = m(P+T) – m(T). The algorithm denoted as double-and-add evaluation algorithm is described as follows.. 35.

(47) Double-and-Add Evaluation Algorithm (Step 2, Miller’s Algorithm) [4] n −1. INPUT: the points P, T, S, and the order m = ∑ bi 2i with bi∈{0,1}, bn-1 = 1 i =0. OUTPUT: fm(S) = fP(S) f1 ←. hP + T (S) ; hP, T (S). f ← f1; Z ← P;. for j ← n-2, n-3, …, 0 do f ←f2. hZ, Z (S) ; Z ← 2Z; h2Z (S). if bj = 1 then f ← f1f. hZ, P (S) ; Z ← Z + P; hZ + P (S). endif endfor return f. 4.3 Point Halving We restrict our attention to elliptic curves E over finite field GF(2n) defined by the equation y 2 + xy = x 3 + ax 2 + b where a, b∈GF(2n), b≠0.. The finite. field GF(2n) can be viewed as a vector space of dimension n over GF(2).. That is,. each c∈GF(2n) can be represented as a vector ( cn −1...c1c0 ) where ci ∈ {0,1} . Let. 36.

(48) P=(xP, yP) be a point on E, where P ≠ −P. The coordinate of Q = 2P = (xQ, yQ) can be computed as follows:. λ = xP +. yP xP. (4.2). xQ = λ2 + λ + a. (4.3). and yQ = xP + xQ (λ + 1) 2. (4.4). Point halving was first proposed by Knudsen with the following operation: given Q=(xQ, yQ), compute P=(xP, yP) such that Q = 2P. Point halving provides fast computation for scalar multiplication on elliptic curve. The basic idea for halving is to solve Eq. (4.3) for λ, Eq. (4.4) for xP, and finally Eq. (4.2) for yP if needed. If G is a subgroup of odd order m in E, point doubling and point halving are automorphisms in G [19]. Therefore, given a point Q∈G, there is a unique point P∈G such that Q = 2P. To uniquely find P, Fong et al. [12] designed a point halving computation algorithm using the trace function Tr : GF(2n)→GF(2) n −1. defined by Tr ( c ) = ∑ ci , where c = ( cn −1...c1c0 ) ∈ GF ( 2 n ). i =0. The halve-and-add method for scalar multiplication uses two kinds of point representation: the usual affine representation P=(xP,yP) and the λ-representation (xP,λP), where λP = xP + yP/xP denotes the slope of the tangent line to the curve at P.. 37.

(49) As shown in the following point halving algorithm, repeated halving can be performed directly on the λ-representation of a point.. Only when a point. addition is required, a conversion to affine coordinate is needed.. Point Halving Algorithm [12]. INPUT: λ-representation (xQ, λQ) of Q OUTPUT: λ-representation (xP, λP) of P=(xP, yP), where Q = 2P. Step 1.. Find a solution λˆ for equation λ2 + λ = xQ + a .. Step 2.. Compute c = xQ(xQ + λQ + λˆ ).. Step 3.. If Tr(c) = 0 then λP ← λˆ , xP ← c + xQ , else λP ← λˆ +1, xP ← c .. Step 4.. Return (xP, λP).. The point halving algorithm requires one field multiplication (Step 2) and three operations: solving the quadratic equation λ2 + λ = xQ + a (Step 1), one trace computation (Step 3), and computing a square root (Step 3). In a normal basis, the time needed for these three operations is negligible in comparison with. 38.

(50) the time needed for a multiplication or an inversion. computed using a number of multiplications.. An inversion can be. The ratio of inversion to. multiplication cost is about 8 in our Pentium III platform. In the next subsection we select a normal basis and introduce arithmetic operations over it. With the normal basis we select, the square root operation at Step 3 can be significantly simplified.. 4.4 Normal Basis Implementation Recall that the binary field GF(2n) can be viewed as a vector space of dimension n over GF(2). That is, there exists a set of n elements α0, α1, …, αn-1, in. GF(2n). such. that. each. c = ∑ ciα i = ( cn −1...c1c0 ) .. c∈GF(2n). can. be. written. in. the. form. In general, there are many bases of GF(2n).. A. typical one is the polynomial basis of the form {1, x, x2, …, xn-1}, and a kind of n −1. special basis called normal basis is the set of the form { β , β 2 ,..., β 2 }. In a normal. basis,. a. field. c = ∑ ci β 2 = ( cn −1...c1c0 ). i. n −1. c 2 = ∑ ci β 2 i =0. i +1. n −1. element The. c. on. squaring. = ∑ ci −1β 2 = ( cn − 2 ...c0cn −1 ) . i. GF(2n) of. c. is. can. represented be. obtained. by by. That is, squaring of c can be. i =0. accomplished by a simple left rotation on the vector representation of c. On the. 39.

(51) other hand, the square root computation is just a right rotation, i.e., c = ( c0cn −1...c1 ) at Step 3 in point halving algorithm.. Therefore the quadratic. equation x 2 + x = c can be solved bitwise at Step 1 in point halving algorithm. These operations are expected to be inexpensive relative to the field multiplication or the field inversion.. The field multiplication in a normal basis is more. complicated, but, with optimization, it can be reduced to a series of n cyclic shifts of the two vector multiplicands. Mullin, Onyszchuk, Vanstone and Wilson [27] introduced optimal normal bases that can optimize the time complexity for field multiplication in GF(2n).. The normal basis implementation is the basic. architecture in the halve-and-add evaluation algorithm to be described in the next subsection.. 4.5 Halve-and-Add Method for Weil Pairing Now we propose a halve-and-add method for the evaluation of rational functions used in the Miller’s algorithm. The evaluation algorithm described in Section 4.2 applies the double-and-add method to compute Weil pairing. To take advantage of point halving, we propose a halve-and-add version of the evaluation algorithm.. 40.

(52) Let the λ-representation of a point P=(xP, yP) be (xP, λP), and the canonical form of a divisor DP be (P) – (O) + div(g), where g is a rational function. Assume that Q=2P with λ-representation (xQ, λQ) corresponds to a divisor DQ with canonical form (Q) – (O) + div(f). Let hP, P ( x, y ) = 0 be the equation of the tangent line at P and h2P ( x, y ) = 0 be the vertical line through Q=2P. By the addition formula of two divisors with canonical form (see Eq. (2.1)), we have. DP + DP = (2P) – (O) + div( g 2. hP, P ) h2P. = (Q) – (O) + div(f).. (4.5). We also have hP, P ( x, y ) = y + y P + λP ( x + xP ) = y + λP x + xP and h2P ( x, y ) = x + xQ . (4.6) 2. From Eqs. (4.5) and (4.6), we have f = g 2. g= f. x + xQ y + λP x + x P. 2. 2 hP, P y + λP x + x P = g2 and thus x + xQ h2P. .. Denote the 1/2-representation of m as (m)1/2 = ( bˆn −1 … bˆ0 ) such that n −1. ⎛1⎞ m = ∑ bî ⎜ i ⎟ mod r , where r is the order of point P. In order to apply the ⎝2 ⎠ i =0 halve-and-add operation in the evaluation of f, we first determine (m)1/2.. A. simple translation was described in [19]. For Weil pairing computation, integer. 41.

(53) m is not only the scalar in evaluating f but also the order of the point P, i.e., mP=O.. To evaluate the rational function fm, we first evaluate fm-1 by using halve-and-add method, and then obtain fm from fm-1. This is because (m)1/2 is always the zero string (00…0) after translation and we can not evaluate fm by using the halve-and-add method directly. The translation of (m-1)1/2 in our algorithm is given as follows. Let n = ⎡log2 m ⎤ , and 2n-1(m-1) mod m =. n −1. ∑c 2 i =0. i. i. = ( cn −1...c0 ) .. Then (m-1)1/2 = ( bˆn −1 … bˆ0 ), where bî = cn −1− i for i = 0, …, n-1. For example, let m = 25 and n = ⎡log2 25⎤ = 5 , we can compute 24×(25-1) mod 25 = 9 and. represent it as (01001). Thus the 1/2-representation of 24 is (10010).. Now we compute Step 2 of the Miller’s algorithm by the following halve-and-add evaluation algorithm.. 42.

(54) Halve-and-Add Evaluation Algorithm. INPUT: points P, T, S, where P is given by λ-representation (xP, λP), and the order m. OUTPUT: fm(S) = fP(S) Find the 1/2-representatin (m-1)1/2.= ( bˆn −1 … bˆ0 ) with bî ∈{0,1}, bˆn −1 =1;. f1 ←. hP + T (S) ; hP, T (S). f ← f1; Z ← P; for j ← n-1, n-2, …, 0 do f← f. 1 xS + xZ ; Z ← Z; 2 2 yS + λZ/2 xS + xZ/2. if bˆ j = 1 then f ← f1f. hZ, P (S) ; Z ← Z + P; hZ + P (S). endif endfor f ← f1f. hZ, P (S) ; Z ← Z + P; hZ + P (S). return f. 43.

(55) In our halve-and-add evaluation algorithm, the halving stage requires 1 inversion, 3 multiplications, 1 squaring, and 1 square root computing, and has an advantage over the doubling. A detailed comparison will be given in the next section.. 4.6 Performance Evaluation In this section we estimate the saved operations in our halve-and-add evaluation algorithm compared with the double-and-add evaluation algorithm. When we consider the arithmetic operations in a normal basis, the time saved by using halving instead of doubling is significant.. In affine coordinates, both. elliptic doubling and addition for scalar multiplication require 1 inversion, 2 multiplications, and 1 squaring. In the λ-representation, halving stage for scalar multiplication requires 1 multiplication and three extra operations: solving the quadratic equation, trace computation, and square root computation.. The. addition stage requires an extra multiplication for the recovery of y-coordinate in the λ-representation. Let the order of the Weil pairing m be represented in binary format by a bit string of length n with k non-zero entries, obviously n≥k. Note. 44.

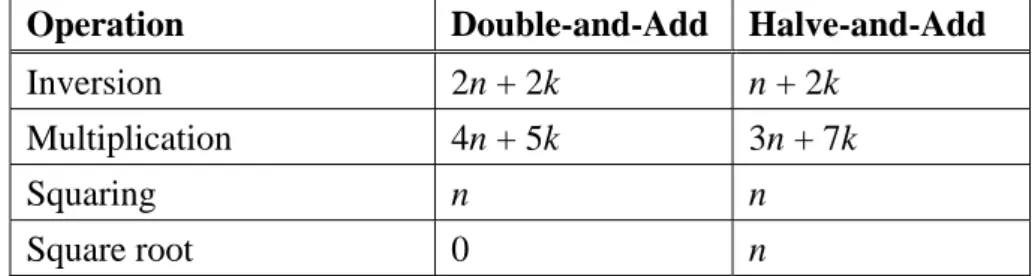
(56) that our halve-and-add method requires the 1/2-representation of m-1 to apply halving and addition. By the translation of (m-1)1/2, (m-1)1/2 is a bit string of length n with k-1 non-zero entries. Since we need an extra addition in the final step to obtain mP from (m-1)P, the total addition in halve-and-add method is still k. The operations needed for the scalar multiplication are listed in Table 1. Table 4.1 Arithmetic Operations for Scalar Multiplication (n≥k) Operation. Double-and-Add. Halve-and-Add. Inversion. n+k. k. Multiplication. 2n + 2k. n + 3k. Squaring. n+k. k. Solving λˆ2 + λˆ = xQ + a. 0. n. Square root. 0. n. Trace computing. 0. n. In affine coordinates, the doubling stage requires 2 inversions (one for the slope of hZ,Z(S), another for h2Z(S)), 4 multiplications, and 1 squaring. Our halving stage requires 1 inversion, 3 multiplications, 1 squiring, and 1 square root computing in the λ-representation. The addition in our halve-and-add method requires two extra multiplications for the recovery of y-coordinate.. The. operations needed for the evaluation of a rational function in Weil pairing are listed in Table 2.. 45.

(57) Table 4.2 Arithmetic Operations for Rational Function Evaluation (n≥k) Operation. Double-and-Add. Halve-and-Add. Inversion. 2n + 2k. n + 2k. Multiplication. 4n + 5k. 3n + 7k. Squaring. n. n. Square root. 0. n. As shown in Tables 1 and 2, by using halvings, we can save 2n inversions, 2n-3k (in general, n≥2k as shown in Table 3) multiplications and n squarings at the cost of solving n quadratic equation, 2n square roots, and n trace computing. Note that, in a normal basis, the time needed to calculate the quadratic equation, square root, and the trace is negligible compared with the time needed to compute a multiplication or an inversion.. To investigate our improvement in computing the Weil pairing, we implement the Boneh-Franklin’s ID-based encryption (IBE) scheme over the NIST recommended curves [11] on a 700MHz Intel Pentium III. Their scheme requires one pairing operation for both encryption and decryption. The recent IBE schemes proposed by Boneh-Boyen [6][7] and Waters [34] pre-compute one pairing operation before encryption, thus require no pairing for encryption but use two pairings for decryption. Their contributions focus on constructing secure provable IBE schemes in different security models such as selective-ID model and. 46.

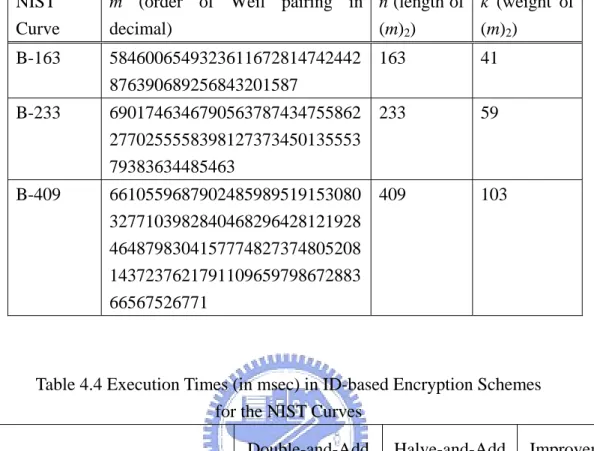
(58) standard model without random oracle.. As our algorithm improves the. computation of pairing which is primitive in IBE schemes, we can implement these new schemes in the future work. Our implementation is programmed in C and uses the free GNU Multiple Precision (GMP) arithmetic library to deal with the big number operations.. The traditional double-and-add method and our. halve-and-add method are both implemented for computation of Weil pairing in the ID-based encryption scheme over NIST recommended curves of different strength. Curves B-163, B-233 and B409 have the same form: y2 + xy = x3 + x2 + b over binary fields GF(2163), GF(2233) and GF(2409), respectively. The orders of the Weil pairing m chosen in these curves are listed in Table 3.. The. representation of elements in the binary field is over a normal basis. The size of message encrypted in our implementation is 160 ASCII characters. Table 4 lists the execution times in the ID-based encryption scheme using double-and-add method and halve-and-add method, and shows the improvements.. The Weil. pairing is the primitive operation for both encryption and decryption in the ID-based encryption scheme.. Therefore, the efficient computation for Weil. pairing improves both encryption and decryption.. 47.

(59) Table 4.3 The Orders of Weil Pairing in the NIST Curves NIST Curve. m (order of Weil pairing in n (length of k (weight of decimal) (m)2) (m)2). B-163. 5846006549323611672814742442 163 876390689256843201587. 41. B-233. 6901746346790563787434755862 233 2770255558398127373450135553 79383634485463. 59. B-409. 6610559687902485989519153080 409 3277103982840468296428121928 4648798304157774827374805208 1437237621791109659798672883 66567526771. 103. Table 4.4 Execution Times (in msec) in ID-based Encryption Schemes for the NIST Curves. Weil Pairing Evaluation B-163 Encryption Decryption Weil Pairing Evaluation B-233 Encryption Decryption Weil Pairing Evaluation B-409 Encryption Decryption. Double-and-Add. Halve-and-Add. Improvement. 10.76. 6.95. 35 %. 16.72. 12.45. 26 %. 12.95. 8.37. 35 %. 41.56. 30.48. 27 %. 76.28. 50.13. 34 %. 46.75. 37.48. 20 %. 126.48. 91.35. 28 %. 198.43. 135.97. 31 %. 150.25. 110.64. 26 %. Our method reduces a number of inversions and multiplications which are expensive in computing the Weil pairing. Overall a 20~35% improvement in encryption/decryption has been accomplished.. 48.

(60) Chapter 5 End-to-End Security for Short Message Service. In the mobile communication systems, security (encryption) offered by the network operator only applies on the wireless link. Data delivered through the mobile network can be acquired by any core network.. Existing end-to-end. security mechanisms are provided at application level and typically based on public key cryptosystem. In this chapter, we first introduce the short message service (SMS) for GSM [21][23].. Then we propose two applicable end-to-end. encryption mechanisms for SMS based on the certificate-based public key cryptosystem and the ID-based public key cryptosystem, respectively. Finally, we also evaluate and compare the delivery overheads between these two mechanisms.. 49.

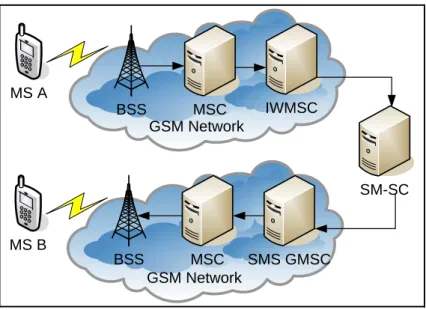
(61) 5.1. Short Message Service Architecture The network architecture of short message service in GSM is illustrated in Fig. 5.1. In this architecture, the short message is first delivered from the mobile station (MS) A to a short message service center (SM-SC) through the base station system (BSS), the mobile switching center (MSC), and then the interworking MSC (IWMSC). The SM-SC then forwards the message to the GSM network through a specific GSM MSC called the short message service gateway MSC (SMS GMSC).. The SM-SC may connect to several GSM networks and to. several SMS GMSCs in a GSM network. Following the GSM roaming protocol, the SMS GMSC locates the current MSC of the message receiver and forwards the message to that MSC. The MSC then broadcasts the message through the BSS to the destination MS B.. In the next sections, we will describe two. encryption mechanisms for end-to-end secure SMS based on certificate-based and ID-based cryptosystems.. 50.

(62) MS A BSS. MSC GSM Network. IWMSC. SM-SC. MS B BSS. MSC SMS GMSC GSM Network. Figure 5.1 GSM short message service network architecture. 5.2. RSA Mechanism The most widely implemented approach to public key encryption is the Rivest-Shamir-Adleman (RSA) scheme [28].. The RSA scheme is a block cipher. in which the original non-ciphered text and cipher text are integers between 0 and n-1 for some n. That is, the block size kRSA is determined by the bit length of the. integer n and regarded as the key size of the RSA scheme. This scheme consists of the following three functions:. Key generation: A user first selects two prime numbers p and q, randomly. chooses e with gcd(e, (p-1)(q-1)) = 1, and calculates d ≡ e-1 mod (p-1)(q-1).. 51.

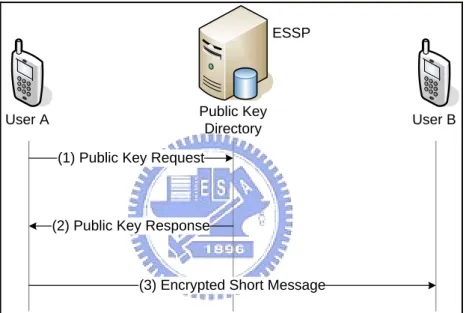
(63) Then the public key is KU = (e, n) and the private key is KR = (d, n), where n = pq.. Encryption: For a given message represented as an integer M < n, the cipher. text is computed by C = M e mod n.. Decryption: For a given cipher text C, the original non-ciphered text is. computed by M = C d mod n.. A RSA mechanism for end-to-end secure SMS is introduced as follows. The end-to-end security service provider (ESSP) plays a role as the CA in the certificate-based public key cryptosystem.. To access the end-to-end security. service, a user first chooses his/her own key pair (KU, KR) and subscribes to the ESSP for requesting a certificate of his/her public key KU.. The ESSP signs the. certificate with its private key and publishes the certificate in the public key directory for public access. When a mobile user A (the sender) wants to encrypt a short message to user B, he/she first sends a public key request (Fig. 5.2 (1)) to the public key directory in short message format.. The public key directory. retrieves user B’s certificate. If it succeeds, user B’s certificate is sent to user A as the public key response (Fig. 5.2 (2)). Once user A is in possession of B’s. 52.

(64) certificate, he/she verifies the certificate with the ESSP’s public key and uses the user B’s public key to encrypt short message for B (Fig. 5.2 (3)). If the request fails (due to unavailability of user B’s certificate), the ESSP will inform user B to subscribe to end-to-end security service if he/she wants to securely communicate with user A.. ESSP. Public Key Directory. User A. User B. (1) Public Key Request. (2) Public Key Response. (3) Encrypted Short Message. Figure 5.2 Procedure of sending an encrypted short message. 5.3. ID-based Mechanism In the above RSA approach, the sender needs to communicate with the public key directory for requesting the public key.. If the request fails (e.g., the. directory server is down or there is no certificate existing for the receiver), the. 53.

(65) sender can not encrypt a short message for the receiver. On the other hand, in an ID-based encryption scheme, the sender simply uses the receiver’s ID (i.e., the telephone number) as his public key without any request and verification. Thus, the sender does not need to access any public key directory before sending an encrypted short message.. The first complete and efficient ID-based encryption scheme was proposed by Boneh and Franklin [8] which uses a bilinear map called Weil pairing over elliptic curves. The bilinear map transforms a pair of elements in group G1 and sends it to an element in group G2 in a way that satisfies some properties. The most important property is the bilinearity that it should be linear in each entry of the pair. Assume that P and Q are two elements (e.g., points on elliptic curves) of an additive group G1. Let e(P, Q) be the element of a multiplicative group G2, which is the pairing applied to P and Q.. Then the pairing must have the. following property:. e(rP, Q) = e(P, Q)r = e(P, rQ),. where r is an integer and rP denotes the element generated by r times of additions on P, e.g., 2P=P+P, 3P=P+P+P and so on.. Weil pairing on elliptic. curves is selected as the bilinear map. That is, the elliptic curve group (the set of. 54.

(66) point collection on elliptic curves) is used as G1 and the multiplicative group of a finite field is used as G2.. The ID-based scheme consists of four algorithms: Setup, Extraction, Encryption, and Decryption. Setup is run by the PKG to generate the master key. and the system parameters. This is done on input of a security parameter kID, which specifies the bit length of the group order and is regarded as the key size of the ID-based scheme. The Extraction algorithm is carried out by the PKG to generate a private key corresponding to the identity of a user. As with regular public key cryptography, the Encryption algorithm takes a message and a public key as inputs to produce a cipher text. Similarly, the Decryption algorithm is executed by the owner of the corresponding private key to decrypt the cipher text. These four functions are described as follows.. Setup: With the parameter kID, the algorithm works as follows:. 1.. Generate a random kID-bit prime p, two groups (G1; +); (G2; *) of order. p, and the Weil pairing e: G1 × G1 → G2. Choose an arbitrary generator P ∈ G1.. 2.. Pick a random number s ∈ Zp* and set Ppub = sP .. 3.. Choose cryptographic hash functions h1:{0, 1}*→G1* and h2:G2 →{0,. 55.

(67) 1}n for some n.. The public system parameters are {p, G1, G2, e, n, P, Ppub, h1, h2} and the master key s is kept in secret by the PKG.. Extraction: For a given string ID∈{0, 1}* as the public key, the algorithm. works as follows:. 1.. Compute QID = h1(ID) ∈ G1.. 2.. Set the private key KR = sQID, where s is the master key held by PKG.. Encryption: To encrypt a message M under the public key KU = ID, the. algorithm works as follows:. 1.. Compute QID = h1(ID) ∈ G1.. 2.. Choose a random r ∈ Zp*.. 3.. Set the cipher text to be C = (U, V) = (rP, M ⊕ h2(e(QID, sP)r)). Decryption: To decrypt a cipher C = (U, V) encrypted using the public key. KU = ID, the algorithm uses the private key KR = sQID to compute M = V ⊕ h2(e(sQID, U)). This decryption procedure yields the correct message due to the. bilinearity of the Weil pairing (i.e., e(sQID, U) = e(sQID, rP) = e(QID, sP)r).. 56.

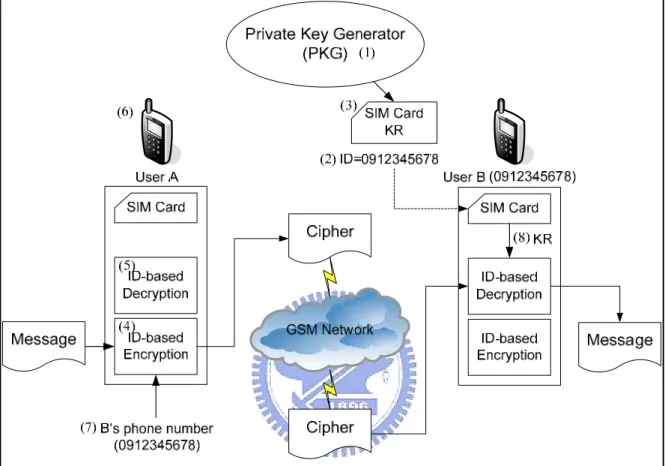
(68) Details of Weil pairing for ID-based cryptosystem can be found in Chapter 4.. Based on an improved algorithm proposed in Chapter 4, an efficient ID-based end-to-end encryption mechanism for mobile services is illustrated in Fig. 5.3. The PKG (Fig. 5.3 (1)) constructs the ID-based cryptosystem and uses, for example, the phone number as the ID (Fig. 5.3 (2)). Every mobile user involved in the ID-based cryptosystem is given a subscriber identity module (SIM) card (Fig. 5.3 (3)) at the subscription time.. The ID (phone number; e.g.,. 0912345678 in Fig. 6) and its corresponding private key KR are loaded in the SIM card by the end-to-end security service provider. Note that for standard GSM/UMTS service, SIM card is always given to a mobile user at the subscription time, and the proposed ID-based encryption scheme can be pre-loaded into the SIM card without incurring any extra overhead. The mobile station contains two security modules: ID-based encryption module (Fig. 5.3 (4)) and ID-based decryption module (Fig. 5.3 (5)). When a mobile user A (the sender; (Fig. 5.3 (6))) wants to encrypt a short message to user B (the receiver), A uses B’s phone number 0912345678 (Fig. 5.3 (7)) as the public key and encrypts the message through the ID-based encryption module. Once user B receives the cipher (the encrypted message), he/she uses the private key KR (Fig. 5.3 (8)). 57.

(69) stored in the SIM card to decrypt the cipher through the ID-based decryption module and obtain the original non-ciphered message.. Figure 5.3 ID-based end-to-end encryption mechanism. To estimate the encryption overheads between the RSA and the ID-based mechanisms, we implement these two encryption schemes and give the evaluation in the next section.. 58.

(70) 5.4 Performance Comparison This section compares the delivery delay of ciphered short messages based on the RSA and the ID-based approaches, respectively. environment is illustrated in Fig. 5.4.. The experimental. Both the sender and the receiver are. notebooks (Fig. 5.4 (1) and (3)) configured with a Pentium-III 500 MHz CPU, 256MB main memory, and 20GB disk space, and running on the Windows XP Professional operating system. To deliver short messages, every notebook is plugged in a NOKIA Card Phone version 2.0 and the short message is sent via the ChungHwa GSM network (Fig. 5.4 (2)) from the sender to the receiver.. Figure 5.4 Experimental environment for encrypted short message. We first note that to support the same security level, the key length for the ID-based and the RSA approaches are different. The ID-based cryptosystem using Weil pairing is over elliptic curves, thus its security level depends on the key length of Elliptic Curve Cryptosystem (ECC). As listed in Table 5.1 [15], a. 59.