On solving rectangle bin packing problems using genetic algorithms

On Solving Rectangle Bin Packing Problems

Using Genetic Algorithms

Shim-Miin Hwang, Cheng-Yan Kao*, Jomg-Tzong Homg

Dept. of Computer Science and Information Engineering

National Taiwan University,Taipei, Taiwan

*All correspondence should

be

sent to the second author

Abstract This paper presents a n application of genetic algorithms in solving rectangle bin packing problems which belong t o the class of NP-Hard optimization problems. There a r e three versions of rectangle bin packing problems to be discussed in this paper: t h e first version is to minimize the packing area, the second version is to minimize the height of a strip packing, and the final version is to minimize the number of bins used to pack the given items. Different versions of genetic algorithms a r e developed t o solve the three versions of problems. Among these versions of genetic algorithms, we have demonstrated two ways of applying the genetic algorithms, either to solve the problem directly or to tune an existing heuristic algorithm so that the performance is improved. Experimental results are compared t o well-known packing heuristics FFDH a n d HFF. From these results, we know that both methods can b e useful in practice.

I.

INTRODUCTION

.

The obvious industrial applications of stock cutting have been a n important stimulus to the research of

two dimensional packing. Further motivation has been driven by the advances in VISI technology in which layouts on chips pose a number of important combinatorial packing problems.

.

It is well known that a n efficient algorithm for finding optimal solutions for bin packing problems has proved to be quite difficult to find. In fact, the decision version of the bin-packing problem "Given C, L, and a n integer bound K, can L be packed into K or fewer bins of capacity C?" is NP-complete, this means that it is unlikely that efficient optimization algorithms can be found for these problems. Thus r e s e a r c h e r s h a v e t u r n e d t o t h e s t u d y of approximation algorithms, that is, algorithms which, although not guaranteed to find a n optimal solution for every instance, usually find near-optimal solutions for most cases.

.

Genetic Algorithms(GAs) [3], [4],

[5],

[6] developed by John Holland in 1975 a r e techniques for optimization and machine learning. A GA is composed of a reproductive plan which provides a n organizational framework for representing the pool of genotypes of a generation. After the successful genotypes are selected from the last

generation, a set of genetic operators a r e used in creating the offsprings of the next generation. Whenever some individuals exhibit better then average performance, the genetic information of these individuals will be reproduced more often. GAS work with a rich database of population and simultaneously climb many peaks in parallel during the search so that the probability of trapping into a local minimum is reduced significantly.

Procedure Genetic-Algori thm begin

t = O initialize P( t) evaluate P( t)

while (not termination-condition) d o begin t = t + l select P( t) from P( t-1) recombine P( t) evaluate P( t) end end

Fig. 1 A simple genetic algorithm

The structure of a simple GA is shown in Fig. 1. The GA simulates a n evolutionary process with n individuals which represent n points in a large search space. From the engineering point of view

,

GAS are a n iterative process where each iteration has two steps, evaluation a n d generation. In the evaluation step, domain knowledge is used t o determine the fitness of a candidate, a measure of its quality. Then a n evaluation function maps a candidate solution into t h e nonnegative real numbers. The generation step includes a selection operator and several modification operators. The selection operator chooses individuals with a probability that corresponds to the relative fitness. Two chosen individuals, called the parents, produce children using the genetic operator crossover. The crossover operator exchanges substring of the codes of the parents a t the same randomly determined point o r points; however, it does n o t create any new genetic material in the knowledge base. The mutation operator, o n the other hand, randomly changes a component in the structure introducing a

new material i n t o t h e knowledge base. From another point of view, the mutation operator acts as a local search close to the current point in the search space while the crossover operator causes larger jumps i n t h e search space. Finally, the descendants replace some individuals in t h e population after the generation step is done. following components:

( 1 ) a genetic representation for potential solutions to the problem,

( 2 ) a way to create a n initial population of potential

solutions,

(3) an evaluation function that plays the role of the environment, rating solutions in terms of their fitness,

(4) genetic operators that alter the composition of children during reproduction,

(5) values for various parameters that the genetic algorithm uses (population size, probabilities of applying genetic operators, etc.)

.

In this paper we will try to solve the three versions of rectangle bin-packing problems, with slightly differences o n their goals, by using GAS. We will denote the version to minimize the packing area as

RBP1, denote the strip packing problems as RBP2,

and denote the version to minimize the number of bins used as RBP3.

A GA for a particular problem must have the

11. Literature Review

.

So far, we have found two papers that solve the rectangle bin packing problems by using CAS. The first work is done by

D.

Smith [ 8 ] . The goal of his CA is to put as many blocks into a single rectangular region as possible. Experimental results have shown that this CA can produce the same packing density 300 times faster than their previously developed deterministic bin packing algorithm which used s o m e heuristics a n d d y n a m i c programming techniques. However, the genetic encoding does not allow for the recognization of characteristic features of packing schemes in their encoding, as most of these characteristics a r e hidden in a n algorithm to place a sequence of rectangles. Thus this approach cannot support the inheritance of certain features by the offsprings.

.

The second paper we have found is by B. Kroger, P.

Schwendering a n d 0. Vornberger [l]. They try to solve the strip bin packing problems (RBPZ in this

paper) by using GAS. Their representation is much more complex than that of Smith. They also devise a s p e c i a l c r o s s o v e r o p e r a t o r f o r t h e i r representation. This representation of packing is better than t h e list representation because the features of the parents are specified more explicitly in the chromosome, a n d thus the offsprings can inherit features from their parents so that the building block hypothesis can be satisfied. They implement their CA o n

a

parallel machine transputer. Experimental results show that this CA i s able to solve large bin packing problems in reasonable time a n d that smaller instances are likely t o be solved optimally. However, the complexity of

the representation makes the design of the genetic operators more difficult a n d the time complexity of evaluating a chromosome is still too high. Also, the cost of applying the associated genetic operators to this representation is much more t h a n t h e associated genetic operators for list representation.

111. On S o l v i n g

RBP1:

M i n i m i z i n g the

Packing

Area

rectangles, we wish to pack them into a rectangular area, so that no two items overlap a n d so that the packing area is minimized. For all items, rotation by 90 degree is allowed. Square packing is preferred.

The problem is stated below: Given a set of

We will denote our GA for solving RBPl as GA1. A. The Representation

.

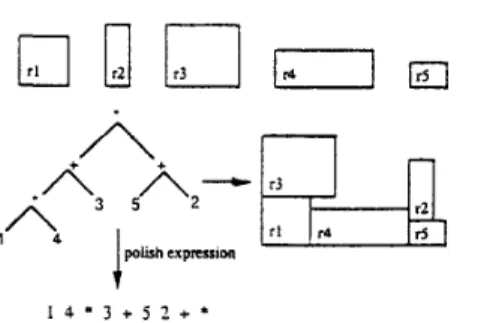
For CA1, we conceptually use a slicing tree (See Fig. 2 ) to represent a solution. A slicing tree is a n

oriented rooted binary tree. Each internal node of the tree is labeled either

*

o r

+,

corresponding to either a vertical o r a horizontal cut, respectively. Each leaf corresponds to a basic rectangle

or

item and is labeled by a identification number between 1 a n d n, where n is the problem size. A slicing tree can be viewed either from top down or from bottom u p fashion. From a top down point of view, a slicing tree specifies how a given rectangle is cut into smaller rectangles by horizontal a n d vertical cuts. From a bottom u p point of view, a slicing tree describes how smaller rectangles are combined. The operator

*

a n d

+

are n o more than left-right and top-down relations for two adjacent rectangles, respectively. Corresponding t o each slicing tree, there exists a polish expression to describe it. The polish expression can be easily obtained through post-order traversal of the slicing tree. Thus, in the implementation of GA1, we actually use the polish expression as o u r internal representation of a packing. Althugh there a r e certain packing that cannot be described by slicing trees (see Fig. 3), we still believe that the slicing tree can represent most good and near optimal packings.

A

t

1 1 * 3 + 5 2 + *

Fig. 2. A slicing tree and its corresponding packing

Fig. 3. A packing that can't slicing tree

be represented by a

.

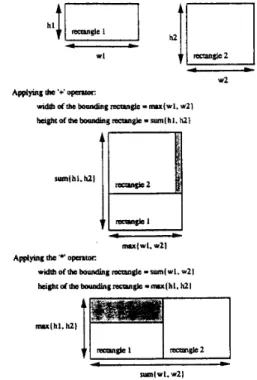
A polish expression can be easily converted to a n actual packing by using a stack of rectangles. A rectangle is specified by its width a n d height. We evaluate a polish expression by scanning it from left to right, if an operand (a number to index the item) is encountered, push the corresponding rectangle to t h e top of the stack; if a n operator is encountered, pop two rectangles from t h e stack as it's operands a n d a p p l y t h e operator, then p u s h t h e newly generated rectangle ( t h e bounding rectangle of its two o p e r a n d s ) back t o t h e stack. When t h e scanning process is over, the rectangle left on t h e stack i s the bounding rectangle. The application of operator

*

a n d

+

is shown in Pig. 4. They are n o more than a sum or m m operation. Eventually, all of the operation can be finished in O( n) time.

Applying rhe '+' opnra:

1

rum(h1. U1

B. The Genetic Operators

.

Rased upon o u r polish expression representation, we design a set of genetic operators, including a crossover a n d several mutations, to manipulate it. The crossover operator in GA1 i s called hybrid crossover. The hybrid crossover works as follows: First, it decompose the polish expression into two parts, t h e index p a r t a n d t h e operator part. The index part is a n ordered list, just like a list of cities to be visited in t h e traveling salesman problem. T h u s we apply t h e partially matched crossover (pmx) [SI o n t h e two selected parents to generate their offsprings a n d use the implementation of pmx by Lin [7]. The operator p a r t specifies the type of operators (+ or *) a n d their position in t h e polish expression. If we have n items to be packed, then we have n-1 operators because

+

a n d

*

a r e both binary operators. The operator p a r t a r e manipulated by uniform crossover [31

.

If we regard t h e relative position of items as schemata, it is easy to see that both t h e children inherit some portion of t h e chromosome from each parent. If t h e parents are good packings, then t h e children may be good ones, too. See Fig. S a n d Fig. 6 for an example of hybrid crossover.

Parent1 1 4 3 2

+

5 *

+

* Parent2 5 1

*

4

+

3 2

+

=>

Index Part Operator Part Parent 1 1 4 1 3 2 51 +4

*s

+5 *5 Parent 2 5 1 1 4 3 21 *2 +3 *4 +5 template 1 1 0 0 Child 1 1 5 1 4 3 2 1 *2 +3

+5

*5 Child 2 4 1 1 3 2

SI

+4 *5 * 4 +5 C h i l d 1 1 5

*

4

+

3 2

+ *

Child2 4 1 3 2

+

*

5

*

+

0 (pmx) ux) =>

Fig. 5 An example of hybrid crossover

Fig. 4 applying t h e

+

a n d

*

operators lo generate the bounding rectangle.

Fig. 6

1.

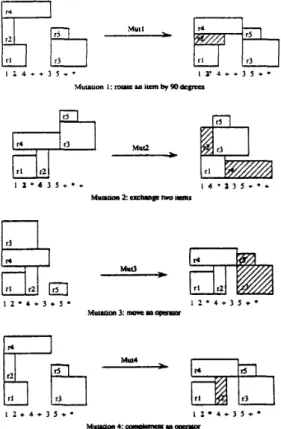
I r l

We h a v e proposed f o u r different mutation operators:

Mutl: rotate a n item

Mut2: randomly exchange two items Mut3: move a n operator

Mut4 complement an operator

Mutation 1 is to randomly choose a n item a n d rotate it by 90 degrees. Mutation 2 is to randomly choose two items and exchange them. Mutation 3 is to move a randomly chosen operator to a new position. Mutation 4 is to replace a randomly chosen operator by the complement operator ( t h e complement of

+

i s

*

and vice versa). All of these mutation operators are applied with a given probability. See Fig. 7 for examples of mutation operators.

.Hull

/1

1 2 - 4 + 3 5 + * Fig. 7 Illustrations of four mutations

.

However, Applying the hybrid crossover and Mut3 operator may cause illegal offspring. To solve this problem, we propose a n algorithm to adjust the positions of operators to make the illegal polish expression legal. The idea of this algorithm is simply t o c o u n t t h e operands(indices) a n d operators(+ or *). Since both the operators

+

and

*

a r e binary operators, t h e application of

+

o r

*

consumes two operands a n d will produce a new operand. Thus, when scanning t h e polish

expression from left to right, t h e accumulated n u m b e r of o p e r a t o r s c a n n o t exceed t h e accumulated number of operands minus one a t any point of the polish expression. See Fig. 8 for a n example of applying the adjustment algorithm. beforeadjustment 2 3

+ *

4

5

1

+

*

count 1 2 1 x invalid afteradjustment 2 3

+

4

*

5 1

+ *

count 1 2 1 2 1 2 3 2 l v a l i d Fig. 8. algorithm

C. The Evaluation Function

.

We first apply the packing algorithm to a polish expression t o obtain its bounding rectangle a n d t h e n u s e this information t o evaluate t h e corresponding packing. However, this information may not be enough to reveal the preference that the s q u a r e packing is preferred. To meet this preference we a d d a penalty function. if t h e bounding rectangle is square or near square, the penalty is zero. When the difference between the width a n d height of t h e bounding rectangle becomes larger, the penalty grows larger, too. For example, given a n previously specified allowable aspect ratio (e.g. AAR = 1.2), we may define the penalty as follows.

if( (width/height)>AARor(width/height)<l/AAR) penalty = (width

-

height)

*

(width

-

height); el se

penalty = 0;

An example of applying the adjustment

Thus the fitness function is:

fitness= l / ( a r e a of t h e bounding rectangle,

+

penalty).

D. Initialization

.

The initialization should generate t h e initial population to represent the entire solution space statistically. To initialize t h e population, we randomly generate a n polish expression with

n

operands a n d (n-1) operators. The n operands are just a random permutation of 1, 2, 3,

...,

n, a n d for each of the n-1 operators, we randomly generate its type ( * o r +) a n d its position in t h e polish expression. Of course, the randomly generated expression may not be a legal polish expression, therefore we need to a p p l y t h e adjustment algorithm to make it legal.

E. The Parameters

.

The population size is empirically set to 2 times the size of the problem (i.e. number of items to be packed). The steady-state reproduction strategy is used with 20 percent of the population updated in each generation. The newly generated offsprings a r e put back into the generation by deleting the least-fit chromosomes. N o duplication of chromosome is allowed to maximize the diversity.

The rate for crossover is set to be 0.3 and the rate for all four mutations is set to be 0.7. The four mutations are selected with equal probability. F. Experimental Results and Discussions

.

The test problems a r e randomly generated as follows: a rectangle is specified by (area, ar), where area is the area of the rectangle a n d is generated randomly from 1 to 100, and ar is the aspect ratio of the rectangle with value randomly generated from 1 t o 4. We test G A 1 for six problems with size ranging from 10 to 60 on a 80286-based PC-AT. Each problem is r u n f o r 10 times

.

The experimental results a r e listed in Fig. 9. The average packing density is a r o u n d 88%. The solution quality can be improved as the running time increased. For example, Fig. 10 shows a n sample packing of 30 items with packing density of 95.6% full. This packing was obtained in 4 0 minutes running time of GAL

problem size P l 10 92.74 3 mins P2 20 89.16 5 mins P3 30 90.62 10 mins p4 40 87.69 18 mins 50 85.20 30 mins P5 p6 60 85.99 57 mins

packing density time elapsed

Fig. 9 Experimental results of GA1

;5.;;;

Fig. 10 A sample packing of 3 0 rectangular items

.

For most problems, the mutation rate of traditional

CAS is supposed t o be very low, e.g. 0.5%, a n d the

GA leaves most of the works of searching t o the crossover operator. However, in the domain of bin packing this is not true because it is very difficult to combine the good features of two good packings. Thus, we take another point of view a n d use the high mutation r a t e instead. Conceptually, the crossover operator causes a larger jumps in the search space a n d the mutation operator acts as a local search close t o t h e c u r r e n t approximate solution in the search space.

IV. O n

S o l v i n g RBPS: M i n i m i z i n g t h e Number of Bins

Used

.

In this section, we demonstrate another way to use

GAS. The two GAS developed in this chapter are called GA3 a n d GA4, respectively. They do not try to solve the problem directly, but to solve it from the point of view of a n existing heuristic packing algorithm. In this case, GA acts like a heuristic improver more than a problem solver. The idea of our heuristic packing algorithm is from algorithm Hybrid First Fit (HFF) [2]. Empirical results of CA3 a n d GA4 a r e c o m p a r e d with t h a t of HFF. Experiences tell us that this is a simple a n d efficient way t o improve the performance of a heuristic algorithm.

.

The problem is stated as below: Let L = { r l , r2,

...,

r n ] be a set of rectangular items, each item r have height h(r) and width w(r). A packing P of L into a collection jB1, B2,

...,

Bm) of H

*

W rectangular bins is a n assignment of each items to a bin a n d a position within that bin, such that (i) each rectangle is contained entirely within its bin, with its sides parallel to the sides of the bin, (ii) no two items in a bin overlap, and (iii) the number of bins used is

minimized. For all items, rotation by 90 degrees is allowed.

A. HFF Heuristic

.

The algorithm HFF is proposed by F.R Chung, M.R Garey and D.S. Johnson [2). A more comprehensive name for the algorithm is FFDH

*

FFD since it is a combination of these two algorithms. It works as follows: First create a strip packing for L using FFDH a n d strip width W, thereby obtaining a collection j b l , b2,

...,

bk) of blocks of nonincreasing heights h l 2 h2 2

...

2 hk, each containing a subset of the rectangular items. If we view these blocks as a new collection of rectangles L' = ( b l , b2,

...,

bk) with h(bi) = hi a n d w(bi) = W, 1

<

i

<

k, we have a n instance of the one-dimensional problem and can apply FFD t o pack the blocks ( a n d hence the rectangles they contain) into

H

*

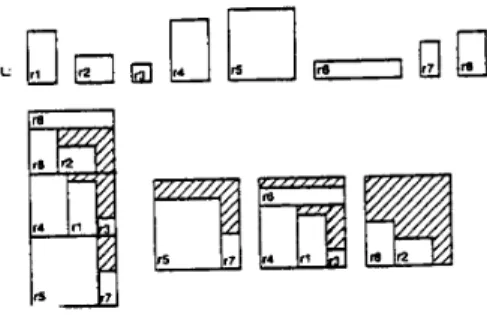
W bins. See Fig. 11 for a n example of HFF.

Fig. 11 An example of HFF

.

From the descriptions of HFF above, we know that HFF is a n off-line algorithm since it reorders the items in non-increasing height before it packs them. The arrangement of non-increasing height ordering of items is also a heuristics embedded in HFF. Thus, we decompose HFF into two parts: the first part is to

V. On Solving RBPZ: Minimizing t h e Height

of A Strip Packing

.

In this section, we continue the idea from the previous sections, a n d develop 3 GAS to solve the strip packing problems RBP2. We denote them as CA2, GAS a n d CA6. The GA2 is modified from G A 1 by using a different evaluation function. GA5 a n d GA6 are modified from GA3 a n d G A 4 with different e m b e d d e d packing heuristics a n d evaluation function. kperimental results are compared with the classical deterministic strip packing algorithm FFDH.

.

The strip packing problems is stated below: Given a set of rectangles pi, with height hi a n d width wi, the goal is to pack them into a vertical strip of width C. so as t o minimize the total height of the strip needed. For all items, rotation by 90 degrees is allowed.

A. Modification of CA1

.

The RBPZ can be viewed as a more constrained version of RBPl with the constraint of keeping the bin width fixed. There a r e two obvious ways of handling the constraints in a GA: either (1) requiring that they are satisfied for every solution generated or ( 2 ) allowing constraint violation for the intermediate solutions a t the expense of some penalty. Kroger, Schwendering and Vornberger [ 1 J

have proposed a GA t o solve t h e strip packing problems with the BOlTOM-LEFT scheme embedded in the genetic operators to meet the bin width constraint a n d to generate good packings. Here, we try t o modify t h e G A l developed in previous chapter t o accommodate the bin width constraint by adding a n penalty function term.

.

Since RBPZ is nothing more than a special case of RBPl with the packing width not exceeding a constant C. If we meet this constraint when minimizing the total packing area, we minimize the height of the strip. Thus the idea from G A 1 can be directly used here. The only modification is t o embed t h e packing width constraint in t h e evaluation function, a n d the goal can be still t o minimize the total packing area as it was before. To minimize the area, we have

fitness = 1 / (area of packing)

To meet the constraint, we add a penalty function term as follows:

if (width of packing I C)

penalty = 0;

else

.

penalty = (width of packing

-

C)

*

height of packing:

The resulting evaluation function is: fitness = 1 / (area of packing

+

penalty). The other parts of CA1 are left unchanged. B. Modifications of GA3 a n d CA4

.

We apply the concepts used in GA3 a n d GA4 t o solve RBPZ. GA5 is modified from GA3 a n d is a combination of GA and First-Fit packing algorithm. G A 6 is modified from GA4 a n d is a combination of GA and Best-Fit packing algorithm. Because what we care in RBP2 is the height of the strip packing, the fitness function can be expressed as below :

.

fitness = 1 / (height of the strip packing) C. Experimental results 8c Discussions

.

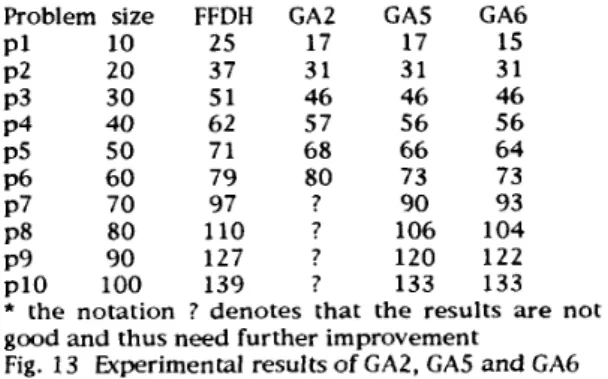
The test problems a r e the same as described in previous chapter. Ten problems with different sizes are tested by the three GAS. The running time of GA2 is roughly equal to the running time of CA1 for the same problem size, and the running time of CAS and GA6 a r e comparable t o GA3 and GA4. The results a r e compared with those obtained by FFDH and shown below:

Problem size FFDH GA2 GA5 GA6

17 17 15 P l 10 25 20 37 31 31 31 P3 30 51 46 46 46 p4 40 62 57 56 56 P5 50 71 68 66 6 4 p6 60 79 80 73 73 P7 70 97 ? 90 9 3 8 0 110 ? 106 104 P8 p9 90 127 ? 120 122 p10 100 139 ? 133 133 * the notation ? denotes that the results a r e not good and thus need further improvement

Fig. 13 Experimental results of GA2, GAS and GA6 From the results above, we recognized that the solution quality of CA2 decrease the problem size sets larger. The results are not good. We guess that this may be because of that the bin width constraint was dealt with as a penalty function, which prunes the solution space too much a n d thus limits the CA2 to d o the search efficiently. That is to say, to deal with the bin width constraint as a penalty may not work for this problem. To make GA solve the strip packing more efficient, we may need to incorporate the constraint in the representation a n d genetic operators so t h a t every offspring meets t h e constraints. The paper by Kroger, Schwendering a n d Vornberger [ l ] demonstrate this idea. The other possible reason is the weight for the penalty function term is too small. This may be tested by increasing the weight of the penalty function term.

.

Although the results of GA2 does not beat FFDH for every instance, the GA2 still have a n advantage over FFDH in that the performance of FFDH is more stable than that of FFDH. For some problem instances, FFDH may obtain a worst case quality solution, but GA2 is expected to adapt itself to have a steady performance.

.

For the results of GAS and GA6, they beats that of FFDH for every cases. This is consistent with o u r discussions in previous chapter. Because GAS a n d G A 6 acts as tuners, their results can not worse than that of FFDH.

decide the packing order (non-increasing height order) a n d the second part is to packing the items according t o the order presented to it. Obviously, the second part of HFF is a n on-line algorithm a n d can be embedded in CA3 as part of the evaluation function. Then t h e work of CA3 is t o find the optimal sequence of items f o r t h e packing algorithm. G A 4 is modified from CA3 with slight differences in their embedded packing algorithm. What i s in GA4 is a best-fit packing algorithm instead of first-fit algorithm in GA3.

B.

The Representation

.

Since most of the packing work is done by the packing algorithm, the only thing we can change is the order of items presented to it. That is, if we change the order of items presented to the packing algorithm, the solution quality may b e improved. Thus, we represent a solution as a n ordered list of items. With this representation, the solution of HFF is included in the solution space because if we let t h e order of items b e non-increasing height, it would produce t h e same solution as that of HFF. Further, rotation of items by 90 degrees is allowed,

so the representation i s extended by added a rotation bit t o each item in the solution vector to indicate their orientations. This extension of the representation n o t only provides a n additional possibility to find solution that is better than that of HFF, but it also enlarge the solution space by the scale of 2n and the size of the final solution space becomes n!

*

2n.

C. The Genetic Operators

.

We apply the partially matched crossover (pmx)

[ 5 ] o n t h e e x t e n d e d list representation of chromosome a n d use the algorithm developed by Lin [7]. TWO mutation operators are proposed, the first is random 2-swap mutation, which randomly selects two components in a chromosome a n d exchange them, a n d the second is the rotation mutation, which rotate a randomly selected gene of a chromosome by 90 degrees.

D.

The Evaluation Function

.

Before we evaluate a chromosome, we have t o construct the actual packing using the embedded packing algorithm. The packing algorithm used in CA3 is a level-oriented first-fit (LFF) algorithm, inspired from algorithm HFF. Suppose the standard bin has width W and height H. It first uses a two- dimensional level-oriented first-fit algorithm to pack t h e set of items into

a

strip of width W. Next, decompose this packing into blocks corresponding to the levels created by the algorithm. Each block can be viewed as a rectangle of width W and height the height of the level. Thus, packing these blocks into rectangular bins of width \.V becomes a simple one-dimensional bin packing problem, where the size of a n block is its height. Then we apply FFD to this one-dimensional problem. The packing algorithm used in CA4 is similar to that being used in CA3. The only difference is that it searches for

the best fit area to pack the incoming item instead of using the firstly found area.

.

The evaluate function is defined as below: fitness= 1 /( bin-used*bin,height+average-height). The first term bin-used

*

bin-height i s t o distinguish the packings by preferring a packing that uses a smaller number of bins. The second term average-height is t o tell t h e difference between packings that uses t h e same number of bins and prefer the smaller average height of all bins.

E Initialization

.

This initial population is created by random permuting the n items, where n is the number of items to be packed. The orientation bit attached to each item is also generated randomly, meaning either n o rotation o r rotating by 90 degrees. F. The Parameters

.

For CA3

and

GA4, the population size is set to be equal t o the n u m b e r of items t o b e packed empirically. The rate for crossover operator is 0.7 and the rate for mutation operators is 0.3. The two mutation operators, random 2-exchange mutation a n d rotation mutation, a r e selected with equal probability. The generational reproduction strategy is used for simplicity.

G. Experimental Results and Discussions

.

The test problems are generated randomly with the width a n d the height of the items uniformed distributed from 1 to the width of the bin. We have r u n the algorithm for 1 0 problems, with problem sizes ranging from 10 to 100. Each problem is tested for 10 times. The results are summarized in Fig. 12.

size min* HFF GA3bins saved G A 4 bins saved p l 1 0 2 2 2 0 2 0 p 2 2 0 3 3 3 0 3 0 p 3 3 0 6 7 6 1 6 1 p4 40 9 11 10 1 10 1 p5 50 12 15 1 4 1 14 1 p6 60 14 18 16 2 16 2 p7 70 16 22 19 3 19 3 p8 80 19 16 24 2 22 4 p9 9 0 22 29 27 2 25 4 p 1 0 1 0 0 2 4 31 28 3 28 3 *min=E(totaI area of items)/(capacity of a bin) Fig. 12 Experimental results of CA3 and CA4

.

From the results above, we see that the solution quality is consistently better than that of HFF. The idea of using a CA to improve a heuristic packing algorithm is very simple, yet useful. It improve the average performance of the heuristic algorithm

and

have high probability t o prevent t h e heuristic algorithm being trapped in the worst case.

References

VL

Conclusions and Future

Works

.

In this paper we demonstrated two different ways of using GAS to solve bin packing problems, either to solve the problem directly (as in CA1 and GA2) or to use the CA t o t u n e a n existed heuristic algorithm (as in GA3, GA4, GAS and GA6) so that t h e performance of t h e heuristic algorithm is improved. The slicing tree representation for a packing in CA1 have the advantage of evaluation efficiency and totally freedom to search without the interference of a heuristic algorithm. And the CA2 shows that the method of adding the bin width constraint as a penalty function may not work alone. That is, we need different way to manipulate the bin width constraint, for example, to embed this constraint in the representation and the associated genetic operators. The value of GA3, GA4, GAS and CA6 are their simplicity. We can use this concept to improve a n algorithm without making too much effort.

.

Using genetic approach to solve the rectangle bin packing problem has a monotone property. The more running time, the better solution you find. This is a practical advantage of this approach. Since CA maintains a population of candidate solutions, w e can choose any good alternative solution from the population as our final solution if the best one (measured by combination of density and penalty violation in G A 1 ) is discarded for some reasons. One disadvantage is that each time w e r u n the algorithm, we will end u p with a different packing, i.e. it is difficult to do reactive packing.

.

The results of o u r CA approach to bin packing problems can be used directly in cutting-stock problems. And with appropriate modifications, CA 1 can be used in the floorplan design of VISI design 191. The modification should be easy by embedding the flexible modules knowledge to the evaluation function.

.

The first direction of research is to incorporate simulated annealing i n t o GAS so t h a t t h e performance is improved. The works by Lin[7] is a good demonstration of this kind of work.

.

Another direction of research is to develop a more powerful representation so that CA1 can manipulate the packings that can't be represented by our slicing tree representation. If t h e representation is modified, t h e corresponding genetic operators should also be designed again. Besides, if we can devise a more efficient crossover operator, then both the quality of the solution and the running time will be improved.

.

Yet another direction of research is to investigate different ways to manipulate the constraints in a CA.

.

Finally, using the idea of CA3 to improve the 1-D bin packing algorithms a n d o t h e r heuristic algorithms is useful in practice.

[ 11 Berthold Kroger, Peter Schwendering and Olive Vornberger, "Parallel g e n e t i c packings of rectangles," proc. of the first workshop o n Parallel Problem Solving from Nature ( P E N l ) , Dortmund, [2] Chung, F.RK., Carey, M.R and Johnson, D.J., "On packing two-dimensional bins," SIAM J. Alg. Disc. Meth., 3, 1982, pp.66-76.

[3] Davis, L. (Editor), Handbook of Genetic Algorithms, V a n Nostrand Reinhold, Reading Mass,

1991.

[4] DeJong, K.A., "Genetic Algorithms: A 10 Year Perspective," Proceedings of the First International conference on Genetic Algorithms, 1985, pp. 169- 177.

[5] Goldberg, D.E, Genetic algorithms: In search, Optimization a n d Machine Learning, Addison- Wesley Publishing Company, Reading Mass, 1989. [6] Holland, J.H., Adaptation in Natural a n d Artificial Systems, the university of Michigan Press, Ann Arbor, 1975.

[7] Lin, F.-T. a n d Kao, C.Y., Incorporating the Genetic Approach to Simulated Annealing in Solving Combinatorial Optimization Problems, Ph.D. Dissertation, National Taiwan Univ., 1991.

Search," Proc. of a n Intern. Conf. o n Genetic Algorithms and Their Application, Pittsburgh P.A., [9] Wong, D.F., Leong H.W., and Liu, C.L, Simulated Annealing For VLSI Design, Kluwer Academic Publishers, 1988.

FRG, Oct. 1-3, 1990, pp.160-164.

[8] Smith, Derek, "Binpacking with Adaptive