Algorithmic aspects of the generalized clique-transversal problem on chordal graphs

(1)

DISCRETE APPLIED MATHEMATICS Discrete Applied Mathematics 66 (1996) 189-203

Algorithmic aspects of the generalized clique-transversal

problem on chordal graphs

Maw-Shang Chang ‘I, Yi-Hua Chen a,‘, Gerard J. Chang b,2,3, Jing-Ho Yan b,2

a

Department of Computer Science and Information Engineering, National Chung Cheng University.

Ming-Shiun, Chiayi 621, Taiwan

bDepartment of Applied Mathematics. National Chiao Tung University, Hsinchu 30050, Taiwan

Received 11 March 1993; revised 29 November 1994

Abstract

Suppose G=( V,E) is a graph in which each maximal clique Ci is associated with an integer ri, where 0 < ri < ICi 1. The generalized clique transversal problem is to determine the minimum cardinality of a subset D of V such that ID n Cij >ri for every maximal clique Ci of G. The problem includes the clique-transversal problem, the i, 1 clique-cover problem, and for perfect graphs, the maximum q-colorable subgraph problems as special cases. This paper gives complexity results for the problem on subclasses of chordal graphs, e.g., strongly chordal graphs, k-trees, split graphs, and undirected path graphs.

Keywords: Clique-transversal set; Neighborhood number; Domination; Dual; Chordal graph; Strongly chordal graph; k-Tree; Split graph; Undirected path graph

1. Introduction

In this paper, G = (V, E) represents a graph with vertex set V of size n and edge

set

E

of size

m.

A

clique

is a subset of pairwise adjacent vertices of

V. An i-clique

is a clique of size

i.

A

maximal clique

is a clique that is not a proper subset of any

other clique. Denote by q(G) the set of all maximal cliques of G.

This paper studies the following generalized clique-transversal problem, which in-

cludes many clique-related problems as special cases. Suppose each maximal clique

Ci of G is associated with an integer ri, where 0 <

ri < ICi 1.

Let R = {(Ci,

ri) : Ci f W(G)}. An R-clique-transversal set

of G is a subset

D

of

V such that ID fl Gil 2 ri

for every Ci E W(G). The

generalized clique-transversal problem

is, given a graph

* Corresponding author. E-mail: gjchang@math.nctu.edu.tw.

’ Supported partly by the National Science Council under grant NSC81-04O8-El94-04. * Supported partly by the National Science Council under grant NSC82-0208-M009-050. 3 Supported partly by DIMACS, Rutgers University.

(2)

190 M.-S. Chang et al. /Discrete Applied Mathematics 66 (1996) 189-203

G and R, to determine the R-clique-transversal number ZR(G) that is the minimum size of an R-clique-transversal set of G. The problem has a natural dual, as follows. A clique-independent set is a collection of pairwise disjoint maximal cliques. The R-clique-independence problem is, given a graph G and R, to determine the R-clique- independence number Q(G) of G that is the maximum value CCrEO ri for a clique- independent set 9 of G. For any R-clique-transversal set D and any clique-independent set 9,

Hence, we have the following weak duality inequality: for any graph

G,

c(R(G)GTR(G)- (1)

Note that the inequality may be strict, as aR(Czn+r) = n < n + 1 = TR(C2n+l) when all ri = 1 and na2.

The concept of chordal graphs was introduced by Hajnal and Suranyi [24] in connec- tion with the theory of perfect graphs (see [21]). A graph is chordal (or triangulated) if every cycle of length greater than three has a chord (i.e., every induced cycle is a triangle). The neighborhood N(v) of a vertex v is the set of all vertices adjacent to v. The closed neighborhood N[v] of v is {v}UN(v). One of the most important properties of a chordal graph G = (V,E) is that its vertices have a perfect elimination ordering, i.e., an ordering vr , ~2,. . . , v, of V such that Ni[vi] is a clique for 1 <i <n, where

Ni[Vj] = {Vk E N[Vj] : i 6 k}. Note that any maximal clique of a chordal graph G is

equal to some Ni[Vi], but an Ni[Ui] is not necessarily a maximal clique. Consequently, a chordal graph has at most n maximal cliques. It is also known that all maximal cliques can be enumerated in O(m + n) time (see [14, 161). In this paper, we study algorithmic aspects of the generalized clique-transversal problem and related problems on subclasses of chordal graphs, such as strongly chordal graphs, k-trees, split graphs, and undirected path graphs.

If we restrict ri = 1 for all maximal cliques Ci of G, the generalized clique- transversal (resp. R-clique-independence) problem becomes the clique-transversal (resp. clique-independence) problem. The corresponding clique-transversal (resp. clique- independence) number is denoted by Q(G) (resp. at(G)). The above weak duality inequality becomes: for any graph G,

w(G)

G

v(G)-

(2)

tic(G) and rc(G) have been studied in [ 1,5,10,36]. In particular, it was proven that determining Q(G) and rc(G) for a split graph G is NP-complete and that there are linear algorithms for finding MC(G) and r=(G) of a strongly chordal graph G (see [5]). Another special case of the generalized clique-transversal problem is the C,r problem described as follows. This problem has in fact been studied in a more general setting (see [8]). For iaja 1, the Ci,j problem is to determine the i, j clique cover number

(3)

M.-S. Chang et al. I Discrete Applied Mathematics 66 (1996) 189-203 191 Q(G) of a graph G, which is the minimum number of j-cliques such that every i- clique of G includes such a j-clique. It is not hard to see that the Ci,r problem is the same as the generalized clique-transversal problem with ri = max{ 1 Ci 1 - i + 1,O) for each maximal clique Cj of G. A classical result of the Ci,j problem is Turan’s theorem, which states that ci,z(&) is equal to the number of edges in a complete (i - 1)-partite graph of n vertices, where any two distinct partite sets have sizes that differ by at most one. The problem has also been studied from an algorithmic point of view by many authors. In particular, it was shown that it is NP-complete on general graphs when i > j> 1 [7,15,28,37], on chordal graphs when i > j>2 [7], on split graphs when i - 1 = j>2 [7], and on split graphs when ia > 1 = j and i is part of the input [8]. On the other hand, there is a polynomial time algorithm for the Cz,r problem, which is exactly the vertex cover problem and is reducible to the maximum independent set problem, on chordal graphs [16], a polynomial-time algorithm for the Ci,r problem on chordal graphs when i is fixed, and an O(m + n) time algorithm for the C,r problem on interval graphs even when i is not fixed [31].

The maximum q-colorable subgraph problem is, given a graph G = (V, E), to determine the maximum size sq(G) of a subset of V that can be partitioned into q disjoint independent sets. The problem has been studied by [13,20,22,23,38]. For any fixed q, the problem is NP-complete for general graphs. It was shown in [8] that for any perfect graph G, +(G) = 1 VI - c,+l,l (G). Consequently, the maximum q-colorable subgraph problem is equivalent to the C,+r,r problem for chordal graphs.

The rest of this paper is organized as follows. Section 2 reviews some terminology that will be applied in this paper. Section 3 gives an O(m + n) time algorithm for the generalized clique-transversal problem on strongly chordal graphs provided that strong elimination orderings are known in advance. We modify this algorithm to get an algorithm for the Ci,r problem so that we do not need to find all maximal cliques explicitly. Section 4 gives a linear time algorithm for the generalized clique-transversal problem on k-trees when k is fixed. Section 5 discusses the NP-complete results on k-trees (with unbounded k) and undirected path graphs.

2. Preliminaries

In this paper, all graphs are finite, undirected, and without loops or parallel edges. A graph is an intersection graph if there is a correspondence between its vertices and a family of sets (the intersection model) such that two vertices are adjacent in the graph if and only if their two corresponding sets have a nonempty intersection. Restricting the sets to subtrees of a tree determines the class of chordal graphs [17]. If the intersection models are further restricted so that each subtree is a path, a proper subclass called the undirected path graphs results [19]. Further restricting the model to rooted trees with paths directed away from the root yields the directed path graphs [18]. Requiring that the tree itself be a path defines the class of interval graphs [14,29].

As Gavril has shown in his papers, the intersection models for chordal graphs can always be chosen so that the nodes of the tree are the maximal cliques of the original

(4)

192 M-S. Chang et al. /Discrete Applied Mathematics 66 (1996) 189-203

graph. Each vertex of the graph then corresponds to the subtree comprising of exactly

those maximal cliques to which it belongs. We call such an intersection model a

clique tree

for the graph.

Other two related subclasses of chordal graphs are split graphs and k-trees. A

split graph

is a graph whose vertex set can be partitioned into the disjoint union of an

independent set and a clique. This concept was first introduced by Fiildes and Ham-

mer [12], who also proved that a graph is split if it and its complement are chordal. A

k-tree is defined recursively as follows: a

Kk

is a k-tree, and if G is a

k-tree

then so is

the graph formed by adding a new vertex to G and making it adjacent to all vertices

of a k-clique in G. In a k-tree of more than

k

vertices, each maximal clique is of

size

k +

1, which is formed by joining a new vertex to a previous existing k-clique. A

clique tree of a k-tree thus can be obtained recursively as follows:

KI

is a clique tree

of

Kk+l,

and if

T

is a clique tree of a k-tree G and G’ is obtain from G by adding a

new vertex v’ adjacent to all vertices in a k-clique C of G, then a clique tree

T’

of G’

can be formed by adding a new vertex v’ adjacent only to v in

T,

where v corresponds

to a

(k + 1 )-clique

of G that includes C.

In conjunction with the study of domination in graph theory, the following subclass

of chordal graphs was studied in [6,11,26]. A

strongly

(or

sun-free) chordal graph

is a graph G =

(V,E)

whose vertex set has a

strong elimination ordering,

i.e., an

ordering vi, ~2,.

. . , V,

of

V

such that

i<j< k

and

Vj, vk E Ni[Vi]

imply

Ni[vi] GNi[vk].

Note that a strong elimination ordering is a perfect elimination ordering. To date, the

fastest algorithm to recognize a strongly chordal graph and give a strong elimination

ordering takes O(mlogn) (see [32]) or O(n2) time (see [35]). Strongly chordal graphs

include trees, block graphs, powers of trees, interval graphs, and directed path graphs.

A

hypergraph

is an ordered pair

H = (V,E)

consisting of a finite nonempty set

V

of

vertices

and a collection

E

of nonempty subsets of

V

called

(hyper)edges.

A

hypergraph is

k-uniform

if each edge is of size

k.

A 2-uniform hypergraph is just

a graph. The

transversal number 7(H)

of a hypergraph

H

is the minimum size of

a subset of vertices that meets all edges of

H.

The

matching number m(H)

of

H

is the maximum size of a pairwise disjoint subclass of

E.

For more terminology on

hypergraphs see [2].

3.

Algorithm on strongly chordal graphs

In this section we give a linear time algorithm for solving the generalized clique-

transversal problem on strongly chordal graphs. Suppose G is a strongly chordal graph

in which every maximal clique Ci is associated with an integer ri, where 0 <ri < ]Ci(.

Let

R = {(Ci,ri): Ci E q(G)}.

W e assume that a strong elimination ordering vl,

~2,.

. .,v,,

is given. Note that a maximal clique of G is equal to some A’i[vi], but an

Ni[Vi] is not necessarily a maximal clique. For simplicity, we may assume that iVi[vi] is

associated with a number

ri = 0

when it is not a maximal clique. It is not hard to see

that D is an R-clique-transversal set of G if and only if ]Ni[oi] fD] >ri for all 1 <i

<n.

(5)

M.-S. Gang et al. IDiscrete Applied Mathematics 66 (1996) 189-203 193

The algorithm is a greedy one. Initially,

D = V

is an R-clique transversal set of G.

It processes the vertices in the order vi,

2~2,. , . , v,,.

At iteration

i, vi

is removed from

D

if ]Nj[uj] n

D( > rj

for all vertices Uj E Si, where

Si =

{Vj E N[Vi] 1 j<i}.

Note that the new

D

is still an R-clique transversal set of G. At the completion of the

algorithm,

D

is a minimum R-clique-transversal set of G.

Algorithm GCT. Solve the generalized clique-transversal problem on strongly chordal

graphs.

Input.

A strongly chordal graph G with a strong elimination ordering ~1, ~2,.

. .

,

0,.

Each maximal clique Ci = Ni[vi] is associated with an integer ri with 0

<ri < lCi[

and

each nonmaximal clique Ni[ui] is associated with

ri = 0.

Output.

A minimum R-clique-transversal

D

of G.

Method

D := V;

for

i =

1 to n do

if INj [Vj] fl

DI > rj

for every vertex uj in Si

then

D := D - {vi};

end for.

Theorem 1.

Algorithm GCT solves the generalized clique-transversal problem on

strongly chordal graphs in O(m + n) time.

Proof. Let

D*

denote the final

D

when the algorithm stops. We shall prove that

D’

is a minimum R-clique-transversal set of G. Since ]Nj[Vj] n

DI arj

for all 1 <j <n at

any iteration,

D*

is an R-clique-transversal set of G.

Choose a minimum R-clique-transversal set M such that IM rl

D* I

is maximum. We

claim that

D* = M.

Suppose

D* # M.

Then

D* - M # 0,

for otherwise the R-clique-

transversal set

D*

is a proper subset of

M,

which contradicts the minimality of

M.

Choose a vertex up E

D* - M.

Suppose

M - D* = 8,

i.e.,

M

is a subset of

D’.

At

iteration

p,

for all

Vj E S,,

INj[Uj]

n

DI 2 INj[vj] n (M U {up})1 2 INj[Vj] nM( + 1 > rj.

Then up must be removed from

D

at iteration

p,

a contradiction. Therefore,

M-D* # 8.

Let

h

be the smallest index such that Vh E

M - D*

and

Q =

{vj :

INj[Uj]

n

(M - {Q})[ < rj}.

By the assumption that

M

is a minimum R-clique-transversal set, Q # 0. It is also

the case that Q G Sh G N[vh]. Since INj[Uj] n

D*( >rj,

by the definition of Q, Nj[Uj] n

(D* - M) # 8

for all vertices Vj of Q. Let s be the smallest index such that v, E Q

and

t

be the smallest index such that u, E N,[v,] n

(D* - M).

By the minimality of s

and the fact that Q c N[uI], Q c NJuJJ.

(6)

194 M.-S. Chang et al. JDiscrete Applied Mathematics 66 (1996) 189-203

For the case where t < h, by the minimality of h and the algorithm, at the beginning of iteration t, MU{u,} CD and so jNi[uj]f~D( 2 IN~[u~]f$Y4U{z+})l > rj for all vertices nj of S,. Therefore vt must be removed from D by the algorithm; this contradicts the assumption that nt E D*.

For the case where t 2 h, we have s <h < t. By the definition of a strong elimination ordering, NJuh] ~N,[v,]. Thus, Q CNs[~~] Civs[v,]. Let M’ = (M - {uh}) U {Q}. If uj 6

Q, then INj[uj] nM’[ 2 INj[uj] n (M - {u})[ >rj

by the definition of Q. If Vj E Q, then j< h < t, Vjul E E, and ]Nj[Uj]

n M’I 2 INj[Vj] n MI -

1 + 1 >rj. Thus, M’ is a minimum R-clique-transversal set of G with IM’

n

D* I > IM

n

D* I, a contradiction to the maximality of (M

n

D* 1. So, D* = M is a minimum R-clique-transversal set of G. To implement the algorithm efficiently, we associate each vertex nj with a variable d(Uj), which is equal to ]Nj[nj]

n

DJ. SO we can check the condition INj[nj]

n

DI > rj in a constant time. Initially, d(nj) = INj[aj]] for 1 <j<n. If ui is removed from D at iteration i, then d(uj) is decreased by 1 for all vertices uj in Si. Altogether, iteration i costs O(ai) time, where di is the degree of vi in G. Hence the running time of the algorithm is O(Cy=r(di + 1)) = O(m + n). 0

Corollary 2. The clique-transversal problem, the Ci,l problem, and the maximum q- colorable subgraph problem can be solved in O(m + n) time on strongly chordal graphs.

To solve the problems in the above corollary by Algorithm GCT, we first need to identify all maximal cliques of G. Although this can be done in a linear time, we shall attempt to avoid this. Note that the algorithm in [5] for the clique-transversal problem on a strongly chordal graph G is able to avoid finding all maximal cliques. The algorithm chooses Ni[Vi] in a special way to guarantee that the final output does get maximal cliques. For the Ci,i problem, and so the q-colorable subgraph problem, the following modification of Algorithm GCT serves this purpose.

Algorithm Cil. Solve the C,i problem on strongly chordal graphs.

Input. A strongly chordal graph G with a strong elimination ordering vi, 212,. . . , v,. Output. A minimum i, 1 clique cover D of G.

Method. D := 0;

for k = 1 to n do Sk := 0; for j = 1 to n do

if Sk < i - 1 for every vertex vk in sj

then Sk := Sk + 1 for every vertex uk in Sj

else D := D U {Uj}; end for.

Note that at any iteration j, every Sk is simply the number of processed vertices in Nk[nk] -D. The algorithm always keeps this value less than i to ensure that D remains an i, 1 clique cover. The correctness of Algorithm Cil can be verified by either a

(7)

M.-S. Chang et al. I Discrete Applied Mathematics 66 (1996) 189-203 195 similar argument as in Theorem 1 or a transformation as follows. Note that

D is an i, 1 clique of G eINk[uk]-Dl<i- 1 for l<k<n

~IN~[u~]nDl~lNk[uk]l-i+l for 16k<n

w ]Nk[uk] n DI 2

max{l&[uk]l -

i + LO} for all A$[uk] E 9?(G).

So the condition in the “if” statement of Algorithm Cil is the same as that in Algorithm GCT. We can also modify the algorithm to get one for the maximum q-colorable subgraph problem, which is equivalent to the C,+i,i problem.

4.

Algorithm on k-trees with bounded

k

This section establishes a linear time algorithm for the generalized clique-transversal problem on k-trees when k is bounded. Suppose G = (V, E) is a k-tree in which each maximal clique Ci is associated with an integer ri, where 0 < ri < ICi]. Let T be a clique tree of G, which is considered to be a rooted tree. For any maximal clique C of G, let G(C) be the subgraph induced by V(C), which is the union of all maximal cliques in the subtree of T rooted at C.

The algorithm will calculate a minimum R-clique-transversal set of G by dynamic programming on T. For each maximal clique C and each subset S of C, let CTR(G(C), S) be a minimum sized R-clique-transversal set of G(C) that contains S. In the following lemma, for any two sets X and Y, MIN {X, Y} is equal to X if 1x1~ ]Y] and

Y otherwise.

Lemma 3.

Suppose Ci is a maximal clique of G, whose children in T are Ci,,

Ci,,..., Ci*. For any subset S of Ci,

= 1 Mm{X, Y} if ISI ari, otherwise, where X = S U

fJ

CTR(G(C,),S n Ci,), j=l Y = MIN{CTR(G(Ci),S U {x}) : X E Ci - S}.

Proof.

Let D* be the set at the right hand side of the above formula. It is clear that if ISI > Ti, then X = S U Usi=1 CTR(G(C,

),

S n Ci,

)

is an R-clique-transversal set of G(Ci) that contains S. For any x E Ci - S, it is also the case that CTR(G(Ci),S U {x}) is an R-clique-transversal set of G(Ci) that contains S. So D’ is an R-clique-transversal set of G(Ci) that contains S.

On the other hand, suppose D is a minimum R-clique-transversal set of G(C) that contains S. If D n Ci contains some vertex x E Ci

-

S,

then D is an R-clique-transversal

(8)

196 M-S. Chang et al. IDiscrete Applied Mathematics 66 (1996) 189-203

set of G(Ci) that contains S

U {x}.

In this case,

IDI~ICTR(G(Ci),SU{x})lbJYIBIL)*J.

If

D II C, = S,

then ISI > ri and each

D n V(Ci, )

is an R-clique-transversal

that contains S

n Ci,

for 1 <j <s. In this case,

set of

G(Ci, )

IDI= PI + 2 I(0 n v(C,)) - Sl

_j=l

= PI + kClD fl

v(cij)I - IG, n sl)

j=l

2ISI +

~(ICTR(G(ci,),SnCi,)l

-

IG, nsl)

j=l

=

ISI +

5

ICTR(G(Gj),S

n

Ci,) -

Sl

i=’

2 IS

U

CTR<G(Gj

1, A’

n

G,

)I

j=l = IXI>lD*l.

Therefore,

D”

is a minimum R-clique-transversal set of G(Ci) that contains S. 0

The above lemma allows us to find a minimum R-clique-transversal set of a k-

tree G recursively from the leaves to the root of

T.

For the case where Ci is a

leaf, s = 0. When the solutions for all children of a maximal clique Ci are found, we

compute

CTR(G(Ci), S)

for all S 5 Ci in nonincreasing order of ISI so that in calculating

CTs(G(Ci),S) we

may assume that

CTs(G(Ci),S’)

is known for all S’ with IS’] > (S(.

Note that the algorithm is exponential in

k,

but linear when

k

is bounded.

Theorem 4.

The generalized clique-transversal problem can be solved in linear time

for k-trees with fixed k.

Corollary 5.

The clique-transversal problem, the Ci,l problem, and the maximum q-

colorable subgraph problem can be solved in linear time for k-trees with fixed k.

Note that precisely the same argument also solves the above problems in linear time

on chordal graphs with bounded clique sizes.

5. NP-complete results

This section establishes NP-complete results on

k-tree

(with unbounded

k)

and undi-

rected path graphs. Besides clique-transversal, we also deal with two related concepts:

domination and neighborhood-covering.

The concept of domination provides a natural model for many location problems in

operations research. In a graph G =

(V,E),

a vertex u is said to

dominate

a vertex v

if u E N[v]. A

dominating set

of G is a subset

D

of

V

such that every vertex in

V

is

dominated by some vertex in

D. The domination number y(G)

of G is the minimum

(9)

M.-S. Chang et al. IDiscrete Applied Mathematics 66 (1996) 189-203 191

size of a dominating set of G. A

k-independent set

is a vertex subset of

V

such that

the distance between any two distinct vertices is greater than

k.

l-independence is the

normal independence. The

k-independence number Q(G)

of G is the maximum size

of a k-independent set of G. 2-independence is a natural dual of domination. We also

have a weak duality inequality: for any graph G,

~((3 <y(G).

(3)

Domination has been studied extensively by many authors during the past two decades

(see [25]).

The concept of neighborhood-covering was first introduced by Sampathkumar and

Neeralagi [34] and then studied by [5,27,30]. This is a vertex-edge variation of the

domination problem. A vertex is said to

dominate an

edge if it dominates both end

vertices of the edge. A

neighborhood-covering set

is a subset

D

of

V

such that every

edge or vertex of G is dominated by some vertex in

D.

(This definition is slightly

different from that in [5,30] where isolated vertices are not required to be dominated by

D.)

The

neighborhood-covering number plv(G)

is the minimum size of a neighborhood-

covering set of G. A

neighborhood-independent set

is a set of edges and isolated

vertices, which are viewed as edges with two identical end vertices, such that no two

distinct edges in the set are dominated by a same vertex in

V.

The

neighborhood- independence number RN(G)

is the maximum size of a neighborhood-independent set

of G. For any graph G,

Q~G) <m(G).

(4)

It is NP-complete to determine UN(G) and IN

for split graphs G [5]. There are

linear algorithms for finding Q(G)

and p&G) of an interval graph G [30] and a

strongly chordal graph G [5]. These problems have been generalized to

k

distance

version in [27].

Besides the weak duality inequalities (2) - (4), these six parameters are related by

the following inequalities: for any graph G,

y(G)

<m(G) <w(G)

and m(G) <w(G) <w(G).

(5)

The first inequality follows from the fact that a neighborhood-covering set is a dom-

inating set. The second inequality follows from the fact that a clique-transversal set

is a neighborhood-covering

set, since each edge or vertex is contained in a maxi-

mal clique. The third inequality follows from the fact that replacing each nonisolated

vertex of a 2-independent set by an edge incident to it results in a neighborhood-

independent set. The last inequality follows from the fact that replacing each edge or

vertex of a neighborhood-independent set by a maximal clique containing it yields a

clique-independent set. As a by-product of the linear time algorithms [5] for deter-

mining p&G), rc(G), UN(G), and at(G) of a strongly chordal graph G, these four

parameters are equal for a strongly chordal graph.

(10)

198 M.-S. Chang et al. IDiscrete Applied Mathematics 66 (1996) 189-203

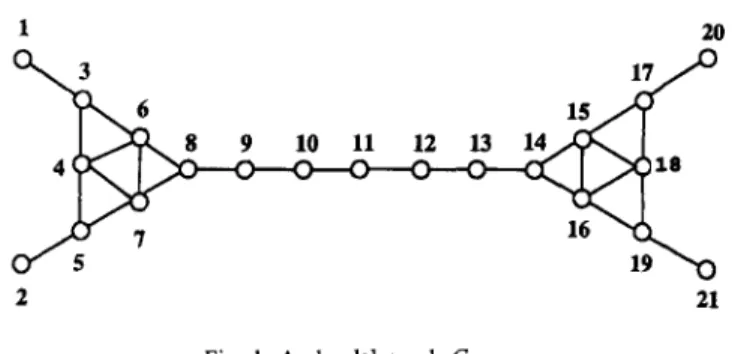
Fig. 1. A chordal graph G.

The inequalities in (5) can be strict even for chordal graphs. Fig. 1 shows an example of such a chordal graph:

y(G) = 7, D’ = (3, 5, 8, 11, 14, 17, 19); p&G) = 8, D* = (3, 5, 8, 10, 12, 14, 17, 19); r=(G) = 9, D* = (3, 5, 7, 9, 11, 13, 16, 17, 19); Q(G) = 7, S* = (1, 2, 8, 11, 14, 20, 21); U&G) = 8, S” = {{1,3}, {2,5}, (6371, (9,101, (12,131, {15,16}, {17,20}, (19,211); Q(G) = 9, S* = {{1,3}, {2,5), {4,6,7}, (8,9}, {lO,ll}, {13,14}, {15,16,18}, {17,20}, {19,21}}.

However, for some subclasses of chordal graphs, the inequalities in (5) can be all equalities. This fact plays an important role in the reductions between NP-complete problems. We shall consider the following subclasses of chordal graphs: split graphs, k-trees with unbounded k, and undirected path graphs.

The following construction of Gi is from [5] and [8] for proving NP-complete results on split graphs. It provides a standard model for our proofs of NP-complete results in k-tree (with unbounded k) and undirected path graphs.

For any hypergraph H = (I’, E), construct the graph Gt = (I’, ,Ei ) with Vt = V U E such that V is a clique in Gi, E is an independent set in Gi, and v E V is adjacent to e E E in Gt if and only if v E e.

The basic idea for the NP-complete results in [5] is that for any hypergraph H,

and

W) = y(G) = P&G I= w(G 1,

m(H) = az(G1) = ~(GI I = dG1); by

PI,

z(H)<k if and only if Ck+t,t(Gt)<]IE] -k.

On the other hand, it is NP-complete to determine z(H) of a 2-uniform hypergraph H, which is known as the “vertex cover” or the “hitting set” problem (see [15]). It is also NP-complete to determine m(H) of a 3-partite 3-uniform hypergraph H, which is called the “three-dimensional matching” problem (see [15]). Hence we have the following results.

(11)

M.-S. Chang et al. I Discrete Applied Mathematics 66 (1996) 189-203 199

Theorem 6 ([5]). It

is NP-complete to determine y(G), p&G), and zc(G) (resp.

az(G), Q,(G), and W(G)) of a split graph G with only degree-2 (resp. degree-3) vertices in the independent set.

Theorem 7 ([8]).

The Ci,l (and hence the maximum q-colorable subgraph) problem

is NP-complete on split graphs.

A similar idea was used in [9] to prove the NP-completeness of the domination problem on k-trees with unbounded k. Extending the argument, we have Theorem 8.

Theorem 8.

It is NP-complete to determine y(G), IN, ZC( G), az(G), a&G), and

ccc(G) of a k-tree G with unbounded k.

Proof.

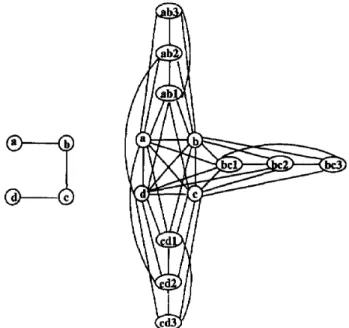
For a hypergraph H = (V,E), we construct an n-tree GZ = (Vz, E2) as follows. For each edge e of H, order the vertices of H into v,,i, v,,J, . . . , v,,, such that e =

bLvl+l-(e/~ %?,“-lel3~. .? II,,,}. Now define the graph G2 = (V2, E2) as

I’2 = VU {eci) : e E E and 1 Qi<n + 1 - lel}, E2 = {uv : u # v in I’}

U {e(‘)eG) : e E E and 1 <j < i<n + 1 - IeI} U {e(‘)Vcj : e E E, 1 <i<n + 1 - IeJ, and i<j<n}.

It is clear that G2 is an n-tree. Fig. 2 shows an example of G2, where H is a 2-uniform hypergraph of four vertices. Note that e(n+l-lel) in G2 plays the same role as e in Gi. G2 is in fact Gi with more e ci) added to make it an n-tree. The theorem follows from the following claim.

Claim.

For any hypergraph H, z(H) =

y(G2) =

pi = zc(G2) am’ m(H) =

~(2(G2) = w(G2) = MG2).

Proof.

Suppose D is a minimum dominating set of G2. For each v E V, e E E

with v E e, 1 <i dn + 1 - lel, replace each eci) E D by v~,~ since v,,, dominates the vertices adjacent to eci), thus we may assume that DC V. For any e E E, since D is a dominating set of G2, e@+‘-lel) is adjacent to some Ve,j E D with n + 1 - (el <j <n; i.e., e meets D at VQ in H. Then D is a transversal set of H. Thus z(H)fy(Gz). On the other hand,

C(e,i) = {e”‘) : 1 <j<i} U {Ve,j : i<j<n},

e E E and 1 d i <n + 1 - lel, are precisely all maximal cliques of Gz. Suppose D is a minimum transversal set of H. For any maximal C(e, i) of

Gz,

there exists Ue,j E e fl D for some n+ 1 - lel <j<n. Since i<n+ 1 - (el, i<j<n and then Ve,j E C(e,i). Thus D is a clique-transversal set of Gz. This gives rc(G2) <z(H). These two inequalities and (5) together imply the first part of the claim.

For any matching A4 of H, {e(n+l-lel) : e E M} is clearly a 2-independent set of G2 with the same size as M. So m(H)<c~(G2). On the other hand, suppose 9 is a

(12)

200 M.-S. CItang et al. IDiscrete Applied Mathematics 66 (1996) 189-203

Fig. 2. A Z-uniform hypergraph H of four vertices and its G2.

maximum clique-independent set of G2. We may assume that B contains only maximal cliques of the type C(e,n + 1 - le]) with e E E. {e E E : C(a,n + 1 - lel) E @‘} is then a matching of H with the same size as 9. Hence, ac(Gz) <m(H). These two inequalities together with (5) imply the second part of the claim, 0

Note that all maximal cliques of G2 are of size n + 1. So the clique-transversal problem is the same as the Cn+r,l problem in G2.

Corollary 9. The generalized clique-transversal problem, the Cj,l problem with non- $xed i, and the maximum q-colorable subgraph problem with nonfxed q are NP-

complete on k-trees with unbounded k.

[4] proved that the domination problem is NP-complete on undirected path graphs by reducing the three-dimensional matching (3DM) problem to it. Extending the argument, we have the following theorem.

Theorem 10. The clique-transversal problem and the neighborhood covering problem are NP-complete on undirected path graphs.

Proof. Consider an instance of the 3DM problem, in which there are three disjoint sets W, X, and Y, each of cardinality q, and a subset A4 of W x X x Y having cardinal@ p, say,

M={mj=(w,,X,,y,):w,EW,x,EX,y,EY,lbi~p}.

The problem is to find a subset M’ of A4 having cardinal@ exactly q such that each w, E W, x, E X, and yt E Y occurs precisely once in a triple of M’.

(13)

M.-S. Chang et al. I Discrete Applied Mathematics 66 (1996) 189-203 201

for mp I

Fig. 3. A clique tree of G3

Consider the 3-partite 3-uniform hypergraph H = (WUXUY,M). Note that m(H) 6q. The 3DM problem is equivalent to asking if m(H) = q.

Given an instance of the 3DM problem, or, equivalently, the corresponding hypergraph H, we construct a clique tree having 6p + 3q + 1 cliques from which we obtain an undirected path graph Gs. The maximal cliques of the tree are explained below.

For each triple mi E M there are six cliques whose vertices depend only upon the triple itself and not upon the elements within the triple: {Ai,Bi, Ci,Di}, {Ai, Bi,Di,Fi}, {Ci,Di,Gi}, {Ai,Bi,Ei}, {Ai,Ei,Hi}, {Bi,Ei,li} for 1 <iip. These six cliques form the subtree corresponding to mi, which is illustrated in Fig. 3. Next, there is a clique for each element of W, X, and Y that depends upon the triples of h4 to which each respective element belongs:

{R,} U {Ai 1 W, E T#i} all W, E W,

{LSS} U {Bj : X3 E mj} all X, E X, {Tt} U {Cj 1 Yt E mj} all y, E Y.

Finally, there is one large clique, the root of the clique tree, which contains {Ai,Bi, Ci : 1 <i < p}. The arrangement of these cliques is shown in Fig. 3. Note that Gs has 9~ + 3q vertices: Ai,Bi,Ci,Di,Ei,Fi,Gi,Hi,li (1 <i<p), R, (1 <r<q), S, (1 <s<q), Tt (1 %t <q). The undirected path corresponding to a vertex u of Gs consists of those cliques containing v in the clique tree. The theorem follows from the following claim.

Claim.

For the 3-partite 3-uniform hypergraph H corresponding to the 3DMproblem,

m(H) = q if and only if y(G3) = pi = ~c(G3) = 2p + q.

Proof.

Suppose D is a minimum dominating set of Gs. Observe that for any i, the only way to dominate the subtree corresponding to mi with two vertices is to choose

(14)

202 M.-S. Chang et al. I Discrete Applied Mathematics 66 (1996) 189-203

Di

and Ei, and that any larger dominating set might just as well consist of Ai, Big

and Ci, since none of the other possible vertices dominate any vertex outside of the

subtree. Consequently,

D

consists of

Ai, Bi,

and Ci for

t mi’s,

and

Di

and

Ei

for

p - t

other

mi’s,

and at least max{3(q -

t),O} R,,S,, T,.

Then

ID(

23t + 2(p - t) +

max{3(q - t),O} 22~ +

q +

max{2(q -

t), t - q}

22~ +

q.

This together with (5) gives 2p +

~<-<(G~)<~N(G~)<ZC(G~).

For the case of y(G3) = pv(G3) = zc(G3) =

2p+q,

the above minimum dominating

set

D

has

t = q

and consists of precisely

Ai, Bi,

and Ci for

q mi’s,

and

Di

and

Ei

for

p - q

other mi’s. Since all

R,, S,, Tt

are. dominated by

D,

the

q

triples ltli for which

Ai, Bi,

and Ci are in

D

form a matching of size

q. So m(H) = q.

Conversely, suppose H has a maximum matching M’ of size

q.

Let

D = {Ai, Bi, Ci : mi E M’} U {Di, Ei : mi E A4 - M’}.

Then

JDJ = 3q +

2(p -

q) =

2p +

q. It

is straightforward to check that

D

is a

clique-transversal set of Gs. So r~(G3)<2p+q

and then y(G3) = pi

= rc(G3) =

2p+q. 0

In the above construction of the clique tree, if we add to each clique some vertices

that appear only in it so that each clique is of size

i,

then we have the following result.

Theorem 11. The Ci,l problem (and hence the maximum q-colorable subgraph prob- lem) is NP-complete on undirected path graphs if i (q) is part of the input.

Acknowledgements

The authors are grateful to the three anonymous referees for many constructive

suggestions.

References

HI

PI [31 [41 PI

161

[71

181

T. Andreae, M. Schughart and Z. Tuza, Clique-transversal sets of line graphs and complements of line graphs, Discrete Math. 88 (1991) 1 l-20.

C. Berge, Graphs and Hypergraphs (North-Holland, Amsterdam, 1973).

A.A. Bertossi, Dominating sets for split and bipartite graphs, Inform. Process. Lett. 19 (1984) 3740. K.S. Booth and J.H. Johnson, Dominating sets in chordal graphs, SIAM J. Comput. 11 (1982) 191-199. G.J. Chang, M. Farber and Z. Tuza, Algorithmic aspects of neighborhood numbers, SIAM J. Disc. Math. 6 (1993) 24-29.

G.J. Chang and G.L. Nemhauser, The k-domination and k-stability problems on sun-free chordal graphs, SIAM J. Algebraic Discrete Methods 5 (1984) 332-345.

M. Confotti, D.G. Comeil and A.R. Mahjoub, k, i-covers I: complexity and polytopes, Discrete Math. 58 (1986) 121-142.

D.G. Comeil and J. Fonlupt, The complexity of generalized clique covering, Discrete Appl. Math. 22 (1988/89) 109-118.

(15)

M.-S. Chang et al. IDiscrete Applied Mathematics 66 (1996) 189-203 203 [9] D.G. Comeil and J.M. Keil, A dynamic programming approach to the dominating set problem on

k-trees, SIAM J. Algebraic Discrete Methods 8 (1987) 535-543.

[IO] P. Erdiis, T. Gallai and Z. Tuza, Covering the cliques of a graph with vertices, Discrete Math., to appear.

[l l] M. Farber, Characterizations of strongly chordal graphs, Discrete Math. 43 (1983) 173-189. [12] S. Fiildes and P.L. Hammer, Split graphs, in: F. Hoffman et al., eds., Proceedings 8th Southeastern

Conference on Combinatorics, Graph Theory and Computing, Louisiana State University, Baton Rouge, Louisiana (1977) 311-315.

[13] A. Frank, On chain and antichain families of a partially ordered set, J. Combin. Theory Ser. B 29 (1980) 176184.

[14] D.R. Fulkerson and O.A. Gross, Incidence matrices and interval graphs, Pacific J. Math. 15 (1965) 835-855.

[ 151 M.R. Garey and D.S. Johnson, Computers and Intractability: A Guide to the Theory of NP-completeness (Freeman, San Francisco, CA, 1979).

[16] F. Gavril, Algorithms for minimum coloring, maximum clique, minimum covering by cliques, and maximum independent set of a chordal graph, SIAM J. Comput. 1 (1972) 180-187.

[ 171 F. Gavril, The intersection graphs of subtrees in trees are exactly the chordal graphs, J. Combin. Theory Ser. B 16 (1974) 47-56.

[18] F. Gavril, A recognition algorithm for the intersection graphs of directed paths in directed trees, Discrete Math. 13 (1975) 237-249.

[19] F. Gavril, A recognition algorithm for the intersection graphs of paths in trees, Discrete Math. 23 (1978) 221-227.

[20] F. Gavril, Algorithms for maximum k-colorings and k-coverings of transitive graphs, Networks 17 (1987) 465470.

[21] M.C. Golumbic, Algorithmic Graph Theory and Perfect Graphs (Academic Press, New York, 1980.) [22] C. Greene, Some partitions associated with a partially ordered set, J. Combin. Theory Ser. A 20 (1976)

69-79.

[23] C. Greene and D. Kleitman, The structure of spemer /c-families, J. Combin. Theory Ser. A 20 (1976) 41-68.

1241 A. Hajnal and J. Suranyi, iiber die Auflo&mg von Graphen in vollstindige Teilgraphen, Ann. Univ. Sci. Budapest Eiitviis Sect. Math. 1 (1958) 113-121.

[25] ST. Hedetniemi and R.C. Laskar, Bibliography on domination in graphs and some definitions of domination parameters, Discrete Math. 86 (1990) 257-277.

[26] A.J. Hoffman, A.W.J. Kolen and M. Sakarovitch, Totally balanced and greedy matrices, SIAM J. Algebraic Discrete Methods 6 (1985) 721-730.

[27] S.H. Hwang and G.J. Chang, /c-Neighborhood covering and independence problems, DIMACS Report 93-03, DIMACS Center, Rutgers University (1993).

[28] R.M. Karp, Reducibility among combinatorial problems, in: R.E. Miller and J.W. Thatcher, eds., Complexity of Computer Computation (Plenum, New York, 1972) 85-103.

[29] C.G. Lekkerkerker and J.C. Boland, Representation of a finite graph by a set of intervals on the real line, Fund. Math. 51 (1962) 4564.

[30] J. Lehel and 2. Tuza, Neighborhood perfect graphs, Discrete Math. 61 (1986) 93-101.

[31] M.V. Marathe, R. Ravi and C. Pandu Rangan, Generalized vertex covering in interval graphs, Discrete Appt. Math. 39 (1992) 87-93.

[32] R. Paige and R.E. Tarjan, Three partition refinement algorithms, SIAM J. Comput. 16 (1987) 973-989. [33] D.J. Rose, Triangulated graphs and the elimination process, J. Math. Anal. Appl. 32 (1970) 597-609. [34] E. Sampathkumar and P.S. Neeralagi, The neighborhood number of a graph, Indian J. Pure Appl.

Math. 16 (1985) 126132.

[35] J.P. Spinrad, Doubly lexical ordering of dense O-l matrices, preprint. [36] Z. Tuza, Covering all cliques of a graph, Discrete Math. 86 (1990) 117-126. [37] M. Yannakakis, Edge-deletion problems, SIAM J. Comput. 10 (1981) 297-309.

[38] M. Yannakakis and F. Gavril, The maximum k-colorable subgraph problem for chordal graphs, Inform. Process. Lett. 24 (1987) 133-137.

Algorithmic aspects of the generalized clique-transversal problem on chordal graphs