Support-Vector-Based Fuzzy Neural Network for
Pattern Classification
Chin-Teng Lin, Fellow, IEEE, Chang-Mao Yeh, Sheng-Fu Liang, Jen-Feng Chung, and Nimit Kumar
Abstract—Fuzzy neural networks (FNNs) for pattern classifica-tion usually use the backpropagaclassifica-tion or C-cluster type learning algorithms to learn the parameters of the fuzzy rules and mem-bership functions from the training data. However, such kinds of learning algorithms usually cannot minimize the empirical risk (training error) and expected risk (testing error) simultaneously, and thus cannot reach a good classification performance in the testing phase. To tackle this drawback, a support-vector-based fuzzy neural network (SVFNN) is proposed for pattern classifica-tion in this paper. The SVFNN combines the superior classificaclassifica-tion power of support vector machine (SVM) in high dimensional data spaces and the efficient human-like reasoning of FNN in handling uncertainty information. A learning algorithm consisting of three learning phases is developed to construct the SVFNN and train its parameters. In the first phase, the fuzzy rules and membership functions are automatically determined by the clustering principle. In the second phase, the parameters of FNN are calculated by the SVM with the proposed adaptive fuzzy kernel function. In the third phase, the relevant fuzzy rules are selected by the proposed reducing fuzzy rule method. To investigate the effectiveness of the proposed SVFNN classification, it is applied to the Iris, Vehicle, Dna, Satimage, Ijcnn1 datasets from the UCI Repository, Statlog collection and IJCNN challenge 2001, respectively. Experimental results show that the proposed SVFNN for pattern classification can achieve good classification performance with drastically reduced number of fuzzy kernel functions.
Index Terms—Fuzzy kernel function, fuzzy neural network (FNN), kernel method, mercer theorem, pattern classification, support vector machine (SVM).
I. INTRODUCTION
A
S IS WIDELY known, both fuzzy logic and neural net-works are aimed at exploiting human-like knowledge processing capability. The fuzzy logic system using linguistic information can model the qualitative aspects of human knowl-edge and reasoning processes without employing precise quantitative analyzes [1]. The neural network is a popularManuscript received May 1, 2003; revised April 12, 2004 and April 6, 2005. This work was supported in part by the Ministry of Education, Taiwan, under Grant EX-91-E-FA06-4-4, and by the Ministry of Economic Affairs, Taiwan, under Grant 94-EC-17-A-02-S1-032.
C.-T. Lin is with the Department of Electrical and Control Engineering/De-partment of Computer Science, National Chiao-Tung University, Hsinchu 300, Taiwan, and also with the Brain Research Center, NCTU Branch, University System of Taiwan, Hsinchu 300, Taiwan (e-mail: ctlin@mail.nctu.edu.tw).
C.-M. Yeh and J.-F. Chung are with the Department of Electrical and Control Engineering, National Chiao-Tung University, Hsinchu 300, Taiwan. (e-mail: yeh120@dragon.ccut.edu.tw; jfchung.ece88g@nctu.edu.tw).
S.-F. Liang is with the Department of Biological Science and Technology, National Chiao-Tung University, Hsinchu 300, Taiwan, and also with the Brain Research Center, NCTU Branch, University System of Taiwan, Hsinchu 300, Taiwan (e-mail: sfliang@mail.nctu.edu.tw).
N. Kumar is with the IBM India Research Lab, Delhi 110016, India. Digital Object Identifier 10.1109/TFUZZ.2005.861604
generation of information processing systems that demonstrate the ability to learn from training data [2]. Much research has been done on fuzzy neural networks (FNNs), which combine the capability of fuzzy reasoning in handling uncertain in-formation and the capability of neural networks in learning from processes [3]–[5]. They have been successfully applied to classification, identification, control, pattern recognition, and image processing, etc. In particular, many learning algo-rithms of fuzzy (neural) classifiers have been presented and applied in pattern classification and decision-making systems [6], [7]. Moreover, several researchers have investigated the fuzzy-rule-based methods for pattern classification [8]–[11].
A fuzzy system consists of a bunch of fuzzyIF–THENrules. Conventionally, the selection of fuzzyIF–THENrules often re-lies on a substantial amount of heuristic observation to express proper strategy’s knowledge. Obviously, it is difficult for human experts to examine all the input–output data to find a number of proper rules for the fuzzy system. Most preresearches used the backpropagation (BP) and/or C-cluster type learning algo-rithms to train parameters of fuzzy rules and membership func-tions from the training data [12], [13]. However, such learning only aims at minimizing the classification error in the training phase, and it cannot guarantee the lowest error rate in the testing phase. In statistical learning theory, the support vector machine (SVM) [14] has been developed for solving this bottleneck. The SVM performs structural risk minimization and creates a clas-sifier with minimized VC dimension. As the VC dimension is low, the expected probability of error is low to ensure a good generalization. The SVM keeps the training error fixed while minimizing the confidence interval. So, the SVM has good gen-eralization ability and can simultaneously minimize the empir-ical risk and the expected risk for pattern classification prob-lems. More importantly, an SVM can work very well in a high dimensional feature space. However, the optimal solutions of SVM rely heavily on the property of selected kernel functions, whose parameters are always fixed and are chosen solely based on heuristics or trial-and-error nowadays. The FNN on the other hand is an approach that is based on adaptive local representa-tions with iterative learning ability. With this motivation, a the-oretical foundation for the FNN using the SVM method is de-veloped in this paper. We exploit the knowledge representation power and learning ability of the FNN to determine the kernel functions of the SVM adaptively, and propose a novel adaptive fuzzy kernel function, which has been proven to be a Mercer kernel. There have been some researches on combining SVM with FNN [15]–[18]. In [15], a self-organizing map with fuzzy class memberships was used to reduce the training samples to speed up the SVM training. The objective of [16]–[18] was on
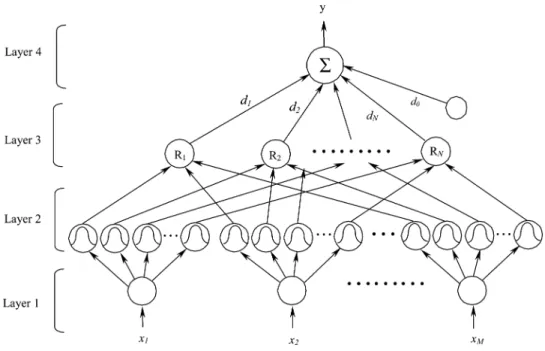
Fig. 1. Structure of the four-layered fuzzy neural network.
improving the accuracy of SVM on multiclass pattern recogni-tion problems. The SVFNN developed in this paper can not only well maintain the classification accuracy, but also reduce the number of support vectors as compared with the regular SVM. The regular SVM suffers from the difficulty of long computa-tional time in using nonlinear kernels on large datasets which come from many real applications. Therefore, one major con-tribution of this paper is to propose a systematical procedure to reduce the support vectors to deal with this problem.
In this paper, we develop a support-vector-based fuzzy neural network (SVFNN) for pattern classification, which is the real-ization of a new idea for the adaptive kernel functions used in the SVM. The use of the proposed fuzzy kernels provides the SVM with adaptive local representation power, and thus brings the advantages of FNN (such as adaptive learning and economic network structure) into the SVM directly. On the other hand, the SVM provides the advantage of global optimization to the FNN and also its ability to minimize the expected risk; while the FNN originally works on the principle of minimizing only the training error. The proposed learning algorithm of SVFNN consists of three phases. In the first phase, the initial fuzzy rule (cluster) and membership of network structure are automatically established based on the fuzzy clustering method. The input space partitioning determines the initial fuzzy rules, which is used to determine the fuzzy kernels. In the second phase, the means of membership functions and the connecting weights be-tween layers 3 and 4 of SVFNN (see Fig. 1) are optimized by using the result of the SVM learning with the fuzzy kernels. In the third phase, unnecessary fuzzy rules are recognized and eliminated and the relevant fuzzy rules are determined. Exper-imental results on five datasets (Iris, Vehicle, Dna, Satimage, Ijcnn1) from the UCI Repository, Statlog collection and IJCNN challenge 2001 show that the proposed SVFNN classification method can automatically generate the fuzzy rules, improve the accuracy of classification, reduce the number of required kernel functions, and increase the speed of classification.
This paper is organized as follows. In Section II, the structure and initial construction of the FNN is presented. Section III de-scribes the proposed adaptive fuzzy kernel with sound theoretic derivations. In Section IV, the learning algorithm of the SVFNN is developed. In Section V, the SVFNN is applied to solve sev-eral classification problems and performance comparisons with other classification methods are made. Finally, the conclusions are summarized in the Section VI.
II. STRUCTURE ANDCONSTRUCTION OFINITIALFUZZY
NEURALNETWORK A. Structure of FNNs
A four-layered FNN is shown in Fig. 1, which is comprised of the input, membership function, rule, and output layers. Layer 1 accepts input variables, whose nodes represent input linguistic variables. Layer 2 is to calculate the membership values, whose nodes represent the terms of the respective linguistic variables. Nodes at Layer 3 represent fuzzy rules. The links before Layer 3 represent the preconditions of fuzzy rules, and the link after Layer 3 represent the consequences of fuzzy rules. Layer 4 is the output layer. This four-layered network realizes the following form of fuzzy rules:
Rule If is and is and is
Then is (1)
where are the fuzzy sets of the input variables , and are the consequent parameter of . For the ease of analysis, a fuzzy rule 0 is added as
Rule If is and and is
Then is (2)
where is a universal fuzzy set, whose fuzzy degree is 1 for any input value , and is the consequent parameter of y in the fuzzy rule 0. Define and as the
output and input variables of a node in layer , respectively. The signal propagation and the basic functions in each layer are described as follows.
Layer 1- Input layer: No computation is done in this layer. Each node in this layer, which corresponds to one input variable, only transmits input values to the next layer directly. That is
(3) where , are the input variables of the FNN.
Layer 2—Membership function layer: Each node in this layer is a membership function that corresponds one linguistic label (e.g., fast, slow, etc.) of one of the input variables in Layer 1. In other words, the membership value which specifies the degree to which an input value belongs to a fuzzy set is calculated in Layer 2
(4)
where is a membership function ,
, . With the use of Gaussian membership function, the operation performed in this layer is
(5) where and are, respectively, the center (or mean) and the width (or variance) of the Gaussian membership function of the th term of the th input variable .
Layer 3—Rule layer: A node in this layer represents one fuzzy logic rule and performs precondition matching of a rule. Here, we use theANDoperation for each Layer 2 node
(6)
where ,
, is
the FNN input vector. The output of a Layer-3 node represents the firing strength of the corresponding fuzzy rule.
Layer 4—Output layer: The single node in this layer is labeled with , which computes the overall output as the sum-mation of all input signals
(7) where the connecting weight is the output action strength of the Layer 4 output associated with the Layer 3 rule and the scalar is a bias. Thus the fuzzy neural network mapping can be rewritten in the following input–output form:
(8)
B. Construction of Fuzzy Rules
For constructing the initial fuzzy rules of the FNN, the fuzzy clustering method is used to partition a set of data into a number
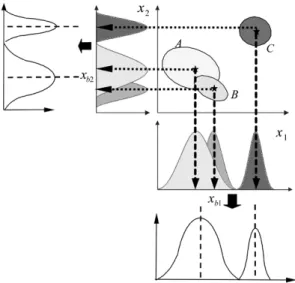
Fig. 2. Aligned clustering-based partition method giving both less number of clusters as well as less number of membership functions.
of overlapping clusters based on the distance in a metric space between the data points and the cluster prototypes. Each cluster in the product space of the input–output data represents a rule in the rule base. The goal is to establish the fuzzy preconditions in the rules. The membership functions in Layer 2 of FNN can be obtained by projections onto the various input variables spanning the cluster space. In this work, we use an aligned clus-tering-based approach proposed in [19]. This method produces a partition result as shown in Fig. 2.
The input space partitioning is also the first step in con-structing the fuzzy kernel function in the SVFNN. The purpose of partitioning has a two-fold objective.
• It should give us a minimum yet sufficient number of clus-ters or fuzzy rules.
• It must be in spirit with the SVM-based classification scheme.
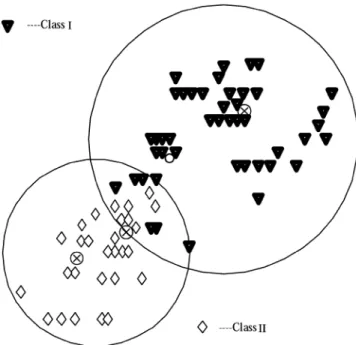
To satisfy the aforementioned conditions, we use a clustering method which takes care of both the input and output values of a data set. That is, the clustering is done based on the fact that the points lying in a cluster also belong to the same class or have an identical value of the output variable. The class infor-mation of input data is only used in the training stage to generate the clustering-based fuzzy rules; however, in testing stage, the input data excite the fuzzy rules directly without using class in-formation. In addition, we also allow existence of overlapping clusters, with no bound on the extent of overlap, if two clus-ters contain points belonging to the same class. We may have a clustering like the one shown in Fig. 3. Thus a point may be geometrically closer to the center of a cluster, but it can belong only to the nearest cluster, which has the points belonging to the same class as that point.
A rule corresponds to a cluster in the input space, with and representing the center and variance of that cluster. For each incoming pattern , the strength a rule is fired can be inter-preted as the degree the incoming pattern belongs to the corre-sponding cluster. It is generally represented by calculating de-gree of membership of the incoming pattern in the cluster [20].
Fig. 3. Clustering arrangement allowing overlap and selecting the member points according to the labels (or classes) attached to them.
For computational efficiency, we can use the firing strength de-rived in (6) directly as this degree measure
(9) where . In the above equation the term
is the distance between and the center of cluster . Using this measure, we can obtain the following criterion for the generation of a new fuzzy rule. Let be the newly incoming pattern. Find
(10) where is the number of existing rules at time . If
, then a new rule is generated, where is a prespecified threshold that decays during the learning process. Once a new rule is generated, the next step is to assign initial centers and widths of the corresponding membership functions. Since our goal is to minimize an objective function and the cen-ters and widths are all adjustable later in the following learning phases, it is of little sense to spend much time on the assign-ment of centers and widths for finding a perfect cluster. Hence, we can simply set
(11)
in (12)
according to the first-nearest-neighbor heuristic [21], where decides the overlap degree between two clusters. Similar methods are used in [22], [23] for the allocation of a new radial basis unit. However, in [22] the degree measure does not take the width into consideration. In [23], the width of each unit is kept at a prespecified constant value, so the allocation result is, in fact, the same as that in [22]. In this paper, the width is taken into account in the degree measure, so for a cluster with larger width (meaning a larger region is covered), fewer rules
will be generated in its vicinity than a cluster with smaller width. This is a more reasonable result. Another disadvantage of [22] is that another degree measure (the Euclidean distance) is required, which increases the computation load.
After a rule is generated, the next step is to decompose the multidimensional membership function formed in (11) and (12) to the corresponding 1-D membership function for each input variable. To reduce the number of fuzzy sets of each input variable and to avoid the existence of highly similar ones, we should check the similarities between the newly projected membership function and the existing ones in each input dimension. Before going to the details on how this overall process works, let us consider the similarity measure first. Since Gaussian membership functions are used in the SVFNN, we use the formula of the similarity measure of two fuzzy sets with Gaussian membership functions derived previously in [24]. Suppose the fuzzy sets to be measured are fuzzy sets and
with membership function
and , respectively. The union
of two fuzzy sets and is a fuzzy set such that , for every . The inter-section of two fuzzy sets and is a fuzzy set such
that , for every . The
size or cardinality of fuzzy set , , equals the sum of the
support values of : . Since the area
of the bell-shaped function, , is
[25] and its height is always 1, it can be approximated by an isosceles triangle with unity height and the length of bottom edge . We can then compute the fuzzy similarity measure of two fuzzy sets with such kind of membership functions. Assume as in [24], we can compute by
(13) where . So the approximate similarity measure is
(14) where we use the fact that
[24]. By using this similarity measure, we can check if two projected membership functions are close enough to be merged into one single membership function . The mean and variance of the merged membership function can be calculated by
(15) (16) Fig. 2 illustrates this procedure, and the detailed algorithm is given in Section IV.
III. ADAPTIVEFUZZYKERNEL
The proposed fuzzy kernel in this paper is defined as shown in (17) at the bottom of the page,
where and
are any two training samples, and is the membership function of the th cluster. Let
the training set be with
explanatory variables and the corresponding class labels , for all where is the total number of training samples. Assume the training samples are partitioned into clusters through fuzzy clustering in Section II. We can perform the following permutation of training samples:
.. .
(18) where , is the number of points belonging to the th cluster, so that we have . Then the fuzzy kernel can be calculated by using the training set in (18), and the obtained kernel matrix can be rewritten as the following form:
. .. ... ..
. . .. ...
(19)
where , is defined as shown in (20) at the bottom of the page. In order that the fuzzy kernel function de-fined by (17) is suitable for application in SVM, we must prove that the fuzzy kernel function is symmetric and positive–definite Gram Matrices [26]. To prove this, we first quote the following theorems.
Theorem 1 (Mercer Theorem [26]): Let be a compact subset of . Suppose is a continuous symmetric function such that the integral operator
(21) is positive; that is
(22) for all . Then we can expand in a uniformly convergent series (on ) in terms of ’s eigen-functions , normalized in such a way that , and positive associated eigenvalues
(23) The kernel is referred to as Mercer’s kernel as it satisfies the above Mercer theorem.
Proposition 1 [27]: A function is a valid kernel iff for any finite set it produces symmetric and positive–definite Gram matrices.
Proposition 2 [28]: Let and be kernels over ,
. Then the function is
also a kernel.
Definition 1 [29]: A function is said to be a positive–definite function if the matrix is positive semidefinite for all choices of points
and all .
Proposition 3 [29]: A block diagonal matrix with the posi-tive–definite diagonal matrices is also a posiposi-tive–definite matrix. Theorem 2: For the fuzzy kernel defined by (17), if the
mem-bership functions , , are
posi-tive–definite functions, then the fuzzy kernel is a Mercer kernel. Proof: First, we prove that the formed kernel matrix
is a symmetric matrix. According to the defi-nition of fuzzy kernel in (17), if and are in the th cluster
if and are both in the th cluster otherwise (17) . .. ... .. . . .. . .. (20)
otherwise
So the kernel matrix is indeed symmetric. By the elementary properties of Proposition 2, the product of two positively defined functions is also a kernel function. And according to Proposition 3, a block diagonal matrix with the positive–defi-nite diagonal matrices is also a positive–defipositive–defi-nite matrix. So the fuzzy kernel defined by (17) is a Mercer kernel.
Since the proposed fuzzy kernel has been proven to be a Mercer kernel, we can apply the SVM technique to obtain the optimal parameters of SVFNN. It is noted that the proposed SVFNN is not a pure SVM, so it dose not minimize the em-pirical risk and expected risk exactly as SVMs do. However, it can achieve good classification performance with drastically re-duced number of fuzzy kernel functions. The way to apply the SVM technique to obtain the optimal parameters of SVFNN is presented in Section IV in details.
IV. LEARNINGALGORITHM OFSVFNN
The learning algorithm of the SVFNN consists of three phases. The details are given below:
Learning Phase 1—Establishing initial fuzzy rules
The first phase establishes the initial fuzzy rules, which were usually derived from human experts as linguistic knowledge. Because it is not always easy to derive fuzzy rules from human experts, the method of automatically generating fuzzy rules from numerical data is issued. The input space partitioning de-termines the number of fuzzy rules extracted from the training set and also the number of fuzzy sets. We use the centers and widths of the clusters to represent the rules. To determine the cluster to which a point belongs, we consider the value of the firing strength for the given cluster. The highest value of the firing strength determines the cluster to which the point belongs. The whole algorithm for the generation of new fuzzy rules as well as fuzzy sets in each input variable is as follows. Suppose no rules are existent initially.
IF is the first incoming input pattern, THEN do
PART 1. Generate a new rule with center
and width ,
IF the output pattern belongs to class
1 (namely, ), for
indicating output node 1 been excited.}
ELSE , for indicating
output node 2 been excited.}
ELSE for each newly incoming input , do
PART 2. Find , as
defined in (9).
IF ,
set and generate
a new fuzzy rule, with ,
and , where decides the overlap degree between two clusters. In addition,
after decomposition, we have ,
, . Do the
following fuzzy measure for each input variable :
Degree
where is defined in (14).
IF Degree
THEN adopt this new membership
func-tion, and set , where is the
number of partitions of the th input variable.
ELSE merge the new membership function with closest one
ELSE If
generate a new fuzzy rule
with ,
, and the respective
consequent weight . In
addition, we also need to do the fuzzy measure for each input variable .
In the previous algorithm, is a prespecified constant, is the rule number at time , decides the overlap de-gree between two clusters, and the threshold determines the number of rules generated. For a higher value of , more rules are generated and, in general, a higher accuracy is achieved. The value is a scalar similarity criterion, which is monotonically decreasing such that higher similarity between two fuzzy sets is allowed in the initial stage of learning. The prespecified values are given heuristically. In general, , , , . In addition, after we determine the pre-condition part of fuzzy rule, we also need to properly assign the consequence part of fuzzy rule. Here we define two output nodes for doing two-cluster recognition. If output node 1 ob-tains higher exciting value, we know this input–output pattern belongs to class 1. Hence, initially, we should assign the proper weight for the consequence part of fuzzy rule. The above procedure gives us means and variances in (9). Another parameter in (7) that needs concern is the weight associated with each . We shall see later in Learning
Phase 2 how we can use the results from the SVM method to
determine these weights.
Learning Phase 2—Calculating the parameters of SVFNN
Through learning phase (1), the initial structure of SVFNN is established and we can then use SVM [30] to find the optimal parameters of SVFNN based on the proposed fuzzy kernels. The dual quadratic optimization of SVM [31] is solved in order to obtain an optimal hyperplane for any linear or nonlinear space:
maximize subject to
and (24) where is the fuzzy kernel in (17) and is a user-specified positive parameter to control the tradeoff between complexity of the SVM and the number of non-separable points. This quadratic optimization problem can
be solved and a solution can be
obtained, where are Lagrange coefficients, and is the number of support vectors. The corresponding support vectors can be obtained, and the constant (threshold) in (7) is
with
(25) where is the number of fuzzy rules (support vectors); the support vector belongs to the first class and support vector belongs to the second class. Hence, the fuzzy rules of SVFNN are reconstructed by using the result of the SVM learning with fuzzy kernels. The means and variances of the membership functions can be calculated by the values of
sup-port vector , , in (5) and (6) and the
variances of the multidimensional membership function of the cluster that the support vector belongs to, respectively. The coef-ficients in (7) corresponding to can be calculated by . In this phase, the number of fuzzy rules can be in-creased or dein-creased. The adaptive fuzzy kernel is advantageous to both the SVM and the FNN. The use of variable-width fuzzy kernels makes the SVM more efficient in terms of the number of required support vectors, which are corresponding to the fuzzy rules in SVFNN.
Learning Phase 3—Removing irrelevant fuzzy rules
In this phase, we propose a method for reducing the number of fuzzy rules learning in Phases 1 and 2 by removing some irrel-evant fuzzy rules and retuning the consequent parameters of the remaining fuzzy rules under the condition that the classification accuracy of SVFNN is kept almost the same. Several methods including orthogonal least squares (OLS) method and singular value decomposition QR (SVD-QR) had been proposed to se-lect important fuzzy rules from a given rule base [32]–[34]. In [32] the SVD-QR algorithm select a set of independent fuzzy basis function that minimize the residual error in a least squares sense. In [33], an orthogonal least-squares method tries to mini-mize the fitting error according to the error reduction ratio rather than simplify the model structure [34]. The proposed method reduces the number of fuzzy rules by minimizing the distance measure between original fuzzy rules and reduced fuzzy rules without losing the generalization performance. To achieve this goal, we rewrite (8) as
(26)
where is the number of fuzzy rules after Learning phases 1 and 2. Now, we try to approximate it by the expansion of a reduced set
and (27)
where is the number of reducing fuzzy rules with , is the consequent parameters of the remaining fuzzy rules, and and are the mean and variance of reducing fuzzy rules. To this end, one can minimize [35]
(28)
where . Evidently, the
problem of finding reduced fuzzy rules consists of two parts: one is to determine the reduced fuzzy rules and the other is to compute the expansion coefficients . This problem can be solved by choosing the more important fuzzy rules from the old fuzzy rules. By adopting the sequential optimization approach in the reduced support vector method in [36], the approximation in (27) can be achieved by computing a whole sequence of reduced set approximations
(29) for . Then, the mean and variance parameters, and , in the expansion of the reduced fuzzy-rule set in (27) can be obtained by the following iterative optimization rule [36]:
(30)
According to (30), we can find the parameters, and , corresponding to the first most important fuzzy rule and then remove this rule from the original fuzzy rule set represented by , and put (add) this rule into the reduced fuzzy rule set. Then the procedure for obtaining the reduced rules is repeated. The optimal coefficients , ,
are then computed to approximate by
[36], and can be obtained as (31)
where (32) and (33), as shown at the bottom of the page, hold, and
(34) The whole learning scheme is iterated until the new rules are sufficiently sparse.
V. EXPERIMENTALRESULTS
The classification performance of the proposed SVFNN is evaluated on five well-known benchmark datasets. These five datasets can be obtained from the UCI repository of machine learning databases [37] and the Statlog collection [38] and IJCNN challenge 2001 [39], [40], respectively.
A. Data and Implementation
From the UCI Repository, we choose one dataset: Iris dataset. From Statlog collection we choose three datasets: Vehicle, Dna and Satimage datasets. The problem Ijcnn1 is from the first problem of IJCNN challenge 2001. These five datasets will be used to verify the effectiveness of the proposed SVFNN classi-fier. The first dataset (Iris dataset) is originally a collection of 150 samples equally distributed among three classes of the Iris plant namely Setosa, Verginica, and Versicolor. Each sample is represented by four features (septal length, septal width, petal length, and petal width) and the corresponding class label. The second dataset (Vehicle dataset) consists of 846 samples belonging to 4 classes. Each sample is represented by 18 input features. The third dataset (Dna dataset) consists of 3186 feature vectors in which 2000 samples are used for training and 1186 samples are used for testing. Each sample consists of 180 input attributes. The data are classified into three physical classes. All Dna examples are taken from Genbank 64.1. The four dataset (Satimage dataset) is generated from Landsat Multispectral Scanner image data. In this dataset, 4435 samples are used for training and 2000 samples are used for testing. The data are classified into six physical classes. Each sample consists of
36 input attributes. The five dataset (Ijcnn1 dataset) consists of 22 feature vectors in which 49 990 samples are used for training and 45 495 samples are used for testing. Each sample consists of 22 input attributes. The data are classified into two physical classes. The computational experiments were done on a Pentium III-1000 with 1024MB RAM using the Linux operation system.
For each problem, we estimate the generalized accuracy using
different cost parameters in (24).
We apply 2-fold cross-validation for 10 times on the whole training data in Dna, Satimage and Ijcnn1, and then average all the results. We choose the cost parameter that results in the best average cross-validation rate for SVM training to pre-dict the test set. Because Iris and Vehicle datasets don’t contain testing data explicitly, we divide the whole data in Iris and Ve-hicle datasets into two halves, for training and testing datasets, respectively. Similarly, we use the above method to experiment. Notice that we scale all training and testing data to be in . B. Experimental Results
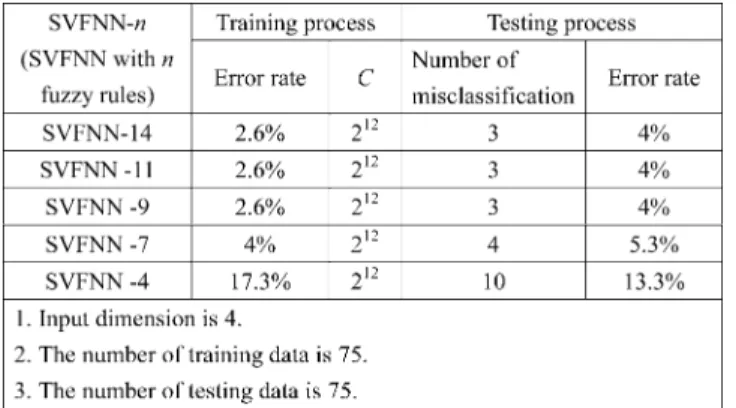
Tables I–V present the classification accuracy rates and the number of used fuzzy rules (i.e., support vectors) in the SVFNN on Iris, Vehicle, Dna, Satimage and Ijcnn1 datasets, respectively. The criterion of determining the number of reduced fuzzy rules is the difference of the accuracy values before and after reducing one fuzzy rule. If the difference is larger than 0.5%, meaning that some important support vector has been removed, then we stop the rule reduction. In Table I, the SVFNN is verified by using Iris dataset, where the constant in the symbol SVFNN-means the number of the learned fuzzy rules. The SVFNN uses fourteen fuzzy rules and achieves an error rate of 2.6% on the training data and an error rate of 4% on the testing data. When the number of fuzzy rules is reduced to seven, its error rate in-creased to 5.3%. When the number of fuzzy rules is reduced to four, its error rate is increased to 13.3%. Continuously de-creasing the number of fuzzy rules will keep the error rate in-creasing. From Tables II–V, we have the similar experimental results as those in Table I.
. .. ... .. . . .. . .. (32) . .. ... .. . . .. . .. (33)
TABLE I
EXPERIMENTALRESULTS OFSVFNN CLASSIFICATION ON THEIRISDATASET
TABLE II
EXPERIMENTALRESULTS OFSVFNN CLASSIFICATION ON THE
VEHICLEDATASET
TABLE III
EXPERIMENTALRESULTS OFSVFNN CLASSIFICATION ON THEDNA DATASET
These experimental results show that the proposed SVFNN is good at reducing the number of fuzzy rules and maintaining the good generalization ability. Moreover, we also refer to some recent other classification performance include support vector machine and reduced support vectors methods [41]–[43]. The performance comparisons among the existing fuzzy neural net-work classifiers [44], [45], the RBF-kernel-based SVM (without support vector reduction) [41], reduced support vector machine (RSVM) [43] and the proposed SVFNN are made in Table VI. These results indicate that the SVFNN classifier produces lower testing error rates as compared to FNN classifiers [44], [45], and uses less support vectors as compared to the regular SVM using
TABLE IV
EXPERIMENTALRESULTS OFSVFNN CLASSIFICATION ON THE
SATIMAGEDATASET
TABLE V
EXPERIMENTALRESULTS OFSVFNN CLASSIFICATION ON THEIJNN1 DATASET
fixed-width RBF kernels [41]. As compared to RSVM [43], the proposed SVFNN can not only achieve high classification accu-racy, but also reduce the number of support vectors quit well. It is noticed that although the SVFNN uses more support vectors in the Ijcnn1 dataset than the RSVM, it maintains much higher classification accuracy than the RSVM. In summary, the pro-posed SVFNN classifier exhibits better generalization ability on the testing data and use much smaller number of fuzzy rules.
VI. CONCLUSION
This paper proposed an SVFNN, which combines the su-perior classification power of SVMs in high-dimensional data spaces and the efficient human-like reasoning of FNN in han-dling uncertainty information. The SVFNN is the realization of a new idea for the adaptive kernel functions used in the SVM. The use of the proposed fuzzy kernels provides the SVM with adaptive local representation power, and thus brings the advan-tages of FNN (such as adaptive learning and economic network structure) into the SVM directly. The major advantages of the proposed SVFNN classification are as follows.
1) The proposed SVFNN can automatically generate fuzzy rules, and improve the accuracy and learning speed of classification.
2) It combined the optimal classification ability of SVM and the human-like reasoning of fuzzy systems. It improved the classification ability by giving SVM with adaptive
TABLE VI
CLASSIFICATIONERRORRATE COMPARISONSAMONG FNN, RBF-KERNEL-BASED
SVM, RSVMANDSVFNN CLASSIFIERS, WHERENA MEANS“NOTAVAILABLE”
fuzzy kernels and increased the speed of classification by reduced fuzzy rules.
3) The fuzzy kernels using the variable-width fuzzy mem-bership functions can make the SVM more efficient in terms of the number of required support vectors, and also make the learned FNN more understandable to human. 4) The ability of the structural risk minimization induction
principle, which forms the basis for the SVM method to minimize the expected risk, gives better generalization ability to the FNN classification.
REFERENCES
[1] K. Tanaka and H. O. Wang, Fuzzy Control Systems Design and
Anal-ysis. New York: Wiley, 2001.
[2] B. Kosko, Neural Networks and Fuzzy Systems. Englewood Cliffs, NJ: Prentice-Hall, 1992.
[3] M. Y. Chen and D. A. Linkens, “Rule-base self-generation and simpli-fication for data-driven fuzzy models,” Fuzzy Sets Syst., vol. 142, pp. 243–265, Mar. 2004.
[4] J. S. Jang, “ANFIS: Adaptive-network-based fuzzy inference system,”
IEEE Trans. Syst. Man. Cybern., vol. 23, no. 3, pp. 665–685, May 1993.
[5] K. Tanaka, M. Sano, and H. Wantanabe, “Modeling and control of carbon monoxide concentration using a neuro-fuzzy technique,” IEEE
Trans. Fuzzy Syst., vol. 3, no. 4, pp. 271–279, Aug. 1995.
[6] L. Y. Cai and H. K. Kwan, “Fuzzy classifications using fuzzy inference networks,” IEEE Trans. Syst., Man, Cybern., pt. B, vol. 28, no. 4, pp. 334–347, Jun. 1998.
[7] J. C. Bezdek, Pattern Recognition with Fuzzy Objective Function
Algo-rithms. New York: Plenum, 1981.
[8] J. C. Bezdek, S. K. Chuah, and D. Leep, “Generalized K-nearest neighbor rules,” Fuzzy Sets Syst., vol. 18, pp. 237–256, Apr. 1986. [9] J.-S. Wang and C. S. G. Lee, “Self-Adaptive neuro-fuzzy inference
sys-tems for classification applications,” IEEE Trans. Fuzzy Syst., vol. 10, no. 6, pp. 790–802, Dec. 2002.
[10] L. I. Kuncheva, “How good are fuzzy IF-THEN classifiers?,” IEEE
Trans. Syst., Man, Cybern., pt. B, vol. 30, pp. 501–509, Aug. 2000.
[11] H. Ishibuchi and T. Nakashima, “Effect of rule weights in fuzzy rule-based classification systems,” IEEE Trans. Fuzzy Syst., vol. 9, pp. 506–515, Aug. 2001.
[12] B. Gabrys and A. Bargiela, “General fuzzy min-max neural network for clustering and classification,” IEEE Trans. Neural Networks, vol. 11, no. 3, pp. 769–783, May 2000.
[13] K. Nozaki, H. Ishibuchi, and H. Tanaka, “Adaptive fuzzy rule-based clas-sification system,” IEEE Trans. Fuzzy Syst., vol. 4, no. 4, pp. 238–250, Aug. 1996.
[14] V. Vapnik, Statistical Learning Theory. New York: Wiley, 1998. [15] S. Sohn and C. H. Dagli, “Advantages of using fuzzy class memberships
in self-organizing map and support vector machines,” in Proc. Int. Joint
Conf. Neural Networks (IJCNN’01), vol. 3, Jul. 2001, pp. 1886–1890.
[16] C. F. Lin and S. D. Wang, “Fuzzy support vector machines,” IEEE Trans.
Neural Networks, vol. 13, pp. 464–471, Mar. 2002.
[17] T. Inoue and S. Abe, “Fuzzy support vector machines for pattern classi-fication,” in Proc. Int. Joint Conf. Neural Networks (IJCNN’01), vol. 2, Jul. 2001, pp. 15–19.
[18] J. T. Jeng and T. T. Lee, “Support vector machines for the fuzzy neural networks,” in IEEE Int. Conf. Systems, Man, and Cybernetics (SMC’99), vol. 6, Oct. 1999, pp. 12–15.
[19] C. F. Juang and C. T. Lin, “An on-line self-constructing neural fuzzy inference network and its applications,” IEEE Trans. Fuzzy Syst., vol. 6, no. 1, pp. 12–32, Feb. 1998.
[20] F. Hoppner, F. Klawonn, R. Kruse, and T. Runkler, Fuzzy Cluster
Analysis: Methods for Classification, Data Analysis and Image Recog-nition. New York: Wiley, 1999.
[21] C. T. Lin and C. S. G. Lee, “Neural-network-based fuzzy logic con-trol and decision system,” IEEE Trans. Comput., vol. 40, no. 12, pp. 1320–1336, Dec. 1991.
[22] J. Platt, “A resource allocating network for function interpolation,”
Neural Computat., vol. 3, pp. 213–225, 1991.
[23] J. Nie and D. A. Linkens, “Learning control using fuzzified self-orga-nizing radial basis function network,” IEEE Trans. Fuzzy Syst., vol. 40, no. 6, pp. 280–287, Nov. 1993.
[24] C. T. Lin and C. S. G. Lee, “Reinforcement structure/parameter learning for neural-network-based fuzzy logic control systems,” IEEE Trans.
Fuzzy Syst., vol. 2, no. 1, pp. 46–63, Feb. 1994.
[25] A. Papoulis, Probability Random Variables and Stochastic
Pro-cesses. New York: McGraw-Hill, 1984.
[26] J. Mercer, “Functions of positive and negative type and their connection with the theory of integral equations,” Philo. Trans. Royal Soc. London, vol. A209, pp. 415–446, 1909.
[27] S. Saitoh, Theory of Reproducing Kernels and Its Application. White Plains, NY: Longman.
[28] N. Cristianini and J. Shawe-Taylor, An Introduction to Support Vector
Machines and Other Kernel-Based Learning Methods. Cambridge, U.K.: Cambridge Univ. Press, 2000.
[29] R. A. Horn and C. R. Johnson, Matrix Analysis. Cambridge, U.K.: Cambridge Univ. Press, 1985.
[30] V. N. Vapnik, The Nature of Statistical Learning Theory. New York: Springer-Verlag, 1990.
[31] B. Schölkopf, C. J. C. Burges, and A. J. Smola, Advances in Kernel
Methods—Support Vector Learning. Cambridge, MA: MIT Press, 1999.
[32] J. Hohensoh and J. M. Mendel, “Two-pass orthogonal least-squares al-gorithm to train and reduce the complexity of fuzzy logic systems,” J.
Intell. Fuzzy Syst., vol. 4, pp. 295–308, 1996.
[33] G. Mouzouris and J. M. Mendel, “A singular-value-QR decomposition based method for training fuzzy logic systems in uncertain environ-ments,” J. Intell. Fuzzy Syst., vol. 5, pp. 367–374, 1997.
[34] J. Yen and L. Wang, “Simplifying fuzzy rule-based models using orthog-onal transformation methods,” IEEE Trans. Syst., Man, Cybern. B, vol. 29, no. 1, pp. 13–24, Feb. 1999.
[35] C. J. C. Burges, “Simplified support vector decision rules,” in Proc. 13th
Int. Conf. Machine Learning, L. Saitta, Ed., San Mateo, CA, 1996, pp.
[36] B. Scholkopf et al., “Input space versus feature space in kernel-based methods,” IEEE Trans. Neural Networks, vol. 10, no. 5, pp. 1000–1017, Sep. 1999.
[37] C. L. Blake and C. J. Merz. (1998) UCI repository of machine learning databases. Dept. Inform. Comput. Sci., Univ. California, , Irvine, CA. [Online]. Available: http://www.ics.uci.edu/~mlearn/MLReposi-tory.html
[38] D. Michie, D. J. Spiegelhalter, and C. C. Taylor. (1994) Machine learning, neural and statistical classification. [Online]. Available: ftp://ftp.stams.strath.ac.uk/pub/
[39] D. Prokhorov. IJCNN 2001 neural network competition. presented at Slide Presentation in IJCNN’01. [Online]. Available: http://www.geoc-ities.com/ijcnn/nncijcnn01.pdf
[40] LIBSVM Datasets of IJCNN2001. [Online]. Available: http://www.csie. ntu.edu.tw/~cjlin/libsvmtools/datasets/
[41] C. W. Hsu and C. J. Lin, “A comparison of methods for multiclass sup-port vector machines,” IEEE Trans. Neural Networks, vol. 13, no. 2, pp. 415–525, Mar. 2002.
[42] Y. J. Lee and O. L. Mangasarian, “RSVM: Reduced support vector ma-chines,” in Proc. 1st SIAM Int. Conf. Data Mining, 2001, pp. 1–17. [43] K. M. Lin and C. J. Lin, “A study on reduced support vector machines,”
IEEE Trans. Neural Networks, vol. 14, no. 6, pp. 1449–1459, Nov. 2003.
[44] H. M. Lee, C. M. Chen, J. M. Chen, and Y. L. Jou, “An efficient fuzzy classifier with feature selection based on fuzzy entropy,” IEEE Trans.
Syst., Man, Cybern. B, vol. 31, no. 3, pp. 426–432, Jun. 2001.
[45] M. R. Berthold and J. Diamond, “Constructive training of probabilistic neural networks,” Neurocomput., vol. 19, pp. 167–183, 1998.
Chin-Teng Lin (F’05) received the B.S. degree from National Chiao-Tung University (NCTU), Taiwan, in 1986, and the Ph.D. degree in electrical engineering from Purdue University, West Lafayette, IN, in 1992. He is currently the Chair Professor of Electrical and Computer Engineering, Dean of Computer Science College, and Director of Brain Research Center at NCTU. He served as the Director of the Research and Development Office of NCTU from 1998 to 2000, the Chairman of Electrical and Control Engineering Department of NCTU from 2000 to 2003, and Associate Dean of the College of Electrical Engineering and Computer Science from 2003 to 2005. His current research interests are fuzzy neural networks, neural networks, fuzzy systems, cellular neural networks, neural engineering, algorithms and VLSI design for pattern recognition, intelli-gent control, and multimedia (including image/video and speech/audio) signal processing, and intelligent transportation system (ITS). He is the coauthor of the book Neural Fuzzy Systems- A Neuro-Fuzzy Synergism to Intelligent
Systems (Prentice Hall, 1996), and the author of Neural Fuzzy Control Systems with Structure and Parameter Learning (World Scientific, 1994). He has
pub-lished over 90 journal papers in the areas of neural networks, fuzzy systems, multimedia hardware/software, and soft computing, including about 60 IEEE journal papers.
Dr. Lin served on the Board of Governors of the IEEE Circuits and Systems (CAS) Society in 2005 and the IEEE Systems, Man, Cybernetics (SMC) Society in 2003–2005. He was the Distinguished Lecturer of the IEEE CAS Society from 2003 to 2005. He is the International Liaison of the International Sym-posium of Circuits and Systems (ISCAS) 2005, in Japan, the Special Session Co-Chair of ISCAS 2006, in Greece, and the Program Co-Chair of IEEE Inter-national Conference on SMC 2006, in Taiwan. He has been the President of Asia Pacific Neural Network Assembly since 2004. He has received the Outstanding Research Award granted by National Science Council, Taiwan, since 1997 to the present, the Outstanding Electrical Engineering Professor Award granted by the Chinese Institute of Electrical Engineering (CIEE) in 1997, the Out-standing Engineering Professor Award granted by the Chinese Institute of En-gineering (CIE) in 2000, and the 2002 Taiwan Outstanding Information-Tech-nology Expert Award. He was also elected to be one of the 38th Ten Outstanding Rising Stars in Taiwan (2000). Dr. Lin currently serves as an Associate Editors of the IEEE TRANSACTIONS ONCIRCUITS ANDSYSTEMS, PARTSIANDPART
II, the IEEE TRANSACTIONS ONSYSTEMS, MAN,ANDCYBERNETICS, the IEEE TRANSACTIONS ONFUZZYSYSTEMS, and the International Journal of Speech
Technology. He is a member of Tau Beta Pi, Eta Kappa Nu, and Phi Kappa Phi
honorary societies.
Chang-Mao Yeh received the B.S. degree in elec-tronics engineering and the M.S. degree in computer science and information engineering from the Na-tional Yunlin University of Science and Technology, Yunlin, Taiwan, R.O.C., in 1994 and 1997, respec-tively. He is currently working toward the Ph.D. degree in electrical and control engineering at the National Chiao-Tung University, Hsinchu, Taiwan, R.O.C.
He is a Lecturer in Information Networking Technology at Chungchou Institute of Technology, Taichung, Taiwan, R.O.C. His current research interests include neuro-fuzzy systems, support vector machine, machine learning, and pattern recognition.
Sheng-Fu Liang was born in Tainan, Taiwan, in 1971. He received the B.S. and M.S. degrees in control engineering from the National Chiao-Tung University (NCTU), Taiwan, in 1994 and 1996, respectively, and the Ph.D. degree in electrical and control engineering from NCTU in 2000.
From 2001 to 2005, he was a Research Assistant Professor in Electrical and Control Engineering, NCTU. In 2005, he joined the Department of Bio-logical Science and Technology, NCTU, where he serves as an Assistant Professor. He has served as the Chief Executive of the Brain Research Center, NCTU Branch, University System of Taiwan, since September 2003. His current research interests are biomedical engineering, biomedical signal/image processing, machine learning, fuzzy neural networks (FNN), the development of brain-computer interface (BCI), and multimedia signal processing.
Jen-Feng Chung received the B.S. degree in com-puter science and information engineering from the Chung-Hua University, Hsinchu, Taiwan, and the M.S. degree in electrical engineering from the Chung-Hua University, Hsinchu, Taiwan, in 1997 and 1999, respectively. He is currently working toward the Ph.D. degree in electrical and control engineering at National Chiao-Tung University, Hsinchu, Taiwan.
His current research interests are neural networks, VLSI signal processing, audio and image signal pro-cessing, and DSP architecture design.
Nimit Kumar recieved the B.Tech. degree from the Indian Institute of Technology, Kanpur, in 2004.
He is currently a Research Trainee at IBM India Research Lab., Delhi, India. His research focuses on statistical learning theory, kernel-based learning, neuro-fuzzy systems, web and text mining, visuo-motor control, and the natural basis of learning.
Mr. Kumar has served as a reviewer for the IEEE TRANSACTIONS ON SYSTEMS, MAN, AND
CYBERNETICSB and the IEEE TRANSACTIONS ON