平面凸多邊形內臨近周邊兩相鄰交叉對角
線長度乘積方程式
(上)
李輝濱
嘉 義 市 輔 仁 高 級 中 學 退 休 教 師壹、前言
從 著 手 進 行 全 面 觀 察 比 對 圓 內 接 四 邉 形 托 勒 密 定 理(Ptolemy theorem)、平 面凸 四 邊 形、 平 面 凸 五 邊 形、平 面 凸 六 邊 形 及 平 面 凸 七 邊 形 等 五 種 圖 形 內 臨 近 周 邊 的 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式 的 公 式 型 態 內 容 架 構 後,再 經 由 深 刻 思 索 的 自 我 發 想,覺 察 意 識 到 可 以 應 用 同 類 歸 納 推 理 法 則 來 將 這 些 已 獲 得 的 五 樣 同 類 公 式 推 廣 延 伸 到 任 何 邉 數 平 面 凸 多 邊 形 的 同 性 質 情 況 上,隨 即 直 觀 地 開 始 對 各 多 邉 形 實 際 依 圖 索 驥,分 析 探 討 各 項 邉 長 組 合、角 度 組 合、邉 長 與 角 度 的 各 樣 適 切 組 合,再 將 這 些 多 項 組 合 式 編 製 成 各 多 邉 形 方 程 式, 並 且 仔 細 逐 項 比 較 而 整 理 出 所 得 方 程 式 間 的 共 同 連 貫 性 質,而 獲 致 一 套 統 整 的 公 式 綜 合 法 則;即 預 先 歸 納 且 詳 細 條 列 出 一 般 多 邉 形 的 常 態 規 則 化 方 程 式,再 按 順 序 逐 一 加 以 嚴 謹 翔 實 的 理 論 推 演 驗 證,以 完 整 建 立 這 所 有 公 式 存 在 的 恆 常 完 美、規 律 秩 序 及 廣 泛 普 遍 的 真 實 正 確 性 ! 以 下 將 詳 盡 的 敘 述 出 憑 藉 著 同 類 歸 納 推 理 法 完 成 的 統 整 綜 合 規 則,用 以 表 明 一 般 化 方 程 式 內 涵 結 構。當 在 理 論 驗 證 時 必 頻 繁 引 用 到 最 普 遍 的 多 邉 形 餘 弦 定 理 公 式 及 平 面 幾 何 學 中 慣 常 應 用 的 輔 助 圖 形 作 圖 法 來 達 成 推 理 實 證 的 演 繹 工 作 。貳、本文
接 著 在 本 文 敘 述 的 導 證 過 程 中,將 詳 盡 列 舉 闡 述 出 平 面 凸 多 邊 形 內 臨 近 周 邊 的 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式 的 綜 合 定 則,並 逐 步 解 說 各 種 不 同 公 式 推 證 時,在 規 則 下 見 證 出 他 們 相 互 之 間 的 一 致 共 同 規 律 秩 序 關 係 ! 而 在 下 列 撰 文 推 理 演 繹 的 運 算 過 程 中, 須 應 用 或 對 照 到 下 述 已 知 的 數 個 基 本 數 學 性 質 ;A. 數學基本性質---引理:
引 理1. 平 面 凸多 邊 形 的 向量 性 質 任 給 一 個 平 面 凸
n
邊形A
1A
2A
3A
4
A
n1A
n,令 邊 長A
1A
2 =V
1的 向 量 為 1V
, 3 2A
A
=V
2的 向 量 為 2V
,
,A
nA
1=V
n的 向 量 為 nV
,則 此 平 面 凸n
邊 形 即 為 此n
個向 量 按 順 序箭 頭 接 箭 尾 相 加 而 成 的封 閉 凸n
邊形 。 依 向 量 加 法 性 質 知 ;
1
0
n mV
m = 1(
cos
)
1(
sin
)
0
nmV
m
mi
nmV
m
mj
此 處
m為V
m在 直 角 座 標 平 面 上 的 方 位 角。 i
為 正 X 軸 方向 的 單 位 向量, j
為 正Y 軸方 向 的 單位 向 量 , 再由 平 面 正 交座 標 系 性 質知 ;0
)
cos
(
1
n mV
m
m 且
1(
sin
)
0
n mV
m
m 現 在 將 頂 點A
1置 於 直 角 座 標 平 面 上 的 原 點 O,如 下 圖 (1),使A
1A
2 邊 完 全 重 疊 並 貼 置 於 X 軸 ,以 使 此n
邊 形 完 全 落 在 第 1 及 第 2 象 限 區域 內(含 X 軸), 則V
1+cos[(
1
)
]
0
2 2
m k k n mV
mm
A
(1) 且sin[(
1
)
]
0
2 2
m k k n mV
mm
A
(2) 圖 1、 凸 n 邊 形證 明 : 由 圖 1. 知 凸
n
邊 形 的內 角 依 次 為A
1,A
2,A
3,
,A
n, 而V
1的 方 位 角
1為 零 , 2V
的 方 位 角
2為 π −A
2 ,V
3的 方 位 角
3為 (π −A
2) (π −A
3),V
4的 方 位 角
4 為 (π −A
2) +(π −A
3) +(π −A
4), … … … … ,V
n的 方 位 角
n為(n−1)π −(A
2+A
3 +A
4 +· · · +A
n ) 。 將 這n
個 方 位 角 全 部 代 入 以 下 方 程 式 中 :0
)
cos
(
1
n mV
m
m 且
1(
sin
)
0
n mV
m
m , 則0
)
cos
(
1
n mV
m
m=
V
1+V
2cos(π −A
2)+V
3cos(2π −A
2−A
3)+
+V
ncos[(n-1) π-
kn2A
k]
0
將 上 列 等 式 改 寫 成 下 式 ; 得V
1+cos[(
1
)
]
0
2 2
m k k n mV
mm
A
(1) 同 理 , 再 得sin[(
1
)
]
0
2 2
m k k n mV
mm
A
(2) 引 理 的 各 邉 長 與 各 頂 角 關 係 證 明 完 成 。 引 理1.的一 組 方程 式(1)與(2)是因 以 線 段A
1A
2 =V
1為 底, 疊 置 在 X 軸 所 求 得 的 結 果, 若 換 成 以A
2A
3=V
2為 底,將 求 得 類 似 的 另 一 組 方 程 式。以 此 類 推,總 共 會 得 出n
組。這n
組 方 程 式 是 非 常 好 應 用 的 , 尤 其 用 在 多 邊 形 尋 找 邊 長 與 內 角 之 間 的 關 係 式 時 至 為 有 效 ! 引 理 2. 在 平 面 上 給 定 一 個 凸n
邊 形A
1A
2A
3A
4....
A
n1A
n, 則 此 凸 多 邊 形 所 有 內 角 總 和 為
2
....
1 4 3 2 1
A
A
A
A
A
n
A
n n 證 明 : 略 。 引 理3. 任 給 一圓 內 接 偶 數邊n
邊 形A
1A
2A
3A
4....
A
n1A
n,n
=2k+2,k 為 自然 數,則 此多 邊 形 的 頂 角 組 合A
1
A
3
A
5
A
7
....
A
n3
A
n1
2
2
1
....
2 8 6 4 2
A
A
A
A
A
nA
nn
證 明 : 略 。引 理4. 三 角 函數 角 度 的 和差 轉 換 公 式
sin α β sin
α cos β cos α sin β
cos α
β
cos α cos β ∓ sin α sin β
引 理5. 在 平 面 上給 定 一 個 凸七 邊 形
A
1A
2A
3A
4A
5A
6A
7,令 線 段 長A
1A
2=V
1,A
2A
3 =V
2, 4 3A
A
=V
3,A
4A
5 =V
4,A
5A
6=V
5,A
6A
7=V
6,A
7A
1=V
7, 如 圖 2. 圖2 則 此 凸 七 邊 形 各 邉 長 與 頂 角 關 係 的 餘 弦 定 理 公 式 為 下 列 方 程 式(3); 2 7V
=V
12+V
22+V
32+V
42+V
52+V
62-2V
1V
2cos A
2-2V
2V
3cos A
3-2V
3V
4cos A
4-2
V
4V
5cos A
5-2V
5V
6cos A
6 + 2V
1V
3cos
A
2
A
3
+ 2V
2V
4cos
A
3
A
4
+ 2V
3V
5cos
A
4
A
5
+2V
4V
6cos
A
5
A
6
- 2V
1V
4cos(
A
2
A
3
A
4)
- 2V
2V
5cos(
A
3
A
4
A
5)
- 2V
3V
6cos(
A
4
A
5
A
6)
+ 2
V
1V
5cos(
A
2
A
3
A
4
A
5)
+ 2V
2V
6cos(
A
3
A
4
A
5
A
6)
- 2
V
1V
6cos(
A
2
A
3
A
4
A
5
A
6)
(3) 證 明 : 應 用 引 理 1. 取n
=7 代入 一 組 方 程式(1)與 (2), 並應 用 引 理 2.再 化 簡 可得1
V
=V
2cos A
2-V
3cos
A
2
A
3
+V
4cos(
A
2
A
3
A
4)
+V
5cos(
A
6
A
7
A
1)
V
6cos(
A
7
A
1)
+V
7cos A
1 (1-1)2 2
sin A
V
-V
3sin
A
2
A
3
+V
4sin
A
2
A
3
A
4
-V
5sin(
A
6
A
7
A
1)
+V
6sin(
A
7
A
1)
V
7sin A
1= 0 (2-1)仿 效 這 組 方 程 式 , 令 將 方 程 式 (1-1)及 (2-1)換 成 以
V
7為 底 , 可 得 下 列 兩 式 ;V
7=V
1cos A
1-V
2cos
A
1
A
2
+V
3cos(
A
1
A
2
A
3)
+V
4cos(
A
5
A
6
A
7)
V
5cos(
A
6
A
7)
+V
6cos A
7 (1-5)V
1sin A
1-V
2sin
A
1
A
2
+V
3sin
A
1
A
2
A
3
V
4sin(
A
5
A
6
A
7)
+V
5sin(
A
6
A
7)
V
6sin A
7= 0 (2-5)將 方 程 式(1-5)及方 程 式(2-5)等號 兩 側 各自 完 全 平 方, 得 2
7
V
=V
12cos A
2 1+V
22cos
2
A
1
A
2
+V
32cos
2(
A
1
A
2
A
3)
+V
42cos
2(
A
5
A
6
A
7)
+V
52cos
2(
A
6
A
7)
+V
62cos A
2 7
2
V
1V
2cos
A
1cos
A
1
A
2
+
2
V
1V
3cos
A
1cos(
A
1
A
2
A
3)
+2
V
1V
4cos
A
1cos(
A
5
A
6
A
7)
—2
V
1V
5cos
A
1cos(
A
6
A
7)
+2
V
1V
6cos
A
1cos A
7-2
V
2V
3cos
A
1
A
2
—2
V
2V
4cos
A
1
A
2
cos(
A
5
A
6
A
7)
+2
V
2V
5cos
A
1
A
2
cos(
A
6
A
7)
—2
V
2V
6cos
A
1
A
2
cos A
7+2
V
3V
4cos(
A
1
A
2
A
3)
cos(
A
5
A
6
A
7)
)
cos(
2
V
3V
5A
1
A
2
A
3
cos(
A
6
A
7)
+2
V
3V
6cos(
A
1
A
2
A
3)
cos A
7)
cos(
2
V
4V
5A
5
A
6
A
7
cos(
A
6
A
7)
+2
V
4V
6cos(
A
5
A
6
A
7)
cos A
7)
cos(
2
V
5V
6A
6
A
7
cos A
70 =
V
12sin A
2 1+V
22sin
2
A
1
A
2
+V
32sin
2(
A
1
A
2
A
3)
+V
42sin
2(
A
5
A
6
A
7)
+V
52sin
2(
A
6
A
7)
+V
62sin A
2 7
2
V
1V
2sin
A
1sin
A
1
A
2
+
2
V
1V
3sin
A
1sin(
A
1
A
2
A
3)
2
V
1V
4sin
A
1sin(
A
5
A
6
A
7)
+
2
V
1V
5sin
A
1sin(
A
6
A
7)
-2
V
1V
6sin
A
1sin A
7-2
V
2V
3sin
A
1
A
2
sin(
A
1
A
2
A
3)
+2
V
2V
4sin
A
1
A
2
sin(
A
5
A
6
A
7)
-2
V
2V
5sin
A
1
A
2
sin(
A
6
A
7)
+
2
V
2V
6sin
A
1
A
2
sin A
7-2
V
3V
4sin(
A
1
A
2
A
3)
sin(
A
5
A
6
A
7)
+2
V
3V
5sin(
A
1
A
2
A
3)
sin(
A
6
A
7)
-2
V
3V
6sin(
A
1
A
2
A
3)
sin A
7)
sin(
2
V
4V
5A
5
A
6
A
7
sin(
A
6
A
7)
+2
V
4V
6sin(
A
5
A
6
A
7)
sin A
7)
sin(
2
V
5V
6A
6
A
7再 將 這 兩 個 完 全 平 方 式 相 加 , 繼 續 應 用 引 理4.及 引 理 2.的 公 式,代入 運 算再 詳 盡 化 簡 , 最 後 就 得 證 出 總 計 有 21 項 式 的 方 程式(3) 。 方 程 式(3)不 僅 僅適 用 於 平 面凸 七 邊 形 ,也 適 用 於 各種 形 狀 的 平面 凹 七 邊 形。
B. 歸 納 平 面 凸 多 邊 形 內 臨 近 周 邊 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 方 程 式 的 綜
合定則
計 算 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 方 程 式 時,發 現 得 到 的 公 式 顯 示 出 兩 對 角 線 長 度 乘 積 的 平 方 式 等 於 若 干 個 兩 邉 長 乘 積 的 平 方 項 的 和 再 加 上 許 多 個 由 四 個 邉 長 乘 積 並 乘 以 無 量 綱 的cosine 函 數項 式 共 同 組合 而 形 成。因 此,公 式 中的 各 項 式 在數 學 運 算 上的 量 綱 都 是邊 長 的 四 次 方 。 圖 3、 平 面凸 n 邊 形 理 論 上 計 算 這 些 公 式 時 , 由 圖 形 的 一 般 性 , 請 參 考 上 圖 3.,選 擇直 觀 的 採取 此 多 邊 形 最 前 緣 的 四 個 頂 點 所 形 成 的 兩 交 叉 對 角 線,而 此 四 頂 點
A
1、A
2、A
3、A
4則 將 多 邉 形 的n
個 邉 長 區 分 成 四 份;第 一 份 為 邉 長A
1A
2 =V
1,第 二 份 是 邉 長A
2A
3 =V
2,第 三 份 邉 長 4 3A
A
=V
3,第 四 份 最 多 邉 長 有n
3
個 邉 為A
4A
5 =V
4,A
5A
6 =V
5,A
6A
7 =V
6,A
7A
8 =V
7,…,A
n3A
n2=V
n3,A
n2A
n1=V
n2,A
n1A
n=V
n1,A
nA
1=V
n 。再 由 這 四 份 的 邉 長 分 別 來 進 行 圖 形 相 對 邉 乘 積 結 合 , 而 歸 納 統 整 出 完 整 的 一 系 列 方 程 式 , 且 比 對 這 所 有 公 式 的 內 涵 型 態 都 能 見 到 它 們 之 間 一 一 展 現 出 最 精 實 相 似 又 彼 此 輝 映 的 一 貫 性 共 同 規 律 秩 序 特 質 ! 以 下 就 是 透 過 比 對 研 究 歸 納 出 的 2 個 綜合 定 則 , 用來 明 列 出 平面 凸 多 邊 形內 臨 近 周 邊 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 方 程 式 , 這 些 被 預 先 列 舉 出 的 每 一 個 凸 多 邊 形 公 式 的 等 號右 側 內 容 恰 好 共 分 成 二 部 份 , 再 看 下 圖3.的 一 般 形平 面 凸
n
邊 形 ; 圖 3 任 給 一 平 面 凸n
邊 形A
1A
2A
3A
4A
5A
6A
7A
8
A
n4A
n3A
n2A
n1A
n , 令 邊 長 線 段 2 1A
A
=V
1,A
2A
3 =V
2,A
3A
4 =V
3,A
4A
5 =V
4,A
5A
6 =V
5,A
6A
7=V
6,A
7A
8 =V
7,…, 2 3 n nA
A
=V
n3,A
n2A
n1=V
n2,A
n1A
n=V
n1,A
nA
1=V
n,4
n
,n
為 正 整 數,現 在 直 覺 選 取 連 接A
1和A
3兩 頂 點 及 其 相 鄰 的A
2和A
4兩 頂 點 使 之 形 成 臨 近 周 邉 兩 對 角 線 長 13 3 1A
d
A
及A
2A
4
d
24, 此 四 頂 點A
1、A
2、A
3、A
4將 這 凸n
邊 形 的 所 有 邉 長 分 隔 編 列 成 兩 組 相 異 集 合;第 一 組 相 對 邊 邉 長 集 合 只 有 兩 元 素 是 {V
1,V
3},而 第 二 組 相 對 邊 的 邉 長 集 合 內 共 計 有n
2
個 元 素,其 集 合 內 的 元 素 是 {V
2,V
4,V
5,V
6,V
7,V
8,…, 4 nV
,V
n3,V
n2,V
n1,V
n},這 兩 組 集 合 皆 為 此 四 頂 點 所 構 成 的 圖 形 中 各 以 相 對 邉 的 邉 長 來 形 成 集 合 。 綜 合 定 則[1]. 公式 中 等 號 右 側內 容 的 第 一部 份 組 成 結構 : (1a) 將 第 一 組 邊 長 集 合 內 兩 元 素 相 乘 並 使 此 乘 積 再 完 全 平 方 , 得( V
V
1 3)
2, (1b) 二 組 邊 長 集 合 的 第 一 個 元 素 是V
2,其 在n
邉 形 圖 形 中 的 對 面 共 有n
3
個 相 對 邉,分 別 為V
4,V
5,V
6,V
7,V
8,…,V
n4,V
n3,V
n2,V
n1,V
n;現 在 取V
2分 別 與 毎 一 個 相 對 邉 邊 長 相 乘,之 後 使 每 一 乘 積 再 各 自 完 全 平 方,然 後 將 此n
3
個 平 方 式 相 加,得( V
V
2 4)
2+( V
V
2 5)
2+( V
V
2 6)
2+( V
V
2 7)
2+( V
V
2 8)
2+… + 2 3 2)
(
V
V
n + 2 2 2)
(
V
V
n + 2 1 2)
(
V
V
n + 2 2)
(
V
V
n ,(1c) 後 再 將(1a).與 (1b).的 所 有 兩 組 的 平 方 項 相 加 , 這 樣 就 構 成 了 被 預 先 表 列 出 的 公 式 中 第 一 部 份 內 容 結 構 的 平 方 項 的 總 和。此 部 份 內 容 共 有
n
2
項,這 完 整 歸 納 得 來 的 第 一 部 份 組 成 結 構 內 容 應 記 為 下 列 型 式 ; 2 3 1)
( V
V
+( V
V
2 4)
2 +( V
V
2 5)
2 +( V
V
2 6)
2 +( V
V
2 7)
2 +( V
V
2 8)
2 + … +(
V
2V
n3)
2 + 2 2 2)
(
V
V
n +(
V
2V
n1)
2+(
V
2V
n)
2 , 綜 合 定 則[2]. 公式 中 等 號 右 側內 容 的 第 二部 份 內 項 數的 組 成 結 構: 公 式 中 第 二 部 分 內 涵 裡 的 每 一 項 是 由 係 數 2 乘 以 此 多邊 形 的 4 個 邊 長 乘 積 再乘 上 cosine 函 數 所 構成 的 , 而 邊長 可 重 複 。此 係 數 2 是 運 算出 的 必然 常 數 。 (2a) 每 一 項 的 4 個 邊長 乘 積 內 容必 須 按 下 述步 驟 依 序 組合 : 由 前 述 綜 合 定 則[1].所獲 得 的共 有n
2
個 兩 邉 長 乘 積 項 依 序 排 列 如 下 ; 3 1V
V
、V
2V
4、V
2V
5、V
2V
6、V
2V
7、V
2V
8、…、V
2V
n3、V
2V
n2、V
2V
n1、V
2V
n。 現 在 將 這n
2
乘 積 項 任 取 2 個 來相 乘 , 總 共就 有C
2n2個 4 邊 長 乘積 項 ,其 組 合 的 各 項 式 形 式 結 構 依 順 序 表 列 於 下 ;V
1V
2V
3V
4,V
1V
2V
3V
5,V
1V
2V
3V
6,V
1V
2V
3V
7, 8 3 2 1V
V
V
V
, … ,V
1V
2V
3V
n3,V
1V
2V
3V
n2,V
1V
2V
3V
n1,V
1V
2V
3V
n, 共 有n
3
個 。 5 4 2 2V
V
V
,V
22V
4V
6,V
22V
4V
7,…,V
22V
4V
n2,V
22V
4V
n1,V
22V
4V
n,共 有n
4
個。 6 5 2 2V
V
V
,V
22V
5V
7,V
22V
5V
8, … ,V
22V
5V
n2,V
22V
5V
n1,V
22V
5V
n, 共 有n
5
個 。 7 6 2 2V
V
V
,V
22V
6V
8, … ,V
22V
6V
n2,V
22V
6V
n1,V
22V
6V
n, 共 有n
6
個 。
3 4 2 2V
nV
nV
,V
22V
n4V
n2,V
22V
n4V
n1,V
22V
n4V
n, 共 有4 個 。 2 3 2 2V
nV
nV
,V
22V
n3V
n1,V
22V
n3V
n, 共 有 3 個 。 1 2 2 2V
nV
nV
,V
22V
n2V
n, 共 有 2 個 。 n nV
V
V
2 1 2 , 僅 有1 個 。因 此 , 得 總 項 數 為 1+2+3+4+…+(
n
5
)+(n
4
)+(n
3
)=2
)
3
)(
2
(
n
n
=C
2n2。 (2b) 每 一 項 的 cosine 函 數裡 呈 現的 角 度 組 合則 以 下 述 之內 角 排 列 法則 來 規 範 : (i) 內 角排 列 法 則 是根 據 每 一個 cosine 項 前的 4 個 邊 長係 數 右 下 標數 字 來 決 定, 請 看 第 一 個 cosine 項 的 邊 長積 係 數 為V
1V
2V
3V
4, 將 其 分 成 前 後 兩 對 ; 前 一 對 是V
1V
2, 這V
1與V
2的 兩 個 邊 長 在 多 邊 形 圖 形 上 所 夾 的 內 角 角 度 是A
2。 後 一 對V
3與V
4在 此 多 邊 形 圖 形 上 所 夾 的 角 度 是A
4。 這A
2+A
4就 是 出 現 於 第 一 個 cosine 項( )內 的 角度 排 列, 組 合 起 來就 成 為V
1V
2V
3V
4cos(A
2+A
4) ! (ii) 然 而 在 (2a).的 敘 述 中 出 現 了 眾 多 的V
2V
iV
j 2 項 ,i
j
, 這 類 型 項 式 的 前 一 對 2 2V
, 其 兩 邉 長V
2在 多 邊 形 圖 形 上 所 夾 的 內 角 角 度 是 零 , 而 後 一 對V
i與V
j的 兩 個 邊 長 在 多 邊 形 圖 形 上 所 夾 的 內 角 角 度 則 仿 照(i).的 規範 。 例 1:V
22V
4V
5這 一 項 就 配 備 著 內 角0
A
5
A
5,組 合 後 就 成 為V
22V
4V
5cos A
5! 例 2:V
22V
5V
8這 一 項 就 配 備 著 內 角 排 列 0A6 A7 A8, 組 合 起 來 就 成 為 V22V5V8 cos(A6 A7 A8)! 公 式 中 任 一 cosine 項( )裡 的角 度 組 合 都以 上 述 之 內角 排 列 法 則來 思 考 操 作。 (2c) 第 二 部 份 內 的 各 cosine 項 前自 然 出 現 的正 負 符 號 則按 下 列 規 律形 成 : 詳 盡 比 對 所 有cosine 項 各 對映 位 置 內 容,發現 任 一 cosine 項 的( )內 所 出 現角 度 組 合 之 內 角 個 數 與 其 本 身 的 正 負 符 號 之 間 存 在 著 特 定 的 關 聯 性 ! 這 個 被 歸 納 出 的 相 關 性 特 徵 如 下 ; (i) 令 任給 一 cosine 項的 四 個 邊長 係 數 為V
aV
xV
bV
y, 現 在 將 此 四 個 邊 長 係 數 拆 分 成 前 後 兩 對 , 前 一 對 是V
aV
x, 這 兩 個 邊 長V
a與V
x依 順 序 由 a 至 x 在 多 邊形 上 所 夾 的 內 角 數 目 有k
1個 。 而 後 一 對 是V
bV
y, 這 兩 個 邊 長V
b與V
y依 順 序 由 b 至 y 在 多 邊形 上 所夾 的 內 角 數目 有k
2個 。 令 k1+k2=k ,k 即 為cosine 項( ) 內 的 角 度 總 數 目,而 這 被 歸 納 出 的 正 負 符 號 關 係 式 為 (1)k1,意 即 由 cosine 項 ( )內的 角 度 總數 目 來 決 定正 負 符 號。當 cosine 項( )內 的 角 度總 數 目 為 奇數 時, 此 cosine 項 係 數為 正。當 cosine 項( )內 的 角 度 總 數目 為 偶 數 時,此 cosine 項 的係 數 為 負 。 (ii) 對 四個 邊 長 乘 積為
V
a2V
bV
y類 型 的 項 式 而 言, 2 aV
的 內 角 數 目k
1= 0,因V
a2的 邉 長 在 多 邊 形 圖 形 上 所 夾 的 內 角 角 度 是 零,即 兩V
a邉 長 重 疊,沒 有 任 何 夾 角。而 y bV
V
的 兩 邉 在 多 邊 形 上 所 夾 的 內 角 數 目 有 k2個 。 故 k1+k2=k2, 這Va2VbVy項 式 前 的 正 負 符 號 關 係 式 則 被 歸 納 為(
1
)
k2 ! 此與(i).的 情形 相 異 。 因 此,此 部 分 每 一 個 被 引 領 的 cosine 項的 完 整 敘 述應 分 別 記 為下 列 兩 種 型式; 1) 1 ( k2
VaVxVbVycos(
Ax(k11) Ax1 Ax+
Ay(k21) Ay1 Ay)。
與
1
)
2(
k2
y b aV
V
V
2cos(
A
y(k21)
A
y1
A
y)。 若 x-1 , x-2 , … , x-(k
1-1)中 任一 個 出 現 負數 或 零 , 那麼 這 個 負 數或 零 必 須 加上 原 凸 多 邊 形 的 總 邊 數 使 其 為 正 。 同 樣 地 , y-1 , y-2 , … , y-(k
2-1) 情形 亦 是 如 此 。 例3: 平面 凸 九邊 形 由 邊 長係 數 為V
5V
6V
7V
2所 帶 領 的 一 個 完 整 cosine 項為 1)51 ( 2V
5V
6V
7V
2cos(A
6
A
8
A
9
A
1
A
2)
= 2V
5V
6V
7V
2cos(A
6
A
8
A
9
A
1
A
2)
例 4: 平面 凸 九邊 形 由 邊 長係 數 為V
4V
5V
7V
1所 帶 領 的 一 個 完 整 cosine 項為 1)41 (2
V4V5V7V1cos(
A5A
8
A
9
A
1)
=
2
V
4V
5V
7V
1cos(
A
5
A
8
A
9
A
1)
例5: 平面 凸 七邊 形 由 邊 長係 數 為V
22V
4V
6所 帶 領 的 一 個 完 整 cosine 項為
1
)
2(
2V
22V
4V
6cos
A
5
A
6
= 2V
22V
4V
6cos
A
5
A
6
例6: 平面 凸 七邊 形 由 邊 長係 數 為V
22V
4V
7所 帶 領 的 一 個 完 整 cosine 項為
1
)
3(
2V
22V
4V
7cos(
A
5
A
6
A
7)
=
2
V
22V
4V
7cos(
A
5
A
6
A
7)
(3) 承上 述[1].與[2].的 操 作守 則 可 得 等號 右 邊 毎 一個 多 邉 形 方程 式 的 總 項式 為 (n
2
)+2
)
3
)(
2
(
n
n
=2
)
2
)(
1
(
n
n
=C
2n1 項 。由 遵 循 上 述 的 2 個 綜 合 定 則即 可 用 來 完整 敘 述 並 清晰 的 排 列 出平 面 凸 多 邊形 內 臨 近 周 邊 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式 。
C. 展 示 平 面 凸 多 邊 形 內 臨 近 周 邊 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 方 程 式 與
驗證
C-1.平 面 凸 四 邊 形 [C-1.a] 展示 平 面 凸 四 邊形 內 兩 交 叉對 角 線 長 度乘 積 方 程 式: 圖 4a 請 看 上 圖 4a.並 參 照 B.的 2 個 綜 合 定 則, 先 列 出 兩組 相 對 邉 邉長 集 合 ; {V
1,V
3}與 {V
2,V
4},得 兩 項 相 對 邉 邉 長 乘 積;V
1V
3、V
2V
4,再 依 循 操 作 定 則 所 指 示 的 運 作 排 列, 得 這 平 面 凸 四 邊 形 內 兩 交 叉 對 角 線 長 度 乘 積 方 程 式 如 下 ;(
d
13d
24)
2
(
V
1V
3)
2
(
V
2V
4)
2
2
V
1V
2V
3V
4cos(
A
2
A
4)
(4) [C-1.b] 證明 平 面凸 四 邉 形 一般 化 方 程 式(4); 請 看 圖 4.範 例 的 作圖 解 說 與 證明 ; 圖4(1) 對 於 四 邊 形
A
1A
2A
3A
4, 在 頂 點A
4處 向 圖 形 內 側 作 一 射 線A
4T
, 使
A
1A
4T
= 3 4 2A
A
A
,又 在 頂 點A
1處 對 圖 形 內 側 作 另 一 射 線A
1T
,使
A
4A
1T
A
4A
2A
3, 此 兩 射 線 交 在 T 點 ; 則
A
1A
4T
A
2A
4A
3 ( 互 為 相 似 形 ) 且 2 3 4 1 4TA
A
A
A
A
。並 繼 續 連 接 T 與A
3兩 點,使 形 成 線 段TA
3 。A
1A
3
d
1 及A
2A
4
d
2。 (2) 由 兩 相 似 三 角 形 對 應 邊 長 必 成 正 比 例 關 係 , 得V
4:
d
2
A
1T
:
V
2
A
4T
:
V
3
可 得V
4:
A
4T
d
2:
V
3, 再 由
A
1A
4A
2=
TA
4A
3 及 兩 對 應 邉 長 成 正 比 例 與 其 夾 角 相 等 的 相 似 形 性 質,可 得 知 兩 相 似 形 關 係
A
1A
4A
2
TA
4A
3,因 此 可 得 2 1 4A
A
A
=
A
4TA
3, 且 有 另 ㄧ 組 正 比 例 關 係 為V
4:
A
4T
d
2:
V
3
V
1:
A
3T
。 (3) 對 作 圖 4.中 的
TA
1A
3言 , 由 餘 弦 定 理 知)
cos(
)
)(
(
2
)
(
)
(
2 1 3 1 3 3 2 1 2 1A
T
A
T
A
T
A
T
A
TA
d
,而 在 上 述(2).的兩 組 正 比 例 關 係 式 中 可 求 得A
1T
(
V
2V
4)
/
d
2 及A
3T
(
V
1V
3)
/
d
2, 將 此 兩 者 代 入 餘 弦 定 理 公 式 內 並 化 簡 、 整 理 , 可 得 下 列 新 方 程 式(4-a);d
12d
22
(
V
1V
3)
2
(
V
2V
4)
2
2
V
1V
2V
3V
4cos(
A
1TA
3)
(4-a) (4) 在 頂 點 T 處 四 周圍 角 度 關 係可 知
A
1TA
3 =2
A
4TA
3
A
1TA
4 =2
A
4A
1A
2
A
4A
3A
2=A
2(頂 角 )+A
4(頂 角 ) ,此 處 對 四 邊 形A
1A
2A
3A
4言, 其 四 個 頂 角 總 和 為2
,所 以 將
A
1TA
3=A
2+A
4 代 入 方 程 式(4-a),即得 證 出 平 面 凸 四 邊 形 兩 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式 為 下 方 程 式(4-b);(
)
(
)
22
1 2 3 4cos(
2 4)
4 2 2 3 1 2 2 2 1d
V
V
V
V
V
V
V
V
A
A
d
(4-b) 又 此 處 的 兩 對 角 線 長d
1=d
13及d
2=d
24,代 入 方 程 式(4-b),即 得下 方 程 式(4);d
132d
242
(
V
1V
3)
2
(
V
2V
4)
2
2
V
1V
2V
3V
4cos(
A
2
A
4)
(4) 平 面 凸 四 邊 形 的 方 程 式(4)等號 右 邊 共 有項 式C
241=C
23= 3 項。 證 明 完成 。C-2. 平 面 凸 五 邊 形 [C-2.a] 展示 平 面 凸 五 邊形 內 臨 近 周邊 兩 相 鄰 交叉 對 角 線 長度 乘 積 方 程式 : 請 看 下 圖 5.並 參 照 B.的 2 個 綜 合定 則,先 列 出 兩 組相 對 邉 邉 長集 合;{
V
1,V
3} 與 {V
2,V
4,V
5},得 3 項 相 對 邉 邉長 乘 積;V
1V
3、V
2V
4、V
2V
5,依 操 作 定 則 的 規 劃 排 列 , 得 這 平 面 凸 五 邊 形 內 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 方 程 式 如 下 ; 圖 5)
cos(
2
)
(
)
(
)
(
)
(
2 1 2 3 4 2 4 5 2 2 4 2 2 3 1 2 24 13d
V
V
V
V
V
V
V
V
V
V
A
A
d
2
V
5V
1V
2V
3cos(
A
1
A
3)
2
V
22V
4V
5cos
A
5 (5) 平 面 凸 五 邊 形 的 方 程 式(5)等號 右 邊 共 有項 式C
251=C
24= 6 項。 [C-2.b] 證明 : 略。 此 證 明 方法 與 下 方 C-5.之 平 面 凸八 邊 形 情 形完 全 相 同 。 C-3. 平 面 凸 六 邊 形 [C-3.a] 展 示 平 面凸 六 邊 形 內臨 近 周 邊 兩相 鄰 交 叉 對角 線 長 度 乘積 方 程 式:請 看 下 圖 6. 並 參 照 B.的 2 個 綜 合 定 則, 先 列 出 兩組 相 對 邉 邉長 集 合 ; {V
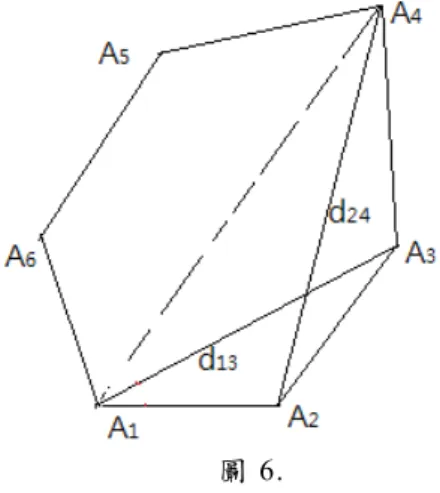
1,V
3}與 {V
2, 4V
,V
5,V
6},得 4 項 相對 邉 邉 長 乘積;V
1V
3、V
2V
4、V
2V
5、V
2V
6,依 操 作 的 規 則 , 得 六 邊 形 內 臨 近 周 邊 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 方 程 式 如 下 ;圖 6.
)
cos(
2
)
(
)
(
)
(
)
(
)
(
2 1 2 3 4 2 4 6 2 2 5 2 2 4 2 2 3 1 2 24 13d
V
V
V
V
V
V
V
V
V
V
V
V
A
A
d
2
V
1V
2V
3V
5cos(
A
2
A
4
A
5)
2
V
6V
1V
2V
3cos(
A
1
A
3)
2
V
22V
4V
5cos
A
5
2
V
22V
5V
6cos
A
6
2
V
22V
4V
6cos(
A
5
A
6)
(6) 平 面 凸 六 邊 形 的 方 程 式(6)等號 右 邊 共 有項 式C
261=C
25= 10 項。 [C-3.b] 證明 : 略。 此 證 明 方法 與 下 方 C-5.之 平 面 凸八 邊 形 情 形完 全 相 同 。 C-4. 平 面 凸 七 邊 形 [C-4.a] 展 示 平 面凸 七 邊 形 內臨 近 周 邊 兩相 鄰 交 叉 對角 線 長 度 乘積 方 程 式 : 請 看 下 圖 7.並 參 照 B.的 2 個 綜 合定 則,先 列 出 兩 組相 對 邉 邉 長集 合;{V
1,V
3} 與 {V
2,V
4,V
5,V
6,V
7},得 出 5 項 相 對邉 邉 長 乘 積;V
1V
3、V
2V
4、V
2V
5、 6 2V
V
、V
2V
7,再 依 操 作 的 完 整 理 念,列 出 七 邊 形 內 臨 近 周 邊 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 方 程 式 如 下 ; 圖 72 24 2 13
d
d
=( V
V
1 3)
2+( V
V
2 4)
2+( V
V
2 5)
2+( V
V
2 6)
2+( V
V
2 7)
2-2V
1V
2V
3V
4cos(
A
2
A
4)
-2