ON THE SPECTRAL THEORY OF WAVE-PROPAGATION IN A WEAKLY RANGE-DEPENDENT ENVIRONMENT

On the spectral theory of wave propagation in a weakly range-

dependent environment

Kuan-Kin Chan

Institute of Communication Engineering, National Chiao Tung University, Hsinchu, Taiwan, Republic of China

(Received 12 September 1985; accepted for publication 30 January 1986)

The spectral theory of wave propagation in a weakly range-dependent environment is deduced from the corresponding theory for a wedge-shaped structure. The solution obtained is compared to that derived previously, which suggests that some modifications are necessary in the previous formulation in order to bring the solution into a symmetric form.

PACS numbers: 43.30.Bp

INTRODUCTION

The adiabatic mode theory • has found wide applications

in the analysis of wave propagation in weakly range-depen- dent environments. Under the assumption of adiabatic ap- proximation, local modes propagate independently with negligible mutual coupling and preserve their identity to adapt themselves smoothly to the slowly changing environ- ments. It fails, however, to apply in a region containing fields of continuous spectrum. A notable example is the wave propagation in a shallow leaky wedge structure, where the trapped adiabatic modal fields may reach their respective cutoffs and begin to radiate across the wedge boundary. Jen-

sen and Kuperman 2 have computed the field numerically via

the parabolic equation method, which vividly displayed the picture of the coupling mechanism involved. Based on this observation, recent advances TM make use of the characteris- tic Green's function, representing the field as a spectral inte- gral, where the adiabatic approximation is extended to in- clude the continuous spectrum contribution by invoking the condition of invariance of local transverse resonance. The spectral integral formulation makes it feasible to treat the modal field constituents, whether discrete or continuous, from a unified point of view. It also substantially broadens the scope of the solution since various well-developed asymptotic techniques can be readily applied. It is most use- ful, in particular, in deriving a uniform representation of the fields in the transition region which is otherwise difficult to obtain. This aspect has been explored extensively in Ref. 3. However, the resultant solution in Ref. 3 is found to be for- mally unsatisfactory since it is not symmetric in form. In this paper we show how a symmetric form can be obtained based on the results in Ref. 4.

I. FORMULATION AND SOLUTION FOR A WEDGE REGION

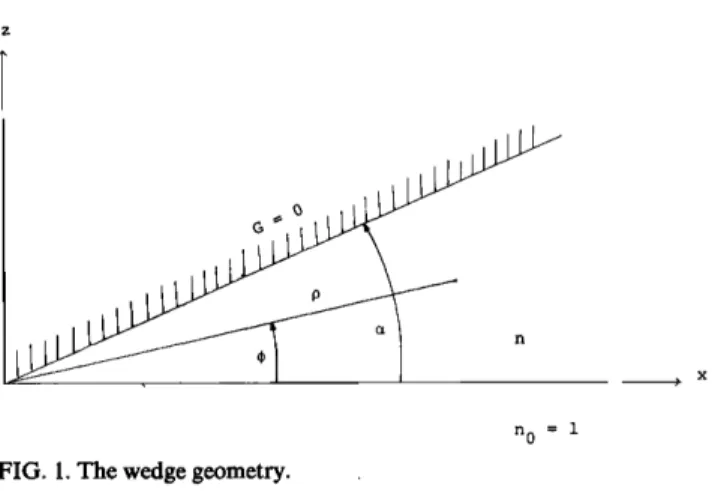
For clarity and completeness, the solution obtained in Ref. 4 is rederived in this section. The model we consider here is a wedge-shaped medium with refractive index n em- bedded in a semi-infinite half-space as shown in Fig. 1. The cylindrical coordinate system is adopted with the bottom interface taken as abscissas. We then seek a solution of the

reduced wave equation (a harmonic time dependence e-

is assumed and deleted throughout),

--fipp+pWa--w

+

) =

),

(la)

with a unit line source located at the position p = (p', •') and satisfying the boundary conditions,

G=O at•=a, •G

G and continuous at • = O, edge condition at p = 0,

radiation condition at p = oo,

where k is the wavenumber associated with the wedge region being considered. To confine our attention to a gradually changing environment, we assume that the wedge angle is small and concentrate our interest in a region sufficiently remote from the edge such that the local arc length (which is approximately the local depth in adiabatic mode theory) remains finite and varies slowly with range.

The problem is a nonseparable one. However, we pro- ceed as in the adiabatic mode theory. But instead of directly constructing the adiabatic eigenfunctions, the method of

characteristic Green's function -• is used. The characteristic

FIG. 1. The wedge geometry.

n0 = 1

1402 J. Acoust. Soc. Am. 79 (5), May 1986 0001-4966/86/051402-04500.80 @ 1986 Acoustical Society of America 1402

Green's function in the angular domain satisfies

+2x

=

sin

k x/A (a - • > )

ik

x[-•-(

a -- 4 < )

eik

•/2--(

a + 4 < )

1 + F(A;

p) e

where A is a spectral variable and F (A; p) is the reflection coefficient resulting from the local boundary condition where the assumption has been made to ignore the back- scattering angular wave under the wedge. A simple evalua- tion invoking boundary conditions yields

or

(4a)

[•pA•

i•(1) ,4]/

r(A;p)

= A

_ 1-• -•

[•pA•

A

+ 1-

i•f(1) A

7 -• . (4b)

The local completeness relation is then given by the spectral

integral

dX

X),

(5)

where the integration contour Cx encircles all the singulari-

ties

of the integrand

g• in the proper

spectral

plane

(Fig. 2).

The pole singularities Am are evaluated through the local

Im)•

... -- = ReX

m

FIG. 2. Contour of integration in the complex A plane.

resonance equation in the denominator in Eq. (3)

1 + F(Am;p)e2inf•-mCt=O

(6)

or, alternatively, by making use of Eq. (4b)

s.

(p) x/(

1

-- 1/n

2)

-- ,•m/D

2 '

sa (p) = ap = arc length

at p extended

by the wedge.

(7) The correct adiabatic modes can be derived from the residue contribution at the poles. In addition, there exists a branch

point singularity at

At, =p2(1- l/n2) ,

(8)

which is responsible for the field radiated across the bottom interface and which does not appear in the adiabatic mode theory. It is, however, inherent in the present approach. The local resonance in Eq. (6) is extended to a spectral variable while maintaining the range dependence through the invar-

iance relation,

1 + F(A;]9)e

2ik'/-i-a

= 1 + F(A ';]9')e

2ik'fi-'a

,

(9)

which

is required

to construct

a solution

that is consistent

with the adiabatic mode theory.

Substitution

of A (p) into the radial equation

leads

to

p-•p

+ k2p-• gp

= -6(p- ). (10)

To solve Eq. (10) let

gp = ]9

-- 1/2fp

ß

One finds

[d

•-•+ k 2 1 '0

2 (A(p) 1 )Ifs,

2 •-

4k2p

2

1/26(

]9 --]9') .

( 11

)

Equation (11 ) can be solved asymptotically by WKB ap- proximation to obtain

g•,,•exp(ik

f••

>

dp•l

A(p) 1

,0

2 •' 4k

2]92

X[_2ik(]9,)1/2191/2(

1 •(]9) 1 )1/4

]92 •' 4k

2]92

( ]9,)2

nt-

4k

2(

]9,)2' '

(12)

where we have ignored the backscattering wave field from the edge, due to the fact that this field will be strongly atten- uated in a leaky wedge structure before reflecting back to the region concerned.

Recall that the exact solution for the Green's function in

a separable

problem

is given

by

5

1403 J. Acoust. Soc. Am., Vol. 79, No. 5, May 1986 Kuan-Kin Chan: Spectral theory in a range-dependent medium 1403

G( p, p') =

_{•-•i c,}

k2

f

_g•'

_(p'

_p';

_A

_{) g+}

_{( q•'}

_q•';

_A

_{) dA}

_.

A simple substitution of Eqs. (3) and (12) would not be justified due to the fact that the solution thus obtained would violate the principle of reciprocity. To remedy this, we re- write Eq. (3) as

sin kx•l (o• -- •bl)

e

i•4-•(a-4:)

d- r'(A2;

p2)e

ik4-•(a

+•)

x , (14)

1 + F(2; p)e

2i•'4T"

where • = •) , •2 = • ( are either the source point or the

observation point while 2•, 2 2 are associated with •, •2, respectively.

Substituting Eqs. (12) and (14) into ( 13 ), we obtain

G( p, p') =

k2f 4c9Lic9A

sinkx/•l(a_41

) ½ik4-•(a--42)_•

F(,•2;P2

)

•-•' c•

t3L/•A

t

k(AA

t) 1/4

1 -3-

r'(A;

p) e

2ik4Ta

(

( p,,)2

4k2( p,,)2

X[__2ikp•/2(p,)•/2(l__/].(p'

•)

(p,)2

+ 4k

2(p,)2 1 p2 •-

1 )1/4(

,•(p) 1)1/4]-1

4k

2p2

Here A is a spectral integration variable whereas A' and A" are related to A through the invariance relation,

L(A;

p) = F(A;

p)e

2i•'4T"

= F(A '; p')e

2i•'•4-•"

= F(A ";p")e

2i•42'"

.

(16)

A scalar factor [ (c•L/c•A ) / (c•L/c•A' ) ] • / 2 has been inserted

in order to preserve the symmetry of the solution. II. TRANSFORMATION INTO LOCAL MODE DESCRIPTION

Although we have adopted a cylindrical coordinate sys- tem for our discussion, all of the relations obtained can be easily cast into forms suitable for a local stratification under the assumption of weak range dependence. Specifically, we first transform all of the angular variables into linear ones via

•=/•/p2,

s(p) =pqb,

s,(p) =pa.

(17)

Next we make use of the following approximations under the assumption of weak range dependence:

p-•x, s(p).•z,

s• (p)-•H(x), the local channel depth. As a result we have for the reflection coefficient

F(A; p)--•F(.e) =

= exp[ - 2i tan-

-

];

•'•, = 1- 1/n 2. (18a) the local resonance equation

, )e

2"' •dxZ•.

1 + F(Am'p

--•l

+

exp

[i(2kx/•,•

H(x)

--

2

tan-]'

•/•b

--

•m

) ]

=0; (18b)

I

the Green's functions

1

exp

[ik ϥ

dxx/1

- •(x) ]

•

-- 2ik [ 1 - •e(x)

]1/4[

1 -- •e(x')

]1/4'

sin k xf• [H(x• ) -- z• ]

g•'-• k(xx')

•/2(•e•e

') •/4

eik

•[H(x2)

-- z2]

_[_

[• (•2)eik

4•[H(x:)

x ;

1 + F (•)e 2ik•-H(x)

and the range-invariant relation

L (A;

p )-•I• (•)e 2ik

4•-H(x)

= I• (• ' )e

2ik

q•'H(x')

(18d)

, (18e)

where the higher-order terms have been neglected in Eq. (18c). Futhermore,

dA

•i

/ c•L

Ic•A

= d(•eP2)

•/ (

(OL

c•L

!0•')

Ic•

) (

(d•

d•

'/d2

/dA

)

')

_d•

(

xx,

)

4 c•L

/c•

Equation (15) reduces, via substitution of Eqs. (18c),

(18d), and (18f) to

k2f40L/O

,

G(

p,

p')

• - •-•. % c3L/c3•

sin k x/• [H(x•) -- z•]

k(•-•-

') TM

eik,•221I-I(x•)

--z21

+ F(•2)eik•[H(x•)

+ z•]

1 + F(•)e 2•ffn(•)

- 2ik [ 1 - •(x) ]]/4[ 1 - •(x') ],/4,

1404 J. Acoust. Soc. Am., Vol. 79, No. 5, May 1986 Kuan-Kin Chan: Spectral theory in a range-dependent medium 1404

which

is the

desired

solution

pertinent

to wave

propagation

in a region with slowly varying boundary interfaces. III. DISCUSSION AND CONCLUSION

Equation (19) is essentially the same as that given in Ref. 3. It is not surprising to see this coincidence, since both

derivations follow the same line of philosophy by assuming

that the invariance of transverse resonance remains valid throughout the entire spectrum as an extension of the adia-

batic mode theory. One notices, however, difference exits

between them regarding the definitions of the depth coordi- nates z> and z <. Literally the z> and z < are defined respec-

tively as the greater and lesser values of the source and obser-

vation depth locations. While these are meaningful in a range-independent situation, ambiquity may arise for the two depths located in different ranges when the channel

depth is a function of the range. Such is the case when one considers the situation as shown in Fig. 3, which shows if the source is specified in a location Q, the depth of an arbitrary observation point P in the shaded region will always appear

to be z>, no matter how one looks from the side of the lower

boundary (with the depth axis upward) or from the side of the upper boundary (with the depth axis downward). In other words, the solution obtained in Ref. 3 is coordinate dependent, i.e., it will depend upon whether the upper or the lower boundary is chosen as the range coordinate axis. A modification is therefore necessary in order to bring the sym- metry into the solution. On the other hand, our present study

shows that the z> and z < are determined via a transforma- tion from their relative orientations •b > and •b < in the angu-

lar domain. They are defined uniquely in a scaled sense such

that the z> and z< represent the depth values with the

greater and the lesser values of the scaled depths z/H(x ) and z'/H( x' ) , respectively.

FIG. 3. The ambiguity region for z>.

To conclude our discussion, the spectral theory for a

weakly range-dependent environment 3 while correctly re-

taining the symmetry of the solution in range, has ignored the symmetric relation in depth and is therefore formally unsatisfactory. This can be readily remedied, as we discussed in this paper, by proper interpretation of the location param-

eters.

•A. D. Pierce, "Extension of the Method of Normal Modes to Sound Prop- agation in an Almost-Stratified Medium," J. Acoust. Soc. Am. 37, 19-27 (1965).

2F. B. Jensen and W. A. Kuperman, "Sound Propagation in a Wedge-

Shaped Ocean with a Penetrable Bottom," J. Acoust. Soc. Am. 67, 564- 1566 (1980).

3K. Kamel and L. B. Felsen, "Spectral Theory of Sound Propagation in an

Ocean Channel with Weakly Sloping Bottom," J. Acoust. Soc. Am. 73, 1120-1130 (1983).

4K. K. Chan, "Radiation of a Line Source in a Leaky Wedge Structure," J.

Chin. Inst. Eng. 7, 147-150 (1984).

5L. B. Felsen and N. Marcuritz, Radiation and Scattering of Waves (Pren-

tice-Hall, Englewood Cliffs, NJ, 1973), pp. 273-288.

1405 J. Acoust. Soc. Am., Vol. 79, No. 5, May 1986 Kuan-Kin Chan: Spectral theory in a range-dependent medium 1405