On-line algorithms for the dominating set problem

(1)

Inform?tion

prc+c=&w

Information Processing Letters 61 (1997) 11-14

On-line algorithms for the dominating set problem

’

Gow-Hsing King, Wen-Guey Tzeng *

Department of Computer and Information Science, National Chiao Tung University, Hsinchu 30050, Taiwan Received 10 July 1996; revised 3 October 1996

Communicated by D. Gries

Keywords: Algorithms; On-line algorithms; Dominating set

1. Introduction

LetG=(VE) withV={1,2,...,n}beanundi-

rected graph. A dominating set of G is a subset V’ 2 V such that for each vertex u E V - V’ there is a ver- tex u E V’ so that (u, U) E E. The minimum dom- inating set problem is to find a set V’ of the mini- mum cardinality, which is known to be NP-complete

[3]. In this paper we consider the on-line version of the problem in two settings. The first setting is that all vertices 1,2,. . . , n in the graph are given in advance. At time interval i the adjacency condition of vertex i to the other vertices is presented. We propose an on-line algorithm of performance ratio l.SJii + cl and show that fi - c2 is a lower bound for the performance ratio that an on-line dominating set algorithm can possible achieve, where ct and c2 are some positive constants. The second setting is that at time interval i the adjacency condition of vertex i to vertices j, j < i, is given. For this setting we show that performance ratio II - 1 is the tight bound.

* Corresponding author. Email: tzeng@cis.nctu.edu.tw.

I This research was supported in part by the National Science Council, Taiwan, R.O.C., under grant NSC 86-2213-E-009-024.

2. The first on-line setting

Suppose all vertices of the graph G are given in advance. At time i the adjacency condition of a vertex i (say) to the other vertices is given. Therefore, without loss of generality, vertices are given in se- quence 1,2,..., n. We present our on-line dominating set algorithm JUMP. Let Di be the set of ver- tices selected by JUMP at time i, where DO = 8. By the nature of the on-line algorithm, Di C Di+l and D = D, is the dominating set returned by JUMP. Let (i,it),(i,iz) ,..., ( i, id, ) be the adjacent edges of vertex i given at time i, where di is the degree of ver- tex i and 1 < il < i2 < . . . < id, 6 n. After time i, vertex u E V is marked as “dominated” if u E Di or there is a vertex ZJ E Di such that (u, U) E E. A vertex that is not “dominated” is an “undominated” vertex. Also, the vertices j, j < i, that are presented before are called “visited”. There are four cases in the following by which the vertex i is put into Di at time i. A vertex in D is classified into one of the three types: j-vertex, r-vertex, and f-vertex. Note that the current vertex is checked from case 1 to case 4 one by one, so a vertex cannot be of two types. We also define a function f on some vertices for later analy- sis.

(2)

G.-H. King, W-G. Tzeng/lnfortnation Processing Letters 61 (1997) 11-14 12 (1) (2) (3) (4)

There are > [m “undominated” vertices among

il,i2,. . . , id,. For this case vertex i is called a j- vertex in

D.

Vertex i dominates all the remaining “undomi- nated” vertices. For this case vertex i is called an r-vertex.

All vertices i,, 1 < s < di are less than i and not in

Di-1,

that is, vertex i’s adjacent vertices are visited and not selected by JUMP such that vertex i is selected to dominate itself. For this case vertex i is called an f-vertex and we define f(i) =i.

There is a vertex j such that j < i, i = jd,, and all vertices j, jl , j2, . . . , jd,__l are not in

Di_1,

that is, vertex i is the last vertex that can dominate vertex j. For each such vertex j, we say that vertex j forces vertex i to be in

D.

For this case also vertex i is called an f-vertex, and we define f(j) = 1.

Correctness. For each vertex i, 1 < i < n, if it is put in Di then it is dominated by itself. If it is not put in

Di then it is dominated either by a vertex u E

Di_1

or by one of its neighbors iP that is not visited yet, that is, i, > i. Therefore, the final

D =

D,

is a dominating set for the graph G.

Performance ratio. We now show that the performance ratio of JUMP is lSfi+q for some constant cl. Let C be a minimum dominating set for G. Lemma 1. There are at most [fi] j-vertices in D.

Proof. Since each j-uertex u in D dominates at least [&’ “undominated” vertices at time u. Once a vertex is marked as “dominated”, it will no longer con- tribute as an “undominated” vertex in case one. There- fore, there are at most In/ [fl] = Lfi] j-vertices in D. 0

Lemma 2. There is at most one r-vertex in D.

Proof. If vertex u is an r-vertex in D then all vertices of G are dominated after time u. No more vertices can be put into D thereafter. 0

Lemma 3.

If

the minimum dominating set C consists of only one vertex then D contains no

f-vertices.

Proof. Let C = {c}. Vertex c is adjacent to all the other vertices. Therefore no f-vertices are put into D before time c. If vertex c is selected as a j-vertex in case one then all vertices are dominated by vertex c. No more vertices can be put into D. Otherwise, vertex c, or some other vertex c’ that dominates all vertices, must be selected as an r-vertex. So, no f-vertices can be put into D. q

We define opt as a mapping of a vertex into one of its dominating vertices in C:

{ i

opt(i) = ifiE C,

min{j 1 j E C, (i, j) E E} if i $ C. We now compare the sets D and C. We define a charge scheme, which distributes weights WI of ver- tices in D to weights w2 of vertices in C. Initially, WI(U) = 1 if and only if u E D and w2( u) = 0 if and only if u E C. Then the performance ratio of JUMP is max{wz(u) 1 u E C} after the weight distribution. The charge scheme is as follows:

For each vertex u E C fl D, the weight of u is charged to itself. That is, w2( U) is increased by WI(U).

For each f-vertex u E D - C, the weight of vertex u is evenly charged to each vertex opt(u), where f(u) = U. That is, w2(opt(u>> is increased by wl(u)/m, where m = I{u 1 f(u) = u}I.

For each j- or r-vertex u E D - C, the weight of vertex u is evenly charged to each vertex u E C. That is, WZ(U) is increased by wl(u)/lCI.

Lemma 4. For each u E C fl D, w2 (u) is not charged by any other f-vertex in D.

Proof. For an f-vertex u E D and u # u charg- ing to w2( u), vertex u must be in D - C. We con- sider only case four by which vertex u is put into D as an f-vertex. There must be a vertex u’ with opt(u’) = u and vertex u’ forces vertex u to be in D, that is, f (u’) = U. However, if vertex u’ forces ver- tex u to be in D, all its adjacent vertices must be vis- ited and not in D,. Therefore vertex u, which is ad- jacent to vertex u’, is not in D, which is a contradic- tion. 0

(3)

G.-H. King, W-G. Tzeng/lnformation Processing Letters 61 (1997) 11-14

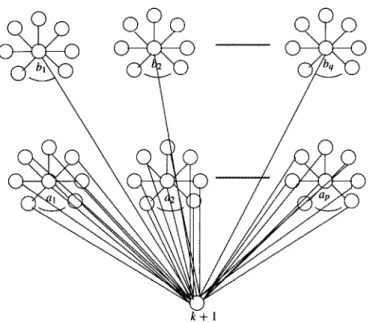
Fig. 1. The structure against on-line dominating set algorithms.

Lemma 5. For each vertex u E C - D, w2( v) is charged by at most [$ij - 1 f-vertices.

Proof. Since vertex v $ D, we let I,, = {U 1 (u, v) E E, vertex u is “undominated” after time v - 1). For an f-vertex u, f(v’) = u and opt(v’) = v, to be charged to w2( v), vertex v’ must be in I,, and f-vertex u is in D - C. Since vertex v is not put into D at time v, it has at most [fl - 1 adjacent “undominated” vertices after time v - 1, that is, IZ,,( < rfl - 1. Therefore, wz(v) is charged at most [fil - 1 times by f-vertices. 0

Lemma 6. If ICI = 1 then the performance ratio of JUMP is at most [Ji;] + 1.

Proof. By Lemma 3 the set D contains no f-vertices if ICI = 1. By Lemmas 1 and 2, IDI < [fi] + 1. The weight We is at most L&i] + 1, where C = {c}. Therefore, the performance ratio of J UMP is at most

LJirJ + 1 if ICI = 1. •i

Lemma 7. The perfomuznce ratio of J U MP is at most 1.5&i + cl for some constant cl.

Proof. By the above lemma we consider only the case that (Cl > 2. Since D consists of at most Ifi] j-

vertices and one r-vertex, for each vertex v E C, w2 (v) is charged at most ( [J;IJ + 1) /2 by j- and r- vertices. Furthermore, by Lemmas 4 and 5, for each vertex v E C, We is charged at most, for n > 2, r&-t1 - 1+ (L&q + 1)/2,

which is 1 Sfi + ct for some constant cl. 0 Lower bound. We now use a strong adversary to prove that fi - c:! is a deterministic lower bound for the performance ratio of the on-line dominating set problem for general graphs in this setting, where c2 is a constant.

Theorem 8. fi - c2 is a lower bound for the per- formance ratio of the on-line dominating set problem for general graphs in this setting.

Proof. Let D be the dominating set selected by an on-line dominating set algorithm. For simplicity, we assume that k = m is an integer. Let S; = (y’,Ei), where I$’ = {i,k + l,i(k - 1) + 3,i(k - 1) +4,... ,i(k-l)+k+l}andE,‘={(i,v) IUE v’ - {i}} for 1 < i < k.

From time intervals 1 to k, vertices 1,2,. . . , k are presented such that vertices al, a2, . . . , up are included in D and vertices 61, b2,. . . , b, are not

(4)

14 G.-H. King, W-G. TzengIlnformation Processing Letters 61 (1997) II-14 included in D by the on-line algorithm, where

{UI,LZZ ,..., a,,bl,bz ,..., b4} = {I,2 ,..., k} and p + q = k. At time interval k + 1, vertex k + I is pre- sented with adjacency to vertices 1 to k and to vertices in V,l,UV&lJ. ~4JV~P-{k+l}.Aftertimek+l,allver-

tices in (Vi, U V& U. 4JV;)-{k+l,b,,bz ,..., bq} are forced to be included i; D with a structure shown inFig.l.ThereforeD={a~,a;!,...,a,,k+l}U{u~

u~(V~,UV&U+..UV~~)-{bl,b2,...,b~}}.Since

p . k + q. k + 1 = n and the minimum dominating set is {bl, b2,. . . , b,, k + l}, the lower bound for the performance ratio is q.(k-l)+p+l 1+q k.(l+q)-2q+l = *+q

3. The second on-line setting

In this setting, at time interval i, the adjacency con- dition of vertex i to the vertices j, 1 < j < i is given. We show that n - 1 is the tight bound for this on-line setting.

First, we present an on-line algorithm for this setting for completeness although it is straightforward. At time i, the algorithm puts vertex i into D if vertex i is not dominated by other vertices j, 1 6 j < i. It is easy to check that the performance ratio of the algorithm is n - 1, in particular, for graphs with a single dominating vertex. We now show that the lower bound isn- 1.

Theorem 9. n - 1 is a deterministic lower boundfor the performance ratio of the on-line dominating set problem in this setting.

Proof. An adaptive adversary is given as follows. Let A be an on-line algorithm. The adversary keeps pro- viding a vertex that is connected to all previous ver- tices till it is not put into D. Let us say that this vertex is k. Then the remaining vertices j, k+ 1 < j < n, are provided as being connected to vertex k only. Algo- rithm A has to choose the remained vertices so that D is{l,2,..., k-l,k+l,k+2 ,..., n}.However, the

minimum dominating set for this graph is {k}. There- fore, n - 1 is a deterministic lower bound. 0

From the above proof, we can see even if the given graph is known to be connected (or permutation, or interval) in advance, the lower bound remains the same. Corollary 10. The deterministic lower boundfor the pelformunce ratio of the on-line dominating set prob-

lem for connected (even for permutation or interval) graphs in this setting is n - 1.

Corollary 11. n - 1 is the tight boundfor the per- formance ratio of the on-line dominating set problem

(even for connected, permutation, or interval graphs) in this setting.

References

[I] M.J. Atallah, G.K. Manacher and J. Urrutia, Finding a minimum independent dominating set in a permutation graph, Discrete Appl. Math. 21 (1988) 177-183.

[2] A. Bar-Noy, R. Motwani and J. Naor, The greedy algorithm is optimal for on-line edge coloring, Inform. Process. fen. 44 (1992) 251-253.

[ 31 M.R. Garey and D.S. Johnson, Computers and Inmzcrabiliry: A Guide to the Theory of NP-completeness (Freeman, San Francisco, CA, 1979).

[4] M.C. Golumbic, AIgorirhmic Graph Theory and Perfect Graphs (Academic Press, New York, 1980).

[5] R.M. Karp, U.V. Vazirani and V.V. Vazirani, An optimal algorithm for on-line bipartite matching, in: Proc. 22ndACM Symp. on Theory of Computing (1990) 352-358. [6] MS. Manasse, L.A. McGeoch and D.D. Sleator, Competitive

algorithms for server problems, J. Algorithms 11 ( 1990) 208-230.

[ 71 A. Srinivasan and C.P. Rangan, Efficient algorithms for the minimum weighted dominating clique problem on permutation graphs, Theoret. Comput. Sci. 91 ( 1991) 1-2 I.