Necessary and sufficient conditions for rearrangeable Log(d) (N, m, p)

(1)

2020 IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 53, NO. 12, DECEMBER 2005

Necessary and Sufficient Conditions for Rearrangeable Log

_d

(N; m; p)

Frank K. Hwang and Wen-Dar Lin

Abstract—We extend previous results on sufficient conditions for

rearrangeable Log2( ) networks to Log ( )

net-works. We show that the original argument using path-intersecting graphs cannot be extended to 2, and we give a new argument. Further, we show our sufficient conditions are also necessary.

Index Terms—Banyan networks, Log( ) networks, rear-rangeable networks.

I. INTRODUCTION

L

EA [2] first proposed the Log (or a multi-Log ) network, which is obtained by vertically stacking up copies of a binary inverse banyan network with inputs and outputs (or a Log network) and identifying their inputs and outputs. One way of doing it is to create a new stage of inputs and a new stage of outputs, and to connect input (output) of the new stage to input (output) of each copy of the Log network (see Fig. 1).

Shyy and Lea [5] extended Log to Log

by replacing the inverse banyan-type network with an extra-stage inverse banyan-type network. Set . They used the extra-stage inverse banyan network , which has stages, with the extra stages constituting a mirror image of the first stages (see Fig. 2). Log can also be ex-tended to Log by replacing inverse banyan networks with -ary inverse banyan networks (i.e., ).

Sufficient conditions for such networks to be either rear-rangeable or strictly nonblocking have been well studied. On the strictly nonblocking side, Lea [2] gave sufficient conditions for Log , Shyy and Lea [5] extended to Log , and Hwang [1] to Log . On the rearrangeable side, Lea [2] gave sufficient conditions for Log , and Lea and Shyy [3] extended it to Log . However, an exten-sion to the -ary verexten-sion has been missing, since the argument used in the binary case cannot be extended to .

It is rare that these sufficient conditions were proven to be also necessary. Lea [2] gave necessary conditions for the rearrange-able Log and Shyy and Lea [5] claimed the necessary conditions for the strictly nonblocking Log to be ob-vious. In this letter, we give a new argument to obtain a suffi-cient condition for the rearrangeable Log , and also

Paper approved by T. T. Lee, the Editor for Switching Systems and Network Performance of the IEEE Communications Society. Manuscript received July 11, 2003; revised January 18, 2005. This work was supported in part by the Republic of China National Science Council under Grant NSC-91-2115-M-009-010 and in part by the Lee and MTI Center for Networking Research at National Chiao Tung University, Hsinchu, Taiwan, R.O.C.

F. K. Hwang is with the Department of Applied Mathematics, Na-tional Chiao Tung University, Hsinchu 30050, Taiwan, R.O.C. (e-mail: fhwang@math.nctu.edu.tw).

W.-D. Lin is with the Institute of Information Science, Academia Sinica, NanKang 115, Taipei, Taiwan, R.O.C. (e-mail: wdlin@iis.sinica.edu.tw).

Digital Object Identifier 10.1109/TCOMM.2005.860073

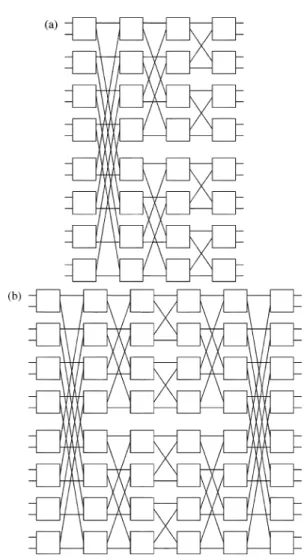
Fig. 1. Log (8; 0; 2) network.

(2)

IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 53, NO. 12, DECEMBER 2005 2021

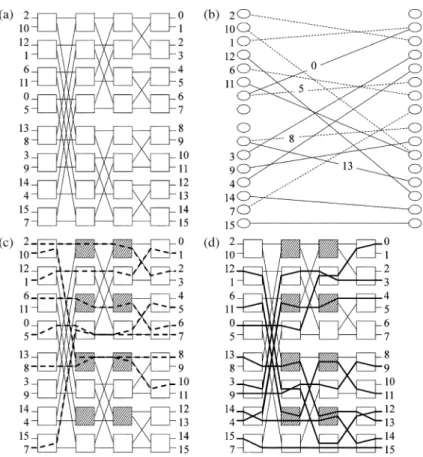
Fig. 3. (a) By mapping all copies ofBY (4; 0) to a single copy, we also map all requests of Log (16; 0; 4) to this copy. The first column indicates the destinations of the inputs. (b) By treating stage-1 (stage-4) outputs (inputs) as nodes, requests as edges, the resulting bipartite graph is two-edge-colorable. Edges (requests) are partitioned into two parts (dash lines and regular lines) according to the colors. (c), (d) The corresponding paths inBY (4; 0) of the two parts.

prove it to be necessary, thus covering the necessary and suf-ficient conditions for the two special cases Log and

Log .

II. MAINRESULTS

We first give a general sketch of Lea’s proof for the rearrange-able Log to see why it can not be extended to the version.

Since is a unique-path network, i.e., there is ex-actly one path for a given request, the given set of requests completely determines the set of paths for all requests. Let link-stage denote the set of links from stage to stage . Construct a path-intersection graph by taking the paths in as vertices, and inserting an edge if the two corresponding paths intersect at either link-stage 1 or link-stage . Then has maximum degree two, since a crossbar allows at most one path to intersect a given path at a given link-stage. Further, each vertex of degree two has one intersection at link-stage 1 and the other at link-stage . Thus, is two-(vertex-)col-orable.

Note that is reduced to copies of if link-stages 1 and are stripped off. For each , we can construct a path-inter-section graph by looking at the intersections at link-stages 2 and . is two-colorable by an analogous reason as . Similarly, we can define and two-color . Note that for even , looks at intersections at the single link-stage , and is also two-colorable. Therefore, all paths

can be colored into colors, such that paths in the same color do not intersect each other.

By routing requests of the same color through one copy of , copies suffice to route all requests. In the -ary version, , we can still construct . But the maximum degree in a is , and equality assumes only when . Therefore, a similar argument would not yield the result that copies suffice.

We now give a different argument to prove.

Theorem 1: Log is rearrangeable if and only if .

Proof: Sufficiency. Theorem 1 is obviously true for

(the network is just a crossbar) and (has a single link-stage where a link can be claimed by at most requests). We prove the general case by induction.

Our strategy is to reduce a Log to sev-eral Log (with as floor notation). For convenience, we map all copies of (of Log , with as floor notation) to a single . In this , two requests (i.e., two paths, since is a unique-path network) intersecting in some links means they must go through different copies of (of Log ). Note that each stage-2 input (stage- output) is involved in at most requests, because only stage-1 inputs (stage- outputs) could generate requests going through it.

Construct a bipartite graph by treating stage-1 outputs and stage- inputs as the two parts, and add an edge if there is a request going through both and . This bipartite graph is

(3)

2022 IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 53, NO. 12, DECEMBER 2005

Fig. 4. (a) We present the routing of dash-line requests [Fig. 3(c)] in the two copies ofBY (4; 0) in Log (16; 0; 4) (two other copies omitted). The four copies ofBY (2; 0) in a BY (4; 0) are drawn in different settings. (b) Each BY (2; 0) and their related requests form Log (4; 0; 2) with a subset of original requests.

-edge-colorable since its degree is bounded by . Partition the requests into parts according to the colors. Assign

copies of (of Log , with as floor notation) to route the requests of each color. Since the requests do not intersect in link-stage 1 and link-stage , we could replace the first and last stages of crossbars by their assigned routes (i.e., the unique paths on the crossbars). The resulting network is a composition of several Log , each with a subset of original requests (see Fig. 4 for an ex-ample). By induction, each Log ) is rear-rangeable for their requests; hence, all requests can be routed by

Log .

Necessity. Fix a link-stage (with as floor notation) link in . Let denote the set of inputs (out-puts) of which can access . It is easy to verify

that and . Since is

a unique-path network, a path starting from to must go through . By assigning requests from to , we con-clude that these requests are routable only if they can be spread to at least copies of . Q.E.D. For easier understanding, we illustrate the concept of

The-orem 1 in Figs. 3 and 4 by using Log as an example. The edge-coloring technique is also used differently in other kinds of rearrangeable networks (see [4] for examples), but we found that it is rare to treat links but not crossbars as vertices.

Theorem 2: Log is rearrangeable (RNB) if and

only if .

Proof: Sufficiency. Theorem 2 holds for (Theorem

1). We prove the general case by induction.

We map all copies of (of Log ) to a single , called , and remove its first and last stages. Then the network is reduced to copies of

, where each stage-1 and stage- crossbar has a link

to each .

Consider and construct a bipartite graph by taking the stage-1 crossbars and the stage- crossbars as the two parts of vertices, and a request from vertex to vertex as an edge. Then the maximum degree of is bounded by , and can be -edge-colored. Associate a color with each of the copies of mentioned in the last paragraph, and route the request through these according to their colors. For a of a given color, by induction, its requests can be routed if there are

copies of it. Since copies of implies copies of for each color,

copies of suffice to route all requests in .

Necessity. By removing the first stages and the last stages of , the network is reduced to copies of

, denoted by for , whose inputs and outputs will be referred as subinputs and suboutputs. Fix a link of the link-stage in a . Let be the link corresponding to in . Let and (in ) assume the roles of and in the necessity proof of

The-orem 1. Then and . Define

. Let for .

It is easily verified that has access to the same set of inputs for all from 1 to . Since an input has access to subinputs, while already has subinputs, it cannot have access to any other subinputs. This holds for all from 1 to . Similarly, we define and subsets of outputs as the counterpart of .

Suppose all inputs in generate requests to . Then there are requests going through (to ), . By Theorem 1, each request goes

(4)

IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 53, NO. 12, DECEMBER 2005 2023

through for some . Since there are , there exists an with at least requests going through it. Thus, at least copies of are

needed. Q.E.D.

REFERENCES

[1] F. K. Hwang, “Choosing the best Log (N; m; p) strictly nonblocking networks,” IEEE Trans. Commun., vol. 46, no. 12, pp. 454–455, Dec. 1998.

[2] C. T. Lea, “Multi-log N networks and their applications in high-speed electric and photonic switching systems,” IEEE Trans. Commun., vol. 38, no. 10, pp. 1740–1749, Oct. 1991.

[3] C. T. Lea and D. J. Shyy, “Tradeoff of horizontal decompostion versus vertical stacking in rearrangeable nonblocking networks,” IEEE Trans.

Commun., vol. 39, no. 6, pp. 899–904, Jun. 1991.

[4] R. Melen and J. S. Turner, “Nonblocking networks for fast packet switching,” in Proc. 8th Annu. Joint Conf. IEEE Comput. Commun.

Soc.: Technol: Emerging or Converging?, vol. 2, 1989, pp. 548–557.

[5] D. J. Shyy and C.-T. Lea, “Log (N; m; p) strictly nonblocking net-works,” IEEE Trans. Commun., vol. 39, no. 10, pp. 1502–1510, Oct. 1991.