ON THE AVERAGE LENGTH OF DELAUNAY TRIANGULATIONS

BIT24 (1984),269-273

ON THE AVERAGE LENGTH OF

DELAUNAY TRIANGULATIONS

R. C. CHANG and R. C. T. LEE Institute of Computer Engineering,

National Chiao Tung University, Hsinchu, Taiwan, 300

Republic of China

Department of Electrical Engineering, National Tsing Hua University, Hsinchu, Taiwan, 300

Republic of China

Abstract.

We shall show that on the average, the total length of a Delaunay triangulation is of the same order as that of a minimum triangulation, under the assumption that our points are drawn from a homogeneous planar Poisson point distribution.

1. Introduction.

Let P be a set of points in the plane. A triangulation of P is a maximal subset of all straight-line segments whose endpoints are in P, that intersect only at their endpoints. A minimum triangulation of P is the triangulation, whose straight-line segment length is minimum among all possible triangulations of P. The Delaunay triangulation is a particular triangulation such that the circumcircle of any triangle in this triangulation contains no point of P in its interior (Delaunay [3], Lee and Schachter [7]). It is also defined as the straight- line dual of the Voronoi diagram for P (Voronoi [16], Shamos [14]). Shamos and Hoey [15] claimed that the Delaunay triangulation was a minimum triangulation. Lawson [6] and Lloyd [9] showed that this is not true by constructing a counterexample.

Denote by DT(P) and MT(P) the Delaunay triangulation and minimum triangulation, respectively. Manacher and Zorbrist [10] showed that Delaunay triangulation does not even approximate minimum triangulation in the worst case. Assuming that P contains n points, Manacher and Zorbrist showed

Q = IDT(P)/MT(P)I >= O(n/log n).

Kirkpatrick [5] showed that in the worst case there exist arbitrarily large point sets P such that the Delaunay triangulation is asymptotically as bad as arbitrary triangulation in approximating minimum triangulation. Kirkpatrick also showed that in the worst case Q >- O(n).

R. C. CHANG AND R. C. T. LEE

But on the average, the Delaunay triangulation is not so bad. Lingas [8] proved Q ~ O(log n) almost certainly if the point set P is uniformly distributed in a unit square.

In the present paper, we shall strengthen Lingas' result by showing that on the average Q = O(1) if the point set P is uniformly distributed in a unit square. In Section 2, we shall introduce the definition of Delaunay triangulations. Section 3 will be devoted to a discussion of the concept of homogeneous planar Poisson point distribution, which can be used to help us find the main result.

Our main result is presented in Section 4. Essentially, our analysis shows that the average total length of a Delaunay triangulation is of the same order as that of a minimum triangulation, under a very reasonable condition. This means that Delaunay triangulations are quite good in the average sense.

2. The definition of Delaunay triangulation.

Given n points {Pl, P2,P3 . . .

Pn}

in the plane, the Voronoi diagram can be defined as follows. Let

H(pi, p~)

be the half plane containing pi and all points closer to p~ than to pj. The region

V(pi) = (-]i~ H(Pi, Pj)

which is the locus of all points closer to the point p~ than any other points is called the Voronoi polygon of Pi. The union of all Voronoi polygons of p[s, 1 < i < n, is called the Voronoi diagram of Pl, P2 ... P,.

The straight-line dual of a Voronoi diagram is a planar graph called Delaunay triangulation. There is a line segment connecting p~ and p~ in Delaunay triangulation if and only if the Voronoi polygons V(p~) and

V(p~)

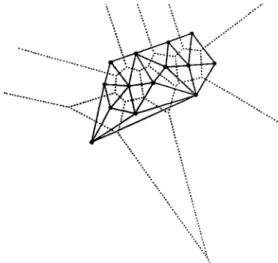
share a common edge.

A Voronoi diagram of 14 points and its dual Delaunay triangulation is shown in Fig. 2-1. \ .... ...

'

...,,

... iiiiiiiiiiiiiiiiiii ...

...

" \ \

""..

\

ON THE AVERAGE LENGTH OF DELAUNAY TRIANGULATIONS 271

Delaunay triangulations have many interesting properties. First of all, the circumcircles of the triangles in a Delaunay triangulation do not contain any other points of P (Lee and Schachter [7]). Another interesting property is shown in the corollary of Lemma 2.1.

LEMMA 2.1 (Lee and Schachter [7]). Given a set P of N points, any triangulation of P has the same number of triangles, N t = 2 ( N - 1 ) - N h , and the same number of edges, N e = 3 ( N - 1 ) - N h, where N h is the number of points on the convex hull

of P.

The following corollary follows from Lemma 2.1.

COROLLARY 2.1. A Delaunay triangulation has the same number of triangles and edges as a minimum triangulation for the same point set.

3. Homogeneous planar Poisson point distribution.

In modeling randomly distributed points in the plane, we usually assume "n points are uniformly distributed in a bounded region of the Euclidean plane" (Shamos [13] pointed out that assuming points uniformly distributed in an unbounded plane is meaningless). In the field of geometric probability, the assumption above can be characterized by a stochastic point process (Goldman [4]) - a homogeneous planar Poisson point distribution.

Let P represent a homogeneous planar Poisson point distributiOn of intensity 2 in the plane, N ( X ) be the number of points in X and IXI be the Lebesgue measure of X for X c E 2. P is completely specified by Lemma 3.1.

LEMMA 3.1 (Miles [12]). (Extreme Poisson Independence Property). I f XI, X 2 ... X,, are arbitrary disjoint,Lebesyue-measurable subsets of E 2, then N ( X 1 ) , . . . , N ( X m ) are mutually independent Poisson random variables with expectation 2lX~l ... ;LIX.,I respectively.

This means that the expected number of points in each domain X 1 ... X m is a random variable depending only on the area IX~l (Lebesgue measure), neither on the shape nor the position of the X[s.

The expectation of the number of points in each X i is therefore equal to 2 (intensity) times the area of Xi.

Besides, the following Lemma indicates that points in each subset are independently and uniformly distributed.

LEMMA 3.2 (Miles [12]). Given N ( X ) = n and 0 < IX[ < oo. These n points are independently and uniformly distributed in X.

4. The average analysis of Delaunay triangulations.

Assume that we put n points into a unit square by a homogeneous planar Poisson distribution. By Lemma 3.2, these n points are uniformly distributed with intensity 2 equal to n. The following Lemmas are crucial in our analysis. LEMMA 4.t (Marks [11]). Let P be a homogeneous planar Poisson point distribution with intensity 2, r be the distance from some point Px to its nearest neighbor and E(r) be the mean value of r. Then E(r) < 1/22 ½.

LEMMA 4.2 (Miles [12]). Let P be a homogeneous planar Poisson point distribution with intensity 2, L be the length of a Delaunay edge of a Delaunay triangle and E(L) be the mean value of L. Then

E(L) = 32/9n2 ½.

Based upon the lemmas above, we can prove the following main theorem. THEOREM 4.1. Let P be a point set with n points which are uniformly distributed in a unit square, E(MT(P)) and E(DT(P)) be the expected total length of minimum triangulation and Delaunay triangulation respectively. Then

E(DT(P))

- o ( 1 ) .

E(MT(P))

PaooF. By Corollary 2.1, these two triangulations have the same number of edges Ne. Since each edge of a minimum triangulation connecting some point p:, is always greater than or equal to the distance of Px to its nearest neighbor, we have on the average,

E(MT(P)) > N," E(r) = N~/22 ½ according to Lemma 4.1.

By Lemma 4.2, E(DT(P)) = 32Nj9z~2 ½. Hence,

E(DT(P)) < 64/9n = O(1).

E(MT(P)) =

5. Concluding remarks.

In this paper we have shown that on the average a Delaunay triangulation is as good as a minimum triangulation, under the assumption that our points are drawn from a homogeneous planar Poisson point distribution. Our results are not very surprising since they are obtained just by combining two results of Marks [11] and Miles [12].

ON THE AVERAGE LENGTH OF DELAUNAY TRIANGULATIONS 273

We believe that both represent quite important research results which should~ be studied by every reader interested in computational geometry. In fact, the present authors [2] successfully applied the result in [11] to show that the average case performance of Bentley's method to solve the planar closest pair problem [1] is a linear function of the number of points.

R E F E R E N C E S

1. J. L. Bentley, Multidimensional divide-and-conquer, Communications of ACM, Vol. 23, No. 4 (1980), 214-229.

2. R. C. Chang and R. C. T. Lee, The average case performance analysis of Bentley's divide-and-

conquer algorithm to solve the planar closest-pair problem, to appear.

3. B. Delaunay, Sur la sphere vide, Bull. Acad. Sci. USSR(VII), Classe Sci. Mat. Nat. (1943),793-800.

4. J. R. Goldman, Stochastic point process: limit theorems, Ann. Math. Statist. 38 (1967), 771-779. 5. D. G. Kirkpatrick, A note on Delaunay and optimal triangulations, Information Processing

Letters, Vol. 10, No. 3 (1980), 127-128.

6. C. L. Lawson, Software for C 1 surface interpolation, in Mathematical Software 111, J. Rice, Ed., Academic Press, New York (1977):

7. D. T. Lee and B. J. Schachter, Two algorithms for constructing a Delaunay triangulation, International Journal of Computer and Information Sciences, Vol. 9, No. 3 (1980), 219-242. 8. A. Lingas, Advances in Minimum Weight Triangulation, Dissertation, Link6ping University,

Sweden (1983).

9. E. L. Lloyd, On trianyulations of a set of points in the plane, Proc. 18th Annual IEEE Conference on the Foundations of Computer Science, Providence (19"77).

10. G. K. Manacher and A. L. Zorbrist, Neither the greedy nor the Delaunay triangulation of a

planar point set approximates the optimal triangulation, Information Processing Letters, VoL 9,

No. 1 (1979), 31-34.

11. E. S. Marks, A lower bound for the expected travel among m random points, Ann. Math. Statist. 19 (1948), 419-422.

12. R. E. Miles, On the homogeneous planar Poisson point process, Mathematical Biosciences, Vol. 6 (1972), 85-127.

13. M. I. Shamos, Geometry and Statistics: Problems at the interface, in Al.qorithms and

Complexity: New Direction and Recent Results, J. F. Traub, Ed., Academic Press, New York

(1976).

14. M. I. Shamos, Computational Geometry, Ph.D. Dissertation, Yale University (1978).

15. M. I. Shamos and D. Hoey, Closest point problems, Proc. 16th Annual IEEE Conference on Foundations of Computer Sciences (1975), 151-162.

16. G. Voronoi, Nouvelles applications des parametres continus a la theorie des formes quadratiques. Deuxieme Memoire: Recherches sur les parallelloedres. Deuxieme reine angew. Math. 134 (1908), 198-287.