Quantum secret sharing using product states

Quantum secret sharing using product states

Li-Yi Hsu*

Department of Physics, Chung Yuan Christian University, Chung-Li, 32023, Taiwan, Republic of China Che-Ming Li

Institute and Department of Electrophysics, National Chiao Tung University, Hsinchu 30050, Taiwan, Republic of China 共Received 19 June 2003; revised manuscript received 28 May 2004; published 28 February 2005兲

This study proposes quantum secret sharing protocols using product states. The first two protocols adopt the quantum key distribution protocol using product states关Guo et al.Phys. Rev. A 64, 042301 共2001兲兴. In these two protocols, the sender does not reveal any information about the qutrits until confirming that each receiver has received a qutrit. This study also considers the security and some possible eavesdropping strategies. In the third proposed protocol, three-level Bell states are exploited for qutrit preparation via nonlocality swapping. DOI: 10.1103/PhysRevA.71.022321 PACS number共s兲: 03.67.Dd, 03.67.Hk

I. INTRODUCTION

The problem of secret sharing is as follows. Alice, the president of a bank, wants to give access to a vault to two vice presidents, Bob and Charlie. Alice knows that one of them, and only one, may be dishonest and she does not know who is the honest one. Nevertheless, any classical secret sharing cannot prevent an eavesdropper with unlimited power from accessing secret bits. On the other hand, it is believed that secret communication using quantum bits can be absolutely secure. In quantum physics, one cannot take a measurement without perturbing the system. That is, an eavesdropper cannot access full information without being detected in quantum secret communication. Recently, people have become interested in quantum secret sharing. Hillery et

al. introduced the quantum secret sharing protocol using

Greenberger-Horne-Zeilinger 共GHZ兲 states 关1兴. Moreover, Koashi and Imoto considered the correlation of the two-qubit Bell state in their quantum secret sharing scheme 关2兴. Ka-rimipour et al. then proposed d-level secret sharing via en-tanglement swapping关3兴. Furthermore, Cabellos suggested a quantum secret sharing scheme using entanglement swap-ping between three-qubit GHZ states and two-qubit Bell states 关4兴. Also, Bagherinezhad and Karimipour introduced the protocol for quantum secret sharing based on the reusable GHZ states as secure carriers 关5兴. In addition, Hillery and Mimih considered quantum secret sharing with restricted classical communication关6兴. Nevertheless, the above quan-tum secret sharing protocols cannot be implemented without entangled states.

This study proposes some quantum secret sharing proto-cols using product states. The obvious advantage of the first two proposed protocols is that there is no need to prepare any entanglement. In quantum cryptography, the nonorthogonal-ity of the state vectors is exploited to detect any possible eavesdropping. For example, using the BB84 or B92 proto-cols, quantum key distribution can be performed without en-tanglement关7,8兴. Therefore, performing quantum secret

shar-ing usshar-ing product states is possible. Notably, Guo et al. considered quantum key distribution using the orthogonal product states关9,10兴. In the protocol of Guo et al., the sender has to prepare one of the two-qutrit bases in a complete set 兵兩␺l典其: 兩␣i典 兩␤i典 兩␺1典 = 兩1典 兩0典, 兩␺2典 = 兩0典 1

冑

2共兩0典 + 兩2典兲, 兩␺3典 = 兩0典 1

冑

2共兩0典 − 兩2典兲, 兩␺4典 = 兩2典 1

冑

2共兩0典 + 兩1典兲, 兩␺5典 = 兩2典 1

冑

2共兩0典 − 兩1典兲, 兩␺6典 = 1

冑

2共兩0典 + 兩1典兲 兩1典, 兩␺7典 = 1

冑

2共兩0典 − 兩1典兲 兩1典, 兩␺8典 = 1

冑

2共兩1典 + 兩2典兲 兩2典, 兩␺9典 = 1

冑

2共兩1典 − 兩2典兲 兩2典. 共1兲 This study writes the Hilbert space of the bipartite complete set basis as HA丢HB. That is, every兩␺l典 with state index l can be written as 兩␣_l典丢兩␤l典, where 兩␣l典苸HA and 兩␤l典苸HB, re-spectively. Bennett et al. proved that full information of an *Electronic address: lyhsu@phys.cts.nthu.edu.tw

unknown兩␺l典 is inaccessible via local operations and classi-cal communication unless the specific joint measurement is performed关11兴. Hence, the nonlocality without entanglement is embedded in the complete set兵兩␺i典其 关11兴. These nonlocal complete sets of product states are graphically illustrated in Fig. 1. In addition, as shown in Fig. 1, indices i, j, k, i

⬘

, j

⬘

, and k

⬘

can be rearranged as different nonlocal complete sets. This study denotes the nonlocal complete sets as that in Fig. 1 by (共i, j,k兲,共i

⬘

, j

⬘

, k

⬘

兲). For example, the complete set 兵兩␺l典其 can be denoted as (共0, 1, 2兲,共1, 0, 2兲). It is easy to verify that (共i, j,k兲,共i

⬘

, j

⬘

, k

⬘

兲) and (共k, j,i兲,共k

⬘

, j

⬘

, i

⬘

兲) indi-cate the same complete set. Consequently, in the three-level two-partite system, 18 complete sets of product states pos-sess nonlocality without entanglement.

It is noteworthy to examine the complete set

(共i, j,k兲,共i

⬘

, j

⬘

, k

⬘

兲). Figure 1 contains four rectangular domi-nos: two horizontal dominos and two vertical dominos. The two horizontal dominos in Fig. 1 are denoted by共i± j兲/i

⬘

and 共j±k兲/k

⬘

, respectively. Similarly, the two vertical dominos in Fig. 1 are denoted by i /共j

⬘

± k

⬘

兲 and k/共i

⬘

± j

⬘

兲, respectively. Obviously, these 18 nonlocal complete sets contain nine dif-ferent horizontal dominos and nine difdif-ferent vertical domi-nos. In addition, the nonlocality in the complete set

(共k, j,i兲,共k

⬘

, j

⬘

, i

⬘

兲) is preserved even if the 兩j典丢兩j

⬘

典 state is excluded关11兴. In this study, the sender never sends states of the兩j典丢兩j

⬘

典 kind. That is, the sender always sends some state lying in some horizontal or vertical domino.

However, if the two distant parties know the order of the local measurements, then both can access full information via local operations and classical communication. For in-stance, the unknown state is one of the bases in the nonlocal complete set (共i, j,k兲,共i

⬘

, j

⬘

, k

⬘

兲) and, moreover, the un-known state is un-known to lie in one of the horizontal dominos. To distinguish the unknown state, at first, the local measure-ment is performed on the Hilbert space H_Bin the basis兵兩0典, 兩1典, 兩2典其. The conditioned local measurement then can be per-formed on the Hilbert space HA. If the outcomes of the mea-surement on HB are兩i

⬘

典 and 兩k

⬘

典, the conditioned local mea-surements are then to be performed in the basis兵兩i典+兩j典,兩i典

−兩j典,兩k典其 and 兵兩j典+兩k典,兩j典−兩k典,兩i典其, respectively. This ap-proach is now accessible to full information via local opera-tions and classical communication. In other words, nonlocal-ity is embedded in the unknown order of the local measurements. That is, since whether an unknown state lies in a horizontal domino or a vertical domino is unknown, the correct order of local measurements cannot still be known.

This study proposes three quantum secret sharing proto-cols. The first two proposed protocols are based on these nonlocal complete sets. Reviewing the quantum key distribu-tion protocol of Guo et al. is helpful. The protocol is as follows关10兴: 共1兲 The sender, Alice, sends the receiver, Bob, one qutrit of a basis state in the complete set兵兩␺_l典其. 共2兲 After receiving the qutrit, Bob informs Alice, via classical commu-nication, that he has received the qutrit.共3兲 Alice sends the other qutrit.共4兲 Bob performs the measurement in the 兵兩␺l典其 basis. The key feature of this protocol is that Alice does not send the second qutrit before ensuring that Bob has received the first qutrit. Thus, Eve, the eavesdropper, is incapable of performing any joint measurement on the two sent qutrits without being detected. However, this protocol implicitly as-sumes that the sending order is always the same. For ex-ample, Alice and Bob both preagree that Alice always sends 兩␣l典苸HA in step共1兲 and then sends 兩␤l典苸HB in step共3兲. If the Hilbert space of the兵兩␺l典其 basis is permuted, the complete set (共0, 1, 2兲,共1, 0, 2兲) becomes another different complete set

(共2, 0, 1兲,共0, 1, 2兲) and vice versa. Thus, the protocol of Guo

et al. is modified as follows. Alice randomly exchanges the

sending order in steps共1兲 and 共3兲. As a result, in step 共4兲, Bob does not know that the first received qutrit is兩␣l典 or 兩␤l典. Bob performs his joint measurement randomly in the basis of the complete set either (共0, 1, 2兲,共1, 0, 2兲) or (共2, 0, 1兲,共0, 1, 2兲). In the next step, Bob must tell Alice his measurement basis via classical communication. Alice then informs Bob which outcomes are to be disregarded via classical commu-nication. Significantly, Alice and Bob consider the permuta-tion effect of the Hilbert spaces. This modified protocol is now adaptable to be used in quantum secret sharing. In the quantum secret sharing protocol of Hillery et al. or Koashi and Imoto, the three-qubit GHZ states or two-qubit Bell states are invariant under the permutation of Hilbert space. In effect, the eavesdropper does not have to consider the effect of the permutation of Hilbert space. However, such an effect is the advantage of the proposed protocol to prevent success-ful cheating.

This paper is organized as follows. Section II considers the effect of the permutation of Hilbert space using a simpler protocol. Section III then explores another protocol, which is the generalization of the protocol in Sec. II. Section IV ana-lyzes the security and investigates some possible eavesdrop-ping strategies on the protocols I and II. Section V discusses the third protocol based on nonlocality swapping. Finally, Sec. VI then draws some conclusions.

II. QUANTUM SECRET SHARING PROTOCOL VIA PRODUCT STATE: PROTOCOL I

In the following proposed protocols, the secret is the state index l of the prepared qubit system兩␺l典. Since the state 兩j典 FIG. 1. The complete set (共i, j,k兲,共i⬘, j⬘, k⬘兲). The complete set

兵兩␺l典其 can represented as (共0, 1, 2兲,共1, 0, 2兲). There are two

horizon-tal dominos and two vertical dominos. For example, the horizonhorizon-tal domino 共i± j兲/i⬘ represents two states 共1/

冑

2兲共兩i典+兩j典兲丢兩i⬘典 and 共1/

冑

2兲共兩i典−兩j典兲丢兩i⬘典; the vertical domino k/共i⬘± j⬘兲. This domino represents two states 共1/

冑

2兲兩k典丢共兩i⬘典+兩j⬘典兲 and 共1/

冑

2兲兩k典丢共兩i⬘典

丢兩j

⬘

典 is discarded, the state index of the other eight basis vectors in the complete set (共i, j,k兲,共i

⬘

, j

⬘

, k

⬘

兲) can be en-coded as three bits in the binary representation. That is, the sender splits the information of three secret bits, l, via send-ing each receiver a qutrit—i.e., sendsend-ing兩␣l典 and 兩␤l典 to Bob and Charlie, respectively. The task of the receivers is to de-termine the state index of the transmitted two-qutrit system. Only when the receivers access full information of the prod-uct states do they decode the secret bits correctly. This study now considers how to modify the quantum key distribution of Guo et al. for quantum secret sharing. The proposed quan-tum secret sharing protocol is as follows.

Protocol I Preparation phase

共1兲 Alice creates two ordered qubit sets of B and C, where

B =兵兩␣l₁典S₁,兩␣l₂典S₂, . . . ,兩␣l_n典S_n其 共2兲 and

C =兵兩␤l₁典S₁,兩␤l₂典S₂, . . . ,兩␤l_n典S_n其. 共3兲 Notably,兩␣_l

i典Si丢兩␤li典Si is a basis vector of the complete set

either (共0, 1, 2兲,共1, 0, 2兲) with Si= 0 or (共2, 0, 1兲,共0, 1, 2兲) with S_i= 1. In addition, Alice permutes the element order in setC based on the bijective function r−1_共x兲:

r−1共x兲 = y, and r共x兲 ⫽ x∀x, y = 1, . . . ,n. 共4兲

That is, the xth element in the ordered set C now becomes the关r−1共x兲兴th element. Therefore, the new ordered set C

⬘

is

C

⬘

=兵兩␤l_r共1兲典S_r共1兲,兩␤l_r共2兲典S_r共2兲, . . . ,兩␤l_r共n兲典S_r共n兲其. 共5兲 共2兲 Alice prepares two n-bit strings b and b

⬘

. Then she performs the three-level Hadama transformation

H =

冢

1 1 1 1 ␻ ␻2 1 ␻2 ␻

冣

, ␻= exp

冉

2␲i 3

冊

, 共6兲

on ith qutrits in the setsB and C

⬘

if the ith bits of b and b

⬘

are 1, respectively.

共3兲 Each time Alice sends the qutrits A 共兩␣l_i典S_i苸HA兲 and B 共兩␤l_r共i兲典S_r共i兲苸HB兲 to Bob and Charlie, respectively. Once Bob and Charlie receive one qutrit, they publicly announce the facts, respectively. Then Alice sends 兩␣l_i+1典S_i+1 and 兩␤l_r共i+1兲典S_r共i+1兲after she confirms their respective receptions.

共4兲 After sending all qutrits and confirmation, Alice an-nounces the strings b and b

⬘

. Bob and Charlie perform H−1 on qutrits A and B for which b and b

⬘

are 1, respectively.

共5兲 Alice publicly announces the function r共m兲. Eventu-ally, Bob and Charlie share n qutrit pairs 兩␣l_i典S_i丢兩␤l_i典S_i, i = 1 , . . . , n.

共6兲 Alice announces the information 共k,k

⬘

兲 of the picked

n

⬘

qutrit pairs. Then Bob performs the measurement on 兩␣l_i典S_i using either the basis 兵兩i典,兩j典,兩k典其 or 兵共1/

冑

2兲共兩i典

+兩j典兲,共1/

冑

2兲共兩i典−兩j典兲,兩k典其. Charlie performs the measure-ment on 兩␤l_i典S_i using either the basis 兵兩i

⬘

典,兩j

⬘

典,兩k

⬘

典其 or 兵共1/

冑

2兲共兩i

⬘

典+兩j

⬘

典兲,共1/

冑

2兲共兩i

⬘

典−兩j

⬘

典兲,兩k

⬘

典其. They publicly an-nounce their respective measurement results. Alice discards the results with the outcomes of inappropriate measurement bases. If there are too many errors for the remaining out-comes, Alice aborts the secret. Otherwise, the other共n−n

⬘

兲 qutrit pairs are used in the revealing phase.

Revealing phase

共7兲 To know the state index li of 兩␣l_i典S_i丢兩␤l_i典S_i, Bob and Charlie discuss who performs the first local measurement in the basis兵兩0典, 兩1典, 兩2典其 and then the other performs the con-ditioned local measurement. For example, Bob and Charlie access a random independent coin flip. If the coin is 0 共1兲, Bob共Charlie兲 and Charlie 共Bob兲 should perform the first and the conditioned local measurements, respectively. In this study, F and S denote the receivers, who perform the first and conditioned measurements, respectively. F tells S his measurement outcome in private.

共8兲 The receiver S performs the second local measurement and then broadcasts the measurement basis and consequently tells the receiver F his measurement outcome in private.

共9兲 Alice tells Bob and Charlie which outcomes should be disregarded owing to the incorrect local measurement order. In this protocol, either兩0典丢兩1典 or 兩1典丢兩0典 are disregarded.

共10兲 This study divides the measurement outcomes based on correct measurement into two subsets: those for which Bob performs the first local measurement, denoted byB, and those for which Charlie performs the first local measurement, denoted by C. On average, there are about equal element numbers of subsetsB and C. Alice randomly selects half of the elements from subsetsB and C, respectively, after which Bob and Charlie then broadcast the selected measurement outcomes, respectively. As a result, Alice checks these out-comes to detect possible eavesdropping behavior. If too many errors occur, Alice announces to abort the secrets.

The proposed protocol is described in detail. At first, we explain steps共1兲, 共2兲, and 共3兲, which are the essential differ-ences from the protocol of Guo et al. 关16兴. Suppose Eve intercepts the qutrits兩␣l_i典S_iand兩␤l_r共i兲典S_r共i兲for any i in step共3兲. Then Eve can perform some joint measurement on兩␣_l

i典Siand 兩␤l_r共i兲典S_r共i兲 before resending one qutrit pair. In this case, Eve can get very little information because she cannot measure 兩␣l_i典S_i丢兩␤l_i典S_i jointly. In the protocol of Guo et al., Alice can send a qutrit at one time关10兴. In the proposed protocol, Alice can send two qutrits at a time in step共3兲. On the other hand, suppose Eve wants to access full information of single qutrit 兩␣l_i典S_i 共兩␤l_r共i兲典S_r共i兲兲. In this case, Eve has to know bi 共bi

⬘

兲 at least. Therefore, step共2兲 is to reduce Eve’s mutual informa-tion when she attacks on only a qutrit. Correspondingly, Al-ice and Bob recover all兩␣l_i典S_i’s and兩␤l_r共i兲典S_r共i兲’s in step共4兲. In step 共5兲, Bob rearranges the order of all 兩␤l_r共i兲典S_r共i兲’s so that Alice and Bob’s ith qutrits are兩␣_l

i典Si’s and兩␤lr共i兲典S_r共i兲, respec-tively.

Second, there are two steps to detect possible eavesdrop-ping attacks. In the preparation phase, Alice tries to detect

possible attacks actively in step 共6兲. Suppose Alice an-nounces the information共k,k

⬘

兲 for the i

⬘

th qutrit pair. In the error-free case, she expects that Bob or Charlie can find some兩␣l_i⬘典S_i⬘or 兩␤l_i⬘典S_i⬘if an appropriate measurement basis is exploited. As a result, deception can be detected if receiv-ers announce wrong outcomes in the appropriate measure-ment basis. In the revealing phase, as previously stated, Bob and Charlie both have full access to information if they per-form the local measurements in the correct order. In step共7兲, if Bob and Charlie randomly decide the person to perform the first local measurement in the basis 兵兩0典, 兩1典, 兩2典其, per-forming the local measurements in the correct order yields a probability 1₂. For the present discussion, Bob is to be the receiver that performs the second local measurement. Mean-while, honest Bob supposes that they both employ the cor-rect order of local measurements and then he tries to guess the complete set to which this product state belongs. For example, Bob knows that Charlie’s measurement outcome is 兩1典 共兩2典兲. In addition, Bob guesses that the product state is a basis vector of the complete set (共0, 1, 2兲,共1, 0, 2兲). Conse-quently, Bob must measure his qutrit in the basis 兵共1/

冑

2兲 ⫻共兩0典±兩1典兲,兩2典其 (兵共1/

冑

2兲共兩1典±兩2典兲,兩0典其). If the measurement outcome of honest Bob in step共8兲 is 兩2典 共兩0典兲, he immediately knows that either they have employed the wrong measuring order or some eavesdropping has occurred. Alice learns the order of the local measurements in step 共8兲. Therefore, in step共9兲, Alice can inform Bob and Charlie which measure-ment outcomes with the incorrect measuremeasure-ment orders is to be dropped over a classical channel. In the above example, if Bob expects that the measurement order is wrong but Alice tells Bob and Charlie to keep this outcome, honest Bob will immediately know that Charlie may have cheated. Moreover, since Bob and Charlie keep the measurement outcomes only when they employ the correct measuring orders, Bob and Charlie generally will have to drop half of the measurement outcomes in step共9兲.

III. QUANTUM SECRET SHARING PROTOCOL VIA PRODUCT STATE: PROTOCOL II

In the previous protocol, the secret can be revealed only when Bob and Charlie perform the local measurements in the correct order. In addition, the sent product state is one of the basis vectors of the complete set, either (共i, j,k兲,共i

⬘

, j

⬘

, k

⬘

兲) or (共i

⬘

, j

⬘

, k

⬘

兲,共i, j,k兲). In general, Alice can prepare a prod-uct state, which can be a basis vector lying in some domino of the 18 nonlocal complete sets. Therefore, protocol I can be modified as follows.

共a兲 As in step 共1兲 of the protocol in Sec. II, Alice prepares a product state, which is one of the basis vectors of the 18 nonlocal complete sets. This study assumes the prepared product state to be one of the basis vectors of the complete set (共i, j,k兲,共i

⬘

, j

⬘

, k

⬘

兲).

共b兲 Following the confirmation in step 共5兲, Alice broad-casts the index 共i

⬘

, j

⬘

, k

⬘

兲 and 共i, j,k兲. Notably, the correct local measurement order remains unknown to Bob and Char-lie.

Now suppose the eavesdropper can intercept two-qutrit system兩␣_l

i典Si丢兩␤li典Sisimultaneously. In addition, Alice does

not reveal any information of the complete set. The eaves-dropper can employ the basis of a nonlocal complete set as the collective measurement basis. For example, suppose that Alice prepares共1/

冑

2兲共兩i典+兩j典兲丢兩i

⬘

典. The eavesdropper inter-cepts both qutrits and then performs some collective measurement with one of the 18 complete set basis. If he chooses one of the complete sets (共i, j,k兲,共i

⬘

, j

⬘

, k

⬘

兲),

(共j,i,k兲,共i

⬘

, j

⬘

, k

⬘

兲), (共i, j,k兲,共i

⬘

, k

⬘

, j

⬘

兲), or (共j,i,k兲,

共i

⬘

, k

⬘

, j

⬘

兲) as the measurement basis, the eavesdropper can access full information without any disturbance. Therefore, the probability of successful and undisturbed eavesdropping is 2₉.

In the quantum key distribution protocol of Guo et al., the sender and receiver preagree on the sending order of qutrits and the measurement basis. The key point is that the sender must ensure that, after sending a qutrit, the receiver has also received a qutrit. In proposed protocol I and its modification, the receivers have to discuss the order of the local measure-ments. The following discussion investigates the quantum secret sharing protocol, in which the receivers do not need to discuss the local measurement order. In following discussion, each complete set is denoted by the corresponding index Si. This protocol is as follows.

Protocol II Preparation phase

The steps from共1兲 to 共6兲 are just about equivalent to those in protocol I. The main difference is that the index Sican be 0, 1,…, 17. Now Bob and Charlie are assumed to hold the ordered sets ofB and C in Eqs. 共2兲 and 共3兲, respectively.

Revealing phase

共7兲 Alice broadcasts the n binary bit strings d as the ap-propriate local measurements. If the ith bit of d is 1共0兲, Bob 共Charlie兲 should F to perform the foremost local measure-ment on qutrit 兩␣_l

i典ki 共兩␤li典ki兲. After the receiver F has

per-formed the first local measurement in the basis兵兩0典, 兩1典, 兩2典其,

F broadcasts that he has performed his measurement. In

ad-dition, F privately informs the other receiver of the measure-ment outcome. For example, let Alice prepare 共1/

冑

2兲共兩i典 +兩j典兲丢兩i

⬘

典. Alice broadcasts that Charlie 共F兲 performs the first local measurement in the basis兵兩0典, 兩1典, 兩2典其.

共8兲 Each time Alice receives the broadcast of F, she then broadcasts the complete set to which the sent product states belong. Since 共1/

冑

2兲共兩i典+兩j典兲丢兩i

⬘

典 is one basis of the four complete sets (共i, j,k兲,共i

⬘

, j

⬘

, k

⬘

兲), (共j,i,k兲,共i

⬘

, j

⬘

, k

⬘

兲),

(共i, j,k兲,共i

⬘

, k

⬘

, j

⬘

兲), and (共j,i,k兲,共i

⬘

, k

⬘

, j

⬘

兲), Alice can pub-licly announce that the state of the prepared qutrits is one of the basis vectors in the complete set (共i, j,k兲,共i

⬘

, j

⬘

, k

⬘

兲).

共9兲 Bob and Charlie must announce some portion of the secret bits to detect possible deception behaviors. Conse-quently, Bob and Charlie perform step共10兲 of the proposed protocol I.

The protocol used in this investigation is described in de-tail. Obviously, Alice initially does not reveal the sending order and measurement basis information, to prevent the eavesdropper from accessing full information without

aware-ness. For example, suppose that Alice prepares one of the following four states: 兩k典丢共1/

冑

2兲共兩i

⬘

典±兩j

⬘

典兲 and 兩i典 丢共1/

冑

2兲共兩j

⬘

典±兩k

⬘

典兲. After Alice broadcasts the measuring or-der and the complete set basis (共i, j,k兲,共i

⬘

, j

⬘

, k

⬘

兲) in step 共8兲, Bob共F兲 performs the measurement in the basis 兵兩0典, 兩1典, 兩2典其. The outcome should be either 兩k典 or 兩i典. Bob then informs Charlie共S兲 of his outcome. After Alice broadcasts the mea-surement basis in step共8兲, Charlie performs his measurement in the basis 兵共1/

冑

2兲共兩i

⬘

典±兩j

⬘

典,兩k

⬘

典其 or 兵共1/

冑

2兲共兩j

⬘

典±兩k

⬘

典, 兩i

⬘

典其, respectively. Charlie should tell Bob his outcome. As a result, Alice can share a secret bit with Bob and Charlie. Notably, if Bob is honest, he will not measure 兩j典 in this example. If Bob measures 兩j典, honest Bob immediately knows that some deception has occurred in the error-free condition.

In general, a quantum secret sharing protocol can be modified to be a quantum key distribution as follows. Bob and Charlie are regarded as the same receiver. In addition, Alice can send the second qutrit only after confirming that the receiver has received the first one. As the sender does in step共4兲 of the proposed quantum secret sharing protocol II, Alice also broadcasts the measurement basis. Nevertheless, this protocol offers minimal advantage over the other quan-tum key distribution schemes.

This study examines how Alice performs the initial prepa-ration. Alice can prepare two supplies of兩0典 and 兩0+1典, re-spectively. To prepare the states兩1典 or 兩2典, Alice can perform the unitary transformation M: 兩t典→兩t+1典 on 兩0典 once or twice, respectively. Similarly, Alice also can prepare some 兩i+ j典 in this manner. If Alice has to prepare 兩i− j典, she may perform the unitary transformation D: diag共1,−1,1兲 fol-lowed by Ms. Both D and M are one-qutrit unitary transfor-mations. Consequently, Alice does not require any pairwise unitary transformation for the preparation. Therefore, physi-cally realizing such preparation will be much easier than the preparation of the Bell states and GHZ states.

Finally, we compare the proposed protocols with quantum secret sharing using GHZ states关1兴. In the error-free case, the efficiency of quantum secret sharing using either GHZ states or product states is nearly 100%. In the case of quan-tum secret sharing using GHZ states, leaving out any re-ceiver, the rest can have no information about the secret bit. In the proposed protocols, any receivers can obtain mutual information even without classical communication. Conse-quently, Eve can gain some mutual information. The pro-posed protocols can reduce Eve’s mutual information in steps 共1兲 and 共2兲. On the other hand, let Eve be able to entangle the sent qubits with ancilla qubits. If the GHZ en-tanglement introduces no errors into secret sharing proce-dures, an eavesdropper can gain no information in this way. Or if Eve can gain information about secret bits, inevitable errors must occur. In the proposed protocols, the ideal eaves-dropping attack is to clone the untangled qutrit states per-fectly. However, the nonorthogonality and no-clone theorem guarantee the impossibility of such an attack.

IV. SECURITY ANALYSIS OF PROTOCOLS I AND II

Now we consider the security of protocols I and II. Recall that four possible states 共兵兩0典,兩1典,共1/

冑

2兲共兩0典+兩1典兲,

共1/

冑

2兲共兩0典−兩1典兲其兲 are exploited in the BB84 protocol. Proto-col II can be regarded as the hybrid of three BB84 protoProto-cols based on three different sets of four states 兵兩i典,兩j典,共1/

冑

2兲 ⫻共兩i典+兩j典兲,共1/

冑

2兲共兩i典−兩j典兲其, where 共i, j兲 are 共0, 1兲, 共1, 2兲, 共2, 0兲, respectively. In addition, the sender smashes the informa-tion共i, j兲 using three-level Hadama transformation. Further-more, the sender must always confirm that the receiver has received the previous qutrit before the next qutrit is sent. Therefore, protocol II is much more secure than the ordinary BB84 protocol. As for protocol I, Guo et al. prove that, in their protocol, an eavesdropper cannot access full informa-tion even if an eavesdropper can intercept 共兩␣l_i典丢兩␤l_i典兲S_i si-multaneously. In addition, an eavesdropper can never inter-cept 共兩␣l_i典丢兩␤l_i典兲S_i simultaneously in protocol I. To access full information in protocols I and II, an eavesdropper has to know the following information after intercepting and before resending the other’s qutrit: the complete set index S_i, the strings b and b

⬘

, and the function r共m兲. In step 共6兲 and the last step of protocols I and II, the sender checks possible eavesdropping. That is, Alice can always find the possible eavesdropping with higher probability than the BB84 proto-col. Next we just consider some possible attacks. Further security proof is considered in Sec. V.

A. Misstate strategy

Since Bob and Charlie have to discuss Alice’s prepara-tion, the intuitive cheating is to lie to the honest receiver. For simplicity, let Bob and Charlie be receivers F and S, respec-tively. If the eavesdropper is receiver S, the simplest method of cheating is to misstate local measurement outcomes to the other receiver. However, such deception can be detected in step共6兲 because the honest receiver can choose and broad-cast a portion of such false outcomes to the sender.

Moreover, the no-clone theorem guarantees that a perfect clone of possible nonorthogonal states is impossible关12兴. In protocol II, if the eavesdropper, Bob or Charlie, takes the intercept-resend strategy, he can access full information us-ing the correct basis with probability 2₉. Otherwise, the eavesdropper will disturb the quantum state. Therefore, the probability of successful eavesdropping without disturbance is 2₉. On the other hand, since receiver S is assumed to per-form his measurement after receiver F, S always can access full information before F. Therefore, if S is the eavesdropper,

S can cheat F by stating false outcomes. This condition also

happens in other quantum secret sharing schemes. In some quantum secret sharing schemes, the two receivers have to discuss Alice’s outcomes关1兴 or preparation 关2兴. In practice, either Bob or Charlie must expose his outcome to the other first. Inevitably, the second receiver to expose his outcome can always have access to full information before the other receiver. However, since the sender is aware of any of incor-rect public measurement outcomes in step共6兲, false outcome statements can be detected.

In addition, the dishonest receiver F can also misstate the outcomes: For example, Alice prepares the product state兩k典 丢共1/

冑

2兲共兩i

⬘

典+兩j

⬘

典兲. If the receiver F misstates his outcome as 兩j典, receiver S can detect this cheating immediately after Alice broadcasts the complete set basis as (共i, j,k兲,

共i

⬘

, j

⬘

, k

⬘

兲) in step 共5兲. Meanwhile, if F misstates the outcome as兩i典, receiver S should perform his local measurement in the basis 兵共1/

冑

2兲共兩j

⬘

典±兩k

⬘

典兲,兩i

⬘

典其. If the outcome is 兩i

⬘

典 with probability 1₂, S can immediately detect the cheating. In ad-dition, Alice is definitely aware of this cheating if the out-come is broadcast in step共6兲. Therefore, any misstatements can be detected.

B. Intecept-resend strategy

For simplicity, we just consider r共m兲=m. Either dishonest Bob 共F兲 or dishonest Charlie 共S兲 can take the intercept-resend strategy. In the quantum key distribution protocol of Guo et al., the eavesdropper can only perform local measure-ments. In the protocol presented here, the eavesdropper can perform any joint measurement. However, only when the eavesdropper performs a correct collective or local measure-ment on these two intercepted qutrits can the eavesdropper access full secret information. Otherwise, the eavesdropper will fail to know the secret. For example, in protocol I, the eavesdropper intercepts the product state 兩0典丢共1/

冑

2兲共兩0典 +兩2典兲. If the eavesdropper performs the measurement in the basis of the complete set (共2, 0, 1兲,共0, 1, 2兲), he will get 共1/

冑

2兲共兩0典±兩2典兲丢兩0典 or 共1/

冑

2兲共兩0典±兩1典兲丢兩2典 with equal probability 1₄. The corresponding density matrix is

1

4共兩00典具00兩 + 兩20典具20兩 + 兩02典具02兩 + 兩12典具12兩兲. 共7兲 Apparently, the eavesdropper cannot gain any information from this density matrix. As a result, the eavesdropper can perform successful eavesdropping with probability 1₂.

This study considers that, in protocol II, dishonest Bob 共F兲 intercepts Charlie’s qutrit and resends a qutrit to Charlie before Alice’s first broadcast in step共4兲. This study assumes that Bob sends Charlie the qutrit兩l

⬘

典, which is equally likely to be兩0典, 兩1典, or 兩2典. Also, it is assumed that Alice sends the quantum system 兩k典丢共1/

冑

2兲共兩i

⬘

典+兩j

⬘

典兲 or 兩k典丢共1/

冑

2兲共兩i

⬘

典 −兩j

⬘

典兲, and then announces that the corresponding complete set is (共i, j,k兲,共i

⬘

, j

⬘

, k

⬘

兲). In addition, Charlie should per-form his local measurement in the basis 兵共1/

冑

2兲共兩i

⬘

典 ±兩j

⬘

典兲,兩k

⬘

典其 after Bob tells him the faithful outcome. If 兩l

⬘

典 =兩j

⬘

典 or 兩i

⬘

典 and Bob honestly tells Charlie the outcomes, then Charlie fails to detect the deception. Nevertheless, if the outcomes are public in step共6兲, Alice can detect the cheating with probability 1₂. If 兩l

⬘

典=兩k

⬘

典, Bob must misstate his out-come to be certain of avoiding Charlie’s detection. Neverthe-less, Alice can definitely detect such cheating if the outcomes are public in step共6兲.

This study now assumes that dishonest Charlie, receiver

S, intercepts Bob’s qutrit and resends the qutrit兩l典, which can

be 兩0典, 兩1典, or 兩2典 with equal probability. Again this study assumes that Alice sends the receivers the quantum system 兩k典丢共1/

冑

2兲共兩i

⬘

典+兩j

⬘

典兲 and then announces that the corre-sponding complete set is (共i, j,k兲,共i

⬘

, j

⬘

, k

⬘

兲). If 兩l典=兩j典, Bob can directly detect the cheating in step共5兲 since Bob’s out-comes should be either兩i典 or 兩k典. If 兩l典=兩k典, the eavesdrop-ping is ineffective. In addition, Charlie’s misstatement is de-tected in step 共6兲. If 兩l典=兩i典, Charlie may misstate his

outcome. However, Alice can detect such cheating in step 共6兲. Suppose that the eavesdropper performs the intercept-resend strategy on every pair of sent qutrits. In this example, only when Charlie resends Bob兩k典 and tells Bob the faithful outcome will Charlie not be found to be cheating. In other words, dishonest Charlie’s cheating must be detected. Impor-tantly, the eavesdropper cannot know the measuring order in advance. That is, Alice can prevent Trojan horse attacks quite well关13兴. Otherwise the proposed protocol will be ineffec-tive.

C. Guo–Li–Shi–Li–Guo strategy

For simplicity, we just consider r共m兲=m. The quantum key distribution protocol of Guo et al. considers the follow-ing eavesdroppfollow-ing strategy. The eavesdropper, Bob or Char-lie, intercepts the other’s qutrit. The eavesdropper performs the orthogonal measurement on one qutrit in the basis兵兩0典, 兩1典, 兩2典其. Based on the outcome, the eavesdropper performs another orthogonal measurement on the other qutrit in some different basis. Guo et al. used only one complete set兵兩␺i典其. Now suppose that the eavesdropper takes such an eavesdrop-ping strategy in our quantum secret sharing protocol II. The eavesdropper first performs an orthogonal measurement on a single qutrit in the basis兵兩0典, 兩1典, 兩2典其. Without loss of gener-ality, the first outcome can be allowed to be兩0典. Furthermore, the eavesdropper infers that the probability of the states兩0典 丢共1/

冑

2兲共兩i

⬘

典±兩j

⬘

典兲 (共i

⬘

, j

⬘

兲=共0,1兲,共1,2兲, or 共2,0兲) and 兩0±k典丢兩k

⬘

典 共k=1, 2 and k

⬘

= 0 , 1 , 2兲 may be prepared with equal probability. Finally, suppose the eavesdropper guesses that the state is one of the states兩0典丢兩i

⬘

± j

⬘

典. The eavesdrop-per then can eavesdrop-perform the nonorthogonal measurement with the following six positive-valued operators:

⌸0±1= 1 2兩0 ± 1典具0 ± 1兩, ⌸1±2= 1 2兩0 ± 2典具0 ± 2兩, ⌸2±1= 1 2兩2 ± 1典具2 ± 1兩, 共8兲

where兩0±1典 denotes the states 共1/

冑

2兲共兩0典±兩1典兲 and so on. It is easy to verify that兺_i,j共⌸_i+j+⌸_i−j兲=1, where 1 denotes the identity operator. Alice is assumed to prepare兩0典丢兩i

⬙

+ j

⬙

典. In this case, the rate that state兩i

⬙

+ j

⬙

典 projects into the ⌸i⬙+j⬙is 1

2. In this way, the probability that an eavesdropper can ac-cess full information without awareness is 1₄.

V. QUANTUM SECRET SHARING PROTOCOL VIA PRODUCT STATE: PROTOCOL III AND A SIMPLE

PROOF OF SECURITY

In this section, we propose another protocol similar to the Ekert protocol 关14兴. Recently, many researches focused on proving the unconditional security of the quantum key dis-tribution关15,16兴. The main theme of proof is to purify the raw two-level Bell states and then measure the syndrome of the stabilizer code关17兴. As a result, the receiver and sender can share perfect Bell states. Nevertheless, in this paper, three-level qutrits are exploited. To prove the unconditional

security of protocols I and II, we first introduce the nonlo-cality swapping关18兴 兩⌿00典共1,2兲兩⌿00典共3,4兲= 1 3

兺

_l=1 9 兩␺l典S_i,共1,4兲兩␺l典S_i,共2,3兲, 共9兲 where 1, 2, 3, 4 are qutrit indices and兩⌿典_共i,j兲 is the three-level Bell state:

兩⌿00典共i,j兲= 1

冑

3共兩00典 + 兩11典 + 兩22典兲. 共10兲 Alice holds the qutrits 1 and 4. Bob and Charlie hold qutrits 2 and 3, respectively. Alice performs the measurement in the basis兵兩␺l典S_i=兩␣l典S_i丢兩␤l典S_i其 of some complete set of set index

Si, where i = 0 , . . . , 17. In this way, Bob and Charlie possess 兩␣l典S_iand兩␤l典S_i, respectively. It is noteworthy that it is non-locality rather than entanglement which is preserved after the measurement关18兴. Therefore, the main idea of the proposed protocol III is as follows. The sender and each receiver ini-tially share the first and second halves of each 兩⌿00典. After performing the purification and the purity test, the sender and each receiver can share perfect three-level Bell states关13兴. Then the sender performs nonlocality swapping and then publicly announces the set index. Finally, the two receivers discuss the state index of the shared states at hand. Never-theless, few papers investigate how to purify multilevel Bell states. Here we propose a quantum privacy amplification al-gorithm共QPA algorithm兲 on three-level Bell states as follows 关19兴. 共1兲 The sender performs the three-level Hadama trans-formation and the receiver performs the inverse Hadama transformation. 共2兲 The sender and receiver each perform two instances of the quantum bilateral controlled-NOT 共CNOT兲 operations,

兩a典兩b典 → 兩a典兩a丣b mod 3典,a,b 苸 兵0,1,2其, 共11兲

between the control pair and target pair. Notably, any of the control pairs and the target pair comprise two qutrits in the initial state兩⌿00典. 共3兲 The sender and each receiver then mea-sure the target qutrits in the basis兵兩0典, 兩1典, 兩2典其. Each receiver publicly announces the measurement outcomes. If the sender finds that the outcomes coincide, they keep the control pair for the next round and discard the target pair. Notably, it is Alice who decides whether a target pair should be kept. In this way, the eavesdropper’s forgery will fail the proposed QPA algorithm. We denote the three-level Bell basis by 兩⌿jk典, where 兩⌿jk典 = 1

冑

3

兺

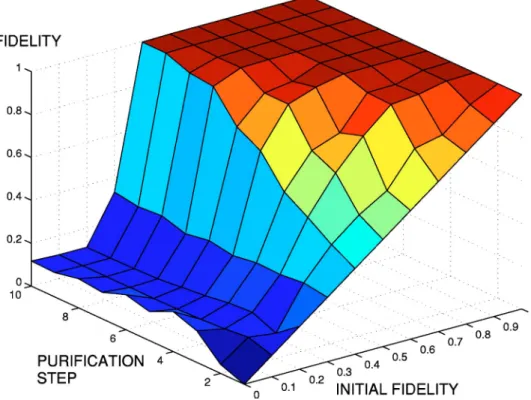
l=0 2 ␻lk_{兩l典兩l + j mod 3典, j,k = 0,1,2. 共12兲} In addition, the fidelity of the state兩⌿jk典 is denoted by pjk. After one round of the proposed QPA algorithm, the new density matrix comprises the survived controlled pairs with 兵p˜_jk其, where p ˜₀₀= N−1共p₀₀2 + p₁₀2 + p₂₀2兲, 共13兲 p ˜₀₁= N−1共p00p10+ p10p20+ p20p00兲, p ˜₀₂= N−1共p00p20+ p10p00+ p20p10兲, 共14兲 p ˜₁₀= A˜20= N−1共p01p02+ p11p12+ p21p22兲, 共15兲 p ˜₁₁= A˜22= N−1共p01p12+ p11p22+ p21p02兲, p ˜₁₂= A˜21= N−1共p01p22+ p11p02+ p21p12兲, 共16兲 and the normalization constant N =共p₀₀+ p₁₀+ p₂₀兲2_{+ 2共p}

01 + p₁₁+ p₂₁兲共p₀₂+ p₁₂+ p₂₂兲. Our simulation of the iterative mapping in Eq. 共16兲 is shown in Fig. 2. Therefore, if the sender and each receiver perform the above QPA algorithm iteratively, they can purify the three-level Bell state 兩⌿00典 with the initial diagonal element p00⬎0.5. Furthermore, if the initial diagonal elements p₁₀= p₂₀= 0, we can purify兩⌿典 even with the initial diagonal element p00⬎

冑

2 − 1.

After purifying the raw entanglement, the sender and each receiver measure the syndrome of the three-ary—i.e., nonbinary—stabilizer code for purity testing 关17兴. In other words, three-ary quantum stabilizer codes are required for purity. Recently, nonbinary quantum stabilizer codes have been studied 关20–25兴. There must exist three-ary quantum stabilizer codes that encode m qutrit into n qutrit and can correct t “nice” errors TkRl, where

T:兩p典 → 兩p + 1 mod 3典, R:兩p典 → exp

冉

2p␲i

3

冊

兩p典 共17兲 关21兴. On the other hand, it is easy to verify

兩⌿kl典 = 共1丢TkRl兲兩⌿00典, ∀l,m = 0,1,2. 共18兲 Suppose that the states shared between Alice and each re-ceiver are assumed to be nearly in state兩⌿00典丢n. The sender and each receiver can correct t nice errors via quantum error correction codes 关15,16,26兴. Still, each receiver should broadcast the necessary measurement results. It is the sender that performs the needed local operations for error correct-ing. As a result, the sender can share perfect state兩⌿00典丢m. Next, the sender performs the nonlocality swapping. Now we propose protocol III of quantum secret sharing as follows.

Protocol III Preparation phase

共1兲 The sender Alice and the each receiver of Bob and Charlie agree on some stabilizer purity testing. In addition, Alice prepares two strings of Bell states

兵兩⌿00典B₁,兩⌿00典B₂, . . . ,兩⌿00典B_n⬘其 and

兵兩⌿00典C₁,兩⌿00典C₂, . . . ,兩⌿00典C_n⬘其 .

共2兲 Alice selects two random n

⬘

-bit strings b and b

⬘

. Alice performs the three-level Hadama transformation on the sec-ond half of兩⌿00典B_iand兩⌿00典C_iif the ith bitvalues of b and b

⬘

are 1, respectively.

共3兲 Alice sends the second half of each 兩⌿00典B_i and 兩⌿00典C_i, i = 1 , . . . , n

⬘

, respectively. Alice holds the first half of 兩⌿00典B_i and兩⌿00典C_i, i = 1 , . . . , n

⬘

.

共4兲 When Bob and Charlie receive their qutrits, they in-form Alice that they have received the qutrit over a classical channel, respectively.

共5兲 Alice announces the bit strings b and b

⬘

after she confirms that all qutrits have been received. Bob and Charlie then perform the three-level inverse Hadama transformation on the qutrits where b and b

⬘

are 1, respectively.

共6兲 Alice and each of Bob and Charlie perform the pro-posed QPA algorithm to purify兩⌿00典. Notably, Alice decides whether the purification is successful. If they fail to purify 兩⌿00典, Alice aborts the secret. Otherwise, Alice performs the following steps.

共7兲 Next they have to perform purity testing via measur-ing the syndrome of the preagreed stabilizer code关17兴.

共8兲 Alice performs nonlocality swapping in the basis of the complete set (共i, j,k兲,共i

⬘

, j

⬘

, k

⬘

兲) with set index Si.

Revealing phase

共9兲 Alice publicly announces the set index Siof the surement basis and who should perform the foremost mea-surement via classical communication.

共10兲 Bob and Charlie discuss the state index of the qutrits at hand.

共11兲 Bob and Charlie must announce some portion of the secret bits to detect possible deception behaviors. Conse-quently, Bob and Charlie perform step 共6兲 of the proposed protocol I.

After nonlocality swapping, Bob and Charlie have to dis-cuss the state index of the shared product state based on Alice’s announcement. The eavesdropper can forge the mea-surement results. Moreover, the eavesdropper can forge the measurement results in the error-correction process of distil-lation. Eventually, the sender and each receiver could share some Bell states other than兩⌿00典. In this case, the state of the qutrits 1 and 4 is not identical that of the qutrits 2 and 3 after the nonlocality swapping in Eq.共9兲. Therefore, any misstate-ment can be detected in step共11兲.

VI. CONCLUSION

This study introduces how to perform the quantum secret sharing via product states. These three proposed protocols can split information and detect eavesdropping simulta-neously using product states. Since the proposed protocols I and II in this study do not require any entanglement, their physical realization is very feasible. This study also investi-gates possible eavesdropping attacks. In addition, this study can revise the quantum key distribution protocols using product states as the quantum secret sharing protocols using product states. Furthermore, we provide a simple proof of protocols I and II.

ACKNOWLEDGMENT

L.Y.H. would like to thank the National Science Council of the Republic of China for financially supporting this re-search under Contract No. NSC. 93–2119–M-033–001.

FIG. 2.共Color online兲 Average fidelity of the proposed three-level quantum privacy amplification, which is a function of the initial fidelity and the number of iterations.

关1兴 M. Hillery, V. Bužek, and A. Berthiaume, Phys. Rev. A 59, 1829共1999兲.

关2兴 M. Koashi and N. Imoto, Phys. Rev. Lett. 79, 2383 共1997兲. 关3兴 V. Karimipour, A. Bahraminasab, and S. Bagherinezhad, Phys.

Rev. A 65, 042320共2002兲.

关4兴 A. Cabello, e-print quant-ph/0009025.

关5兴 S. Bagherinezhad and V. Karimipour, Phys. Rev. A 67, 044302共2003兲.

关6兴 M. Hillery and J. Mimih, Phys. Rev. A 67, 042304 共2003兲. 关7兴 C. H. Bennett and G. Brassard, in Proceedings of IEEE

Inter-national Conference on Computers, Systems and Signal Pro-cessing共IEEE, New York, 1984兲, p. 175.

关8兴 C. H. Bennett, Phys. Rev. Lett. 68, 3121 共1992兲.

关9兴 L. Goldenberg and L. Vaidman, Phys. Rev. Lett. 75, 1239 共1995兲.

关10兴 G.-P. Guo, C.-F. Li, B.-S. Shi, J. Li, and G.-C. Guo, Phys. Rev. A 64, 042301共2001兲.

关11兴 C. H. Bennett, D. P. DiVincenzo, C. A. Fuchs, Tal Mor, E. Rains, P. W. Shor, J. A. Smolin, and W. K. Wootters, Phys. Rev. A 59, 1070共1999兲.

关12兴 W. K. Wootters and W. H. Zurek, Nature 共London兲 299, 802 共1982兲.

关13兴 N. Gisin, G. Ribordy, W. Tittel, and H. Zbinden, Rev. Mod.

Phys. 74, 145共2002兲.

关14兴 A. K. Ekert, Phys. Rev. Lett. 67, 661 共1991兲.

关15兴 P. W. Shor and J. Preskill, Phys. Rev. Lett. 85, 441 共2000兲. 关16兴 H.-K. Lo and H. F. Chau, Science 283, 2050 共1999兲. 关17兴 H. Barnum, C. Crépeau, D. Gottesman, A. Smith, and A. Tapp,

in Proceedings of The 43rd Annual IEEE Symposium on Foun-dations of Computer Science (FOCS’02) 共IEEE, New York, 2002兲, pp. 16–19.

关18兴 L. Y. Hsu, Phys. Rev. A 65, 062302 共2002兲.

关19兴 D. Deutsch, A. Ekert, R. Jozsa, C. Macchiavello, S. Popescu, and A. Sanpera, Phys. Rev. Lett. 77, 2818共1996兲.

关20兴 E. Knill, e-print quant-ph/9608048.

关21兴 A. Ashikhmin and E. Knill, IEEE Trans. Inf. Theory 47, 3065 共2001兲.

关22兴 E. Rains, e-print quant-ph/9703048.

关23兴 A. Ashikhmin and S. Litsyn, IEEE Trans. Inf. Theory 45, 1206 共1999兲.

关24兴 R. Matsumoto and T. Uyematsu, IEICE Trans. Fundamentals

83, 1206共2000兲.

关25兴 E. Knill, e-print quant-ph/9608049.

关26兴 Charles H. Bennett, David P. DiVincenzo, J. A. Smolin, and W. K. Wootters, Phys. Rev. A 54, 3824共1996兲.