Effect of atomic position on the spontaneous emission of a three-level atom in a coherent photonic-band-gap reservoir

(1)

Effect of atomic position on the spontaneous emission of a three-level atom

in a coherent photonic-band-gap reservoir

Szu-Cheng Cheng,1,

*

Jing-Nuo Wu,2,† Tzong-Jer Yang,3and Wen-Feng Hsieh2 1

Department of Physics, Chinese Culture University, Taipei, Taiwan, Republic of China 2

Department of Photonics, National Chiao Tung University, Hsinchu, Taiwan, Republic of China 3

Department of Electrical Engineering, Chung Hua University, Hsinchu, Taiwan, Republic of China 共Received 10 May 2008; revised manuscript received 6 September 2008; published 5 January 2009兲 The effect of atomic position on the spontaneous emission and optical spectra of a three-level atom embed-ded in a photonic crystal was studied by considering the coherent two-band photonic-band-gap共PBG兲 reser-voir. With the definite phase difference between the fields of the air band and dielectric band in this coherent PBG reservoir, we found that this coherent property grows stronger and results in the spectrum shift and the appearance of dark lines and kinks as the width of band gap gets smaller; and the variation of the atomic position leads to large shift of spectral peak. The averaged spectra of the system with an ensemble of atoms embedded in the dielectric region are blueshifted while those of atoms in the air region are redshifted. The spectra peaks can even shift more than 75% of the half width at half maximum. The feasible experimental systems composed of an ensemble of molecules共quantum dots or fluorescence dye兲 in photonic crystals are discussed.

DOI:10.1103/PhysRevA.79.013801 PACS number共s兲: 42.50.Gy, 42.70.Qs

I. INTRODUCTION

It is well known that spontaneous emission共SE兲 rate and optical properties of atoms can be modified effectively by placing the atoms in photonic band gap 共PBG兲 materials 关1–10兴, where the density of modes of the reservoirs has

significant deviation from that of free space vacuum. This modification changes the atomic coherence and quantum in-terference effects and provides potential application to quan-tum optical communication. The related atomic coherence effects include the electromagnetically induced transparency 共EIT兲关11兴, lasing without inversion 关12,13兴, slow

propaga-tion of light 关14兴, and nonlinear effects at low light level

关15兴.

Here we propose a different point of view on varying the SE and optical resonant spectra through changing the relative position of the embedded atom in photonic crystals共PCs兲. It originates from the fact that the strength of photon-atom in-teraction depends on the atomic position 关16兴 and the

two-band reservoir becomes coherent and can interfere with each other, which results from the definite phase difference be-tween the air-band and dielectric-band fields of PBG 关17兴.

One band approximation is valid when the PBG is relatively wide and the transition frequencies of the atoms is near the air or dielectric band edge. For the photonic crystals with narrow band gap, the photon-atom coupling between the em-bedded atom and the system has to consider the contribution of both electric fields from the air-band and dielectric-band reservoirs. Existence of both reservoirs leads to a stronger photon-atom coupling关16兴, and the time evolution decay of

the excited population of a two-level atom has been shown faster than that in the one-band approximation. Although atomic coherence in a⌳-type three-level atom embedded in

a PBG structure has been studied using the two-band model 关18–20兴, it was assumed that the atom inside PCs interacted

with two incoherent PBG reservoirs. The results of Ref.关18兴

revealed that the photon-atom coupling strengths of both res-ervoirs were the same and independent of the position of the embedded atom. In this paper, a⌳-type three-level atom em-bedded in a PBG structure is studied共Fig.1兲. One transition

level of the atom共兩2典↔具1兩兲 lies near the PBG edge; the other transition 共兩2典↔具0兩兲 is far from the PBG edge and couples with the Markovian reservoir. We investigate the spontane-ous emission spectrum of atoms in the PBG reservoir with a coherent property, which depends on the embedded position of the atom and the width of the band gap. The variation of the atomic position and band-gap width would lead to the change of the SE rate and the spectra of absorption and dis-persion. These results provide a new degree of freedom to vary the SE and optical properties in PCs, especially for nonlinear optical phenomena.

This paper is organized as follows. In Sec. II, we derive the atom-field coupling Hamiltonian, where the position de-pendence of the atom-field coupling constants is considered, and show that this position dependence of the atom-field couplings is induced by the phase difference of the air-band and dielectric-band fields at different locations of the embed-ded atom. In Sec. III, we apply the Schrödinger picture to describe the interaction of the embedded atom with the PBG reservoir. We then calculate the SE spectrum in the free space vacuum and discuss it under the different band-gap widths and relative positions of the atom. In Sec. IV, we discuss the optical properties of the system by adding a weak probe laser to the system. Absorption and dispersion spectra of the system are studied. Finally, we summarize our results in Sec.V.

II. ATOM-FIELD COUPLING HAMILTONIAN

Considering the system of an excited atom embedded in a photonic crystal under the Coulomb gauge⵱·Aជ= 0, one can *FAX:_{⫹886-2-28610577. sccheng@faculty.pccu.edu.tw}

(2)

write the interaction Hamiltonian of the atom with a radia-tion field as

H = − e

mPជ· AជPC, 共1兲

where e and m are the charge and mass of single electron in the atom, Pជ is the momentum of the electron without spin, and the radiation field for the reservoir of a photonic crystal is described by the quantized vector potential AជPC. This

vec-tor potential can be expressed as 关16兴 AជPC共rជ0,t兲 =

兺

n

冕

BZ dkជ 共2␲兲3

冑

ប 2⑀0␻n,kជV

⫻关Aជn,kជ共rជ0兲aˆn,kជe−i␻kជt+ Aជ_n,kជ* 共rជ0兲aˆn,kជ +

ei␻_kជt_{兴, 共2兲}

where V is the volume of a unit cell of the lattice,⑀₀ is the Coulomb constant, n is the energy band index in the first Brillouin zone representing the air band by a and the dielec-tric band by d, and the integral is over each band in this region of kជ space. In addition, aˆ_n,kជ+ and aˆn,kជ are the creation

and annihilation operators for a field mode with energy band index n, wave vector kជ, and frequency ␻kជ. Here the Bloch

modes Aជ_n,kជ satisfy the Bloch-Floquet theorem Aជ_n,kជ共rជ₀+ Rជ兲 = eikជ·Rជ_Aជ

n,kជ共rជ0兲 and a reduced zone scheme for kជis adopted. If

only dipole contribution of the electronic charge distribution is considered, the interaction Hamiltonian for the field modes in PCs could be expressed as关2兴 HPC⬇ − e mPជ· AជPC共rជ0,t兲 = − iប

兺

n,kជ

g_n,kជ共兩j典具i兩aˆ_n,kជe−i␻kជt_{− aˆ}

n,kជ + ei␻kជt兩i典具j兩兲, 共3兲 where gn,kជ= ␻ij ប共2⑀0ប␻kជV兲 1/2_d ij ជ _{· E}ជ n,kជ * _共r_ជ 0兲 is the position-dependent

coupling strength of the atom with the photonic crystal field modes共n兲, dជijis the atomic dipole moment for the transition

兩i典→兩j典 with basis vectors 兵兩i典其 forming a complete orthogo-nal set of the atomic system, and ␻ij=␻i−␻j is the atomic

transition frequency between levels兩i典 and 兩j典. Note that rជ₀is designated to be the position of the atomic nucleus. We shall assign Eជ

a,kជ

* _共r_ជ

0兲 and Eជ_d,kជ* 共rជ0兲 as the atom-coupling fields from

the air band and dielectric band, respectively.

In discussing the physical origin of the PBG, Joannopo-ulos et al.关17兴 applied the electromagnetic variational

theo-rem and found that the low-frequency modes concentrate their energy in the high dielectric constant regions and the high-frequency modes in the low dielectric regions. Since the low dielectric regions are often air regions, they therefore refer to the high-frequency modes as the “air band” and the low-frequency modes as the “dielectric band.” The PBG 共fre-quency difference兲 arises due to this difference in field en-ergy location. The corresponding distributions of electric fields of one-dimensional photonic crystals are plotted in

Figs.2共a兲and2共b兲. These distributions of electric fields from the two-band reservoir are two coherent waves with ␲/2 phase difference and can thus be given by

Eជ a,kជ

* _共r_ជ

0兲 = Ekជcos␪共rជ0兲⑀ˆ, Eជ*_d,kជ共rជ0兲 = Ekជsin␪共rជ0兲⑀ˆ , 共4兲

where⑀ˆ is a unit vector of the electric field, the angle

param-eter␪共rជ0兲 “sees” by the active atom located at rជ0within a unit

cell关21兴, and a single amplitude Ekជis contained in these two

coherent eigenmode fields. The position-dependent effect on the atom-field coupling is thus constructed to illustrate the connection of the atomic actual position with angle param-eter␪共rជ0兲关22兴. This effect is absent in the previous two-band

model关23兴, in which two independent eigenmode fields were

used for the two-band reservoir. Notice that our two-band model reduces to the single-band model as␪共rជ0兲=0 共or ␲2兲.

) (

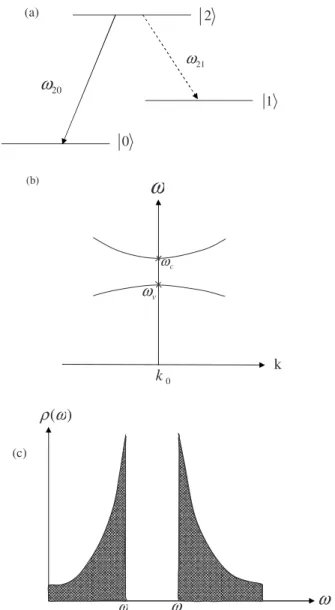
ω

(3)

III. SPONTANEOUS EMISSION IN THE FREE-SPACE RESERVOIR

Consider a ⌳-type three-level atom, whose energy dia-gram is shown in Fig.1, being embedded inside a PBG struc-ture. The atom is assumed to be initially excited in state兩2典. The transition between 兩2典↔具1兩 is considered to be near resonant with the band edge of the PBG reservoir, while the transition between兩2典↔具0兩 is assumed to be far away from the PBG edge, and is coupling with the free-space reservoir. In a rotating-wave approximation, the interaction Hamil-tonian for a three-level atom and the electromagnetic field in a photonic crystal can be written as

H =ប

兺

␭

g_␭e−i共␻␭−␻20兲t兩2典具0兩aˆ

␭+ប

兺

a

ga共rជ0兲e−i共␻a−␻21兲t兩2典具1兩aˆa

+ប

兺

d

gd共rជ0兲e−i共␻d−␻21兲t兩2典具1兩aˆd+ H.c. 共5兲

Here g_␭characterizes the coupling constant of the atom with the free-space vacuum modes␭ while the position-dependent coupling strength of the atom with the air共dielectric兲 -band-reservoir modes a共d兲 has the form of

ga共d兲共rជ0兲 = ␻21 ប

冋

ប 2⑀₀␻a共d兲V

册

1/2 dជ21· Eជa共d兲 * _共r_ជ 0兲. 共6兲

We denoted the atomic transition frequency as␻ijphotonic

eigenmode frequency as ␻a共d兲, and fixed polarization

orien-tation of atomic dipole moment dជ21关24兴.

In the single photon sector, the wave function of the sys-tem could be described as

兩⌿共t兲典 =␣2共t兲兩2,兵0␭,0a,0d其典 +

兺

␭ ␣0␭共t兲兩0,兵1␭ ,0a,0d其典 +

兺

a ␣1a共rជ0,t兲兩1,兵0␭,1a,0d其典 +

兺

d ␣1d共rជ0,t兲兩1,兵0␭,0a,1d其典. 共7兲

Here ␣2共t兲 and ␣0␭共t兲 are the probability amplitudes of the

system in the states 兩2,兵0_␭, 0a, 0d其典 and 兩0,兵1_␭, 0a, 0d其典,

which describe the atom in the state 兩2典 with no photon and in the state 兩0典 with a single photon in the mode ␭, respec-tively. The probability amplitudes of the system in the states 兩1,兵0␭, 1a, 0d其典 and 兩1,兵0␭, 0a, 1d其典共the atom in the state 兩1典

and a photon in either the air or dielectric band兲 are consid-ered to be functions of atomic position and assumed to be

␣1a共rជ0,t兲 =␣1kជ共t兲cos␪共rជ0兲, ␣1d共rជ0,t兲 =␣1kជ共t兲sin␪共rជ0兲.

共8兲 This assumption comes from the position-dependent electric fields of the two-band reservoir and makes the probability of the system in atomic level 兩1典 to be 兩␣1kជ共t兲兩2.

As the SE rate is studied, we assume the atom is initially excited in state 兩2典. By substituting the interaction Hamil-tonian and single-photon wave function into the time-dependent Schrödinger equation, we have the time evolution of the probability amplitudes,

id dt␣2共t兲 =

兺

_␭ g␭␣0␭共t兲e −i共␻_␭−␻20兲t +

兺

a ga共rជ0兲␣1a共rជ0,t兲e−i共␻a−␻21兲t +

兺

d gd共rជ0兲␣1d共rជ0,t兲e−i共␻d−␻21兲t, 共9兲 id dt␣0␭共t兲 = g␭␣2共t兲e i_共␻_␭−␻20兲t_, 共10兲 id dt␣1a共rជ0,t兲 = ga共rជ0兲␣2共t兲e i共␻_a−␻₂₁兲t , 共11兲 id dt␣1d共rជ0,t兲 = gd共rជ0兲␣2共t兲e i共␻_d−␻₂₁兲t . 共12兲

Combining these equations with position-dependent coupling strength and probability amplitudes 关Eqs. 共6兲 and 共8兲兴, we

obtained the integrodifferential equation

d dt␣2共t兲 = −

兺

_kជ gkជ 2

冕

0 t d␶␣2共␶兲

⫻关sin2_␪_e−i共␻d−␻21兲t_{+ cos}2␪_e−i共␻a−␻21兲t兴

⫻ 关sin2_␪ei共␻_d−␻₂₁兲␶ + cos2␪ei共␻a−␻21兲␶兴 −

兺

␭ g_␭2

冕

0 t d␶␣₂共␶兲e−i共␻␭−␻20兲共t−␶兲_, 共13兲 (b) (a)

FIG. 2. 共Color online兲共a兲 The electric field profile of dielectric-band modes and共b兲 air-band modes from the two-band reservoir of one-dimentional photonic crystals. The high-dielectric region is in blue共darker兲 color and low-dielectric region in yellow 共faint兲 color.

(4)

where we have approximated ga共rជ0兲⬵gkជcos␪共rជ0兲

and gd共rជ0兲⬵gkជsin␪共rជ0兲 with real constant gkជ

=␻_ប21共_2⑀ប

0␻kជV兲

1/2_E

kជ共dជ21·⑀ˆ兲 which agrees with the case of single

amplitude for electric fields. The first summation reveals the quantum interference of two atomic-emission channels along with the two-band PBG reservoir共␻21⬵␻aand␻21⬵␻d兲. It

could be further dealt with by defining the the memory func-tions共or kernels兲 from the PBG reservoir as

K1共t兲 =

兺

kជ g_kជ2e−i共␻d−␻21兲t₌␤3/2

冕

冑

t. 共16兲 The Laplace transforms of these memory kernels are

K˜1共s兲 =␤3/2ei␲/4/共2

冑

s + i␦v兲, K˜2共s兲 =␤3/2e−i␲/4/共2

冑

s + i␦c兲,

共17兲 which have two singularities exhibiting two dark lines of the SE spectrum 关18兴.

Our aim is to derive the long time spontaneous emission spectrum of the transition兩2典↔具0兩 within the Markovian res-ervoir, namely, S共␦␭兲⬀兩␣0␭共t→⬁兲兩2 with the detuning

fre-quency ␦_␭=␻_␭−␻₂₀. The long-time probability amplitude

␣0␭共t→⬁兲 could be also obtained from the final-value

theo-rem ␣_0␭共t→⬁兲=lims→0关s␣˜0␭共s兲兴 with ␣˜0␭共s兲 being the

Laplace transform of ␣0␭共t兲 in Laplace variable s. Through

performing the final-value theorem and Laplace transform, we have

S共␦_␭兲 ⬀␥兩˜␣₂共s = − i␦_␭兲兩2_, _共18兲

with ␣˜₂共s兲 being the Laplace transform of the probability

amplitude␣2共t兲 and given by

␣ ˜₂共s兲 = 兵1 − sin2_␪_共r_ជ 0兲cos2␪共rជ0兲关˜␣2共s + iD␻兲K˜1共s + iD␻兲 +␣˜₂共s − iD_␻兲K˜₂共s − iD_␻兲兴其 ⫻ 关s +␥/2 + cos4_␪_共r_ជ 0兲K˜2共s兲 + sin4␪共rជ0兲K˜1共s兲兴−1, 共19兲 where D_␻=␻a−␻dis the frequency difference of the air-band

and dielectric-band modes at a fixed wave vector and K˜1共s兲

and K˜2共s兲 are the Laplace transforms of the memory kernels

expressed in Eq. 共17兲. We can approximate the frequency

difference D_␻by the band gap⌬=␻c−␻v⬵D␻because most

of the PBG density of states 共DOS兲 is contributed from the states near band edges关see Fig.1共c兲兴. Here we have applied the Weisskopf-Wigner result关25兴 to the free-space modes ␭

and used the iterative method once in this nonlocal differ-ence equation␣˜₂共s兲 to get the SE spectrum:

␣ ˜₂共s兲 ⬵␣˜₂共0兲共s兲兵1 − sin2_␪_共r_ជ 0兲cos2␪共rជ0兲关␣˜2共0兲共s + iD␻兲 ⫻K˜1共s + iD␻兲 +␣˜2共0兲共s − iD␻兲K˜1共s − iD␻兲兴其共20兲 with␣˜₂共0兲共s兲=关s+␥/2+cos4_␪_共rជ 0兲K˜2共s兲+sin4␪共rជ0兲K˜1共s兲兴−1.

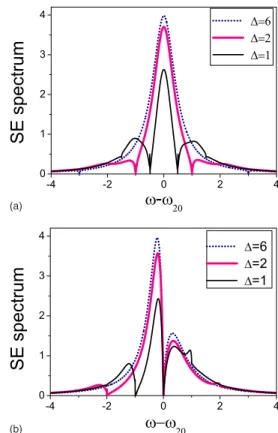
The SE spectra were plotted as a function of detuning frequency ␦_␭=␻−␻20 for several gap widths 共⌬兲 in Fig.3.

The symmetric case in which the atomic transition frequency

␻21is chosen at the middle of the gaps is shown in Fig.3共a兲. (b)

(a)

FIG. 3. 共Color online兲 The SE spectra for several gap widths 共⌬兲. The parameters 共in units of coupling constant␤兲 are decay rate ␥=1, ␪共rជ0兲=␲/4, PBG width ⌬=6 共dotted line兲, ⌬=2 共faint solid line兲, ⌬=1 共dark solid line兲, and 共a兲 detuning frequency of band edge ␦c= −␦v=⌬/2 for the symmetric cases; 共b兲␦c= 0, ␦v= −⌬ for

(5)

As expected for the large gap width ⌬=6, the excited atom mainly couple to the free-space vacuum and thus the spec-trum shows a single Lorentzian peak关18兴, which is referred

to as the free-space light. However, as decreasing the gap width, other than the main peak, we observed two symmetric side lobes separated by zeros, which result from strong cou-pling of the excited atom through the兩2典→兩1典 transition with the PBG reservoir at these two band edges, where we have the largest DOS. The zeros are also termed the dark lines 关26兴. These two side lobes originate from the atomic

free-space transition coupling to the PBG vacuum, which are re-ferred to as the PBG light. This coherent coupling effect grows stronger for the smaller gap widths. For the asymmet-ric case, in which the atomic transition frequency ␻₂₁ is lo-cated at the air-band edge, the spectrum of the larger PBG is close to that of the single-band case 关2,3兴; whereas, as

de-creasing the gap width, the free-space light will be signifi-cantly quenched by the atom’s emitting the PBG light or loss population through the兩2典→兩1典 transition. These results dra-matically differ from those of the previous model 关18–20兴,

which considered the non-Markovian reservoir as two inco-herent PBG reservoirs and showed no intensity quench. Our model reveals, for the smaller gap width, an apparent quan-tum interference effect 共quench in the main peak and en-hance dark lines at the band edges兲 as a result of considering the fields of the non-Markovian reservoir as coherent mode fields. The interference of the free-space light with PBG light from the air band is the same as that from the dielectric band for the symmetric case, whereas it is enhanced in the air band for the asymmetric case 共␻21at the air-band edge兲. Besides,

this quantum interference effect also happens when the field modes from the air band interfere strongly with the modes from the dielectric band via the atom. Its result is shown by two shallow kinks of two side lobes for the symmetric case and by an abrupt kink of the right-hand side lobe for the asymmetric case in small gap width ⌬=1.

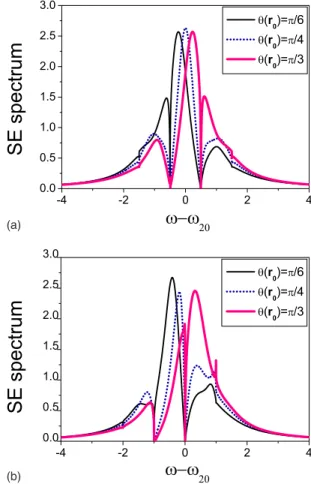
Next, we shall consider how the SE spectrum is affected by the relative position of the atom in a Wigner-Seitz cell which is described by the position-dependent parameter

␪共rជ0兲. Both the symmetric case and the asymmetric case were

considered for narrow gap 共⌬=1兲 and shown in Figs. 4共a兲 and4共b兲. As increasing the␪共rជ₀兲 value, we observed that for both the symmetric and asymmetric cases, the free-space light makes a blueshift with increasing ␪共rជ0兲 but does not

have much change in intensities. The increase of␪共rជ0兲 causes

the growth of the dielectric-band field strength 关Eជ

d,kជ

* = Ekជsin␪共rជ0兲⑀ˆ兴 and thus the stronger coherent coupling with

the dielectric-band field to push the free-space light toward the air band. Therefore the interference between the free-space light and the air-band PBG light is then enhanced. It results in the blueshift and increasing radiated power of the air-band PBG light. For the asymmetric case共␻21at the

air-band edge兲, the resonant effect enhances the more radiated power of the air-band PBG light such that the radiated power of the air-band PBG light eventually becomes stronger than that of the free-space light at␪共rជ0兲=␲/3.

When we consider the system of an ensemble of nonin-teracting atoms embedded in photonic crystals at symmetry-inequivalent positions with low density per unit cell, the

av-eraged SE spectra shown in Fig. 5 reveal large values of peak-frequency shift. The system with atoms embedded in the dielectric region has blueshift spectra, while those of at-oms in air are redshifted. The variation of atomic embedded region results in the spectra shift up to 46.9关Fig.5共a兲兴 and

77.8关Fig.5共b兲兴 percentage of the half width at the half

maxi-mum. This evident phenomenon can be observed in the ex-perimental system of an ensemble of CdSe-ZnSe quantum dots embedded in an inverse opal consisting of air spheres in TiO2关27兴 or ensemble of dye molecules in silica opals 关28兴.

The phenomenon of atomic-position dependent spectrum had also been observed experimently by Akahan et al. 关29兴.

In order to fabricate a high-Q nanocavity in a silicon-based two-dimensional photonic-crystal slab, they tuned the posi-tion of air rods to get a gentler electric field profile at the cavity edges. The peak frequency of the resonant spectrum shifts with the position of the air rods which is shown in Fig.

4. The distribution of the electric field in the cavity is changed because of the movement of the air rods. The air-rods position-dependent spectrum has the same mechanism as that of our result in which atomic position changes field distribution.

(b) (a)

FIG. 4. 共Color online兲 The SE spectra for several atomic posi-tion parameters ␪共rជ0兲. The parameters 共in units of␤兲 are ␥=1, ⌬ = 1, ␪共rជ0兲=␲/6 共dark solid line兲, ␪共rជ0兲=␲/4 共dotted line兲, ␪共rជ0兲 =␲/3 共faint solid line兲, and 共a兲 ␦_c= −␦_v= 0.5 for the symmetric cases;共b兲␦c= 0, ␦v= −1 for the asymmetric cases共␦c=␻c−␻21,␦v

(6)

IV. THE ABSORPTION AND DISPERSION FOR A PROBE LASER FIELD

In this section we shall discuss the absorption and disper-sion properties of the system by applying a weak probe laser 关30兴 with field angular frequency␻⬵␻20 to the atomic

ini-tial ground state 兩0典. When the perturbed behavior of the system to the probe laser pulse is considered, we add a free-space decay rate ␥ to the excited state 兩2典 and express the effective Hamiltonian as

H =

冋

ប⍀ei␦t兩0典具2兩 + ប

兺

a

ga共rជ0兲e−i共␻a−␻21兲t兩2典具1兩aˆa

and

b1a共rជ0,t兲 = b1kជ共t兲cos␪共rជ0兲, b1d共rជ0,t兲 = b1kជ共t兲sin␪共rជ0兲

共24兲 to the position-dependent coupling strength and probability amplitudes. Substituting these equations into the time-dependent Schrödinger equation, we obtained the time evo-lution of the probability amplitudes

id

dtb0共t兲 = ⍀b2共t兲, 共25兲

(b) (a)

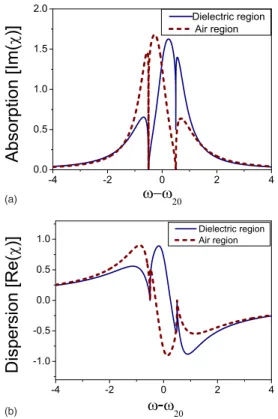
FIG. 6. 共Color online兲共a兲 Absorption and 共b兲 dispersion of the system. The parameters are ␥=1, ␦_c= −␦_v= 0.5 共symmetry case兲, ⌬=1 共narrow gap兲, and ␪共rជ0兲=␲/6 共dark solid line兲; ␪共rជ0兲=␲/4 共dotted line兲;␪共r0ជ 兲=␲/3 共faint solid line兲.

(b) (a)

FIG. 5. 共Color online兲 The averaged SE spectra of the system with atoms symmetric-inequivalently embedded in air region and dielectric region. The parameters 共in units of ␤兲 are ␥=1, ⌬=1, ␲/4艋␪共rជ0兲艋3␲/4 for the dielectric region 共solid line兲 and −␲/4 艋␪共rជ0兲艋␲/4 for the air region 共dashed line兲, and 共a兲 ␦c= −␦v

= 0.5 for the symmetric cases;共b兲␦c= 0,␦v= −1 for the asymmetric

(7)

id dtb2共t兲 = ⍀b0共t兲 −

冉

␦+ i ␥ 2

冊

b2共t兲 + ei␦t

兺

kជ

gkជb1kជ共t兲e−i共␻a−␻21兲tcos2␪共rជ0兲

+ ei␦t

兺

kជ

gkជb1kជ共t兲e−i共␻d−␻21兲tsin2␪共rជ0兲, 共26兲

id

dtb1kជ共t兲 = e −i␦t

gkជb2共t兲ei共␻a−␻21兲tcos2␪共rជ0兲

+ e−i␦tgkជb2共t兲ei共␻d−␻21兲tsin2␪共rជ0兲. 共27兲

共t −␶兲e iD_␻t sin2␪cos2␪. 共29兲 Our aim of the absorption and dispersion properties can be obtained from the steady-state linear susceptibility ␹ of the system. Under the assumption of a weak laser-atom in-teraction and兩0典↔兩2典 transition occurring in the Markovian reservoir, this linear susceptibility can be expressed as关18兴

␹共␦兲 = −4␲Ꭽ兩dជ20兩2

⍀ b0共t → ⬁兲b₂*共t → ⬁兲. 共30兲

We assume that the Rabi frequency ⍀Ⰶ␥ 共decay rate兲,

b0共t兲⬇1 for all times, and the atomic-density related

con-stant 4␲Ꭽ兩dជ20兩2⬅1 with one embedded atom in the system.

Here the long-time behavior of the probability amplitude

b2共t→⬁兲 could be resolved from the final-value theorem and

the Laplace transform, so the linear susceptibility is

␹共␦兲 = − 1

␦− i␥/2 − i cos4␪共rជ0兲K˜₂*共− i␦兲 − i sin4␪共rជ0兲K˜₁*共− i␦兲

共31兲 with K˜₁*and K˜₂*being the complex conjugates of the Laplace transforms of the non-Markovian kernels, which are deter-mined by the PBG model in Eq. 共17兲. The absorption (−Im关␹共␦兲兴) and dispersion (Re关␹共␦兲兴) spectra of the probe

field are thus affected by the DOS of the PBG reservoir. Besides, these spectra are also affected by the atomic posi-tion inside the PC because of the posiposi-tion-dependent angle

␪共rជ0兲.

The absorption and dispersion spectra for the two-coherent-band system were plotted based on Eq.共31兲 in Fig. 6. The absorption spectra exhibits similar behavior to the spontaneous-emission ones having a central peak with two side lobes and blueshift in the central peak at increasing

␪共rជ0兲. The two-band absorption profiles of the

atomic-position dependence is shown in Fig. 6共a兲 for the atomic resonance␻₂₁at the middle of the gap共symmetric case兲. The transparent windows are independent of the relative position of the atom关␪共rជ0兲兴 because they are determined by the DOS

of the PBG reservoir 关18兴. As the field strength from the

dielectric band of the PBG reservoir grows stronger关␪共rជ₀兲 is increased兴, the central peak of absorption is lying close to the air-band edge 共right-hand side兲. And the absorption on the air-band side lobe is enhanced while the dielectric-band side lobe is suppressed due to coherence coupling and quantum interference effect. As␪共rជ₀兲 increases, stronger coupling with the dielectric-band field pushes the free-space absorption line

(b) (a)

FIG. 7. 共Color online兲共a兲 Averaged absorption and 共b兲 disper-sion of the system with atoms symmetric-inequivalently embedded in the air region and the dielectric region. The parameters are ␥ = 1, ␦_c= −␦_v= 0.5 共symmetry case兲, ⌬=1 共narrow gap兲, and ␲/4 艋␪共rជ0兲艋3␲/4 for the dielectric region 共solid line兲 and −␲/4 艋␪共rជ0兲艋␲/4 for the air region 共dashed line兲.

(8)

共central peak兲 toward the air-band edge. Stronger quantum interference between this central-peak light and the PBG light of the air band enhances the air-band side lobe intensity. This quantum interference effect is due to the coherence of the PBG reservoir, which has a more enhanced effect for the smaller PBG. The coherent property can also affect the trans-mission of the probe light shown in Fig.6共b兲. The frequency of the slow velocity photon shifts toward the blue side for increased ␪共rជ₀兲. That is, the slow photons with higher fre-quency represent the stronger coupling with the dielectric-band field. When the experimentally feasible system of an ensemble of noninteracting atoms embedded in the photonic crystal at different region is considered, the averaged absorp-tion spectra shown in Fig. 7共a兲also exhibit large values of peak-frequency shift with 49.2% of the half width at half maximum. The frequency shift of the slow photon in the averaged dispersion spectra shown in Fig. 7共b兲 reaches 57.1% of the peak-to-peak width. This noticeable result could be verified in the experimental system with quantum dots of several nm 共4.5 nm兲 in the air and dielectric region 共130–380 nm兲, respectively, of photonic crystals as in Ref. 关27兴.

V. CONCLUSION

We have studied the effect of atomic position on the spec-tra of spontaneous emission, absorption, and dispersion of a three-level atom with ⌳ configuration in a PBG reservoir using the two-band isotropic effective-mass model. With the consideration of the definite phase difference between the air-band and dielectric-band fields, we found that the two-band reservoir is coherent and can interfere with each other. The coupling strength of the atom with this coherent reser-voir depends on the embedded position of the atom. This is quite different from the previous two-band studies, which took the PBG reservoir as two independent and incoherent

reservoirs and assumed equal strength of coupling between the atom and each individual reservoir of the PBG. Our SE spectra show the coherence phenomenon of the PBG reser-voir through the intensity changes of the free-space light and PBG light. Besides, for the small PBG, the spectra of the PBG light reveal quantum interference effect of the PBG reservoir by means of kinks of side lobes. The atomic position-dependent coupling strength is shown by the blue-shift of the free-space light in SE spectra, in which the phe-nomenon of atomic-position dependent spectra has been ob-served in experiment关29兴. The profiles of the absorption and

dispersion show the coherent and quantum interference prop-erties, too. With the variation of atomic position 关␪共rជ0兲兴, we

could observe the coherent property of the reservoir by the shift of the free-space absorption line. The intensity changes of the absorption side lobe illustrate the quantum interfer-ence effect of the system with the small PBG. The coherent property could also be observed in the dispersion spectra, whose frequencies of the slow photons vary with atomic po-sition parameter ␪共rជ0兲. It results in the change of the

refrac-tion index with the atomic posirefrac-tion. When we consider the practical system in experiment, the averaged spectra of the system with an ensemble of noninteracting atoms embedded in photonic crystals at symmetry-inequivalent positions show large values of peak-frequency shift up to 77.8% of the half width at half maximum. This consequence is visible in the system of an ensemble of CdSe-ZnSe quantum dots embed-ded in an inverse opal made of air spheres in TiO₂ 关27兴 or

dye molecules in silica opals关28兴.

ACKNOWLEDGMENTS

We greatly acknowledge partial support from the National Science Council of the Republic of China under Contracts No. NSC 96-2914-I-009-017, No. NSC 95-2119-M-009-029, No. NSC 96-2112-M-034-002-MY3, and No. NSC 96-2628-M-009-001.

关1兴 R. F. Nabiev, P. Yeh, and J. J. Sanchez-Mondragon, Phys. Rev. A 47, 3380共1993兲.

关2兴 S. John and T. Quang, Phys. Rev. A 50, 1764 共1994兲. 关3兴 A. G. Kofman, G. Kurizki, and B. Sherman, J. Mod. Opt. 41,

353共1994兲.

关4兴 T. Quang, M. Woldeyohannes, S. John, and G. S. Agarwal, Phys. Rev. Lett. 79, 5238共1997兲.

关5兴 S.-Y. Zhu, H. Chen, and H. Huang, Phys. Rev. Lett. 79, 205 共1997兲.

关6兴 Y. Yang, S.-Y. Zhu, and M. S. Zubairy, Opt. Commun. 166, 79 共1999兲.

关7兴 S. Bay, P. Lambropoulos, and K. Molmer, Opt. Commun. 132, 237共1996兲.

关8兴 S. Bay, P. Lambropoulos, and K. Molmer, Phys. Rev. A 55, 1485共1997兲.

关9兴 S. Bay and P. Lambropoulos, Opt. Commun. 146, 130 共1998兲. 关10兴 N. Vats and S. John, Phys. Rev. A 58, 4168 共1998兲.

关11兴 S. E. Harris, Phys. Today 50 共7兲, 36 共1997兲.

关12兴 S. E. Harris and L. V. Hau, Phys. Rev. Lett. 82, 4611 共1999兲. 关13兴 M. O. Scully, S.-Y. Zhu, and A. Gavrielides, Phys. Rev. Lett.

62, 2813共1989兲.

关14兴 L. V. Hau, Phys. World 14 共9兲, 35 共2001兲. 关15兴 S. E. Harris, Phys. Rev. Lett. 62, 1033 共1989兲.

关16兴 N. Vats, S. John, and K. Busch, Phys. Rev. A 65, 043808 共2002兲.

关17兴 J. D. Joannopoulos, S. G. Johnson, J. N. Winn, and R. D. Meade, Photonic Crystals: Molding the Flow of Light, 2nd ed. 共Princeton University Press, Princeton, NJ, 2008兲, URL: http:// ab-initio.mit.edu/book

关18兴 D. G. Angelakis, E. Paspalakis, and P. L. Knight, Phys. Rev. A

64, 013801共2001兲.

关19兴 M. Woldeyohannes and S. John, J. Opt. B: Quantum Semiclas-sical Opt. 5, R43共2003兲.

关20兴 S. R. Entezar and H. Tajalli, J. Phys. B 39, 2959 共2006兲. 关21兴 R. Sprik, B. A. van Tiggelen, and A. Lagendijk, Europhys.

(9)

关22兴 For example, if one defines ␪共r0ជ 兲=0 in the middle of the air region of the unit cell, then the middle of the dielectric region of the unit cell corresponds to␪共r0ជ 兲=␲/2. Therefore these two coherent fields can be directly read from Fig.2once the posi-tion of the single active atom is given.

关23兴 Y. Yang and S.-Y. Zhu, Phys. Rev. A 61, 043809 共2000兲. 关24兴 Y.-S. Zhou, X.-H. Wang, B.-Y. Gu, and F.-H. Wang, Phys. Rev.

Lett. 96, 103601共2006兲.

关25兴 S. John and T. Quang, Phys. Rev. Lett. 74, 3419 共1995兲. 关26兴 E. Paspalakis, D. G. Angelakis, and P. L. Knight, Opt.

Com-mun. 172, 229共1999兲.

关27兴 I. S. Nikolaev, P. Lodahl, A. F. van Driel, A. F. Koenderink, and W. L. Vos, Phys. Rev. B 75, 115302共2007兲.

关28兴 R. A. L. Vallée, K. Baert, B. Kolaric, M. Van der Auweraer, and K. Clays, Phys. Rev. B 76, 045113共2007兲.

关29兴 Y. Akahane, T. Asano, B.-S. Song, and S. Noda, Nature 共Lon-don兲 425, 944 共2003兲.

关30兴 C.-G. Du, Z.-F. Hu, C. F. Hou, and S.-Q. Li, Chin. Phys. Lett.