Spin-orbit splitting in semiconductor quantum dots with a parabolic confinement potential

(1)

Spin-orbit splitting in semiconductor quantum dots with a parabolic confinement potential

O. Voskoboynikov,1,2C. P. Lee,2 and O. Tretyak1

1

National Chiao Tung University, 1001 Ta Hsueh Rd., Hsinchu, 30010, Taiwan, R.O.C. 2_{Kiev Taras Shevchenko University, 64 Volodymirska st., 252030 Kiev, Ukraine} 共Received 10 May 2000; revised manuscript received 6 October 2000; published 2 April 2001兲

We present a theoretical study of the effect of spin-orbit interaction on the electron energy spectrum of cylindrical semiconductor quantum dots. The study is based on a simple effective one-band approximation. The dependence of energy levels on parameters of the dots and the applied external magnetic field is studied. Contributions of the bulk inversion asymmetry共the Dresselhaus term兲 and the system inversion asymmetry

共the Rashba term兲 to the spin splitting of the electron energy states are discussed. The spin splitting of electron

states with nonzero angular momentum is demonstrated theoretically for InSb and InAs small quantum dots at zero magnetic field. We find a ‘‘crossing’’ of the electron energy states with the same angular momentum and different spin polarizations in a nonzero magnetic field.

DOI: 10.1103/PhysRevB.63.165306 PACS number共s兲: 71.70.Ej, 85.35.Be

Experimental and theoretical investigations of spin-dependent confinement and transport in semiconductor quan-tum heterostructures have attracted considerable attention in recent years共see Refs. 1–7, and references therein兲. The in-creasing interest in this topic stems from two facts. First, advances in semiconductor technology have made it possible to create structures which possess electrical properties that are highly sensitive to electron spin. So-called ‘‘spintronics’’ devices can be controlled by the electron-spin polarization.8,9 Second, one can use a quite general physical approach to clarify unusual spin-dependent phenomena in low-dimensional semiconductor quantum structures.1–5,10–13

Electron spin can significantly impact the electronic prop-erties of quantum structures through different mechanisms. Among possible spdependent interactions there is an in-teraction between orbital angular and spin momenta of an electron known as spin-orbit共SO兲 interaction.14,15Despite its relativistic nature, SO interaction can play an observable role in the energy-band structure of many semiconductors. When the potential through which the carriers move is inversion asymmetric, spin-orbit interaction removes the spin degen-eracy even without an external magnetic field. While the SO interaction impact on the electron quantum confinement in semiconductor quantum wells and quantum wires has been extensively studied theoretically and experimentally共see for instance Refs. 1, 2, 10, and 11兲, SO interaction in semicon-ductor quantum dots 共QD’s兲 has largely been uninvestigated.16

In a zinc-blende crystal with bulk inversion asymmetry

共BIA兲, energy bands are split for a given direction of the

electron wave vector.14,17–19 Additional spin splitting in semiconductor quantum structures may also occur owning to the structure confinement potential invention asymmetry

共SIA兲.15,19_{Since SO interaction has been used successfully in} experimental result interpretations for various quantum well and quantum wire structures, it also appears to provide a well-defined contribution to the spin properties of QD’s. Clearly, SO interaction depends heavily on the quantum

sys-tem geometry as well as the effective external and internal fields. With advanced semiconductor technology, QD’s are easily realizable within a wide range of dot geometrical shapes and built-in fields.20 Therefore, the spin-dependent phenomenon in those structures is of worthwhile interest.

The goal of this paper is to start a theoretical discussion of how SO interaction can affect the electron energy states and magnetic properties of QD’s. Spin-orbit interaction is de-scribed by two contributions to the effective one-band spin dependent Hamiltonian. One of them arises from the bulk Hamiltonian, and was first considered by Dresselhaus

共BIA兲.14,17 _{The second contribution, known as the Rashba} term, represents the spin-orbit interaction of an electron moving in a QD confinement potential 共SIA兲.4,15 The Cou-lomb interaction between electrons is neglected for simplic-ity. However, a recent investigation21 indicated that the ef-fect of electron-electron interaction in systems with strong confinement can enhance the SO interaction. The following discussion clearly reveals that principal consequences of the SO interaction can be described with the used simplifica-tions.

This study next considers SO interaction in semiconduc-tor cylindrical quantum dots with a quasi-two-dimensional confinement for electrons.16,22,23Widely used to describe QD energy states, this model can successfully describe the elec-tronic properties of circular disk-shaped quantum dots 共arti-ficial atoms兲24,25as well as QDs formed in two-dimensional electron-gas systems by external electric16,26 and strain fields.27In cylindrical coordinates, we consider a quasi-two-dimensional effective parabolic lateral confinement potential28,29

Vc共␳兲⫽

1 2m␻0

2_␳2_, _共1兲

whereប␻0 is the characteristic confinement energy,␳ is the radius vector, and the electron effective mass is given by4

1 m共E兲⫽ 1 m共0兲 Eg共Eg⫹⌬兲 共3Eg⫹2⌬兲

冋

2 E⫹Eg ⫹ 1 E⫹Eg⫹⌬

册

; 共2兲

(2)

⫺ i 2ប␻c共E,B兲 ⳵ ⳵␾ ⫹1₈m共E兲␻c 2_共E,B兲_␳2_⫹V c共␳兲⫹Vso D_共_␳ ,␾兲⫹Vso R_共_␳ ,␾兲 ⫹1₂␴z␮Bg共E兲B, 共5兲 where ␻c共E,B兲⫽ eB m共E兲 is the electronic cyclotron frequency,

g共E兲⫽2

冋

1⫺ 1 m共E兲

⌬

3共Eg⫹E兲⫹2⌬

册

共6兲

is the effective Lande˙ factor of the semiconductor,30 ␮B

⫽eប/2m0 is the Bohr magneton, and m0 is the free-electron mass.

An analysis of the problem begins by considering a situ-ation in which the dot height is adequately large共that condi-tion is evaluated below兲, so that the Dresselhaus term is ne-glected. Under this circumstance, the energy eigenfunction of Hamiltonian 共5兲 takes the well-known form

⌿n,l,␴⫽ 1

冑

2␲exp共il␾兲Rn,l,␴共␳兲, with a radial part Rn,l,␴(␳) that satisfies

冋

d2 d␳2⫹ 1 ␳ d d␳⫺ l2 ␳2⫹ m2共E兲⍀_␴2共E,B兲␳2 ប2 ⫹⌸l␴共E,B兲

册

Rn,l,␴共␳兲⫽0, 共7兲 where ⍀_␴2_共E,B兲⫽_␻ 0 2_⫹␻c 2_共E,B兲 4 ⫹␴␣ m共E兲␻₀2 ប ␻c共E,B兲, 共8兲 ⌸l␴共E,B兲⫽ 2m共E兲 ប2

再

E⫺ បl 2 ␻c共E,B兲 ⫺␴

冋

␮B 2 g共E兲B⫹l␣m共E兲␻0 2

册冎

,

and␴⫽⫾1 refers to the electron-spin polarization along the z axis. The solution to Eq. 共7兲 has been known for a long time共see, for example, Ref. 23兲. The electron energy levels are given by En,l,␴⫽ប⍀␴共En,l,␴,B兲共2n⫹兩l兩⫹1兲⫹l ប␻c共En,l,␴,B兲 2 ⫹␴

冋

␮B 2 g共En,l,␴兲B⫹l␣m共En,l,␴兲␻0 2

册

_, _共9兲 and the corresponding normalized radial wave functions are given by R_n,l,_␴共␳兲⫽& ␳␴

冋

n! 共n⫹兩l兩兲!

册

1/2 exp

冉

⫺ ␳ 2 2␳_␴2

冊

⫻

冉

␳ 2 ␳␴2

冊

兩l兩/2 L_n兩l兩

冉

␳ 2 ␳␴2

冊

, 共10兲 where␳_␴⫽(ប/m⍀_␴)1/2_{, and L} n

兩l兩 _{is the generalized Laguerre}

polynomial.31

Equation共9兲 shows the dependence of the electron energy on the quantum numbers兵n,l,␴其 and the external magnetic field B by taking into account the nonparabolicity of the semiconductor dispersion relation 关Eq. 共2兲兴.

(3)

Consider how the Rashba spin-orbit interaction impacts the energy spectrum of narrow-gap semiconductor QD’s. The main value of interest is the spin splitting in the electron energy:

⌬En,l共B兲⫽En,l,⫹1共B兲⫺En,l,⫺1共B兲. 共11兲 First we analyze a situation without an external magnetic field. The dispersion relation 关Eq. 共9兲兴 in this case can be written as

En,l,␴⫽ប␻0

冋

2n⫹1⫹兩l兩

冉

1⫹␴S共l兲 ␣ r₀2

冊册

,

where r0(E)⫽

冑

ប/m(E)␻0 is an effective QD lateral size andS(l) is the sign of l. The spin splitting

⌬En,l共0兲⫽ប␻0 2l␣

r₀2 共12兲

is a weak function on n 关due to effects of nonparabolicity that come to Eq. 共9兲 with r0(En,l,␴)兴. The dependence of

⌬En,l(0) on l is of primary concern in this study, and we examine the lowest-energy levels when n⫽0. The spin-orbit interaction separates states with the same orbital momentum and different spin directions. However, states with parallel spin and l共antiparallel spin and l兲 remain twofold degener-ate. This is the well-known Kramers degeneracy. Doubly de-generate electron states with parallel directed spin and l have

the highest energy. This level hierarchy obviously depends on the sign of the Rashba constant.

Our calculations for InSb, InAs, and InxAs1⫺xGs QDs are presented as practical examples. The band parameters and the estimated geometrical parameters of the dots are taken from the available literature, and are listed in Table I. Figure 1 presents the amount of spin splitting for QD’s as a function of the orbital quantum number l at n⫽0 and zero magnetic field. According to this figure, the Rashba spin-orbit splitting can have a well-pronounced magnitude for QD’s with rela-tively small effective sizes.

The Rashba spin splitting at zero magnetic field leads to an unusual behavior of the QD energy spectrum when a magnetic field is present. Figure 2 displays the calculated spectrum of InSb QD’s as a function of the magnetic field B for a set of 兵n,l,␴其 with n⫽0 and l⫽0,⫾1,⫾2,⫾3 using the parameters of Table I. For comparison, inset a shows the spectrum of InSb QD’s with the same parabolic confinement potential but without spin-orbit interaction. The spin-orbit interaction provides a ‘‘crossing’’ of the energy levels with the same orbital momentum but different spins when

⌬En,l(Bcr)⫽0 共see inset b in Fig. 2兲. Using the linear ap-proximation for the dispersion relation关Eq. 共9兲兴 allows us to derive the conditions for the crossing of energy levels. A straightforward consequence of solution共10兲 is that the area covered by the electron in state 兩n,l

典

⫽Rn,l,␴ in a low mag-netic field is Sn,l⫽␲

具

l,n兩␳2兩n,l

典

⫽␲␳0

2

(2n⫹兩l兩⫹1).37 Us-ing dispersion relation共9兲 and this expression reveals that, at the point of the crossing,

FIG. 1. The Rashba spin splitting vs the orbital angular momen-tum for n⫽0 at zero magnetic field for Insb, InAs, and In0.55Al0.45AsQD’s.

TABLE I. QD parameters.

Semiconductor m(0)/m0 Eg共eV兲 ⌬ 共eV兲 ␣ 共Å2兲 ប␻0共eV兲 r0(0) 共Å兲

InSb 0.014a 0.24a 0.81a 500 0.025b 148 InAs 0.04c 0.42a 0.38a 110 0.019c 100 In0.55Al0.45As 0.076d 1.45d 0.34d 4.4 0.043e 48 a_{Reference 32.} b_{Reference 33.} c_{Reference 34.} d_{Reference 35.} e_{Reference 36.}

FIG. 2. Energy states for an InSb QD with Rashba spin-orbit interaction (n⫽0; inset a shows a spectrum without sporbit in-teraction; the arrows in inset b show electron-spin polarizations兲.

(4)

⌽n,l ⌽0 ⫽⫺l共2n⫹兩l兩⫹1兲

冋

បg 2m0␻0␣⫹共2n⫹兩l兩⫹1兲

册

⫺1 , 共13兲

where ⌽n,l⫽BcrSn,l is the magnetic flux corresponding to the effective 兵n,l,␴其 state area at the crossing point and⌽0 is the magnetic flux quantum. Equation 共13兲 becomes very simple when g→0.38 For such a case, ⌽n,l/⌽0⫽⫺l. For narrow-gap semiconductors, the magnitude of g in quantum structures has not yet been totally clarified.39Nevertheless, if g is a negative number with 兩g兩⬎2(2n⫹兩l兩⫹1)m0␻0␣/ប

⬅g0(2n⫹兩l兩⫹1), it follows from Eq. 共13兲 that the crossing exists for positive l. For the case of InSb QD’s considered here, g0⬇3.2.

Figure 3 shows how the Rashba spin splitting depends on the external magnetic field and l for InSb QD’s. The calcu-lated spin splitting follows the general tendency described above. The calculated magnitudes of the spin splitting and the magnetic fields at level crossing (Bcr) allow us to discuss more realistic theoretical models of the phenomena, and to verify the effect experimentally.

Next consider a situation when the effective sizes of the quantum dot are such that the Dresselhaus term must be con-sidered as well. In this situation, Eq. 共5兲 can be solved by following the scheme proposed in Refs. 10 and 40. The so-lution can be represented in the spinor form

⌿共␳,␾兲⫽

兺

n,l eil␾R_n,l0 共␳兲

冋

A_ln

冉

1 0

冊

⫹Bl n

冉

0 1

冊册

, 共14兲

1/2 共2n⫹兩l兩⫹1兲 ⫹lប␻c共E,B兲 2 ⫹␴

冋

␮B 2 g共E兲B⫹l␣m共E兲␻0 2

册

_. System of equations 共15兲 can be written in the vector form: Al⫽MˆBl_⫺1 and Bl⫽NˆAl_⫹1.40 The energy spectrum of the QD has to be numerically calculated from the following equation:

det共1ˆ⫺Mˆ N兲⫽det共1ˆ⫺N¯ Mˆ兲⫽0. 共16兲 The chosen basic set 兵Rn,l(␳)其 provides a very quick con-vergence for the roots of Eq.共16兲, with an increasing number n. For nmax⬃15, the net error for the lowest four energy levels is ⬍10⫺4 for InSb QD’s in a magnetic field near the crossing points.

First we assume that ␣⫽0 describes the spin splitting produced by the Dresselhaus term only. Calculation results indicate that, at zero magnetic field, the spin splitting re-mains for all states with 兩l兩⭓1. However, in contrast to the Rashba splitting, the Dresselhaus splitting between pairs of twofold degenerate levels is proportional to ␤2/ប␻0␳0

2 and

FIG. 3. Dependence of the spin splitting for InSb QD’s on ex-ternal magnetic field and orbital momentum共only the Rashba spin-orbit interaction is included兲.

(5)

does not depend on the sign of ␥c constant. The Kramers degeneracy also remains for兵n⫽0,兩l兩⭓1,␴其 levels.

When the Rashba term is included in Eqs. 共15兲, the total

共Dresselhaus and Rashba兲 spin splitting sign heavily depends

on the dot height. For InSb quantum dots with the same parameters as in Fig. 3 and z0⫽35 Å, ␥c⫽160 eV Å3 共Ref. 17兲 at zero magnetic field, the BIA term dominates in the total spin splitting for 兵0,⫾1,␴其 states that is about ⬃5.5 meV. Since ␤ depends heavily on the dot height, the SIA term becomes dominant for z0ⲏ50 Å. In addition, at z0

⬇80 Å, the Dresselhaus term can be neglected.

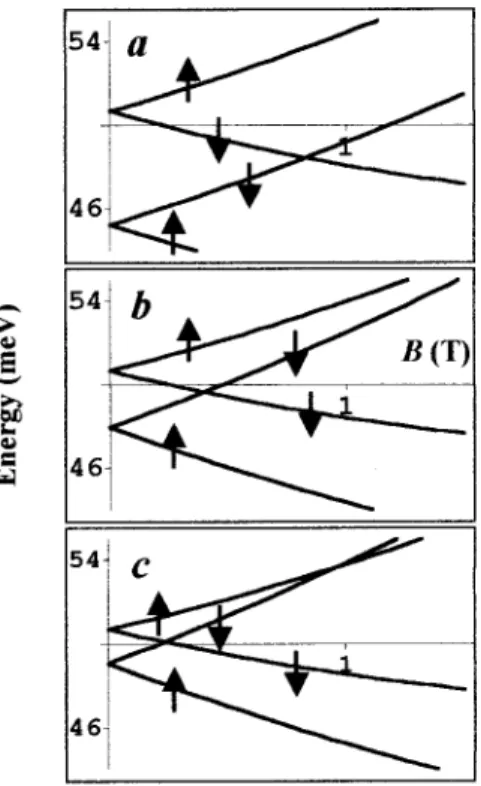
Consider the eventual changes of spin splitting at zero magnetic field for ‘‘thin’’ quantum dots, in which the energy-state crossing demonstrates a different behavior. Fig-ure 4 presents the calculation results for 兵0,⫾1;␴其 states of InSb quantum dots at a magnetic field near the crossing point. In contrast to Fig. 2共b兲, for the dot size z0⫽35 Å, the Dresselhaus splitting is strong enough to remove the crossing between states with the same l at low magnetic fields 关Fig. 4共a兲兴. When the dot height increases, the Dresselhaus split-ting weakens 关Fig. 4共b兲兴, and then (z0ⲏ45 Å) the crossing appears at relatively large magnetic fields. For z0⫽70 Å, the electron energy-level positions are extremely close to those when only the Rashba term is included 关Fig. 4共c兲兴.

In planar semiconductor systems共e.g., in quantum wells兲, the electron energy spectrum is insensitive to the sign of ␣. In quantum dots, however, it is sensitive. Therefore, BIA and SIA contributions to the total spin splitting can either sum up or subtract from each other, depending on the sign of␣but independent on the sign of ␥c. In our calculation above we

described the first situation when ␣⬎0. To our knowledge, the absolute signs of those constants remain a controversial issue共see Ref. 2 and references therein兲. As an example, Fig. 5 兵0,⫾1,␴其 presents energy-state positions for ␣⬍0. For a negative ␣ we found a cancelation of the Rashba-Dresselhaus terms when z0⫽46 Å and B→0 关Fig. 5共a兲兴. In addition, increasing the dot height leads to the appearance of a crossing. However, in contrast to the positive ␣case, the crossing between electron energy states has l⫽⫺1 关Fig. 5共b兲兴. Therefore, a possible measurement of the␣-dependent characteristics of quantum dots can determine the sign of ␣, and provide additional information about the effective spin-orbit interaction.

In conclusion, we presented a study of the effect of spin-orbit interaction on the electronic spectrum of narrow-band semiconductor quantum dots. Calculations were made on the basis of an effective one-dimensional spin-dependent Hamil-tonian within the envelope-function approximation. For the parabolic confinement potential model a well-pronounced spin splitting was found for QD’s with parameters of InSb and InAs.

Our results further demonstrate that the magnitude and sign of the effect depend on the effective size of the QD, and can gain a measurable value for relatively small QD’s of narrow-gap semiconductors. For relatively thin cylindrical quantum dots, the Dresselhaus mechanism of the spin split-ting is dominant. However, with increasing dot height, the Rashba term becomes dominant.

The main goal of the paper is to call attention to spin-splitting effects for QD’s. In our calculation, a simple model and conventional parameters of the semiconductor band structures are used. A real three-dimensional calculation should be performed. However, the major finding is as fol-lows: the spin splitting at zero magnetic field and the l-state crossing with external magnetic field are clear physical phe-nomena which are independent of the model. Therefore, the crossing of electron energy levels with different spins may lead to unusual magnetic properties of QD’s.

This work was supported by the National Science Council of R.O.C. under Contract No. NSC89-2215-E009-013.

FIG. 4. 兵0,1,␴其 energy states for InSb QD’s with Rashba and Dresselhaus spin-orbit interactions: 共a兲 z0⫽35 Å, 共b兲 z0⫽46 Å,

and共c兲 z0⫽70 Å. The other parameters are the same as in Fig. 2.

FIG. 5. 兵0,1,␴其 energy states for InSb QD’s with Rashba (␣

⫽⫺500 Å2

) and Dresselhaus spin-orbit interactions:共a兲 z0⫽46 Å

(6)

1_{Can-Ming Hu, Junsaka Nitta, Tatsushi Akazaki, Jiro Osaka, P.}

Pfeffer, and W. Zawadzki, Phys. Rev. B 60, 7736共1999兲.

2_{D. Richards and B. Jusserand, Phys. Rev. B 59, R2506}_共1999兲. 3

E. A. de Andrada e Silva, Phys. Rev. B 60, 8859共1999兲.

4_{E. A. de Andrada e Silva, G. C. La Rocca, and F. Bassani, Phys.}

Rev. B 55, 16 293共1997兲.

5_{A. Voskoboynikov, Shiue Shin Liu, C. P. Lee, and O. Tretyak, J.}

Appl. Phys. 87, 1共2000兲.

6_{A. G. Mal’shukov and K. A. Chao, Phys. Rev. B 61, R2413} 共2000兲.

7_{P. N. Racec, T. Stoica, C. Popescu, M. Lepsa, and Th. G. van de}

Roer, Phys. Rev. B 56, 3595共1997兲.

8_{S. Datta and B. Das, Appl. Phys. Lett. 56, 665}_共1990兲. 9_{B. E. Kane, Nature}_{共London兲 393, 133 共1998兲.}

10_{A. V. Moroz and C. H. W. Barnes, Phys. Rev. B 61, R2464} 共2000兲; 60, 14 272 共2000兲.

11_{E. Silveira, M. K. Kelly, C. E. Nebel, G. Bo¨hm, G. Abstreiter,}

and M. Stutzmann, Physica E 2, 929共1998兲.

12_{L. I. Magaril, D. A. Romanov, and A. V. Chaplik, Zh. Eksp. Teor.}

Fiz. 113, 1411共1998兲关JETP 86, 771 共1998兲兴.

13_{L. I. Magaril and A. V. Chaplik, Pis’ma Zh. Eksp. Teor. Fiz. 64,}

466 共1996兲关JETP Lett. 64, 460 共1996兲兴; Zh. Eksp. Teor. Fiz. 115, 1478共1999兲关JETP 88, 815 共1999兲兴.

14_{G. Dresselhaus, Phys. Rev. 100, 580}_共1955兲.

15_{Yu. A. Bychkov and E. I. Rashba, J. Phys. C 17, 6039}_共1984兲. 16_{T. Darnhover and U. Ro¨ssler, Phys. Rev. B 47, 16 020}_共1993兲. 17_{G. E. Pikus, V. A. Marushchak, and A. N. Titkov, Fiz. Tekh.}

Poluprovodn. 22, 185 共1988兲关Sov. Phys. Semicond. 22, 115

共1988兲兴.

18_{F. G. Pikus and G. E. Pikus, Phys. Rev. B 51, 16 928}_共1995兲. 19_{T. Hassenkam, S. Pedersen, K. Baklanov, A. Kristensen, C. B.}

Sorensen, P. E. Lindendorf, F. G. Pikus, and G. E. Pikus, Phys. Rev. B 55, 9298共1997兲.

20_{D. Bimberg, Semiconductors 33, 951}_共1999兲.

21_{Guang-Hong Chen and M. E. Raikh, Phys. Rev. B 60, 4826} 共1999兲.

22_{P. A. Maksym and T. Shakraborty, Phys. Rev. Lett. 65, 108} 共1990兲.

23_{F. Geerinckx, F. M. Peeters, and J. T. Devreese, J. Appl. Phys.}

68, 3435共1990兲.

24_{S. Tarchua, T. Honda, D. G. Austing, Y. Tokura, K. Muraki, T.}

H. Oosterkamp, J. W. Janssen, and L. P. Kouwenhoven, Physica E 3, 112共1998兲.

25_{A. Lorke and R. J. Luyken, Physica B 256-258, 424}_共1998兲. 26_{Ch. Sikorski and U. Merkt, Phys. Rev. Lett. 62, 2164}_共1989兲. 27

R. Rinaldi, P. V. Giugno, R. Cingolani, H. Lipsanen, M. Sopanen, J. Tulkki, and J. Ahopelto, Phys. Rev. Lett. 77, 342共1996兲.

28_{V. Fock, Z. Phys. 47, 446}_共1928兲.

29_{A. V. Madhav, T. Chakraborty, Phys. Rev. B 49, 8163}_共1994兲. 30_{L. M. Roth, B. Lax, and S. Zwerdling, Phys. Rev. 114, 90}_共1959兲. 31_{Handbook of Mathematical Functions, edited by M. Abramowitz}

and I. A. Stegum共Dover, New York, 1965兲.

32_{G. Bastard, Wave Mechanics Applied to Semiconductor} Hetero-structures共Les Edition de Physique, Les Ulis, 1990兲.

33_{P. Junker, U. Kops, U. Merkt, T. Darnhofer, and U. Ro¨ssler,}

Phys. Rev. B 49, 4794共1994兲.

34_{M. A. Cusack, P. R. Briddon, and M. Jaros, Phys. Rev. B 54,}

2300共1996兲.

35_{Shun Lien Chuang, Physics of Optoelectronic Devices}

共Wiley-Interscience, New York, 1995兲.

36_{S. Fafard, R. Leon, D. Leonard, G. Medeiros-Ribeiro, M.}

Oestre-ich, P. M. Petroff, K. Uchida, N. Miura, H. Akiyama, and H. Sakaki, Phys. Rev. B 53, 16 458共1996兲.

37_{R. B. Laughlin, Phys. Rev. B 27, 3383}_共1983兲.

38_{P. C. Main, A. S. G. Thornton, R. J. A. Hill, S. T. Stoddart, T.}

Ihn, L. Eavels, K. A. Benedict, and M. Henini, Phys. Rev. Lett. 84, 729共2000兲.

39_{A. A. Kiselev, E. L. Ivchenko, and U. Ro¨ssler, Phys. Rev. B 58,}

16 353共1998兲.

40_{Yu. A. Bychkov, V. I. Melnikov, and E. I. Rashba, Zh. Eksp.}