A Systematic Space-Time Code Design and Its Maximum-Likelihood Decoding for Combined Channel Estimation and Error Correction

A Systematic Space-Time Code Design and Its

Maximum-Likelihood Decoding for Combined

Channel Estimation and Error Correction

Chia-Lung Wu*, Mikael Skoglund", Po-Ning Chen" and Yunghsiang S. Han+

*Dept. of Comm. Eng., National Chiao-Tung Univ., Taiwan, ROC Email: clwu@banyan.cm.nctu.edu.tw.qponing@mail.nctu.edu.tw

t

School of Electrical Engineering, Royal Institute of Technology, Sweden Email: skoglund@ee.kth.se

+Graduate Institute of Comm. Eng., National Taipei Univ., Taiwan, ROC Email: yshan@mail.ntpu.edu.tw

Abstract-Several previous works have confirmed that a joint design that combines channel estimation, channel coding and space-time transmission can improve the system performance over that of a separate design. These conclusions are however in general based on unstructured solutions obtained using computer search. The coding gain of these joint designs is therefore limited by both the computer-searchable "short" code length and the compromise between "suboptimal" performance and "high" complexity of their optimal decoding.

At this background, we propose a systematic space-time code construction for joint channel estimation and error correction for a two-transmit-antenna and half-rate system. Also proposed is its

maximum-likelihood decoder that follows a priority-first search

principle. Our systematic code construction, together with a fairly low-complexity optimal decoder, then allows one to work with longer codes with no sacrifice in performance. For codes of short block length, our simulations illustrate that the codes we propose have comparable performance to the best computer-searched codes. For codes of long block lengths that are almost beyond the searchable range of existing computer systems, our codes are still better than some reference designs based on separate channel estimation and error correction components.

1. INTRODUCTION

Coding and transmission schemes for noncoherent receivers used in multiple-input multiple-output (MIMO) flat-fading channels can be roughly classified into two categories.1

Schemes in the first category devise the space-time constella-tionsfor a given noncoherent receiver structure using computer search [1], [3], [10], while schemes in the second category couple the well-known space-time block codes with blind detection [11], [12], [15]. A brief summary of these schemes is as follows.

1There are some notable papers that deal with similar problems, but cannot

be classified into the two categories. For example, both [5] and [6] consider the so-called training codes that incorporate training symbols into their

codewords. As anticipated, the receiver estimates the channel coefficients via training symbols. Such designs are very different from ours, which combines channel estimation and error correction by adopting joint maximum-likelihood decoding at the receiver. In [4], a noncoherent code is constructed through a mapping from coherent code. The code structure however only allows for a suboptimal efficient decoder.

In [1], Beko et al. propose a two-phase code design ap-proach, where the first phase produces a rough space-time code constellation that is subsequently refined in the second phase through a search-based geodesic descent optimization algorithm (GDA). In [3], Borran et al. uses the Kullback-Leibler distance as a design criterion to partition the signal space into several subsets, resulting in a reduction of number of parameters to be computer-searched. The authors in [10] construct unitary space-time signals by random search upon a Fourier-based structure, which only requires optimizing L-1

parameters instead ofL (L - 1)/2 in the correlation matrix, where L is the number of space-time signals.

On the other hand, [11], [12] and [15] incorporate blind detection to existing space-time block codes. Based on the semidefinite relaxation (SDR) approach, an efficient subopti-mal blind detection scheme is also suggested by Ma et al. in [11]. Later in [12], Ma further addresses the necessary properties for the family of orthogonal space-time block codes that can well co-work with blind detection.

Two main problems of designing codes or signal constel-lations based on unconstrained computer-search are that the design complexity is in general high, especially for codes of long block length, and the codes often need to be redesigned when design assumptions change. Moreover, their decoding depends mostly on operationally intensive exhaustive search, which further prevents their practical use in the case of long block lengths. Obviously, these problems can be solved by realizing a systematic code construction and its respective low-complexity decoder. Such an approach designed under two-transmit-antenna and half-rate condition is presented in this paper.

Furthermore, one main difference between our work and the existing works on combining known space-time block codes with blind detection, is that we aim at achieving a coding gain in contrast to targeting only improved diversity gains at maximum rate.

The paper is organized in the following fashion. Section II introduces the system model. Section III presents our code

design scheme that is devised based on the unitary and full-rank properties. Section IV derives the maximum-likelihood metric that can be used by priority-first search decoding. Simulations are summarized and discussed in Section V.

In this work, superscripts "H" and "T" are specifically reserved for the matrix operations of Hermitian transpose and transpose, respectively.

II. SYSTEM MODEL

We consider an MIMO system with AT transmit antennas and AR receive antennas. The N x AR complex received

matrix Y == [YlY2 ... YAR] is then given by

Y==JBIHI

+

N,

where JB== [b1 b2 ... bAT]is the N x AT transmitted code

matrix, and N == [nl n2 ... nAR]is an N x AR zero-mean

complex Gaussian matrix with independent and identically distributed elements and covariance matrix

1 0 0

0 1 0

E[ninf] ==0-2

0 0 1 _NxN

Also, b, == [b1,i b2,i ... bN,i]T is the bipolar codeword

transmitted by antenna i with each i;n E {

±

1/

VAT}.

Likewise,Yj == [Yl,j Y2,j ... YN,j]T is the received vector at the jth receive antenna.

Because IHI is assumed an unknown constant matrix, the Gaussian assumption on the additive noise matrix N im-mediately gives that the maximum-likelihood (ML) decision about the transmitted codeword should be made based on the generalized likelihood ratio test (GLRT) as

i

== arg min minI/Y - JBIHII/2

JB IHI

== arg minI/Y - JBrHrl/ 2

JB

== arg min1/(JI_{N -} TIDB)YI/2, (1) JB

where rHr ~ (JBTJB)-lJBTy is the least-square estimate ofIHI

with respect to codewordJB and received matrixY,and TIDB ~JB(JBTJB)-lJBT

is a function of the codewordJB. Here,JIN denotes an N xN identity matrix.

III. CODE DESIGN

A. Criteria for Good Codes

Several criteria for good codes have been proposed in the literature [1], [7], [8], [16]. We will in particular center on two of them: unitary and pairwise full-rank.

Firstly, it has been derived in [16] that unitary codewords, i.e., JBTJB== (N/AT) .JIAT , can maximize the average signal-to-noise ratio (SNR) regardless of the statistics on IHI. It has also been shown that whenIHIis zero-mean complex Gaussian distributed, a unitary signal maximizes the capacity [14] and

ISIT 2009, Seoul, Korea, June 28 - July 3, 2009 minimizes the union bound of word error rate (WER) [2] at high SNR. These results suggest that a good code can perhaps be constructed by collecting unitary codewords.

Secondly, it is better to have full-rank codeword pairs, where a pair of codewords, JB(i) and JB(j), is said to be pair-wisely full-rank if

rank([JB(i) JB(j)

J)

== 2AT ,

subject to N

2:

2AT .This is because at fairly high SNR, the

average error probability is well approximated by the sum of pair-wise word error rates, namely, the union bound [1]. Also at fairly high SNR, the pair-wise word error is in tum well approximated by

Pr (

B

=

JE(j)

I

JE(

i) transmitted)

~

Q

(~lllHIIIJAmin(JLij))

(2) where

and Amin (ILi j ) is the smallest eigenvalue ofILi j .Here, "@"

in-dicates the Kronecker product, and Q(x) ~

k

Jxoo

e-t 2/2dt

is the area under the tail of a standard Gaussian probability density function. Hence, if [JB(i) JB(j)] do not achieve full column rank, we can obtain by [8] that

detIJB(i)T (JIN - TIDB(j»)JB(i) I==o.

This subsequently implies that Amin (ILi j ) ==0,and (2) will be

close to 1/2 at fairly high SNR, which is a situation that a good code should avoid.

Therefore, a code that satisfies both the above criteria should guarantee a good pairwise-error-based union bound (whichin tum hints to have a good performance). This viewpoint will be confirmed by the subsequent simulations.

B. The Proposed Code Design

Denote the information sequence by k == [k1 k2 ... kK]T , where k, E {

±

1}. The corresponding codeword is then proposed to be

JB _ _1_

[k

k

8

s]

-VAT

-k8s k

where "8" denotes the Hadamard product, and

[l K- rK/ 21] , if k1 == -1

-lrK/21

s==

[l K- rK/ 21] 8_-lrK/21 d, otherwise.

In the above equation, lk represents a k x 1 all-one vector, and d ~ [(-1 )0 (-1)1 ... (-1 )K-1 ]T .

It can be easily examined that the unitary criterion is satisfied, i.e., JBTJB == (N/AT) .JIAT . It remains to show that the code just introduced satisfies pair-wise full-rank criterion.

Case 1: 8 i

==

8 j

==

8.

In this case,

IV. PRIORITY-FIRST SEARCH DECODING

and

whereW ~ Re{(ATIN)

2:::1

Yjyf},

and tr(·) is the trace matrix operation. By letting

In this section, we will derive the recursive decoding metric that can be used by the priority-first search algorithm [9]. Since the metric proposed is nondecreasing along every path in the code tree, the optimality of the decoding result is certified [16].

Continuing the derivation in (1) by noting that

II

JIDB112

AT,we obtain (3)

Now, let (ki , 8 i ) and (kj , 8 j ) be respectively the vector pairs that define codewords 1ffi(i) and 1ffi(j). Denote for conve-nienceCj,i

==

k_j88i. We then prove that Al

i-

(N

I

A_{T )2}and

A2

i-

(N

I

AT)2 _{by differentiating the following two cases.}

I

1 AT I

(3){=} det JIA T

~

(N/A

T)2

t;>'kUkUf

-=I-

0

{=} det

I~

(1

~ (N~T)2)

ukufl-=l-

O.

for 1

<

i,j ::;2K with i

i-

j. By denoting respectively the kth eigenvalue and kth eigenvector ofAi,jA[j by Ak and Uk, the validity of(3) can be verified by showing that Ak

i-

(N

I

A_{T )2} for every kbecause

LetAi,j ~1ffi(i)T1ffi(j). Then for the validity of the pair-wise

full-rank criterion, it suffices to prove that det!JIA T

~ (N/~T)2Ai,jALI-=I-

_0,

Then, A..A!.

==

[(k

Tk

j_{)2 0 ]} ~,J ~,J 0 (kTk_j)2 So, Al

==

A2

==

(kTkj)2

<

(NIAT)2. we have AT

[T]

'" b.b!

==

_1_ Ml _M2 L.J ~ ~ A M M ' i=l T 2 1

This reduces the decoding criterion to Case 2: 8i

i-

8j.

In this case,

which gives

k

==

arg min {-tr (MlIIJ)) - tr (M2JE)} ,

k

where IIJ)~Wl,l

+

W2,2, JE ~W l,2 - Wf2' and Wl,l, W l,2 and W2,2 are the corresponding submatrices of

W

==

[Will Wl,2]. W l,2 W2,2

Since the decision criterion is intact by adding a constant independent of the codewords,

T

[c

0]

Ai,j Ai,j

==

0 c '

where c~ (IIAT)2(lkT(kj

+

kj 8 d)12

+

IkT(Cj,j - Cj,i)12) . Accordingly, Al

==

A2

==

C

<

(N

I

AT)2.

We end this section by commenting that our design can be viewed as a high-dimensional variation of Alamouti codes. Hence, the unitary property is satisfied simply by the Alam-outi code structure. By properly introducing the additional Hadamard product, our code can further fulfill the pairwise full-rank property.

ISIT 2009, Seoul, Korea, June 28 - July 3, 2009

Fig. 1. Comparison of word error rates (WERs) between the codes constructed in Section III-B (Proposed-N) and the codes obtained from simulated annealing search (SA-N). The codeword lengths arc taken to be equal toN = 4,6,8, 10, 12 and 14. 20 10',---~ 10' ,---~ 10-1 ~10-2 ~10-2

_I

=

~~o~~sed-41 ~ I

=

~~~~sed-6 1 10 ' 10 ' 0 10 15 20 0 5 10 10' SNR (dB) 10' SNR (dB) ~10-2 _~ 10-2

1-8A-8

1

1-

8A-1O

1

_ ___ Propose d-a _ ___ Propose d-10

10 ' 10 ' 0 5 10 15 20 0 5 10 15 10' SNR (dB) 10' SNR (dB) ~10-' ~10-'

_I

=

~~~~~ed-121 _I

=

~~~~~ed-14 1 10 ' 10 ' 0 5 10 15 20 0 5 10 15 SNR (dB) SN R (dB)

Figure I shows that the best (structureless) computer-searched codes only have about 0.4 dB advantage over the constructed codes for N = 4, 6, . .. , 12.

We also compare our code with a multiple-antenna system that uses the (17,12, 3) nonlinear channel code/ in combina-tion with the Alamouti code and a 7-bit training sequence. In particular, the code bits are mapped to the two transmit antennas using the Alamouti code before its transmission, and the rece iver will estimate IHI in terms of a least square estimator based on the 7 training bits. The result in Figure 2 illustrates that this communication system perform s 0.7 dB worse than the constructed code. In a technically infeasible situation that assumes the receiver can achieve a perfect estimate of IHI with merely 7 training bits, the typic al communication system outperform s the constructed code by only 0.5 dB.

We would like to emphasize that to search the best code by computers for codeword length greater than 14 is very operational intensive even if there are only two transmit antennas. For example, it took about three weeks to cool down the simulated-ann ealing search when N

=

14 and

AT = 2. It can be anticipated that the search time will grow exponentially with the code word length. Thus, the systematic code construction that we propose may be a good alternative as far as long code is concerned.

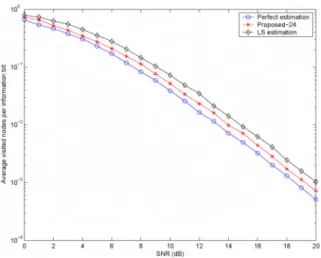
Figure 3 shows the decoding compl exity of the priority-first search decoder for constructed code of length 24. The com-plexity is defined as the average number of node expansions per information bit. Since the numb er of node expansions is half of the number of tree branch metrics computed (i.e., two recursions of j-function values), the equivalent complexity of exhaustive decoding is correspondingly (2K

₊

_{1 - 1) .AT/ K.} In the case of (24, 12) code with two transm it antennas, this number is equal to 1365.17. It is then clear from the figure

j

A

AR

;:. L

Re{Ym,jY~,j

+

Ym+K,jY~+K,J,

dm n

=

J=1 , for 1 :::::m,n ::::: N 0, otherwise

j

A

AR

;:.

LRe{Ym,jY~+K,j

-

Ym+K,jY~,j }'

em n= J=1 , for 1 :::::m , n ::::: N 0, otherwise

Finally, the decoding metric j inside the parenthesis of (4) can be computed recursivel y as

j(k(£))

=

g( k(£)) - -y(k(£)) , where k ef )= [k1 k2 ••• k£V ,

g( k( H l) )

=

g(k (£))- (3( k( H1) ),

and dm,n and em,n are respectively the elements in matrices

]JJ) andJE and can be expressed as

K m -y(k (£))

= -

L L ( Idm,n ll{ sm

=

sn } m=£+1n=£+1

+

lem,nl l{sm -1= sn })

~

K

IAR

{I

+

NT

m~1 ~

R e

~

Ym+tK ,r X

to

to(

- 1)" 1" .

ul]<k(e))

}

p

=

It

+

(-I )t(i

+

j)/ 2J,q

=

t

+ Ii -

j l(_ 1)t, and

(r)(k ) _ (r)(k) 1 k i *

U i ,j (HI) - Ui ,j (£)

+

~ H l SHI YHl+j K,r '

In the above equation, I{-} denotes the set indicator function. V. S IMULATI ON RE SULTS

In this section , we compare the performance of the code constructed in Section III with the codes obtained by computer search. The criterion used in the simulated annealing code search algorithm follows that in [2] (also, [7] and [8]). We take AR

=

1 in our simulations, and assum e that IHI is

zero-mean compl ex Gaussian with E [IHIIHIII ]

=

(1/AT) ][A T ' The average SNR is then give by

2

lO'r--.,---,---,---r---,.--,--,--.,..---===~ Fig. 2. Comparison of WERs among the codes constructed in Section III-B (Proposed-24) and the system using a (17,12) nonl inear code in combination with the Alamouti code and a 7-bit training sequence. The cod eword length is equal to N = 24.

[6] H. EI Gamal, D. Akt as, M. O. Damen, "Noncohcrent space -time coding: An algebraic perspe ctive" ,IEEE Trans. Inform. Theory, vol. 51, no. 7,

pp . 2380-2390, July 2005 .

[7J J. G iese and M. Skoglund, " Space-time code design for unknown frequency-selective channels,"Proc. IEEE. Int. Conf Acoust., Speech, Signal Process., Orlando, FL, USA, May 2002.

[8J J. G iese and M. Skoglund, "Single- and multiple-antenna constellations for communication over unknown frequency-selective fading channels,"

IEEE Trans. Inform. Theory, vol. 53, no. 4, pp. 1584-1594, Apr il 2007.

[9] Y.S. Han and P.-N. Chen , "Se quential decoding of convolutional codes,"

The Wiley Encyclopedia of Telecommun ications, edited 1. Proak is, John

Wiley and Sons, Inc., 2002.

[10] B. Hochwald, T. L. Marzetta, T.J. Richardson, W Sweldens, and R. Urbanke, " Systematic design of unitary space-time constellations,"

IEEE Trans. Inform. Theory, vol. 46, no. 6, pp. 1962-1973, Sept. 2000 .

[II] W-K. Ma, B.-N. Vo,T.N. Davidson and P.-c. Ching, "Blind ML detec-tion of orthogonal spac e-tim e block codes: efficient high-performance implementations,"IEEE Trans. Signal Process., vol. 54, no. 2, pp.

738-751 , Feb. 2006 .

[12] W-K. Ma, "Blind ML detection of orthogonal space -time block codes: Ident ifiability and code construction," IEEE Trans. Signal. Process.,

vol. 55, no. 7, pp. 3312-3324, July 2007 .

[I3 J F. J. MacWilli ams and N. J.A.Sloan e,The Theory of Error-Correcting Codes Amsterdam, The Netherlands: North-Holland, 1977.

[14] T.L. Marzetta and B.M. Hochwald, "Capacity of a mobil e multiple-antenna communication link in Rayle igh nat- fading,"IEEE Trans. In-form. Theory, vol. 45, no. I, pp. 139-157, Jan. 1999.

[lSI V.Tarokh andA.R. Calderbank, " Space-time block code s from orthogo-na l des igns,"IEEE Trans. Inform. Theory, vol. 45 , no. 5, pp. 1456-1467,

July 2007 .

[16] C.-L. Wu, P.-N. Chen, Yunghsian g S. Han and M.-H. Kuo, "Maximum-likelihood priority-first search deeodable codes for combined channel estimation and error correction," In review,IEEE Trans. Inform. Theory. 20 18 -e-PFSD 16 14 10 12 SNR (dB) 10 12 SNR (dB) 14 16 18 20

Fig. 3. The decoding complexity of the priority-first search decoder (PFSD) for the constructed code of length N = 24.

that the priority-first search decoder significantly improve the decoding complexity whenit is compared with the exhaustive decoder.

REFERE NCES

[I] M. Beko , J. Xavi er andV. A.N. Barros o, "N onco herent communication in multiple-antenna system: receiver des ign and codebook construction,"

IEEE Trans. Signal Process., vol. 55, no. 12, pp. 5703-5715, Dec. 2007.

[2] M. Brehler and M. K. Varanasi, "Asymptotic error probability anal ysis of quadratic receivers in Rayleigh fading channels with applic ation s to a unified analysis of coherent and noncoherent space-time receivers,"

IEEE Trans. Inform. Theory, vol. 47 , no. 6, pp. 2383-2399, Sept. 2001.

[3] M. J. Borran ,A. Sabharwal and B. Aazhang , "On des ign criteria and construction of non coherent space-tim e constellations,"IEEE Trans. In-form. Theory, vol. 49, no. 10, pp. 2332-2351 , Oct. 2003.

[4] A.M. Cipriano, J.-C. Belfiore , "noncoherent Codes over the Grassman-nian",IEEE Trans Wireless Commun., vol. 6, no. 10, pp 3657-3667,

Oct. 2007.

[5] P. Dayal , M. Brehle r and M. K. Varanasi , " Leveraging coherent space-time codes for noncoherent communication via training",IEEE Trans. Inform. Theory, vol. 50, no. 9, pp. 2058-2080, Sept. 2004.