Blind-Channel Identification for
MIMO Single-Carrier Zero-Padding
Block-Transmission Systems
Yi-Sheng Chen and Ching-An Lin
Abstract—We propose a blind identification method for mul-tiple-input multiple-output (MIMO) single-carrier zero-padding block-transmission systems. The method uses periodic precoding on the source signal before transmission. The estimation of the channel impulse response matrix consists of two steps: 1) obtain the channel product matrix by solving a lower-triangular linear system; 2) obtain the channel impulse response matrix by com-puting the positive eigenvalues and eigenvectors of a Hermitian matrix formed from the channel product matrix. The method is applicable to MIMO channels with more transmitters or more receivers. A sufficient condition for identifiability is simply that the channel impulse response matrix is full column rank. The design of the precoding sequence which minimizes the noise effect in covariance matrix estimation is proposed and the effect of the optimal precoding sequence on channel equalization is discussed. Simulations are used to demonstrate the performance of the method.
Index Terms—Blind identification, block transmission, multiple-input multiple-output (MIMO) channel, periodic precoding, zero padding (ZP).
I. INTRODUCTION
M
ULTIPLE-INPUT multiple-output (MIMO) communi-cation systems employing multiple transmit and receive antennas have received much attention due to the potential im-provement in data transmission rate and link reliability they can offer. However, to exploit the potential advantage of MIMO sys-tems, accurate channel state information is required. Channel can be identified or estimated using training signal which requires ad-ditional bandwidth. As a means to eschew the need of training signal and the associated bandwidth requirement, blind identifi-cation of MIMO channels has been the focus of much research. Many blind identificationalgorithms havebeendeveloped for var-ious transmission systems (see [33]–[35] for a detailed review), including single-carrier (SC) block-transmission systems.SC block-transmission systems can be generally classified into three kinds: the first with cyclic prefix (CP) insertion (SC-CP systems) [1]–[7], the second with zero padding Manuscript received January 8, 2007; revised June 14, 2007. First published February 2, 2008; last published July 10, 2008 (projected). This work was sup-ported by the National Science Council under Grant NSC-93-2213-E009-041. This paper was recommended by Associate Editor P. Regalia.
Y.-S. Chen is with the Department of Communications Engineering, Feng Chia University, Taichung 40249, Taiwan, R.O.C. (e-mail: yischen@fcu.edu. tw).
C. A. Lin is with the Department of Electrical and Control Engineering, National Chiao Tung University, Hsinchu 30010, Taiwan, R.O.C. (e-mail: calin@cc.nctu.edu.tw).
Digital Object Identifier 10.1109/TCSI.2008.916418
(SC-ZP systems) [8]–[13], and the third with nonZP (SC-NZP) [36]–[38]. All these schemes are used to remove interblock interference (IBI) [8], [12]–[14], [36]. Discussions on these three kinds of systems can be found in [1]–[13], [36]–[38]. In this paper, we consider blind identification of the MIMO SC-ZP block-transmission system.
In the literature, to the best of our knowledge, there are two methods for blind identification of MIMO SC-ZP block-trans-mission systems. The subspace method [12] is suitable for white channel noise, while the eigen-decomposition method [13] can be used in the case when the channel noise is temporally and spatially colored.
Blind-channel identification using periodic precoding/mod-ulation, originally proposed in [21], has become an active research area, because it imposes no restriction on the loca-tions of channel zeros. Many different methods in this class have been proposed for SISO/MIMO series transmission sys-tems [20]–[26]. Wu and Lee [7] is the first to apply periodic precoding for blind identification of SISO SC-CP block-trans-mission systems. Their method exploits the circulant structure for computational advantage in solving the channel product matrix. It is shown that channel impulse response can be iden-tified up to a phase ambiguity by an eigenvalue-eigenvector decomposition.
We propose a method for blind identification of MIMO SC-ZP block-transmission systems with periodic precoding. The estimation of the channel impulse response matrix con-sists of two steps: 1) obtain the channel product matrix by solving a lower-triangular linear system; and 2) obtain the channel impulse response matrix by computing the positive eigenvalues and eigenvectors of a Hermitian matrix formed from the channel product matrix. The method is applicable to MIMO channels with more transmitters or more receivers. A sufficient condition for identifiability is simply that the channel impulse response matrix is full column rank. The design of the precoding sequence which minimizes the noise effect in covariance matrix estimation is proposed and the effect of the optimal precoding sequence on channel equalization is dis-cussed. Simulations are used to demonstrate the performance of the method and to compare it with a subspace method [12]. Compared with the subspace method [12], the identifiability condition of the proposed method is more relaxed than the irreducible condition required in [12]. As a result, the proposed method is suitable for more practical scenarios.
This paper is organized as follows. Section II is the system model and problem statement. In Section III, we describe the identification method, discuss the design of precoding 1549-8328/$25.00 © IEEE
Fig. 1. MIMO SC-ZP block-transmission baseband model with periodic precoding.
sequences, and propose an identification algorithm. The effect of the precoding scheme on channel equalization is discussed in Section IV. Simulation results are given in Section V. Section VI concludes this paper.
Notations used in this paper are quite standard: Bold upper-case is used for matrices, and bold lowerupper-case is used for vec-tors. and denote the transpose and conjugate transpose of , respectively. denotes the identity matrix of dimension . is the submatrix formed from the th row to the th row and from the th column to the th column of . The symbols and stand for the set of real numbers and the set of complex numbers, respectively.
II. SYSTEMMODEL ANDPROBLEMSTATEMENT Consider the -input -output discrete-time SC-ZP block-transmission baseband model shown in Fig. 1. At the transmitting end, the -input signal vector
is first multiplied by a positive -periodic sequence, , to obtain
, where is similarly
de-fined as and , . Then is
passed through a serial-to-parallel block whose output is Then is zero padded as
(2.1)
where . Finally, is converted to via
a parallel-to-serial block and transmitted through the MIMO FIR channel. At the receiving end, the -output received signal
vector is
, where is the signal component at the output and is the channel noise seen at the receivers. Here and are similarly defined as . is the channel coefficient
ma-trix whose th element , , is the
impulse response from the th transmitter to the th receiver, and is the order of the MIMO channel. We
assume that . Group the sequence of as
and define similarly as , we have
(2.2)
where is a block lower-triangular
Toeplitz matrix with the first block column being , and is a block upper-triangular Toeplitz matrix with the first
block row being .
The problem we study in this paper is blind identification of the MIMO channel coefficient matrices ,
using second-order statistics of the received data. We assume that the receivers are synchronized with the transmitters. In addition, the following assumptions are made throughout the paper.
(i) An upper bound of the channel order is known, , and is a multiple of .
(ii) The source signal is a zero mean white sequence
with , where is the
Kronecker delta function. The noise is white zero
mean with . In
ad-dition, the source signal is uncorrelated with the noise
, i.e., , .
(iii) The channel impulse response matrix is full column rank, i.e., rank .
III. BLIND-CHANNELIDENTIFICATION
In this section, we derive the proposed method under assump-tions (i), (ii), and (iii). We propose an optimal design of the pre-coding sequence, which takes into account the noise effect in the estimation of covariance matrix of the received data, so as to in-crease the accuracy in the computation of the channel product matrix and thus reduce the channel estimation error. With the proposed optimal precoding sequence, the computation of becomes particularly simple. Taking eigen-decomposi-tion of , we obtain the channel impulse response matrix up to a unitary matrix ambiguity. The proposed method can be used in the case of more transmitters or more
re-ceivers .
A. Identification Method
We first derive the proposed method for the case where noise is absent, the channel order is known, and there are more receivers, i.e., . We assume that . We discuss the case where noise is present in Section III-B. The effect of channel order overestimation is discussed in Section III-E. The
case is discussed in Section III-F.
Due to ZP of and [see (2.1)], we know and (2.2) can be written as
(noiseless case), where . Let
first rows of . Then ,
where and
. Due to
peri-odic precoding, we know for
, and hence can be written as
(3.1) where is similarly defined as , and
..
. ... . ..
Define as the matrix whose first block
sub-diagonal entries are all (i.e.,
), and all remaining entries are zero. Then . Taking expectation of , we get the covariance matrix
(3.2)
Since , (3.2) can be
written as
(3.3)
From [32, p.414], we know that the general matrix equation can be equivalently expressed as a
matrix-vector equation form, ,
where is the vec-function which stacks up columns of a matrix. Hence, the matrix (3.3) can be written in the following vector form:
(3.4) Here is a block Toeplitz lower-triangular matrix shown as follows:
..
. ... . .. ...
(3.5)
where and is a block diagonal
matrix with on the diagonal blocks. Since is square, the solution to (3.4) is
(3.6) provided . The elements of the channel product matrix obtained in (3.6) are then used to form a Hermitian matrix as follows:
(3.7)
Since rank by assumption (iii), rank .
Since is Hermitian and positive semidefinite, has posi-tive eigenvalues, say, . We can expand as
(3.8)
where is a unit norm eigenvector of associated with . We can thus choose the channel impulse response matrix to be
(3.9) We note that can only be identified up to a unitary matrix
am-biguity , i.e., , since .
The ambiguity matrix is intrinsic to blind identification of multiple input systems using only second-order statistics tech-nique [16]–[19]. The ambiguity can be resolved using a short pilot block sequence [12].
Remark: The method uses only , the first received blocks of , to identify the channel product matrix , since the lower-triangular structure of the sparse matrix makes it easy to compute , which can be seen in Section III-C. We can use more than block rows of for identifica-tion. However, the computational load increases as more data are used. Computation of using more data is formu-lated in Appendix A.
B. Optimal Design of the Precoding Sequence
When the noise is present, the covariance matrix contains the contribution of noise. Thus, (3.2) becomes
(3.10) where . In this case, (3.4) becomes
(3.11) From (3.6), an approximate solution of is
It follows from (3.12) and (3.11) that
(3.13)
where the vector in (3.13)
is the solution of . Since the matrix is com-pletely determined by the precoding sequence , we seek to choose so that is minimized. To this end, we need to analyze the relations between and . By expanding the
ma-trix equation , we find that for ,
.. .
(3.14)
and for all other indexes . We write (3.14) as the fol-lowing matrix equation,
..
. ... . .. ... ... ... (3.15)
where is a lower-triangular Toeplitz matrix, for
, and for ,
, . Hence, ,
the relations between and , is reduced to (3.15), and mini-mization of is equivalent to minimization of , which is a nonlinear function of . Then the problem is to minimize by choosing , subject to suitable constraints. Specifically, we formulate the problem as
(3.16) (3.17) Roughly, constraint (3.16) requires that at each instant, the
power gain is no less than with ;
constraint (3.17) normalizes the power gain of the precoding sequence of each transmitter to 1.
It is easy to show that for , the problem has a unique global minimizer given by and . For gen-eral case, the standard Kuhn-Tucker conditions of the nonlinear minimization problem do not seem to yield easily a unique analytical solution. However, the problem can be easily solved numerically (for fixed and ), say, using the Matlab Optimization Toolbox. Extensive numerically solutions, with different , , and initial guesses, have indicated that a global minimizer exists and is given by
(3.18)
In the following, we show that the solution (3.18) is also the global minimizer of an upper bound of . We know , where is the 2-induced norm of . Since is tri-angular and Toeplitz, it follows from [29] that for any fixed in-teger
(3.19)
where and . Hence, we
know . Since for any and
, (see Appendix B) and
, we know for any fixed , is an increasing function of , and for any fixed ,
is a decreasing function of . Hence, to minimize , we should choose as small as possible and choose as large as
possible subject to and .
It follows that (3.18) is a global minimizer of the upper bound .
Since and , the optimal precoding
sequence is
. (3.20)
We consider next the effect of on channel identification. From (3.15) and [27], [28], we know , where is a lower-triangular Toeplitz matrix with
as its first column, and
. (3.21) Then
(3.22)
For the optimal solution in (3.18), the corresponding in (3.21) can be expressed as follows:
. (3.23) The following proposition shows that is a continuous and strictly increasing function of on . In other words, for
, decreases as decreases, and thus as decreases, the noise effect in the estimation of the covariance matrix is reduced and hence identification performance im-proves.
and
for Proof: See Appendix C. C. Computation of
With the precoding sequence chosen as in (3.20), the matrix in (3.5) becomes
..
. ... . .. ... (3.24)
where , and . The inverse of can be
obtained by forward substitutions as
..
. ... . .. ... (3.25)
where and
for . The solution in
(3.12) is thus quite easy to compute once the precoding sequence is designed.
D. Identification Algorithm
We have proposed a new method for the identification of the MIMO channels for the SC-ZP block-transmission system using optimally designed periodic precoding sequences. With ZP, the computation of the channel product matrix becomes par-ticularly simple, since it amounts to solving a lower-triangular linear system. The channel impulse response matrix is then computed, up to a unitary matrix ambiguity, from the channel product matrix via an eigen-decomposition. We summarize the proposed method as the following algorithm.
Algorithm:
1) Select the optimal precoding sequence given by (3.20), and form as in (3.25).
2) Collect the received data as and pick up the first block entries of as . Then esti-mate the covariance matrix via the time average: , where is the number of data block.
3) Compute to obtain the
ele-ments of .
4) Form the matrix as in (3.7), and obtain the channel im-pulse response matrix (3.9) by computing the largest eigenvalues and the associated eigenvectors of . E. Channel Order Overestimation
So far we have assumed that the channel order is known. If only an upper bound is available, then following the same process given in Section III-A, we
ob-tain where
. Then we can also obtain . Note that the last block columns and block rows of are zero. Hence, again, rank and has positive eigenvalues. Each of the associated eigenvectors
has the form where .
Thus, we can identify the channel impulse response matrix, up to a unitary matrix ambiguity, from the eigenvectors associated with the positive eigenvalues of .
F. More Transmitters Than Receivers
In the above discussions, we assume that there are more re-ceivers than transmitters, i.e., . If there are more
transmit-ters, i.e., , then either or .
If , then is a tall matrix and assumption (iii) is generically satisfied. Hence, the proposed method still
ap-plies. If , then rank and assumption
(iii) does not hold. Hence, the proposed method is applicable to the more transmitters case, provided the additional condition
is satisfied.
IV. CHANNELEQUALIZATION
Once the received data is available
and the channel is identified, the minimum mean-square error (MMSE) or zero forcing (ZF) equalization methods [8] can be used to recover the modulated sources . For example, with an MMSE equalizer
where , we estimate by .
Since the precoding scheme is applied at the transmitter, we need to multiply the estimated by to obtain an estimate of , where is similarly defined as , and
. In other words, the estimated can be obtained by
(4.1) From (4.1), we know the equalization performance is related to and . Because is formed from the estimated channel coefficients, we expect good channel identification to bring an accurate and thus improves the equalization performance. Also we know using the optimal precoding sequence in (3.20), the identification performance improves as decreases. Hence, using a small brings good channel estimation and improves the accuracy of , which is expected to improve the equalization performance. However, using a
small would make the diagonal gain in
, , becomes large, which results in large noise amplification at the receivers and hence is more likely to
cause decision error. Therefore, using a small would amplify the noise and the equalization performance deteriorates as decreases.
In summary, although decreasing improves the accuracy of , it would cause an increased amplification of noise, and vice versa. Hence, there is a tradeoff on the selection of when channel equalization is performed. In the work of [7], [20], [23], [26], this tradeoff is also observed. We will give a simulation example to demonstrate this tradeoff in Section V.
V. SIMULATION
In this section, we generate 100 two-input two-output random channels for each simulation (except simulation 2) with order to demonstrate the performance of the proposed method. Each element in the channel impulse response matrix is gener-ated by a zero-mean complex circular Gaussian random variable with unit variance. The length of symbol blocks is , which is zero padded to blocks of length . It
means and transmission efficiency is .
The source symbols are independent and identically distributed (i.i.d.) Gray-coded quadrature phase-shift keying (QPSK) sig-nals. The signal-to-noise ratio (SNR) at the output is defined as . The channel noise is zero mean, temporally and spatially white Gaussian. The channel normalized root-mean-square error (NRMSE) is defined as
where denotes the Frobenius norm. is
the estimate of the th random channel
after removing the unitary matrix ambiguity by the least squares method [17], and is the number of random channels. is the average Frobenius norm of random channels.
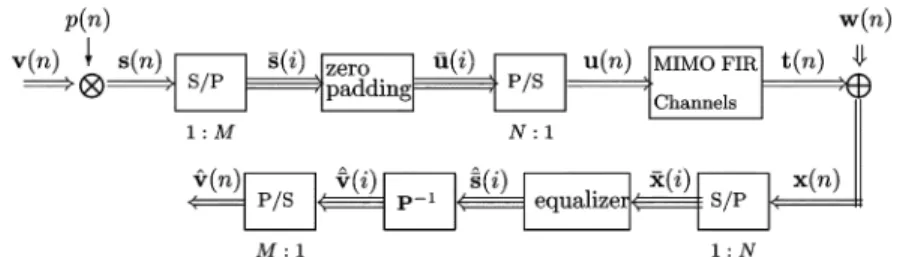
Simulation 1–optimal selection of the precoding sequence In this simulation, we use 5 precoding sequences which all satisfy (3.16) and (3.17) to illustrate the effect of the pre-coding sequences on the identification performance. The first sequence are chosen based on (3.20) for , i.e.,
is chosen as . The sequences , , ,
and are chosen as , ,
, and (i.e., no precoding), respectively. Fig. 2 shows that for dB, the NRMSE decreases as the number of symbol blocks increases for every precoding sequence. As expected, the optimal precoding sequence yields the smallest NRMSE.
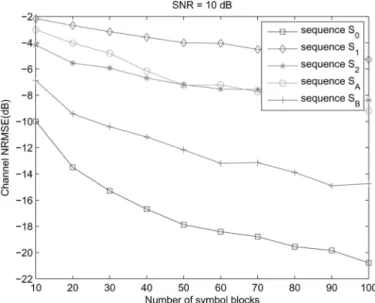
Simulation 2–tradeoff in selecting
In this simulation, we use the optimal precoding sequences which satisfy (3.20) with various to test the effect of on the identification and MMSE equalization performances. The number of symbol block is 100. To get more smoother curves, we use 1000 random channels for simulation. Fig. 3 shows that the identification performs better for smaller . Fig. 4(a) shows that for , the bit error rate (BER) performance deteriorates as decreases. Fig. 4(b) shows that for large ,
, the BER performance improves as decreases. Fig. 4 shows
Fig. 2. Channel NRMSE for different numbers of symbol blocks.
Fig. 3. Channel NRMSE at various SNR levels.
that there is a tradeoff between identification accuracy and noise amplification: a small means large noise amplification and an accurate channel estimate, and vice versa. For this example, it seems that is a good choice for BER performance.
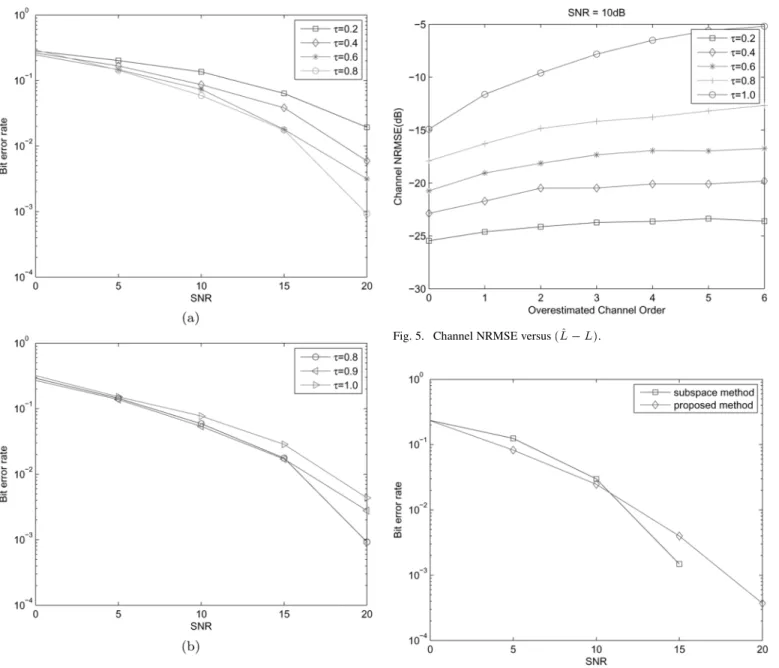
Simulation 3–channel order overestimation
In this simulation, we use precoding sequence that satisfies (3.20) with different and fix the number of symbol blocks at 100. For each upper bound , , we choose
and for simulation such that the transmission efficiency is maintained at . Fig. 5 shows the NRMSE in-creases with increasing channel order overestimation for each . We see that periodic precoding improves robustness to channel order overestimation. For example, without precoding , the NRMSE increases about 7 dB for . With pre-coding , the corresponding increase in NRMSE is about 3 dB.
Simulation 4–comparison with the subspace method In this simulation, we use the precoding sequence that sat-isfy (3.20) with . We compare the MMSE equalization
Fig. 4. BER versus output SNR.
performances of the proposed method and the subspace method [12] for MIMO SC-ZP systems. The number of symbol block is 100. Fig. 6 shows that the equalization performance of the pro-posed method is better than those of the subspace method for dB. The subspace method gives smaller BER than the proposed method for dB.
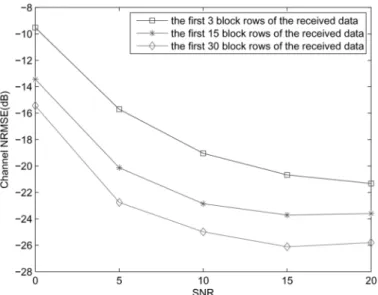
Simulation 5–identification using more recieved data In this simulation, we use the first 3, 15, and 30 block rows of to form the covariance matrices for identification. We use the precoding sequences that satisfy (3.20) with
and fix the number of symbol blocks at 100. Fig. 7 shows that when we use more received data, the identification performance improves. However, as we indicate at the end in Section III-A, the computational load of solving increases as more data are used. If we define a “flop” to be a single complex mul-tiplication or addition [30], then due to the sparse and lower-tri-angular structure of , there requires about 4.3 flops to solve for the first 3 block rows of ; while for the first 15 and 30 block rows of , the solution of is
Fig. 5. Channel NRMSE versus(^L 0 L).
Fig. 6. Comparison with the subspace method.
obtained via the least square approach, which is solved by the QR factorization [30, p.240], and the flop counts are roughly 8.4 and 3.44 flops, respectively.
VI. CONCLUSION
In this paper, we propose a new method for blind identifica-tion of MIMO channels for the SC-ZP block-transmission sys-tems using periodic precoding. The identifiability condition is simply that the channel impulse response matrix is full column rank. The performance of identification algorithm depends on the choice of the precoding sequence. We propose a two-level optimal precoding scheme that minimizes the noise effect in the estimation of the covariance matrix . The effect of the op-timal precoding sequence on channel equalization is also dis-cussed.
Compared with the subspace method [12], the proposed method is shown to have better performance from low to medium SNR. Besides, the computations involved in the
Fig. 7. Channel NRMSE for different sizes of received data.
algorithm are relatively simple: only covariance matrix es-timation, a multiplication of by a lower triangular matrix to obtain , and an eigen-decomposition
of a matrix, the main
computa-tional load; whereas, the computations of the subspace method requires a covariance matrix estimation, and two main computational loads: an eigen-decomposition of a matrix and a singular value
decomposi-tion of a matrix. Since
and , the subspace method requires substantially more computations than the proposed method.
APPENDIX
A) Computation of Using More Received Data:
If we use , the
first blocks of for identification, then it is easy to verify that
where is similarly defined as and
for .
Here we define as the matrix
whose first block sub-diagonal entries are all (i.e., ), and all
re-maining entries are zero; and with
and all remaining entries are zero.
Taking expectation of , we get the covariance matrix
(A.1)
Write the matrix equation (A.1) in the following vector form:
(A.2)
Since is a tall matrix, the
solu-tion to (A.2) is
(A.3) provided is full column rank, by appropriate selection of the precoding sequence.
B) Proof of :
Let and write in (3.19) as
Since
for
and , we have .
C) Proof of Proposition 3.1:
Let and , then according to (3.25),
and for
, and . Hence, by
computation, we obtain
and
Because and for
REFERENCES
[1] H. Sari, G. Karam, and I. Jeanclaude, “Transmission techniques for digital terrestrial TV broadcasting,” IEEE Signal Process. Mag., vol. ???, no. 2, pp. 100–109, Feb. 1995.
[2] B. Gyselinckx and M. Engels, “Training sequence versus cyclic prefix—A new look on single-carrier communication,” IEEE Commun.
Lett., vol. 5, no. 7, pp. 292–294, Jul. 2001.
[3] D. Falconer, S. L. Ariyavisitakul, A. Benyamin-Seeyar, and B. Eidson, “Frequency domain equalization for single-carrier broadband wireless systems,” IEEE Signal Process. Mag., vol. ???, pt. 4, pp. 58–66, Apr. 2002.
[4] Y. H. Zeng and T. S. Ng, “Pilot cyclic prefixed single-carrier commu-nication: Channel estimation and equalization,” IEEE Signal Process.
Lett., vol. 12, no. 1, pp. 56–59, Jan. 2005.
[5] J. Coon, S. Armour, M. Beach, and J. McGeehan, “Adaptive frequency-domain equalization for single-carrier multiple-input multiple-output wireless transmissions,” IEEE Trans. Signal Process., vol. 53, no. 8, pp. 3247–3256, Aug. 2005.
[6] J. Coon, J. Siew, M. Beach, A. Nix, S. Armour, and J. McGeehan, “A comparison of MIMO-OFDM and MIMO-SCFDE in WLAN environ-ments,” in Proc. IEEE Global Telecommun. Conf., Dec. 2003, vol. 6, pp. 3296–3301.
[7] J. Y. Wu and T. S. Lee, “Periodic-modulation-based blind-channel identification for the single-carrier block transmission with fre-quency-domain equalization,” IEEE Trans. Signal Process., vol. 54, no. 3, pp. 1114–1130, Mar. 2006.
[8] A. Scaglione, G. B. Giannakis, and S. Barbarossa, “Redundant filter bank precoders and equalizers—Part I: Unification and optimal de-signs and Part II: Blind-channel estimation, synchronization, and di-rect equalization,” IEEE Trans. Signal Process., vol. 47, no. 7, pp. 1988–2022, Jul. 1999.
[9] S. Ohno, “Performance of zero-forcing equalizers for single-carrier zero-padded transmission over fading channels,” in Proc. IEEE Int.
Conf. Acoustics, Speech, Signal Process., May 2004, vol. 4, pp.
1017–1020.
[10] Z. Wang, X. Ma, and G. B. Giannakis, “Optimality of single-carrier zero-padding block transmission,” in Proc. Wireless Commun.,
Net-working Conf., Mar. 2002, vol. 2, pp. 660–664.
[11] Z. Wang, X. Ma, and G. B. Giannakis, “OFDM or single-carrier block transmission?,” IEEE Trans. Commun., vol. 52, no. 3, pp. 380–394, Mar. 2004.
[12] Y. H. Zeng and T. S. Ng, “A semi-blind-channel estimation method for multiuser multiantenna OFDM systems,” IEEE Trans. Signal Process., vol. 52, no. 5, pp. 1419–1429, May 2004.
[13] Y. S. Chen and C. A. Lin, “Blind identification of MIMO channels in zero-padding block-transmission systems,” IEEE Trans. Signal
Process., vol. 55, no. 2, pp. 764–772, Feb. 2007.
[14] B. Muquet, Z. Wang, G. B. Giannakis, M. D. Courville, and P. Duhamel, “Cyclic prefixing or zero padding for wireless multicar-rier transmissions?,” IEEE Trans. Commun., vol. 50, no. 12, pp. 2136–2148, Dec. 2002.
[15] W. Hachem, F. Desbouvries, and P. Loubaton, “MIMO channel blind identification in the presence of spatially correlated noise,” IEEE Trans.
Signal Process., vol. 50, no. 4, pp. 651–661, Mar. 2002.
[16] Z. Ding, “Matrix outer-product decomposition method for blind mul-tiple channel identification,” IEEE Trans. Signal Process., vol. 45, no. 12, pp. 3053–3061, Dec. 1997.
[17] Z. Ding and L. Qiu, “Blind MIMO channel identification from second order statistics using rank deficient channel convolution matrix,” IEEE
Trans. Signal Process., vol. 51, no. 2, pp. 535–544, Feb. 2003.
[18] J. Shen and Z. Ding, “Direct blind MMSE channel equalization based on second-order statistics,” IEEE Trans. Signal Process., vol. 48, no. 4, pp. 1015–1022, Apr. 2000.
[19] X. Cao and R. Liu, “General approach to blind source separation,”
IEEE Trans. Signal Process., vol. 44, pt. 3, pp. 562–577, Mar. 1996.
[20] A. Chevreuil, E. Serpedin, P. Loubaton, and G. B. Giannakis, “Blind channel identification and equalization using periodic modulation pre-coders: Performance analysis,” IEEE Trans. Signal Process., vol. 48, no. 6, pp. 1570–1586, Jun. 2000.
[21] E. Serpedin and G. B. Giannakis, “Blind channel identification and equalization with modulation induced cyclostationarity,” IEEE Trans.
Signal Process., vol. 46, no. 7, pp. 1930–1944, Jul. 1998.
[22] E. Serpedin, A. Chevreuil, G. B. Giannakis, and P. Loubaton, “Blind channel and carrier frequency offset estimation using periodic mod-ulation precoders,” IEEE Trans. Signal Process., vol. 48, no. 8, pp. 2389–2405, Aug. 2000.
[23] C. A. Lin and J. Y. Wu, “Blind identification with periodic modulation: A time-domain approach,” IEEE Trans. Signal Process., vol. 50, no. 11, pp. 2875–2888, Nov. 2002.
[24] A. Chevreuil and P. Loubaton, “MIMO blind second-order equalization method and conjugate cyclostationarity,” IEEE Trans. Signal Process., vol. 47, no. 2, pp. 572–578, Feb. 1999.
[25] H. Bölcskei, R. W. Heath, Jr, and A. J. Paulraj, “Blind channel es-timation in spatial multiplexing systems using nonredundant antenna precoding,” in Proc. 33rd Annu. IEEE Asilomar Conf. Signals, Syst.,
Computers, Oct. 1999, vol. 2, pp. 1127–1132.
[26] C. A. Lin and Y. S. Chen, “Blind identification of MIMO channels using optimal periodic precoding,” IEEE Trans. Circuits Syst. I, Reg.
Papers, vol. 54, no. 4, pp. 901–911, Apr. 2007.
[27] R. E. Bach, JR and Y. Baram, “Recursive inversion of externally de-fined linear systems by FIR filters,” IEEE Trans. Autom. Contr., vol. 34, no. 6, pp. 635–637, Jun. 1989.
[28] D. Commenges and M. Monsion, “Fast inversion of triangular Toeplitz matrices,” IEEE Trans. Autom. Contr., vol. 29, no. 3, pp. 250–251, Mar. 1984.
[29] N. J. Higham, “A survey of condition number estimation for triangular matrices,” SIAM Rev., vol. 29, no. 4, pp. 575–596, Dec. 1987. [30] G. H. Golub and C. F. Van Loan, Matrix Computions, 3rd ed.
Balti-more, MD: The Johns Hopkins University Press, 1996.
[31] B. O’Hara and A. Petrick, The IEEE 802.11 Handbook: A Designer’s
Companion, 2nd ed. New York: IEEE Press, 2005.
[32] P. Lancaster and M. Tismenetsky, The Theory of Matrices With
Appli-cations. Reading, MA: Academic, 1984.
[33] K. Abed-Meraim, W. Qiu, and Y. Hua, “Blind system identification,”
Proc. IEEE, vol. 85, no. 8, pp. 1310–1332, Aug. 1997.
[34] Z. Ding and Y. Li, Blind Equalization and Identification. New York: Marcel Dekker, 2001.
[35] G. B. Giannakis, Y. Hua, P. Stoica, and L. Tong, Signal Processing
Advances in Wireless and Mobile Communications Volume I: Trends in Channel Identification and Equalization. Upper Saddle River, NJ: Prentice-Hall, 2001.
[36] G. Leus and M. Moonen, “Semi-blind-channel estimation for block transmissions with non-zero padding,” in Proc. 35rd Annu. IEEE
Asilomar Conf. Signals, Syst., Comput., Nov. 2001, vol. 1, pp.
762–766.
[37] O. Rousseaux, G. Leus, P. Stocia, and M. Moonen, “A stochastic method for training based channel identification,” in Proc. 7th Int.
Symp. Signal Process. Appl., Jul. 2003, vol. 1, pp. 657–660.
[38] J. Coon, M. Beach, J. McGeehan, and M. Sandel, “Channel and noise variance estimation and tracking in unique-word based single-carrier systems,” in Proc. 1st Int. Symp. Wireless Commun. Syst., Sep. 2004, pp. 51–55.
Yi-Sheng Chen received the B.S. and the M.S. degrees, both in electrical engineering from the Na-tional Chung Hsing University, Taichung, Taiwan, R.O.C., in 1997 and 1999, respectively, and the Ph.D. degree in electrical and control engineering from the National Chiao Tung University, Hsinchu, Taiwan, R.O.C., in 2006.
He was with the military service from 1999 to 2001, and with the Kaohsiung Rapid Transmit Corporation from 2001 to 2002. Since Aug., 2007, he has been with the Department of Communications Engineering, the Feng Chia University, where he is an assistant Professor. His current research interests are in signal processing and communication.
Ching-An Lin received the B.S. degree from the National Chiao Tung University, Hsinchu, Taiwan, R.O.C., in 1977, the M.S. degree from the University of New Mexico, Albuquerque, in 1980, and the Ph.D. degree from the University of California, Berkeley, in 1984, all in electrical engineering.
He was with the Chung Shan Institute of Science and Technology from 1977 to 1979 and with Inte-grated Systems Inc. from 1984 to 1986. Since June, 1986, he has been with the Department of Electrical and Control Engineering, the National Chiao Tung University, where he is a Professor. His current research interests are in control and signal processing.