有五階對稱的晶格嗎？

S C I E N C E

有五階對稱的晶格嗎？

作者 科里澤克 Michal K ížek 梭茨 Jakub Šolc 莎可娃 Alena Šolcová 譯者 黃俊瑋 作者簡介 科里澤克是捷克科學院數學所的教 授；梭茨是捷克科技大學的數學助 理教授；莎可娃是捷克科技大學的 數學副教授。

克卜勒的馬賽克

日耳曼學者克卜勒（

Johannes Kepler

，

1571–1630

），做為布拉 格神聖羅馬帝國皇帝魯道夫二世的宮廷數學家，尤其以天文學上的發現 著名。他從第谷•布拉赫（

Tycho Brahe

）觀察火星的數據，所推得的 三大行星運動定律，時至現今依舊令人們欽佩。克卜勒另一個傑出的發 現是克卜勒方程式，這方程式描述了行星在公轉軌道上時間和位置之間 的關係。這個方程式現在通常是從克卜勒第一與第二定律，利用無窮小 量微積分推導，但是克卜勒當時則是利用橢圓和圓的幾何性質就得到此 結論。 然而克卜勒也研究純數學的問題，例如他有一個關於球體最密堆 積方式的著名猜想。關於這個猜想，在

[12]

裡所談「以電腦為基礎的證 明」，其有效性仍然有討論的餘地，因為它的證明不是整數算術的證明 （而是浮點電腦的算術）。克卜勒也被認為是「結晶學」的創始人之 一，當他經過布拉格的查理斯大橋時，被美麗的雪花所震攝。他在

1611

年〈關於六角雪花〉這篇論文中問到，為什麼所有的雪花皆具有六階對 稱性，即便它們的形狀都不相同。克卜勒建構出三個像星星狀的有趣多 面體：星型八面體，以及另外兩個具有六條五階旋轉對稱軸的星形多面 體，參見

[23]

以及圖

1

與圖

2

。 圖1. 克卜勒星型多面體，左邊的星狀八面體是由兩個正四面體所組 成的立體圖形，它剛好可以塞入一個正立方體（正六面體） 裡。右邊的立體是星型12面體，我們可以看到有12個「五角金 字塔」，事實上，它們恰巧接在正12面體的12個面上。如果我 們把這種星型的頂點以稜邊連接起來，便形成一個正20面體。 圖2. 布拉格查爾斯廣場的克卜勒大星狀20面體，鄰近克卜勒 故居。它的正向對稱（亦即旋轉而非鏡射）是單交錯群  A5，它可用來證明五次多項式沒有根式解。

書裡，他處理了如何用凸正多邊形做平面鋪磚（即 馬賽克）的問題，其中任兩相鄰的正多邊形必須共 邊。此外，他還要求每一頂點必須具有同樣的類 型(n1, n2,· · · , nk)，也就是說，頂點被同樣的 n1邊 形、n2 邊形等等所環繞。這裡我們要把_k 元數組 (n1, n2,· · · , nk)和(nk,· · · , n2, n1)視為等價，也就 是說，這與環繞的多邊形是順時針或逆時針順序無 關 。 除 此 ， 我 們 也 將_k 元 數 組 (n1, n2,· · · , nk)和 (n2,· · · , nk, n1)視為等價，亦即從哪一個多邊形開始 編號並不重要。這樣的鋪磚方式我們稱之為半正規 （

semi-regular

）。特別當n1= n2=· · · = nk  時， 則稱為正規。當某一種鋪磚方式可以利用平移、旋 轉、鏡射、伸縮，或者上述變換的組合而得到另一種 鋪磚方式時，我們就將這兩種鋪磚方式視為等價。 克卜勒定理：恰存在十一種不同的半正規平面鋪磚 法，其中三種是正規的。 以下，我們概述這個證明的主要想法（詳見

[15]

）。

正

ni

邊形的內角等於

ni

− 2

n

i

180

◦ 因此，對於

(n1, n2,· · · , nk)

型的頂點而言，下面有 關於半正規鋪磚法存在性的必要（但非充分）條件 成立： n1− 2 n1 180◦+n2− 2 n2 180◦+· · · +nk− 2 nk 180◦= 360◦ 從上式我們可導出一個丟番圖整數方程式：

（

1

）

1

n

1

+

1

n

2

+

_{· · · +}

1

nk

=

k

_{− 2}

2

（

1

）式右邊必須是正的，因此

k_{≥ 3}。又由於一個 點最多可被六個正三角形環繞，但因其它的正

n

邊 形內角更大，因此我們進一步獲得了（

1

）式可解的 必要條件為

k_{≤ 6}。為了清楚表示，我們將依據數組 的大小把所有可能產生的

k

元數組進行排序，底下 是

17

組關於方程式（

1

）的解： ( 3 , 7 , 42 )　( 3 , 8 , 24 )　( 3, 9 , 18 ) ( 3 , 10 , 15 )　( 3 , 12 , 12 )　( 4 , 5 , 20 ) ( 4 , 6 , 12 )　( 4 , 8 , 8 )　( 5 , 5 , 10 )　( 6 , 6 , 6 ) 四元數組： ( 3 , 3 , 4 , 12 )　( 3 , 3 , 6 , 6 )　( 3 , 4 , 4 , 6 ) ( 4 , 4 , 4 , 4 ) 五元數組： ( 3 , 3 , 3 , 3 , 6 )　( 3 , 3 , 3 , 4 , 4 ) 六元數組： ( 3 , 3 , 3 , 3 , 3 , 3 ) 然而，並非上述所有解都能夠對應到半正規平面 鋪磚，以

(5

,

5

,

10)

為例，我們可以在一個點環繞 二個正五邊形以及一個正十邊形，但是你簡單檢查一 下，就知道光靠這種方式並不足以鋪滿整個平面。 以下，我們不再依數組大小進行排序。在逐一檢 查各種情況之後，我們獲得底下可以鋪滿整個平面的

11

組解（如下頁圖

3

所示）： ( 3 , 3 , 3 , 3 , 3 , 3 ) 　( 4 , 4 , 4 , 4 )　( 6 , 6 , 6 ) ( 3 , 12 , 12 )　( 4 , 8 , 8 )　( 4 , 6 , 12 ) ( 3 , 6 , 3 , 6 )　( 3 , 4 , 6 , 4 )　( 3 , 3 , 4 , 3 , 4 ) ( 3 , 3 , 3 , 4 , 4 )　( 3 , 3 , 3 , 3 , 6 ) 注意到，圖

3

中最後兩種鋪磚方式互為鏡像，因 此是等價的，它們是同一鋪磚方式的左手形式與右手 形式，其餘的鋪磚方式則都具有鏡射軸。 我們發現克卜勒的半正規鋪磚並不存在五階旋轉 對稱，但是它們包含了二階、三階、四階或六階旋轉 對稱，亦即對克卜勒馬賽克圖案中某個適當的點，旋 轉360◦/k，k∈ {2, 3, 4, 6}，並且不考慮顏色，那麼 我們可以得到同一種馬賽克樣式。但是，克卜勒嚮往 五階對稱性。在他的《世界的和諧》一書中，可以發 現許多至少局部具有五階對稱性的馬賽克圖案（參見 下頁圖

4

）。

1 8 5 0

年 ， 法 國 數 學 家 兼 晶 體 學 家 布 哈 維 （

Auguste Bravais

）證明了三維空間中的晶格不存 在五階對稱。請注意，此結論僅限於歐氏空間裡，至

S C I E N C E 圖3. 克卜勒馬賽克圖案。最後的兩個是互為鏡像的圖形，因此是 等價的。其餘的鋪磚方式則都有鏡射軸，它們的類型包含： ( 3, 3, 3, 3, 3, 3 )　( 4, 4, 4, 4 ) 　( 6, 6, 6 ) ( 3, 12, 12 )　( 4, 8, 8 )　(4, 6, 12 ) ( 3, 6, 3, 6 )　( 3, 4, 6, 4 )　( 3, 3, 4, 3, 4 ) ( 3, 3, 3, 4, 4 )　( 3, 3, 3, 3, 6 )　( 3, 3, 3, 3, 6 ) 於雙曲（或橢圓）空間則是另外一回事（請參見艾雪 （

M. C. Escher

）著名的藝術作品）。

潘洛斯的馬賽克

令 （

2

）

α = 1 + √ 5 2

以及

β = 1₋√5 2 它們是一元二次方程式_x2_{− x − 1 = 0的根，其中α} 被稱為黃金分割比（

golden section

），它是我們 所知最神祕的無理數之一（底下將會談到），總在某 些人們意想不到的場合出現（例如

[13]

）。 黃金分割比表現了古代的美學比例（見

[17]

）， 邊長比為α的矩形，往往被視為是最美的矩形。正

20

面體中兩相對稜邊的凸包（

convex hull

）所構成 的矩形便是一例（如圖

5

）。正五邊形對角線長與邊 長的比是α。如果把正五邊形對角線分成兩段，其中 較長的一段成等於邊長時，這兩段線段的長度比也是 α。另外，正十邊形外接圓半徑與其邊長的比也是α 。而邊長為

1

的正

12

面體與正

20

面體，其體積分別為 2 + 7α/2 以及5(1 + α)/6。 克卜勒發現一種

30

個面皆全等的多面體（克 圖4. 克卜勒在《和諧的世界》中對五階對 稱的試驗。克卜勒將正n邊形排成 像圓的形狀。他試圖以其他正n邊 形來填滿中間的區域，就像我們在圖 Y之中看到的一樣。以同樣的手法， 他將十個正五邊形排成一圈，中間的 區域形成了正十邊形（圖Z）。克卜 勒的主要結果呈現在圖Aa中，請注 意，圖中兩個十邊形重疊的部分，恰 與較小的潘洛斯磚形狀相同。 卜 勒 菱 形

30

面 體 ），這個多面體是五個方向各異 但中心相同的正立方體交集（參考圖

6

與圖

7

）， 這

30

個面都是菱形，而且這些菱形對角線長的比 值也是α =−1/β。溫克巴赫（

H. Unkelbach

） 於

1940

年左右所發現的菱形

60

面體也具有相同的 面（參見

[9]

、

[27]

）。更令人驚奇的是，這個被 選 為

Wolfram Alpha

搜 尋 引 擎 視 覺 標 誌 的

60

面體，一般被認為存在於大自然界中，是鋁銅鋰 合 金 （Al6Cu3Li） 緩 慢 固 化 過 程 中 所 形 成 準 晶 體 （

quasicrystal

）聚集體中的核心部分（見

[11]

）。 在 四 維 空 間 裡 ， 中 心 在 原 點 的 正 四 維 單 形 （

simplex

，相當於二維的正三角形、三維的正四面 體），其頂點坐標同樣可利用黃金分割比來表示，分 別為： 圖5. 左 邊 是 正 八 面 體 。 而 右 邊 的 正2 0面 體 ， 具 有 六 條 五 階 對 稱 的旋轉軸。

（

3

）

v

1

=

(3α

− 1, β, β, β)

T

v

2

=

(β, 3α

− 1, β, β)

T

v

3

=

(β, β, 3α

− 1, β)

T

v

4

=

(β, β, β, 3α

− 1)

T

v

5

=

(

−2, −2, −2, −2)

T 在四維空間中，存在另一種正多胞超體，稱為

600

胞，這是相當奇特的數學物件，它的三維「邊 界」是由

600

個正四面體所組成（參見

[6]

，

[25]

）。 這個三維超曲面共包含了

720

條邊，並形成

72

個有相 同中心，但彼此不共邊的正十邊形（類似地，正八面 體的表面包含了十二條邊，並形成三個不共邊的正方 形）。而這個

600

胞的外接球半徑與其邊長之比也是 α。除此之外，還有其他類似的例子。 在

1970

年 代 初 期 ， 英 國 的 數 學 家 與 物 理 學 家 潘 洛 斯 （

Roger

Penrose

），發現 利用兩種菱形磚， 可以在平面鋪磚時 形成局部的五階對稱（如圖

8

），並且與黃金分割比 有緊密的關係。這兩類菱形磚皆有相同的邊長，第一 類菱形磚的銳角等於72◦_{，而第二類菱形磚的銳角則} 為36◦_{。它們都被稱為潘洛斯磚（}

Penrose tiles

_）。 我們可以簡單地驗證： 2α 假設兩類磚的邊長皆為

1

，那麼第一類潘洛斯磚的

面積為

sin 72◦_{= 2 sin 36}◦_{cos 36}◦_{，而第二類則為}

sin 36◦_{。因此，他們的面積比也是黃金分割：}

sin 72◦_{: sin 36}◦_{= 2 cos 36}◦_{= α}

潘洛斯自己承認他曾受到克卜勒《世界的和諧》 研究的啟發，該書也檢驗了正五邊形磚的鋪磚法。想 建構潘洛斯鋪磚時，所有的磚片都必須滿足 潘洛斯 規則： 如圖

9

，磚片相連時必須使相同顏色的粗曲線 相連。 潘洛斯鋪磚最令人驚奇的性質是它們並不滿足非 無聊的平移對稱性（如圖

8

）。將潘洛斯鋪磚沿任一 向量移動皆不會與原來的鋪磚相同，即使環繞於某一 給定頂點的所有磚片組合數是有限的也一樣。若一種 鋪磚方式不滿足任何非無聊的平移對稱性，則稱其為 非週期（

nonperiodic

）鋪磚，上述定義來自

[22]

。 關於潘洛斯鋪磚有相當多的文獻，這裡我們只提 到最源頭的論文

[20]

，圖

9

所示的菱形磚第一次就是 出現在這篇文章中。 潘洛斯定理：每一種使用潘洛斯磚的平面鋪磚法，若 滿足潘洛斯規則，則其為非週期鋪磚。 相關證明可參考

[10]

。 成。這個多面體有六條五階對稱的旋轉 軸。 圖7. 五個正立方體的聯集，其交集區域即 為克卜勒的菱形30面體，這個圖形 也有六條五階對稱的旋轉軸，而且其 凸包構成正12面體（相反地，在正 12面體找八個適當的頂點，其凸包 就是一個正立方體）。 圖8. 潘洛斯的非週期性鋪磚。 圖9. 想 製 造 非 週 期 的 潘 洛 斯 鋪 磚 ， 需 要 使 用 兩 種 潘 洛 斯 磚，並將上面同樣顏色的粗曲線 相連。這麼一來，我們甚至可以得到一種馬賽克圖 案，具有針對某一特定點的整體平面五階對稱性。

S C I E N C E 如果違反潘洛斯規則，就有可能利用潘洛斯磚做 出週期性的鋪磚法。舉例來說，我們可以將這些磚片 排成無限長的長條，並建構出週期性的鋪磚。不過為 了做出非週期性的鋪磚，光是假設任兩個相鄰的磚片 不形成平行四邊形並不夠，我們仍然可以利用潘洛斯 磚來構成週期性鋪磚，例如讓每個頂點環繞四片磚， 而其角度分別為

36◦_、72◦_、144◦_、108◦_{（永遠依這個} 順序），注意到這個例子不滿足潘洛斯規則。另外， 潘洛斯鋪磚的想法還可推廣到高維空間中。

1980

年，卡茲（

André Katz

）發現一種非週期 性的平面鋪磚方式，並在局部上形成七階旋轉對稱（ 參見圖

10

）。他的三種磚片類型同樣是菱形，其銳 角依序為

180◦_/7

_、

₃₆₀◦_/7、以及

₅₄₀◦_{/7，更詳細的} 說明請參見文獻

[21][26]

。 值得提醒的是，我們可以只用單一形狀的圖形， 就能以非週期性的方式鋪滿平面，例如等腰直角三角 形。事實上，我們只要用著名的烏朗螺線便足以構 造這樣的例子（見圖

11

），這個螺線是

1963

年波蘭 數學家烏朗（

Stanislaw Ulam

）所提出的。其中， 質數寫在黑色的正方格，其它的數則寫在白色的正方 格。接著將所有的黑色正方格以斜率為

1

的對角線隔 成兩個等腰直角三角形，而白色正方格則以斜率為 −1的對角線隔成兩個等腰直角三角形。這樣便得到 以一種磚片所構成的非週期性鋪磚。

半正多面體

希臘哲學家柏拉圖在其對話錄〈蒂邁歐斯篇〉 （

Timaios

）之中提到三維空間中的五種正多面體。 正多面體又被稱為柏拉圖物體，是滿足所有面都是全 等正多邊形，並且每一頂點都被同樣多面所環繞的 凸多面體。需要注意的是「凸」這個假設是不可或 缺的。因為存在例如一種非凸的多面體，它的表面由

20

個全等正三角形所組成，而且每個頂點均環繞了 五個面。 所謂 半正多面體 是一種凸多面體，它的面都是 正多邊形，而且各頂點的立體角之間都是正向或反向 全等的。注意到，一個立體角跟它的鏡像彼此是反向 全等的。 柏拉圖物體是半正多面體的特例，它們的表面是 由單一正多邊形所組成。半正多面體的表面則由兩種 以上的正多邊形組成。半正多面體可以被分成阿基米 德立體（

Archimedean solid

）、正角柱（

regular

prism

）與正反角柱（

regular antiprism

）。我們可 以採取類似研究平面半正則鋪磚的方法，就像前述 用丟番圖不等式來證明克卜勒定理一樣，去探究這類 立體的存在性。所謂正角柱，有兩個相對平行的正n 邊形底面，其它的面都是正方形；相對地，反正角柱 也有兩個平行但錯開的正n邊形底面，而其它的面 都是正三角形。正角柱的特例之一是正立方體；相對 地，正反角柱的特例之一是正八面體。關於

13

種阿 基米德立體的研究，則出現於克卜勒的《世界的和 諧》第二章。 在

1905

年左右，第

14

種阿基米德立體被發現， 這主要是透過將圖

12

中第十個圖形的「上層」旋轉 45◦後得到的結果（參見

[24]

的圖

27

），不過這個圖 形並沒有整體的對稱性。而圖

12

裡的最後兩種多面 體，都分別有左手形式與右手形式的存在，就像圖

3

中克卜勒最後的兩種鋪磚方式一樣。這些分類的歧 異，肇因於阿基米德立體一詞的定義不幸地不統一。 另外，注意到有一些半正多面體也有六條五階對稱的 旋轉軸。 典型的足球是一種包含

12

個正五邊形與

20

個正 六邊形的阿基米德立體（請參見圖

12

中的第四個立 圖10. 卡茲的非週期性鋪磚。 圖11. 烏 朗 的 正 整 數 螺 旋 方 格。其中質數部份的底 色是灰黑色的。 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

{(x1, x2,· · · , x8)∈ Z8∪ (Z + 1 3) 8 | 8  i=1 xi≡ 0 mod 2} 對應於這些中心的所有沃羅諾胞（

Voronoi cells

） 正好形成這個有趣半正多面體的特定複製組合。

四維空間中的五階對稱

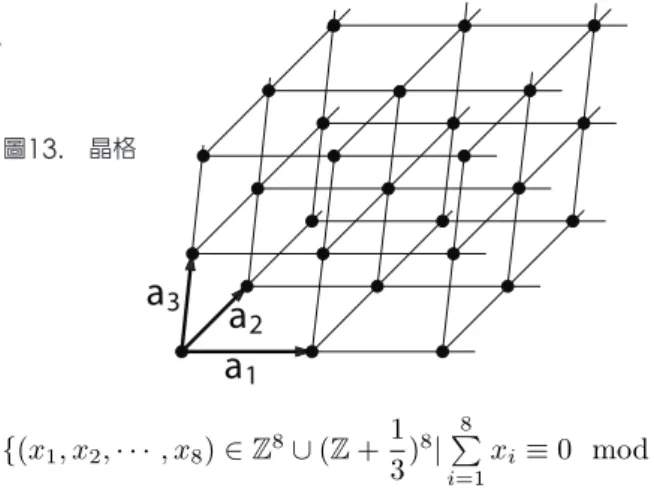
所謂三維空間的晶格是由彼此全等的平行六面體 晶胞之稜邊所構成，這些平行六面體是由三個線性獨 立的向量

a1, a2, a3∈ R3

所定義的（參見圖

13

）。 我們假設晶格是無限的，並且對向量ai的任 意整數倍數皆具有平移對稱性。法國結晶學家布哈 維研究了三維空間中晶格的點對稱群，亦即將整個 晶格映至自身並具有至少一個固定點的等距變換（ 參見

[4]

）。這裡的對稱指的是正向全等變換（亦 即不考慮反射與旋轉反射的情況）。這些晶格的對 稱是依某個軸旋轉k_{· 360}◦_{/n，其中k是整數，而} n_{∈ {1, 2, 3, 4, 6}}。因此，晶格可能具有二階、三階、 四階、以及六階的對稱性，但不具有五階對稱性。由 此可以立刻得到下面的定理： 布哈維定理：三維空間中不存在具有五階對稱的晶格 五 階 對 稱 僅 會 局 部 地 出 現 ， 而 原 子 排 列 成 正

20

面 體 的 準 晶 體 便 是 這 樣 的 例 子 （ 參 見

[

18

]

） 。利用考克斯特群（

Coxeter group

）的方法， 陳 （

L. Chen

）、 穆 迪 （

R. Moody

）、 佩 特 拉 （

J. Patera

）在

[5]

中，詳細地分析了以五階對稱 為基礎的非晶體根系（

noncrystallographic root

system

）以及與其相關的準晶體。 現在考慮在高維空間中的無界晶格，這個晶格被 線性獨立的向量a1, a2,· · · , ad ∈ Rd所定義，並且令 V = _d i=1 ciai| ci∈ Z  體圖形）。這種多面體共有

60

個頂點，並且出現在 化學的分子模型上。因為有一種穩定的碳分子，也就 是所謂的富勒烯巴克球

C60，它的

60

個碳原子，正好 落在這種半正多面體的頂點上。另外，有些粉塵與病 毒的形狀也是半正多面體。 構造球面的分割時，通常是對正

20

面體表面的 三角形進行再分割而得。正

20

面體（參見圖

5

）也 被用於將空間分割成銳角四面體的過程（參見

[8]

、

[12]

）。正立方體是唯一可以用來鋪滿三維空間中的 柏拉圖物體。三維空間也可利用正四面體與正八面體 透過下述方式來鋪滿：讓每個正三角形的面，恰被一 個正四面體與一個正八面體所共有。由於鑽石正具有 這樣的晶格，因此它是最硬的礦物。 這裡我們要特別指出，阿基米德立體可以被推廣 至更高維度的_Rd_{空間。對於d > 3，除了正多面體、} 角柱與反角柱之外，恰只存在七種半正多面體，其 中三種落在維度

d = 4

時，而當

d = 5, 6, 7, 8

時，則 各有一種半正多面體（參見

[1]

）。舉例來說，在四 維空間裡有一種半正多面體，它有十個頂點，其「表 面」是由五個正四面體以及五個正八面體所組成，同 時它具有五階對稱性。 R8_{空間可利用一種對稱群為E8（參見}

[28]

_） 的半正多面體來鋪滿。值得一提的是，這種立體圖 形的內切球可以形成_R8_{的最密堆積（參見}

[16]

_與

[19]

）。其中每個球與其它

240

個球相接，而這個 性質可以被應用來構造最有效率的漢明錯誤更正碼 （

Hamming error-correcting code

）。這些球的 球心所構成的集合為：

S C I E N C E 表示這個晶格的格點所形成的集合。另外如果 一個變換_{A : V → V} 會保持距離，則稱之為保距變 換（

isometry

），也就是說，對所有的x_{∈ V}，滿 足A(x) = x，其中 · 表示歐氏距離。如果存 在一個非恒等的保距變換_{A : V → V}，滿足對所有的 x_{∈ V}，A5_{(x) = x} ，那麼我們就稱此晶格具有五階 對稱性。 令

ei= (0, 0,· · · , 0, 1, 0, · · · , 0)

為

d

維空間中， 第

i

個分量為

1

的標準基底。並令 P =        0 0 _{· · · 0 1} 1 0 _{· · · 0 0} 0 1 _{· · · 0 0} . .. 0 0 · · · 1 0        為 一 個d_{× d}的 置 換 矩 陣 （

p e r m u t a t i o n

matrix

）。那麼

ei+1= P ei

，其中

i = 1,· · · , d − 1

，而且

e1= P ed

。 於是，我們可以得下列結果： 系理：對任意 d_{≥ 2} 的整數，Pd _{為 d× d 的單位} 矩陣。 由此可得到一個直接的結論：_R5_{空間中的超立} 方體晶格具有五階對稱性。接著自然會聯想到下面的 問題：在維度比五小的空間中，是否存在一個具有 五階對稱的晶格？當_{d = 4}時，答案是肯定的（詳見

[7]

、

[18]

）。然而，想要看到四維空間中的複雜幾 何圖形絕非易事。從（

2

）式中

α

和

β

的關係，我們 可以定義線性獨立的單位向量： （

4

）

a1= (1, 0, 0, 0)T, a2= (− 1 2, α 2, β 2, 0) T_, a3= (0, β 2, α 2, 1 2) T_{, a} 4= (0, 0, 0,−1)T 並定義鏡射變換

γi（見

[18]

）： （

5

）

γi(ai) = −ai γi(aj) = ai+ aj |i − j| = 1 γi(aj) = aj |i − j| > 1 其中

i, j∈ {1, 2, 3, 4}。稍後我們將證明

γi

是唯 一決定的（參見（

6

）式）。另外從（

4

）我們可以 簡單地驗證，兩個以上且足標相鄰的向量

ai

相加之 和，仍然是單位向量。 γi

的鏡射平面與向量

ai

正交，並且通過原點。 足標相鄰的

γi

與

γj

_{，它們的鏡射平面之夾角為}

₁₂₀◦ ，這是因為

aT iaj =−1/2。如果足標

i 與

j 之差的絕 對值比

1

大時，那麼

γi

與

γj

_{的鏡射平面彼此正交。} R4_{中，上述向量對應的晶格是由全等的四維平} 行六面晶胞的稜邊所組成。而其頂點所形成的集合是

V = 4 i=1 ciai| ci ∈ Z  V顯然對每個向量ai的整數倍都具有平移對稱 性。底下我們將證明當d = 4時，此晶格具有五階對 稱性。 定理：存在一個從集合V 至本身的非恒等保距變換 A

，滿足 A5_{(x) = x,} ∀ x ∈ V 。 證明：定義下述保距變換： A = γ1γ3γ2γ4 利用（

5

），我們可以得到： A(a1) = γ1γ3γ2(a1) = γ1γ3(a1+ a2) = γ1(a1+ a2+ a3) = a2+ a3 A(a2) = γ1γ3γ2(a2) =−γ1γ3(a2) = _−γ1(a2+ a3) =−a1− a2− a3 A(a3) = γ1γ3γ2(a3+ a4) = γ1γ3(a2+ a3+ a4) = γ1(a2+ a3+ a4) = a1+ a2+ a3+ a4 A(a4) = −γ1γ3γ2(a4) =−γ1γ3(a4) = −γ1(a3+ a4) =−a3− a4 從這些結果可以發現，_A

是從離散集合

V

映至 V

的線性算子，並滿足： a1 → a2+ a3→ a4→ –(a3+ a4) → –(a1+ a2)→ a1 a2 → −(a1+ a2+ a3)→ –(a2+ a3+ a4) → a3→ a1+ a2+ a3+ a4→ a2 經過類似檢查後，我們得到

_A5_(a i) = ai

，對所 有的

i = 1, 2, 3, 4

皆成立，因此，_A5

_{是恒等變換。} 接著更深入地檢視前述定理中的算子_A，我們可 以利用矩陣來表示它。由於映射γi都是由鏡射的正交 矩陣所唯一決定，其中 （

6

）

Ai= I− 2aiaTi , i = 1, 2, 3, 4 也就是說，對所有的

x∈ R4_，r i(x) = Aix

，其中

A1=    00 10 01 00 0 0 0 1    A2= 1 2    αβ β1 α1 00 0 0 0 2    A3= 1 2     2 0 0 0 0 α 1 β 0 1 β α 0 β α 1     A4=     1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 ₋₁     因此

_A

可由底下的正交矩陣來表示： A = A1A3A2A4= 1 2     −1 −α −β 0 1 0 α _−β 1 β 0 _−α −1 1 1 1     若令

ϕ = 72◦

_以及

_{ψ = 144}◦

_，則

_A

_{的特徵值為：} （

7

）λ1,2= cos ϕ± i sin ϕ, λ3,4 =− cos ψ ± i sin ψ

因為它們皆非實數，因此

A(x) = Ax

的唯一固 定點為零，再根據前述定理，可知

A5

_{是單位矩陣。} 我們提醒一下，下述矩陣的特徵值與矩陣

A

相同： A4_{= A}−1 _{= A}T ₌ 1 2     −1 1 1 −1 −α 0 β 1 −β α 0 1 0 −β −α −1     附記：前述定理中的算子

_A

以及其所對應的矩陣

A 並非唯一。例如我們可以令 B =     a b c c a c b c a c c b d a a a     其中

a =_−α/4、b = (α + 2)/4、c =_{−(β + 1)/4}、 d = (3β_{− 1)/4}

，我們發現

B5

_{也是單位矩陣，這是} 因為 （

8

）vi+1= Bvi, i = 1, 2, 3, 4

以及

v1= Bv5 其中 vi 為正四維單形的頂點（參見（

3

）式）。 又因為B4_{= B}−1 _{= B}T_{，所以B是正交矩陣。B的} 特徵值與（

7

）式相同。另外，在

[7]

中還給出另一個 具有類似性質的矩陣，其分塊對角矩陣表示為 D =     cos ϕ _{− sin ϕ} 0 0 sin ϕ cos ϕ 0 0 0 0 cos ϕ _{− sin ϕ}     階對稱的格。而這只需考慮正六維單形以及類似於 （

8

）式的關係即可。

短結

在十七世紀初期，克卜勒思考具有五階對稱性 的週期馬賽克圖案。許多其他學者也希望發現具 有這種對稱性的平面馬賽克圖案或是空間晶格。然 而，

1850

年布哈維證明了二維與三維空間中的晶 格，只具有二階、三階、四階與六階對稱性。 本文中，我們展示了四維空間的特殊晶格具有五 階對稱性，並且給出具體的構造演算法。五階對稱在 低維度的歐氏空間中只能局部出現，例如某些克卜 勒的馬賽克圖畫，或是

1970

年代早期出現的著名潘 洛斯鋪磚。如果從實質上是抽象多維的構造物做低維 的投影，可以製造出真實空間中具有局部對稱性的圖 形，並顯示出與某些合金裡準晶體原子排列的相關 性，這個技術未來或許會有廣泛的應用。

本文出處　Notices 59 (2012) no.1, AMS。感謝三位作者提供本

文圖片。 譯者簡介　黃俊瑋為師大博士班，主修數學史。譯有《數學偵探 物語》，並與洪萬生教授等人合著《摺摺稱奇：初登大雅之堂的 摺紙數學》。 本文參考資料請見〈數理人文資料網頁〉 http://yaucenter.nctu.edu.tw/periodical.php 延伸閱讀

+

蔡蘊明譯〈具有黃金比例的晶體〉網頁，此為2011年 諾貝爾化學獎之大眾新聞稿。《臺大科學教育發展中 心》http://case.ntu.edu.tw/blog/?p=9938

+

林水田〈準晶的發現〉《科學發展》472期（2012） 。http://ejournal.stpi.narl.org.tw/NSC_INDEX/ Journal/EJ0001/10104/10104-09.pdf

+

翁秉仁〈正多邊形拼貼〉網頁。《國科會高瞻計畫自 然科學教學資源平台》http://case.ntu.edu.tw/hs/ wordpress/?p=34915