The elastic fields of a line force or dislocation in an anisotropic wedge

(1)

~ Pergamon

T H E ELASTIC F I E L D S OF A L I N E F O R C E O R

D I S L O C A T I O N IN A N A N I S O T R O P I C W E D G E

K U A N G - C H O N G W U

Institute of Applied Mechanics, National Taiwan University, Taipei, Taiwan (Received 11 September 1996 ; in revised form 16 July 1997)

Abstract--An elasticity analysis for a line force or dislocation in an infinite anisotropic wedge is presented. A solution in integral form is derived by the Mellin integral transform method. It is shown that the solution integral can be expanded into eigenfunction series by residue theorem. The asymptotic fields as the radial distance approaches zero or infinity are discussed. © 1998 Elsevier Science Ltd. All rights reserved.

1. INTRODUCTION

One o f the basic solutions in elasticity is the fields produced by a line force or a line dislocation. The solutions due to these line singularities are important in constructing integral equations for boundary value problems. F o r example, the conventional b o u n d a r y integral equations are based on the line force solution (Rizzo, 1967). Some new b o u n d a r y integral equations are established using both line force and dislocation solutions (Wu et al., 1992). The dislocation solutio is also widely used to set up integral equations for solving crack problems.

The solution for a line dislocation in an infinite anisotropic medium has been obtained by Eshelby et al. 0953), Stroh (1958), Willis (1970), Malen and Lothe (1970), and Malen (1971). Malen's (1971) treatment also includes a line force. The solution for an anisotropic half-space subject to a line force a n d / o r a line dislocation has been considered by Head (1953, 1965), Chou (1966), Tucker (1969), Willis (1970), Barnett and Lothe 0 9 7 5 ) . The problem where the force is at the tip o f an anisotropic wedge was studied by Barnett and Lothe (1975). Similar plane strain solutions for anisotropic wedges subject to b o u n d a r y traction was provided by Bogy (1972) with focus on stress singularities at apex. An anisotropic wedge under a concentrated couple at the tip was investigated by Ting (1988) and Hwu and Ting (1990). The near-tip fields of a wedge with a line force or dislocation were derived by Wu and Chang (1993).

In this paper a line force or a line dislocation in an anisotropic wedge is considered. Stroh's formalism for anisotropic elasticity and Mellin integral transform are employed to derive the full solution in a compact and explicit form. The solution is expressed either in terms o f an integral or eigenfunction series by evaluating the residues of the integral.

The plan of the paper is as follows. In Section 2 the basic equations are given. The solution in integral form is derived in Section 3. The eigenfunction series solution is derived in Section 4. Asymptotic fields are discussed in Section 5. Finally some remarks are made.

2. BASIC EQUATIONS

In the following discussion vectors or matrices are denoted by bold-faced letters. A subscript c o m m a denotes partial differentiation and repeated Latin indices imply summation from 1-3 unless noted otherwise. Summation over Greek indices is indicated explicitly.

F o r a homogeneous anisotropic body, the generalized H o o k e s law and the equations o f equilibrium are given as

(2)

3 4 8 4 K . - C . W u

~ij = Cij~uk,,

(1)

~,jj = 0 (2)

where u~ and ao is the displacement and stress component, respectively, Ciakt is the component of the elasticity tensor. If the displacement u depends only on x~ and x2, so does the corresponding stress tensor a. In view of eqn (2), a stress function ~b can be introduced such that

O'il : - - (~i,2, 0"i2 = (~i,1, i = 1,2, 3 (3)

Substitution of eqn (3) into eqn (1) yields

Qu,1 +Ru,2 = -4~,2

RTu, I +Tu,2 = ~b,l (4)

where the components of the three by three matrices Q, R, and T are defined as

Ri~ = Cilk2 Tik = C~2k2

Equation (4) can be rewritten as (Chadwick and Smith, 1977)

w,2 = Nwl (5)

where the six-dimensional vector w and six by six matrix N stand for

N = (7)

N3 Nf

and the three by three matrices NI, N 2 and N3 are given by

N1 = - T - 1 R r (8)

Nz = T -~ = N ~ (9)

N3 = R T - ~ R r - Q = N~ (10)

In terms of polar coordinates r and 0 eqn (5) can be expressed as (Ting, 1996)

w,0 = rN(0)wr (11)

where

N(0) = IN1(0) N2(0) ] (12)

N3(0) N1 (0)rJ

(3)

and N 2 (0) ~--- T-1 (0) N3 (0) = R ( 0 ) T - ' ( O ) R r ( O ) - Q(0) Qik(O) = Gjksnj(O)ns(O) Ri~(O) = cij~,nj(O)ms(O) Ti~(O) = c,jk, m j ( O ) m s ( O ) nr(0) = [cos 0, sin 0, 0] mr(0) = [ - sin 0, cos 0, 0]

Applying the Mellin transform to eqn (11) with respect to r, we get

where ¢~,0 = - 2N(0)~ @(0) = f o w(0, r ) r ~- l d r (14) (15) (16) (17)

(18)

(19)

(20)

(21) (22) N r = J N J where the six by six matrix J is defined as

13

being the three by three identity matrix. Comparing eqn (24) with eqn (23), we can set Since

is the Mellin transform o f w.

Consider the following eigenvalue problem (Stroh, 1958) :

N¢ = pC (23)

where p is the eigenvalue and ~ is the right eigenvector o f N. Equation (23) provides six roots, p~, K = 1 , . . . , 6. Since PK are complex if the strain energy is positive definite (Eshelby el al., 1953), we can let

PK+3 ----ff~, ~[p~] > 0 ~ + 3 = ~ , X = 1,2,3

where 3 denotes imaginary part and overbar stands for complex conjugate. Let ! / b e the left eigenvector o f N determined by

(4)

3486 K.-C. Wu

~/= J ¢ (25)

As the left eigenvector r/and the right eigenvector ~ associated with different eigenvalue o f p are orthogonal to each other, we can normalize the eigenvectors such that

~/[¢r = 5=r (26)

where 6~r is Kronecker's delta. The six by six identity matrix I6 can be expressed as the following spectral representation (Hoffman and Kunze, 1961):

6

I6 = E ¢ ~i']ff (27)

x=l

and the matrix N(0) in eqn (11) as (Ting, 1996)

N(0) = + ~(0)'

_{,<~, Q(0) Cat[}

₍₂₈₎

where (~(0) = cos 0 +p~ sin 0 and (~(0)' is the derivative o f (~(0) with respect to 0. Equation (28) indicates that ¢K and !/~ are right and left eigenvectors, respectively, and (~(0)'/~(0) is the corresponding eigenvalue of N(0). With eqn (28) into eqn (21), the general solution of

can be expressed as

~(0) = G(0, 0o ;,~)~(00)

where the six by six matrix G is given by

K=I k ~ J Cx I'/T

and 0o is an arbitrary angle.

The matrix G has the following properties :

G(00,00 ; 2) = G ( 0 , 00 ; 0) = I6 G(0, 00 ; 2) = G(0, 0, ;2)G(0,, 00 ; 2) G(0, 0o ; - 2 ) G ( 0 , 00 ;2) = I6 (29)

(30)

(31) (32) (33) If we let

_-r<

71

~

LB~J

q~ = J ~ = A~ (34)

where A~ and B~ are three-dimensional vectors, the matrix G can be partitioned into four three by three submatrices as follows,

(5)

where

G,(0,0o;2) = ~ (~(0)"~-~A~B~ (36)

G2(0,0o;2)=

~', ( ~ ( 0 ) y ~ A ~ A r (37)

G3(0,0o;2)

= ~

( ~ ( 0 ) ~-~B~Br (38)

Some identities which will be useful later are listed here (Hwu and Ting, 1990)"

,=, ~ , - ~ 0 ) ) log

\~(0o),,i ~01~ = Urn( O,

0o)(-N(0,

0o))"

(39)

N(0, 0o) -- c o s ( 0 - 0o)I 6 + s i n ( 0 - 0o)N(0o) (40)

l fo'

1~(0, 0o) = ~

N(~o) d~o

(41)

0

In eqn (39) m and n are arbitrary integers. The matrix N(0, 0o) has the following properties :

N1(0,00)m(0o) = m(0), N3(0,0o)m(0o) = 0 (42)

where m(0) is given by eqn (20).

3. INTEGRAL SOLUTION

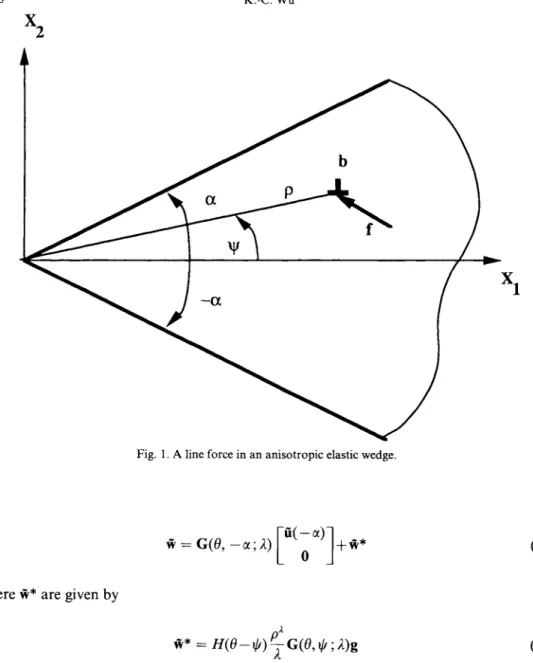
Consider the wedge shown in Fig. 1. The x I axis is taken as the bisector of the wedge. The wedge is free of tractions at 0 = + a. A line force f and a dislocation with Burgers vector b are located at r = p and 0 -- ¢. The boundary conditions at 0 = _ a and the jump conditions at 0 = ¢ are described, respectively, by

~---~r (r, + ~) =

o

(43)

w ( r , ~h + ) - w(r, ~ - ) = -

H(r--

p ) g (44)

where H is the Heaviside step function and gr = [b r, fr]. Applying the Mellin transform to eqns (43) and (44), we have

(2 -- 1)q~( + ~, 2-- 1) = 0 (45)

p~

~ ( ~ + ) - ~ ( t p - ) = ~-g (46)

An expression for ,k which satisfies the traction-free conditions at 0 = - a and the jump conditions at 0 = ¢ is given by

(6)

3488 K.-C. Wu

b

f

X 1

Fig. 1. A line force in an anisotropic elastic wedge.

w h e r e ~* are given by

(47)

p,l

if* =

H(O- ~) -~ G(O,

0 ; 2)g (48)

T h e v e c t o r f i ( - - e ) in ~ is d e t e r m i n e d b y the traction-free c o n d i t i o n s at 0 = e as 2

fi( ~) 1 _{2 G ; ~ (e' - c~ ; 2)(G3 (e, ~ ; 2)b + G r ( e , ~ ; 2)f)} ₍₄₉₎

T h e solution w in the physical d o m a i n is o b t a i n e d b y the Mellin inversion t h e o r e m as

~c+ic~

w = 2r~ijc ~ r - ~ d 2

w h e r e c is a p r o p e r real n u m b e r .

4. E I G E N F U N C T I O N E X P A N S I O N S

(50)

T h e integration c o n t o u r in e q n (50) for w c a n be closed b y a d d i n g to the line o f 9t[2] = c a semicircle o f infinite r a d i u s to the right o r the left in the c o m p l e x 2 plane, d e p e n d i n g o n w h e t h e r r > p o r r < p. H e r e 9112] s t a n d s f o r the real p a r t o f 2. T h e integral o f e q n (50) c a n then be e v a l u a t e d b y the residues at the poles o f ~ which are l o c a t e d in the

(7)

regions 9t[2] > c for r > p and 9112] < c for r < p. If the displacement is required to be bounded at the tip and the stress vanish at infinity, c is chosen to be in the open strip

- 9 1 1 2 t ] < 9112] < 0, where 2~ denotes the location of the pole o f ~ with the smallest real

part. Since the term if* in eqn (47) only has a simple pole at 2 = 0 where the residue is a constant, the term will be omitted in the following discussion for simplicity. Also to simplify the notation, G3(~, - ~ ; 2 ) will be denoted as G3(2).

Consider the following eigenvalue problem :

G 3 ( 2 ) q i : A~q~ no sum on i (51) where Ae and qi, i = 1, 2, 3, are the eigenvalues and eigenvectors of G3(2 ). As G3(2) is symmetric, the eigenvectors q~ and q: can be normalized such that

q.rqj = fi,j (52)

and the eigenvalue Ai can be expressed as

Ai = q/rG3(2)qi no sum on i (53)

A crucial step in evaluating the residues is to express G3(2) as the following spectral representation (Wu and Chiu, 1996)"

3

G3(2) = ~ A,qiq r (54)

i=1

The inverse of G3(2) can then be represented as

G3(2) - l = k 1 r

i= I A~ qiqi

(55)

Substitution of eqn (55) into eqn (49) yields

f i ( - ~ ) = - qi i = I (56) where G(2) = q,(2)T(G3 (~, ~ ; 2 ) b + G~r(~, ~9 ; 2)t) (57) D i = 2 A i (58)

With eqn (56), r-Xff o f e q n (50) can be expressed as

. .

± c ,

- = , (59)

where

W ( r , O ; 2 ) =

,,=l (60)

(8)

3490

Since

K.-C. Wu

Di(2 )

: 0 (61/

IG3(A)I = AIA2A3 (62)

Equation (61) implies that at the poles G3(2 )- 1 is singular.

A pole o f order m exists at 2 = 2" if 2* satisfies not only eqn (61) but

O~Y)(2 *) =jA~/-I)(2*)+2A~Y)(2 *) = 0, j = 1,2 . . . m - 1 (63) where D~ j} denotes the j-th derivative o f

Di

with respect to 2. By taking m-th derivative o f eqn (51) with respect to 2, setting A~ j) = 0 , j < m, and pre-multiplying the resulting equation by qT, A~ m) c a n be expressed as

{ m

m!

F_(O~(m--"~

(64) A}m) = q r k----~'t)~ l!( ~-Z- l) ./`-'3 "li

_]

where

:

)

. , . :

(65)

Note that A~ m) depends only on qi and its derivative with respect to 2 up to q~m-1). F o r example, for m = 1,

A~ = q/rG~q, (66)

Thus, once qi is obtained, whether A~ vanishes or not can be readily checked.

It is obvious that if 2" is a pole o f ff so is 2" and q(2*) = q(2*). We show in the following that - 2 * is also a pole. Using eqn (33), we have

Equation (67) yields

(67)

G3 ( - 2 ) G , (2)q(2) + A(2)G, ( - 2)Tq(2) = 0 (68) By pre-multiplying eqn (68) by q ( - 2 ) T, we have

q( - 2)rGi ( - 2) rq(2)

A ( - 2 ) = - A ( 2 ) (69)

q( -- 2) r C I (2)q(2)

Since by definition A(2*) = 0, it follows from eqn (69) that - 2 * is a root and from eqn (68)

q ( - 2*) = yG, (2")q(2") (70)

(9)

(0-~A(2)) ~= _~. = ( - l Y ( 5 A ( - 2 ) ) ~=~"

(71) Equation (69) implies that i f 2 * is order m, - 2 * is also o f order m.

It is obvious that Di(0) = 0 and 2 = 0 is always a pole. M o r e o v e r as &(0) = 0, a n d D~(0) = 0, i = 1, 2, 3, 2 = 0 is o f order two. It can be shown that 2 = 1 is also a pole regardless o f the wedge angle. F o r 2 = 1, by setting m = 1, n = 0 in eqn (39), we have

G3(1) = N3(--c~, a) (72)

F r o m eqn (42), the corresponding eigenvector is given by

q(1) = m(~) (73)

It is remarkable that the eigenvector q(1) is independent o f the elastic constants and is perpendicular to the wedge face at 0 = ~. F r o m eqn (39) with m = n = 1, the matrix G ; (1) can be expressed as

= X[~3 (--~, ~)N 1 (--~, ~) + I'~TT(--oc, cx)N3 ( - - ~ , a)] (74) Substituting eqns (73) and (74) into eqn (66), we have

A' (1) = - rcm(~) rlq 3 (~, -- a ) m ( -- ~) (75) where eqn (42) has been used. Let ~* be the critical wedge angle such that

m(a)qq3 (:, -

~ * ) m ( - c~*) = 0 (76) The pole at 2 = 1 is o f order two when a = ~* and is simple otherwise. Equation (76) has also been given by ( H w u and Ting, 1990) for a wedge subject to a couple at the tip.

By s u m m i n g the residues at the poles, w for r > p can be expressed as

W = W o + ~ w. (77)

n = l

and for r < p

w = ~ w _ . (78)

where - w 0 , - w , , and w_, are the residues o f eqn (59) at 2 = 0, 2,, and - 2 , , respectively. Each term in eqn (77) or eqn (78) satisfies the traction-free conditions on the wedge faces and thus, eqns (77) and (78) are actually eigenfunction expansions o f w for r > p and r < p, respectively.

Consider first the general terms in the eigenfunction expansions for the special angles

= r n r c / 2 , m = 1, 2. The case for m = 1 corresponds to a half-space and m = 2 to a semi-

infinite crack. The matrix G3(2 ) in these cases can be simplified as

G3 (2) = sin(mnA)L (79)

(10)

3492 K.-C. Wu 3

L = - 2 i E B~B~r

~c=l

(80)

It follows that Ai = sin(mT~2)L~, i = 1, 2, 3, L~ > 0 being the eigenvalues o f L and that the eigenvectors qi are those o f L. It is apparent that 2n =

n/m, n

being an integer, is a simple pole regardless o f the elastic constants. Evaluation o f the residue o f eqn (59) at 2, yields

(--1)n (p)n/m ( m'IT,

d ~ T , @ ; w . - G 0, • (81) nT~ 2 ' 0 J W - n G 0, •

ntF

1

(82) mr 2 ' 0 where (83)

By substituting eqn (98) with ~ =

m~/2,

m = 1, 2 and eqn (81) into eqn (77) or eqn (82) into eqn (78), the resulting series can be summed to yield the following closed form expressions : 1 u = - (~[ACmh] +..~[AD,,fi]) (84) 7~ 1 = - (~[BC~h] + ~[BDmfi]) (85)

where A = [A~, A2, A 3 ] , B = [B~, B> B3] , h = A r f + Brb, C 1 and D1 for a half-space are given by

( e l ) i j ---- l o g ( r ( , ( O ) --p~,(@))Sij (86)

(DI)ij = log (r~e~)pj

p(i(~t))yij

(87)

and C2 and

D 2

for a semi-infinite crack are

(C2)ij = l o g ( ~ - - ~ ) 6 i j

(88)

(D2)a = l o g ( - ~ - - ~ ) Yij (89)

with Y = B - 1 R The form o f the solution for a half-space is also given by Ting (1996). F o r simplicity it is assumed that for ~ :~ 7r/2, re, only one o f the eigenvalues Ai vanishes at the pole 2., n > 0. The eigenvalue is simply denoted by A(2.) and the corresponding eigenvector by q(2.). F r o m eqn (59), the terms w., n ~> 0 in eqn (77) are given by

(11)

w.

- (m__l).,c92m_, (2--2.)"

W(r, 0"2) 7q(2)1"] (90)

' L o JJl~=~°

if the pole at 2 = 2. is o f order m. While the terms w_., n > 0 in eqn (78) are obtained by

W_ n ( m _ l ) # o ~ - - 1

(2+2.)"

W(r,0.R)rq(2)] ']

(91)

'

L

0

J)l~=-~.

If 2. is a simple pole, eqns (90) and (91) reduce to

w. - 2.A'(2.) W(r, 0 ; 2.) (92)

w_.(2.) = - w . ( - 2 . ) (93)

5. ASYMPTOTIC FIELDS

F o r definiteness let 2. in eqns (77) and (78) be arranged in increasing real parts. In this section the leading terms Wo and Wl as r --* oe and w_ ~ as r --* 0 are discussed.

F r o m preceding discussion 2 = 0 is a pole o f order two. The expression for w0 derived from eqn (90) with m = 2 is given by

- 0 ±

-

. . . ,,

[qT}

94>

where

f

rC(O) "~. T

w'(,,0;0>

= - ' o = (95)

In eqn (94) certain constant terms, which are related to rigid body translations are omitted. By differentiating eqn (51) with respect to 2 at 2 = 0, we have

G ; (0)q~ = A~(0)q; (96)

and

3 T

= 2 (97)

G ' 3 1 (0) i=l A i ( 0 )

With eqn (97), eqn (94) can be rewritten as

w 0 = W'(r, 0 ; 0) I G ~ ( ~ ) - If ~ ₍₉₈₎

Equation (98) represents the solution for a force f acting on the tip (Barnett and Lothe, 1975).

Since 2 = 1 is always a pole, 2~ is either less than or equal to one. If2~ < 1, wl and w_~ are simply given by eqn (90) and eqn (91), respectively, with n = 1. In this case the stresses corresponding to w_~ are proportional to r ~ - i and are singular at the tip. The result has been derived by Wu and Chang (1993) using a different approach.

(12)

3 4 9 4 K . - C . W u

If 21 = 1 and A'(1) ~ 0 or a 4: ~*, ~* being the critical angle determined by eqn (76),

and N 3 ( - - a * , 0~*) ( - I ) is defined as

N3(--a*, ~*) (-1) __ Here

where

wl - A,(1)~N(--e, 0) (99)

where A'(1) is given by eqn (75) and M is the moment exerted by the force with respect to the tip :

M = pm(~')rf (100)

Equation (99) has been derived by H w u and Ting (1990). The near field w_,, obtained by eqn (93), represents a rigid body rotation fl given by

1

f~ - - - m r ( ~ ) ( N r ( - a, ff)b + N ~ ( - ~, ~)f) (lO l)

pA'(1)

If 2~ = 1 and A'(1) = 0 or ct = a*, the pole is of order two. The far field w~ can be derived from eqn (90) with m = 2. The result can be expressed as

W 1 = W l I - l - W 1 2 (102)

p{c'+clog(p/r)

h'c'~ G ( _ a., 0 ; 1) Ira(0*) ]

= r \

h

cr(

Vm(a*)-] ~ . , [ q ' ; 1 ) l ) w l z = h r G ' ( - ~ * ' 0 ; I ) L 0 J + G ( - ~ , 0 ; I) C = C j

h

h ' - - G ' ( - ~ * , O ; 1) = q'(1) = m ( ¢ ) r F (q'(1)rN~(~, ~*) -7rm(~k)rlql (a*, ~))F + (q'(1)rNr(~b, ~*) -nm(~k)rlq3 (~ *, ff))b 1 n 1 m

~A (1)+ga (1)

rdq(- ~, 0)N(- ~, 0)

rcN3 (-- a*, a*) <- 1>1q3 (a*, - a * ) m ( - c¢*)

1 1

- A~q2q~+ ~ q 3 q 3 ~ (105)

where &, i = 2, 3 are two nonzero eigenvalues o f S 3 ( - - a * , a * ) and qg, i = 2, 3 are the corresponding eigenvectors. It can be shown that the moment exerted by the force is balanced solely by that produced by Wlz. In fact wll contains a term multiplied by log(p) and is not related to the ordinary moment of force. Equation (102) is also applicable to isotropic material. Indeed the expressions for the corresponding stresses have been checked (103)

(104) the pole is simple. The far field wl is given by eqn (92) as

(13)

to agree w i t h t h o s e d e r i v e d b y S t e r n b e r g a n d K o i t e r (1958). T h e n e a r field w_~ c a n be o b t a i n e d f r o m eqn (91) w i t h m = 2. T h e r e s u l t is i d e n t i c a l w i t h t h a t d e r i v e d b y W u a n d C h a n g (1993) a n d will n o t be r e p r o d u c e d here. 6. CONCLUDING REMARKS T h e c o m p l e t e s o l u t i o n d u e to a line f o r c e o r a line d i s l o c a t i o n in a n a n i s o t r o p i c w e d g e is d e r i v e d . W i t h S t r o h ' s f o r m a l i s m the s o l u t i o n is e x p r e s s e d in a n e x p l i c i t a n d c o m p a c t f o r m . S e v e r a l s o l u t i o n s in the existing l i t e r a t u r e a r e i n c l u d e d in the s o l u t i o n o b t a i n e d here. In p a r t i c u l a r the s o l u t i o n s for a w e d g e s u b j e c t to a f o r c e ( B a r n e t t a n d L o t h e , 1975) a n d a c o u p l e (Ting, 1988 ; H w u a n d Ting, 1990) a t the tip a p p e a r as t e r m s for ). = 0 a n d 2 = 1, respectively, in the e i g e n f u n c t i o n series o f the p r e s e n t s o l u t i o n . It is s h o w n t h a t the c r i t i c a l w e d g e a n g l e as d i s c u s s e d b y H w u a n d T i n g (1990) is the o n e t h a t gives rise to a d o u b l e p o l e a t 2 = 1.

REFERENCES

Barnett, D. M. and Lothe, J. (1975) Line force loadings on anisotropic half-spaces and wedges. Phys. Norv. 8, 13-22.

Bogy, D. B. (1972) The plane solution for anisotropic elastic wedges under normal and shear loading. ASME Journal of Applied Mechanics 39, 1103-1109.

Chadwick, P. and Smith, G. D. (1977) Foundations of the theory of surface waves in anisotropic materials. Advances in Applied Mechanics 17, 303-376.

Chou, Y. T. (1966) On dislocation-boundary interaction in an anisotropic aggregate. Phys. Status Solidi B15, 123-127.

Eshelby, J. D., Read, W. T. and Shockley, W. (1953) Anisotropic elasticity with applications to dislocation theory. Acta Metallica 1, 251-259.

Head, A. K. (1953) Interaction of dislocations and boundaries. Philosophical Magazine 44, 92-94. Head, A. K. (1965) The dislocation image force in cubic polycrystals. Phys. Status Solidi B10, 481-484. Hoffman, K. and Kunze, R. (1961) Linear Algebra. Prentice-Hall, New Jersey.

Hwu, C. and Ting, T. C. T. (1990) Solution for the anisotropic elastic wedge at critical angles. Journal of Elasticity

24, 1-20.

Malen, K. (1971) A unified six-dimensional treatment of elastic Green's functions and dislocations. Phys. Status Solidi B44, 661-672.

Malen, K. and Lothe, J. (1970) Explicit expressions for dislocation derivatives. Phys. Status Solidi B39, 287-296. Rizzo, R. (1967) An integral equation approach to boundary value problems in classical elastostatics. Quarterly

Journal of Applied Mathematics 25, 83-95.

Sternberg, E. and Koiter, W. T. (1958) The wedge under a concentrated couple : a paradox in the two-dimensional theory of elasticity. ASME Journal of Applied Mechanics 25, 575-581.

Stroh, A. N. (1958) Dislocations and cracks in anisotropic elasticity. Philosophical Magazine 7, 625-646. Ting, T. C. T. (1988) The anisotropic elastic wedge under a concentrated couple. Quarterly Journal of the

Mechanics of Applied Mathematics 41, 563-578.

Ting, T. C. T. (1996) Anisotropic Elasticity--Theory and Applications. Oxford University Press, New York. Tucker, M. O. (1969) Plane boundaries and straight dislocations in elastically anisotropic materials. Philosophical

Magazine 19, 1141-1159.

Willis, J. R. (1970) Stress field produced by dislocations in anisotropic media. Philosophical Magazine 21, 931- 949.

Wu, K.-C. and Chang, F.-T. (1993) Near-tip fields in a notched body with dislocations and body forces. ASME Journal of Applied Mechanics 60, 936-941.

Wu, K.-C. and Chiu, Y.-T. (1996) Analysis for elastic strips under concentrated loads. ASME Journal of Applied Mechanics, submitted.

Wu, K.-C., Chiu, Y.-T. and Hwu, Z.-H. (1992) A new boundary integral equation formulation for linear elastic solids. ASME Journal of Applied Mechanics 59, 344-348.

The elastic fields of a line force or dislocation in an anisotropic wedge

~ Pergamon