平面凸七邊形內中央兩相鄰交叉對角線
長度乘積方程式
李輝濱
嘉 義 市 輔 仁 中 學 退 休 教 師壹、前言
首 先 來 探 討 一 個 受 規 範 的 圓 內 接 七 邊 形 的 特 例 情 況 : 即 任 意 給 定 一 個 圓 內 接 七 邊 形 7 6 5 4 3 2 1A
A
A
A
A
A
A
,令 其 各 邉 線 段 長A
1A
2 =V
1,A
2A
3 =V
2,A
3A
4 =V
3,A
4A
5 =V
4,A
5A
6 =V
5,A
6A
7 =V
6,A
7A
1 =V
7, 見 下 圖 1. , 在 圖 形 中 央 任 意 選 定 兩 相 鄰 交 叉 對 角 線 長 14 4 1A
d
A
,A
2A
5
d
25 的組 合,也 還有 其 它 多 種組 合;如;A
2A
5
d
25,A
3A
6
d
36 的 組 合 及A
3A
6
d
36與A
4A
7
d
47的 組 合 , … … 等 。 圖 1 圖 2. (a) 連 接 對 角 線 長A
1A
5
d
15,A
2A
4
d
24, 使 形 成 一 圓 內 接 四 邊 形A
1A
2A
4A
5, 見 上 圖 2., 由 托 勒 密定 理 Ptolemy theorem 得d
14d
25
V
1V
4
d
24d
15 (1) (b) 圖 2.中 , 令 角 度m
A
1A
5A
6, 角 度k
A
7A
1A
5, 對 四 邊 形A
1A
5A
6A
7言可 得 ;
d
15
V cos
5m
+V
6cos[
m
(
A
6)]
+V cos
7k
=
V
5cos(
A
7)
+V
6cos[(
A
7)
(
A
6)]
+V
7cos(
A
6)
=
V
5cos A
7+V
6cos(
A
6
A
7)
V
7cos A
6 (b-1) 再 令 角 度x
A
3A
4A
2, 角 度y
A
4A
2A
3, 對 三 角 形A
2A
3A
4言 可 得 ;
24d
V cos
2y
+V cos
3x
, 因 對 六 邊 形A
1A
2A
4A
5A
6A
7言 , 可 得 下 列 頂 角 關 係 ;A
1
(
A
4
x
)
A
6
2
A
7
(
A
2
y
)
A
5
A
1
A
4
A
6
2
x
且A
2
A
5
A
7
2
y
,代 入d
24 中, 得d
24
V
2cos(
A
2
A
5
A
7)
+V
3cos(
A
1
A
4
A
6)
(b-2) 將 方 程 式(b-1)與(b-2)一 起 代入 方 程 式(1),經 演 算 後, 整 理 , 得下 列 方 程 式;
25 14d
d
V
1V
4
V
2V
5cos
A
7cos(
A
2
A
5
A
7)
+V
2V
6cos(
A
6
A
7)
cos(
A
2
A
5
A
7)
V
2V
7cos
A
6cos(
A
2
A
5
A
7)
V
3V
5cos
A
7cos(
A
1
A
4
A
6)
+
V
3V
6cos(
A
6
A
7)
cos(
A
1
A
4
A
6)
V
3V
7cos
A
6cos(
A
1
A
4
A
6)
(2) (c) 再 對四 邊 形A
1A
5A
6A
7言 , 有 下 列 的 邉 長 與 頂 角 正 弦 值 關 係 式 ;0 =
V sin
5m
+V
6sin[
m
(
A
6)]
V sin
7k
=V sin
5m
V
6sin(
m
A
6)
V sin
7k
0 =V
5sin A
7
V
6sin(
A
6
A
7)
V
7sin A
6 (c-1) 又 對 三 角 形A
2A
3A
4言 , 可 得 ; 0 =V sin
2y
V sin
3x
0 =
V
2sin(
A
2
A
5
A
7)
V
3sin(
A
1
A
4
A
6)
(c-2) 將 方 程 式(c-1)與 (c-2)式 相 乘, 經 演 算 後, 整 理 , 得下 列 方 程 式;0 =
V
2V
5sin
A
7sin(
A
2
A
5
A
7)
+V
2V
6sin(
A
6
A
7)
sin(
A
2
A
5
A
7)
V
2V
7sin
A
6sin(
A
2
A
5
A
7)
V
3V
5sin
A
7sin(
A
1
A
4
A
6)
V
3V
6sin(
A
6
A
7)
sin(
A
1
A
4
A
6)
+V
3V
7sin
A
6sin(
A
1
A
4
A
6)
(3) (d) 將 方程 式(2)減 去方 程 式(3),再 經 運 算 ,化 簡 整 理 後, 得 下 列 方程 式 ;
25 14d
d
V
1V
4
V
2V
5cos(
A
2
A
5)
+V
2V
6cos(
A
2
A
5
A
6)
V
2V
7cos(
A
2
A
5
A
6
A
7)
V
3V
5cos(
A
1
A
4
A
6
A
7)
+V
3V
6cos(
A
1
A
4
A
7)
V
3V
7cos(
A
1
A
4)
(4) 這 方 程 式(4)就 是 圓 內 接 七 邊 形 內 中 央 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式 的 面 積 型 量 綱 公 式 , 因 為 公 式 裡 的 各 項 量 綱 都 是 長 度 的 平 方 。 (e) 再 將方 程 式(b-2)與 (c-1)式 相乘 , 得 下 列方 程 式 ;0 =
V
2V
5sin
A
7cos(
A
2
A
5
A
7)
+V
2V
6sin(
A
6
A
7)
cos(
A
2
A
5
A
7)
V
2V
7sin
A
6cos(
A
2
A
5
A
7)
+V
3V
5sin A
7cos(
A
1
A
4
A
6)
V
3V
6sin(
A
6
A
7)
cos(
A
1
A
4
A
6)
V
3V
7sin A
6cos(
A
1
A
4
A
6)
(e-1) 再 將 方 程 式(b-1)與 (c-2)式 相乘 , 得 下 列方 程 式 ;0 =
V
2V
5cos
A
7sin(
A
2
A
5
A
7)
+V
2V
6cos(
A
6
A
7)
sin(
A
2
A
5
A
7)
V
2V
7cos A
6sin(
A
2
A
5
A
7)
+V
3V
5cos A
7sin(
A
1
A
4
A
6)
將 方 程 式(e-1)與 (e-2)式 兩 式相 加 , 經 演算 後 , 整 理, 得 下 列 方程 式 ; 0 =
V
2V
5sin(
A
2
A
5)
+V
2V
6sin(
A
2
A
5
A
6)
V
2V
7sin(
A
2
A
5
A
6
A
7)
+V
3V
5sin(
A
1
A
4
A
6
A
7)
V
3V
6sin(
A
1
A
4
A
7)
+V
3V
7sin(
A
1
A
4)
(5) (f) 比 較方 程 式 (4)式 與 (5)式 ,見 到 兩 者的 cos 項 與 sin 項 的 係 數與 角 度 組 合均 對 應 相 同 , 可 將 兩 者 相 組 合 ; 今 將 兩 式 的 等 號 兩 側 各 自 完 全 平 方 後 , 再 相 加 , 並 經 一 連 串 三 角 函 數 角 度 的 和 差 轉 換 公 式 運 算 , 化 簡 , 先 得 到 下 列 方 程 式 ;
2 25 2 14d
d
V
12V
42+V
22V
52+V
22V
62+V
22V
72+V
32V
52+V
32V
62+V
32V
72
2
V
2V
3V
52cos A
3
2
V
2V
3V
62cos
A
3
2
V
2V
3V
72cos
A
3
2
V
1V
2V
4V
5cos(
A
2
A
5)
+2
V
1V
2V
4V
6cos(
A
2
A
5
A
6)
2
V
1V
2V
4V
7cos(
A
2
A
5
A
6
A
7)
2
V
1V
3V
4V
5cos(
A
1
A
4
A
6
A
7)
+2
V
1V
3V
4V
6cos(
A
1
A
4
A
7)
2
V
1V
3V
4V
7cos(
A
1
A
4)
2
V
22V
5V
6cos
A
6+2
V
22V
5V
7cos(
A
6
A
7)
2
V
2V
3V
5V
6cos(
A
1
A
2
A
4
A
5
A
7)
+2
V
2V
3V
5V
7cos(
A
1
A
2
A
4
A
5)
2
V
22V
6V
7cos
A
7+2
V
2V
3V
5V
6cos(
A
6
A
3)
+2
V
2V
3V
6V
7cos(
A
3
A
7)
)
cos(
2
V
2V
3V
5V
7A
6
A
7
A
3
+2
V
2V
3V
6V
7cos(
A
7
A
3)
2
V
32V
5V
6cos
A
6+2
V
32V
5V
7cos(
A
6
A
7)
2
V
32V
6V
7cos
A
7 (6) 對(6)式再 作 角 度轉 換 , 繼 續運 算 化 簡 ,並 重 新 整 理排 列 後 , 得下 列 方 程 式;
2 25 2 14d
d
V
12V
42+[V
22V
52+V
32V
52
2
V
2V
3V
52cos A
3] +[V
22V
62+V
32V
62
2
V
2V
3V
62cos
A
3]+[V
22V
72+V
32V
72
2
V
2V
3V
72cos
A
3])
cos(
2
V
1V
2V
4V
5A
2
A
5
+2
V
1V
2V
4V
6cos(
A
2
A
5
A
6)
)
cos(
2
V
1V
2V
4V
7A
2
A
5
A
6
A
7
+2
V
1V
3V
4V
5cos(
A
2
A
3
A
5)
)
cos(
2
V
1V
3V
4V
6A
2
A
3
A
5
A
6
2
V
1V
3V
4V
7cos(
A
1
A
4)
+[
2
V
22V
5V
6cos
A
6+2
V
22V
5V
7cos(
A
6
A
7)
2
V
22V
6V
7cos
A
7] +[
2
V
32V
5V
6cos
A
6+2
V
32V
5V
7cos(
A
6
A
7)
2
V
32V
6V
7cos
A
7] +4
V
2V
3V
5V
6cos
A
3cos
A
6
4
V
2V
3V
5V
7cos
A
3cos(
A
6
A
7)
這 方 程 式(7)就 是 圓 內 接 七 邊 形 內 中 央 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式 的 面 積 平 方 型 量 綱 公 式,因 為 公 式 裡 的 各 項 量 綱 都 是 長 度 的 四 次 方。事 實 上,方 程 式(7)與方 程 式(4)是 等 價 方 程 式 , 兩 者 都 是 同 樣 在 描 述 圓 內 接 七 邊 形 內 中 央 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式。又 因 為 圓 內 接 七 邊 形 各 內 角 的 任 意 加 法 組 合 無 特 定 關 係 值,除 了 七 個 內 角 和 恰 為5π外 , 所 以 根 據 此 觀 點 可 以 作 一 個 猜 想 : 即 此 方 程 式 (7)應 當 也 是 平 面 凸 七 邊 形 內 中 央 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式 的 面 積 平 方 型 量 綱 公 式 。 再 重 新 檢 視 方 程 式(6)的 原 型 式 , 將 其 與 平 面 八 邊 形 面 積 型 餘 弦 公 式 作 一 個 項 式 相 對 應 的 比 對,可 發 覺 到 兩 者 之 間 呈 現 極 高 度 融 合 相 關 性,這 微 妙 特 徵 令 人 思 索 到 可 用 餘 弦 定 理 公 式 與 新 構 圖 出 的 平 面 八 邊 形 之 間 作 一 個 完 美 縝 密 的 連 結 ! 進 而 應 用 此 關 連 性 嚴 謹 的 推 導 出 平 面 凸 七 邊 形 方 程 式(7)式 。 接 下 來,要 尋 求 適 切 方 法 特 以 證 明 出 這 預 想 的 平 面 凸 七 邊 形 內 中 央 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式 的 面 積 平 方 型 量 綱 公 式 。 並 將 推 證 出 的 公 式 與 方 程 式(7)作 一 個 完 整 的 對 照 比 較,即 能 呼 應 出 先 自 圓 內 接 七 邊 形 的 規 則 特 例 思 考 起 較 容 易,然 後 逐 步 規 劃 分 析 擴 展 到 繁 複 的 一 般 化 平 面 凸 七 邊 形 的 研 究 情 形 。
貳、本文
在 研 析 推 導 廣 義 的 平 面 凸 七 邊 形 內 中 央 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式 之 前,為 了 要 完 整 且 有 條 理 地 導 證 出 應 得 的 型 態 關 係 式,則 必 在 下 列 撰 文 推 理 演 繹 的 運 算 過 程 中 , 需 應 用 或 對 照 到 下 述 已 知 的 幾 個 數 學 應 用 性 質 ;一、數學應用性質─引理
引 理1. 平 面 四 邉 形 餘 弦 定 理 : 在 平面 上 給 定 一個 凸 四 邊 形A
1A
2A
3A
4, 如 圖 3。 令 線 段A
1A
2 =V
1,A
2A
3 =V
2,A
3A
4 =V
3,A
4A
1=V
4, 則 此 凸 四 邊 形 的 面 積 型 餘 弦 公 式 為 圖 3 圖 4
V
42=V
12+V
22+V
32- 2V
1V
2cos A
2-2V
2V
3cos A
3+ 2V
1V
3cos
A
2
A
3
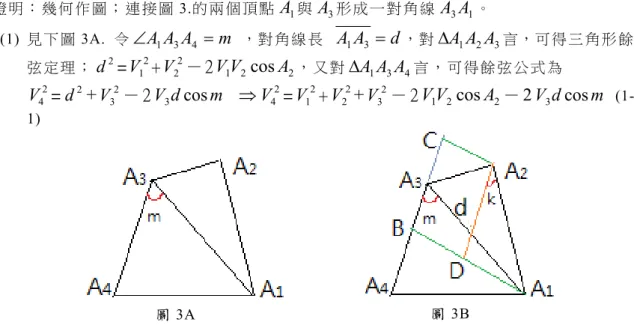
(L-1) 因 上 列 公 式 中 各 項 的 量 綱 都 是 邊 長 的 平 方 , 故 稱 為 面 積 型 餘 弦 公 式 。 證 明 : 幾 何 作 圖 ; 連 接 圖 3.的 兩 個 頂 點A
1與A
3形 成 一 對 角 線A
3A
1。 (1) 見 下 圖 3A. 令
A
1A
3A
4
m
,對 角線 長A
1A
3
d
,對
A
1A
2A
3言,可 得 三 角 形 餘 弦 定 理 ;d
2=
V +
12V -2
22V
1V
2cos A
2, 又 對
A
1A
3A
4言 , 可 得 餘 弦 公 式 為 2 4V =
2d
+
2 3V
- 2
V cos
3d
m
2 4V =
2 1V +
2 2V +
2 3V
- 2
V
1V
2cos A
2-
2
V cos
3d
m
(1-1) (2) 現 在要 證 明 方 程式(1-1)的 最末 項 中d cos 在
m
圖 形 上 的 幾 何 意 義 ; 上 圖 3B。 (i) 延 長線 段A
3A
4,使 成 直 線A
4A
3C
,通 過 頂 點A
2作 一 直 線A
2D
平 行 直 線A
4A
3C
。 (ii) 通 過 頂 點A
2作 一 直 線A
2C
垂 直 於 直 線A
4A
3C
, 使 C 點 為 垂 足 點 。 (iii) 再 通過 頂 點A
1作 一 直 線A
1B
垂 直 於 直 線A
4A
3C
, 使 B 點 、 D 點 為 垂 足 點 。 (iv) 由 直 角
A
1A
3B
性 質 知d cos
m
的 值 恰 為 投 影 線 段 長A
3B
, 同 理V
2 在 直 線C
A
A
4 3 上 的 投 影 線 段 長 為A
3C
, 而 線 段 長A
3C
恰 等 於V
2cos(
A
3)
= 3 2cos A
V
。 (v)V
1在 直 線A
4A
3C
上 的 投 影 線 段 長 為A
2D
CB
線 段 ; 因A
2D
平 行CB
, 令k
D
A
A
1 2 ,則 頂 角A
3與A
2的 關 係 為A
3+ (A
2-k) =
A
3+A
2=
+ k,而 線 段 長A
2D
恰 等 於V cos
1k
, 但 由V
1cos
A
2
A
3
=V
1cos
k
=
V cos
1k
, 得 線 段 長A
2D
=V cos
1k
=
V
1cos
A
2
A
3
。(vi) 因 此 , 由
A
3B
+A
3C
=CB
=A
2D
, 得d cos
m
=V
2cos A
3
V
1cos
A
2
A
3
。(3) 最 後 將 此
d cos
m
的 值 代 入 方 程 式 (1-1), 即 得 證 出 方 程 式 (L-1) 。事 實 上 , 方 程 式 (L-1)不 僅 適 用 於 圖 3.凸 四 邉 形 , 也 適 用 於 如 圖 4.的 凹 四 邉 形 ; 只
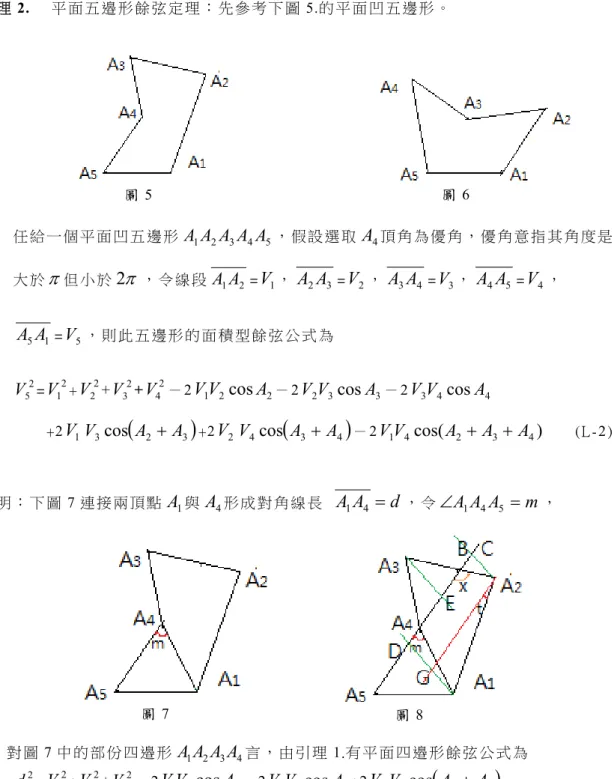
要 仿 效 上 述 構 圖 要 領 即 可 完 整 證 明 出 平 面 凹 四 邉 形 餘 弦 定 理 為 方 程 式 (L-1)。 引 理2. 平 面 五 邉 形 餘 弦 定 理 : 先 參 考 下 圖 5.的 平面 凹 五 邊形 。 圖 5. 任 給 一 個 平 面 凹 五 邊 形
A
1A
2A
3A
4A
5, 假 設 選 取A
4頂 角 為 優 角 , 優 角 意 指 其 角 度 是 大 於
但 小 於2
, 令 線 段A
1A
2=V
1,A
2A
3 =V
2,A
3A
4 =V
3,A
4A
5 =V
4, 1 5A
A
=V
5, 則 此 五 邊 形 的 面 積 型 餘 弦 公 式 為 2 5V
=V
12+V
22+V
32+V
42-2V
1V
2cos A
2-2V
2V
3cos A
3-2V
3V
4cos A
4+2
V
1V
3cos
A
2
A
3
+2V
2V
4cos
A
3
A
4
-2V
1V
4cos(
A
2
A
3
A
4)
( L -2 )證 明 : 下 圖7 連 接 兩頂 點
A
1與A
4形 成 對 角 線 長A
1A
4
d
, 令
A
1A
4A
5
m
,
(1) 對 圖 7 中 的 部 份四 邉 形
A
1A
2A
3A
4言 , 由 引 理 1.有 平 面 四 邉 形餘 弦 公 式 為2
d
=V
12+V
22+V
32-2V
1V
2cos A
2-2V
2V
3cos A
3+2V
1V
3cos
A
2
A
3
又 對
A
1A
4A
5言 , 可 得 三 角 形 餘 弦 公 式 為V
52=d
2+V
42-2V cos
4d
m
圖 5 圖 6
V
52=V
12+V
22+V
32+V
42-2V
1V
2cos A
2-2V
2V
3cos A
3+ 2V
1V
3cos
A
2
A
3
-2V cos
4d
m
(2-1) (2) 仿 效引 理 1.的 幾何 作 圖 法,作 出 圖 8.,即延 長 線 段A
4A
5使 形 成 一 直 線CA
4A
5,另 作 三 綠 色 直 線A
3E
、A
2B
與A
1D
相 互 平 行 且 皆 與 直 線CA
4A
5相 垂 直。使 得B
、D
、E
三 點 都 是 垂 足 點。再 通 過 頂 點A
2作 一 直 線A
2G
平 行 直 線CA
4A
5,使G
點 為 垂 足 點。 (3) 圖 8 中, 由 直 角
A
1A
4D
性 質 知d cos
m
的 值 恰 為 投 影 線 段 長A
4D
, 同 理V
3在 直 線CA
4A
5上 的 投 影 線 段 長 為A
4E
, 恰 等 於V
3cos(
A
4
)
=
V
3cos A
4。 (4)V
2 在 直 線CA
4A
5 上 的 投 影 線 段 長 為BE
, 恰 等 於 V2cos[A3(A4)] =)
cos(
3 4 2A
A
V
。 (5)V
1在 直 線CA
4A
5上 的 投 影 線 段 長 為BD
=A
2G
線 段 長 , 因BD
平 行A
2G
, 令t
G
A
A
1 2 , 由 圖8.中 知 x=A
3+ (A
4
)
且 x+ (A
2 )
t
, 則A
2+A
3+A
4 =t
2
V
1cos
A
2
A
3
A
4
=V
1cos
2
t
=V cos
1t
=A
2G
=BD
。(6) 在 直線
CA
4A
5上,線 段 長BD
=線 段 長A
4D
+A
4E
+BE
,故 得A
4D
=BD
-A
4E
-BE
d cos
m
=V
1cos
A
2
A
3
A
4
V
2cos(
A
3
A
4)
+V
3cos A
4 。 (7) 將 此d cos
m
關 係 式 直 接 代 入 方 程 式 (2-1)中 , 即得 證 出 方 程式 (L-2) 。 事 實 上,方 程 式 (L-2)不 僅 適用 於 凹 五 邉形,也 適 用於 凸 五 邉 形;只 要 仿 效上 述 引 理 1. 與 引 理 2.構 圖 要 領 即 可 完 整 證 明 出 平 面 凸 五 邉 形 餘 弦 定 理 為 方 程 式 (L-2)。 若 換 成 選 取 頂 角A
3為 優 角 如 圖 6. , 則 同 樣可 推 證 得 方程 式 (L-2) 。 引 理3. 平 面 六 邉 形 餘 弦 定 理 : 在 平 面 上 給 定 一 個 凸 六 邊 形A
1A
2A
3A
4A
5A
6, 令 線 段 長 2 1A
A
=V
1,A
2A
3=V
2,A
3A
4 =V
3,A
4A
5 =V
4,A
5A
6 =V
5,A
6A
1 =V
6,則 此 六 邊 形 的 面 積 型 餘 弦 公 式 為 : 2 6V
=V
12+V
22+V
32+V
42+ 2 5V
-2V
1V
2cos A
2-2V
2V
3cos A
3-2V
3V
4cos A
4 -2V
4V
5cos A
5+2V
1V
3cos
A
2
A
3
+2V
2V
4cos
A
3
A
4
+2
V
3V
5cos
A
4
A
5
-2V
1V
4cos(
A
2
A
3
A
4)
-2
V
2V
5cos(
A
3
A
4
A
5)
+2V
1V
5cos(
A
2
A
3
A
4
A
5)
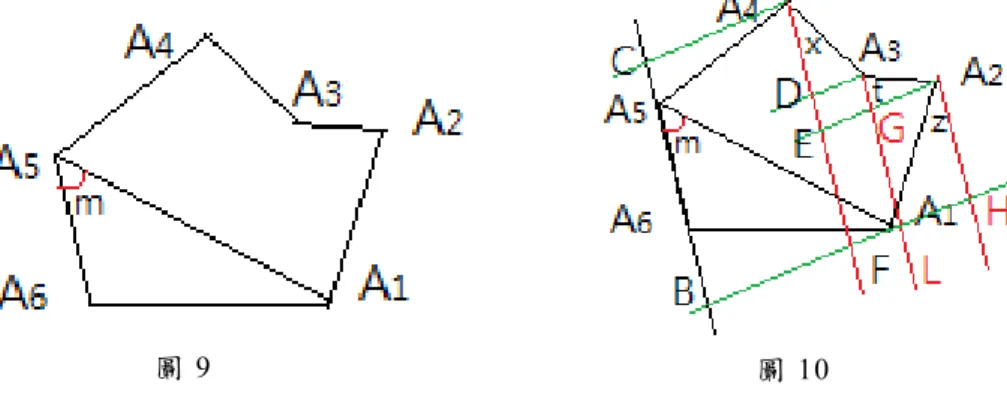
(L-3)證 明:方 程 式 (L-3)也 適 用 於凹 六 邉 形,以 頂角
A
3為 優 角 的 凹 六 邉 形 來 推 證 之;參 見 下 圖 9. 連 接 兩 頂 點A
1與A
5形 成 一 對 角 線 , 使 對 角 線 長 度A
1A
5
d
,(1) 令
A
1A
5A
6
m
, 對 圖9.中 的 部份 凹 五 邉形A
1A
2A
3A
4A
5言 , 有 餘 弦 公 式 為2
d
=V
12+V
22+V
32+V
42-2V
1V
2cos A
2-2V
2V
3cos A
3-2V
3V
4cos A
4+2
V
1V
3cos
A
2
A
3
+2V
2V
4cos
A
3
A
4
-2V
1V
4cos(
A
2
A
3
A
4)
又 對
A
1A
5A
6言 , 可 得 三 角 形 餘 弦 公 式 為V
62=d
2+V
52-2V cos
5d
m
2 6
V
=V
12+V
22+V
32+V
42+V
52-2V
1V
2cos A
2-2V
2V
3cos A
3-2V
3V
4cos A
4-2
V cos
5d
m
+2V
1V
3cos
A
2
A
3
+2V
2V
4cos
A
3
A
4
-2
V
1V
4cos(
A
2
A
3
A
4)
(3-1) (2) 仿 效 引 理 1.與 2.的 幾 何 作 圖 法 , 作 出 圖 10., 其 中 四 直 線A
2H
、A
3GL
、A
4F
與B
A
CA
5 6 相 互 平 行,另 四 綠 色 直 線A
4C
、A
3D
、A
2GE
與HA
1FB
相 互 平 行 且 皆 與 直 線A
2H
、A
3GL
、A
4F
與CA
5A
6B
相 垂 直。而B
、C
、D
、E
、F
、G
、H
七 點 都 是 垂 足 點 。 故 四 邉 形A
4CBF
、A
3DEG
、A
2EFH
皆 為 長 方 形 。 (3) 對 直角
A
1A
5B
言,d cos
m
的 值 恰 為 投 影 線 段 長A
5B
,同 理V
4在 直 線CA
5A
6B
上 的 投 影 線 段 長 為A
5C
, 恰 等 於V
4cos(
A
5)
=
V
4cos A
5=A
5C
。 (4) 由A
4F
平 行CA
5A
6B
,令
A
3A
4D
x
,得A
4+A
5=
x
,而V
3在 直 線A
4F
上 的 投 影 線 段 長 為A
4D
, 恰 等 於V
3cos
x
V
3cos(
A
4
A
5)
=A
4D
。 (5) 由A
4F
平 行A
3GL
,令
A
2A
3G
t
,得x
+A
3
t
=
,故A
3+A
4+A
5=2
t
, 而V
2 在 直 線A
3GL
上 的 投 影 線 段 長 為A
3G
=DE
, 恰 等 於V cos
2t
=)
cos(
3 4 5 2A
A
A
V
=A
3G
=DE
。 (6) 由A
2H
平 行A
3GL
,令
A
1A
2H
z
,得z
+A
2
t
=
,故z
=3
(A
2
A
3 +A
4+A
5) , 而 邉 長V
1在 直 線A
2H
上 的 投 影 線 段 長 為A
2H
。 再 由 圖 10 知A
2H
=EF
=V cos
1z
=
V
1cos
A
2
A
3
A
4
A
5
。 (7) 因 四 邉 形A
4CBF
為 長 方 形 , 得A
5C
+A
5B
=CB
=A
4F
=A
4D
+DE
+EF
, 故A
5B
=m
d cos
=A
4D
+DE
+EF
A
5C
=
V
3cos(
A
4
A
5)
+V
2cos(
A
3
A
4
A
5)
2 3 4 5
1
cos
A
A
A
A
V
V
4cos A
5 。 至 此 找 到d cos
m
的 完 整 值 。(8) 將 此
d cos
m
的 完 整 值 直 接 代 入 方 程 式 (3-1)中,即 得 證 出 方程 式 (L-3)。方 程 式 (L-3)不 僅 適 用 於 凹 六 邉 形 , 也 適 用 於 凸 六 邉 形 ; 只 要 仿 效 上 述 引 理 1.與 引 理 2.及 引 理 3.構 圖 要 領 即 可 完 整 證 明 出 平 面 凸 六 邉 形 餘 弦 定 理 為 方 程 式 (L-3) 。凹六 邉 形 有各 樣 不 同 型 態 ; 如 另 有 頂 角A
2是 單 一 優 角 情 形 , 頂 角A
4是 單 一 優 角 情 形 ,A
2與A
4同 為 優 角 情 形 (其 餘 頂 角 為 劣 角 ),… 等。只 需 仿 效 上 述 作 圖 要 領,這 所 有 型 態 的 凹 六 邉 形 其 具 有 的 餘 弦 定 裡 皆 為 方 程 式 (L-3) 。 引 理4. 平 面七 邉 形 餘 弦定 理:在 平面 上 給 定 一個 凸 七 邊 形A
1A
2A
3A
4A
5A
6A
7,令 其 各 邉 線 段 長A
1A
2 =V
1,A
2A
3 =V
2,A
3A
4 =V
3,A
4A
5 =V
4,A
5A
6 =V
5,A
6A
7=V
6, 1 7A
A
=V
7, 見 下 圖 11., 則此 七 邊 形的 面 積 型 餘弦 公 式 為 : 圖 11 2 7V
=V
12+V
22+V
32+V
42+ 2 5V
+V
62-2V
1V
2cos A
2-2V
2V
3cos A
3-2V
3V
4cos A
4-2
V
4V
5cos A
5-2V
5V
6cos A
6+2V
1V
3cos
A
2
A
3
+2V
2V
4cos
A
3
A
4
+2V
3V
5cos
A
4
A
5
+2V
4V
6cos
A
5
A
6
-2V
1V
4cos(
A
2
A
3
A
4)
-2
V
2V
5cos(
A
3
A
4
A
5)
-2V
3V
6cos(
A
4
A
5
A
6)
+2V
1V
5cos(
A
2
A
3
A
4
A
5)
+2V
2V
6cos(
A
3
A
4
A
5
A
6)
-2V
1V
6cos(
A
2
A
3
A
4
A
5
A
6)
(L-4) 證 明 : 略 。 方 程 式 (L-4)不 僅適 用 於 凸 七邉 形,也 適用 於 凹 七 邉形;只 要 仿效 上 述 引 理 3. 構 圖 要 領 即 可 完 整 證 明 出 所 有 平 面 七 邉 形 餘 弦 定 理 為 方 程 式 (L-4)。 引 理 5. 平 面 八邉 形 餘 弦 定理 : 在 平 面上 給 定 一 個凸 八 邊 形A
1A
2A
3A
4A
5A
6A
7A
8, 令 線 段 長A
1A
2 =V
1,A
2A
3 =V
2,A
3A
4 =V
3,A
4A
5 =V
4,A
5A
6 =V
5,A
6A
7 =V
6,A
7A
8 =V
7,A
8A
1=V
8, 見 下 圖 12a.,則 此 八邊 形 的 面 積型 餘 弦 公 式為 :2 8
V
=V
12+V
22+V
32+V
42+ 2 5V
+V
62+ 2 7V
-2V
1V
2cos A
2-2V
2V
3cos A
3-2V
3V
4cos A
4 -2V
4V
5cos A
5-2V
5V
6cos A
6-2V
6V
7cos A
7+2V
1V
3cos
A
2
A
3
+ 2
V
2V
4cos
A
3
A
4
+2V
3V
5cos
A
4
A
5
+2V
4V
6cos
A
5
A
6
+ 2
V
5V
7cos
A
6
A
7
-2V
1V
4cos(
A
2
A
3
A
4)
-2V
2V
5cos(
A
3
A
4
A
5)
-2V
3V
6cos(
A
4
A
5
A
6)
-2V
4V
7cos(
A
5
A
6
A
7)
+2V
1V
5cos(
A
2
A
3
A
4
A
5)
+ 2
V
2V
6cos(
A
3
A
4
A
5
A
6)
+2V
3V
7cos(
A
4
A
5
A
6
A
7)
-2V
1V
6cos(
A
2
A
3
A
4
A
5
A
6)
-2V
2V
7cos(
A
3
A
4
A
5
A
6
A
7)
+ 2V
1V
7cos(
A
2
A
3
A
4
A
5
A
6
A
7)
(L-5) 證 明 : 略 。 方 程 式 (L-5)不 僅適 用 於 凸 八邉 形,也 適用 於 圖 12b.凹八 邉 形;只 要仿 效 引 理 3.構 圖要 領 即 可完 整 證 明 出所 有 平 面 八邉 形 餘 弦 定理 為 方 程 式(L-5)。二、平面凸七邊形內中央兩相鄰交叉 對角線長度乘積一般化方程式
平 面 上 給 定 一 個 凸 七 邊 形A
1A
2A
3A
4A
5A
6A
7,令 線 段 長A
1A
2 =V
1,A
2A
3 =V
2,A
3A
4 =V
3,A
4A
5 =V
4,A
5A
6 =V
5,A
6A
7=V
6,A
7A
1=V
7,見 下 圖 13,在 圖 形 中央 選 定 兩相 鄰 交 叉 對 角 線 長A
1A
4
d
14,A
2A
5
d
25 的 組 合 , 則 此 平 面 凸 七 邉 形 內 中 央 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式 為 下 列 型 (7a)式 ; 圖 12a 圖 12b 圖 13
2 25 2 14d
d
V
12V
42+[V
22V
52+V
32V
52
2
V
2V
3V
52cos A
3] +[V
22V
62+V
32V
62
2
V
2V
3V
62cos
A
3]+[V
22V
72+V
32V
72
2
V
2V
3V
72cos
A
3])
cos(
2
V
1V
2V
4V
5A
2
A
5
+2
V
1V
2V
4V
6cos(
A
2
A
5
A
6)
)
cos(
2
V
1V
2V
4V
7A
2
A
5
A
6
A
7
+2
V
1V
3V
4V
5cos(
A
2
A
3
A
5)
)
cos(
2
V
1V
3V
4V
6A
2
A
3
A
5
A
6
2
V
1V
3V
4V
7cos(
A
1
A
4)
+[
2
V
22V
5V
6cos
A
6+2
V
22V
5V
7cos(
A
6
A
7)
2
V
22V
6V
7cos
A
7] +[
2
V
32V
5V
6cos
A
6+2
V
32V
5V
7cos(
A
6
A
7)
2
V
32V
6V
7cos
A
7] +4
V
2V
3V
5V
6cos
A
3cos
A
6
4
V
2V
3V
5V
7cos
A
3cos(
A
6
A
7)
+
4
V
2V
3V
6V
7cos
A
3cos
A
7 (7a)證 明:連 接 兩 頂 點