高效RSA密碼系統解密方法及實作

全文

(1)國立交通大學電機資訊學院資訊學程碩士論文. 高效 RSA 密碼系統解密方法及實作. An Efficient Decryption Method for RSA Cryptosystem And Implementation. 研究生：陳嘉耀指導教授：葉義雄. 中華民國. 教授. 九十四年六月. i.

(2) 高效 RSA 密碼系統解密方法及實作 An Efficient Decryption Method for RSA Cryptosystem And Implementation 研究生：陳嘉耀. Student： Chia-Yao Chen. 指導教授：葉義雄. Advisor：Dr. Yi-Shiung Yeh. 國立交通大學. 電機資訊學院資訊學程碩士論文 A Thesis Submitted to Degree Program of Electrical Engineering and Computer Science College of Electrical Engineering and Computer Science National Chiao Tung University in Partial Fulfillment of the Requirements for the Degree of Master of Science In Computer Science June 2005 Hsinchu, Taiwan, Republic of China. 中華民國. 九十四年六月. i.

(3) 高效 RSA 密碼系統解密方法及實作. 學生:陳嘉耀. 指導教授:葉義雄博士. 國立交通大學電機資訊學院資訊學程﹙研究所﹚碩士班. 摘. 要. RSA密碼系統在電子商務與安全的網際網路存取等許多應用中是一種最有吸引力與歡迎的安全技巧。為了安全性的考量，RSA密碼系統必須在大的指數與模數下執行模指數運算，因此需要大量的計算成本。所以，在許多RSA的應用中，使用者會使用較小的公開金鑰來加快加密運算，相對的，在解密的運算還是需要大量的計算。本篇論文提出一有效率的解密實現方法，其架構在中國剩餘定理與RSA強質數的標準上。在TMS320C55x family of signal processors上實作，此新方法大約只須16%傳統解密方法的計算成本，與僅運用中國乘餘定理的解密法相比，大約只須55%的計算成本。換句話說，我們所提出的方法大約比運用中國乘餘定理的解密法快1.8倍。所以本方法非常適合加快RSA的解密運算。. ii.

(4) An Efficient Decryption Method for RSA Cryptosystem And Implementation Student: Chia-Yao Chen. Advisor: Dr. Yi-Shiung Yeh. Degree Program of Electrical Engineering Computer Science National Chiao Tung University Abstract In this thesis an efficient method to implement RSA decryption algorithm is proposed. In applications such as electronic commerce and internet access security, RSA cryptosystem is the most attractive and most popular security technique. For security reason, RSA cryptosystem has to execute modular exponentiation with large exponent and modulus. The RSA cryptosystem needs a very high computational cost. In many RSA applications, users use a small public key to speed up the encryption operation. However, the decryption operation has to take more computational cost to perform modular exponentiation by this case.. In. this thesis we propose an efficient decryption method not only based on Chinese Remainder Theorem (CRT) but also on the strong prime of RSA criterion. On the TMS320C55x family of signal processors, the proposed decryption method only needs 16% computational costs of the original decryption method. Compared with the computational cost of decryption method based on CRT, our proposed decryption method only needs 55% computational costs. Therefore, our proposed method is very useful in accelerating the speed of the RSA decryption operation. iii.

(5) 致. 謝. 能夠順利完成論文，首先要謝謝指導老師葉義雄教授，在這兩年中給予我各方面的教導。還要感謝淡江大學黃仁俊老師及蘇豐富學長的指導及黃龍信學長在實作上的協助。當然也要感謝所有的口試委員，因為他們細心使論文更加完善。能順利完成學業，要感謝辦公室各級長官的體諒，特別是彭仁岡處長、林副座、徐副座及張姐，還有所有學長姐的幫忙，在功課方面，除了要感謝黃定宇學長、薛明宏學長外，還要感謝那群一起奮鬥的專班同學。最後要感謝我的父母，由於他們的寬容，讓我可以隨心所欲的作我想作的事，特別是我的媽媽。. 陳嘉耀. 中華民國. 九十四年六月. iv.

(6) Contents Chapter 1 Introduction..........................................................................................1 Chapter 2 RSA .....................................................................................................4 2.1 Algorithm ................................................................................................4 2.2 The Security of RSA.............................................................................6 2.2.1 Brute Force: ..................................................................................6 2.2.2 The Factoring Problem .................................................................6 2.2.3 Timing Attack..............................................................................10 2.3 Strong Prime........................................................................................13 2.4 Chinese Remainder Theorem ..........................................................14 Chapter 3 New Decryption Method .................................................................18 Chapter 4 Computational complexity..............................................................25 Chapter 5 Implementation ................................................................................30 Chapter 6 Conclusion ........................................................................................36 REFERENCES ..................................................................................................37. v.

(7) List of Figures FIGURE 1 MIPS-YEARS NEEDED TO FACTOR [13] ........................................................8 FIGURE 2 THE STRUCTURE OF STRONG PRIME ...........................................................14 FIGURE 3 NEW DECRYPTION METHOD FOR RSA CRYPTOSYSTEM..............................20. vi.

(8) List of Tables TABLE 1 PROGRESS IN FACTORIZATION [13].................................................................7 TABLE 2 COMPARISON AMONG THREE TYPES OF DECRYPTION METHODS .................29 TABLE 3 THE FEATURES OF TMS320C55X [32].........................................................31 TABLE 4 PARAMETERS OF THE RSA DECRYPTION ......................................................32 TABLE 5 NUMBERS OF CPU CLOCK CYCLES FOR REALIZATION RSA DECRYPTION BETWEEN THREE METHODS (KEY LENGTH = 2048 BITS).............................32 TABLE 6 NUMBERS OF CPU CLOCK CYCLES FOR REALIZATION RSA DECRYPTION BETWEEN THREE METHODS (KEY LENGTH = 1024 BITS).............................32 TABLE 7 NUMBERS OF CPU CLOCK CYCLES FOR REALIZATION RSA DECRYPTION BETWEEN THREE METHODS (KEY LENGTH = 512 BITS)...............................33 TABLE 8 THE MEMORY SPACES FOR REALIZATION RSA DECRYPTION BETWEEN THREE METHODS (KEY LENGTH = 2048 BITS) ........................................................34 TABLE 9 THE MEMORY SPACES FOR REALIZATION RSA DECRYPTION BETWEEN THREE METHODS (KEY LENGTH = 1024 BITS) ........................................................34 TABLE 10 THE MEMORY SPACES FOR REALIZATION RSA DECRYPTION BETWEEN THREE METHODS (KEY LENGTH = 512 BITS)...............................................34. vii.

(9) Chapter 1 Introduction With the rapid progress of modern information technology, security is an important technique of many applications. The RSA cryptosystem was proposed by R. Rivest, A. Shamir, L. Adleman in 1978 [2]. It is the most popular and well-defined security primary technique. RSA is a cryptosystem widely used to ensure data privacy in many fields such as communication and PKCS#1 standard lines out a way of encrypting data using the RSA cryptosystem [3]. Moreover, in digital signature and digital envelope, RSA provides non-repudiation and confidentiality of communication [3]. Actually, many good security protocols using RSA cryptosystem are applied in the modern information technology, for example, virtual private networks, electronic commerce, and secure Internet access. RSA cryptosystem is easy to understand and implement. It is based on modular exponentiation. This modular exponentiation is performed by repeated modular multiplications. In general, the modular multiplication has to be performed a certain number of times to ensure security, but the consequence is that the RSA operation has to take much more computational cost for security consideration. In order to include RSA cryptosystem practically in many protocols, it is desired to devise faster encryption and decryption operations. Under this consideration, many hardware implementation methods have been proposed [4, 5, 6], in which high speed can be achieved but not flexibility. In these applications, users usually select a small number such as 3, 17, or 65537 to be the public key to speed up the encryption operation [7]. 1.

(10) However, by this way, the corresponding decryption operation costs more computational time because of the larger private key. Another choice is the Chinese Remainder Theorem (CRT). The decryption operation can be accelerated by applying the CRT [8, 9, 10] if the prime factors of modulus are known. It is reasonable that someone who holds the private key can get the prime factors of modulus. By means of the CRT, the speed for the RSA decryption operation could be 4 times faster [6]. In addition, Hayashi proposed a new modular exponentiation method [12] to improve the computational time of RSA. In his method, the modular exponentiation with the modulus n transforms into two substitute operations with factorable moduli n + 1 and n + 2. If moduli n + 1 and n + 2 can be factored, user can apply CRT to these modular operations modulo to n + 1 and n + 2 for each.. The final result can be generated by. Hayashi’s formula. But this method is not very practical, especially when n is an odd number; it would be a difficult job to factor n + 2. We propose an efficient method to implement RSA decryption operation in this thesis. This method is not only based on CRT but also on the strong prime of RSA criterion. The security of RSA is based on the difficulty of factoring problem. So, the prime factors of modulus of RSA algorithm must be strong primes. The large modular exponentiation result can be generated from small exponents and moduli. The proposed method enhances the performance of RSA algorithm. The rest of this article is organized as follows: we will briefly review RSA algorithm in Chapter 2. In Chapter 3 we introduce our new decryption method. In Chapter 4 we analyze the computational complexity. In Chapter 5 we talk about the implementation of new 2.

(11) decryption method. Finally, we make some conclusion in Chapter 6.. 3.

(12) Chapter 2 RSA RSA cryptosystem is a typical public-key cryptosystem.. Although. the cryptanalysis neither proved nor disproved RSA’s security, it dose suggest confidence level in the algorithm. RSA gets its security from the difficulty of factoring large number. The public and private keys are functions of a pair of large prime numbers. Recovering the plaintext from the public key and the ciphertext is conjectured to be equal to factoring the product of the two primes.. 2.1 Algorithm RSA algorithm can be described briefly as follows: ⅠKey Generation: 1. Choose two large strong primes, p and q. 2. Calculate n = p⋅q. 3. Compute Euler value of n: Φ(n) = (p - 1)(q - 1) 4. Find a random number e satisfying 1 < e < Φ(n) and gcd(e,. Φ(n)) = 1. 5. Compute a number d such that d = e-1 mod Φ(n) Public key = {e , n} Private key = {d , n} ⅡEncryption: Plaintext:. m satisfying m < n,. Ciphertext:. c = me mod n. ⅢDecryption: 4.

(13) m = cd mod n. [Example 1] Let p = 47 and q = 59, then n = pq = 2773 and (p-1)(q-1) = 2668. The value of e must be chosen somewhere between 1 and 2668. Assume e = 17. The value of d is 157.Assume further that the alphabet is represented by decimal values, i.e. a = 01, b = 02, c =03, etc. and a blank space is given the value 00. The plaintext is given as: m = RSA CRYPTOSYSTEM or in decimal representation by: m = 1819 0100 0318 2516 2015 1925 1920 0513 The plaintext is enciphered by an individually encrypted message, which contains a block of four digits: m1 = 1819 m2 = 0100 m3 = 0318 m4 = 2516 m5 = 2015 m6 = 1925 m7 = 1920 m8 = 0513 The first block is encrypted as: 181917 mod 2773 = 0818 Performing the same operation on the subsequent blocks generates an encrypted message: c = 0818 1952 0578 2666 0774 0246 2109 0772 Decrypting the message requires performing the same 5.

(14) exponentiation using the decryption key of 157, so 0818157mod2773 = 1819 = m1 The rest of the plaintext can be recovered in this manner.. 2.2 The Security of RSA There are three possible approaches to attack the RSA algorithm as follows: Brute force, Mathematical attacks, and time attacks. z Brute force: This involves trying all possible private keys. z Mathematical attacks: There are several approaches, all equivalent in effect to factoring the product of two primes. z Timing attacks: These depend on the running time of the decryption algorithm.. 2.2.1 Brute Force: To defense the Brute-force attack, the approach for RSA cryptosystem is the same as for other cryptosystems ─ use a large key space. That mean, the larger the number of bits in e and d, the better. However, because the calculations involved, both in key generation and in encryption/decryption, are complex, the larger the key length, the slower the system operates.. 2.2.2 The Factoring Problem Three approaches to attacking RSA mathematically can be identified as follows: z Factor n into its two prime factors. This enables calculation of Φ(n) = (p - 1)(q - 1) and d = e-1 mod Φ(n). 6.

(15) z Direct Determine Φ(n). This enables determine of d = e-1 mod Φ(n). z Direct Determine d. Most discussions of the cryptanalysis of RSA have focused on the task of factoring n into two prime factors. Determine Φ(n) given n is equivalent to factoring n. With all known algorithms, determine d only given e and n, appears to be at least as time-consuming as the factoring problem. To factor a large n with only two large prime factors is a hard problem, but not as hard as it used to be. With great computational capability, this problem can be solved in reasonable time. In table 1 shows the progress in factorization. The level of effort is measured in MIPS-years: a million-instructions-per-second processor running for Table 1 Progress in Factorization [13]. one year, which is about 3 × 1013 instructions executed. A 200-MHz Pentium is about a 50-MIPS machine. The threat to larger key sizes is twofold: the continuing increase in computing capability, and the continuing refinement of factoring algorithm. If a different algorithm is used, it can result in a tremendous speedup. It can expect further refinements in the 7.

(16) generalized number field sieve, and the use of an even better algorithm is also a possibility. For example, a related algorithm, the special number field sieve, can factor number with a specialized from considerably faster than the generalized number field sieve. In Figure 1 we compar the performance of two algorithms. It is reasonable to. Figure 1 MIPS-years Needed to Factor [13] expect a breakthrough that would enable a general factoring performance in about the same time as the special number field sieve, or even better. Thus, we need to be careful in choosing a key size for 8.

(17) RSA. In the near future, a key size in the range of 1024 to 2048 bits seems reasonable. In some special case, there are some factoring algorithms, which can easy to factor n such like Pollard’s p - 1 algorithm. z Pollard’s p - 1 algorithm Pollard’s p - 1 algorithm [17] is efficient only if n has a prime factor p such that p - 1 is smooth. The algorithm can be described as follows: 1. Select a ∈ ℤ/Nℤ at random. Select a positive integer k that is divisible by many prime powers, for example, k = lcm(1,2,…,B) for a suitable bound B (the larger B is the more likely the method will be to succeed in producing a factor, but the longer the method will take to work). 2. Compute ak = ak mod N. 3. Compute d = gcd (ak-1 , N). 4. If 1 < d < N, then d is a nontrivial factor of N, output d and go to step 6. 5. If d is not a nontrivial factor of N and still want to try more experiment, then go to step 2 to start all over again with a new a and/or a new k, else go to step 6. 6. Terminate the algorithm. The Pollard’s p - 1 algorithm is usually successful in the fortunate case where N has a prime divisor p for which p – 1 has no large prime factors. Suppose that (p – 1)|k and that pɫa.. 9.

(18) Since |(ℤ/pℤ)* | = p – 1 and ak ≡ 1 (mod p), thus p| gcd (ak-1 , N). In many cases, p = gcd (ak-1 , N). [Example 2] Input N = 540143, and B = 8 let k = 840 = 23*3*5*7, and a = 2 gcd (2840 – 1 mod 540143 , 540143) = gcd (53046 , 540143) = 421 421 is a factor of 540143. In fact, 540143 = 421*1283. The drawback of this algorithm is that it requires N to have a prime factor p such that p – 1 has only “small” prime factors. In RSA algorithm, it would be very easy to Factor n into its two prime factors, if p - 1 or q - 1 has only “small” prime factors. Note that the p + 1 algorithm, proposed by H. C. Williams in 1982, is an algorithm very similar to Pollard’s p - 1 algorithm. It is efficient only if n has a prime factor p such that p + 1 is smooth.. 2.2.3 Timing Attack The main idea of timing attack is that a snooper can determine a private key by keeping track of how long a computer takes to decipher message [20]. Timing attacks are applicable not only to RSA, but also to other public-key cryptography system. This attack is alarming for two reasons: It comes from a completely unexpected direction and it is a ciphertext-only attack. The attack assumes that the attacker knows the design of the 10.

(19) target system, although practically this could probably be inferred from timing information. The attack can be tailored to work with virtually any implementation that does not run in fixed time, but is first outlined using the simple modular exponentiation algorithm below which computes R = cd mod n, where d is w bits long: Let s0 = 1. For k = 0 to w - 1: If (bit k of d) is 1 then Let Rk = (sk • c) mod n. Else Let Rk = sk. Let sk+1 = Rk2 mod n. End. Return (Rw-1). The attack allows someone who knows exponent bits 0…(b-1) to find bit b. To obtain the total exponent, begin with b equal to 0 and repeat the attack until the total exponent is known. Because the first b exponent bits are known, the attacker can compute the first b iterations of the ″For″ loop to find the value of sb. The next iteration requires the first unknown exponent bit. If this bit is ″1″, Rb = (sb • c) mod n will be computed. If it is ″0″, the operation will be skipped. The attack will be described first in an extreme hypothetical case. Suppose the target system uses a modular multiplication function that is normally extremely fast but occasionally takes much more time than an entire normal modular exponentiation. For a few sb and c values the calculation of Rb = (sb • 11.

(20) c) mod n will be extremely slow, and by using knowledge about the target system's design the attacker can determine which these are. If the total modular exponentiation time is ever fast when Rb = (sb • c) mod n is slow, exponent bit b must be zero. Conversely, if slow Rb = (sb • c) mod n operations always result in slow total modular exponentiation times, the exponent bit is probably set. Once exponent bit b is known, the attacker can verify that the overall operation time is slow whenever sb+1 = Rb2mod n is expected to be slow. The same set of timing measurements can then be reused to find the following exponent bits. Although the timing attack is a serious threat, there are simple countermeasures that can be used, including the following: z Constant. exponentiation. time:. Ensure. that. all. exponentiation takes the same amount of time before returning result. This is a simple fix but does degrade performance. z Random delay: Better performance could be achieved by adding a random delay to the exponentiation algorithm to confuse the timing attack. If defenders do not add enough noise, attackers could still succeed by collecting additional measurements to compensate for the random delay. z Blinding: Multiply the ciphertext by a random number before performing exponentiation. This processed prevents the attacker from knowing what ciphertext bits are being processed inside the computer and therefore prevents the bit-by-bit analysis essential to the timing attack. 12.

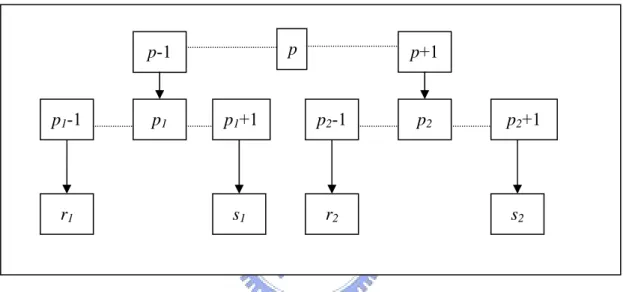
(21) 2.3 Strong Prime The security of RSA depends critically on the problem of factoring n into its prime factors p and q.. Therefore it is important. for the user to select primes p and q in such a way that the problem of factoring n = p×q is computationally infeasible for an adversary. The recommended way of maximizing the difficulty of factoring n is to choose p and q as strong primes.. Ogiwara [21, 22, 23] defined. that a prime p is said to be strong if p satisfies the following constraints: 1. p - 1 should contain a large prime factor p1 so that p – 1 = p1×α, where gcd(p1, α) = 1. 2. p + 1 should contain a large prime factor p2 so that p + 1 = p2×β, where gcd(p2, β) = 1. 3. p1 - 1 has a large prime factor r1 so that p1 – 1 = r1×χ, where gcd(r1, χ) = 1. 4. p1 + 1 has a large prime factor s1 so that p1 + 1 = s1×δ, where gcd(s1, δ) = 1. 5. p2 - 1 has a large prime factor r2 so that p2 – 1 = r2×ε, where gcd(r2, ε) = 1. 6. p2 + 1 has a large prime factor s2 so that p2 + 1 = s2×γ, where gcd(s2, γ) = 1. These ‘level-3 prime’ numbers r1, s1, r2 and s2 can be easily found by a probabilistic primarily test.. There are many methods. have been proposed to generate strong primes for RSA [21, 24, 25, 26].. These methods first use level-3 primes to find ‘level-2 primes’ 13.

(22) p1 or p2.. Similarly we use the level-2 primes to find the ‘level-1. prime’ p.. In these methods, the bit length of the level-(i + 1) prime. is about half of the bit length of the level-i prime. Figure 2 shows the strong prime structure.. Another prime q also can be generated. by the same method. The private key holder knows these secret values essentially, because he should select these secret values to generate his private key by himself.. p. p-1. p1-1. r1. p1. p+1. p1+1. p2-1. s1. r2. p2. p2+1. s2. Figure 2 The Structure of Strong Prime. 2.4 Chinese Remainder Theorem The Chinese remainder Theorem (CRT) is a really method of solving certain system of congruence. Suppose m1,m2,…,mr are pairwise relatively prime positive integers, and suppose a1,a2,…,ar are integers. Then the system of r congruences x ≡ a1 mod m1 x ≡ a2 mod m2 :. x ≡ ar mod mr has a unique solution modulo M = m1×m2×…×mr, which is given by 14.

(23) r. x ≡ ∑ a iM iYi mod M i =1. where Mi = M/mi and yi = Mi-1 mod mi, for 1≤ i ≤ r. [Example 3] Let x ≡ 2 mod 3 x ≡ 3 mod 5 x ≡ 2 mod 7 M = m1 m2 m3 = 105 M1 = M / m1 = 35 y1 = M1-1 mod m1= 35-1 mod 3 = 2 M2 = 21 and y2 = 1 M3 = 15 and y3 = 1 x. = (a1M1y1 + a2M2y2 +a3M3y3 ) mod M = (2*35*2 + 3*21*1 +2*15*1 ) mod 105 = 23. The CRT is very useful in Cryptography and its applications very broad. When the factors of the modulus N (i.e., p and q) are assumed to be known, the RSA decryption operation can be speeded up by using the CRT [8, 9]. By using the CRT, the computation of M = Cd mod N can be partitioned into two parts: Mp = Cpdp mod p, Mq = Cqdq mod q, where Cp = C mod p, dp = d mod ( p－1), Cq = C mod q, dq = d mod (q－1). 15.

(24) Finally, we use CRT to compute M as follows: M = ( Mp ( q-1 mod p) ) q + Mq ( p-1 mod q) ) p) mod N. This reduces computation time since dp, dq < d and Cp, Cq < C. In fact, their sizes are bout half the original sizes. In the ideal case we can have a speedup of about 4 times. In this case, dp, dq, q-1 mod p and p-1 mod q can be predict. The extra operations are Cp = C mod p, Cq = C mod q and M = Mp ( q-1 mod p) q + Mq ( p-1 mod q ) p) mod N. Compared with the calculation of Mp and Mq, the time spent on the extra operations is negligible. Therefore, in most cases, the speedup is close to 4 times. Another RSA decryption algorithm based on CRT can be described as follows: a = cd mod p.. Compute:. b = cd mod q. u*q = 1 mod p If a ≥ b mod p, then cd mod n = (((a – (b mod p))*u)mod p)*q +b If a < b mod p, then cd mod n = (((a + p – (b mod p))*u)mod p)*q +b If a and b can be easily computed, this algorithm will be more efficient. [Example 4] From example 1, m1 = 1819, c1 = 0818, m3 = 0318, c3 = 0578, e = 17, d = 157, p = 47 and q = 59, a1 = cd mod p = 818157 mod 47 = 33 b1= cd mod q =818157 mod 59 = 49 16.

(25) u = 59-1 mod 47 = 4 a1 < b1 m1 = (((33 + 47 – (49 mod 47))*4)mod 47)*59 +49 = 1819. a2 = cd mod p = 578157 mod 47 = 36 b2= cd mod q =578157 mod 59 = 23 a2 ≥ b2 m3 = (((36 – (23 mod 47))*4)mod 47)*59 +23 = 0318 The result is the same with the result in example 1.. 17.

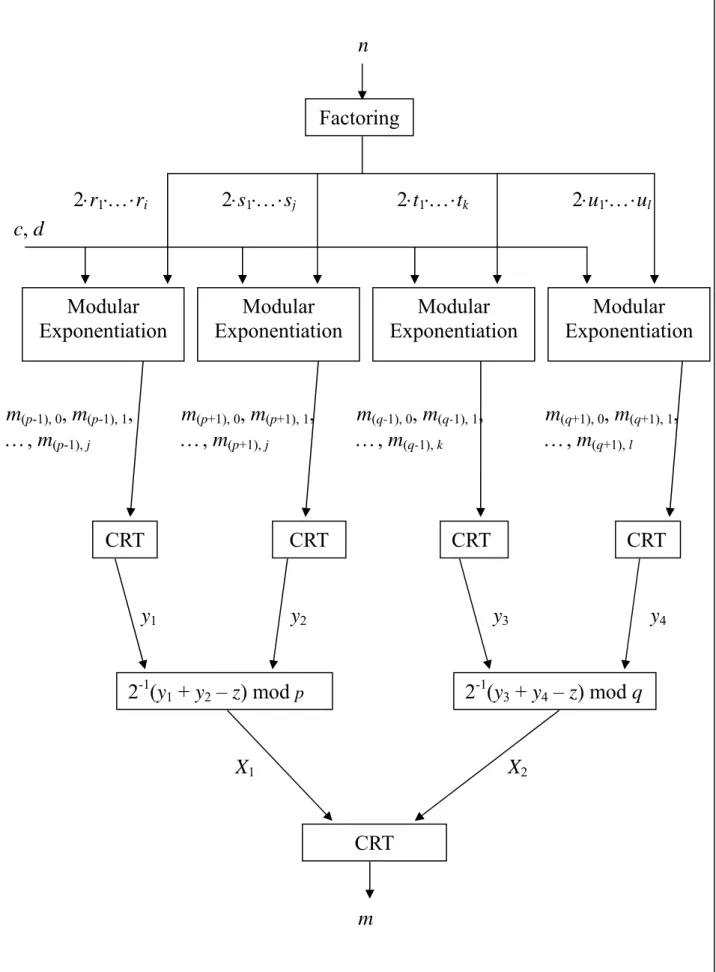
(26) Chapter 3 New Decryption Method In this Chapter, we propose an efficient RSA decryption method based on strong prime criterion. If the highest concern is to ensure data security, the prime factors p and q of modulus n in RSA cryptosystem must be strong primes. It is reasonable that the private key holder knows the prime factors of p – 1, p + 1, q – 1 and q + 1. The proposed decryption method is based on the strong primes of RSA criterion and Chinese Remainder Theorem (CRT). The private key holder performs the decryption procedure: cd mod n by our method as the following steps: Step 1: Factor p – 1, p + 1, q – 1, and q + 1 to get their prime factors. We assume that moduli p – 1, p + 1, q – 1, and q + 1 be expressed as follows. p – 1 = 2 ⋅ r1⋅…⋅ri, p + 1 = 2 ⋅ s1⋅…⋅sj, q – 1 = 2 ⋅ t1⋅…⋅tk, q + 1 = 2 ⋅ u1⋅…⋅ul. Step 2: Compute the modular exponentiation with prime factors of p – 1 as the modulus. Then, apply the CRT to generate individually y1 = cd mod (p - 1), y2 = cd mod (p + 1), y3 = cd mod (q - 1), y4 = cd mod (q + 1), The detail steps are as follows: 2.1 Compute c(p-1),i = c mod riαi, i = 1, …, h. 2.2 Compute d(p-1), i = d mod Φ(riαi), i = 1, …, h. 18.

(27) 2.3 Compute the modular exponentiation m(p-1),i = c(p-1),id(p-1),i mod riαi, i = 1, …, h. 2.4 Apply the CRT to generate y1 = cd mod (p – 1) based on m(p-1),i, i = 1, …, h. Step 3: Compute X1 = 2-1(y1 + y2 – z) mod p where z = 0 if y1 ≥ y2; otherwise z = 1,and X2 = 2-1(y3 + y4 – z) mod q where z = 0 if y3 ≥ y4; otherwise z = 1. Step 4: Apply the CRT to calculate the final result m = cd mod n based on X1 and X2. Figure 3 shows the diagram of our decryption method. The numbers p – 1, p + 1, q - 1 and q + 1 can be individually decomposed into three prime factors at least in step 1. The bit lengths of riαi (i = 1, …, h) are shorter than p -1. The bit lengths of d(p-1), i (i = 1, …, h) are shorter than d. In general, the complexity of modular exponentiation depends on the bit length of exponent and modulus. The total computation time of Step 2 to get y1 = cd mod (p -1) is shorter than compute y1 by computing cd mod (p -1) directly. The efficient results are similar to y2 = cd mod (p + 1), y3 = cd mod (q - 1) and y4 = cd mod (q + 1). The proposed decryption method is more efficient than the original method. In chapter 4 we will prove these results in detail. In Step 3, we use (y1, y2) to compute X1, and (y3, y4) to compute X2. Theorem 1 demonstrates that X1 and X2 are generated as Step 3 correctly.. 19.

(28) n Factoring. 2⋅r1⋅…⋅ri. 2⋅s1⋅…⋅sj. 2⋅t1⋅…⋅tk. 2⋅u1⋅…⋅ul. c, d. Modular Exponentiation. m(p-1), 0, m(p-1), 1, …, m(p-1), j. Modular Exponentiation. m(p+1), 0, m(p+1), 1, …, m(p+1), j. CRT. Modular Exponentiation. m(q-1), 0, m(q-1), 1, …, m(q-1), k. CRT. y1. Modular Exponentiation. m(q+1), 0, m(q+1), 1, …, m(q+1), l. CRT. y2. CRT. y3. 2-1(y1 + y2 – z) mod p. 2-1(y3 + y4 – z) mod q. X1. X2 CRT. m. Figure 3 New Decryption Method for RSA Cryptosystem 20. y4.

(29) [Lemma 1] Given y1 = X mod (p – 1), y2 = X mod (p + 1) where 0 ≤ X < (p2 - 1)/2, and p is a prime, then X = (p + 1)y1/2 – (p –1)y2/2 + (p – 1)(p + 1)z/2 where z = 1 or 0. Proof: From y1 = X mod (p – 1) and y2 = X mod (p + 1), we have y1 + (p – 1)z1 = X. (1). y2 + (p + 1)z2 = X. (2). z1 and z2 are two positive integers Equation (1) × (p+1): (p + 1)y1 + (p + 1)(p – 1)z1 = (p + 1)X.. (3). Equation (2) × (p - 1): (p - 1)y2 + (p + 1)(p – 1)z2 = (p - 1)X.. (4). Equation (3) – Equation (4): 2X = (p + 1)y1 – (p –1)y2 + (p – 1)(p + 1)(z1 - z2) Let z = z1 - z2 X = (p + 1)y1/2 – (p –1)y2/2 + (p – 1)(p + 1)z/2. (5). We will proof z is 0 or 1 in Equation (5) by contradiction as follows: Case 1: Assume that z < 0.Since y1 ≤ p - 2 and y2 ≥ 0, it follows that X = (p + 1)y1/2 – (p –1)y2/2 + (p – 1)(p + 1)z/2 X ≤ (p + 1) (p –2)/2 - (p – 1)(p + 1)/2 = -(p + 1)/2 X < 0. This result contradicts the given condition X ≥ 0. Hence, z is not 21.

(30) smaller than 0. Case 2: Assume that z > 1.Since y1≥0 and y2≤ p, it follows that X = (p + 1)y1/2 – (p –1)y2/2 + (p – 1)(p + 1)z/2 X ≥ –(p –1)p/2 + (p – 1)(p + 1) = (p – 1) (p + 2)/2 X > (p – 1) (p + 1)/2. This result contradicts the given condition X < (p2 - 1)/2. Hence, z is not larger than 1. By Cases 1, 2 and z1, z2 are integers, z must be either 0 or 1.. Q.E.D.. [Theorem 1] Given y1 = X mod (p – 1), y2 = X mod (p + 1) where 0 ≤ X < (p2 - 1)/2, and p is a prime, then X = 2-1(y1 + y2 – z) mod p The value of z is if y1 ≥ y2 ; z = 0, otherwise ; z = 1. Proof: By Lemma 1, X = (p + 1)y1/2 – (p – 1)y2/2 + (p – 1)(p+1)z/2, where z is either 0 or 1. We get X = 2-1(y1 + y2 – z) mod p,. (6). where z is either 0 or 1. In addition, we will demonstrate the conditions of Equation (6) that z 22.

(31) = 0 or z = 1. By Equation (2) – Equation (1) y2 – y1 = (p – 1)z1 – (p + 1)z2 = (p – 1) (z1 – z2) – 2z2 where y1 ≥ 0, y2 ≥ 0, p > 0 , both z1 and z2 are two positive integers. Let (z1 – z2) = z. y2 – y1 = (p – 1) z – 2z2. (7). By Equation (2), and 0 ≤ X < (p2 - 1)/2, 0 ≤ y2 ≤ p, we get 0 ≤ y2 + (p + 1) z2 < (p2 - 1)/2. Hence, we get 0 ≤ z2 < (p – 1)/2. By Equation (7), y2 – y1 > (p – 1)z – (p - 1) = (p – 1) (z – 1).. (8). Case 1: y1 ≥ y2 Since y1 ≥ y2, from Equation(8) 0 ≥ y2 – y1 > (p – 1) (z – 1) 0 > (p – 1) (z – 1) and, (p – 1) > 0, 0> z – 1 1> z By Lemma 1, z = 0. Case 2: y1 < y2 The value of z must be a positive integer. Thus z = 1. To sum up, z = 0 if y1 ≥ y2; otherwise z = 1. [Example 4]( y1 < y2) Let p = 19, X = 169 p + 1= 20 = 4*5 p – 1 = 18 =3*6 23. Q.E.D..

(32) y1 = 169 mod 18 = 7 y2 = 169 mod 20 = 9 y1 < y2 y ≡ 2-1(7 +9 -1) mod 19 ≡ 17 mod 19 [Example 5]( y1 ≥ y2) Let p = 2773, X = 9202 p+1 = 2774 = 38*73 p-1 = 2772 = 36*77 y1 = 9202 mod 2772 = 940 y2 = 9202 mod 2774 = 330 y1 ≥ y2 y ≡ 2-1(330 + 940) mod 2773 ≡ 635 mod 2773 Although we need to compute the multiplicative inverse of 2 modular p in Step 3, Theorem 2 provides an efficient method to compute the inverse value. [Theorem 2] Let p be a prime, the multiplicative inverse of 2 modulo p can be computed by 2-1 mod p = (p + 1)/2. Proof: 2 × (p + 1)/2 = p + 1 ≡ 1 mod p. The multiplicative inverse of 2 modulo p is equal to (p + 1)/2.. 24. Q.E.D.

(33) Chapter 4 Computational complexity In this chapter we will demonstrate our proposed decryption method, which is more efficient than the original decryption method and decryption method based on CRT.. First, we will define some. denotations as follows: MODE(y, z) denotes an operation of modular exponentiation (xy mod z). M(w), A(w) and Mod(w) denote operations of multiplication, addition and modulus with the bit length of operand is w. l(w) denotes lengths of w. S denotes an operation of shift. By the additional chain method [27] the modulo operation cd mod n can be expressed as: (9) MODE(d, n) = 1.5 × l(d)[M(l(n) + 2 Mod(l(n)) + 1). The multiplication and addition operations can be expressed as follows [28]: M(w) = 3M(w/2) + 5A(w) + 2S,. (10). A(w) = w/32.. (11). Also, the modular operation could be expressed as the following equations based on the divide and conquer concept [29]: Mod(w) = Mod(w/2) + 4M(w/2) + 1.5A(w) + 3S.. (12). Without loss of generality, we assume all of Mod(32), M(32), A(32) and S take one clock cycle. By the equations (10) and (11), we get M(1024). =. 3M(512) + 5A(1024) + 2S. =. 3M(512) + 162. =. 3[3M(256) + 5A(512) + 2S] + 162 25.

(34) =. 9M(256) + 408. =. 9[3M(128) + 5A(256) + 2S] + 408. =. 27M(128) + 786. =. 27[3M(64) + 5A(128) + 2S] + 786. =. 81M(64) + 1380. =. 81[3M(32) + 5A(64) + 2S] + 1380. =. 243M(32) + 2352. =. 2595.. By the equations (10), (11) and (12), we get Mod (1024) =. Mod(512) + 4M(512) + 1.5A(1024) + 3S. =. [Mod(256) + 4M(256) + 1.5A(512) + 3S] + 3295. =. [Mod(128) + 4M(128) + 1.5A(256) + 3S] + 4294. =. [Mod(64) + 4M(64) + 1.5A(128) + 3S] + 4577. =. [Mod(32) + 4M(32) + 1.5A(64) + 3S] + 4646. =. 4657. We use the recursion down to the 32-bit level, then M(128) = 9M(32) + 50A(32) + 8S, M(256) = 27M(32) + 190A(32) + 26S, M(512) = 81M(32) + 650 A(32) + 80 S, M(1024) = 243M(32) + 2110A(32) + 242S, Mod(128) = Mod(32) + 16M(32) + 49A(32) +14S, Mod(256) = Mod(32) + 52M(32) + 261A(32) +49S, Mod(512) = Mod(32) +160M(32) +1045A(32) + 156S, Mod (1024) = Mod (32) + 484M(32) + 3693A(32) + 479S. In order to ensure data security, the bit length of modulus should be 1024 at least. By Equation (9), the original decryption method can be repressed as 26.

(35) MODE(d, n) = 1.5 × 1024[M(1024) + 2 Mod(1024)+1]. = 3072Mod(32) + 1860096M(32) + 14585856A(32) + 1843200S + 1536. = 18293760 That is to say, the original decryption method should take 18293760 clock cycles. In the decryption method based on CRT, we assume that l(p) and l(q) are equal.. Thus the length of the exponent is about n/2.. The total. number of operations of the decryption method based on original CRT is equal to: 2MODE(d/2, n/2) + A(3d/2) + 4M(n/2) + 2Mod(n/2) + Mod(n), that is: MODE(d, n) = 2{1.5× 512[M(512) + 2 Mod(512) + 1]} + A(1536) + 4M(512) + 2Mod(512) + Mod(1024) = Mod(1024) + 1540M(512) + 3074Mod(512) + A(1536) + 1536 = 2[243M(32) + 2110A(32) + 242S] + Mod (32) + 484M(32) + 3693A(32) + 479S + 1540[81M(32) + 650 A(32) + 80S] + 3074[Mod(32) +160M(32) +1045A(32) + 156S] + 48A(32) + 1536 = 3075Mod(32) + 617550M(32) + 4221291A(32) + 603707S + 1536 = 5447159 By this case, the decryption method takes 5447159 clock cycles. In our proposed method, p - 1, p + 1, q - 1 and q + 1 can be factored 27.

(36) into at least three numbers. Without loss of generality, we assume that bit length of the largest prime factor is about l(n)/4 and others are about l(n)/8 [21, 22, 24, 25].. The total number of operations of our proposed. method is 4[2MODE(d/4, n/4) + A(3d/4) + 4M(n/4) + 2Mod(n/4) + Mod(n/2)] + 2[2A(n/2) + M(n/2) + Mod(n/2)] + 4A(n/2) + 2M(n/2) + Mod(n/2) MODE(d, n) = 4{2{1.5× 256[M(256) + 2 Mod(256) + 1]} + A(768) + 4M(256) + 2Mod(256) + Mod(512)} + 2[2A(512) + M(512) + Mod(512)] + 4A(512) + 2M(512) + Mod(512) = 8A(512) +4M(512) + 7Mod(512) + 3088M(256) + 6152Mod(256) + 4A(192) + 3072 =6159Mod(32) + 404724M(32) + 2202459A(32) + 383148S + 3072 =2995062 It takes 2995062 clock cycles. The original decryption method take 18293760 clock cycles. The decryption method based on CRT takes 5447159 clock cycles; however, our proposed method only takes 2995062 clock cycles. If we suppose the computational costs of the original decryption method is 100%, Compared with the original decryption method, the decryption method based on CRT takes 30% computational costs, but our proposed method takes only approximately 16%. The result will show in the table 2. The 28.

(37) speed of our proposed method is almost 1.8 times faster than the decryption method based on CRT only. Table 2 Comparison Among Three Types of Decryption Methods Clock Cycles. Computational Cost. Original Decryption Method. 18293760. 100%. Decryption Method Based on CRT. 5447159. 29.78%. New Decryption Method. 2995062. 16.37%. 29.

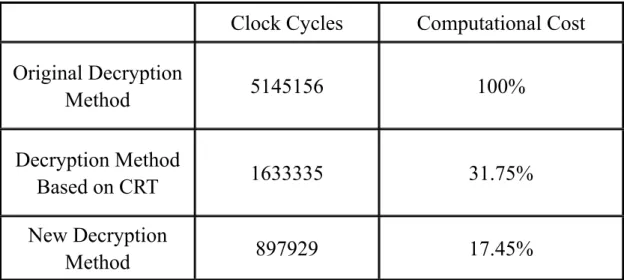
(38) Chapter 5 Implementation In order to evaluate the performance of our method, we examine these. methods. mentioned. above. based. on. Texas. Instruments. TMS320C55x family of signal processors. In table 3[34], we show the features of TMS320C55x. In addition, we assume the calculated CPU clock cycles of the realization of the RSA decryption with the following parameters as Table 4. The CPU clock cycles needed for processing the original RSA decryption method, decryption method based on the CRT, and our proposed method are given in Table 5, Table 6, and Table 7. The critical factor in influencing the speed of RAS decryption is the computation of modular multiplication. We apply the square and multiply algorithm to compute the modular exponentiation [27]. The square and multiply algorithm needs 3n/2 modular multiplications for an n-bit exponent. The original RSA decryption method needs modular multiplication only one time. The decryption method based on the CRT needs modular-multiplication two times. Because there is a difference in the length of d and n in modular multiplication, the clock cycles needed by the decryption method based on the CRT are less and the speed of this method is faster than the speed of the original decryption method. However, as our proposed method needs modular multiplication four times and the length of d and n is much shorter, the clock cycles needed are much less and the speed is much faster. As demonstrated in Table 6, due to the characteristics of chip TMS320C55x, the clock cycles needed by original decryption method is more than the clock cycles assessed in chapter four. Nevertheless, the 30.

(39) Table 3 The Features of TMS320C55x [32] High-Performance, Low-Power, Fixed-Point. – 6.25-/5-ns Instruction Cycle Time. TMS320C55x Digital Signal Processor (DSP). – 160-/200-MHz Clock Rate – One/Two Instructions Executed per Cycle – Dual Multipliers (Up to 400 Million Multiply-Accumulates Per Second (MMACS)) – Two Arithmetic/Logic Units – One Internal Program Bus – Three Internal Data/Operand Read Buses – Two Internal Data/Operand Write Buses. Instruction Cache. 24K Bytes. 160K x 16-Bit On-Chip RAM. – Eight Blocks of 4K × 16-Bit Dual-Access RAM (DARAM) (64K Bytes) – 32 Blocks of 4K × 16-Bit Single-Access RAM (SARAM)(256K Bytes). 16K × 16-Bit On-Chip ROM. 32K Bytes. 8M × 16-Bit Maximum Addressable External Memory Space 32-Bit External Memory Interface (EMIF). – Asynchronous Static RAM (SRAM) – Asynchronous EPROM – Synchronous DRAM (SDRAM) – Synchronous Burst SRAM (SBSRAM). On-Chip Peripherals. – Two 20-Bit Timers – Six-Channel Direct Memory Access(DMA) Controller – Three Multichannel Buffered Serial Ports (McBSPs) – 16-Bit Parallel Enhanced Host-Port Interface (EHPI) – Programmable Digital Phase-Locked Loop (DPLL) Clock Generator – Eight General-Purpose I/O (GPIO) Pinsand Dedicated General-Purpose Output (XF). On-Chip Scan-Based Emulation Logic IEEE Std 1149.1 (JTAG) Boundary ScanLogic 3.3-V I/O Supply Voltage 1.6-V Core Supply Voltage. 31.

(40) Table 4 Parameters of The RSA Decryption RSA modulus n. 2048bits. 1024bits. 512bits. RSA exponent length. 2048bits. 1024bits. 512bits. message length. 2048bits. 1024bits. 512bits. level-1 prime length. 1024bits. 512bits. 256bits. level-2 prime length. 512bits. 256bits. 128bits. Table 5 Numbers of CPU Clock Cycles for Realization RSA Decryption between Three Methods (Key Length = 2048 bits) Clock Cycles. Computational Cost. Original Decryption Method. 269083092. 100%. Decryption Method Based on CRT. 55491364. 20.62%. New Decryption Method. 30634747. 11.37%. Table 6 Numbers of CPU Clock Cycles for Realization RSA Decryption between Three Methods (Key Length = 1024 bits) Clock Cycles. Computational Cost. Original Decryption Method. 35635338. 100%. Decryption Method Based on CRT. 9985827. 28.02%. New Decryption Method. 5506659. 15.45%. 32.

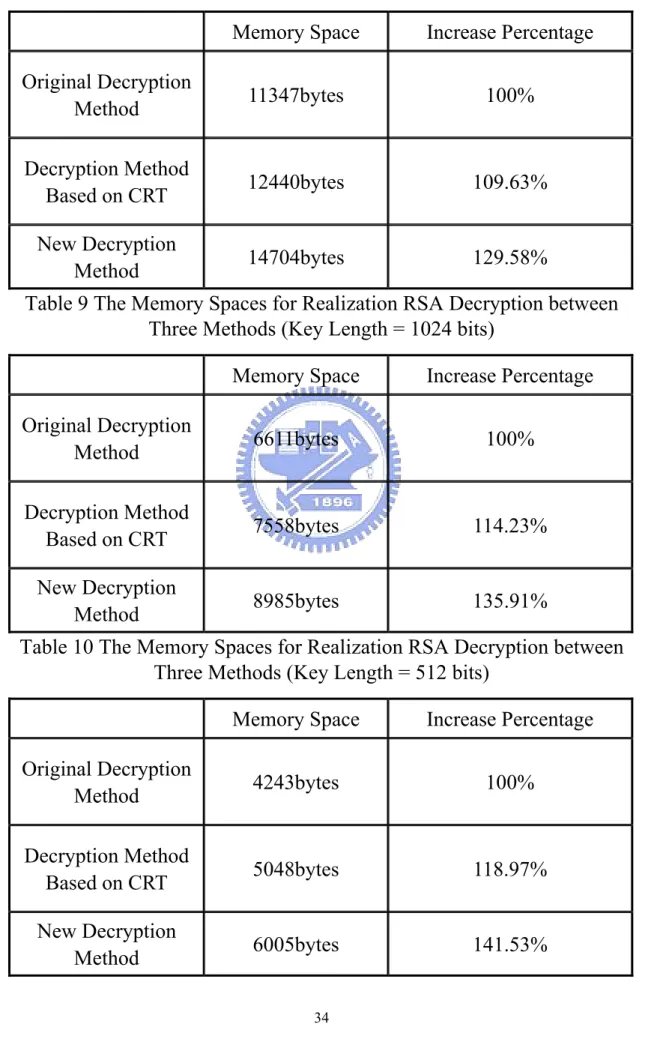
(41) Table 7 Numbers of CPU Clock Cycles for Realization RSA Decryption between Three Methods (Key Length = 512 bits) Clock Cycles. Computational Cost. Original Decryption Method. 5145156. 100%. Decryption Method Based on CRT. 1633335. 31.75%. New Decryption Method. 897929. 17.45%. computational cost needed by each kind of decryption method is almost the same with the computational cost that we assessed before. Comparing the results in Table 5, Table 6, and Table 7, we find that, with the increase of key length, the computational costs which can be saved by decryption method based on the CRT and by our new decryption method also increase. Let’s take another example. In table 7, when the key length is 2048bits, the decryption method based on the CRT only needs 20% of the computational cost of original decryption method. Furthermore, our new decryption method only needs 11% of the computational cost of original decryption method. The memory spaces needed for processing the original RSA decryption method, decryption method based on the CRT, and our proposed method are given in Table 8, Table 9, and Table 10. As demonstrated in Table 8, Table 9, and Table 10, our new decryption method and decryption method based on the CRT need more memory space respectively than original decryption method does. When key length is 1024bits, the memory space needed by decryption method based 33.

(42) Table 8 The Memory Spaces for Realization RSA Decryption between Three Methods (Key Length = 2048 bits) Memory Space. Increase Percentage. Original Decryption Method. 11347bytes. 100%. Decryption Method Based on CRT. 12440bytes. 109.63%. New Decryption Method. 14704bytes. 129.58%. Table 9 The Memory Spaces for Realization RSA Decryption between Three Methods (Key Length = 1024 bits) Memory Space. Increase Percentage. Original Decryption Method. 6611bytes. 100%. Decryption Method Based on CRT. 7558bytes. 114.23%. New Decryption Method. 8985bytes. 135.91%. Table 10 The Memory Spaces for Realization RSA Decryption between Three Methods (Key Length = 512 bits) Memory Space. Increase Percentage. Original Decryption Method. 4243bytes. 100%. Decryption Method Based on CRT. 5048bytes. 118.97%. New Decryption Method. 6005bytes. 141.53%. 34.

(43) on the CRT is 14% more than the memory space needed by the original decryption method. The memory space needed by our proposed method is 36% more than the memory space needed by the original decryption method. Comparing the results in Table 8, Table 9, and Table 10, we find that, with the increase of key length, the memory space increased by decryption method based on the CRT and by our new decryption method is lessening respectively. For example, in Table 8, when key length is 2048bits, the memory space of decryption method based on the CRT increases 10% and the memory space of our proposed method only increases 30%. As demonstrated by the results of implementation, when little amount of memory space is increased, the speed of RSA decryption operation can be greatly accelerated. Furthermore, when the key length is increased, the memory space needed to increase is reducing, but the speed of RSA decryption operation can be accelerated much significantly. Therefore, as it can be seen from the results of implementation, our new decryption method is more efficient than other two kinds of decryption method.. 35.

(44) Chapter 6 Conclusion In this thesis, we propose an efficient method to implement RSA decryption algorithm. This decryption method is not only based on CRT but also on the strong prime of RSA criterion. By our computational performance analysis, the 1024 bits RSA original decryption method without any tricks must require 18256896 clock cycles. The decryption method based on CRT takes 5447159 clock cycles. However, our proposed decryption method only takes 2995062 clock cycles. The complexity of our proposed method is only 16% of that of the original decryption method. Compared with decryption method based on CRT, our proposed method reduces approximately 45% computational costs. In a word, on the TMS320C55x family of signal processors, the speed of our proposed method is almost 1.8 times faster than the speed of the decryption method based on CRT. Our method can be applied not only decryption operation but also signing phase of digital signature. This efficient decryption method can enhance the performance of the RSA algorithm.. 36.

(45) REFERENCES [1] R.-J. Hwang, F.-F. Su, Y.-S. Yeh and C.-Y. Chen, ″An Efficient Decryption Method for RSA Cryptosystem″, Proc. The IEEE 19th International Conference on advanced Information Network and Applications, vol.1 pp.585-590, 2005. [2] R. Rivest, A. Shamir, and L. Adleman, ″A method for obtaining digital signature and public-key cryptosystems″, Commun. of ACM, vol.21, no.2, pp.120-126, 1978. [3] RSA Laboratories, PKCS#1: RSA Cryptography, Version 2.1, 2002 [4] A. Cilardo, A. Mazzeo, L. Romano, and G. P. Saggese, ″Exploring the design-space. for. FPGA-based. implementation. of. RSA″,. Microprocessors and Microsystems, vol.28, pp.183-191, 2004. [5] G. P. Saggese, L. Romano, N. Mazzocca and A. Mazzeo, ″A tamper resistant hardware accelerator for RSA cryptographic applications″, Journal of Systems Architecture, vol.50, pp.711-727, 2004. [6] N. Koblitz, A course in Number Theory and Cryptology, 2nd Edition, Graduate Text in Mathematics, vol.114, Springer, Berlin, Germany, 1994. [7] B. Schneier, Applied Cryptography: protocols, algorithms, and source code in C, 2nd ed, John Wiley & Sons, Inc., 1996. [8] Johann Groβschädl, ″The Chinese remainder theorem and its application in a high-speed RSA crypto chip″, Proc. 16th IEEE Annual Computer Security Applications Conference, pp.382-393, 2000. [9] J.-J. Quisquater, and C. Couvreur, ″Fast decipherment algorithm for RSA public-key cryptosystem″, Electronics Letters, vol.18, no.21, pp.905-907, 1982. 37.

(46) [10] M. Shand, and J. Vuillemin, ″Fast implementation of RSA cryptography″, Proc. 11th Symposium on Computer Arithmetic, pp.252-259, 1993. [11] D. W. Davies, W. L. Price, Security for Computer Network, 2nd Edition, , John Wiley & Sons, 1994. [12] A. Hayashi, ″A new fast modular multiplication method and its application. to. modular. exponentiation-based. cryptography″,. Electronics and Communications in Japan vol.83, no.12, pp.88-93, 2000. [13] W. Stallings, Cryptography and Network Security: principles and practices, 3nd ed, Prentice Hall International, Inc., 2002. [14] Jan C. A. van der Lubbe, Basic Methods of Cryptography, Cambridge University Press, 1999. [15] D. R. Stinson, Cryptography: Theory and Practice, 2nd ed, Chapman & Hall/CRC, 2002. [16] A. J. Menezes, P. C. van Oorschot, S. A. Vanstone, Handbook of Applied Cryptography, CRC Press LLC, 1997. [17] J. M. Pollard, ″Theories on Factorization and Testing Primality″, Proc. Cambridge Philosophical Society, vol.76 pp.521 - 528, 1974. [18] H. C. Williams, ″A p + 1 Method of Factoring″, Mathematics of Computation, vol.39 pp.225 - 234, 1982. [19] S.. Y.. Yan,. Number. Theory. for. Computing,. 2nd. Edition,. Springer-Verlag Berlin Heidelberg, 2002. [20] P. Kocher, ″Timing Attacks on Implementation of Diffie-Hellman, RSA, DSS, and Other System.″, Proc. Crypto ‘96, pp.104-113,1996. [21] M. J. Ganley, ″Note on the generation of P0 for RSA keysets″, Electronics Letters, vol.26, no.6, pp.369, 1990. [22] M. Ogiwara, ″A Method for Generating Cryptographically Strong 38.

(47) Primes″, IEICE Trans. Fundamentals, E73, vol.6, pp.985-994, 1990. [23] R. D. Diaz, and J. M. Masque, ″Optimal strong primes″, Information Processing Letters, vol.93, pp.47-52, 2005. [24] C.-S. Lai, W.-C. Yang, and C.-H. Chen, ″Efficient method for generating strong primes with constraint of bit length″, Electronics Letters, vol.27, no.20, pp.1807-1808, 1991. [25] J. Gordon, ″Strong RSA keys″, Electronics Letters, vol.20, no.12, pp.514-516, 1984 [26] L. Batina, S. B. Örs, B. Preneel, and J. Vandewalle, ″Hardware architectures for public key cryptography, Integration″, VLSI Journal, vol. 34, pp.1-64, 2003. [27] D. E. Knuth, Seminumerical Algorithms, Volume 2 of The Art of Computer Programming, 3rd edition, Addison-Wesley, Reading, MA, USA, 1997. [28] Davida GI, Wells DL, and Kam JB, ″A database encryption system with subkeys″, ACM Trans. Database Systems, vol.6, pp.312-328, 1981. [29] M.-S. Hwang, ″Dynamic participation in a secure conference scheme for mobile communications″, IEEE Trans. Vehicular Technology, vol.48, no.5, pp.1469-1474, 1999. [30] G. Dorðević, T. Unkašević, and M. Markocić, ″Optimization of modular reduction procedure in RSA algorithm implementation on assembler of TMS320C54x signal processors″, Proc. of the IEEE 14th International Conference on Digital Signal Processing, pp.811-814, 2002. [31] ANSI Standard X9.31, Digital Signatures Using Reversible Public Key Cryptography for the Financial Services Industry (rDSA), 1998. [32] C-H Wu, J-H Hong, and C-W Wu, ″RSA Cryptosystem Design 39.

(48) Based on the Chinese Remainder Theorem″, Proc. of the 2001 conference on Asia South Pacific design automation, pp.391- 395, 2001. [33] RSA Laboratories, ″RSAREF: A Cryptographic Toolkit,″ Version 2.0, 1994, avail-able via FTP from rsa.com. [34] Texas Instruments, TMS320VC5510 Fixed-Point Digital Signal Processor Data Manual, Literature Number: SPRS076D, June 2000.. 40.

(49)