Yu-Ju Lu, Tingxian Xie, Jing-Wen Fang, Hua-Chieh Shao, and Jim J. Lin
Citation: The Journal of Chemical Physics 128, 184302 (2008); doi: 10.1063/1.2913517 View online: http://dx.doi.org/10.1063/1.2913517
View Table of Contents: http://scitation.aip.org/content/aip/journal/jcp/128/18?ver=pdfcov Published by the AIP Publishing
Articles you may be interested in
Infrared laser spectroscopy of C H 3 H F in helium nanodroplets: The exit-channel complex of the F + C H 4 reaction
J. Chem. Phys. 124, 084301 (2006); 10.1063/1.2168450
Mode-correlated product pairs in the F + CHD 3 DF + CHD 2 reaction J. Chem. Phys. 119, 8289 (2003); 10.1063/1.1611877
Insights into dynamics of the F + CD 4 reaction via product pair correlation J. Chem. Phys. 119, 4997 (2003); 10.1063/1.1592153
Time delay as a tool to identify the signatures of reactive resonance: F + HD and F + H 2 reactions J. Chem. Phys. 119, 1462 (2003); 10.1063/1.1582172
F + D 2 reaction at ultracold temperatures
J. Chem. Phys. 116, 9222 (2002); 10.1063/1.1472515
Dynamics of the F
2reaction with the simplest
-bonding molecule
Yu-Ju Lu,1Tingxian Xie,1,2Jing-Wen Fang,1,3Hua-Chieh Shao,1and Jim J. Lin1,4,a兲1
Institute of Atomic and Molecular Sciences, Academia Sinica, Taipei 10617, Taiwan 2
Department of Physics, Dalian Jiaotong University, Dalian, Liaoning 116028, People’s Republic of China 3
Department of Chemistry, National Taiwan University, Taipei 10617, Taiwan 4
Department of Applied Chemistry, National Chiao Tung University, Hsinchu 30010, Taiwan
共Received 25 February 2008; accepted 2 April 2008; published online 8 May 2008兲
The reaction of F2+ C2H4has been investigated with crossed molecular beam experiments and high level ab initio calculations. For a wide range of collision energies up to 11 kcal/mol, only one reaction channel could be observed in the gas phase. The primary products of this channel were identified as F + CH2CH2F. The experimental reaction threshold of collision energy was determined
to be 5.5⫾0.5 kcal/mol. The product angular distribution was found to be strongly backward, indicating that the reaction time scale is substantially shorter than rotation. The calculated transition state structure suggests an early barrier; such dynamics is consistent with the small product kinetic energy release measured in the experiment. All experimental results consistently support a rebound reaction mechanism, which is suggested by the calculation of the intrinsic reaction coordinate. This work provides a clear and unambiguous description of the reaction dynamics, which may help to answer the question why the same reaction produces totally different products in the condensed phase. © 2008 American Institute of Physics.关DOI:10.1063/1.2913517兴
I. INTRODUCTION
Regarding the fluorination in organic chemistry,1 F2
+ C2H4 reaction is an important benchmark as it is the
sim-plest reaction of F2 with-bonding systems. If this simple
reaction can be understood, the mechanism may be extended to larger systems. Due to the small number of participating atoms, it should be feasible to study this reaction with high level ab initio calculations to reach a precision of the so-called chemical accuracy. Definitive experimental results of this reaction are also extremely desirable as to provide a test of the theories. Although there have been quite a number of experimental2–11and theoretical12–19investigations on the action of fluorine with ethylene, the reaction mechanism re-mains unclear. For convenience of discussion, we list three most likely primary product channels together with the calculated20reaction enthalpies:
F2+ C2H4
→ C2H4F + F, ⌬H0 K0 = − 7.8 kcal/mol 共R1兲,
→C2H3F + HF, ⌬H0 K0 = − 100.4 kcal/mol 共R2兲,
→C2H4F2, ⌬H0 K0 = − 118.5 kcal/mol 共R3兲.
R1 has been observed in the gas phase.2–4The released F atom can initiate a series of exothermic chain reactions, which may lead to explosion. Kapralova et al.2reported the temperature dependence for R1 and showed the rate constant of reaction共1兲 can be expressed as follows:
kl= 8.0⫻ 10−14exp共− Ea/RT兲 cm3molecule-1s−1, and
Ea= 4.6 kcal/mol.
Farrar and Lee5studied the decomposition of chemically activated C2H4F from F + C2H4reaction in a crossed
molecu-lar beam setup. They employed a pyrolysis method to gen-erate the F atom source from a F2gas mixture. The reactive
signal of R1 was observed as a by-product from the reaction of C2H4with the residue F2in their beam source.
For the F2+ C2H4reaction in the condensed phase,
inves-tigations using the matrix isolation technique have provided some important results. Hauge et al.6studied the reactions of F2with a series of small hydrocarbons in F2or Ar matrices at
15 K. They concluded that propylene, butadiene, and cyclo-hexene reacted spontaneously with F2 even at this low
tem-perature; ethylene and allene reacted with F2 when the
ma-trix was exposed to infrared light in the wavelength range from 1 to 4m. For ethylene, the observed products were 1,2-difluoroethane共R3兲, vinyl fluoride and HF 共R2兲. Neither the small alkane nor alkyne reacted, even exposed to the infrared light for a long time. Their results suggest that the activation energies of the F2 reactions with these hydrocar-bons may be in the order of propylene⬇butadiene ⬇cyclohexene⬍ethylene⬇allene⬍alkyne, alkane.
Frei and co-workers7–10 investigated the infrared photo-induced reaction of F2· C2H4complex in N2or Ar matrices at
12 K. They excited various vibrational levels of C2H4in the
complex and monitored the reaction with Fourier-transform infrared absorption spectroscopy. Products of both R2 and R3 have been observed. The lowest excitation frequency which leads to the product formation is 1896 cm−1
共5.4 kcal/mol兲, indicating a reaction threshold. For
vibra-a兲Electronic mail: jimlin@gate.sinica.edu.tw.
THE JOURNAL OF CHEMICAL PHYSICS 128, 184302共2008兲
0021-9606/2008/128共18兲/184302/10/$23.00 128, 184302-1 © 2008 American Institute of Physics This article is copyrighted as indicated in the article. Reuse of AIP content is subject to the terms at: http://scitation.aip.org/termsconditions. Downloaded to IP:
tional transitions between 1896 and 4209 cm−1, deviations
from a smooth rise of the quantum yield with energy have been attributed, in part, to mode selectivity. Similar HF/DF branching ratios close to 1.1 were found for the reactions of F2 with three different isomers of C2H2D2. Based on this
observation, the contribution of an abstraction reaction of F + C2H2D2F to the HF共DF兲 formation was ruled out because
at such a low temperature, the author expected significant isotope effect for the F atom attacking back on the CH or CD bond.9They concluded7–10that the F2+ C2H4 reaction under
the cryogenic matrix-isolation conditions involves a vibra-tionally hot 1,2-difluoroethane intermediate, followed by a decomposition via either R2 or R3; the product branching ratio originates in a competition between the HF共DF兲 elimi-nation and the thermal stabilization of the vibrational excited intermediate. The later process can be enhanced by two or-ders of magnitude with the addition of a second C2H4in the
matrix cage. It is less conclusive, however, for how the 1,2-difluoroethane intermediate is formed. Two possibilities have been mentioned:共i兲 a one-step four-center addition of F2 to
the CvC-bond and共ii兲 a rapid sequential process within the same matrix cage, F2+ C2H4→C2H4F + F→C2H4F2.
Grover et al.11studied the reaction of F2with benzene in
a crossed molecular beam experiment and determined the energy threshold of generating C6H6F + F products to be
13.9⫾0.5 kcal/mol. The angular distribution of the C6H6F
product was observed to be slightly backward with respect to the F2 beam direction. Theelectron system of benzene is
more stable than that of C2H4 due to the resonance effect.
Thus, a larger threshold for F2+ C6H6 reaction may be expected.
When reliable ab initio calculations were lacking, Raff12 reported a semiempirical potential energy surface共PES兲 with the central structure being 1,2-difluoroethane, in which the barrier height of R3 was set to be 12.3 kcal/mol for the concerted, planar, four-center addition of F2 across the
eth-ylene double bond. A series of dynamic studies13–15 have been performed on this PES for reactions in the gas phase and matrix-isolation conditions. Although this empirical PES yielded equilibrium geometries, reaction enthalpies, and fun-damental vibrational frequencies in fair-to-good accord with experimental values, there was no reliable input for the prop-erties of the transition states at that time.12 Therefore, the results should be used with caution.
There have been some earlier ab initio investigations on F2+ C2H4 reaction but the employed calculation levels are
probably not high enough to describe the reaction. Yamabe et al.16 proposed a four-center transition state for a concerted ␣-addition using the Hartree–Fock and third-order Møller– Plesset calculations with 3-21G basis sets. The reported bar-rier is about 51 kcal/mol, which is even higher than the bond dissociation energy of F2共D0= 37 kcal/mol兲. Iwaoka et al.17
suggested a nonconcerted mechanism with the MP2/6-31 + G calculation, in which one CuF bond is formed first at the transition state structure. The calculated reaction barrier is 23 kcal/mol.
Recently, Wang et al.18 investigated the mechanism for the addition of F2 to C2H4 using density functional theory
共DFT兲 with large basis sets. They proposed a two-step
diradi-cal mechanism: the first step is low-barrier attack of F2 on
C2H4 to produce a diradical intermediate of
FuFuCH2uCH2 structure; the second step is the
com-plete dissociation of the FuF bond, producing F + CH2FuCH2 共R1兲. For the first step, the obtained barrier
height differs with the used functional; 1.8 kcal/mol using B3LYP and 6.3 kcal/mol with BHH 共half-and-half func-tional兲. Qi et al.19
studied this reaction with calculations of direct dynamics based on DFT and plane-wave basis sets. The authors found all three channels 共R1, R2, and R3兲 in their simulations.
The abovementioned experimental and theoretical re-sults in literature give rise to an immediate question as to why this reaction leads to totally different products in the gas phase than in the matrices which simulate a condensed phase surrounding. The chosen matrices consisted of N2 or Ar,
which should be inert enough in order to neglect chemical effects induced by the matrix itself. However, sterical caging effect in the condensed phase may be an important factor. Another arising question is: are the present theoretical calcu-lations able to account for all the experimental observations? With this contribution, we would like to answer the above questions with crossed molecular beam experiments and high level ab initio calculations.
In our crossed molecular beam experiments, R1 was ob-served to be the only product channel for a wide range of collision energy up to 11 kcal/mol. The translational energy and angular distributions of the corresponding products were recorded. The collision energy threshold for the reaction was determined. In addition, possible reaction paths have been searched with high level ab initio calculations. Among the three possible primary channels, only a reaction path corre-sponding to R1 could be found under modest energy range. Energetics of R1 was determined using the CCSD共T兲 calcu-lation extrapolated to the complete basis set limit 共CBSL兲. The results obtained from various ab initio methods were compared and discussed. Combining the experimental and computational results, an unambiguous mechanism is given in this paper.
II. METHODS A. Experimental
The experimental setup was similar to our previous works.21,22Therefore, only the essential parts of this experi-ment are given here. The F2molecular beam was generated
by expanding 5% F2/He mixture or neat F2 gas 共Spectra
Gases, Inc.兲 through a fast pulsed valve23共Even-Lavie valve, high repetition rate model,艋1000 Hz兲. The nozzle tempera-ture was controlled to be at room temperatempera-ture or a cryogenic temperature共⬃150 K兲 to generate different beam velocities. The mean speed of the neat F2 beam was 700 m/s from the
room temperature nozzle and 535 m/s from the cryogenic nozzle. The expansion of the seeded 5% F2/He gas through
the room temperature nozzle leads to a mean velocity of 1530 m/s.
The C2H4gas共Linde, ⬎99.99%兲 was seeded in He with
two different concentrations of 4% and 10%. The gas mix-tures were expanded through a similar pulsed valve to form This article is copyrighted as indicated in the article. Reuse of AIP content is subject to the terms at: http://scitation.aip.org/termsconditions. Downloaded to IP:
the molecular beams. To increase the beam speed, the respec-tive nozzle is heatable. The C2H4 beam speed was tuned between 1500 and 1860 m/s by varying the seeding ratio and nozzle temperature. Both molecular beams were colli-mated by sharp-edge skimmers共Beam Dynamics, Inc.兲 to an angular divergence of about⫾1.3° 关full width at half maxi-mum共FWHM兲兴.
Both molecular beams passed through further collima-tors cooled by a helium refrigerator and collided with each other under 90°. Following the reaction, the neutral products traveled a fixed distance to an ionizer. After ionization, the charged products were selected by a quadrupole mass filter and entered a Daly detector coupled with a multichannel sca-lar共MCS兲 共EG&G ORTEC兲 to do ion counting. The time-of-flight共TOF兲 spectra accumulated by the MCS were recorded and transferred into the product velocity distributions. The laboratory共LAB兲 frame angular distribution was obtained by integrating the TOF data for each given LAB angle. Scatter-ing experiments of Ar+ C2H4and F2+ N2were performed to
confirm that the observed signals in the F2+ C2H4 crossed
beam experiments were not affected by the impurities in the F2and C2H4samples.
To transform the data taken at the LAB frame to the center-of-mass共CM兲 frame, a forward convolution program was applied to simulate all TOF spectra and angular distri-bution. We input the experimental parameters共spreads of the beam velocities and flight distance, etc.兲 and iteratively ad-justed the CM-frame translational energy distribution P共ET兲 and angular distribution P共CM兲 until a best fit was obtained.
The Jacobian factor of the LAB-CM transformation has been included in the program.
The experimental studies were performed using two dif-ferent apparatuses. The majority of the results presented here were obtained with the apparatus equipped with an electron-impact ionizer in the detector.24For measuring photoioniza-tion efficiency spectra, a second crossed molecular beam apparatus25 coupled with the synchrotron radiation facility26 was employed. The product flight distance is 10.1 cm in the synchrotron apparatus and 24.2 cm in the electron-impact apparatus. For a better velocity resolution, the TOF analysis was based on the electron-impact results.
For determination of the relative reaction cross section as a function of collision energy, the C2H4 and F2 beam
intensities need to be known. The C2H4 beam intensity was measured using a fast ionization gauge 共Beam Dynamics, Inc.兲 operated at a reduced electron-impact energy 共⬃23 eV兲 at which the He buffer gas produced no signal while C2H4 can still be efficiently ionized. The F2beam intensity could
be deduced from the attenuation measurements, in which the C2H4 beam was slightly attenuated共⬍9%兲 by collisions of
the F2beam.
B. Ab initio calculation
In this work, the complete active space self-consistent field共CASSCF兲 calculation with the second-order multiref-erence perturbation theory 共CASPT2兲 corrections27–29 was used to explore the PES. It has been found that the CASPT2 calculation is computational efficient to predict not only the
geometries of stable species but also transient structures along the reaction path.30 We believe that it is important to use a multireference method to check the calculation of a reactive PES, especially when breaking/formation of a chemical bond is involved.
All calculations have been performed without setting the molecular symmetry, i.e., using the C1 point group. This
al-lows us to avoid unnecessary bias in choosing active orbitals. All employed active spaces have been carefully chosen and tested. The geometry optimization and zero point energy 共ZPE兲 calculations were obtained mainly using the CASPT2 methods. Dunning basis sets31,32 共cc-pVNZ and aug-cc-pVNZ, N = T, Q, 5兲 were employed. The barrier height and reaction enthalpy were obtained using single-point CCSD共T兲 calculations33,34
based on the respective CASPT2 optimized geometries. The CCSD共T兲 energy was extrapolated to CBSL using the following scheme:22 the Hartree–Fock energy was extrapolated with an exponential function, exp共−␥1N兲; the CCSD共T兲 correlation energy was
extrapolated with a function35 of ␥2N−3. Whenever the
QCISD共T兲 analytical gradients36
were available, the QCISD共T兲 approach was used to double-check the geometry optimization. All calculations were performed with the MOL-PRO 2006.1quantum chemistry package.37
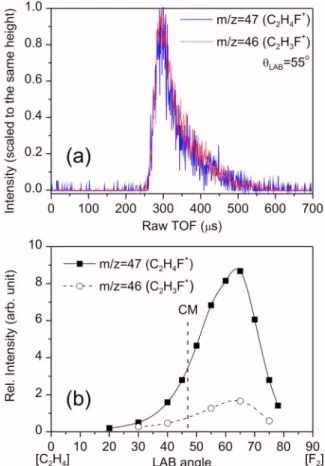
FIG. 1. 共Color online兲 共a兲 A comparison of typical TOF spectra at m/z = 47 and 46. The data were recorded with the electron-impact ionizer at 70 eV;共b兲 LAB-frame angular distributions of the reactive signals at m/z = 47 and 46. The experimental data are connected with a spline fit for visu-alization. The corresponding : LAB angle of the center of mass is shown as a vertical dashed line. The data were recorded with the photoionization detector at 11 eV photon energy. The collision energy is 11.4 kcal/mol in both cases.
184302-3 Dynamics of F2reaction with C2H4 J. Chem. Phys. 128, 184302共2008兲
III. RESULTS
A. Crossed beam experiments
The first goal of this study is to identify the primary product channel共s兲 among the three possible ones: R1, R2, and R3. In the crossed molecular beam reaction of F2
+ C2H4, we have searched for signals with the
mass-to-charge ratios m/z=47, 46, and 66, which correspond to the parent masses of the possible products, C2H4F共R1兲, C2H3F 共R2兲, and C2H4F2共R3兲, respectively. In the experiments,
sig-nals of reactive scattering could be observed at m/z=47 and 46. The existence of R1 can be verified with the observation of the m/z=47 signal. On the other hand, there are two likely contributions to the m/z=46 signal. One is from the C2H3F
products of R2; the other is from dissociative ionization of the C2H4F共R1兲 product. For the latter case, the signal of the
daughter ion usually has the same arrival time and angular distribution as its parent ion. A comparison of representative TOF spectra and LAB-frame angular distribution at m/z = 47 and 46 is shown in Fig.1. The identical shapes of TOF spectra and angular distributions strongly suggest that both masses are from the same neutral product C2H4F. The
reac-tion energetics provide further evidence to discriminate R2. From the enthalpy of the reactions, it is obvious that the
available energy of R2 products is much larger than that of R1 products. The translational energy release for producing two closed-shell molecules like HF + C2H3F is usually large
because the PES should be very repulsive in the exit valley. Therefore, the recoil velocity of the C2H3F product of R2 should be much larger than that of the C2H4F product of R1. The noise at earlier arrival times in the experimental TOF spectra is quite low, thus we can be sure that there is no faster product observed at m/z=46. Hence, the observed m/z=46 signal should stem from the dissociative ionization of the C2H4F product. Regarding the possibility of R3, its
product angular distribution in the LAB frame will be very narrow because the recoil velocity is zero. Such hypothetical signal has not been observed in the crossed beam experi-ments. Again, energetically, the R3 product is unlikely to be observed in the gas phase because its exothermicity is larger than the energy required to break a chemical bond or to eliminate a HF molecule.
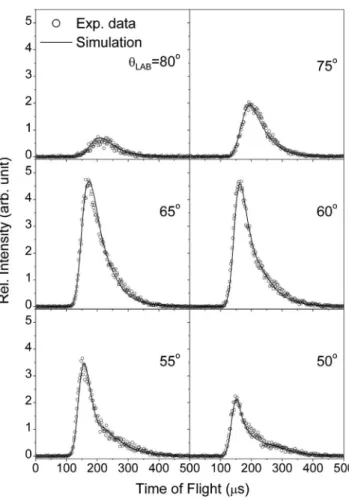
Figure 2 shows the experimental TOF spectra of the C2H4F product from the F2+ C2H4crossed beam reaction at
11.0 kcal/mol collision energy. The ion of m/z=46, which is a daughter ion of the C2H4F product, was chosen because of
its higher signal-to-noise ratio. Figures 1 and 2 show the product distributions in the LAB frame. In order to compre-hend the underlying reaction dynamics, the experimental TOF data and angular distribution were transformed to the CM frame using the forward convolution method described in Sec. II A. The best-fit results in the CM frame are plotted in Fig. 3共a兲. Initially, one single P共ET兲 distribution was as-sumed to describe the entire dataset. However, the product scattered in the backward direction was consistently slower than at other CM angles. Therefore, a slower P共ET兲 for the backward direction共CM= 180°兲 and a faster P共ET兲 for CM angles between 0° and 110° were used, connected by a lin-early interpolated P共ET兲 distribution for the region between 110° and 180°. The resulting best fit for a collision energy of FIG. 2. TOF spectra of the C2H4F products from the F2+ C2H4crossed
beam reaction at 11.0 kcal/mol collision energy. The data were recorded at
m/z=46 共C2H3F+兲, which is a daughter ion of C2H4F. The molecular beam
speeds used in the experiment were 1530 m/s for F2 and 1840 m/s for
C2H4; the corresponding LAB angle of the center of mass is about 48°.
Here, the 0° in the LAB frame is defined as the C2H4beam direction; the F2
beam direction is at 90°.
FIG. 3. CM-frame translational energy distribution P共ET兲 and angular
dis-tribution P共CM兲 used to simulate the R1 experimental data. 共a兲 The colli-sion energy is 11.0 kcal/mol. Slightly different P共ET兲 distributions were
used for different CM angles; for CM angles in between 110° and 180°, an interpolated P共ET兲 was used. 共b兲 The collision energy is 6.6 kcal/mol.
6.6 kcal/mol is shown in Fig.3共b兲. At this collision energy, we used only one P共ET兲 distribution to fit all of the TOF spectra recorded.
Figure4shows a comparison between the experimental and simulated LAB-frame angular distributions of the C2H4F
product at 11.0 and 6.6 kcal/mol collision energies. Figure4
clearly shows a highly asymmetric product angular distribu-tion with a pronounced bias toward the LAB angles larger than that of the CM. Checking the LAB-frame angular dis-tributions at several collision energies in the range of 5.3 to 11 kcal/mol always gave a similar trend. It is obvious from Figs. 3 and4 that the CM-frame angular distributions are peaking preferentially in the backward direction.
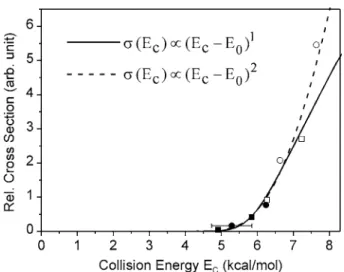
No reactive signal could be found at collision energies smaller than 5.0 kcal/mol, while significant signals have been observed at higher collision energies. This threshold behavior is consistent with the previous gas-phase kinetic study2 and matrix-isolation infrared-excitation investi-gations.7–10 To determine the reaction threshold, the excita-tion funcexcita-tion of R1, i.e., the relative reacexcita-tion cross secexcita-tion as a function of collision energy was measured. The result is shown in Fig. 5, which was determined by the following procedure:共i兲 the LAB-frame angular distribution was mea-sured at every selected collision energy;共ii兲 the peak height of the angular distribution was normalized with respect to both F2 and C2H4 beam intensities. Then, the normalized
peak height was plotted as a function of collision energy to give the data points in Fig. 5. This approach neglects the Jacobian factor of the LAB-CM transformation. However, we found that this factor varies very little within the collision
energy range in Fig.5. The resulting error of not including the Jacobian factor is less than 5%, thereby smaller than other experimental uncertainties. A more significant influ-ence is the width of the collision energy. From the measured spreads of the molecular beam speeds, the width of the col-lision energy can be deduced. It is indicated as a horizontal error bar in Fig.5. The experimental excitation function was fitted with two simple forms, a linear form 共Ec兲⬀共Ec − E0兲1or a quadratic form共Ec兲⬀共Ec− E0兲2, for the collision
energy Ec higher than the threshold energy E0. Both
func-tions have been convoluted with the derived collision energy spread. The E0obtained are 5.8⫾0.2 and 5.3⫾0.3 kcal/mol
for the linear and quadratic functions, respectively. Account-ing for both results, we suggest the collision energy threshold for R1 to be 5.5⫾0.5 kcal/mol.
To vary the molecular beam speed, we could heat the C2H4 nozzle to 413 K or cool the F2 nozzle to 150 K. In
order to check the influence of the nozzle temperature and the resulting change in vibrational distributions of the reac-tants, the experiment was designed to have conditions of different nozzle temperatures distributed in a narrow range of collision energy. In Fig. 5, the nozzle temperature combina-tions are indicated with different symbols as open/closed symbols for heated/RT C2H4 nozzle and square/circle sym-bols for cryo/RT F2 nozzle 共heated=413 K; RT=300 K; cryo= 150 K兲. From these data, we cannot find any signifi-cant correlation with the nozzle temperature; all data points fall into a smooth line with deviations smaller than experi-mental uncertainties. This result indicates either the vibra-tional excitation in our molecular beams is negligible or its effect is too small to be observed.
B. Calculations
To further investigate the reaction mechanism of R1, the transition state was searched with the CASPT2 and QCISD共T兲 methods. For all CASPT2 results presented here, FIG. 4. The experimental and simulated LAB-frame angular distributions of
R1 product signals with their schematic Newton diagrams. 共a兲 Ec
= 11.0 kcal/mol; C2H4, 1840 m/s at 0°; F2, 1530 m/s at 90°. 共b兲 Ec
= 6.6 kcal/mol; C2H4, 1720 m/s at 0°; F2, 700 m/s at 90°. In both panels,
the corresponding LAB angle of the center of mass is shown as a vertical dashed line. The Newton circles represent the corresponding recoil veloci-ties of the C2H4F product.
FIG. 5. The relative reaction cross section of R1 as a function of collision energy. Two functions convoluted with the collision energy spread are shown as the solid and dashed lines. The horizontal error bar indicates the width共FWHM兲 of the collision energy spread. Different symbols of the data points indicate the nozzle temperature used in the experiments: open/closed symbols for heated/RT C2H4nozzle; square/circle symbols for cryo/RT F2
nozzle共heated=413 K; RT=300 K; cryo=150 K兲.
184302-5 Dynamics of F2reaction with C2H4 J. Chem. Phys. 128, 184302共2008兲
the active spaces have been carefully chosen to ensure that there is no orbital switching along the reaction paths and that the chemically important molecular orbitals such as the /*orbitals of C2H4 and/*orbitals of F2 are included
in the active spaces. Although we did not constrain the sym-metry in the calculation共C1point group was used in all input
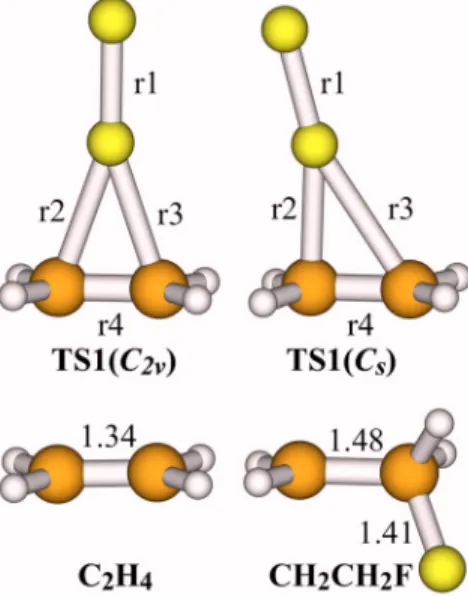
files兲, two kinds of transition state 共TS1兲 geometries were found for R1. The point groups of the two TS1 structures can be assigned as C2v and Cs. The optimized geometries are shown in Fig. 6. Both C2v and Cs structures of TS1 have been verified as a first-order saddle point on the PES. The vibrational frequency analysis for both structures shows that there is one imaginary frequency, of which the normal-mode displacement vector corresponds to the motions of the FuF bond dissociation and CuF bond formation.
Both C2vand Csgeometries of TS1 can be located using CASPT2 calculations with different initial guess geometries. We have checked a few active spaces from 关共4e,4o兲 关four
active electrons distributed in four active orbitals兴 to 共6e,8o兲. Selected results with important geometry param-eters are listed in TableI. It can be seen in Table Ithat the active spaces have only little effect on the transition state geometry. For example, TS1a and TS1b are almost the same, and so are TS1c and TS1d. The QCISD共T兲 calculation pre-dicts a Cs transition state共TS1 g兲 with a slightly longer r1 and slightly shorter r2, r3.
To check the effect of the augmented basis sets on the geometry calculation, a CASPT2共6e,6o兲 calculation was per-formed to locate the transition state with the basis sets: H = cc-pVDZ; C, F = aug-cc-pVTZ. The resulting geometry TS1e is very similar to TS1d with the largest difference in bond length to be only 0.04 Å. In addition, TS1f was ob-tained with larger basis sets on H. The resultant geometry is again very similar to TS1e. These results indicate that the type and size of the basis sets used have only minor effects on the TS1 geometry.
To clarify these C2v and Cs structures of TS1, we per-formed single-point CCSD共T兲 calculations with the same ba-sis sets. The results共see Table I兲 indicate practically no
en-ergy difference for these structures at the CCSD共T兲 level, independent of being of C2v or Cs symmetry. We have also checked the single-point CCSD共T兲 energy for a few interpo-lated geometries between the C2v and Cs structures. A smooth path connecting these two structures without any bar-rier could be obtained. These results indicate the PES is very flat in the region between the C2vand Csstructures of TS1. It is important to mention that the product valley of R1 has to be a lower symmetry than C2v. For the C2v transition state, symmetry lowering is inevitable for product formation. We believe that the actual path of R1 may go though anyone of the C2v and Cs transition state structures or any geometry between/near them. With the above argument of symmetry lowering, we have chosen the Cs structure of TS1 for the following discussions.
From TS1e, an intrinsic reaction coordinate共IRC兲 which connects TS1e to both reactant valley and product valley was obtained with a CASPT2 calculation关active space: 共6e,6o兲; basis sets: H = cc-pVDZ; C, F = aug-cc-pVTZ兴. At each struc-ture on the IRC, single-point energy calculations were per-FIG. 6. 共Color online兲 Optimized geometries of C2H4, CH2CH2F and the
C2vand Csstructures of the transition state共TS1兲. The C2H4geometry was
calculated with QCISD共T兲 using the basis sets: H=cc-pVDZ; C, F = aug-cc-pVTZ. The CH2CH2F geometry was calculated with CCSD共T兲
us-ing the same basis sets. See TableIfor details of TS1 structures. Unit: Å.
TABLE I. Comparison among TS1 geometries obtained with selected methods. Method of the geometry optimization: TS1a and TS1d: CAS-PT2共6e,6o兲/cc-pVDZ 共H兲, cc-pVTZ 共C,F兲 with different initial guess ge-ometries; TS1b: CAS-PT2共6e,8o兲/pVDZ 共H兲, pVTZ 共C,F兲; TS1c: CAS-PT2共4e,4o兲/pVDZ 共H兲, cc-pVTZ共C,F兲; TS1e: CAS-PT2共6e,6o兲/cc-pVDZ 共H兲, aug-cc-pVTZ 共C,F兲; and TS1f: CAS-PT2共6e,6o兲/cc-pVTZ 共H兲, aug-cc-pVTZ 共C,F兲; TS1g: QCISD共T兲/cc-pVDZ 共H兲, cc-pVTZ 共C,F兲. Symmetry Eb+277.74 r1 r2 r3 r4 ⬔FFC TS1a C2v −0.0034 1.650a 2.078 1.355 161.0 TS1b −0.0033 1.654 2.075 1.357 160.8 TS1c Cs −0.0021 1.627 1.946 2.365 1.358 164.0 TS1d −0.0021 1.628 1.947 2.356 1.358 163.8 TS1e −0.0026 1.624 1.962 2.315 1.360 163.4 TS1f −0.0029 1.620 1.985 2.325 1.357 163.2 TS1g −0.0028 1.700 1.850 2.252 1.372 158.5
aUnit: Å and deg.
bSingle-point energy calculated with CCSD共T兲/cc-pVTZ 共C,H兲; aug-cc-pVTZ 共F兲. Unit: hartree. 1 hartree
= 627.5096 kcal/mol.
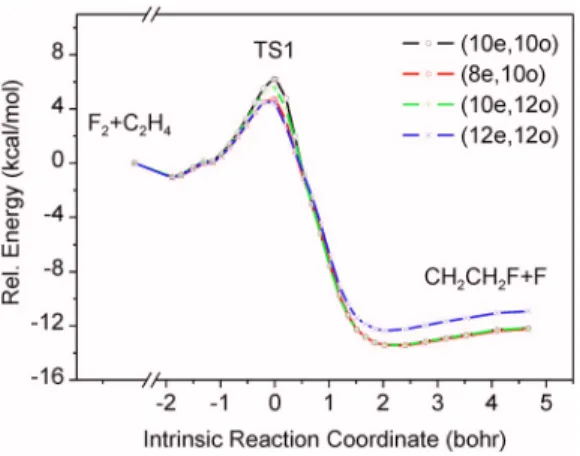
formed with larger active spaces up to共12e,12o兲. The results are shown in Fig.7. All relative energy curves in Fig.7have a similar shape but the barrier heights are slightly different. The lowest barrier height 共ZPE not included兲 is about 4.6 kcal/mol for the CASPT2 calculations using 共8e,10o兲 and共12e,12o兲 active spaces. The higher values are 5.6 and 6.2 kcal/mol for 共10e,12o兲 and 共10e,10o兲 active spaces, re-spectively.
With the results shown in Figs.6and7, the reaction path of R1 can be described as a simple rebound type, in which one fluorine atom transfer is the major atomic motion along the reaction coordinate. A single barrier, separates the prod-ucts from the reactants. It can be anticipated that the flux of the reaction is controlled by the TS1 barrier, acting as a kinetic bottleneck. To overcome this barrier, the favorable orientation of the approaching F2 is roughly normal to the
C2H4molecular plane. The structure of the C2H4subsystem
varies little from the reactant valley to TS1, with a slightly elongated CuC bond distance for TS1. The analysis of the CASSCF molecular orbitals suggests the coupling of the *orbitals of C2H4with the/*orbitals of F2 to be the
most important interaction for the TS1 structure. On the IRC, there are van der Waals wells in both entrance and exit val-leys. The well depths are about 1 kcal/mol, which is in the range of typical van der Waals interactions. The reaction is exothermic, i.e., the newly formed CuF bond is stronger than the FuF bond of F2.
Figure 8 shows the effect of the basis sets on the TS1 barrier height共ZPE not included兲 at the CCSD共T兲 level. Five families of basis sets were tested. As can be seen in Fig.8, the use of the augmented basis sets on fluorine has the most significant effect. For TS1, partial charge transfer to the F atoms was observed in the calculation. In this situation, the augmented basis sets are required to adequately describe the diffuse character of the atoms with 共partially兲 negative charge. The quality of the basis sets is less crucial for the rest of atoms, especially for the H atoms as the CH bonding character varies only slightly along the IRC. In order to per-form more efficient computation, relatively smaller basis sets were selected for the H atoms. If an extrapolation scheme is performed on the size of the basis sets for C and F atoms, the
calculated potential energy barriers converge to about 6.8 kcal/mol 共without ZPE correction兲 at all basis set selec-tions.
The results of the ZPE calculations and CCSD共T兲 ener-gies are summarized in Table II. The ZPE-corrected CBSL barrier height for TS1 is 7.8 kcal/mol or 7.1 kcal/mol using the individual CASPT2 or the QCISD共T兲 frequencies 共not scaled兲, respectively. The lower value of 7.1 kcal/mol is still 1.6 kcal/mol higher than the experimental threshold of 5.5⫾0.5 kcal/mol. This discrepancy seems significant and may locate on the borderline of the statistical CCSD共T兲 accuracy.38,39 A possible source of error to account for this discrepancy lies in the ZPE calculation. The structure of the C2H4 subsystem of TS1 is quite similar to that of the
reac-tant, suggesting the ZPE correction should be small. It is possible that the ZPE of TS1 is overestimated especially for the CASPT2 calculation, and/or that the harmonic approxi-mation is not very good for TS1. As for the CCSD共T兲 energy, CCSD共T兲 is a single-reference based calculation, which may be less reliable if the electronic wave function of the studied system is of significant multireference character. For exam-ining this issue, we have checked the value of the T1
diag-nostic of the CCSD共T兲 calculation. It has been recommended40,41 that if T1 is larger than 0.02, the results from single-reference electron correlation methods limited to single- and double-excitations should be viewed with cau-tion, i.e., the CCSD calculation may be less reliable.42 For the studied structures, T1 is about 0.017 for TS1; 0.013 and 0.011 for F2 and C2H4, respectively. The T1 values are all small, suggesting that the single-reference methods such as CCSD, CCSD共T兲, and MP2 may be applicable. Nevertheless, although the discrepancy between the calculated and experi-mental reaction threshold seems significant, it is still in the reasonable range of statistical errors of CCSD共T兲 calcula-tions. Other corrections, e.g., for core/valence and scalar relativistic effects and higher order correlation may improve the energy calculation at higher computational expense.39 Moreover, for transitions states, the error estimation of an ab initio calculation is not well established yet.
Figure9shows the result of a two-state CASSCF calcu-FIG. 7. 共Color online兲 CASPT2 energy curves with various active spaces.
The geometry points were obtained from the intrinsic reaction coordinate 共IRC兲 calculation of TS1e with CASPT2共6e,6o兲/cc-pVDZ 共H兲; aug-cc-pVTZ共C,F兲.
FIG. 8.共Color online兲 Basis set effects on the potential energy difference of TS1 to reactants. Single-point calculations were performed with CCSD共T兲 using various family of Dunning basis sets, noted as vNz= cc-pVNZ; avNz= aug-cc-pVNZ. TS1f geometry was used for TS1. CBSL= Complete basis set limit.
184302-7 Dynamics of F2reaction with C2H4 J. Chem. Phys. 128, 184302共2008兲
lation along the same IRC in Fig. 7. Although the energy calculation at the CASSCF level is not very accurate, Fig.9
provides qualitative potential energy curves of the ground state and the first excited state. The energy gap between these two electronic states is quite large at the reactant valley and becomes smaller for the product side. It is expected that there are degenerate electronic states at the product valley which consists of two radicals, F + CH2CH2F. The energy gap at the TS1 geometry is about 2.8 eV, suggesting a multireference calculation may not be necessary for TS1.
C. H-atom migration and photoionization efficiency spectrum
With the synchrotron facility, the photoionization effi-ciency 共PIE兲 spectrum of the C2H4F product was measured
at 9 kcal/mol collision energy. The corresponding ionization threshold was determined to be 8.9 eV from the abrupt rise of the PIE curve. Additionally, the PIE spectrum of C2H4
was also measured and the ionization threshold determined is in good accord with the literature value of 10.5 eV.43
How-ever, it is less straight forward to compare the experimental photoionization threshold of C2H4F to the result from a
con-ventional ab initio calculation. We found that the ionic form of CH2CH2F is not a stable structure on the PES, which can
isomerize to a more stable structure of CH3CHF+ without
any barrier.44,45 The experimental PIE signal usually corre-sponds to a photoionization process with a good Franck– Condon factor. A simple model of harmonic oscillators is not applicable in this case because the considered structure is very far from the equilibrium geometry. A fair description of the Franck–Condon factor and the interpretation of the PIE spectrum therefore require further theoretical investigation. On the neutral PES both isomers CH2CH2F and CH3CHF
are stable structures separated by a high barrier共see Fig.10
for details兲. In our experimental conditions, the internal en-ergy of the CH2CH2F product should be less than
20 kcal/mol, which is not enough for this H-atom migration process.
TABLE II. CCSD共T兲 results and zero-point energies for the reaction path of R1. Basis sets共NH, NC, NF兲b
CASPT2 QCISD共T兲 Expt. 共2,3,3兲 共3,3,3兲 共3,4,4兲 共3,5,5兲 CBSLc
Energy共hartree兲 ZPE共hartree兲d
F2 −199.3136 −199.3136 −199.3657 −199.3839 −199.3995 0.0021 0.0021 0.0021
C2H4 −78.4206 −78.4387 −78.4574 −78.4643 −78.4699 0.0506 0.0504 0.0492
CH2CH2F −178.1208 −178.1390 −178.1839 −178.1999 −178.2135 0.0534
F −99.6278 −99.6278 −99.6529 −99.6616 −99.6690
TSla −277.7248 −277.7429 −277.8129 −277.8375 −277.8585 0.0543 0.0530 Relative energy共kcal/mol兲e ⌬ZPE 共kcal/mol兲
TS1 barrier 6.15 6.24 6.66 6.95 7.08 1.02 0.29
⌬H0 K0 −8.42 −8.55 −8.12 −7.95 −7.81 0.48 aCalculated at the TS1f geometry.
bNotation for the basis sets: H = cc-pVN
HZ; C = cc-pVNCZ; F = aug-cc-pVNFZ;
cCBSL= complete basis set limit. The Hartree–Fock energies were extrapolated with a function of exp共−␥
1N兲. The CCSD共T兲 correlation energies were
extrapolated with a function of␥2N−3.
dZPE= vibrational zero-point energy, which is calculated using the basis sets: H = cc-pVDZ; C = cc-pVTZ; F = aug-cc-pVTZ. The active spaces used for the
CASPT2 calculations are共6e,6o兲 for singlet species, and 共5e,5o兲 for doublet species. Experimental data are from Ref.43.
e⌬ZPE
QCISD共T兲is included in TS1 barrier;⌬ZPECASPT2is used in⌬H0 K0 .
FIG. 9. 共Color online兲 Two-state CASSCF potential energy curves calcu-lated with共10e,10o兲 active space. The geometries used are the same as those on the IRC shown in Fig.7.
FIG. 10. 共Color online兲 Potential energy curve on the intrinsic reaction coordinate共IRC兲 for the H-atom migration from the CH2CH2F product to
CH3CHF. Calculation method: CASPT2共5e,5o兲/aug-cc-pVTZ.
IV. DISCUSSION
The average kinetic energy release共ET兲 can be obtained from the product translational energy distribution P共ET兲. The total available energy Eavlfor the R1 products is given by the
sum of the collision energy and the reaction exothermicity of 7.8 kcal/mol. The fraction of the excess energy released as translation共fT=具ET典/Eavl兲 was determined to be fT= 0.27 and fT= 0.29 for the collision energies of 6.6 and 11 kcal/mol, respectively. This means that more than 70% of the available energy is deposited into the product’s internal degrees of freedom. In this reaction, the structure of TS1 was found to be more similar to the reactants than to the products. Thus, according to Polanyi’s rule,46,47 TS1 can be classified as an early barrier and the available energy is likely to excite the vibrational motion of the products. Polanyi’s rule also sug-gests that a translational excitation of the reactants is more efficient in promoting the reaction than vibrational excita-tions. Although Polanyi’s rule was initially proposed for a triatomic A + BC reaction, it seems applicable to the F2
+ C2H4reaction because that the reaction path of R1 is very
similar to a simple atom transfer reaction and the C2H4 sub-system is spectatorlike along the reaction path from the re-actant valley to TS1. In addition, the equilibrium structure of the CH2CH2F product is quite different from the TS1 struc-ture, also suggesting vibrational excitation of the products induced by the structure change in the exit valley.
The experimental angular distribution is highly asym-metric, indicating the reaction time scale is much shorter than the rotational period of the collision complex. This ob-servation can clearly rule out the contribution of any long lifetime reaction intermediate such as 1,2-difluoroethane. The strongly backward distribution may be explained by a rebound mechanism.47 For R1, head-on-like collisions with small impact parameters are more efficient to overcome the potential energy barrier; such collisions can lead to sharply backward products if the FuFu共C2H4兲 interaction lies on
a linear line—an ideal rebound condition. The calculated TS1 geometry and energetics are in good agreement with this picture. Practically, there would be reasonable ranges for the impact parameters and cone of acceptance, resulting in the width of the product angular distribution. In brief summary, these results strongly indicate the following:
共i兲 the reaction time scale is much shorter than the com-plex rotation period;
共ii兲 collisions at small impact parameters dominate in the reactive events; and
共iii兲 the interaction between the three subunits, F, F, and 共C2H4兲, is approximately linear.
Our reaction threshold of R1 is slightly higher than the reported activation energy of 4.6 kcal/mol obtained from a kinetic study in the temperature range of 300 to 430 K.2 Un-der these comparably hot conditions, however, a thermal ex-citation of the F2vibration is possible to promote the reaction
leading to the observed lower threshold. The fundamental vibrational frequency of F2is 894 cm−1, corresponding to an
energy gap of 2.55 kcal/mol. From the Boltzmann distribu-tion, the ratio of F2共v=1兲/F2共v=0兲 can be estimated to be
5.0% at 430 K and 1.4% at 300 K. The increase in F2共v
= 1兲 population is quite significant when the temperature is raised above room temperature. It is very likely that the F2共v=1兲+C2H4 reaction has a significant lower threshold than the F2共v=0兲+C2H4 reaction. Therefore, the amount of thermal excitation of the reactants may have significant con-tribution to the empirical activation energy.
Wang et al.18studied the reaction with DFT calculations and proposed a diradical intermediate, which can be formed through a low barrier. The corresponding transition state has C2v symmetry and its geometry 共r1=1.794 Å; r2, r3 = 1.975 Å; and r4 = 1.330 Å兲 is quite similar to our TS1a and TS1b. However, in the crossed beam experiments, we have observed highly asymmetric product angular distribution, in-dicating the reaction time scale is substantially shorter than rotation. This finding does not support the mechanism of a stable intermediate. The stability of the diradical may be too small to have a significant effect. In Fig.7, a van der Waals well can be seen in the product valley but the well depth is quite shallow in comparison with the DFT results18 of 5.6 kcal/mol 共B3LYP兲 or 4.0 kcal/mol 共BHH兲. We believe that the multireference CASPT2 calculation should provide a better description than the DFT calculations for the exit val-ley which has significant diradical character. On the other hand, from the product valley, it is quite feasible to form the structure of 1,2-difluoroethane if the ejected F atom is let to attack back to the radical site 共the unpaired electron on the carbon atom兲 of the CH2CH2F. In the gas phase, there is
essentially very little probability for this process but it should be quite likely in the condensed phase. Cage effect in high density environments, such as a cryogenic matrix, effectively hinders the escape of the F atom. The F + CH2CH2F reaction is a typical process of radical-radical recombination which is usually barrierless. Therefore, R3 product may be formed through this sequential process following R1. The initially produced 1,2-difluoroethane is highly vibrationally excited. It can decompose to HF + CH2CHF or be stabilized through
efficient energy transfer in the condensed phase. In this study, a detailed computational search for a direct reaction path related to either concerted addition共R3兲 or HF forma-tion 共R2兲 led to no results. Combining these theoretical ef-forts with the experimental observation that only R1 is ob-served in the gas phase, we strongly suggest that R2 and R3 observed in the condensed phase are most likely due to the cage effect and fast sequential reactions following R1.
V. SUMMARY
The F2+ C2H4 reaction has been investigated with
crossed molecular beam experiments and high level ab initio calculations in detail. R1 has been found to be the only pri-mary product channel in the gas phase. The experimental reaction threshold has been determined to be 5.5⫾0.5 kcal/mol. The translational energy and angular dis-tributions of R1 products have been recorded. The strongly backward angular distribution indicates a typical rebound re-action mechanism discriminating mechanisms involving a stable intermediate. The calculated transition state of R1 can be classified as an earlier barrier, which is consistent with the 184302-9 Dynamics of F2reaction with C2H4 J. Chem. Phys. 128, 184302共2008兲
small fraction of product translational energy release 共fT ⬵0.28兲 observed in the experiments. The reaction path of R1 has been calculated while other concerted-addition paths could not be found. The previous condensed-phase results can be explained by secondary reactions following R1 due to the cage effect.
Our ongoing research includes F2 reactions with other
unsaturated hydrocarbons such as C3H6, C4H8, and C2H2.
Preliminary results show that the barriers for the F2reactions
with C3H6 and C4H8 are significantly lower than that of F2
+ C2H4 reaction, while the F2+ C2H2 reaction has a much
higher barrier. A direct formation of HF could not been ob-served in either of these reactions.
ACKNOWLEDGMENTS
National Science Council 共Grant No. NSC95-2113-M-001-041-MY3兲 and Academia Sinica, Taiwan supported this work. We thank Professor Yuan T. Lee and Dr. Jens Riedel for valuable comments and National Synchrotron Radiation Research Center, Taiwan for the use of facilities.
1For example, see R. D. Chambers, Fluorine in Organic Chemistry
共Blackwell, Oxford, 2004兲; M. Sawaguchi, S. Hara, and N. Yoneda, J. Fluorine Chem. 105, 313共2000兲; S. Rozen, Acc. Chem. Res. 21, 307 共1988兲; S. T. Purrington, B. S. Kagen, and T. B. Patrick,Chem. Rev. 共Washington, D.C.兲86, 997共1986兲; R. F. Merritt, J. Am. Chem. Soc. 89,
609共1967兲.
2G. A. Kapralova, A. M. Chaikin, and A. E. Shilov, Kinet. Katal. 8, 421
共1967兲.
3Z. K. Gyul’bekyan, O. M. Sarkisov, and V. I. Vedeneev, Kinet. Katal. 15,
993共1974兲.
4V. L. Orkin and A. M. Chaikin, Kinet. Katal. 23, 438共1982兲. 5J. M. Farrar and Y. T. Lee,J. Chem. Phys. 65, 1414共1976兲.
6R. H. Hauge, S. Gransden, J. L.-F. Wang, and J. L. Margrave,J. Am.
Chem. Soc. 101, 6950共1979兲.
7H. Frei, L. Fredin, and G. C. Pimentel,J. Chem. Phys. 74, 397共1981兲. 8H. Frei and G. C. Pimentel,J. Chem. Phys. 78, 3698共1983兲. 9H. Frei,J. Chem. Phys. 79, 748共1983兲.
10H. Frei and G. C. Pimentel,Annu. Rev. Phys. Chem. 36, 491共1985兲. 11J. R. Grover, Y. Wen, Y. T. Lee, and K. Shobatake,J. Chem. Phys. 89,
938共1988兲.
12L. M. Raff,J. Phys. Chem. 91, 3266共1987兲. 13L. M. Raff,J. Phys. Chem. 92, 141共1988兲. 14L. M. Raff,J. Chem. Phys. 93, 3160共1990兲. 15L. M. Raff,J. Chem. Phys. 95, 8901共1991兲.
16S. Yamabe, T. Minato, and S. Inagaki, J. Chem. Soc., Chem. Commun.,
532共1988兲.
17T. Iwaoka, C. Kaneko, A. Shigihara, and H. Ichikawa,J. Phys. Org.
Chem. 6, 195共1993兲.
18B.-W. Wang, L. Chan, S. P. Chan, Z.-D. Chen, and Z.-F. Liu,J. Chem.
Phys. 120, 9467共2004兲.
19Y. Qi, K.-L. Han, and A. J. C. Varandas, Chin. J. Chem. Phys. 20, 109
共2006兲.
20The electronic energy U is calculated with the CCSD共T兲 method at the
complete basis set limit for R1共see TableII兲 and at the basis sets: H = cc-pVTZ; C = cc-pVQZ; F = aug-cc-pVQZ for R2 and R3. The vibra-tional zero-point energy is calculated with the CASPT2 methods. ⌬H0 K0 =⌬U+⌬ZPE. See TableIIfor details.
21Y.-J. Lu, L. Lee, J.-W. Pan, H. A. Witek, and J. J. Lin,J. Chem. Phys. 127, 101101共2007兲.
22Y.-J. Lu, L. Lee, J.-W. Pan, T. Xie, H. A. Witek, and J. J. Lin,J. Chem.
Phys. 128, 104317共2008兲.
23U. Even, J. Jortner, D. Noy, and N. Lavie,J. Chem. Phys. 112, 8068
共2000兲.
24J. J. Lin, D. W. Hwang, S. Harich, Y. T. Lee, and X. Yang,Rev. Sci.
Instrum. 69, 1642共1998兲.
25J. J. Lin, Y. Chen, Y. Y. Lee, Y. T. Lee, and X. Yang,Chem. Phys. Lett. 361, 374共2002兲.
26See: http://140.110.203.42/bldoc/21AU9WL.htm or www.nsrrc.org.tw. 27H.-J. Werner,Mol. Phys. 89, 645共1996兲.
28P. Celani and H.-J. Werner,J. Chem. Phys. 112, 5546共2000兲. 29P. Celani and H.-J. Werner,J. Chem. Phys. 119, 5044共2003兲. 30L. B. Harding, S. J. Klippenstein, and A. W. Jasper,Phys. Chem. Chem.
Phys. 9, 4055共2007兲.
31T. H. Dunning, Jr.,J. Chem. Phys. 90, 1007共1989兲.
32R. A. Kendall, T. H. Dunning, Jr., and R. J. Harrison,J. Chem. Phys. 96,
6796共1992兲.
33M. J. O. Deegan and P. J. Knowles,Chem. Phys. Lett. 227, 321共1994兲. 34P. J. Knowles, C. Hampel, and H.-J. Werner,J. Chem. Phys. 99, 5219
共1993兲; J. Chem. Phys. 112, 3106共E兲 共2000兲.
35T. Helgaker, W. Klopper, H. Koch, and J. Noga,J. Chem. Phys. 106,
9639共1997兲.
36G. Rauhut and H.-J. Werner,Phys. Chem. Chem. Phys. 3, 4853共2001兲. 37H.-J. Werner, P. J. Knowles, R. Lindh et al.,
MOLPRO, Version 2006.1, a package of ab initio programs共see http://www.molpro.net兲.
38T. Helgaker, T. A. Ruden, P. Jørgensen, J. Olsen, and W. Klopper, J.
Phys. Org. Chem. 17, 913共2004兲.
39D. Feller and K. A. Peterson,J. Chem. Phys. 126, 114105共2007兲. 40T. J. Lee and G. E. Scuseria, in Quantum Mechanical Electronic
Struc-ture Calculations with Chemical Accuracy, edited by S. R. Langhoff
共Kluwer, Dordrecht, 1995兲, pp. 47–108.
41T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., Symp. 23, 199共1989兲. 42For CCSD共T兲, T
1slightly larger than 0.02 may be acceptable, but there is
no recommended critical value of T1 for CCSD共T兲 calculations in the literature.
43See: http://webbook.nist.gov/cgi/cbook.cgi?ID⫽C74851&Units⫽SI&
Mask⫽20#Ion-Energetics.
44Calculated with B3LYP, MP2, QCISD, and CASPT2 methods using
cc-pVTZ basis sets.
45Experimental adiabatic ionization energy of CH
3CHF is 7.93 eV; See:
http://webbook.nist.gov/cgi/cbook.cgi?ID⫽C52067193&;Units ⫽SI&Mask⫽20#Ion-Energetics.
46J. C. Polanyi,Acc. Chem. Res. 5, 161共1972兲.
47R. D. Levine, R. B. Bernstein, Reaction Dynamics and Chemical Reac-tivity共Oxford University Press, Oxford, 1987兲.