以微積分的方法證明
任意三角形外角和為
360∘
連威翔
適 園 有 限 公 司
壹、前言
在 數 學 傳 播 27 卷 4 期 的 《 以微 積 分 的 方法 求 四 邊 形面 積 公 式 》一 文 當 中 ,作 者 透 過
微 積 分 的 手 法 , 重 新 證 明 了 可 表 示 出 四 邊 形 面 積 的 Bretschneider 公 式 , 其證 明 過 程 請參
考[1]。 根 據 作 者 在 [1]中 所 言 , 其 證 明 的 想 法 是 來 自 微 積 分 基 本 定 理 , 而 作 者 計 算 微 分 時
所 用 的 參 數 , 是 四 邊 形 的 其 中 一 個 角 度 。
或 許 是 受 到[1]文 的 影 響 , 筆 者 也 找 出 了 一 種 透 過 微 積 分 手 法 來 證 明 任 意 三 角 形 的 外
角 和 為360°(從而可知任意三角形的內角和為180°)。不過,與[1]文不同的地方是,筆者將
引 入 坐 標 與 向 量 來 進 行 證 明,且 計 算 微 分 時 所 用 的 參 數 是 長 度。底 下 第 二 節 中,筆 者 將 會
介 紹 自 己 的 證 明 過 程 。
貳、筆者的證明
對 於 任 意 的 三 角 形,我 們 先 以 逆 時 針 方 向 沿 著 三 角 形 邊 界 繞 一 圈,繞 圈 的 同 時 也 為 三
角 形 的 三 個 頂 點 命 名 為
, ,
。為 三 點 命 名 後 的 結 果,下 圖 的 兩 個 三 角 形,顯 示 出 其 中 兩
種 可 能 :
圖 1
我 們 以 上 圖 中 左 邊 的
Δ
為 例 , 設
∠
, 。 接 著 , 我 們 以 為 原 點 、 射 線
的 方 向 為 軸 正 向 , 在
Δ
所 在 的 平 面 建 立 坐 標 系 , 則 如 下 圖 :
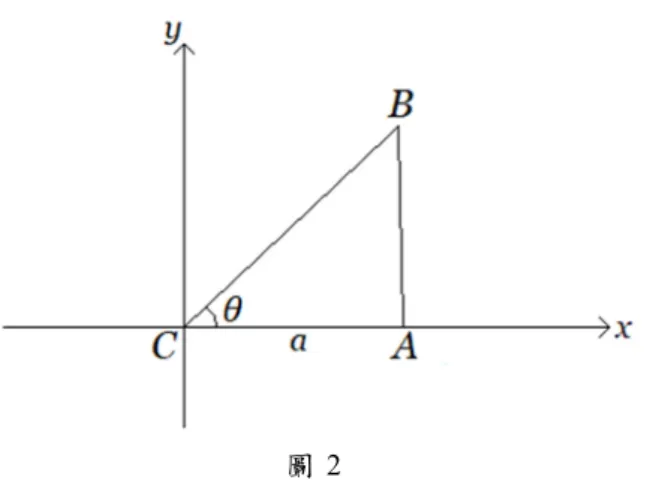
圖 2
注 意 點 將 在 軸 上 方。為 了 研 究 上 圖 中
Δ
的 外 角,我 們 在 上 圖 中 畫 出 射 線 ,並 在 該
射 線 上 取 一 動 點 。 接 著 , 連 接 另 一 個 射 線 後 , 則 如 下 圖 :
圖 3
上 圖 中 , 我 們 也 假 設 了
Δ
的 三 個 外 角 為
, ,
。
在 圖 3 中,筆 者想 證 明 無 論動 點 的 位 置為 何,都 將滿 足Δ 之 外 角 和 為360°,即證
明 圖3 中 有
2 … 1
的 結 果。證 明 1 式之後,只要取動點 的位置為圖 3 中的 點,這樣就證明了Δ 的 外 角
和 為360°,從而也證出Δ 的 內 角 和 為180°。
所 以,接 下 來 準 備 介 紹 的 證 明 中,最 重 要 的 第 一 步 將 放 在 如 何 證 明 1 式。筆者的證明
如 下 :
證 明 : 圖 3 中 ,假 設 , 則 點 坐 標 可 表 為
cos , sin
因 為 有 , 0 ,可知
cos , sin
cos ,
sin
, 0
圖 3 中 ,
∙
兩 向 量 的 夾 角 , 我 們 可 透 過 內 積 的 定 義 計 算cos 之值如下:
cos
∙
cos
√
2 cos
… 2
至 於cos 的計算,同理也有
cos
∙
cos
√
2 cos
… 3
因 為0 , 可 知sin 非負,因此利用(2)式計算後可得
sin
1
cos
sin
√
2 cos
… 4
接 著 , 因 為0 , 可 知sin 為正,因此利用(3)式計算後可得
sin
1
cos
sin
√
2 cos
… 5
為 了 底 下 計 算 的 方 便 , 我 們 先 分 別 利 用 2 , 3 兩式求出
cos
sin
2 cos
… 6
cos
sin
2 cos
… 7
此 時 , 若 將 2 式的等號左端的cos 對 微分,利用微分連鎖規則可得
cos
cos
∙
sin ∙
因 此 有
1
sin
∙
cos
… 8
將 4 , 6 兩式代入上式,可知
sin
2 cos
… 9
另 一 方 面,仿 照 8 式的求法,將 3 式的等號左端的cos 對 微分,利用連鎖規則處理後再
移 項 得
1
sin
∙
cos
… 10
將 5 , 7 兩式代入上式,可知
sin
2 cos
… 11
至 此 , 將 9 , 11 兩式相加,可得
0
因 此 可 知 圖3 中 的 之值 與 的長 度 無 關 ,即 與 的 位 置無 關 。 可 假設
… 12
其 中 為 與 無 關 的 待 定 常 數 。
圖 3 中 , 取 0時, , 兩點重合,此時由圖 3 可知有
將 上 述 , 之值代入 12 式後,可得
2
而 在 將 上 式 中 的 移 項 之 後 , 即 得
2
至 此 我 們 就 證 得 1 式,即圖 3 中無論 的位置為何,Δ 的 外 角 和 恆 為360°。
最 後 , 若 取 動 點 為 圖 3 中 的 點的 位 置 ,即 可 證 明 了圖 3 中Δ 的 外 角 和 為360°,
也 因 此 可 推 論 出Δ 的 內 角 和 為180°
參、證明之後的反思
在 一 個 證 明 之 中,通 常 會 在 某 些 假 設 之 下 進 行 一 些 推 論。在 第 二 節 的 證 明 中,讀 者 是
否 有 看 出 筆 者 用 上 了 哪 些 重 要 的 假 設 呢 ?
在 數 學 傳 播 27 卷 2 期 的 《 三角 形 內 角 和等 於180°與畢氏定理》一文當中,作者在畢
氏 定 理 成 立 的 條 件 下 , 證 明 了 任 意 三 角 形 內 角 和 等 於180°,其證明過程請參考[2]。
然 而 在 本 文 第 二 節 的 最 後,我 們 也 證 明 了 任 意 三 角 形 內 角 和 等 於180°。請注意本文第
二 節 中 , 當 我 們 計 算 4 , 5 兩式時,用上了三角恆等式
cos
sin
1 … 13
其 中 是 廣 義 角 , 因 為0 。 關 於 廣 義 角 三 角 函 數 的 定 義 , 請 參 考 下 圖 :
圖 4
其 中 設 。 透 過 上 圖 , 我 們 可 定 義 底 下 的 廣 義 角 正 、 餘 弦 函 數 值 :
cos
,
sin
圖 4 中,設 在 軸上 且 。在 畢 氏 定 理 成 立 的 條 件 下,將 有 ,
又 因 為
| |,
| |
, 因 此 可 知
上 式 同 除 後 , 即 得 13 式。因此, 13 式是在畢氏定理成立之下才有的結果。
至 此,若 回 顧 第 二 節 的 證 明 過 程,可 發 現 當 我 們 以 廣 義 角 三 角 函 數 中 的 恆 等 式 13 算
出 4 , 5 兩式的結果時,其實就已經悄悄假設畢氏定理成立。因此,就「假設畢氏定理成
立 」這 點 而 言,本 文 第 二 節 的 證 明 與[2]文的 證 明 是一 樣 的,即 使 兩 個 證 明看 起 來 是 如此 不
同 。
肆、結語
從 參 考 資 料[1]的 有 趣 內 容 , 到 本 文 第 二 節 所 介 紹 的 探 討 過 程 , 我 們 可 發 現 高 等 數 學
的 基 礎 科 目 之 一 的 微 積 分,也 有 著 許 多 的 初 等 應 用。仍 在 高 中 階 段 就 讀 的 同 學 們,若 能 好
好 學 習 微 積 分 , 相 信 對 於 日 後 的 應 用 也 會 有 許 多 助 益 。
最 後,要 藉 此 機 會 謝 謝 台 大 數 學 系 王 藹 農 退 休 教 授 與 莊 武 諺 教 授 熱 心 提 供 意 見 供 筆 者
參 考 。
參考資料
張 海 潮
(2003): 以微 積 分 的 方法 求 四 邊 形面 積 公 式 。數 學 傳 播 季 刊 , 27(4),59-63。
張 海 潮、王 彩 蓮(2003):三 角形 內 角 和 等於
180°與畢氏定理。數 學傳播季刊,27(2),44-46。