9 Springer-Verlag 1996 Printed in Austria
A Parallel Algorithm for Solving Special Tridiagonal
Systems on Ring Networks
K.-L. Chung, W.-M. Yan and J.-G. Wu,
Taipei
Received September 26, 1994; revised October 9, 1995Abstract-- Zusammenfassung
A Parallel Algorithm for Solving Special Tridiagonal Systems on Ring Networks. The solution of special linear, circulant-tridiagonal systems is considered. In this paper, a fast parallel algorithm for solving the special tridiagonal systems, which includes the skew-symmetric and tridiagonal-Toeplitz systems, is presented. Employing the diagonally dominant property, our parallel solver does need only local communications between adjacent processors on a ring network. An error analysis is also given. On the nCUBE/2E multiprocessors, some experimental results demonstrate the good performance of our stable parallel solver.
AMS Subject Classifications: 65F05, 15A23
Key words: nCUBE/2E multiprocessors, matrix perturbation, parallel algorithm, performance, ring network, tridiagonal Toeplitz linear systems.
Ein parelleler Algorithmus zur Liisung spezieller Tridiagonalsysteme auf Ring-Netzwerken. Wir betrachten die I.Ssung einer Klasse yon speziellen tridiagonalen Gleichungssystemen, die sehiefsymmetrische und TSplitz-Systeme einschlieBt, trod geben einen schnellen, parallelen, Algorithmus dafiir an. Bei Vorliegen von Diagonal-Dominanz ben6tigt unser paralleler Solver nur Kommtmikation zwischen benachbarten Prozessoren auf einem Ring-Netzwerk. Eine Fehleranalyse wird angegeben. Einige experimentelle Resultate, die auf einem nCUBE/2E Ger~it gewonnen wurden, zeigen das gute Verhalten unseres stabilen, parallelen Solvers.
1. Introduction
Throughout this paper, matrices are represented by uppercase letters, vectors by bold lowercase letters, and scalars by plain lowercase letters. The superscripts T correspond to the transpose operation. Consider an n • n linear system
Anx=y,
(1)
/
/31 3" /32)
c~ /3 3' A n = o~ /3 3'/3~
o, /3~ n•
where
386 K.-L. Chung et al.
and 1/31> [a + y 1. Solving this special linear system arises in many applications, e.g., numerical methods for differential equations [10], [9], [16], [15]. When setting /31 = / 3 / u ( u = 1 or 2),/3~ = / 3 / v ( v = 1 or 2), a = 3', and /32 = /32 = PY( P
= 0 or 1, if p = 1 then it implies u = v = 1), Boisvert [1] gave a survey to describe many fast serial algorithms for solving this class of special tridiagonal systems. These algorithms are Gaussian elimination [5], cyclic reduction [10], special LU factorization [16], [11], reversed triangular factorization [6], [7], [8], [1], and Toeplitz factorization with Sherman-Morrison formula [9]. Recently, Yah and Chung [17] presented a new algorithm for solving (1) sequentially when setting o~ = y =/32 ~-/32 and /31 =/3~ =/3. Based on cyclic reduction method by Golub and Hockney [10], Bondeli and Glander [2] presented a parallel cyclic reduction for solving (1) when setting a = y = 1, fil = fi~ =/3, and f12 = fl~ = 0. Following the approach in [17], this paper presents a new and fast parallel algorithm for solving the special tridiagonal system of (1). Employing diagonally dominant property, our parallel solver does need local communications between adjacent processors on a ring network. An error analysis for our parallel algorithm is also given. On the n C U B E / 2 E multiprocessors, some experimental results are illustrated to demonstrate the good performance of our stable parallel solver.
In Section 2 of this paper, we first describe the three-phase parallel solver on the ring network and the corresponding error analysis. Then, the parallel pseudo code is given. Section 3 contains performance results on the n C U B E / 2 E multiprocessors. Section 4 concludes the paper.
2. The Parallel Algorithm and its Analysis
Our parallel solver consists of three phases called the Toeplitz factorization, the substitution procedure, and the update procedure, respectively. Suppose that we have a ring network with p processors. In what follows, we will show how each phase can be accomplished on the ring network in a highly parallel way.
Let
2.1 Phase 1: Toeplitz factorization
y
,~ /3
o1
)qxq
L, =
(
1 ] a 7 - b 1 J a , and U' = - b 1 - b 1a/
a , ( 3 )which implies that a - 7b =/3 and - a b = a. This implies that b = - a / a and a = (/3+~/(/32 - 4 7 a ) ) / 2 . Since we wish the matrices L' and U ' t o be diago- nally dominant, we will select the sign so that the absolute value of a is greater than max([ a I, [71). That is, when/3 > [ a + 7 I, we chose a = (/3 + ~/(/3 2 _ 4 7 a ) ) / 2 ,
from which a > (la + yl + ~/((a + 7) 2 - 4 7 a ) ) / 2 = (la + 71 + [a - 71)/2 =
max(lal, 171).
When /3 < - [ a + 7[, we chose a = (/3 - ~/(/32 _ 4 7 a ) ) / 2 , t h e n a < [ - [ a + 7 1 - ~ / ( ( a + 7) 2 - 4 y a ) ] / 2 = ( - l a + 7 l - [ a - 71)/2=
-max(l~l, 171).
Since one of our choices always makes
lal > max(lal, 17l),
hence the bidiagonal Toeplitz matrices L' and U' are diagonally dominant 9 The computation of a and b provides the Toeplitz factorization of the matrix A' (phase 1 in our parallel solver), which can be done by each processor in O(1) time on the ring network.2.2 Phase 2: Substitution Procedure
For convenience, suppose n is a multiple of the number of processors used, i.e.,
9 1T 2 T p T T
n = p q . Initially, we partition y mto p parts and y = ( y ,y , . . . , y ) , where y i = ,:1r176 :2"(~ . ,y(qO)T . . for 1 < i _<p. The ith processor first solves A q z / = yi, . 1 _< i _<p, where zZ = ,~1('(~ z(i)2 ,. . . , Z(q~ T. That is, the ith processor solves EqUqz' , i
= yi. It can be verified that each processor in the ring network needs about 5q time to perform the forward and backward substitution procedure for solving
LqUqz i = y i (second phase in our algorithm) sequentially. Let w = A n z - y , where z = ( z : , z : , . . . ,zPT) T and w = (Wl, W 2 .. . . ,wn) T, then we have
-,:~ + ~ - ~ p ~ - (az~ 1~ + 7 z ? ) = ( ~ 1 - a ) z ~ 1~ + &z~P~,
W1 = (BIZ} 1)-]- I 2 t'2~q ]
Wn
= ( ~2Z~ 1) q-OLz(P)q-1 "]- /3~ Z(p)) -- I[ OIz(P)q-1 -t- flZ~ v))
=/3~Z~ 1) q- ( ~ - / 3 ) Z(p),
:~-<'~
+/3z~i~ + 7z~+1~)- ( ~ . o + ~z~O)= 7z~+,, for 1 <g <_p- 1
Wiq ~- I "*'q-1
wi.+ 1= (.~z~ + ~z~ ,+,~ + 7z~ ~+ ~) - (az~ ~+ 1~ + 7 4 ~ + , ) = . . 4 o + ( / 3 - a ) z ~ ' + 1,
for 1 < i < p - 1,
Wgq+i =O, O <_i < _ p - 1 , 2 < j < q - 1.
Consequently, it follows that
p - 1
A n Z - - Y =gpen
+ h p e l + E (gieiq +hieiq+l), (4) i=1388
K.-L. Chung et al.
where
gi---
TZ~ i+I),
hi = ~ i) -~- ( / 3 - a)z~ i+1), 1 <_i < p - 1, (5) gp = (/3~ - / 3 ) z ~ p) +/3~ z~ 1), h e = ( 13 l - a)z~ 1) +/3 2 Z~q p). (6) By (4), the solution of x in (1) will be determined approximately, say, z - p, in Section 2.3 later, where A p = gpe n + hpe 1 + •iP-ll(gieiq + hieiq + 1). To estimatethe bound of IIAx - yH/Itylf, we need the following lemma. Here Iloll denotes the
infinite norm of a vector.
Lemma 1. [4]
if
L =
I: ,o
ll lo
ll lo
, II01 >
II11,
then IIL-lyll ~ II01-1ll---~ ILylJ"Similarly, we have the inequality
1
IIU-lyll ~ Ilyll
lu01- lull
for the upper bidiagonal matrix
U
US
)
U 0 U 1
U = , lu01 > lull.
U 0 Ul
UO
From A q z , i = y', 1 _< i < p , Lemma 1, and the above inequality, it gives 1
I]zil] = ]t(L'q U~ )-~yill = HU~-l(L,q
lyi)H _< l a l - 171 llL'qlyi]]
1 1
< Ilyql -< I~yl[ for 1 < i < p .
- l a l - lyl(1 - lb[) ( [ a ] - lyl)(1 - [bl)
(7)
2.3 Phase 3." Update Procedure
By (4), in what follows, the solution of x in (1) will be determined approximately and only local communications between adjacent processors on the ring network are needed. Then, the bound of IIAx - yIl/I~yll will be derived.
F r o m a - "yb = 13 a n d - a b = a , it derives to c = - "y/a, t h e n w e h a v e 'y + 13c + a r 2 = 0. L e t a + f i b + 'yb 2 = 0. I f w e let
(o
o)
pk = , . . . , 0 , 1 , b , . . . , b ~ , O , . . . , a n d k n - k q k = ( O , . . . , O , c t , . . . , C , 1 ,0,.~0 ) T
k n - k f o r q _< k _ n - q. H e r e w e a s s u m e q > m a x ( s , t). I n addition, w e let P l = (1, b . . . b ~- 1, b ~, 0 , . . . , O) T a n d qn = ( 0 , . . . , O, c t, c t - 1 .. . . , c, 1) r. A c c o r d i n g l y , it gives A P k = ( 0 , . . . , 0 , ' y , 1 3 + ' y b , k \ a + f i b + 'yb 2 . . . . , a b s - 2 + f i b s-1 + "yb s, a b s - 1 + 13b ~, a b * , O , . . . , 0 ) n - k ... ... o) k n - k= 'yek_ 1 + a e k + a b e ( - "yb ek+s + ek+s+l)
= 'Y%-1 + a % + oeb*( - c % + , + %+~+1), (8)
A q k
= ( 0 , . . . , O, "yC t, f l c t + "yet-1, ogct+ tic t- 1 + " y c t - 2 , . . . , OlC 2 + tiC + "y, OLC + fl,
\
k
n - k
= ( 0 .... , O , ' y c t , - - o ~ c t + l , o , . . . , O , a , oe,O~ O)
k n - k
='yC t ek_t_ 1 -- Cek_ t +aek-t-O~ek+ 1
= 7 c t ( % _ t - 1 - - b e k _ t ) + a % + ~ % + 1 ,
Al% = ( 131 q- 'yb, ol + fib + ' y b 2 , . . . , olb s - 2 + f i b s - 1 + T b 2, olb s-1
+ fib*, a b * , O . . . O, fi~) T
= ( ~31 -}- 7 b ) % - TO "*+* es+ 1 + oebSes+2 + ~2en
390
w h e r e
K.-L. Chung et al.
= y'2el + 18;% + abS( - C e s + , + e,+2 ), (10)
Aq,~ = ( 182,0,..., O, y c t, 18c t + 3,c t- 1, a C t q_ 18C t - 1 jr_ a C t - 2 . . . . , Oft 2
+18c + ~,, ~c + 18~)r
= 182el -k y c t % _ t _ l - a c t + l e n _ t q- ( a c n t- 18~)e n
= 182% + Y2e~ + y c t ( % - t - I - b % - t ) , (11)
e2 = a c + N , ~4 = 182 + e b . By (8), (9), (10), and (11) for 1 < i < p - 1, we have
A ( uiPiq+ l + viqiq ) = (,yu i + avi)eiq + ( au i + a vi)eiq+ l
+ u i a b S ( - c e i q + s + l + eiq+s+2) + U i ~ l c t ( e i q _ t _ 1 - b e i q _ t ) ,
(12)
+ U p O l b S ( - C e s + 1 + e s + 2 ) -t- V p T C t ( e n _ t _ l -- b % _ t ) .
(13) L e t yui + a v i = g i and aui + a v i = h i for l _ < i _ < p - 1 ; 18~Up + y2Vp=gp and y'2Up + 182v. = hp. Therefore, it gives
L e t a g i -- ah i Yhi - ag i bt i -~" a 7 - - a2 v i = a T - a2 , 1 _< i _<p - 1, (14) y 2 h p - t 8 2 g p T'2gp -- 1 8 ; h p
% ~';~2-182/3~' vp ~;~2-18218;
(15)
p - 1p = (Upp 1 + Vpq,,) + E (uiPiq+, + viqiq), (16)
i = l
by (12), (13), (14), and (15), we have A p ~ gpe n + hpe~ + F,P-ll(gieiq + hieiq + 2).
L e t x = z - p, t h e n we have the following t h e o r e m . T h e o r e m 2 . [4]
[IA~x-y[I
< max (max(Luiabq, iv, yc'O) l<_i<_p
t ! S ! t
where
171
la+abl+lao~l
h,l(lal + I/3- 2al)
T]I
~- 1Ol7 --a21(lal- 171)(1 - I b l ) ' '/72
~---l a y _
aZl(lal_
171)(1 --Ibl)'
172(/31 - a) -/32/3;I +1/32(/3 + 72 -/3~)1
nl =
1%72 -/32/3~l(lal- 171)(1 -Ibl)
'
lY~/3; - / 3 ; ( / 3 1 - a ) l +
I%( N -/3)
- / 3 ; / 3 2 1~[=
1%72 -/32/3;l(lal- 171)(1 -Ibl)
2.4 Parallel Psuedo Code
For simplicity, suppose the size of the linear system of (1) ( = the size of y in (1)), n, is much greater than the number of processors, p, used in the ring network, and n is a multiple of p. Initially, the n data of y are partitioned into p parts, i.e., each processor stores n / p data. The processor with address 0 (node - id = O) wants to compute x l , x 2 , . . . , Xn/p; the processor with address 1 (node - id = 1) wants to compute Xn/p+l, X n / p + 2 , . . . , X 2 n / p , and so on. In our parallel algo- rithm, each node performs the following pseudo-code.
/ * initially the vector y is stores in x * / / * all the concerning variables are local * /
q ~ n / p
/ * Phase 1: Toeplitz factorization * /
if fi > 0 t h e n a <-- [/3 + ~/( ]3 2 _ 4 y ~ ) ] / 2 e l s e a <--- [/3 - ~/(/3 2 _ 4 y a ) ] / 2 e n d i f
b ~ - a / a ; c ~ - 7 / a ; d ~ 1 / a
/ * Phase 2: Substitution procedure * /
for i := 2 to q d o x i = x i + b * x i _ 1 e n d f o r / * forward substitution * /
xq=d*Xq
for i := q - 1 downto 1 d o x i = d * xi+ 1 + c * x i e n d f o r / * backward substitution
, /
/ * Phase 3: Update procedure * /
if p = 1 t h e n
t l --->xq; t2 ---~x 1
e l s e
send x 1 to n o d e - [ ( i d - 1) mod p]; send
Xq
to n o d e - [ ( i d + 1) mod p] receive the value from n o d e - [ (id - 1) mod p] and store it in t lreceive the value from n o d e - [ ( i d + 1) mod p] and store it in t2
e n d i f
if n o d e - i d = p - 1 t h e n if n o d e - i d = 0 t h e n
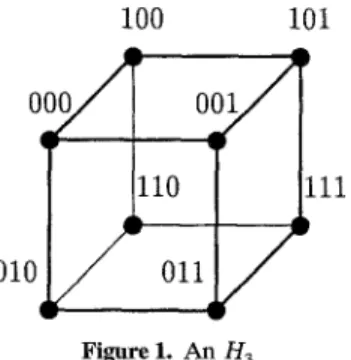
392 K.-L Chung et al, "Yz ~ a * c +/3~; y~ ~ / 3 1 + 7 b . . . . * g ' h ) / d e t ; u d e t ~ (3'z3'~ /32/32), v ~ (3'2 - ! 3 z * ~ ( 3 " 2 * h - f l 2 * g ) / d e t else g*-- y * x l ; h ~ a , t l + ( / 3 - a ) , x l ; d e t ~ a , 3 " - a 2 ; u ~- ( a * g - a * h ) / d e t g ~ ( / 3 ~ - / 3 ) * X q + ~ * t Z ; h ~ / 3 2 * X q + ( ~ l - a ) * t 2 ; 7 2 <-- OZ * C + [3~; 3"t 2 ~-- f i l + 3"b t . ! d e t ~ (723'~ - f12/32), v ,-- (3'~ * g - fi2 * h ) / d e t endif e l s e if n o d e - i d = 0 then g<--- y , t 2 ; h <--- a * Xq + ( / 3 - a ) * t2; d e t <--- o~ * y - a 2 ; v <-- (3' * h - a * g ) / d e t g ~ ( fl~ - fl ) * tl + /3~ * x~; h ~ /32 * tl + ( fll - a ) * x l ; y2 ~ a * c + /3~; 3"2 ~- /31 + 7 b ! ! , d e t ~ (3'2"/2 - / 3 z / 3 2 ) , u <-- (3'2 * h - / 3 2 * g ) / d e t else g<-- Y * Xl; h <-- a * t 1 + ( f l - a ) * x l ; d e t <-- a * 3 ' - a 2 ; u ~ ( a * g - a * h ) / d e t g<-- 3 ' * t2; h ~ a * Xq + ( / 3 - a ) * t 2 ; d e t ~ a * 3 , - a 2 ; v ~ ( 3 ' * h - a * g ) / d e t endif endif t ~ q - 1; s ~ q - 1; p o w e r ~ u f o r i := 1 to s do x i e-- x i - p o w e r ; p o w e r ~ b * p o w e r endfor p o w e r ~ v for i := 0 to t - 1 do Xq_ i ~ xq _ / - p o w e r ; p o w e r ~ c * p o w e r endfor 3. Experimental Results T h e k - d i m e n s i o n a l h y p e r c u b e n e t w o r k , Hk, has 2 ~ n o d e s a n d k 2 k - 1 e d g e s , w h e r e two n o d e s a r e l i n k e d w i t h a n e d g e if a n d o n l y if t h e i r b i n a r y strings differ in o n e bit. F i g u r e 1 i l l u s t r a t e s a n H 3. B a s e d o n t h e p a r a l l e l p s e u d o c o d e d e s c r i b e d in S e c t i o n 2.4 a n d t h e e m b e d d i n g m e t h o d t o m a p a r i n g n e t w o r k i n t o
the hypercube [13], we have implemented our parallel solver for solving (1) on a 16-node n C U B E / 2 E multiprocessors.
Our parallel program has been executed on the machine with 1, 2, 4, 8, and 16 processors, respectively, and the n C U B E / 2 E parallel C source code for solving (1) is listed in [4]. Five sets of data corresponding to the five cases, namely, the symmetric Toeplitz tridiagonal case [17], the skew-symmetric Toeplitz tridiago- nal case [8], the circulant-symmetric Toeplitz tridiagonal case [1], the symmetric near-Toeplitz tridiagonal case [1], and the circulant-skew-symmetric Toeplitz case [8], respectively, are taken to demonstrate the performance of our parallel solver.
In our implementations, we let Yi = rand(), a = 1, and/3 = 4 for all cases, where the function 'rand()' denotes a random number generator. In the first set of data, we let y--- a = 1, /31 =/3~ =/3 = 4, and /32 =/3~ = 0, representing the sym- metric Toeplitz tridiagonal case. In the second set of data, T = - a = - 1, /31 =/3~ =/3 = 4, and /32 =/3; = 0, representing the skew-symmetric Toeplitz tridiagonal case. In the third set of data, 3/= a =/32 =/3; = 1, and /31 =/3~ =/3 = 4, representing the circulant-symmetric Toeplitz trigonal case. In the fourth set of data, Y = a = 1, /31 = fl~ = / 3 / 2 = 2, and /32 =/3; = 0, representing the symmetric near-Toeplitz tridiagonal case. In the fifth set of data, 3' = - a =/32 =
t _ _ !
- / 3 2 - 1 , and /31 =/31 = / 3 = 4 , representing the circulant-skew-symmetric Toeplitz case.
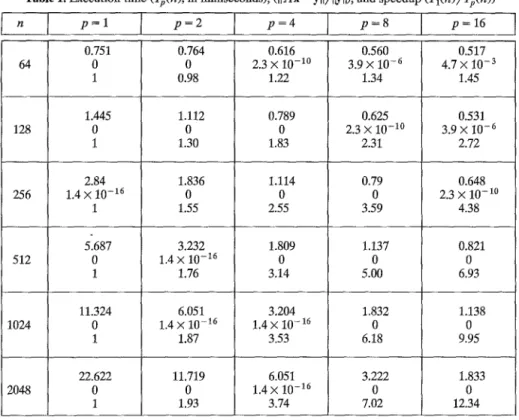
Since the execution times for all these cases are identical, and the relative residuals, I l A x - yll/l~yll, are of the same order. In Table 1, we only list the execution time
(Tp(n)),
H A x - yI[/[~YL[, and the speedup(Tl(n)/Tp(n))
for the first set of data, where n denotes the problem size,Tl(n)
denotes the time required when one processor is used,Tp(n)
denotes the time required when p processors are used. In the table, each entry has three values. The first value shows the execution time, the second value shows the sup-norm of the relative residual, and the third value denotes the speedup. It is shown that our parallel solver has good scalability and stability. The relative residual is small (less than 10 -15 ) when each processor processes more than 32 data.We also reorder the sequence of data communication operations in order to
100 101
A A
0 ~ 1 1 1
010
394 K.-L. Chung et al.
Table 1. Execution time (Tp(n), in milliseconds), (llAx - YI[/[~II), and speedup (Tl(n)/Tp(n))
n I p = l 0.751 64 0 1 128 1.445 0 1 2.84 256 1.4 • 10 -16 512 1024 2048 p=2 p = 4 p=8 p=16 0.764 0 0.98 1.112 0 1.30 1.836 0.616 2.3 • 10 -1~ 1.22 0.789 0 1.83 1.114 0.560 3.9 x 10 - 6 1.34 0.625 2.3 • 10 -1~ 2.31 0.79 0.517 4.7 • 10 -3 1.45 0.531 3.9 • 10 -6 2.72 0.648 2.3 • 10 -1~ 5.687 0 1 11.324 0 1 22.622 0 1 1.55 3.232 1.4 • 10 -16 1.76 6.051 1.4 • 10 -16 1.87 11.719 0 1.93 2.55 1.809 0 3.14 3.204 1.4 • 10-16 3.53 6.051 1.4 • 10 -16 3.74 3.59 1.137 0 5.00 1.832 0 6.18 3.222 0 7.02 4.38 0.821 0 6.93 1.138 0 9.95 1.833 0 12.34
hide the long communication latency. We let each node send its Xq to its
neighboring node at the begining of Phase 2, and read the value from another node in the receiving buffer after it sends its x~ to another neighboring node in Phase 3. However, the experiment shows that the execution time makes no difference with that of using the original communication sequence. Since either one of the communication operations sends and receives one double precision number. The messages are very short. The total communication time of a message with length L between two nodes is dominated by the start-up time, which is about 150/xs [14]. This cannot be hidden by sending the message a long time before receiving it by another processor.
4. Concluding Remarks
The significance of solving special tridiagonal Toeplitz linear systems is due to its use in many areas such as using finite difference methods to solve linear constant-coefficient boundary-value problems and solving uniform B-spline curve/surface fitting problems. We have presented an efficient parallel algo- rithm for solving special tridiagonal Toeplitz systems on the ring network. Employing diagonally dominant property, our parallel solver does need local communications between adjacent processors on the ring network. A n error analysis has also been provided. The corresponding implementation has been done on the n C U B E / 2 E multiprocessors.
Acknowledgements
The authors would like to thank the referees for several valuable comments. These comments improved the quality and presentation of this paper. The research was supported in part by the National Science Council of R.O.C. under contracts NSC85-2121-M011-002 and NSC-852213-E003- 001.
References
[1] Boisvert, R. F.: Algorithms for special tridiagonal systems. SIAM J. Sci. Stat. Comput. 12,
423-442 (1991).
[2] Bondeli, S., Gander, W.: Cyclic reduction for special tridiagonal systems. SIAM J. Matrix Anal. Appl. 15, 321-330 (1994).
[3] Chung, K. L., Yan, W. M.: A fast algorithm for cubic B-spline curve fitting. Comput. Graphics
18, 327-334 (1994).
[4] Chung, K. L., Yan, W. M., Wu, J. G.: A parallel algorithm for solving special tridiagonal systems on ring networks. Research Report, Dept. Inform. Mgmt., National Taiwan Inst. of Tech. (May 1994).
[5] Dongarra, J. J., Moler, C. B., Bunch, J. R., Stewart, G. W.: LINPACK User's Guide. New York: SIAM Press 1979.
[6] Evans D. J., Forrington, C. V. D.: Note on the solution of certain tridiagonal systems of linear equations. Comput. J. 5, 327-328 (1963).
[7] Evans, D. J.: An algorithm for the solution of certain tridiagonal systems of linear equations. Comput. J. 15, 356-359 (1972).
[8] Evans, D. J.: On the solution of certain Toeplitz tridiagonal linear systems. SIAM J. Numer.
Anal. 17, 675-680 (1980).
[9] Fischer, D., Golub, G., Hald, O., Levia, C., Winlund, O.: On Fourier-Toeplitz methods for separable elliptic problems. Math. Comput. 28, 349-368 (1974).
[10] Hockney, R. W.: A fast direct solution of Poisson's equation using Fourier analysis. J. ACM 12,
95-113 (1965).
[11] Malcolm, M. A., Palmer, J.: A ~fast method for solving a class of tridiagonal linear systems. Comm. ACM 17, 14-17 (1974).
[12] Ro]o, O.: A new method for solving symmetric circulant tridiagonal systems of linear equations. Comput. Math. Appl. 20, 12, 61-67 (1990).
[13] Saad, Y., Schltz, M. H.: Topological properties of hypercubes. IEEE Trans. Comput. 37,
867-872 (1988).
[14] Schmidt-Voigt, M.: Efficient parallel communication with nCUBE 2S processor. Parallel Comput. 20, 509-530 (1994).
[15] Smith, G. D.: Numerical solution of partial differential equations: finite difference methods, 3rd ed. Oxford: Oxford University Press, 1985.
[16] Widlund, O. B.: On the use of fast methods for separable finite difference equations for the solution of general elliptic problems. In Sparse matrices and their applications (Rose, D. J., Willoughby, R. A., eds.), pp. 121-131. New York: Plenum Press 1972.
[17] Yan, W. M., Chung, K. L.: A fast algorithm for solving special tridiagonal systems. Computing
52, 203-211 (1994).
Dr. tC-L. Chung Mr. W.-M. Yah
Department of Information Management Department of Computer Science National Taiwan Institute of Technology and Information Engineering No. 43, Section 4, Keelung Road, National Taiwan University, Talpei, Taiwan 10672, R.O.C Taipei, Taiwan 10764, R.O.C. Dr. J.-G. Wu
Department of Information and Computer Education
National Taiwan Normal University, Taipei, Taiwan 10610, R.O.C.