A smart method makes DFT more precise for power system frequency estimation

A Smart Method Makes DFT More Precise for Power System Frequency

Estimation

Jun-Zhe Yang

Chih-Wen

Liu

Department of Electrical Engineering, National Taiwan University, Taipei, Taiwan Abstract

- A

precise digital algorithm based on Discrete

Fourier Transforms (DFT) to estimate the kequency of a sinusoid with harmonics in real-time is proposed. This algorithm that we called the Smart Discrete Fourier Transforms (SDFT) smartly avoids the errors that arise when frequency deviates from the fundamental frequency, and keeps all the advantages of the DFT e.g., immune to harmonics of fundamental Erequency, obtaining easily the parameters of amplitude and phase, and even the recursive computing can be used in SDFT. These make the SDFT more accurate than conventional DFT based techniques. In addition, this method is recursive and very easy to implement, so it is very suitable for use in real-time. We offer the simulation results compared with conventional DFT method and second-order Prony method to validate the claimed benefits of SDFT.

Keywords: Discrete Fourier Transforms (DFT), Frequency estimation, phasor measurement.

I. Introduction

Frequency is one of the most important quantities in power system operation because it can reflect the dynamic energy balance between load and generating power. So frequency is always regarded as an index of the operating practices, and utilities can know the system energy balance situations by observing frequency variations. Frequency may vary very fast in the transient events such that it is difficult to track it accurately. In addition, there are many devices, such as power electronic equipment and arc fumaces, etc. generating lots of harmonics and noise in modem power systems. It is therefore essential for utilities to seek and develop a reliable method that can measure frequency in presence of harmonics and noise.

With the advent of the microprocessor, more and more microprocessor-based equipments have been extensively used in power systems. Using such equipment is known to provide accurate, fast responding, economic, and flexible solutions to measurement problems [

11.

Therefore, all we have to do is to find the best algorithm and implement it.

There have been many digital algorithms applied to estimating frequency during recent years, for example Modified Zero Crossing Technique [2], Level Crossing Technique [3], Least Squares Error Technique [4-61, Newton method [7], Kalman Filter [8-10], Prony Method [ll], and Discrete Fourier Transform (DFT) [12], etc. For real-time use, most of the aforementioned methods have trade-off between accuracy and speed [ 131. A smart digital algorithm, namely Smart Discrete Fourier Transform (SDFT) is presented and tries to meet the real-time use. SDFT has the advantages that it can obtain exact solution when frequency deviates from hdamental frequency, its speed is even faster than DFT, and it can get exact solution in the presence of harmonics.

The organization of this paper is as follows: We describe in very detail the SDFT in section 11. DFT, Prony method and SDFT are tested by four examples in section 111. Finally, we give a conclusion in section IV.

11. The Proposed Digital Algorithm

This section presents the algorithm of the SDFT that estimates the frequency and phasor from a voltage/current signal. Consider a sinusoidal input signal of frequency

0 = 2nf given by:

where X : the amplitude of the voltage/current signal,

4

: the phase angle of the voltage/current signal Suppose that x ( t ) is sampled with a sampling rate (60*N) Hz waveform to produce the sample set { ~ ( k ) }

k

60N x ( k ) =

x

cos(0

-

+

4)

The signal x ( t ) is conventionally represented by a phasor (a complex number)

X

X

= XeJ* = x c o s ~

+

jXsinQ (3)

Then x ( t ) can be expressed as

where

*

denotes complex conjugate.

Moreover, the fundamental frequency (60Hz) component

of DFT of { ~ ( k ) is given by 2nk

2 N-I N k=O

i, = - C x ( k

+

r ) e - ' y

Combing Eq.(4) and Eq.(5) and taking frequency deviation ( w = 2n(60

+

Af)) into consideration, we obtain:

We rearrange Eq.(6) as the following 2 j z ( l + z ) r N - l j 2 n X k N k=O e N 60 C e 6 0 N x, =

-

-.

(2+f) x -J2"(1+df)r N-1 -~2n-*k N k=O +-e 6o

C e

We use the following identity to simplify Eq.(7) NB sin - sin - 2 N - l ,=O

Then Eq.(7) can be expressed as

2 n ( 2

+

-) Af

60 where

e l

=

*

, and 6 = -

60 N N

Rearranging Eq.(9) further, we obtain

Ifwedefine A, and B, as

Then Eq.(9) can be expressed as

So far the development of the algorithm of SDFT are the same as the conventional DFT method. So the SDFT can keep all advantages of DFT such as recursive computing manner. But in the DFT, it assumes that the frequency deviation is small enough to be ignored, and it always considers

2,

II! A , , so traditional DFT based methods incur error in estimating frequency and phasor when frequency deviates from nominal frequency (60 Hz). If we want to get exact solution, we must take B, into consideration. So we define

And from Eq.(lO), we will find the following relations Arcl = A, * a

B,,l = B,

*

a-' Then

=A,,

+

B,+I =A, * a

+

B, *a-' i + 2 = 4 + 2 + Br+2 =

4+1*

a + B,+I

*

a-'

(17) (1 8) If we multiply ' a ' on both sides of Eq.( 17) and Eq.( 1 S), respectively, then we get

.?r+l

* a

= A,

*

a 2

+

B, (19)

(20)

* *

x r + 2 a = A,+I

*

aZ + B,+I

Subtracting Eq.( 13)ftom Eq.( 19) and subtracting Eq.( 17) from Eq.(20), respectively, we obtain

2r+l

*

a

- 2,

= A, (aZ

-

1)

ir+Z

*

a - i,+, = Arrl (a' - 1) Dividing Eq.(22) by Eq.(21), we get

Then rearrange Eq.(23) as follows

Solve W 2 4 ) to obtain

C l = . Then from the

definition of 'a' in Eq.( 14), we can get the exact solution of the frequency.

(2, + i r + z ) k J ( i r + i r + 2 ) 2 - 4 i , + , *

%+I

(25)

60N

f = 60

+

Af = cos-' (Re( U))

*

-

2%

From Eq.(25), it is observed that SDFT can provide exact frequency using ?,

,

?,+, and ?,+, in the absence of noise. Moreover, we can estimate phasor after getting exact ' f' by the following equations:

i"+, *U-;,

112 -1

A, =-

Actually, if we assume that

x ( t ) = XI cos(wt

+

4,)

+

X , cos(3wt

+

$,) from the beginning of development of the algorithm, we will derive a polynomial equation similar to Eq.(24) that provide exact frequency in the presence of 3'd harmonic. We use SDFT, that has taken 3rd harmonic into consideration to distinguish ffom SDFT. Of course, any other integral order harmonic still can be taken into consideration, for example SDFT,, and SDFT,,, take 3rd, 5" harmonic and 3rd, 5Ih, 7 I h harmonic

into consideration respectively.

Although we can take all of the harmonics into consideration, we still need digital filter to decay noise and high order harmonics. The advantages of digital filter are no voltage drop, no temperature drift, no noise addition, and don't care any filter element feature. Besides these, digital filter can be implemented in microprocessor-based equipment. These make us choose the digital filter to filter noise and high order harmonics. There are many digital filters that we can choose eg., hanning, hamming and Blackman window. In simulations we will use Blackman window for filtering.

111. Simulation Results

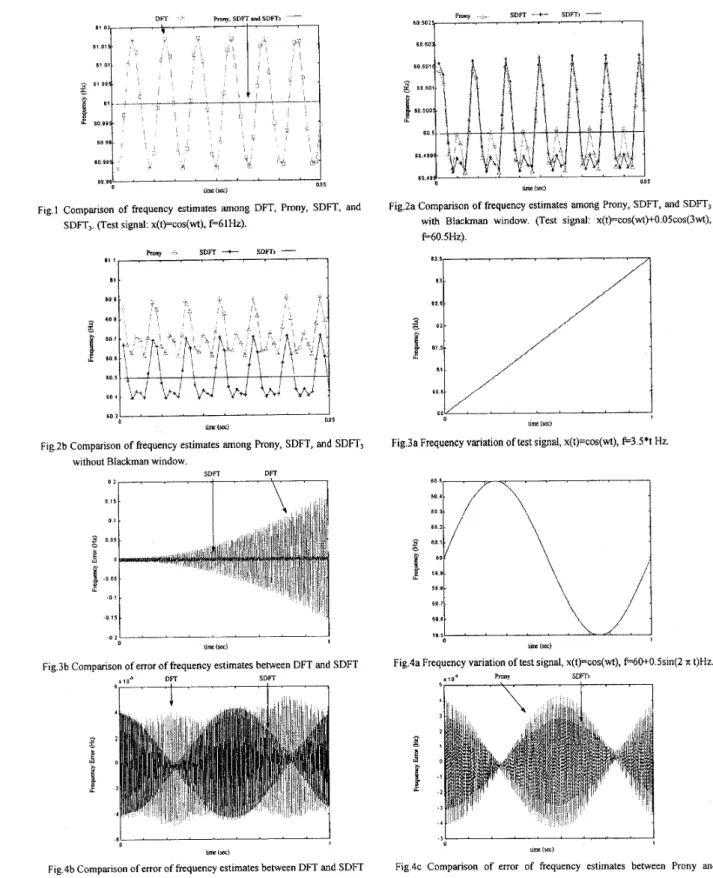
Simulation results presented in this section were all simulated from Matlab and showed for a fair comparison to DFT method and Prony method. In Fig.1, we showed that SDFT could obtain an exact solution identical to the Prony method under frequency deviation in a pure

sinusoidal waveform. Fig. 1 also shows the performance of SDFT, method and conventional DFT method. It is

observed that conventional DFT method gives the wrong frequency estimates. In Fig 2a, SDFT, is observed to obtain the exact solution. When the SDFT and Prony methods test the same signal as SDFT, but filtered by a Blackman window (window size = 16) for estimation, we find that the SDFT and Prony methods have similar performance. In Fig 2b, the same test signal without Blackman window tests SDFT and Prony, we find that Prony is worser than SDFT in the presence of harmonic. In Fig.3a, the frequency of test signal is changed linearly from 60Hz to 63.5Hz during 1 second. From Fig.3b, we can observe that the error of DFT increases with the frequency deviation. However, the absolute error of SDFT is bounded below a small value. In FigAa, the frequency is changed as sin wave and 3'd harmonic is also added in test signal during 1 second. We can observe the errors of DFT and SDFT in Fig.4b, and the errors of Prony and SDFT, in FigAc. Although SDFT, can resist the effect of the 3rd harmonic, the effect of frequency variation makes SDFT, get some small errors. Anyway, from Fig4 we can conclude that SDFT-based algorithms (SDFT, SDFT,) are better than DFT method and Prony method for frequency estimation. By comparison of computation speed, Table 1 shows the AMD K6-200 CPU time of each method. There are 960 data per second computed by each method (the test signal is the same as Fig.3a) without Blackman windows to estimate the frequency, while adding a Blackman window will add 0.91 second to the computation. We find that SDFT is the fastest method in these computation, even faster than DFT, because SDFT counts frequency directly, but DFT has to count phase first and then use the phase difference to count frequency. The faster speed of SDFT over the Prony method is because recursion can be used in

SDFT.

Table 1 computation time

I

Prony

I

DFT SDIT

I

SDIT~ SDFT,~SDIT~= time@)

I

2.03

I

0.71

I

0.54

I

1.01

1

1.71

1

3.44

IV. Conclusion

In this paper we introduce the SDFT method and demonstrate its performance. SDFT both keeps the advantages of DFT and also deals with the cause of frequency deviation errors, while taking integral harmonics into consideration. These aspects make SDFT a fast, accurate and harmonic-resisting method. But we do not suggest taking all the harmonics into consideration, since that would require too much computation time. Alternatively, using a smooth window to decay the high order harmonics and just taking the low order harmonics power systems under real-time demands.

into consideration will be more efficient and suitable for

Fig1 Comparison of frequency estimates among DFT, Prony, SDFT, and SDFT,. (Test signal: x(t)=cos(wt), f-61Hz).

OD5 lim (16)

6 0 1 1 ' ' ' ' ' ' " "

Fig.2b Comparison of frequency estimates among Prony, SDFT, and SDFT, without Blackman window.

SDFI D F I

0 _{um 6"}

Fig 3b Comparison of error of frequency estimates between DFT and SDFT

, 1 0 1 DFI SDFI

I " I ' ' ' ' I ' ' I

UM(Uc)

Fig.4b Comparison of error of frequency estimates between DFT and SDFT

~ , b y , . , S D F I - .t- ,SDFI>, -,

.

,

60 I 0 1

60 3 0

U M (=)

Fig.2a Comparison of frequency estimates among Prony, SDFT, and SDFT, with Blackman window. (Test signal: x(t)=cos(wt)+O.OScos(3wt),

F60.5Hz).

Fig.3a Frequency variation of test signal, x(t)=cos(wt), f-3.5*t Hz

Fig.4a Frequency variation of test signal, x(t)=cos(wt), M(HOSsin(2 K t)Hz.

i 1 0 = m S D F b

I ' ' \ . ' ' I' ' ' I

F i g . 4 ~ Comparison of error of frequency estimates between Prony and

[31

[41

Reference

P J Moore, R D Carranza, A T Johns, “Model System Tests on a New Numeric Method of Power System Frequency Measurement”, IEEE Transactions on Power Delivery, Vol. 11, No. 2, April 1996, pp. 696- 701

Miroslav M. Begovic, Petar M. Djuric, Sean Dunlap, Arun G. Phadke, “Frequency Tracking in Power Networks in the Presence of Harmonics”, IEEE Transactions on Power Delivery, Vol. 8, No. 2, April 1993, pp. 480-486.

C.T.Nguyen, K.Srinivasan, “A New Technique for Rapid Tracking of Frequency Deviations Based on Level Crossings”, IEEE Transacfions on Power Apparatus and Systems, Vol. PAS-103, No.8, August 1984,

I. KAMWA, R. GRONDIN, “Fast Adaptive Schemes for Tracking Voltage Phasor and Local Frequency in Power Transmission and Distribution Systems”, IEEE Transactions on Power Delivery, Vol. 7, No. 2, April 1992, pp. 789-795.

M.S. Sachdev, M.M. Giray, “A Least Error Squares Technique For Determining Power System Frequency”, IEEE Transacfions on Power Apparatus andSystems, Vol. PAS-104, No. 2, February 1985, pp. 437- 443.

M.M. Giray, M.S. Sachdev, “Off-Nominal Frequency Measurements In Electric Power Systems”, IEEE Transactions on Power Delivery, Vladimir V. Tenia, Milenko B. Djuric, Branko D. Kovacevic, “Voltage Phasor and Local System Frequency Estimation Using Newton Type Algorithm”, IEEE Transactions on Power Delivery, Vol.

M.S. Sachdev, H.C. Wood, N.G. Johnson, “Kalman Filtering Applied To Power System Measurements For Relaying”, IEEE Transactions. on Power Apparatus and System, Vol. PAS-104, No. 12, December Adly A.Girgis, T. L. Daniel Hwang, ”Optimal Estimation of Voltage Phasors and Frequency Deviation Using Linear and Non-Linear Kalman Filter: Theory and Limitations”, IEEE Transactions o n Power Apparatus and Syslems, Vol. 103, No. IO, October 1984, pp. Adly A. Girgis, William L. Peterson, “Adaptive Estimation of Power System Frequency Deviation and its Rate of Change for Calculating Sudden Power System Overloads”, IEEE Transactions on Power Delivery, Vol. 5,No. 2, April 1990, pp. 585-594.

Tadeusz Lobos and Jacek Rezmer, “Real-Time Determination of Power System Frequency”, IEEE Transactions on Instrumentation and measurement, Vol. 46, No. 4, August 1997, pp. 877-88 1. A. G. Phadke, J. S . Thorp, M. G. Adamiak, ”A New Measurement Technique for Tracking Voltage Phasors, ‘Local System Frequency, and Rate of Change of Frequency”, IEEE Transactions on Power Apparatus andSystems, V01.102, No. 5 , May 1983, pp. 1025-1038.

Ph. Denys, C. Counan, L. Hossenlopp, C. Holweck, ”Measurement Of Voltage Phase For The French Future Deffence Plan Against Losses Of Synchronism”, IEEE Transactions on Power Delivery, Vo1.7, No.1, Jan 1992, pp. 62-69

pp.2230-2236.

Vol. 4, NO. 3, July 1989, pp. 1573-1578.

9, NO. 3, July 1994, pp. 1368-1374

1985, pp. 3565-3573.

2943-2949.

Biographies

Wen

Liu

was bom in Taiwan in 1964. He received the B.S. degree in Electrical Engineering from National Taiwan University in 1987, Ph.D. degree in electrical engineering from Come11 University in 1994. Since 1994, he has been with National Taiwan University, where he is associate professor of electrical engineering. His research interests include application of numerical methods to power system, motor control and GPS time transfer.

Jun-Zhe Ymg was bom at Tainan, Taiwan,

in 1971. He received his B.S. degree in electrical engineering from Tatung Institute

of Technology in 1992 and M.S. degree fiom National Taiwan University in 1995. He is presently a graduate student in the electrical

%-

engineering department, National Taiwan University, Taipei, Taiwan