http://ssc.sagepub.com/
Social Science Computer Review
http://ssc.sagepub.com/content/23/2/221
The online version of this article can be found at:
DOI: 10.1177/0894439304273270
2005 23: 221
Social Science Computer Review
Hsu-Chih Wu and Chuen-Tsai Sun
What Should We Do Before Running a Social Simulation?: The Importance of Model Analysis
Published by:
http://www.sagepublications.com
can be found at:
Social Science Computer Review
Additional services and information for
http://ssc.sagepub.com/cgi/alerts Email Alerts: http://ssc.sagepub.com/subscriptions Subscriptions: http://www.sagepub.com/journalsReprints.nav Reprints: http://www.sagepub.com/journalsPermissions.nav Permissions: http://ssc.sagepub.com/content/23/2/221.refs.html Citations:
What is This?
- Mar 28, 2005
Version of Record
>>
What Should We Do Before
Running a Social Simulation?
The Importance of Model Analysis
HSU-CHIH WU CHUEN-TSAI SUN
National Chiao Tung University
Before running a model simulation, it is important to accumulate as much information about the model as possible. Although an analysis of relations among model components is considered a promising means of accomplishing this task, the social simulation literature offers very little guidance in perform-ing such analyses. We use an analytical framework to demonstrate how model analysis can facilitate the simulation process, with the Iterated Prisoner’s Dilemma serving as a primary example. Our results show that the analysis was helpful in identifying important strategies and simulation phenomena, thus reducing the amount of work required for the simulation. We suggest that this framework is applicable to other types of two-person matrix games, and that the methods we use are also suitable for other macro- or agent-based simulation models.
Keywords: social simulation; Prisoner’s Dilemma; model analysis
C
omputer simulation is gaining significant attention in terms of its potential use in soci-ology (Halpin, 1999). Increased computing power and advancements in such areas as agent-based computation (Brent, 1999; Brent, Thompson, & Vale, 2000), and Distributed Artificial Intelligence are making social simulation efforts more practicable and reliable. Social simulations are increasingly being adopted to complement or substitute for more tra-ditional social science methods, including empirical experimentation, theoretical and statis-tical analysis, and explanations using natural language (Goldspink, 2002).Detailed discussions of social simulations can be found in the literature (Fishwick, 1995; Hanneman & Patrick, 1997; Jacobsen & Bronson, 1995). Common methodologies include the following steps: (a) model creation (constructing a model based on an existing theory, hypothesis, or empirical data), (b) model execution (running a model to produce data), and (c) model verification (assessing a model’s ability to operate as intended) and validation (analyzing data to ensure that a model is working as intended; Goldspink, 2002).
Although it is rarely included in lists of social simulation methodologies, theoretical and statistical model analyses play important roles in the social simulation process. During the creation phase, model structures and relationships are based mostly on theories or hypothe-ses. Theoretical variables are defined and quantified, and relationships among them are encoded (Jacobsen & Bronson, 1995). In the words of Hanneman and Patrick (1997), any model being constructed is “one concrete realization of the prior theory.” During the
verifi-221
Social Science Computer Review, Vol. 23 No. 2, Summer 2005 221-234 DOI: 10.1177/0894439304273270
cation phase, the simulated results are statistically analyzed for purposes of interpretation and/or explanation (Axelrod, 1997).
There are few discussions in the social simulation literature of useful analytical tasks to be performed after a model is created but before simulation begins. At this point, it is important to determine appropriate model parameters or parameter sets based on empirical experience or existing data. The importance of analysis at this phase is the focus of this article. We believe that presimulation model analysis can help reduce simulation complexity as well as assist in the identification of appropriate simulation parameters. We use an analytical frame-work based on the Iterated Prisoner’s Dilemma (IPD)—a mathematical model frequently used to assess conflicts of interest—to demonstrate how model analysis can facilitate the simulation process.
In a classic version of the Prisoner’s Dilemma game, two players must decide whether each move they make will be one of cooperation or defection; payoffs are determined by a combination of moves. In the payoff matrix presented as Table 1, if Players A and B decide to cooperate with each other, both receive payoff R. If A cooperates and B defects, then A receives S and B receives T. If both players defect, each receives payoff P.
Players restricted to a single move are most likely to achieve a maximum outcome if they defect. However, the longer the game, the more advantageous it is for both players to act in mutual cooperation. Because most real-world dilemmas are iterated, researchers have spent more time studying IPDs than single-move PD games (Axelrod, 1984). Two additional rea-sons why we chose IPD as our analytical model are (a) as a classical model, it has been widely studied and used in the social sciences, political science, computer science, and eco-nomics, and therefore a considerable number of research reports are available for verifica-tion purposes; and (b) it is mathematically simple but analytically intractable, thus making it a representative model to illustrate the importance of presimulation model analysis.
In this article we discuss the importance of presimulation model analysis, present an ana-lytical framework for IPD, describe the results, discuss the framework, and offer our conclusion.
WHY ANALYZE BEFORE SIMULATION?
The most important motivation for presimulation analysis is to learn as much as possible about a model, based on the assumption that the more one knows, the easier it will be to run a proper simulation. In this section, we describe how a presimulation analysis helps in defin-ing model scope, reducdefin-ing simulation complexity, and choosdefin-ing appropriate simulation parameters.
TABLE 1
Payoff Matrix and Value Constraints for the Iterated Prisoner’s Dilemma (IPD) Model
Cooperation Defection
Cooperation R/R S/T
Defection T/S P/P
Defining Model Scope
Defining a model’s scope is an important first step toward increasing model efficiency; it is surprising how often this step is overlooked in the social simulation literature. Whenever a simulation run provides significant findings, the data and the model clearly need to be inspected in terms of validity. However, it is equally important to determine the conditions under which a particular model is successful, as well as the possibility of achieving success under other conditions.
Following model construction, concepts and entities are defined as parameters or vari-ables. Prior to each new simulation run, individual parameters must be set to specific values to satisfy some condition. A simulation run is not equivalent to a simulation model. In this article, we define a simulation run as an instance of the model. In theoretical terms, a compre-hensive understanding of a model requires simulations of all possible model instances, but doing so is usually considered impractical. A simulation model M can be defined as
M = (P1, P2, . . . , Pn),
where P1, P2, . . . , Pnrepresent n parameters of M. Letting N denote the number of possible
model instances and |Pi| denote the number of possible values of parameter Pi, then N = |P1| • |P2| • . . . |Pn|.
Each parameter has its own constraints. Examples of discrete parameters include the size of a population in a societal model and the number of nodes in a social network model (Stocker, Green, & Newth, 2001). Here the number of possible values is finite; however, other parameters are considered continuous and infinite—for instance, tax rates in a simula-tion of tax and welfare systems. Most social simulasimula-tion models contain discrete and continu-ous parameters; even in simple models, the number of instances is usually large or infinite. Each instance represents a tiny part of the model.
The impossibility of simulating all model instances implies a need to choose an appropri-ate model instance or set of model instances. We want to emphasize the importance of know-ing the number of potential choices before choosknow-ing what appears to be the most appropriate because the success of one model instance implies overall model success; however, the fail-ure of one model instance does not imply overall model failfail-ure. It is easier to figfail-ure out the relationship between a model and a model instance when its scope is defined.
Reducing Model Complexity
The second step toward a successful simulation involves reducing model complexity. When the scope of a model is defined, it is no longer necessary to run all possible model instances. Unnecessary instances should be skipped to make the simulation process more efficient. The two types of model instances that can be skipped are the following:
1. Unreasonable instances, meaning that a parameter setting does not match real-world condi-tions. These can be further divided into two categories: (a) instances with unreasonable parame-ter values, which are not under the constraints of the corresponding parameparame-ters and (b) unrea-sonable parameter combinations, meaning that individual parameter values that are considered reasonable become unreasonable when they are combined with other reasonable parameter val-ues because of their correlational relationships.
2. Equivalent instances, meaning that instances may appear to be completely different but never-theless produce identical simulation results, or have identical meanings from the perspective of the model. An analysis of equivalent instances can provide information about whether an instance should be simulated. It may be unnecessary to simulate reasonable or important instances in cases where simulation results from equivalent instances are produced.
Analyses of unreasonable or equivalent instances reduce the number of potentially appro-priate model instances. Using the metaphor of a highway map, the scope of a model provides the number of possible ways to get from point A to point B, while reduced model complexity provides answers to questions such as “Which routes will not get us from point A to point B?” and “Which individual routes lead to the same destination?” By reducing the numbers of unreasonable and equivalent instances, it becomes easier to choose the appropriate parame-ter settings for running a successful simulation.
Choosing Appropriate Model Instances
The final presimulation analytical step is determining appropriate model instances—that is, instances that resemble most other instances or that have significant importance. Most model instance selections in the social simulation literature are based on empirical data or hypotheses. However, a simulation instance with significant results must be tested to deter-mine if it is representative of other instances and if other instances will produce identical or similar outcomes. Answering such questions becomes more difficult when model instance determinations are not based on theoretical or statistical analyses.
AN ANALYTICAL FRAMEWORK FOR
THE ITERATED PRISONER’S DILEMMA
Our proposed framework focuses on relationships among memory-n deterministic strate-gies in IPD. A strategy is considered deterministic if its behavior is consistent within the con-text of certain conditions; if the behavior changes even though the conditions remain unchanged, the strategy is considered nondeterministic. Regarding memory-n strategies, moves of cooperation and defection are determined by the historical moves of two players. A memory-n strategy determines any individual move in correspondence to the moves made during the previous n rounds. The most important IPD strategies (e.g., Tit-for-Tat and PAVLOV) belong to this category of memory-n strategies (Axelrod, 1984; Nowak & Sigmund, 1993). Tit-for-Tat also belongs to the strategy category in which the historical moves of opponents (instead of both players) are considered. This strategy class can also be used in our analytical framework. The reasoning behind our decision to focus on memory-n strategies is twofold: All strategies in the class that considers only opponent’s moves also belong to the memory-n class, and the current literature reflects today’s strong research interest in memory-n strategies.
We chose a finite state machine—a dynamic system that changes its behavior at discrete moments—to represent interactions between deterministic memory-n strategies. A finite state machine consists of a finite set of internal states and a transition function that deter-mines new system states as a function of the current state plus input. Interactions between two memory-n strategies can be expressed as finite state machines by defining individual states in terms of two players’ preceding n moves. As a simple example, let Siand Sjbe two
memory-1 strategies that can be expressed as (P0, P1, P2, P3), where P0, P1, P2, P3∈{C, D}
(with C denoting cooperation and D defection). P0, P1, P2, and P3represent the respective
moves). If Si= (C, D, C, D) and Sj= (C, D, D, C), the resulting interactions can be presented
as a finite state machine with a transition diagram equal to that shown in Figure 1. All possi-ble Siand Sjbehaviors are shown in this figure. For example, if Siand Sjmade defection
moves in the previous round, Siwill make another defection move and Sjwill make a
cooper-ative move, resulting in a transition from DD to DC.
The finite state machine that represents interactions between two memory-n determinis-tic strategies, Siand Sj, from Si’s perspective is formally defined as FSM(Si|Sj). Because the
behaviors of Siand Sjare deterministic, there is only one outgoing link for each state in FSM(Si|Sj). Starting from any state, the behavior of FSM(Si|Sj) will be periodically
repeated—that is, any interactive behavior between two memory-n deterministic strategies will be periodically repeated.
According to the so-called shadow of the future assumption (Axelrod, 1984), stable coop-eration between two players increases as the potential that they will meet again increases (thus making defection an unprofitable strategy). This means that the finite state machine will be run an infinite number of times. Because the interaction behavior of two memory-n deterministic strategies is periodically repeated, the traversal probability of each state can be calculated. Each state represents Siand Sj’s past n moves, including moves in their preceding
game. The traversal probability of each state can be accumulated to derive the probability of each combination of the preceding game; that is
FCC= the probability that the result of the preceding game was CC
FCD= the probability that the result of the preceding game was CD
FDC= the probability that the result of the preceding game was DC
FDD= the probability that the result of the preceding game was DD.
The expected payoff E(Si|Sj) can be obtained as
E(Si|Sj) = FCC× R + FCD× S + FDC× T + FDD× P,
where R, S, T, and P are the values in the payoff matrix of the IPD. When Simeets Sjfor an
infinite duration, Si’s expected payoff E(Si|Sj) can be obtained from FSM(Si|Sj) and Sj’s
expected payoff E(Sj|Si) from FSM(Sj|Si).
Based on the expected payoffs from each strategy pair, two criteria were established for examining strategy properties: the ability to exploit others and the ability to form clone clusters. S15 S9 S7 S13 S11 S6 S0 S4 S2 S1 S14 S8 S10 S3 S12 S5
<
<
<
<
Ability to Exploit Others
This ability is determined by the relationship between E(Si|Sj) and E(Sj|Si). Sjis said to
exploit Siif E(Si|Sj) <E(Sj|Si). This is expressed as
Si→Sjif E(Si|Sj)<E(Sj|Si), meaning that Sjexploits Si, or
Si= Sjif E(Si|Sj) = E(Sj|Si), meaning that Siand Sjreceive the same payoff.
Note that the combination of Si→Sjand Sj→Skdoes not imply Si→Sk; the relationship
between Siand Skis determined by E(Si|Sk) and E(Sk|Si). However,
Si→Sjimplies E(Si|Sj) < E(Sj|Si), and
Sj→Skimplies E(Sj|Sk) < E(Sk|Sj).
From these two inequalities, nothing is known about E(Si|Sk) or E(Sk|Si), and the
relation-ship between Siand Skremains undetermined.
To show relations among more than two strategies, we defined an exploitation chain as
SC1→ SC2→ …SCk, where strategy exploits SC1if j > i.
For an exploitation chain Si→Sj→Sk, for example, Si→Sj, Sj→Sk, and Si→Sk.
Ability to Form Clone Clusters
The ability of strategies to form clone clusters is determined by the expected payoff when they play with their clones—that is, E(Si|Si). If the E(Si|Si) is high, then two players using the same
strategy Siwill receive relatively higher payoffs. This effect is more apparent in spatial models, in
which strategies only interact with their neighbors (Brauchli, Killingback, & Doebeli, 1999; Grim, 1996; Ishibuchi, Nakari, & Nakashima, 1999; Lindgren & Nordahl, 1994).
RESULTS OF OUR FRAMEWORK
We applied our proposed framework to memory-1 strategies, notated as (P0, P1, P2, P3).
Our 24deterministic strategies, named S
0, S1, . . . , S15, represent (C, C, C, C), (C, C, C, D), (C, C, D, C), (C, C, D, D), . . . (D, D, D, D), respectively.
Relations among the abilities of all strategies to exploit others are known as exploitation
relations. Exploitation relations between paired memory-1 deterministic strategies are listed
in Table 2. Assume an element Tijin Row i and Column j, and
Tij= 0 if Si= Sj,
Tij= 1 if Sj→Si, and
Tij= –1 if Si→Sj.
Three strategy sets are defined as WINk= {Si| Si→Sk},
LOSEk= {Si| Sk→Si}, and
WINkconsists of a set of strategies exploited by Sk, LOSEkconsists of a set of strategies
capable of exploiting Sk, and DRAWkcontains strategies that result in identical payoffs when
they meet Sk. Exploitation relations among these 16 strategies were constructed by WINk,
LOSEk, and DRAWk(0 k ≤ 15). Strategies were said to be equivalent if they had the same
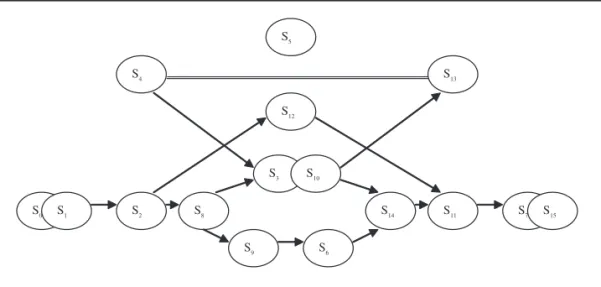
WIN, LOSE, and DRAW sets. We identified three sets of equivalent strategies: { S0, S1}, { S3, S10}, and { S7, S15}, with their exploitation chain expressed as
{ S0, S1}→{ S3, S10}→{ S7, S15}. (1)
We then identified all possible exploitation chains based on (1):
{ S0, S1}→S2→S8→{ S3, S10}→S11→S14→{ S7, S15} (2)
S4→{ S3, S10}→S11→S14→{ S7, S15} (3)
{ S0, S1}→S2→S8→{ S3, S10}→S13 (4)
{ S0, S1}→S2→S12→S11→{ S7, S15} (5)
{ S0, S1}→S2→S8→S9→S6→S11→S14→{ S7, S15}. (6)
A graphic representation of exploitation chains for memory-1 deterministic strategies— that is, relationships among the various strategies’ abilities to exploit each other—is pre-sented in Figure 2. As shown, if a path exists from Sito Sj, then Si→Sj. We added a “=” link to
indicate the single exception—that is, a path exists from S4to S13, but S4=S13. S5, which
receives the same payoff when it interacts with any other memory-1 deterministic strategy, is shown as an isolated vertex in Figure 3. This is the well-known strategy Tit-for-Tat.
Exploitation relations among all memory-1 deterministic strategies are shown in Figure 3. The principle for determining the exploitative capabilities of Siand Sjis
TABLE 2
Exploitation Relations between Paired Memory-1 Strategies
S0 S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 S11 S12 S13 S14 S15 S0 0 0 –1 –1 0 0 –1 –1 –1 –1 –1 –1 –1 –1 –1 –1 S1 0 0 –1 –1 0 0 –1 –1 –1 –1 –1 –1 –1 –1 –1 –1 S2 1 1 0 –1 0 0 –1 –1 –1 –1 –1 –1 –1 –1 –1 –1 S3 1 1 1 0 1 0 0 –1 1 0 0 –1 0 –1 –1 –1 S4 0 0 0 –1 0 0 0 –1 0 0 –1 –1 0 0 –1 –1 S5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 S6 1 1 1 0 0 0 0 –1 1 1 0 –1 0 0 –1 –1 S7 1 1 1 1 1 0 1 0 1 1 1 1 1 0 1 0 S8 1 1 1 –1 0 0 –1 –1 0 –1 –1 –1 0 –1 –1 –1 S9 1 1 1 0 0 0 –1 –1 1 0 0 –1 0 0 –1 –1 S10 1 1 1 0 1 0 0 –1 1 0 0 –1 0 –1 –1 –1 S11 1 1 1 1 1 0 1 –1 1 1 1 0 1 0 1 –1 S12 1 1 1 0 0 0 0 –1 0 0 0 –1 0 0 0 –1 S13 1 1 1 1 0 0 0 0 1 0 1 0 0 0 0 0 S14 1 1 1 1 1 0 1 –1 1 1 1 –1 0 0 0 –1 S15 1 1 1 1 1 0 1 0 1 1 1 1 1 0 1 0
Si=Sjif there is a “=” link between them, or if no traversal path exists between Siand Sj;
Si→Sjif a traversal path exists from Sito Sj; and
Sj→Siif a traversal path exists from Sjto Si.
The ability of strategies to form clone clusters is also referred to as a clustering relation. Strategy Si’s clustering ability is determined by E(Si|Si)—the expected payoff that results
from interactions with its clones. A list of E(Si|Si) for all memory-1 deterministic strategies is
presented in Table 3. S2 S8 S3 S10 S7 S15 S4 S13 S12 S9 S6 S14 S11 S0 S1
Figure 2: Exploitation Chains for Memory-1 Deterministic Strategies
S2 S8 S3 S10 S7 S15 S4 S13 S12 S9 S6 S14 S11 S0 S1 S5
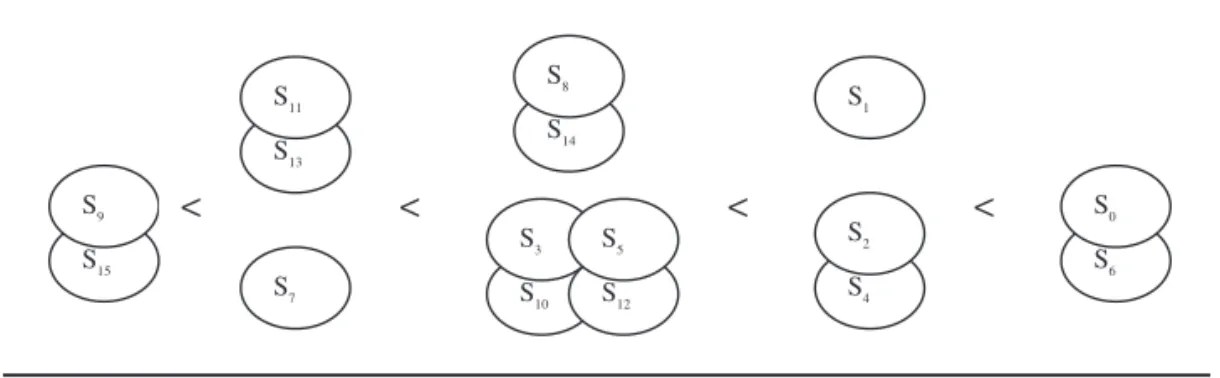
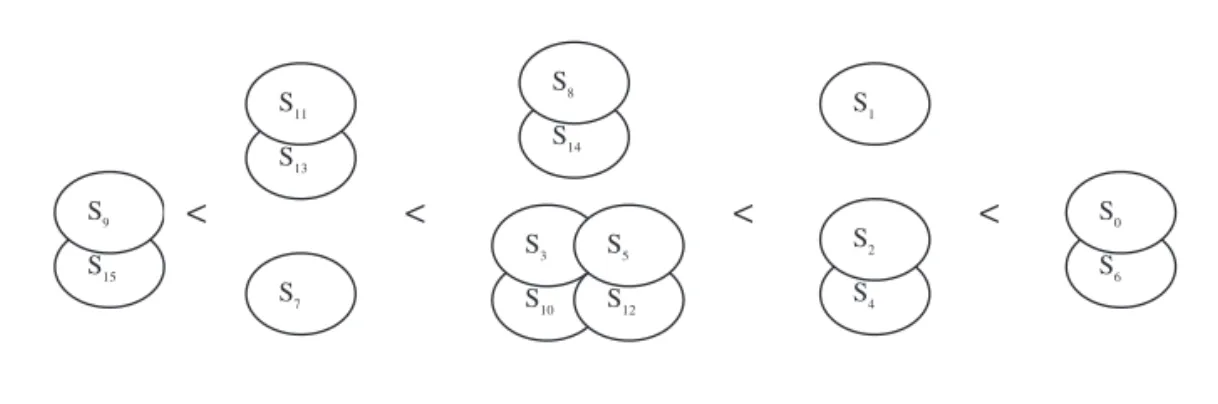
Recall that R, S, T, and P in the Prisoner’s Dilemma payoff matrix satisfy T > R >P > S, and that 2R > S+T. According to these constraints, the clustering relations of all memory-1 deter-ministic strategies are as follows:
If S+T > R+P: S9, S15< S7< S11, S13S14, S8< S3, S5, S10, S12< S1< S2, S4< S0, S6. If S+T < R+P: S9, S15< S11, S13< S7< S3, S5, S10, S12< S14, S8< S2, S4< S1< S0, S6. If S+T = R+P: S9, S15< S7, S11, S13< S3, S5, S8, S10, S12, S14< S1, S2, S4< S0, S6.
Relations between {S1} and {S2, S4}, between {S8, S14} and {S3, S5, S10, S12,}, and between
{S7} and {S11, S13} are determined by the values of (S+T) and (R+P). Because the focus of this
article is on relations that are independent of the value of the payoff matrix, {S1} and {S2, S4}
are viewed as one set of strategies, {S8, S14} and {S3, S5, S10, S12,} a second set, and {S7} and
{S11, S13} a third. A graphic representation of the ability of memory-1 deterministic strategies
to form a clone cluster is shown in Figure 4.
It can be argued that the use of a value-independent analysis contradicts one of our stated reasons for performing a presimulation analysis—that is, defining model scope—because model scope may depend on the payoff matrix value. The payoff matrix values indeed may affect the analytical result of relation between strategies. However, we firmly believe that neglecting to perform an analysis of relations that are independent of payoff matrix values would make it difficult to determine whether results were the consequence of the IPD prob-lem nature or payoff matrix values. In short, a value-independent analysis highlights rela-tions based on the native properties of the IPD model, whereas a value-dependent analysis emphasizes how different values affect exploitation and clustering relations.
TABLE 3
E(Si|Si) for Memory-1 Deterministic Strategies
Strategy E(Si|Si) Strategy E(Si|Si)
S0 R S8 R P+ 2 S1 3 4 R P+ S 9 P S2 2 4 R S T+ + S 10 R S T P+ + + 4 S3 R S T P+ + +4 S11 S T+ + 24 P S4 2 4 R S T+ + S 12 R S T P+ + + 4 S5 R S T P+ + + 4 S13 S T+ + 2P 4 S6 R S14 R P+2 S7 R+ 34 P S15 P
DISCUSSION
Relations Among All Memory-1 Deterministic Strategies
Before examining the important strategies revealed in Figures 3 and 4, we look at rela-tions between the two criteria. A good strategy should exploit others to receive a higher pay-off, and a clone cluster should be strong enough to repel invasions. In terms of examining strategy properties, these two criteria hold equal importance. Strategies that exploit others but fail to form strong clone clusters will likely spread throughout an environment until it becomes saturated, then become susceptible to invasions from other strategies. S15(always
defect, regardless of the opponent’s move) is typical of this kind of strategy. On the other hand, strategies with a strong ability to form clone clusters but that are easily exploited have low survival rates, because their exploitation usually occurs before their clone clusters can be formed; S0(always cooperate, regardless of the opponent’s move) is one example of this kind
of strategy.
The strategy order in Figure 3 is almost exactly opposite that of Figure 4. Accordingly, strategies that exploit others find it difficult to get along with their clones, whereas strategies that get along well with their clones are more likely to be exploited. Among memory-1 strate-gies, strength in one criterion usually implies weakness in another. The midorder strategies in Figures 3 and 4 are considered important because they show a certain degree of dual strength and have, therefore, attracted the greatest attention from Prisoner’s Dilemma researchers (Axelrod, 1984; Kraines & Kraines, 2000; see also Table 4).
In addition to their greater survival potential, these midorder strategies are parts of a dividing line between nice and nonnice strategies. S3, S5, S10, and S12divide the two lists
sym-metrically. Most of the strategies on the left side of Figure 3 and the right side of Figure 4 will cooperate following a CC round, indicating that they are so-called nice strategies that will never defect first (Axelrod, 1984). Most of the strategies on the right side of Figure 3 and left side of Figure 4 are considered nonnice, but with some important exceptions. S7, a nice
strat-egy, is located on the right side of Figure 3 and the left side of Figure 4. S6and S9are located in
the middle of Figure 3; however, in Figure 4 S6is on the right side and S9the left. For this
rea-son, those strategies have become the focus of numerous investigations. S6is an example of
the well-known PAVLOV strategy (Nowak & Sigmund, 1993), and S7is an example of a
RETALIATOR strategy (Brauchli et al., 1999). S15 S9 S7 S13 S11 S6 S0 S4 S2 S1 S14 S8 S10 S3 S12 S5
<
<
<
<
Characteristics of Important Strategies Revealed by the Framework
In this section, we discuss two memory-1 strategies that are located in particular positions within our proposed framework: Tit-for-Tat and PAVLOV. Both are considered good illus-trations of how our proposed framework provides satisfactory explanation of important strategies properties.
Tit-for-Tat. The isolation of S5(the Tit-for-Tat strategy) in Figure 3 means that it cannot
exploit other strategies nor is it easily exploited. According to our proposed framework, the success of a Tit-for-Tat strategy is based on its (a) ability to attain equal chances of survival with any other strategy and (b) strong clustering capability. This supports Axelrod’s (1984, 1997) conclusion that a Tit-for-Tat strategy among predominantly ALLD strategies (i.e., strategies that encourage defection regardless of an opponent’s move) can resist invasion by most defective strategies (see also, Nowak & Sigmund, 1992).
PAVLOV. S6is an example of the well-studied PAVLOV strategy. Among all memory-1
deterministic strategies, it is the only one whose exploitation and clustering abilities are higher than average. According to Nowak and Sigmund (1993), PAVLOV holds an advan-tage over Tit-for-Tat because (a) it can correct occasional mistakes and (b) it resists invasions by strict cooperators. The first property is not observable from the information in Figures 3 and 4 because occasional mistakes do not occur in deterministic strategies. However, the sec-ond property is obvious because the ability of S6to exploit others is higher compared to most
nice strategies. Furthermore, its ability to form clone clusters is the strongest among all memory-1 deterministic strategies; this explains why it can resist invasion by strict coopera-tors. Another important property that distinguishes PAVLOV from Tit-for-Tat is that it loses against ALLD because it alternates between cooperation and defection. This property is explained well in Figure 3.
The identification of important strategies and common phenomena by our proposed framework underscores the idea that some simulations are not necessary if appropriate ana-lytical procedures are followed. This is not to say that analysis can completely replace simu-lation, which is required to verify predicted phenomena. The key word here is verification and not discovery, the difference being the amount of required simulation work. If the pur-pose of simulation is to verify certain properties, fewer model instances are needed; if the purpose is to discover unknown phenomena, more model instances are needed to reflect as many conditions as possible. In either case, theoretical analysis helps reduce unnecessary simulation efforts and provides guidance toward anticipated results.
TABLE 4
Common Memory-1 Deterministic Strategies
Strategy Name Representation Description
S3 Stubborn (C, C, D, D) Repeats first round move regardless of
opponent’s move.
S5 Tit-for-Tat (C, D, C, D) Repeats opponent’s previous move.
S10 Bully (D, C, D, C) Defects against a cooperator but
cooperates if punished.
S12 Fickle (D, D, C, C) Changes strategy each round
An important property of our framework is its directed graph representation for exploita-tion relaexploita-tions. Assume three strategies (A, B, and C) and their cyclical exploitaexploita-tion relaexploita-tions (A→B, B→C, and C→A). In environments where only A and B exist, the dominant B will always exploit A. If C appears in the same environment, B will become less dominant because C can exploit it. Because A can exploit C, the arrival of C increases A’s and decreases B’s survival potential. No such cycle exists in any subset of the 16 memory-1 strategies; how-ever, a number of “semi-cycles” are observable—for instance, ALLC→ALLD / ALLD = Tit-for-Tat / Tit-for-Tat = ALLC. Previous studies have shown that Tit-for-Tat affects ALLC and ALLD domination; however, further investigation (based on topological strategy rela-tions and payoff matrix values) is required to better understand this property.
Framework Generalization
The framework is suitable for analyzing other types of two-person matrix games—for instance, so-called chicken games that are very similar to the PD except for slight differences in their payoff matrix value constraints (i.e., T > R > S > P).
The framework can also be applied to spatial IPD models, which have different emer-gence behaviors than nonspatial models because of an opponent selection bias—that is, players must be neighbors. Assume an environment restricted to ALLC and ALLD players. For all ALLC players in a nonspatial model, the probabilities of meeting another ALLC player are equal. In contrast, in a spatial model containing clusters of ALLC players, the probability of a player in the center of a cluster to meet an ALLC player would be 100% because all of its neighbors would be ALLC players. Our framework addresses interaction patterns between two players regardless of the spatial or nonspatial status of the model in question. It can be applied to spatial models to better understand interaction patterns between strategies; however, more research is required on how players contact and select their opponents.
The framework’s methodology is summarized as follows: (a) identify interaction patterns between two agents, (b) use these patterns to determine the expected payoff for each agent, (c) identify relationships between the agents according to their expected payoffs, and (d) construct strategy relations based on pair-wise relations. The primary purpose of this meth-odology is to analyze a model from the perspective of interactions between two individuals. Although it can be applied to other types of agent-based and macro simulations, interaction patterns may be very different from those observed in the PD. For multiagent systems whose agents have deterministic behaviors, our finite state machine representation for pattern inter-action is applicable. For nondeterministic multiagent systems, it would be inappropriate (or impossible) to use our finite state machine representation at Step (1). However, regardless of how two agents interact, the status of either agent changes following an interaction. The change of agent status may be transformed into the expected payoff after interaction. Once the expected payoff is identified, Steps (3) and (4) can proceed.
CONCLUSION
In this article, we reemphasized the importance of presimulation analysis in social simu-lations. By analyzing various relationships among model components, the scope of the model can be defined, the complexity of a model reduced, and appropriate parameter set-tings identified—all leading to increased simulation efficiency. Theoretical analyses can reduce and/or complement the weaknesses of social simulations. For simple models, analy-sis is required to determine why a simulation is needed and why certain parameters should be
chosen. For complex models, analysis reduces unnecessary work and guides the direction of a simulation toward discovery. An analysis of relationships between or among strategies pro-vides a global view of a model’s scope and helps to establish important strategies and appropriate parameter settings.
An analytical framework based on the IPD was used as our primary example. Using this framework, many well-known strategies’ properties and simulation phenomena were revealed. This indicates that (a) the framework is capable of providing rich and integrated information, which is crucial to investigating and simulating the IPD and (b) appropriate analysis is needed prior to a simulation to reduce unnecessary effort. We suggest that our proposed framework is suitable for analyzing other types of two-person matrix games, and the framework methodology can be extended to other agent-based simulation models to investigate relationships among agents.
Although we want to emphasize the importance of presimulation analysis, we make no claim that analytical approaches can replace simulations, nor are they to be considered supe-rior to simulation approaches in any other manner. In each case, advantages and disadvan-tages are clear. We believe the integration of simulative and analytical approaches will become an increasingly important topic in future social simulation studies. Further investi-gation to clarify their complementary properties would be necessary.
REFERENCES
Axelrod, R. (1984). The evolution of cooperation. New York: Basic Books.
Axelrod, R. (1997). Advancing the art of simulation in the social science. In Simulating social phenomena (pp. 21-40). Berlin, Germany: Springer-Verlag.
Brauchli, K., Killingback, T., & Doebeli, M. (1999). Evolution of cooperation in spatially structured populations.
Journal of Theoretical Biology, 200, 405-417.
Brent, E. (1999). Sociology: Modeling social interaction with autonomousagents. Social Science Computer Review,
17, 313-322.
Brent, E., Thompson, A., & Vale, W. (2000). Sociology: A computational approach to sociological explanations.
Social Science Computer Review, 18, 223-235.
Fishwick, P. A. (1995). Simulation model design and execution. Englewood Cliffs, NJ: Prentice Hall.
Goldspink, C. (2002). Methodological implications of complex systems approaches to sociality: Simulation as a foundation for knowledge. Journal of Artificial Societies and Social Simulation, 5.
Grim, P. (1996). Spatialization and greater generosity in the stochastic prisoner’s dilemma, Biosystems, 37, 3-17. Halpin, B. (1999). Simulation in sociology, American Behavioral Scientist, 42, 1488-1508.
Hanneman, R., & Patrick, S. (1997). On the uses of computer-assisted simulation modeling in the social sciences.
Sociological Research Online, 2.
Ishibuchi, H., Nakari, T., & Nakashima, T. (1999). Evolution of neighborly relations in a spatial IPD game with cooperative players and hostile players. In Congress on Evolutionary Computation, 2.
Jacobsen, C., & Bronson, R. (1995). Computer simulations and empirical testing of sociological theory.
Sociologi-cal Methods and Research, 23, 479-506.
Kraines, D. P., & Kraines, V. (2000). Natural selection of memory-one strategies for the iterated prisoner’s dilemma.
Journal of Theoretical Biology, 203, 335-355.
Lindgren, K., & Nordahl, M. G. (1994). Evolutionary dynamics of spatial games, Physica D, 75, 292-309. Nowak, M., & Sigmund, K. (1992). Tit for Tat in heterogeneous populations. Nature, 355, 250-252.
Nowak, M., & Sigmund, K. (1993). A strategy of Win-Stay, Lose-Shift that outperforms Tit-for-Tat in the Prisoner’s Dilemma game. Nature, 364, 56-58.
Stocker, R., Green, G. D., & Newth, D. (2001). Consensus and cohesion in simulated social networks, Journal of
Artificial Societies and Social Simulation, 4.
Hsu-Chih Wu is a Ph.D. candidate in the department of Computer and Information Science at National Chiao Tung University in Hsinchu, Taiwan. He is currently conducting his dissertation research. His research
interests include analysis of strategies in game theory, distributed artificial intelligence, and information visualization on evolutionary systems. He can be contacted at e-mail: gis86534@cis.nctu.edu.tw. Chuen-Tsai Sun received his B.S. degree in electrical engineering (1979) and his M.A. degree in history (1984), both from National Taiwan University, Taiwan. He received his Ph.D. degree in computer science from the University of California at Berkeley in 1992. From 1991 to 1992, he was with the Lawrence Livermore National Laboratory, California, where he participated in research projects on fuzzy neural net-works. Since 1992 he has been with National Chiao Tung University, Taiwan, where currently he is a profes-sor in the Department of Computer and Information Science. He is currently engaged in research and teach-ing in the areas of creative evolutionary systems, Web-based collaborative learnteach-ing, and computer simulation in social studies. He is also in charge of one community university in Hsinchu City, Taiwan. He can be contacted at e-mail: ctsun@cis.nctu.edu.tw.