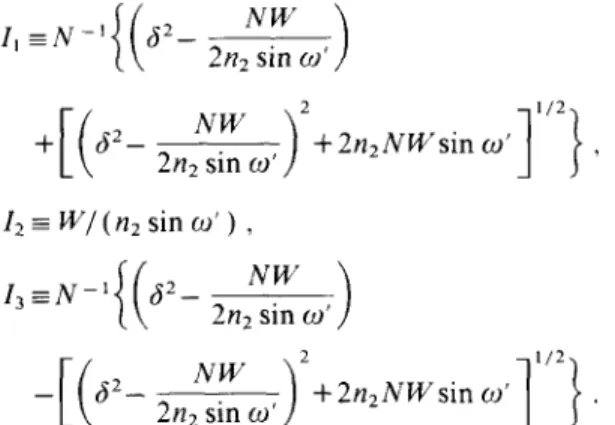Optical switching of a nonlinear slab in total internal reflection state

(1)

O P T I C A L S W I T C H I N G O F A N O N L I N E A R SLAB IN T O T A L I N T E R N A L R E F L E C T I O N STATE

Yi-Yen W U and Chun Hsiung C H E N

Department of Electrical Engineering, National Taiwan University, Taipei, Taiwan, Republic of China Received 16 August 1989

A study of a plane wave obliquely incident on a nonlinear slab of positive Kerr coefficient in total internal reflection (TIR) state is reported. Various bistable and multi-valued transmissions are investigated as the incident power varies. Especially, the mechanism of the resonant transmission is analyzed in detail, and an explanation of the invariance phenomenon in the first jump positions is proposed, Finally, a method for designing good bistable switchings is given.

1. Introduction

Nonlinear interface problems have received much attention recently because they are potentially useful as ultra-fast optical switches and logic elements, and the operating power can be greatly reduced [ 1,2 ]. A series o f theoretical works on nonlinear interfaces in total internal reflection ( T I R ) state were published. Typical examples are the plane-wave theory [ 3 ] and the study o f 2D gaussian beams under slowly-vary- ing envelope approximation [4,5 ], which all predict the switching behavior o f the transmittivity. Re- cently, Chen and Mills [6] have discussed the nor- mal incidence o f a plane wave on a nonlinear slab, in which bistable and resonant transmissions were found. The bistable and multi-stable phenomena have found applications in the fields such as optical switching [7,8], optical circuit, and optical m e m o r y [9 ], which are essential to the development o f optical c o m m u n i c a t i o n and optical computers [10].

In this paper, a plane wave obliquely incident on a nonlinear slab o f positive Kerr coefficient in T I R state is studied. In section 2, general results will be presented and multi-valued actions o f transmittivity will be discussed. In section 3, the existence and characteristics o f the resonant transmission will be examined and formulae for calculating the resonant transmission directly will also be derived. In section 4, a unique p h e n o m e n o n o f the T I R state, invariance of the first j u m p position under the slab-length's

variation, will be pointed out and c o m p u t e d results for the first j u m p will also be compared with the pre- vious results for a nonlinear interface [3,4].

2. Mathematical formulation and general results Let a .f-polarized plane wave

Ei.~ =.lEo exp [ - ik~ (x cos q/+ z sin ~,) ]

be obliquely incident on a nonlinear slab as shown in fig. 1, where d is the slab length and q/is the incident angle. The symbol ~'cr=COS-~(X//~-3/E~ ) de- notes the T I R angle o f the interface between two linear media el and ~3. Express the transmitted wave and the wave in the slab as

~cr

z=O

YA e2

L

>Z

z=d

(2)

Et=yTEo

exp [ - ik2(x cos ~' + z sin gt' ) ] ,

E=yEoe(z)

e x p [ i 0 ( z ) ] exp( - i k ~ x cos ~u) . Then by the following the process o f ref. [6], one has the relations for the wave fields

l(z' ) f ( A I + ~ Z I 2 _ ½ N _ 1 3 W 2 ) _ I / 2 d I l(d' ) = _ + 2 ( d ' - z ' ) , (1) l ( d ' ) =

W/(n2

sin q / ) = IT[ e , (2) ½ N I 2 ( 0 ) - ( 6 2 + n 2 sin2q/) I ( 0 ) + [4n 2 sin2q/ + ~ 2 W / ( n 2 sin ~,' ) - 2 n ~ W s i n ~u-n2 W s i n ~r

- N W 2 / ( 2 n 2 sin2~ ' ) ] = 0 .

(3) Here new variables and p a r a m e t e r s are introduced:

k i ~ ~

( i = 0 , 1, 2, 3),

z' =koz, d ' - k o d ,

n i ~

x/ei/eo, 62n 2 c o s 2 ~ , - n 2, l(z' )=-eZ(z ' ), N-~,E2/eo,

~,' =-cos -~ (k~cos

~'/k2),

while A and W are integra-

tion constants. Basically, only the relationship between the transmittivity I TI 2 and N is needed. F r o m

( ! ), l(z' )

m a y be expressed in terms o f j a c o b i a n elliptic functions [11] and (3) is the resultant nonlinear equation for W, which can be solved by the d a m p e d Newton method [ 12 ]. A nonlinear slab with positive coefficient in T I R state means e , > 0 and ~ 2 > 0 , so

l(z' )

can be expressed as (i) N ~ n 2 s i n 2 ~ ' + ~ 2,

2n:

sin oJ'

+

/ +2n2NWsino)'

2n2 sin m' ' h =- W~ (n2 sin e)' ) ,

13 ~ N - I { ( ~ 2 - 2n;N-~09, )

2n2 sin

J +2n2NWsin

.

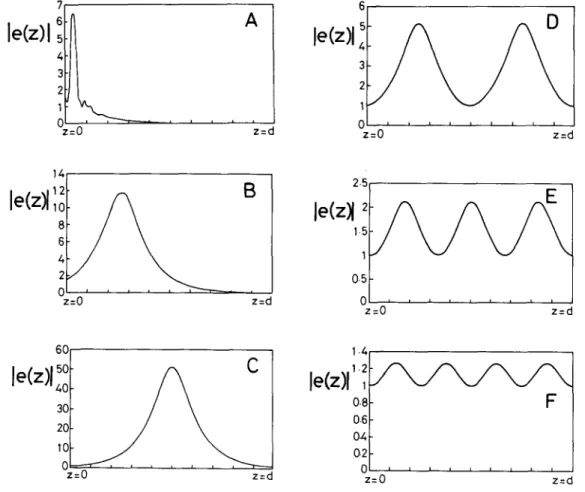
Eq. (3) is solved for several cases, as illustrated in figs. 2-5. It should be r e m e m b e r e d that if e, is fixed, then the variation of N is equivalent to the variation o f incident optical power. Figs. 2 and 3 show Wpical examples for multi-valued transmissions. Note that resonant transmissions ( I T I 2 = 1 ) occur at C, D, E, F (fig. 2) which also show periodicity and s y m m e t r y in field distributions (fig. 3). If N increases from zero, then a sudden switching of transmittivity takes place when passing through the first j u m p as defined in fig. 2. Certainly, there are m o r e j u m p s if N is further increased. The first j u m p is emphasized here because it represents the transition from surface waves to oscillatory waves, as indicated by A - C in fig. 3. These i m p o r t a n t characteristics will be examined rigorously in later sections.

To gain a better insight to the multi-valued trans- 11 (12 - - 1 3 ) +13(11 - 1 2 ) c n 2 ( • ) I ( z ' ) = (12_13)..1_(11_12)cn2(.) ,

O<~z'<~d',

c n ( ' ) - - c n

( ~ N ) l / 2 ( l u - 1 3 ) l / 2 ( d ' - z ' ) I i - 1 3 J " (4a) (ii)

N>n~

sin2~ ' +~2,

l ( z ' ) = l ~ +(12-11)cn2(.),

O<~z' <~d' ,

cn(. )

=-en{ ( ½N)l/2(I2 -13)'/2(d ' - z ' ) I2 - I , - ]

12 -- 13 J " ( 4 b ) In both cases,

1.2 ¢-

I!

0.81 0.E

0.Z

0.~

f-C D ~ E~-~b t ~ F B m p qL- A I -O~;-S I0-~ 10 °3 10 -~ 10 -I Fig. 2. Transmittivity I TI 2 versus N ( = ~ , E ~ / ~ o ) . q = e 2 = 1.93 %, e3= 1.88 Co, d = 10 20 (20: free-space wavelength), q / = 7 °, q/or = 9 . 2 3 ° .

(3)

7

le(z)l 6

5 4 3 1 ,

o=

A

i z=d 14

I )112

e ( z 10 8 6 4 2 0 z=O

B

z=d

2.5

le(z)l 2

1.5 1 0.5 I I I I I I I I I Z=0 Z=, 60 z : O z : ( 1.4

le(z)l' ~f~J~/'~J~,

°, I

0.6 04 0.2 0 I z=O

F

I I Z ~ I

Fig. 3. Field-amplitude distributions l e(z) I in the slab corresponding to the states defined in fig. 2.

1.2 missions, the cases with different slab-lengths a n d

i n c i d e n t angles are considered, respectively, in fig. 4 1

a n d fig. 5. T h e m u l t i - v a l u e d actions become notable 0.8

as the slab-length increases or the i n c i d e n t angle de-

creases. In figs. 4 a n d 5, bistable t r a n s m i s s i o n curves ~ 06

are also observed, which are very useful in optical E

switching. As will be shown in section 4, good bist- ~ 04 _{t _}

able curves can be o b t a i n e d in general situation. "~ 02

(Here good bistable curves m e a n the ones with very ]

0 great contrast for switching w i t h i n a narrow bistable

region.) Note that the above conclusions are not - 0 2

limited to small i n c i d e n t angles which must be as- s u m e d in refs. [ 3 - 5 ]. As for n u m e r i c a l results, only symmetric configurations (El = e2) are presented.

~. ~ " " . . . " L L - . . . : ". ~ " "'.... /I . ." : .. _: _'. ,. _,. _/i I : . . ".. / , / : "'. "'. / : ".. ", / • • . . . ' , l I . . I X "~ .:----~:~:7 . . . . d=1 8~, ~ o ... ..:::-::,.). - - a = 3 1 0 ~ o ... d=10.0 "h o 0 0.005 001 0.015 0.02 0 0 2 5 0.03 N

Fig. 4. Transminivity I TI 2 versus N for three values of d. tl =t2= 1.93 to, ts= 1.88 to, ~= 7 °, ~uc,= 9.23 °.

(4)

12 0., O~

i

i'" ...

- - - 1 ~ = 3 2 ' '~, =25 ° ... 1~ =18" . . . ' . . . " : : : : -. v . v ... ...

0.5 1 15 2 25 3 35 4 4.5

N Fig. 5. T r a n s m i t t i v i t y I TI z v e r s u s N f o r t h r e e v a l u e s o f ~. q = ~2 = 1 0 , 1 % , % = 5 %, d = 0 . 2 4 3 20, ~cr = 45.3 °.

3. Analysis of resonant transmissions

First, the necessary condition for the existence o f resonant transmissions is derived. Putting I ( 0 ) = 1 and I T I 2 = I in (3) gives

< =~2, (5)

which is the desired condition. Thus resonant transmissions never occur in asymmetric configurations. Next, with ~1=~2, I ( 0 ) = 1 , and 1 T I 2 = 2 be substi- tuted into (4), one has cn(. )2= 1. Then by the pe- riodic nature of the jacobian cosine function c n ( . ) , one may derive the desired formulae for resonant transmissions, (i)

N<~n2sin2q/ +62,

(½N)'/2(I~-13)'/2d'=2nK(Ii~--7)3)

n = 1 , 2 , 3 ... M . (6a) (ii)

N>n 2

s i n 2 q / + 5 2 ,

(½N)l/2(1-13)l/2d'=2nK(~-13)l-ll ,

n = ( M + 1 ), ( M + 2 ) , ( M + 3 ) , .... (6b) Here K(. ) is the elliptic integral o f the first kind. Ob- viously, the periodicity and symmetry o f the field distributions are simply the results o f c n ( . ) . Cal-

culations have also proved that eq. (6) is consistent with the numerical results c o m p u t e d from eq. (3). Fig. 3 is a typical example where C, D, E, F corre- spond to n = 1, 2, 3, 4 in eq. (6). Further compari- sons with ref. [6] show that the resonant transmission here is of different nature.

4. Analysis of the first jump

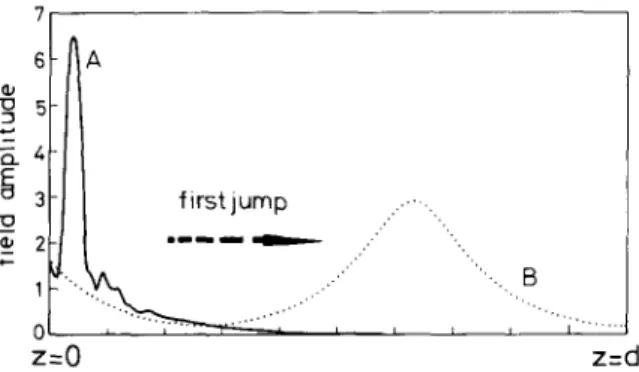
The first j u m p is defined, in fig. 2, as the state where the first switching action takes place when N increases from zero. The first j u m p position, occur- ring at N = N o , has the intuitive meaning that, if ~ t i r = - - s i n - l ( J ( ~ 3 + % N ) / E l ), then No is approxi- mately the value of N for ~'tir=~'. Then it is found that the position of the first j u m p is almost i nvariant under variation o f the slab length, an important phe- n o m e n o n which can also be concluded from fig. 4. This p h e n o m e n o n may be explained by the following consideration. Specifically, the wave field is essen- tially confined to the region a r o u n d the nonlinear interface before the first j u m p (refer to fig. 6 for il- lustration), which is similar to the well-known concept o f T I R in the linear theory. Thus the first j u m p should mainly depend on the physical condition o f the interface at z = 0 and is not influenced by the thickness o f the slab. The wave field is not confined to the interface immediately after the first jump, which is also shown in fig. 6.

By the invariance argument, our first j u m p result for a nonlinear slab problem can be used to compute the one for a nonlinear interface problem merely by letting the slab-length approach infinity. The plane-

6 A 0a

g 8

. m ~_4 3 f i r s t j u m p _..... _.. . - " '"-.. B 0 " ' " " . . . " " - . , . . . . z = 0 z = d

Fig. 6. Field-amplitude distributions l e(z) fore and after the first jump in fig. 2.

(5)

Table 1

Positions of first jump from three different approaches. Ourresults ReK [3] Re£ [4]

5 ° 0.0210 0.0212 0.0263

7 ° 0.0110 0.0106 0.0124

8 ° 0.0061 0.0062

wave t h e o r y o f a n o n l i n e a r interface was c o n s i d e r e d in ref. [3] a n d a 2D gaussian b e a m i n c i d e n t on a n o n l i n e a r interface was discussed in ref. [ 4 ] . C o m - p a r i s o n o f the p o s i t i o n s o f the first j u m p for three cases is given in table 1, where g o o d a g r e e m e n t is observed. The m e c h a n i s m s for multi-valued actions and resonant t r a n s m i s s i o n s are different for these three cases by noting the different b o u n d a r y c o n d i t i o n s at infinity. But the first j u m p p o s i t i o n s are m a i n l y de- t e r m i n e d by the physical c o n d i t i o n at the interface. This again explains the g o o d a g r e e m e n t in the first j u m p p o s i t i o n s for these three cases.

F r o m the a b o v e c o n s i d e r a t i o n , a m e t h o d for ob- taining g o o d bistable switchings is then p r o p o s e d by selecting

( p o s i t i o n o f first j u m p )

( p o s i t i o n o f first r e s o n a n t t r a n s m i s s i o n ) , where the first resonant t r a n s m i s s i o n is calculated by eq. ( 6 ) . Typical examples are d - - 3 . 1 0 2o in fig. 4 and ~,=25 ° in fig. 5.

5. Conclusions

Two unique p h e n o m e n a associated with T I R state, the resonant t r a n s m i s s i o n a n d the first j u m p , have been a n a l y z e d in detail. A s i m p l e m e t h o d has also been p r o p o s e d for designing g o o d bistable switchings, F r o m a sufficient c r i t e r i o n for i n s t a b i l i t y [ 13 ],

dlTIE/dN<O

a n d

IdlTlE/dN[> IT[E/N,

( 7 )

it is easy to verify that the p r o p o s e d bistable transmission curves have only two stable states [ 1 4 ] , which m e a n s practical bistable switchings can exist. T h e stability p r o b l e m o f the m u l t i - v a l u e d t r a n s m i s - sions (fig. 2) is difficult to analyze a n d chaotic results o f stability are expected. A p p l i c a t i o n s o f the m u l t i - v a l u e d transmissions, such as m u l t i - v a l u e d logic [ 15 ], are possible after the stability p r o b l e m o f the m u l t i - v a l u e d t r a n s m i s s i o n s is investigated in detail.

Acknowledgement

This work was s u p p o r t e d by the N a t i o n a l Science Council, R e p u b l i c o f China, u n d e r G r a n t N S C 79- 0417-E002-07.

References

[ l ] D.A.B. Miller, M.H. Mozolowski, A. Miller and S.D. Smith, Optics Comm. 27 (1978) 133.

[ 2 ] D.A.B. Miller, C.T. Seaton, M.E. Prise and S.D. Smith, Phys. Rev. Lett. 47 (1981) 197.

[3] A.E. Kaplan, Soy. Phys. 45 (1977) 896.

[4 ] P.W. Smith and W.J. Tomlinson, IEEE J. Quantum Electron. QE-20 (1984) 30.

[ 5 ] W.J. Tomlinson, J.P. Gordon, P.W. Smith and A.E. Kaplan, Appl. Optics 21 (1982) 2041.

[6] W. Chen and D.L. Mills, Phys. Rev. B 35 (1987) 524. [7] P.W. Smith, Phil. Trans. R. Soc. Lond. A 313 (1984) 349. [8] A.C. Walker, F.A.P. Tooley, M.E. Prise, J.G.H. Mathew,

A.K. Kar, M. R. Taghizadeh and S.D. Smith, Phil. Trans. R. Soc. Lond. A 313 (1984) 249.

[9] S.D. Smith, Phil. Trans. R. Soc. Lond. A 313 (1984) 195. [ I0] A. Huang, Proc. IEEE 72 (1984) 780.

[ l l ] L.M. Milne-Thomson, Jacobian elliptic functions tables (Dover, New York, 1950).

[12]J.M. Ortega and W.C. Rheinboldt, Iterative solution of nonlinear equations in several variables (Academic Press, New York, 1970).

[ 13 ] W. Chen and D.L. Mills, Phys. Rev. B 36 (1987) 6269. [ 14 ] H.M. Gibbs, Optical bistability (Academic Press, New York,

1985).

[15] R. Arrathoon, Optical computing (Marcel Dekker, New York and Basel, 1989).