熱帶圓錐曲線之研究 - 政大學術集成

全文

(1)國立政治大學應用數學系數學教學碩士在職專班碩士學位論文. 學. 熱帶圓錐曲線之研究. ‧. ‧ 國. 立. 政治大. On Tropical Conics. n. er. io. sit. y. Nat. al. Ch. i Un. v. engchi 撰碩專班學生：黃馨儀. 指導教授：蔡炎龍博士. 中華民國九十九年八月二十三日.

(2) 中文摘要本篇文章主要研究熱帶幾何之圓錐曲線，即二元二次多項式“根”的圖形。在文章中，我們以二元二次多項式係數關係做曲線的分類，歸納出20種熱帶圓錐曲線圖形，並證明此為完整的熱帶圓錐曲線之分類。然後，我們進一步討論如何調整二元二次多項式係數使圖形平移。最後，提出以熱帶直線輔助熱帶圓錐曲線快速作圖的方式。. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. i. i Un. v.

(3) 英文摘要 The purpose of the present study is to investigate conics -the graphs of the “roots” of quadratic polynomial- in tropical geometry. First, we induct and classify twenty types of tropical conics based on the relation between the coefficients and roots in quadratic polynomial. Second, evidences are provided to prove the classification thorough and intact. Then, we further discuss how to modify the quadratic polynomial in order to translate the graphs. Finally, suggestion about how to use tropical line to assist the graphing of tropical conics more efficiently is provided.. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. ii. i Un. v.

(4) 目錄中文摘要. i. 政治大緒論 ...................................................................................................... 立熱帶幾何簡介.......................................................................................... 英文摘要. ii. 第一章. 1. 學. ‧ 國. 第二章. 3. 第三章熱帶多項式 ............................................................................................. 6. 第四章熱帶多項式的“根”................................................................................... 9. ‧. 第五章熱帶圓錐曲線......................................................................................... 14. y. Nat. 第六章熱帶圓錐曲線的作圖方式........................................................................ 45. er. io. sit. 第七章結論 ...................................................................................................... 51 參考文獻 ............................................................................................................ 52. n. al. Ch. engchi. iii. i Un. v.

(5) 第一章. 緒論. 熱帶幾何起源於約20年前，來自巴西的數學家與電腦科學家Imre Simon是這個理論的先驅，熱帶幾何的名稱也源自於此。最近幾年，大家開始漸漸瞭解到熱帶幾何在. 政治大具有一般化且令人滿意的定義。有些在古典幾何中非常著名的定理，例如：Bezout’s 立 theorem [3]，在熱帶幾何裡面也是成立的。還有，Mikhalkin也在熱帶幾何中，證明. 組合數學、計算機代數，以及代數幾何上的重要性，一些觀念在熱帶幾何中，也已經. ‧ 國. 學. 給定虧格(genus)g和次數d，通過3d + g − 1個點的平面曲線個數 [4]。在文章中，將介紹一些關於熱帶幾何的基礎概念，而我們最主要的目的是熱帶半. ‧. 環(R ∪ {−∞}, ⊕,

(6) )，在熱帶半環中，重新定義熱帶幾何中的“加法”及“乘法”，使得. y. Nat. 數字運算在熱帶幾何中變得更加簡單！並證明在熱帶幾何中，加法及乘法的交換律、. io. sit. 分配律成立，而且在加法及乘法運算都有一個單位元素。接著，介紹熱帶幾何中的多. n. al. er. 項式及多項式性質，並舉例說明什麼是一元m次多項式的“根”，然後，將“根”的概念. i Un. v. 推廣到n元m次熱帶多項式，進一步定義出熱帶多項式的“根”。. Ch. engchi. 第五章及第六章內容為本文最主要的研究成果。在第五章中，結合牛頓多邊形分割的方式，先猜測出熱帶圓錐曲線可能有20種型式。在定理A中，以討論二元二次熱帶多項式係數的方式，確實證明出共有20種型式的熱帶圓錐曲線，並由證明過程得知，每一種牛頓多邊形分割與二元二次熱帶多項式係數間的對應關係，也就是說，我們能夠知道在何種係數關係下，可以得到想要的牛頓多邊形分割。然後，再進一步，由定理B提出如何調整二元二次熱帶多項式的係數，使得熱帶圓錐曲線能在xy平面上平移。第六章熱帶圓錐曲線作圖的想法，是由定理A證明過程中分析而得到，最主要是希 1.

(7) 望能發揮“化繁為簡”的精神，利用熱帶直線幫助熱帶圓錐曲線作圖。由於，熱帶圓錐曲線共有20種型式，且以熱帶圓錐曲線的基本作圖方式，我們共需要做15次的討論才可完成圖形，不過，熱帶直線的圖形只有一種型式，若能利用熱帶直線來幫助熱帶圓錐曲線的作圖，找出兩者之間的關聯性，或許能夠在作圖上節省許多時間。. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. 2. i Un. v.

(8) 第二章. 熱帶幾何簡介. 我們研讀的基本目標是熱熱帶半環 (R∪{−∞}, ⊕,

(9) )，並依據Grigory Mikhalkin的方式 [5]，在熱帶半環中，重新定義基本的加法運算及乘法運算如下：. 政治大. 定義 1. 若x, y ∈ R ∪ {−∞}，則：. 立. (1) x ⊕ y = max (x, y)，換句話說，熱帶加法是求出兩個元素的最大值。. ‧ 國. 學. (2) x

(10) y = x + y，換句話說，熱帶乘法是求出兩個元素的和。. ‧. 範例 1. 3 ⊕ 7 = max (3, 7) = 7. Nat. io. sit. y. 範例 2. 3

(11) 7 = 3 + 7 = 10. n. al. er. 範例 3. 3 ⊕ 3

(12) 7 = 3 ⊕ 10 = 10 範例 4. 3

(13) (1 ⊕ 7) = 3

(14) 7 = C 10 h. engchi. i Un. v. 範例 5. 3

(15) 1 ⊕ 3

(16) 7 = 4 ⊕ 10 = 10 範例 6. 依據熱帶加法及熱帶乘法定義，我們可以製成熱帶加法表格，如表 2.1，以及熱帶乘法的表格，如表 2.2，這是兩個連小學生都能輕易記憶的表格，因為在熱帶幾何中，把加法和乘法變簡單了。許多計算上熟悉的公設在熱帶幾何中仍然維持正確，假設x, y, z ∈ R ∪ {−∞}，則以下為熱帶幾何中不變的性質 [1], [6]： 3.

(17) ⊕. 1. 2. 3. 4. 5. 6.

(18). 1. 2. 3. 4. 5. 6. 1. 1. 2. 3. 4. 5. 6. 1. 2. 3. 4. 5. 6. 7. 2. 2. 2. 3. 4. 5. 6. 2. 3. 4. 5. 6. 7. 8. 3. 3. 3. 3. 4. 5. 6. 3. 4. 5. 6. 7. 8. 9. 4. 4. 4. 4. 4. 5. 6. 4. 5. 6. 7. 8. 9. 10. 5. 5. 5. 5. 5. 5. 6. 5. 6. 7. 8. 9. 10. 11. 6. 6. 6. 6. 6. 6. 6. 6. 7. 8. 9. 10. 11. 12. 表 2.2: 熱帶乘法表格. 表 2.1: 熱帶加法表格. 政治大. 定理 1. 熱帶加法及熱帶乘法的結合律成立。也就是說，x ⊕ (y ⊕ z) = (x ⊕ y) ⊕ z，. 立. 而且x

(19) (y

(20) z) = (x

(21) y)

(22) z. ‧ 國. 學. 證明: 因為 max(x,max (y, z)) = max (x, y, z) = max(max(x, y), z)，所以x ⊕ (y ⊕ z) = (x ⊕ y) ⊕ z。因為 x + (y + z) = (x + y) + z，所以x

(23) (y

(24) z) = (x

(25) y)

(26) z。. ‧. 定理 2. 熱帶加法及熱帶乘法的交換律成立。也就是說，x ⊕ y = y ⊕ x，而. sit. y. Nat. 且x

(27) y = y

(28) x。. er. al. n. 以x

(29) y = y

(30) x。. io. 證明 : 因為 max (x, y) = max (y, x)，所以x ⊕ y = y ⊕ x。因為 x + y = y + x，所. Ch. engchi. i Un. v. 定理 3. 熱帶加法及熱帶乘法的分配律成立。也就是說，x

(31) (y ⊕ z) = x

(32) y ⊕ x

(33) z。證明: 因為x+ max (y, z) = max(x+y, x+z)，所以x

(34) (y ⊕z) = x

(35) y ⊕x

(36) z。定理 4. 在熱帶加法及熱帶乘法的運算都有一個單位元素，例如：x ⊕ −∞ = −∞ ⊕ x = x ， x

(37) 0 = 0

(38) x = x。也就是說，−∞是熱帶加法單位元素， 0 是熱帶乘法單位元素。證明: 因為−∞ 小於任意實數，所以x ⊕ −∞ = x。因為任意實數加上0值不改變，所以x

(39) 0 = x。 4.

(40) 定理 5. 若x 6= −∞，則乘法反元素存在且唯一，例如：x

(41) (−x) = 0。也就是說，−x是x的乘法反元素。證明: 因為x 6= −∞，所以x ∈ R，且x + (−x) = 0，所以x

(42) (−x) = 0，即−x是x的乘法反元素。以上我們的討論僅限於熱帶加法及熱帶乘法兩種運算方式，那是否有相對應的熱帶減法或熱帶除法? 事實上，並沒有熱帶減法，我們不能說 x 等於 10 減 12，因為12 ⊕ x = 10的解並不存在。但是，當限制b 6= −∞時，我們可以有a b = a − b。. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. 5. i Un. v.

(43) 第三章. 熱帶多項式. 令變數x1 , x2 , . . . , xn 為代表熱帶半環(R ∪ {−∞}, ⊕,

(44) )中不等於−∞的元素。一個單項式是這些變數的任意乘積，且每一個變數可重複出現。根據交換律，我們可以. 政治大

(45) 立 x

(46) x

(47) x

(48) x

(49) x

(50) x =x x x x. 把單項式中的這些變數分類，並利用指數符號來簡化單項式的表示方式，例如： x2

(51) x1. 3. 1. 4. 2. 3. 2 3 2 1 2 3 4. 2. (3.1). ‧ 國. 學. 一個單項式表示一個函數從Rn 到R。當我們用典型的運算方式計算(3.1)式時，我們得到一個線性函數：. ‧. x2 + x1 + x3 + x1 + x4 + x2 + x3 + x2 = 2x1 + 3x2 + 2x3 + x4. Nat. n. al. er. io. 註記 1. 熱帶單項式都是整係數線性函數。. sit. y. 每一個整係數線性函數都是以這種方式出現。因此，我們知道：. i Un. v. 定義 2. 一個熱帶多項式是由有限個熱帶單項式線性組合而成：. Ch. engchi. p(x1 , x2 , . . . , xn ) = a1

(52) xi11 xi22 . . . xinn ⊕ a2

(53) xj11 xj22 . . . xjnn ⊕ . . . ⊕ am

(54) xt11 xt22 . . . xtnn (3.2) 在(3.2)式中a1 , a2 , . . . , am 為實數且i1 , . . . , j1 , . . . , t1 , . . . , tn 為整數。每一個熱帶多項式表示一個函數從Rn 到R，當我們用典型的運算方式計算(3.2)式，則我們得到有限個線性函數所成集合的最大值，即 p(x1 , x2 , . . . , xn ) =max(a1 + i1 x1 + . . . + in xn , a2 + j1 x1 + . . . + jn xn , . . . , am + t1 x1 + . . . + tn xn ) 6.

(55) 由David Speyer及Bernd Sturmfels的文章 [7]，我們可以得知定理6.中，關於p(x1 , x2 , . . . , xn )的三個性質，並歸納出註記2的結論。定理 6. 上述函數p(x1 , x2 , . . . , xn ) : Rn −→ R有下列三個重要的性質： (1) p是連續的 (2) p是分段線性的，且分段的個數是有限的 ) ≤ 21 (p(x) + p(y))對於所有的x, y ∈ Rn (3) p是凸函數，也就是說，p( x+y 2 我們知道如果每一個函數如果滿足上述的三個性質，則可以表示成有限個線性函數所成集合的最大值。因此，我們得到：. 政治大. 註記 2. 有n個變數x1 , x2 , . . . , xn 的熱帶多項式，確實是在Rn 上具有整係數的分段線性. 立. 凸函數。. ‧. ‧ 國. 學. 下面範例中，我們取一元三次熱帶多項式為例子，作圖說明註記2。. n. er. io. sit. y. Nat. al. Ch. engchi. i Un. v. 圖 3.1: p(x) = a

(56) x3 ⊕ b

(57) x2 ⊕ c

(58) x ⊕ d的函數圖形. 範例 7. 考慮一元三次熱帶多項式的一般情況： p(x) = a

(59) x3 ⊕ b

(60) x2 ⊕ c

(61) x ⊕ d. (3.3). 為了畫出這個函數圖形，我們先將下列四條直線畫在 xy 平面上：y = 3x + a, y = 2x + b, y = x + c, y = d。則 p(x) 是取 x 為一實數，代入上述四條直線方程式 7.

(62) 中，所得到的最大 y 值。也就是說，p(x) 的圖形由四條直線中取出較高的線段所組成。如果在d − c ≤ c − b ≤ b − a的條件下畫出這四條直線，則p(x)的圖形在x = b − a，x = c − b，x = d − c 時為折點，如圖 3.1，因此，我們可將 p(x) 分解成三個一次式的乘積： p(x) = a

(63) (x ⊕ (b − a))

(64) (x ⊕ (c − b))

(65) (x ⊕ (d − c)). (3.4). 具有一個變數的m次熱帶多項式，可被唯一表示為m個一次熱帶多項式的乘積，也就是說，熱帶多項式滿足代數基本定理。特別地，在熱帶幾何中，兩個不同的熱帶多項式可被表示為相同的熱帶多項式的乘積，例如：. 治 x ⊕ −3

(66) x⊕2 政大 2. 立. =x2 ⊕ −1

(67) x ⊕ 2. ‧ 國. 學. =(x ⊕ 1)2. 因此，我們可將每一個分解成相同熱帶多項式乘積的熱帶多項式視為相同的熱帶多項. ‧. n. al. sit. io. (x ⊕ 0)

(68) (y ⊕ 0)

(69) (x

(70) y ⊕ 0). er. Nat. 不成立，例如：. y. 式。但是，當熱帶多項式的變數為兩個或兩個以上時，熱帶多項式的唯一分解性質並. i Un. v. =(x

(71) y ⊕ x ⊕ 0)

(72) (x

(73) y ⊕ y ⊕ 0). Ch. engchi. 在Gao和Lauder的文章中曾經提到，對於一個給定的熱帶多項式，能夠建立一個法則，使得此熱帶多項式有不可簡化的分解方式是重要的 [2]。. 8.

(74) 第四章. 熱帶多項式的“根根”. 一個熱帶多項式函數 p(x) : Rn −→ R 是將 Rn 中的元素代入給定有限個線性函數，並取出最大值。現在，我們想知道熱帶多項式p(x)的“根”到底是什麼? 當 n = 1，. 政治大多項式乘積，如(3.4)式，仿照一般多項式的概念，我們可以說{b − a, c − b, d − c}為立 p(x) 的“根”。接著，我們根據此概念，把熱帶多項式根更具體定義如下：且 p(x) 為(3.3)式中的一元三次多項式時，我們知道 p(x) 可以分解為三個一次熱帶. ‧ 國. 學. 定義 3. 令熱帶多項式函數 p(x) : Rn −→ R，則熱熱帶多項式 p(x)的的根為{x ∈ Rn |x代. ‧. 入給定有限個線性函數中，使得最大值至少出現兩次}，稱此集合為hypersurface，並以符號H(p)代表此集合。也就是說，x ∈ H(p) ⇔ 在 x 時， p 的圖形一定不是線性。. y. Nat. H(p) = {b − a, c − b, d − c}. n. al. Ch. er. io. sit. 範例 8. 令p(x) = a

(75) x3 ⊕ b

(76) x2 ⊕ c

(77) x ⊕ d，則. i Un. v. 且由p(x)的圖形，如圖 3.1，我們可以知道在 {b − a, c − b, d − c} 時，p的圖形不是線性。. engchi. 接下來，考慮兩個變數的多項式： p(x, y) = ⊕(i,j) cij

(78) xi

(79) y j. cij ∈ R. 首先，我們討論p(x, y)的最高次數為1的情形，並在xy平面上畫出H(p)的圖形。範例 9. 考慮二元一次多項式的一般情況： p(x, y) = a

(80) x ⊕ b

(81) y ⊕ c 9. a, b, c ∈ R.

(82) 圖 4.1: 二元一次多項式a

(83) x ⊕ b

(84) y ⊕ c的根在xy平面上的圖形. 則 H(p) 為所有使得函數 p(x) 非線性的 (x, y) 所成的集合。H(p) 的圖形，包含了在. 政治大. xy 平面上，以點 (c − a, c − b) 為原點，往 (1, 1)、(−1, 0)、(0, −1) 三個方向所畫出. 立. 的射線，如圖 4.1，我們稱此圖形為熱帶幾何中的直線，簡稱為熱熱帶直線。熱帶直線包. 學 ‧. ‧ 國. 含了一個頂點及三條射線。. n. er. io. sit. y. Nat. al. Ch. engchi. i Un. v. 圖 4.3: 任兩條熱帶直線交於一點. 圖 4.2: 任兩點決定一條熱帶直線. 註記 3. 任兩點決定一條熱帶直線，如圖 4.2。註記 4. 任兩條熱帶直線交於一點，如圖 4.3。當p(x, y)為二元二次多項式的一般情況時，H(p)的圖形就比較複雜。我們以下面範例說明在二元二次多項式時，H(p)的作圖方式： 10.

(85) 範例 10. p(x, y) = −1

(86) x2 ⊕ 1

(87) xy ⊕ −1

(88) y 2 ⊕ 1

(89) x ⊕ 1

(90) y ⊕ −1，則H(p)為使得集合 {−1 + 2x, 1 + x + y, −1 + 2y, 1 + x, 1 + y, −1} 中的最大值至少能出現2次以上的(x, y)。因此，我們先分別假設最大值為6個元素中其中一項，然後，檢驗此最大值是否能出現2次，並逐一收集所有滿足條件的(x, y)畫在xy平面上。討論方式如下： (1) 如果最大值為−1 + 2x，且−1 + 2x = 1 + x + y，即x − y = 2，則2 ≤ x; (2) 如果最大值為−1 + 2x，且−1 + 2x = −1 + 2y，即x − y = 0，則x無解; (3) 如果最大值為−1 + 2x，且−1 + 2x = 1 + x，即x = 2，則y ≤ 0; (4) 如果最大值為−1 + 2x，且−1 + 2x = 1 + y，即y = 2x − 2，則x無解;. 政治大 (5) 如果最大值為−1 + 2x，且−1 + 2x = −1，即x = 0，則y無解; 立. ‧ 國. 學. (6) 如果最大值為1 + x + y，且1 + x + y = −1 + 2y，即x − y = −2，則2 ≤ y; (7) 如果最大值為1 + x + y，且1 + x + y = 1 + x，即y = 0，則0 ≤ x ≤ 2;. ‧. (8) 如果最大值為1 + x + y，且1 + x + y = 1 + y，即x = 0，則0 ≤ y ≤ 2;. y. Nat. al. er. io. sit. (9) 如果最大值為1 + x + y，且1 + x + y = −1，即x = −y − 2，則y無解;. n. (10) 如果最大值為−1 + 2y，且−1 + 2y = 1 + x，即x = 2y − 2，則y無解;. Ch. engchi. i Un. v. (11) 如果最大值為−1 + 2y，且−1 + 2y = 1 + y，即y = 2，則x ≤ 0; (12) 如果最大值為−1 + 2y，且−1 + 2y = −1，即y = 0，則x無解; (13) 如果最大值為1 + x，且1 + x = 1 + y，即x − y = 0，則−2 ≤ x ≤ 0; (14) 如果最大值為1 + x，且1 + x = −1，即x = −2，則y ≤ −2; (15) 如果最大值為1 + y，且1 + y = −1，即y = −2，則x ≤ −2。因此，得到圖 4.4, 圖 4.4即為H(p)的圖形. 11.

(91) 圖 4.4: −1

(92) x2 ⊕ 1

(93) xy ⊕ −1

(94) y 2 ⊕ 1

(95) x ⊕ 1

(96) y ⊕ −1的根在xy平面上的圖形. 政治大. 立. io. sit. y. ‧. ‧ 國. 學. Nat. 圖 4.5: 圖 4.4所對應的牛頓三角形分割. n. al. er. 當p(x, y)為二元二次多項式時，我們稱H(p)的圖形為熱帶幾何中的圓錐曲線，. i Un. v. 簡稱為熱熱帶圓錐曲線。每一個熱帶圓錐曲線最多包含四個頂點，三條線段及六條射. Ch. engchi. 線，而且每一個熱帶圓錐曲線均對應一種以(0, 0), (0, 2), (2, 0)為頂點的牛頓三角形分割 [8]。範例10中H(p)的圖形，如圖 4.4，其對應的三角形分割，如圖 4.5實線部分，此三角形分割中包含四個三角形，三條在內部的線段，及六條邊界的線段。在圖 4.5中，虛線代表H(p)的圖形。接著，我們將說明如何找出與熱帶曲線所對應的牛頓多邊形分割 [3]，令p(x, y) = max {ai1 x + ai2 y + bi , i = 1, 2, 3, · · · , n}，假設 p 的最高次數為 d，則(ai1 , ai2 )為三角形4d := {(a1 , a2 )|a1 > 0, a2 > 0, a1 + a2 6 d}中的格子點，考慮相異兩. 12.

(97) 點(ak1 , ak2 )，(as1 , as2 )，k, s ∈ {1, 2, 3, · · · , n}且k 6= s。若有一點(x1 , y1 ) ∈ R2 使得 p(x1 , y1 ) = ak1 x1 + ak2 y1 + bk = as1 x1 + as2 y1 + bs 則在(ak1 , ak2 )及(as1 , as2 )兩點間作一線段，那麼我們可得到4d 的分割，使得此分割圖形的每一邊對應到 H(p) 的邊，並與 H(p) 的邊垂直，且每一個有界的區塊對應到 H(p) 的頂點，我們稱此分割為 H(p) 對應的牛頓三角形分割。. 立. 政治大. ‧. ‧ 國. 學. io. sit. y. Nat. 圖 4.6: 無法對應到熱帶曲線的牛頓多邊形分割. n. al. er. 但是，並非每一個牛頓多邊形分割都可以對應到一種熱帶曲線，如圖 4.6。若. i Un. v. 此牛頓多邊形分割可以對應到一種熱帶曲線Γ，則我們可以知道Γ對應到牛頓多邊. Ch. engchi. 形分割中E4 與E3 的兩線段應該相交，但對應到E4 與E2 的兩線段不相交，因此，對應到E2 的線段長度需要比對應到E1 的線段長度要大，按照這樣的方式討論下去，我們會得到E1 的線段長度大於E1 的線段長度的矛盾情形，因此，圖 4.6中的牛頓多邊形分割確實沒有辦法對應到一種熱帶曲線。事實上，每一種可以對應到熱帶曲線的牛頓多邊形分割我們稱為正正則牛頓多邊形分割 (regular Newton polyhedral subdivisions)。不過，我們要強調牛頓多邊形分割決定熱帶曲線的組合型式，而非熱帶曲線本身的圖形，例如圖 4.4中的線段長度或位置是會隨著p的係數而改變的。. 13.

(98) 第五章. 熱帶圓錐曲線. 我們已經知道每一種熱帶曲線都可以對應到一種牛頓多邊形分割，但是，並非所有的牛頓多邊形分割都可以對應到一種熱帶曲線，而且，牛頓多邊形分割只能決定熱. 政治大討論出熱帶圓錐曲線可能的型式，並在xy平面找出與之對應的圖形。立令p(x, y) = max {2x + a, x + y + b, 2x + c, x + d, y + e, f }，我們可以知道熱. 帶曲線的組合型式，而非熱帶曲線本身的圖形。現在，我們要先以牛頓多邊形的分割. ‧ 國. 學. 帶圓錐曲線必對應到以(0, 0), (0, 2), (2, 0)為頂點的牛頓三角形分割，而此牛頓三角形分割的所有情形共有20種，如圖 5.1，因此，我們可以猜測熱帶圓錐曲線的型式應該. ‧. 有20種。. y. Nat. 接下來，將利用範例10作圖的方式，討論出熱帶圓錐曲線在xy平面上的所有圖. er. io. al. sit. 形，並找出每一個圖形所對應的三角形分割。. n. 定理A. 熱帶圓錐曲線在xy平面上的所有圖形有20種不同的形式。即熱帶圓錐曲線可. Ch. i Un. v. 以對應到以(0, 0), (0, 2), (2, 0)為頂點的20種牛頓三角形分割。. engchi. 證明: 將二元二次多項式的一般式表示如下：. p(x, y) = ax2 ⊕ bxy ⊕ cy 2 ⊕ dx ⊕ ey ⊕ f. a, b, c, d, e, f ∈ R. 當 a + c < 2b, a + f < 2d, c + f < 2e 時，“根”在 xy 平面上的圖形，依下面七種情形分別討論如下：假設f − d = e − b < d − a 且 d − b = f − e < e − c，將每一種可能解的狀況討論如下: 14.

(99) 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. i Un. v. 圖 5.1: 以(0, 0), (0, 2), (2, 0)為頂點的20種牛頓三角形分割. 15.

(100) 圖 5.2: 熱帶圓錐曲線之一. 圖 5.3: 圖 5.2對應的牛頓三角形分割. (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則d − a ≤ x;. 政治大. (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. 立. c−a ，則x無解; 2. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則y ≤ d − b;. ‧ 國. 學. (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則x無解; f −a ，則y無解; 2. ‧. (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. sit. y. Nat. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則e − c ≤ y;. n. al. er. io. (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則f − d ≤ x ≤ d − a;. i Un. v. (8) 如果最大值為b + x + y，且b + x + y = e + y，即x = e − b，則f − e ≤ y ≤ e − c;. Ch. engchi. (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則y無解; (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則y無解; (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則x ≤ f − d; (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. f −c ，則x無解; 2. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則(x, y) = (f − d, f − e);. 16.

(101) (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則y ≤ f − e; (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則x ≤ f − d。綜合上述結果，此時圖形如圖 5.2.. 政治大圖 5.4: 熱帶圓錐曲線之二圖 5.5: 圖 5.4對應的牛頓三角形分割立. ‧ 國. 學. 假設f − d < e − b < d − a 且 f − e < e − c < d − b，將每一種可能解的狀況討論如下:. ‧. (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則d − a ≤ x; c−a ，則x無解; 2. er. io. al. sit. y. Nat. (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. v. n. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則y ≤ d − b;. Ch. engchi. i Un. (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則x無解; (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. f −a ，則y無解; 2. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則d − b ≤ y; (7) 如果最大值為b+x+y，且b+x+y = d+x，即y = d−b，則c+d−2b ≤ x ≤ d−a; (8) 如果最大值為b + x + y，且b + x + y = e + y，即x = e − b，則y無解; (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則y無解; 17.

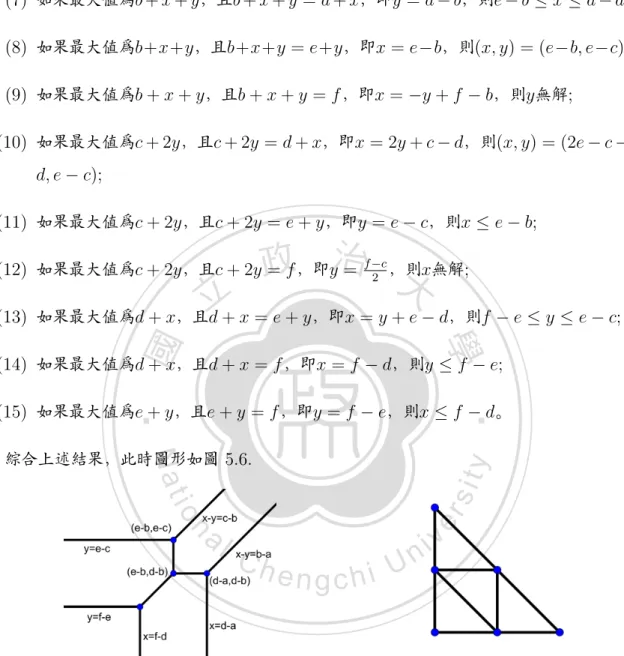
(102) (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則e − c ≤ y ≤ d − b; (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則x ≤ 2e − c − d; (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. f −c ，則x無解; 2. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則f − e ≤ y ≤ e − c; (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則y ≤ f − e; (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則x ≤ f − d。綜合上述結果，此時圖形如圖 5.4.. 立. 政治大. ‧. ‧ 國. 學 y. Nat. 圖 5.7: 圖 5.6對應的牛頓三角形分割. n. er. io. al. sit. 圖 5.6: 熱帶圓錐曲線之三. i Un. v. 假設f − d < e − b < d − a 且 f − e < d − b = e − c，將每一種可能解的狀況討論如下:. Ch. engchi. (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則d − a ≤ x; (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. c−a ，則x無解; 2. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則y ≤ d − b; (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則x無解; (5) 如果最大值為a + 2x，且a + 2x = f ，即x = 18. f −a ，則y無解; 2.

(103) (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則e − c ≤ y; (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則e − b ≤ x ≤ d − a; (8) 如果最大值為b+x+y，且b+x+y = e+y，即x = e−b，則(x, y) = (e−b, e−c); (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則y無解; (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則(x, y) = (2e − c − d, e − c); (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則x ≤ e − b;. 政治，則x無解; 大. (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. 立. f −c 2. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則f − e ≤ y ≤ e − c;. ‧ 國. 學. (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則y ≤ f − e;. ‧. (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則x ≤ f − d。. Nat. n. al. er. io. sit. y. 綜合上述結果，此時圖形如圖 5.6.. Ch. engchi. 圖 5.8: 熱帶圓錐曲線之四. i Un. v. 圖 5.9: 圖 5對應的牛頓三角形分割. 假設f − d < e − b < d − a 且 f − e < d − b < e − c，將每一種可能解的狀況討論如下:. 19.

(104) (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則d − a ≤ x; (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. c−a ，則x無解; 2. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則y ≤ d − b; (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則x無解; (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. f −a ，則y無解; 2. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則e − c ≤ y; (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則e − b ≤ x ≤ d − a;. 治政 (8) 如果最大值為b + x + y，且b + x + y = e + y，即x大 = e − b，則d − b ≤ y ≤ e − c; 立 ‧ 國. 學. (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則y無解; (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則y無解;. ‧. f −c ，則x無解; 2. io. sit. Nat. (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. y. (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則x ≤ e − b;. er. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則f − d ≤ y ≤ d − b;. al. n. iv n C (14) 如果最大值為d + x，且d + x = = f − d，則y ≤ f − e; hfe，即x ngchi U. (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則x ≤ f − d。綜合上述結果，此時圖形如圖 5. 假設e − b < f − d < d − a 且 d − b < f − e < e − c，將每一種可能解的狀況討論如下: (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則d − a ≤ x; (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y = 20. c−a ，則x無解; 2.

(105) 圖 5.10: 熱帶圓錐曲線之五. 圖 5.11: 圖 5.10對應的牛頓三角形分割. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則y ≤ d − b;. 政治大. (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則x無解;. 立. (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. f −a ，則y無解; 2. ‧ 國. 學. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則e − c ≤ y;. ‧. (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則f − d ≤ x ≤ d − a;. sit. y. Nat. (8) 如果最大值為b + x + y，且b + x + y = e + y，即x = e − b，則f − e ≤ y ≤ e − c;. n. al. er. io. (9) 如果最大值為b+x+y，且b+x+y = f ，即x = −y +f −b，則d−b ≤ y ≤ f −e;. i Un. v. (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則y無解;. Ch. engchi. (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則x ≤ e − b; (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. f −c ，則x無解; 2. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則y無解; (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則y ≤ f − e; (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則x ≤ e − b。. 21.

(106) 圖 5.12: 熱帶圓錐曲線之六. 圖 5.13: 圖 5.12對應的牛頓三角形分割. 綜合上述結果，此時圖形如圖 5.10.. 政治大. 假設f − d < d − a = e − b 且 f − e < d − b < e − c，將每一種可能解的狀況討論如下:. 立. ‧ 國. (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. 學. (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則d − a ≤ x; c−a ，則x無解; 2. ‧. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則y ≤ d − b;. y. Nat. (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. al. er. io. sit. (4) 如果最大值為a+2x，且a+2x = e+y，即y = 2x+a−e，則(x, y) = (d−a, d−b); f −a ，則y無解; 2. n. iv n C (6) 如果最大值為b + x + y，且b +hxe + y = c + 2y，即x n g c h i U − y = c − b，則e − c ≤ y; (7) 如果最大值為b+x+y，且b+x+y = d+x，即y = d−b，則(x, y) = (d−a, d−b); (8) 如果最大值為b + x + y，且b + x + y = e + y，即x = e − b，則d − b ≤ y ≤ e − c; (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則y無解; (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則y無解; (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則x ≤ e − b; 22.

(107) (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. f −c ，則x無解; 2. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則f − e ≤ y ≤ d − b; (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則y ≤ f − e; (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則x ≤ f − d。綜合上述結果，此時圖形如圖 5.12.. 立. 政治大. ‧ 國. 學. 圖 5.14: 熱帶圓錐曲線之七. 圖 5.15: 圖 5.14對應的牛頓三角形分割. ‧ y. sit. io. al. er. 論如下:. Nat. 假設f − d < d − a < e − b 且 f − e < d − b < e − c，將每一種可能解的狀況討. v. n. (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則e − b ≤ x;. Ch. engchi. i Un. (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. c−a ，則x無解; 2. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則y ≤ 2d − a − e; (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則d − a ≤ x ≤ e − b; (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. f −a ，則y無解; 2. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則e − c ≤ y; (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則x無解; 23.

(108) (8) 如果最大值為b+x+y，且b+x+y = e+y，即x = e−b，則a+e−2b ≤ y ≤ e−c; (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則y無解; (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則y無解; (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則x ≤ e − b; (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. f −c ，則x無解; 2. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則f − e ≤ y ≤ 2d − a − e; (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則y ≤ f − e;. 政治大. (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則x ≤ f − d。. 立. 綜合上述結果，此時圖形如圖 5.14.. ‧. ‧ 國. 學. n. Ch 圖 5.16: 熱帶圓錐曲線之八. er. io. sit. y. Nat. al. iv n i U 圖 5.16對應的牛頓三角形分割 e n g c圖h 5.17:. 當 2b ≤ a + c, a + f < 2d, c + f < 2e 時，“根”在 xy 平面上的圖形，依下面三種情形分別討論如下：假設a + 2e < c + 2d，將每一種可能解的狀況討論如下: (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則當2b = a + c 時，d − a ≤ x; (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y = 24. c−a ，則d 2. − a ≤ x;.

(109) (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則y ≤ d −. a+c ; 2. (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則x無解; (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. f −a ，則y無解; 2. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則當2b = a + c 時，d −. a+c 2. ≤ y;. (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則當2b = a + c 時，(x, y) = (d − a, d −. a+c ); 2. 政治大. (8) 如果最大值為b + x + y，且b + x + y = e + y，即x = e − b，則y無解;. 立. (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則y無解;. ‧ 國. 學. (10) 如果最大值為c+2y，且c+2y = d+x，即x = 2y +c−d，則e−c ≤ y ≤ d− a+c ; 2. f −c ，則x無解; 2. sit. y. Nat. (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. ‧. (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則x ≤ 2e − c − d;. io. n. al. er. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則f − e ≤ y ≥ e − c;. v. (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則y ≤ f − e;. Ch. engchi. i Un. (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則x ≤ f − d。綜合上述結果，此時圖形如圖 5.16. 假設a + 2e = c + 2d，將每一種可能解的狀況討論如下: (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則當2b = a + c 時，d − a ≤ x; (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. 25. c−a ，則d 2. − a ≤ x;.

(110) 圖 5.18: 熱帶圓錐曲線之九. 圖 5.19: 圖 5.18對應的牛頓三角形分割. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則y ≤ e − c;. 政治大. (4) 如果最大值為a+2x，且a+2x = e+y，即y = 2x+a−e，則(x, y) = (d−a, e−c);. 立. (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. f −a ，則x無解; 2. ‧ 國. 學. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則當2b = a + c. ‧. 時，(x, y) = (d − a, e − c);. y. Nat. (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則當2b = a + c. er. io. sit. 時，(x, y) = (d − a, e − c);. (8) 如果最大值為b + x + y，且b + x + y = e + y，即x = e − b，則當2b = a + c. n. al. Ch. 時，(x, y) = (d − a, e − c);. engchi. i Un. v. (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則y無解; (10) 如果最大值為c+2y，且c+2y = d+x，即x = 2y+c−d，則(x, y) = (d−a, e−c); (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則x ≤ d − a; (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. f −c ，則x無解; 2. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則f − e ≤ y ≥ e − c;. 26.

(111) (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則y ≤ f − e; (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則x ≤ f − d。綜合上述結果，此時圖形如圖 5.18.. 政治大圖 5.20: 熱帶圓錐曲線之十圖 5.21: 圖 5.20對應的牛頓三角形分割立. ‧ 國. 學. 假設c + 2d < a + 2e，將每一種可能解的狀況討論如下:. ≤ x;. Nat. c−a ，則e 2. −. a+c 2. ≤ x;. io. er. (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. y. a+c 2. sit. 時，e −. ‧. (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則當2b = a + c. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則y ≤ 2d − a − e;. al. n. iv n C ; (4) 如果最大值為a+2x，且a+2x h = e+y，即y =i 2x+a−e，則d−a ≤ x ≤ e− a+c 2 engch U (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. f −a ，則x無解; 2. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則當2b = a + c 時，e − c ≤ y; (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則當x無解; (8) 如果最大值為b + x + y，且b + x + y = e + y，即x = e − b，則當2b = a + c 時，(x, y) = (e −. a+c ,e 2. − c); 27.

(112) (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則y無解; (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則y無解; (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則x ≤ e − (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. a+c ; 2. f −c ，則x無解; 2. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則f − e ≤ y ≤ 2d − a − e; (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則y ≤ f − e; (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則x ≤ f − d。綜合上述結果，此時圖形如圖 5.20.. 立. 政治大. 當 a + c < 2b, 2d ≤ a + f, c + f < 2e 時，“根”在 xy 平面上的圖形，依下面三種. ‧. ‧ 國. 學. 情形分別討論如下：. n. er. io. sit. y. Nat. al. Ch. i Un. v. i 圖 5.22對應的牛頓三角形分割 e n g c圖h 5.23:. 圖 5.22: 熱帶圓錐曲線之十一. 假設a + 2e < 2b + f ，將每一種可能解的狀況討論如下: (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則 f −a ≤ x; 2 (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. c−a ，則x無解; 2. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，當2d = a + f 時，則y ≤ d − b; 28.

(113) (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則x無解; (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. f −a ，則y 2. ≤. a+f 2. − b;. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則e − c ≤ y; (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則當2d = a + f 時，(x, y) = (d − a, d − b); (8) 如果最大值為b + x + y，且b + x + y = e + y，即x = e − b，則f − e ≤ y ≤ e − c; (9) 如果最大值為b+x+y，且b+x+y = f ，即x = −y+f −b，則 a+f −b ≤ y ≤ f −e; 2. 政治大. (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則y無解;. 立. (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. 學. ‧ 國. (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則x ≤ e − b; f −c ，則x無解; 2. ‧. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則y無解;. sit. y. Nat. (14) 如果最大值為d + x，且d + x = f ，即x = f − d，當2d = a + f 時，則y ≤ d − b;. n. al. er. io. (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則x ≤ e − b。. Ch. 綜合上述結果，此時圖形如圖 5.22.. engchi. 圖 5.24: 熱帶圓錐曲線之十二. i Un. v. 圖 5.25: 圖 5.24對應的牛頓三角形分割. 29.

(114) 假設a + 2e = 2b + f ，將每一種可能解的狀況討論如下: (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則e − b ≤ x; (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. c−a ，則x無解; 2. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，當2d = a + f 時，則y ≤ d − b; (4) 如果最大值為a+2x，且a+2x = e+y，即y = 2x+a−e，則(x, y) = (e−b, f −e); (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. f −a ，則y 2. ≤ f − e;. 政治大. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則e − c ≤ y;. 立. (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，當2d = a + f 時，. ‧ 國. 學. 則(x, y) = (d − a, d − b);. ‧. (8) 如果最大值為b + x + y，且b + x + y = e + y，即x = e − b，則f − e ≤ y ≤ e − c;. y. sit. io. er. (e − b, f − e);. Nat. (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則(x, y) =. (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則y無解;. al. n. iv n C (11) 如果最大值為c + 2y，且c + 2yh=ee + y，即y n g c h i= eU− c，則x ≤ e − b; (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. f −c ，則x無解; 2. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，當2d = a + f 時，則(x, y) = (e − b, f − e); (14) 如果最大值為d + x，且d + x = f ，即x = f − d，當2d = a + f 時，則y ≤ d − b; (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則x ≤ e − b。. 30.

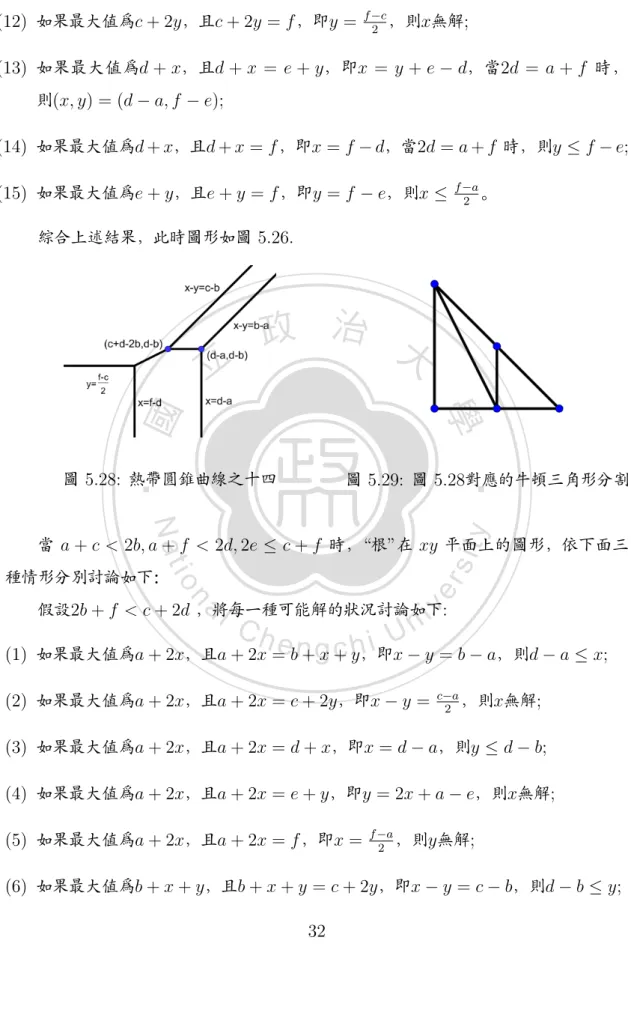
(115) 圖 5.26: 熱帶圓錐曲線之十三. 圖 5.27: 圖 5.26對應的牛頓三角形分割. 綜合上述結果，此時圖形如圖 5.24.. 政治大 (1) 如果最大值為a + 2x，且a 立+ 2x = b + x + y，即x − y = b − a，則e − b ≤ x; 假設2b + f < a + 2e，將每一種可能解的狀況討論如下:. ‧ 國. c−a ，則x無解; 2. 學. (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. ‧. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，當2d = a + f 時，則y ≤ 2d − a − e;. y. Nat. (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. n. al. Ch. er. io. sit. ≤ x ≤ e − b; (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則 f −a 2 f −a ，則y 2. n engchi U. ≤ f − e;. iv. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則e − c ≤ y; (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則x無解; (8) 如果最大值為b+x+y，且b+x+y = e+y，即x = e−b，則a+e−2b ≤ y ≤ e−c; (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則y無解; (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則y無解; (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則x ≤ e − b; 31.

(116) (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. f −c ，則x無解; 2. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，當2d = a + f 時，則(x, y) = (d − a, f − e); (14) 如果最大值為d + x，且d + x = f ，即x = f − d，當2d = a + f 時，則y ≤ f − e; (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則x ≤. f −a 。 2. 綜合上述結果，此時圖形如圖 5.26.. 立. 政治大. ‧. ‧ 國. 學. 圖 5.28: 熱帶圓錐曲線之十四. 圖 5.29: 圖 5.28對應的牛頓三角形分割. y. Nat. sit. 當 a + c < 2b, a + f < 2d, 2e ≤ c + f 時，“根”在 xy 平面上的圖形，依下面三. n. al. er. io. 種情形分別討論如下：. i Un. v. 假設2b + f < c + 2d ，將每一種可能解的狀況討論如下:. Ch. engchi. (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則d − a ≤ x; (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. c−a ，則x無解; 2. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則y ≤ d − b; (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則x無解; (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. f −a ，則y無解; 2. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則d − b ≤ y; 32.

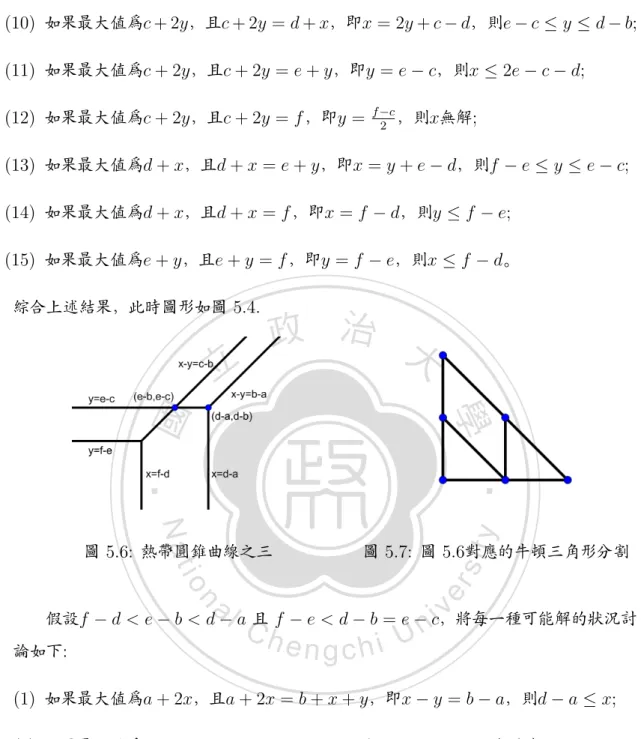
(117) (7) 如果最大值為b+x+y，且b+x+y = d+x，即y = d−b，則c+d−2b ≤ x ≤ d−a; (8) 如果最大值為b + x + y，且b + x + y = e + y，即x = e − b，則y無解; (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則y無解; ≤ y ≤ d − b; (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則 f −c 2 (11) 如果最大值為c+2y，且c+2y = e+y，即y = e−c，則當2e = c+f 時，x ≤ f −d; (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. f −c ，則x 2. ≤ f − d;. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則當2e = c + f. 政治大. ); 時，(x, y) = (f − d, f −c 2. 立. (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則y ≤. f −c ; 2. ‧ 國. 學. (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則當2e = c + f 時，x ≤ f − d。. ‧. 綜合上述結果，此時圖形如圖 5.28.. n. er. io. sit. y. Nat. al. Ch. engchi. 圖 5.30: 熱帶圓錐曲線之十五. i Un. v. 圖 5.31: 圖 5.30對應的牛頓三角形分割. 假設2b + f = c + 2d ，將每一種可能解的狀況討論如下: (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則d − a ≤ x; (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y = 33. c−a ，則x無解; 2.

(118) (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則y ≤ d − b; (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則x無解; (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. f −a ，則y無解; 2. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則d − b ≤ y; (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則f − d ≤ x ≤ d − a; (8) 如果最大值為b + x + y，且b + x + y = e + y，即x = e − b，則當2e = c + f 時，(x, y) = (f − d, d − b);. 政治大. (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則(x, y) =. 立. (f − d, d − b);. ‧ 國. 學. (10) 如果最大值為c+2y，且c+2y = d+x，即x = 2y+c−d，則(x, y) = (f −d, d−b);. ‧. (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則當2e = c + f. ≤ f − d;. io. er. f −c ，則x 2. sit. Nat. (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. y. 時，(x, y) = (f − d, d − b);. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則當2e = c + f. n. al. Ch. 時，(x, y) = (f − d, d − b);. engchi. i Un. v. (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則y ≤ d − b; (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則當2e = c + f 時，(x, y) = (f − d, d − b)。綜合上述結果，此時圖形如圖 5.30. 假設c + 2d < 2b + f ，將每一種可能解的狀況討論如下: (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則d − a ≤ x; 34.

(119) 圖 5.32: 熱帶圓錐曲線之十六. 圖 5.33: 圖 5.32對應的牛頓三角形分割. (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. c−a ，則x無解; 2. 政治大. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則y ≤ d − b;. 立. (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. 學. ‧ 國. (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則x無解; f −a ，則y無解; 2. ‧. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則 f −c ≤ y; 2. sit. y. Nat. (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則f − d ≤ x ≤ d − a;. n. al. er. io. (8) 如果最大值為b + x + y，且b + x + y = e + y，即x = e − b，則當2e = c + f 時，(x, y) = (e − b, e − c);. Ch. engchi. i Un. v. (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則d − b ≤ y ≤. f −c ; 2. (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則y無解; (11) 如果最大值為c+2y，且c+2y = e+y，即y = e−c，則當2e = c+f 時，x ≤ e−b; (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. f −c ，則x 2. ≤. c+f 2. − b;. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則y無解; (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則y ≤ d − b; 35.

(120) (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則當2e = c + f 時，x ≤ e − b。綜合上述結果，此時圖形如圖 5.32.. 圖 5.35: 圖 5.34對應的牛頓三角形分割治政大. 圖 5.34: 熱帶圓錐曲線之十七. 立. 當 2b ≤ a + c, 2d ≤ a + f, c + f < 2e 時，“根” 在 xy 平面上的圖形，. ‧ 國. 學. 將每一種可能解的狀況討論如下:. (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，當2b = a + c. ‧. 時，則e − b ≤ x;. y. Nat. c−a ，則e 2. io. sit. (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. −. a+c 2. ≤ x;. n. al. er. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，當2d = a + f 時，則y ≤ f − e;. Ch. engchi. i Un. v. −a (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則 f ≤ x ≤ e − a+c 2; 2. (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. f −a ，則y 2. ≤ f − e;. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，當2b = a + c 時，則e − c ≤ y; (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則x無解;. 36.

(121) (8) 如果最大值為b + x + y，且b + x + y = e + y，即x = e − b，當2b = a + c時，則(x, y) = (e − b, e − c); (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則y無解; (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則y無解; (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則x ≤ e − (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. a+c ; 2. f −c ，則x無解; 2. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，當2d = a + f 時，. 政治大. 則(x, y) = (f − d, f − e);. 立. (14) 如果最大值為d + x，且d + x = f ，即x = f − d，當2d = a + f 時，則y ≤ f − e;. ‧ 國. 學. (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則x ≤. ‧. 綜合上述結果，此時圖形如圖 5.34.. f −a 。 2. n. er. io. sit. y. Nat. al. Ch. engchi. 圖 5.36: 熱帶圓錐曲線之十八. i Un. v. 圖 5.37: 圖 5.36對應的牛頓三角形分割. 當 2b ≤ a + c, a + f < 2d, 2e ≤ c + f 時，“根” 在 xy 平面上的圖形，將每一種可能解的狀況討論如下: (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則當2b = a + c 時，d − a ≤ x; 37.

(122) (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. c−a ，則d 2. − a ≤ x;. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則y ≤ d −. a+c ; 2. (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則x無解; (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. f −a ，則y無解; 2. (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則當2b = a + c 時，d −. a+c 2. ≤ y;. (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則當2b = a + c. 政治大 (8) 如果最大值為b + x + y，且b 立 + x + y = e + y，即x = e − b，則y無解; 時，(x, y) = (d − a, d −. a+c ); 2. ‧ 國. 學. (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則y無解;. ‧. (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則 f −c ≤ y ≤ d − a+c ; 2 2 (11) 如果最大值為c+2y，且c+2y = e+y，即y = e−c，則當2e = c+f 時，x ≤ f −d; ≤ f − d;. er. io. al. f −c ，則x 2. sit. y. Nat. (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. v. n. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則當2e = c + f 時，(x, y) = (f − d,. f −c ); 2. Ch. engchi. i Un. (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則y ≤. f −c ; 2. (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則當2e = c + f 時，x ≤ f − d。綜合上述結果，此時圖形如圖 5.36. 當 a + c < 2b, 2d ≤ a + f, 2e ≤ c + f 時，“根” 在 xy 平面上的圖形，將每一種可能解的狀況討論如下: (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則 f −a ≤ x; 2 38.

(123) 圖 5.38: 熱帶圓錐曲線之十九. 圖 5.39: 圖 5.38對應的牛頓三角形分割 c−a ，則x無解; 2. (2) 如果最大值為a + 2x，且a + 2x = c + 2y，即x − y =. 政治大. (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則當2d = a + f. 立. 時，y ≤ d − b;. (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. f −a ，則y 2. ≤. a+f 2. − b;. ‧. ‧ 國. 學. (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則x無解;. sit. y. Nat. ≤ y; (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則 f −c 2. io. er. (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則當2d = a + f 時，(x, y) = (d − a, d − b);. al. n. iv n C U = e − b，則當2e = c + f (8) 如果最大值為b + x + y，且b + h xe+nyg=ceh+iy，即x 時，(x, y) = (e − b, e − c);. (9) 如果最大值為b+x+y，且b+x+y = f ，即x = −y+f −b，則 a+f −b ≤ y ≤ 2. f −c ; 2. (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則y無解; (11) 如果最大值為c+2y，且c+2y = e+y，即y = e−c，則當2e = c+f 時，x ≤ e−b; (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. 39. f −c ，則x 2. ≤. c+f 2. − b;.

(124) (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則y無解; (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則當2d = a + f 時，y ≤ d − b; (15) 如果最大值為e + y，且e + y = f ，即y = f − e，則當2e = c + f 時，x ≤ e − b。綜合上述結果，此時圖形如圖 5.38.. 立. 政治大. 圖 5.40: 熱帶圓錐曲線之二十. ‧ 國. 學. 圖 5.41: 圖 5.40對應的牛頓三角形分割. ‧. 當 2b ≤ a + c, 2d ≤ a + f, 2e ≤ c + f 時，“根” 在 xy 平面上的圖形，將每一種可能解的狀況討論如下:. sit. y. Nat. io. 時， f −a ≤ x; 2. er. (1) 如果最大值為a + 2x，且a + 2x = b + x + y，即x − y = b − a，則當2b = a + c. al. n. i vc−a f −a n C ，則 2 ≤ x; (2) 如果最大值為a + 2x，且a + 2x −y = h=ecn+g2y，即x chi U 2 (3) 如果最大值為a + 2x，且a + 2x = d + x，即x = d − a，則當2d = a + f 時，y ≤. f −c ; 2. (4) 如果最大值為a + 2x，且a + 2x = e + y，即y = 2x + a − e，則當2e = c + f 時，(x, y) = ( f −a , f −c ); 2 2 (5) 如果最大值為a + 2x，且a + 2x = f ，即x =. 40. f −a ，則y 2. ≤. f −c ; 2.

(125) (6) 如果最大值為b + x + y，且b + x + y = c + 2y，即x − y = c − b，則當2b = a + c ≤ y; 時， f −c 2 (7) 如果最大值為b + x + y，且b + x + y = d + x，即y = d − b，則當2d = a + f 時，(x, y) = ( f −a , f −c ); 2 2 (8) 如果最大值為b + x + y，且b + x + y = e + y，即x = e − b，則當2e = c + f 時，(x, y) = ( f −a , f −c ); 2 2 (9) 如果最大值為b + x + y，且b + x + y = f ，即x = −y + f − b，則當2b = a + c 時，(x, y) = ( f −a , f −c ); 2 2. 政治大. (10) 如果最大值為c + 2y，且c + 2y = d + x，即x = 2y + c − d，則當2d = a + f. 立. 時，(x, y) = ( f −a , f −c ); 2 2. ‧ 國. 學. (11) 如果最大值為c + 2y，且c + 2y = e + y，即y = e − c，則2e = c + f 時，x ≤ f −c ，則x 2. ≤. f −a ; 2. ‧. (12) 如果最大值為c + 2y，且c + 2y = f ，即y =. f −a ; 2. y. Nat. (13) 如果最大值為d + x，且d + x = e + y，即x = y + e − d，則當2d = a + f. er. io. sit. 時，(x, y) = ( f −a , f −c ); 2 2. (14) 如果最大值為d + x，且d + x = f ，即x = f − d，則當2d = a + f 時，y ≤. al. f −c ; 2. n. iv n C U 。 (15) 如果最大值為e + y，且e + y =hfe ，即y = c + f 時，x ≤ f −a 2 n g=cfh−ie，則當2e 綜合上述結果，此時圖形如圖 5.40. 由上述討論可知，熱帶圓錐曲線有20種不同形式。我們可以模仿Andreas Gathmann [3]的方式，將某些特殊圖形做出如下定義：定義 4. 當熱帶圓錐曲線ax2 ⊕ bxy ⊕ cy 2 ⊕ dx ⊕ ey ⊕ f 在 xy 平面上的圖形中，有四個頂點，三條線段及六條射線，稱此圖形為非非退化圖形。即此圖形所對應的牛頓三角形分割恰為四個面積等分的小三角形。 41.

(126) (a). (b). (c). (d). 政治大. 圖 5.42: 四種非退化的熱帶圓錐曲線及其對應的牛頓三角形分割. 立. 結論 1. 由定理A，我們可以歸納在p(x, y)的係數滿足何種條件時，會出現四種非退化. ‧ 國. 學. 的圖形，及其所對應的牛頓三角形分割，如圖 5.42：. ‧. (1) 當 a+c < 2b, a+f < 2d, c+f < 2e 且 e−b < f −d < d−a 及 d−b < f −e > e−c 時，熱帶圓錐曲線ax2 ⊕ bxy ⊕ cy 2 ⊕ dx ⊕ ey ⊕ f 型式，及其所對應的牛頓三角. Nat. sit. y. 形分割，如圖 5.42(a).. n. al. er. io. (2) 當 a+c < 2b, a+f < 2d, c+f < 2e 且 f −d < e−b < d−a 及 f −e < d−b < e−c. i Un. v. 時，熱帶圓錐曲線ax2 ⊕ bxy ⊕ cy 2 ⊕ dx ⊕ ey ⊕ f 型式，及其所對應的牛頓三角形分割，如圖 5.42(b).. Ch. engchi. (3) 當 a+c < 2b, a+f < 2d, c+f < 2e 且 f −d < d−a < e−b 及 f −e < d−b < e−c 時，熱帶圓錐曲線ax2 ⊕ bxy ⊕ cy 2 ⊕ dx ⊕ ey ⊕ f 型式，及其所對應的牛頓三角形分割，如圖 5.42(c). (4) 當 a+c < 2b, a+f < 2d, c+f < 2e 且 f −d < e−b < d−a 及 f −e < e−c < d−b 時，熱帶圓錐曲線ax2 ⊕ bxy ⊕ cy 2 ⊕ dx ⊕ ey ⊕ f 型式，及其所對應的牛頓三角形分割，如圖 5.42(d).. 42.

(127) 定理B. 若 ax2 ⊕ bxy ⊕ cy 2 ⊕ dx ⊕ ey ⊕ f 的圖形在xy平面上平移 (t, s)，則平移後，新圖形方程式為a0 x2 ⊕ b0 xy ⊕ c0 y 2 ⊕ d0 x ⊕ e0 y ⊕ f 0 ，其中 a0 = a − 2t, b0 = b − t − s, c0 = c − 2s, d0 = d − t, e0 = e − s, f 0 = f 。證明: 取出定理A中的 20 種形式分別討論，討論方式說明如下，以滿足a + c < 2b, a + f < 2d, c + f < 2e 且f − d < e − b < d − a 及 f − e < d − b < e − c的圖形為例：首先，說明新圖形形式不變，即a0 + c0 < 2b0 , a0 + f 0 < 2d0 , c0 + f 0 < 2e0 且f 0 − d0 < e0 − b0 < d0 − a0 及 f 0 − e0 < d0 − b0 < e0 − c0 。因為a + c < 2b，所以(a0 + 2t) + (c0 + 2s) < 2(b0 + t + s)，整理可得a0 + c0 < 2b0 .. 政治大因為c + d < 2e，所以(c + 2s) + f < 2(e + s)，整理可得c + f 立. 因為a + f < 2d，所以(a0 + 2t) + f 0 < 2(d0 + t)，整理可得a0 + f 0 < 2d0 . 0. 0. 0. 0. 0. < 2e0 .. (d0 + t) − (a0 + 2t)，整理可得f 0 − d0 < e0 − b0 < d0 − a0 .. 學. ‧ 國. 因為f − d < e − b < d − a，所以f 0 − (d0 + t) < (e0 + s) − (b0 + t + s) <. 因為f − e < d − b < e − c，所以f 0 − (e0 + s) < (d0 + t) − (b0 + t + s) <. ‧. (e0 + s) − (c0 + 2s)，整理可得f 0 − e0 < d0 − b0 < e0 − c0 ，由上述討論結果可知新圖形. sit. y. Nat. 形式不變。. 再來，說明新圖形交點為舊圖形交點平移 (t, s)，由定理A知，此形式交點共. io. n. al. er. 有4個，且令新圖形交點分別為A01 (e0 − b0 , e0 − c0 ), A02 (e0 − b0 , d0 − b0 ), A03 (d0 − a0 , d0 −. Ch. i Un. v. b0 ), A04 (f 0 − d0 , f 0 − e0 )；舊圖形交點分別為A1 (e − b, e − c), A2 (e − b, d − b), A3 (d − a, d − b), A4 (f − d, f − e)。. engchi. 新交點A01 (e0 − b0 , e0 − c0 ) = ((e − s) − (b − t − s), (e − s) − (c − 2s)) = (e − b + t, e − c + s). 新交點A02 (e0 − b0 , d0 − b0 ) = ((e − s) − (b − t − s), (d − t) − (b − t − s)) = (e−b+t, d−b+s). 新交點A03 (d0 −a0 , d0 −b0 ) = ((d−t)−(a−2t), (d−t)−(b−t−s)) = (d − a + t, d − b + s). 新交點A04 (f 0 − d0 , f 0 − e0 ) = (f − (d − t), f − (e − s)) = (f − d + t, f − e + s). 由上述結果可知A1 , A2 , A3 , A4 平移 (t, s) 可分別得到 A01 , A02 , A03 , A04 ，因此，新圖形交點為舊圖形交點平移 (t, s)。 43.

(128) 總結，由於新圖形形式不變，且新圖形交點為舊圖形交點平移 (t, s)，因此， a0 x2 ⊕ b0 xy ⊕ c0 y 2 ⊕ d0 x ⊕ e0 y ⊕ f 0 的圖形，可由 ax2 ⊕ bxy ⊕ cy 2 ⊕ dx ⊕ ey ⊕ f 的圖形在 xy 平面上平移 (t, s) 而得。同理，其餘形式可由上述討論方式得證。. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. 44. i Un. v.

(129) 第六章. 熱帶圓錐曲線的作圖方式. 根據第五章定理A的證明所得到的圖形中，發現到熱帶圓錐曲線與熱帶直線圖形的關聯性，並進一步，將此特性歸納為具體的作圖步驟。接著，我們如何利用熱帶直線. 政治大. 的作圖方式，將熱帶圓錐曲線 ax2 ⊕ bxy ⊕ cy 2 ⊕ dx ⊕ ey ⊕ f 的圖形，在 xy 平面上作圖步驟如下：. 立. ‧ 國. 學. 步驟一: 從二元二次熱帶多項式中，分別取出有x和y的項，化簡為下列兩式： a

(130) x⊕b

(131) y⊕d. (6.1). ‧. b

(132) x⊕c

(133) y⊕e. Nat. y. (6.2). n. al. d

(134) x⊕e

(135) y⊕f. Ch. er. io. sit. 再來取出一次項及常數項部分，形成一個二元一次熱帶多項式：. n engchi U. iv. (6.3). 步驟二: 若a + c ≤ 2b，a + f ≤ 2d，c + f ≤ 2e，則把(6.1)，(6.2)，(6.3)三式代表的熱帶直線圖形畫在xy平面上。若a + c > 2b，取b0 = 取d0 =. a+f ；若c 2. + f > 2e，取e0 =. a+c ；若a 2. + f > 2d，. c+f ，並將以上三式中的b用b0 替代， 2. 或d用d0 替代，或e用e0 替代再開始作圖。步驟三: 將步驟二中，三條熱帶直線的頂點，以及任意兩熱帶直線的交點，代入熱帶圓錐曲線ax2 ⊕ bxy ⊕ cy 2 ⊕ dx ⊕ ey ⊕ f 檢驗，若點坐標均屬於熱帶圓錐曲線，則跳到下一步驟；若點坐標不屬於熱帶圓錐曲線，則刪除由點坐標所延伸的射線和線段，直到碰到其他熱帶直線或熱帶直線的頂點為止。 45.

(136) 步驟四: 若圖形是一個完全相連的圖形，則跳到下一步驟；若圖形未完全相連，則作一線段，連接被分開的某一熱帶直線。步驟五: 若圖形中無多餘射線，則圖形即為所求；若圖形中有多餘射線，刪除多餘的射線，則圖形即為所求。刪除射線方式如下：若a + c < 2b，則保留由(6.1)，(6.2)二式中往(1, 1)方向所作出的射線，刪除掉由(6.3)式中往(1, 1)方向所作出的射線；若a + d < 2f ，則保留由(6.1)，(6.3)二式中往(0, −1)方向所作出的射線，刪除掉由(6.2)式中往(0, −1)方向所作出的射線；若c + e < 2f ，則保留由(6.2)，(6.3)二式中往(−1, 0)方向所作出的射線，刪除掉由(6.3)式中往(−1, 0)方向所作出的射線。. 政治大. 為了使上述作圖步驟能更清楚，下面將舉三個範例說明作圖步驟：. 立. 學. ‧ 國. 範例 11. 以−1

(137) x2 ⊕ 0

(138) xy ⊕ −1

(139) y 2 ⊕ 2

(140) x ⊕ 0

(141) y ⊕ 0為例說明作圖方式：. ‧. (6.4). 0

(142) x ⊕ −1

(143) y ⊕ 0. y. (6.5). 2

(144) x⊕0

(145) y⊕0. sit. (1) 依照上述步驟一及步驟二的方法取出下列三式：. (6.6). Nat. io. n. al. er. −1

(146) x ⊕ 0

(147) y ⊕ 2. Ch. engchi. i Un. v. 圖 6.1: (6.4), (6.5), (6.6)三式代表的三條熱帶直線及交點. 46.

(148) 圖 6.2: 刪除部分圖形. 圖 6.3: 圖 6.2的刪除結果. (2) 把(6.4)，(6.5)，(6.6)三式中所代表的熱帶直線圖形畫在xy平面上，如圖 6.1。. 政治大 (3) 把熱帶直線頂點(3, 2)、(0, 1)、(−2, 0)及交點(1, 2)、(0, 2)、(−1, 1)代入檢驗，點立坐標(0, 1)、(0, 2)均不屬於熱帶圓錐曲線，則刪除由點坐標(0, 1)、(0, 2)所延伸的. ‧ 國. 學. 射線和線段，如圖 6.3。. ‧. n. er. io. sit. y. Nat. al. Ch. engchi. i Un. v. 圖 6.4: 連接線段AB. (4) 取A(−1, 1)、B(1, 2)兩點，作線段AB連接被分開的熱帶直線0

(149) x ⊕ −1

(150) y ⊕ 0，如圖 6.4。圖 6.4中並無多餘射線，則圖形即為所求。範例 12. 以1

(151) x2 ⊕ 3

(152) xy ⊕ 1

(153) y 2 ⊕ 3

(154) x ⊕ 3

(155) y ⊕ 1為例說明作圖方式：. 47.

(156) (1) 依照上述步驟一及步驟二的方法取出下列三式：. 立. 1

(157) x⊕3

(158) y⊕3. (6.7). 3

(159) x⊕1

(160) y⊕3. (6.8). 3

(161) x⊕3