ELEMENT PERTURBATION PROBLEMS OF OPTIMUM SPANNING-TREES WITH 2-PARAMETER OBJECTIVES

(1)

Information

Processing

Letters

Information Processing Letters 53 ( 1995) 55-59

Element perturbation problems of optimum spanning trees

with two-parameter objectives

1

Yung-Cheng Chang a, Lih-Hsing Hsu b,*

a Institute of Computer Science and Information Engineering, National Chiao Tung University, Hsinchu, 30050, Taiwan, ROC b Department of Computer and Information Science, National Chiao Tung University, Hsinchu, 30050, Taiwan, ROC

Communicated by K. Ikeda; received 24 November 1993

Abstract

Let G = (YE) be a graph. We associate with each edge ei E E an ordered pair of rational numbers (ai, bi) . Let the weight of a spanning tree T, w(T), be defined as xeiET ai + netET bi. A spanning tree T in G is called a w-optimum spanning tree if w(T) > w( T’) for all spanning trees T’ in G. The function w is one instance in a class of two-parameter objectives. Hassin and Tan-k proposed a unified approach for solving the class of two-parameter objective optimum spanning tree problems. Let s be an objective in the class and Fs( G) denote the weight of the s-optimum spanning tree of G. The element perturbation problem of the s-optimum spanning tree is to compute FS (G - ek) for all ek E E. With Hassin and Tank’s approach, let

ts(p, q) be the complexity of computing the s-optimum spanning tree where p = [VI and q = IEl. In this paper, we present an approach to solve the element perturbation problem of the s-optimum spanning tree in t,(p, q).

Keywords: Combinatorial algorithms; Complexity; Spanning trees; Matroid

1. Introduction and notation

Most of the graph definitions used in this paper are standard (see, e.g., [ l] ). Here, we limit ourselves to defining the most commonly used terms and those that may produce confusion. G = (YE) is called a graph ifVisafinitesetandEisasubsetof{(u,u) 1 (u,u> is an unordered pair of V, where u # u}. We say V is the vertex set of G and E is the edge set of G. Let p = ]V]andq=IEl.Let,!?beasubsetofE.WeuseG-E

to denote the graph G’ = (YE - I?). In particular, we use G - ek to denote the graph G - {ek}, where

ek E E. Graph H = (V’, E’) is called a subgraph of GifV’CVandE’s Efl(V’xV’).Asubgraph

H = (V’, E’) of G with V’ = V is called a spanning subgraph of G. A spanning tree of G is a connected

spanning subgraph of G that contains exactly p - 1 edges. We also use T to denote the spanning tree with edge set T. D = ((I, A) is called a directed graph if the vertex set U is a finite set and the arc set A is a subset of{[u,u] 1 [u,u] isanorderedpairofU,whereu # u}. We use [u, u] to denote the arc incident from u to v.

Let G = (YE) be a graph. We associate with each edge ei E E an ordered pair of rational num- bers (ai, bi). For a subset E’ of E, define A( E’) =

C~,EE~ Q an d B(E’) = CelEE, bi. Let g be a real

valued function defined in R2. The problem of max-

* Corresponding author. Email: lhhsu@cc.nctu.edu.tw.

I This work was supported in part by the National Science Coun- cil of the Republic of China under contract NSC83-0208-M009- 034.

(2)

56 E-C. Chang, L.-H. Hsu/Infortnation Processing Letters 53 (1995) 55-59

imizing g( A( T) , B(T) ) over all spanning trees

T of G has been discussed by Hassin and Tamir [3]. Finding a spanning tree T which maximizes (C e,Er ~i)~ + (CeZEr bi)2Y (CeiErai + l-Ie,Er bi or l-I&T ai + neiET bi, respectively) can be transformed into the problem of maximizing A(T)2 + B(T)2 (A(T) + expB’(T) with B’(T) = CeiErlogbi or exp A’(T) + exp B’(T) with A’(T) = zeiET log ai

and B’(T) = CeiET log bi, respectively). Hassin and Tamir proposed a unified strategy which yields strongly polynomial algorithms for a class of two- parameter maximization problems that includes the above three objective functions. Note that the problem of minimizing the cost/reliability ratio over all spanning trees of a graph [2] is modeled as lX,,r bil C~,ET ai and also solved in [ 31.

Let s(T) = g(A(T),B(T)) be one of the above two-parameter objectives. The weight of a spanning tree T is the objective value of s(T). A spanning tree T in G is called an s-optimum spanning tree if s(T) 3 s( T’) for all spanning trees T’ of G. Find- ing the s-optimum spanning tree with respect to s is called the s-MST problem. We use t,(p, q) to denote the time complexity of solving the s-MST problem with Hassin and Tamir’s approach. Let F,(G) denote the weight of the s-optimum spanning tree of G if G is connected; otherwise, F,(G) = -ca The element

perturbation problem (EPP) of the s-optimum span- ning tree, s-EPP for short, is to compute F, (G - ek) for all ek E E. A naive method of solving the s-EPP is to repeatedly apply Hassin and Tamir’s algorithm to compute F, (G - ek) for every ek. This approach takes

O(qt,(p,q)) time. However, F,(G - ek) = f(G) if the edge ek is not in the s-optimum spanning tree. Thus, we can reduce the time to O( pts (p, q) > . In this paper, we present a t,(p, q) algorithm for solving the s-EPP

The study of the s-EPP is interesting for several reasons. First, the concept of the EPP can be gen- eralized to combinatorial optimization problems. Re- cently, Hsu, Leu, and Sung discussed general EPP strategies [ 51. If we solve the EPP of a combinatorial optimization problem, we can find the second optimal solution(s) and the critical element(s). A naive method of solving an EPP is to repeatedly solve the original problem. To avoid repeated execution of an algorithm, we extract and reuse information from what we have solved. Several EPPs can then be solved with

the same time complexity as the original problem [ 4- 7,9]. Algorithms that reuse information in this way are called recycling algorithms [ 51. It has been observed that recycling strategies are problem-dependent. It is interesting to collect as many recycling strategies as possible. Hassin and Tamir’s algorithm is a unified approach for a class of interesting problems. Thus, it is worthwhile to investigate the corresponding recycling strategy. Also, since the two-parameter maximum spanning tree problem is a topic in matroid theory [ 81, we expect that our approach may lead to some insights into matroid theory.

2. Previous work

To make this paper self-contained, we first review the basic strategy of Hassin and Tamir’s approach as proposed in [ 31. Assume that (ai, bi) # (uj, bj) if ei # ej to avoid degenerate cases. Let T* be the s- optimum spanning tree with respect to the objective function s. We call a spanning tree T a local optimal spanning tree if there is no pair of elements ei, ej E E such that ei E T, ej $ T, and T’ = T - {ei} + { ej} is a spanning tree which yields a larger weight than T does. Hassin and Tamir divided the R2 plane into a number of cells and showed that all points in a cell produce at most one local optimal spanning tree. Obviously, the s-optimum spanning tree T* is one of these local optimal spanning trees. T* will be contributed by the unique cell in R2 containing (A (T*) , B( T*) > .

Let (A, B) be a point in R2. Define a directed graph DQ(G) with the vertex set being the edge set E of G. In short, we use D_.Q to denote DA,B( G) . Let ei, ej be distinct elements in E. [ ei, ej] is an arc in DA,B if andonlyifg(A--ai+aj,B-bi+bj) > g(A,B).An equivalence in R2 can be defined by (A, B) N (C, D) if and only if DA,B = Dc,D.

Let ei, ej E E, ei # ej. Define the function gij(A,B)=g(A-ui+uj,B-bi+bj) -g(A,B). The equivalence regions in R2 are induced by the set of q( q - 1) gij( A, B) functions. Define Rij =

{(A,B) 1 g(A-ai+Uj,B-bi+bj) > g(A,B)}* Let f : R2 + Rk be a mapping of R2 into Rk. Fur- ther, let zj, ei, ej E E, ei # ej be a collection of subsets in Rk such that (A, B) E Rij if and only if f(A, B) E Tij for ei, ej E E, i # j. Suppose there exists a polynomial hij( x1,. . . , xk) such that

(3)

Z-C. Chang, L.-H. Hsu/lnformation Processing Letters 53 (199.5) 5.5-59 57 Kj =

((X17.

.-7Xk)

1

hij(xlt- ..,xk) > 0). Then

the number of equivalence regions is bounded by the number of topological components induced on Rk by the set of polynomials hij. If d, the maximum degree of hij, and k, the dimension of Rk, are constant and in- dependent of q, then it can be proved that the number of equivalence regions will be a polynomial in q.

For ease of exposition, we use the weight function w(T) = CeiET ai +neiET bi as the objective. In the w- MSTproblem,g(A(T),B’(T)) =A(T)+expB’(T) with A(T) = CeiET ai, B’(T) = Ce,ET log bi. Given

a point (A,B) = (A(T),B’(T)), Rij = ((A,B) 1

(A - ui + uj) + exp (B - logbi +logb;) > A + expB}= {(A,B) 1 -ai+aj > (l-bj/bi)expB}. Set f(A, B) = expB and zj = {x 1 -ai + Uj >

~(1 - bj/bi)}. Hence, (A,B) E Rij if and only

if f(A, B) E Tij for every pair of distinct edges

ei, ej E E. The number of equivalence regions is

O(q2> for the w-MST problem. These regions cor-

respond to the partition of the line induced by the points dij = bi(uj - ui)/(bi - bj), where ei,ej E E

and ei # ej. Each equivalence region defines a DA,B, where (A, B) is a point in that region.

Let E(DA,B) be the arc set of D,+,B. Let 7’1 and T2 be two distinct spanning trees of G. We say that T2 is a DA,B-improvement of Tl if there exist ei E Tl and ej $! Tl such that [ei, ej] E E(DAJ) and T2 = Tl - {ei} + {ej}, i.e., T2 is obtained from Tl by a single

edge swap. A spanning tree T of G is DA,*-optimal if there exists no spanning tree T’ of G which is a D,Q- improvement of T. In [3], the following theorem is presented.

Theorem 1. There is at most one D,+B-optimal spun-

ning tree ofG for every (A, B) in R2.

We use T*,J to denote the DA,B-optimal spanning tree if it exists. Let r( DA,B) (ei) be the set {ej 1

[ei, ej] E E(D,Q)} for ei E E. Also let X(DAJ) be the set {ei 1 the two endpoints of ei in G are on different connected components of the graph H = (YrA,B (ei))}. In short, we use ~,J,B( ei) to denote r( DA,J) (ei) and XA,B to denote X( DA,J). The fol- lowing theorem is also from [ 31.

Theorem 2.

If

the DA*B-optimal spanning tree T,Q exists, then the edge set

of

TAJ is exactly XAJ.

This theorem states that a necessary condition for the existence of the DA,B-optimal spanning tree is that XA,J forms a spanning tree. If XA,J forms a spanning tree, it is a candidate solution. It is suggested in [ 31 that we do not have to verify that the candidate solution is DA,B-optimal. To reduce the computational complexity, it will suffice simply to find the candidate solution. The s-optimum spanning tree is a candidate solution which has maximum weight with respect to s. The following algorithm proposed in [3], Algo- rithm 1, finds X,Q and then tests whether it forms a candidate solution in a D,Q.

Algorithm 1.

Step 1. Compute ~A,B (e,) for all e, E E. Step 2. Set XA,B = 4.

Step 3. For each e, E E do the following:

If the two endpoints of e, are disconnected in H =

(~~A,B(ex)), set XA,B = XA,B u {ex).

Step 4. If XA,B does not form a spanning tree, stop and

conclude that the DA,J has no DA,n-optimal solution. Otherwise, XA,B forms the candidate solution. Obviously, step 1 in Algorithm 1 takes O(q2) time. Step 3 needs q tests to see if the endpoints of e, are not connected in H = ( Y~A,B (e,) ). Each test takes

O(q) time. Hence, step 3 takes 0( q2) time. Step 4

is completed in O(p) time. Hence, the complexity of Algorithm 1 is 0( q2). For the weight function w(T), we can find the w-optimum spanning tree by finding all candidate solutions among all 0( q2) different DA,JS. Then we select the candidate solution with maximum weight to be the w-optimum spanning tree. The whole process takes 0( q”) time.

3. The EPP strategy

Although our EPP strategy is independent of the equivalence region construction, we use the w-EPP as an example to demonstrate our method. We want to extract some useful information when computing F,,,(G) and then reuse this information to compute

F, ( G - ek ) s. Assume we are given a graph G = ( YE)

and each edge ei E E is associated with an ordered pair of rational numbers (ai, bi). Let T’ be the w- optimum spanning tree of G and Tek be the w-optimum spanning tree of G - ek,

(4)

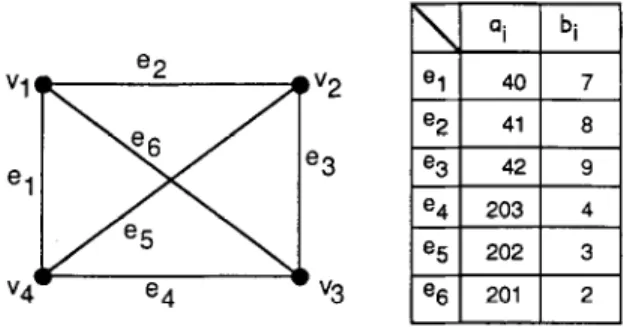
58 E-C. Chmg, L.-H. Hsu/Infornmtion Processing L.etters 53 (1995) 55-59 “1 e2 e6 e1 e3 El “2 e5 “4 e4 “3

Fig. I. A graph G = (YE) and the (ai. bi) for every edge.

Fig. 1 is an example of a graph G with four vertices. The (ui, bi) s are listed in the table. In this example,

T* = {eh,es,ec}, Tel = Te2 = Te’ = T*, and Te4 = Tes = Te6 = {el, e2, e3).

To apply Hassin and Tamir’s algorithm, we need to construct D,QS for all equivalence regions in

R’. There are 0(q2) different D,QS for G. When constructing a DA,B, we create an arc [ei,ej] if g(A-ai+uj,B--logbi+logbj) > g(A,B), where

g(A(T),B’(T)) = A(T) +expB’(T). Let DXB be

DA,J (G - ek) . From the construction of a DA,B, we

know that if [et, ej] is an arc in DTB, [ei,ej] must be an arc in DA,J. We have the following lemma.

Lemma 3. D& is the subgraph of DA,B induced by

the vertex set E - {ek}. Moreover, r( DzB) (ei) is exactly ~A,B (ei) - { ek}, where ei # ek.

With Lemma 3, we can easily obtain DzB from

D,Q for every (A, B) in R* and ek E E. Fig. 2(a) is

D30r,~~s40, where G is the graph in Fig. 1. Fig. 2(b) is DZKI log40. SincetheO DA,BScOverall (A,B)sin

R*, the 02 Bs induced by E - { ek} from the DA,B (G) s

will also cover all (A, B)s.

Let XRB be X( DAJ (G - ek) ) . We want to obtain XFB from XA,B. Note that the two endpoints of an ei in XA,B are on different connected components of the graph H = (Yr~,~(ei)). Let ei be an edge in X2, but not in XA,J. The two endpoints of ei are connected in H = ( v ~A,B (ei) ) but are not connected in H’ = (v!rA,~(ei) - {ek}). In other words, ek is a

cut edge of the connected component in H connecting

the two endpoints of ei. We use ReAIB to denote the set {ei 1 ek is a cut edge of the connected component in H connecting the endpoints of ei}. We have the following theorem. e2 e1 e6 e6

&

e3 e4 @I

Fig. 2. (a) The Dm,lOg 40 for G in Fig. 1. (b) The D$, ,Og 4. for G-q.

Theorem 4. X2,B = XA,B - {ek} U RTB.

PrOOf. Obviously, ek $! X2, Since ek $! Dz,B.

From the above discussion, ’ if ei is an edge of X”” _{A,B -} xA.B, ei E R2.B. Suppose ei is in XAJ and

ei # ek. Then the endpoints of ei are not connected in H = (vr~,~(ei)). The endpoints of ei are not connected in H’ = (v!rA,B(ei) - {ek}), which is a subgraph of H. Hence, ei is in XT,B. Therefore, XT, = xA,B - {ek) u RT,B. 0

In Fig. 2, Xsc~t~s40 is (e4, es, es}, which forms the

T*. es is not in X30o,t~~40 because r300,10g40(es) =

(e4, es, e6) forms a conne&d component connecting the two endpoints of es in G. From Theorem 4, X”” _{300,log 40 -}- (e4, es,e6} - {es} U {e3}, where es iS the only element in R&,,,,,. Hence, D&, ,0g4o con- tributes the candidate solution XF&, ,0g4o = {es, e4, e6) to compete for the w-optimum spanning tree of G-es.

Let e, E E and e, = (u,,u,), where u,,u, E V.

The following algorithm, Algorithm 2, finds RT,B for

every ek in E with respect to DA,B.

Algorithm 2.

Step 1. For each e,, E E, set R2,B = 4. Step 2. For each e, E E do the following:

Construct rA,& (e,) . If the two endpoints of e, are connected in H = (v!rA,B (e,) ), find every CUt edge eY in the connected component that connects u, to u, and set Rz,B = RzsB U {e,}.

(5)

K-C. Chang, L.-H. Hsu/lnformation Processing Letters 53 (1995) 55-59 59

struction of a ~A,B( e,) requires O(q) time. The cut edges can be found with depth-jrst search techniques starting from ux or ux in O(q) time [ lo]. Hence, step 2 can be performed in 0(q2) for all e, E E. The loop in step 2 assigns the e, to all the Ry,‘s, where ek is a cut edge of the connected component in H that con- nects 24, to u,. Hence, step 2 constructs R& for all t?k E E.

Note that the w-EPP algorithm reuses the XA,J obtained from Algorithm 1. Even if the XA,B fails to form a candidate solution for DA,~,, the X2, may become a candidate solution for D2B. After the’execution of Al- gorithms 1 and 2 for DA,B; the X&s can also be found in 0(q2) time by setting X& = XAJ - {ek} U R&

for all ek E E. We conclude that the w-EPP can be solved in 0( q”) time.

Hassin and Tank’s unified approach for finding local solutions applies to a class of maximization problems that construct equivalence regions in various ways. Our Algorithm 2 for a DA,B is independent of the method of constructing the equivalence regions. Hence, our strategy can be applied to this entire class of problems. If we define the weight function s(T) as (Ce,U G)~ + (CeiET bi)2, neiET ai + fle,ET bi, Or ILET bil CGET ai and use Hassin and Tank’s approach, the time compexity is the same for solving the s-MST problem and the S-EPP

References

[ 11 J.A. Bondy and U.S.R. Murty, Graph Theory with Applicarions (Elsevier, New York, 1976).

[2] R. Chandrasekaran and A. Tamir, Polynomial testing of the Query “Is ab > cd?” with application on finding a minimal cost reliability ratio spanning tree, Discrete Appl. Math. 9 (1984) 117-123.

[3] R. Hassin and A. Tamir, Maximizing classes of two- parameter objectives over matroids, Math. Oper. Res. 14 (1989) 362-375.

[4] L.H. Hsu, R.H. Jan, Y.C. Lee, C.N. Hung and MS. Chem, Finding the most vital edge with respect to minimum spanning tree in weighted graphs, Inform. Process. L&t. 39 (1991) 277-281.

[ 51 L.H. Hsu, SC. Leu and T.Y. Sung, Second optimal solutions, critical elements and recycling algorithms, submitted for publication.

[6] C.N. Hung, L.H. Hsu and T.Y. Sung, The most vital edges for matchings in a bipartite graph, Networks 23 ( 1993) 309- 313.

[7] N. Katoh, T. Ibaraki and H. Mine, An efficient algotithm for K shortest simple paths, Networks 12 (1982) 41 l-427. [ 81 J. Lee and J. Ryan, Matroid applications and algorithms,

ORSA J. Comput. 4 (1992) 70-98.

[9] K. Malik, A.K. Mittal and S.K. Gupta, The k most vital arcs in the shortest path problem, Oper. Res. L&t. 8 ( 1989) 223-227.

[ 101 R.E. Tarjan, Depth-first search and linear graph algorithms, S1AM.l. Compur. 1 (1972) 146-160.