An Efficient JMC Algorithm for the Rhythm Query
in Music Databases
Ye-In Chang
∗, Jun-Hong Shen
†, Chen-Chang Wu
∗, and Han-Ping Chou
∗∗Dept. of Computer Science and Engineering National Sun Yat-Sen University Email: changyi@cse.nsysu.edu.tw †Dept. of Information Communication
Asia University Email: shenjh@asia.edu.tw
Abstract—The rhythm query is the fundamental tech-nique in music genre classification and content-based retrieval, which are crucial to multimedia applications. Recently, Christodoulakis et al. has proposed the CIRS algorithm that can be used to classify music duration sequences according to rhythms. In order to classify music by rhythms, the CIRS algorithm locates M axCover which is the maximum-length substring of the music duration se-quence, which can be covered (overlapping or consecutive) by the rhythm query continuously. However, this algorithm will repeatedly generate unnecessary results during the processing, resulting in the increase of the running time. To reduce the processing cost in the CIRS algorithm, we propose the JMC (Jumping-by-M axCover) algorithm which provides a pruning strategy to find M axCover incrementally. From our experimental results, we have shown that the running time of our proposed algorithm could be shorter than that of the CIRS algorithm.
Index Terms—music databases, music duration se-quence, rhythm queries.
I. INTRODUCTION
In recent years, music becomes more popular due to the evolution of the technology [1], [2], [3]. Vari-ous kinds of music around us become more complex and huge [4], [5]. This explosive growth in the mu-sic has generated an urgent need for new techniques and tools that can intelligently and automatically transform the music into useful information and classify the music into correct music group precisely [6]. The rhythm query for music databases is the fundamental technique in music genre classification and content-based retrieval, which are crucial to multimedia applications.
In [7], Christodoulakis et al. proposed a kind of problem for rhythm queries. In the CIRS algorithm, a rhythm is represented by a sequence of “Quick”
(Q) and “Slow” (S) symbols, which corresponds to
the (relative) duration of notes, such that S = 2Q.
In order to classify music by rhythms, the CIRS algorithm locates the M axCover, which is the maximum-length substring of the music duration sequence which can be covered (overlapping or consecutive) by the rhythm query continuously.
This algorithm uses the notated music data of durations for the rhythm query. As compared with the rhythm query using audio music data, the CIRS algorithm can save a lot of time. Although the CIRS algorithm has the above advantages, it does not apply any pruning strategy to reduce the process-ing cost. This is because that the CIRS algorithm cannot decide how long one rhythm of “S”(slow) is. Therefore, it needs to trace all different du-ration values occurring in the dudu-ration sequence, and regards each different duration value as one rhythm of “S”(slow). So that, as the number of different duration values increases, the processing time of the CIRS algorithm increases. Therefore, in this paper, we proposed the JMC
(Jumping-by-M axCover) algorithm to avoid tracing all different
duration values, in order to speed up answering the rhythm query. From our experimental results, we have shown that the running time of our proposed algorithm could be shorter than that of the CIRS algorithm.
Onset time: 0 50 100 200 220
50 50 100 20 Interval:
S1
DSeq
Fig. 1. Two equivalent definitions of a musical sequence
Section 2, we present our proposed algorithm. The experimental results are presented in Section 3. Finally, we conclude this paper in Section 4.
II. THEJUMPING-BY-MAXCOVER ALGORITHM
In [7], Christodoulakis et al. proposed a new model for song classification based on dancing rhythms. Although their CIRS algorithm can find the interesting result (the q-cover), it takes long time. Therefore, we propose an efficient algorithm named Jumping-By-M axCover (JMC), which re-quires shorter time to solve the same Maximal
Cov-erability problem. In this section, we first describe
formal definitions of duration sequences, the rhythm representation, q-match, q-cover and the M aximal
Coverability problem [7], and then present the
pro-posed JMC (Jumping-By-M axCover) algorithm.
A. Definitions
1) Duration Sequences: A musical sequence can
be thought of as a sequence of occurrences of events [7]. Consider a music signal having 5 musical events occurring at 0th, 50th, 100th, 200th and 220th milliseconds. Then, sequence S1 = [0, 50, 100, 200,
220] can be regarded as the corresponding sequence representing the music signal under consideration, as shown in Figure 1. Alternatively, we can repre-sent the same music signal by stating the duration of the consecutive musical events, instead of the start time. In this algorithm, duration sequence DSeq = [50, 50, 100, 20] represents the same music signal, as shown in Figure 1.
2) The Rhythm Representation: In particular,
there are two types of intervals in the rhythm of a song: quick (Q) and slow (S). Quick means that the duration between two onsets is q milliseconds, while the slow interval is equal to 2q. For example, tango, the dancing rhythm, is given as sequence SSQQS.
Definition 1.: A rhythm Rhy is a string Rhy = Rhy[1]Rhy[2]...Rhy[m], where Rhy[j] ∈ Q, S, for
all 1 ≤ j ≤ m.
1 2 3 4 5 6 7
20 30 50 100 40 10 90
Solid
Q :
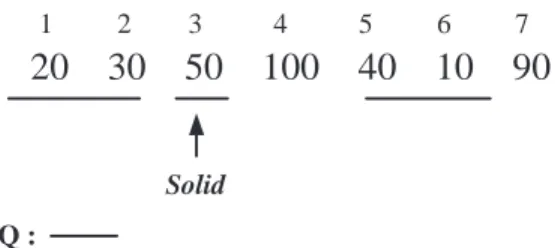
Fig. 2. The rule of q-matching and solid for q = 50
3) q-Match:
Definition 2.: Let Q represent an interval of q ∈ N+
milliseconds, and S represent an interval of 2q milliseconds. Then, Q is said to q-match with substring DSeq[i..i′] of duration sequence DSeq, if
and only if
q= DSeq[i] + DSeq[i + 1] + ... + DSeq[i′],
where 1 ≤ i ≤ i′ ≤ n. If i = i′, then the matching
is said to be solid. Similarly, S is said to q-match with DSeq[i..i′], if and only if either one of the
following conditions is true
• i= i′ and DSeq[i] = 2q, or
• i 6= i′ and there exists i ≤ i1 < i′ such that q= DSeq[i] + DSeq[i + 1] + ... + DSeq[i1] = DSeq[i1+ 1] + DSeq[i1+ 2] + ... + DSeq[i′].
As with Q, the match of S is said to be solid, if i = i′. In a word, duration sequence DSeq can
be transformed to Q and S by accumulating the consecutive ones.
For example, Figure 2 shows that duration se-quences DSeq[1..2] , DSeq[3] and DSeq[4..5] = 50 can be transformed to Q, because DSeq[1] + DSeq[2] = 20 + 30 = 50 = q and so on. Moreover,
duration sequence DSeq[3] is a solid S because of DSeq[3] = 50 = q.
We use an example to illustrate the q-match for a rhythm from the duration sequence. Consider the duration sequence shown in Figure 3-(a). We want to get the q-match for rhythm Rhy = QSS
and q = 50 from this sequence. First, we need to transform the DSeq to the Q S representation. We have DSeq[1] + DSeq[2] = 25 + 25 = 50 = q and DSeq[3] = 100 = 2q, so we transform DSeq[1..2]
and DSeq[3] to Q and S, and so on. In fact, there are many possible results of the transforming. Next, we can find sequences DSeq[1..5] and DSeq[5..8] are
Rhy Rhy S : Q : q -cover 1 25 2 25 3 100 4 50 5 50 6 50 7 50 8 100 9 50 (a) Rhy Rhy q -cover 1 25 2 25 3 100 4 50 5 50 6 50 7 50 8 50 9 100 (b)
Fig. 3. q-cover of Rhy = QSS in DSeq, for q = 50: (a) overlapping; (b) consecutive.
matched to Rhy = QSS. That is, we have match
sequence M atchSeq = (1, 5), (5, 8), 4) q-Cover:
Definition 3.: A rhythm Rhy is said to q-cover
substring DSeq[i..i′] of duration sequence DSeq, if
and only if there exist integers i1, i′1, i2, i′2, ..., ik, i′k,
for some k ≥ 1, such that
• Rhy q-matches DSeq[iℓ..i′ℓ], for all 1 ≤ ℓ ≤ k,
and
• i′ℓ−1 ≥ iℓ− 1, for all 2 ≤ ℓ ≤ k.
In short, the q-covering DSeq consists of the over-lapping or consecutive MatchSeq’s.
In Figure 3-(a), MatchSeq’s are DSeq[1..5] and
DSeq[5..8]. Joining the overlapping MatchSeq’s
be-comes the q-cover. Therefore, we can find rhythm
Rhy = QSS q-covers DSeq[1..8] for q = 50. In
the same way, in Figure 3-(b), we can join the consecutive MatchSeq’s, resulting in the q-cover
DSeq[1..9].
5) The Maximal Coverability Problem: In this
paper, we focus on locating M axCover, the maximum-length substring of the music duration sequence, for rhythm queries. This is called the
Maximal Coverability problem defined as follows
[7]:
Definition 4. (Maximal Coverability problem):
Given a duration sequence DSeq = DSeq[1]...DSeq[n], DSeq[i] ∈ N+
, and a rhythm
Rhy = Rhy[1]...Rhy[m], Rhy[j] ∈ {Q, S}, find
the longest substring DSeq[i..i′] of DSeq that is q-covered by Rhy among all possible values of q.
Moreover, the following restriction is applied on the above problem.
Definition 5. (At least one event is solid.): For
each match of Rhy with a substring t[i..i′], there
must exists at least one S in Rhy whose match in t[i..i′] is solid; that is, there exists at least one 1 ≤ j ≤ m such that Rhy[j] = DSeq[k] = 2q, i≤ k ≤ i′, for some value of q.
B. The Proposed JMC Algorithm
The basic idea of the JMC algorithm contains the following five steps:
1) Finding all occurrence of S.
2) Transforming the areas around all the S into sequences of Q and S.
3) Finding the Matchings. 4) Finding the M axCover. 5) Updating Cut-Sequence.
Our JMC algorithm does a while loop from Step 2 to Step 5, until the cut-sequence is empty.
First, we will describe a portion of our algorithm which is similar to the CIRS algorithm to gener-ate the maximal q-cover (M axCover) by duration sequence DSeq and rhythm query Rhy. Next, we will introduce our proposed data structure,
cut-sequence, which can prevent generating useless
se-quences. We introduce the detail of each procedure in the following section.
1) Step 1: Finding All Occurrence of S: In this
step, we use the procedure which is similar to the first step in the CIRS algorithm [7]. We need to find all occurrences of S = Dif f V [ ].V alue in DSeq, where Dif f V[ ].V alue means the different
duration value in DSeq. According to the chosen
Dif f V[ ].V alue, in Step 2, we can transform the
areas around each of those occurrences to sequences of Q and S. Then, we have to repeat the above pro-cess for every possible value of Dif f V[ ].V alue. A
single scan through the input string suffices to find all occurrences of Dif f V[ ].V alue.
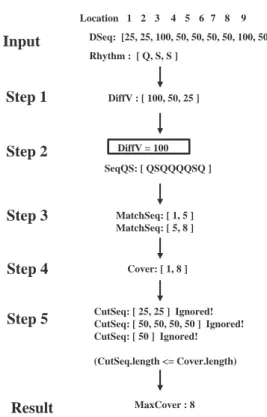
Basically, this step contains two parts: (a) finding all different values and recording their locations;
DSeq: [25, 25, 100, 50, 50, 50, 50, 100, 50] Rhythm : [ Q, S, S ] DiffV : [ 100, 50, 25 ] Input Step 1 Step 2 Step 3 Step 4 Result MaxCover : 8 SeqQS: [ QSQQQQSQ ] DiffV = 100 MatchSeq: [ 1, 5 ] MatchSeq: [ 5, 8 ] Cover: [ 1, 8 ]
Step 5 CutSeq: [ 25, 25 ] Ignored!CutSeq: [ 50, 50, 50, 50 ] Ignored! CutSeq: [ 50 ] Ignored! (CutSeq.length <= Cover.length)
Location 1 2 3 4 5 6 7 8 9
Fig. 4. A tracing example by using our JMC algorithm
TABLE I THE RESULT OFSTEP1 DiffV[].Value Location[ ] 100 3, 8 50 4, 5, 6, 7, 9 25 1, 2
(b) sorting all locations by Dif f V[ ].V alue in
the descending order. Take musical sequence DSeq shown in Figure 4 as a running example. According to the two parts mentioned above, we can get the result as shown in Table I.
2) Step 2: Transformation: The task of this step
is to transform DSeq, which is a sequence of integers, to SeqSQ, which is a sequence consisting of Q and S, by the chosen Dif f V[ ].V alue. Each
sequence belonging to SeqSQ is a sequence over
Q, S for the chosen q = (Dif f V[ ].V alue / 2) .
In this step, our goal is to identify all the
q-matches of Rhy in duration sequence DSeq.
For each occurrence of the current symbol
Dif f V[ ].V alue = 2q = S, we try to convert the
area surrounding such an S into sequences or a tile of Q. When we cannot continue to make Q, we check whether we can make S instead.
Note that we first try to make Q, and in case of a failure, we try for one S. Consider DSeq shown in Figure 4. It is easy to observe that in this way, we can only find S, if S is solid. The reason is that according to the definition, we cannot have S that cannot be divided into two consecutive Q’s. If we cannot make either of them, we mark the end of the sequence. Therefore, each sequence DSeq ∈ SeqSQ consists of at least one solid S.
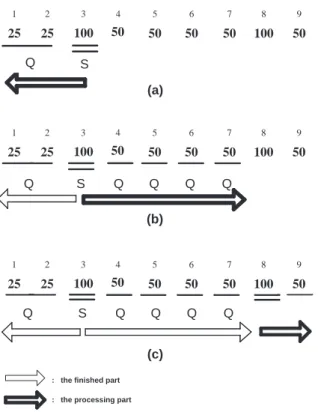
This step spends the longest time in CIRS algo-rithm [7]. By using the notion of cut-sequence men-tioned in Step 5, our proposed algorithm reduces the generation of SeqSQ and increases the efficiency for the later steps. Consider musical sequence DSeq shown in Figure 5, where we use Dif f V[1].V alue (= 100) to be 2q, i.e., q = 50. In Figure 5-(a),
the first solid S, DSeq[3] (= 2q), at location 3 is
located, and the transformation before this solid S is then performed. After that, the transformation after this solid S is performed as shown in Figure 5-(b). Figure 5-(c) shows that the second solid S is located and the remaining transformation is performed. The transformed result SeqSQ in the proposed JMC algorithm is shown in Step 2 of Figure 4.
3) Step 3: Finding Matchings: During the
match-ing step, the followmatch-ing restriction of q-match should be obeyed [7]. One S symbol in the rhythm query can be regarded as two consecutive Q symbols in the duration sequence, but the two consecutive Q symbols in the rhythm query cannot be combined as one S symbol in the duration sequence.
In this step, we consider each SeqSQ, for
Dif f V[ ].V alue and identify all the q-matches of Rhy in SeqSQ. To do that efficiently, we exploit
a bit-masking technique as described below. We first define some notations that we use for sake of convenience. We define Ss and Sr to indicate
an S in SeqSQ and Rhy, respectively. Qs and Qr are defined analogously. We first perform a
preprocessing as follows. We construct Seq01 from SeqSQ where each Ss is replaced by 01 and each Qs is replaced by 1, as shown in Table II. We also
construct Rhy’ from Rhy where each Sris replaced
by 10 and each Qr is replaced by 0, as shown in
(a)
(b)
: the finished part : the processing part
1 25 2 25 3 100 4 50 5 50 6 50 7 50 8 100 9 50 Q S Q S Q Q Q Q 1 25 2 25 3 100 4 50 5 50 6 50 7 50 8 100 9 50 1 25 2 25 3 100 4 50 5 50 6 50 7 50 8 100 9 50 Q S Q Q Q Q (c)
Fig. 5. Transforming DSeq into SeqSQ, for q = 50: (a) the processing before the first solid S; (b) the processing after the first solid S; (c) the processing after the second solid S.
TABLE II THE BITMASKING TABLE
Ss Qs Sr Qr
01 1 10 0
Seq01, where I includes each position of “1” of Ss in SeqSQ. This completes the preprocessing.
For example, if SeqSQ = QSQQQQSQ, we have
Seq01 = 1011111011 and I = [3,9]. It is easy to
see that no occurrence of Rhy can start at i ∈ I.
After the preprocessing is done, at each position i
∈ I of Seq01, we perform a bitwise “OR” operation
between Seq01[i..i+ |Rhy′| − 1] and Rhy’. If the
result of the “OR” operation is all 1’s, then we have found a match at position i of Seq01. However,
we need to ensure that there is a solid S in the match. To achieve that, we simply perform a bitwise “XOR” operation between Seq01[i..i + |Rhy′| − 1]
and 1Rhy′
and only if the result of this “XOR” returns a nonzero value, we go on with the “OR” operation stated above.
1 25 2 25 3 100 4 50 5 50 6 50 7 50 8 100 9 50 Q S Q Q Q Q S Q 1 01 1 1 1 1 01 1 0 10 1 0 (Match) 01 0 1 0 0 1 0 10 (Match) 0 1 01 0 S : Q : SeqSQ DSeq Seq01 Rhy'
Fig. 6. Finding matchings of Rhy = QSS(01010) in DSeq, for q = 50
We now discuss the correctness of q-match. Our encoding obeys the restriction of q-match. (Recall that a match occurs when the result of the bitwise OR operation is all 1’s.)
1) Qs(= 1) and Qr(= 0) always matches: (1 OR
0 = 1).
2) QsQs(= 11) always matches with Sr(= 10):
(11 OR 10 = 11).
3) SS(= 01) can only match with Sr(= 10) : (01
OR 10 = 11).
4) Since Ss(= 01) cannot give a match with QrQr(= 00): (01 OR 00 = 01).
According to Rhy = QSS, we can find the matching sequences, M atchSeq’s, in DSeq[1..5]
and DSeq[5..8], as shown in Figure 6. In this step,
we use the Dif f V[1].V alue = 100 to be 2q. The
result is shown in Step 3 of Figure 4.
4) Step 4: Finding MaxCover: In this step, we
use MatchSeq’s generated in Step 3 to process the
q-cover. Checking the start and end location of
each MatchSeq, we can combine the overlapping or consecutive MatchSeq’s. Overall, the running time of this step is decided by the number of MatchSeq’s. Therefore, the running time of this step is shorter than that of Step 2 and related to the sequence generated in Step 2. Moreover, we maintain a global variable MaxCover to keep track of the longest cover so far.
Figure 7 shows M axCover of the running ex-ample for rhythm Rhy = QSS and q = 50. In this figure, M atchSeq’s DSeq[1..5] and DSeq[5..8] are
combined into q-cover DSeq[1..8]. The result is the
length of M axCover = 8, as shown in Step 4 of Figure 4.
5) Step 5: Updating Cut-Sequence: In this step,
MatchSeq 1 25 2 25 3 100 4 50 5 50 6 50 7 50 8 100 9 50 MatchSeq
Fig. 7. Finding covers of Rhy = QSS in DSeq, for q = 50
1 25 2 25 3 100 4 50 5 50 6 50 7 50 8 100 9 50 Input Duration First round Second round Third round 25 25 50 50 50 50 50 25 25
Fig. 8. The cut-sequence for input in the different rounds
sequence according to duration sequence DSeq and
Dif f V[].V alue, the difference duration value of DSeq, in each loop. We can observe that if there is a
value in DSeq that is larger than Dif f V[].V alue,
this value will not be transformed to an S or Q rhythm in the following step. This value is a cut point of DSeq. It cuts off DSeq into two or less subsequences. Two larger values cut off DSeq into three or less subsequences, and so on. We can ig-nore all the cut-sequences, whose length are shorter than that of M axCover, which is updated in each round. After updating cut-sequences and pruning impossible ones, the remaining cut-sequences are the input data in the next round. Figure 8 shows the cut-sequences in the different rounds.
Following the previous example, Figure 8 shows that the input DSeq’s for the next round, which are generated by cut-sequence CutSeq’s, are [25,25], [50, 50, 50, 50] and [50]. All of the lengths of
DSeq’s are shorter than M axCover = 8 at present.
Therefore, we prune all of DSeq’s, as shown in Step 5 of Figure 4. That is, there are no existing DSeq for the next round. At this point, the processing of the proposed JMC algorithm is completed. The final result is as follows:
TABLE III THE RHYTHM QUERIES[8]
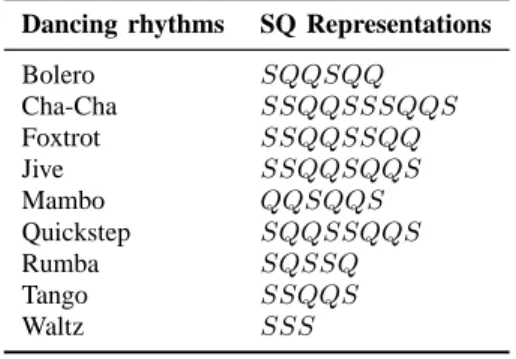
Dancing rhythms SQ Representations
Bolero SQQSQQ Cha-Cha SSQQSSSQQS Foxtrot SSQQSSQQ Jive SSQQSQQS Mambo QQSQQS Quickstep SQQSSQQS Rumba SQSSQ Tango SSQQS Waltz SSS
• Given a duration sequence DSeq = [25, 25,
100, 50, 50, 50, 50, 100, 50], and a rhythm Rhy = QSS, the length of the longest substring,
MaxCover, is 8 for q = 50.
III. PERFORMANCE
In order to evaluate the performance of our pro-posed algorithm, we compare our JMC (Jumping-by-M axCover) algorithm with the CIRS Algorithm [7]. We generate the synthetic data that are similar to the duration sequence of the “ballroom dance” music. Moreover, we use the duration sequence as the input data to compare these two algorithms in the total running time.
A. Generation of Synthetic Data
The musical sequences (e.g. a song) can be considered as a series of onsets (or events) that correspond to music signals, such as drum beats. They are the intervals between those events, which characterize the song. In order to obtain the reliable results, we generate synthetic duration sequences as one song. Therefore, we generate several different duration sequences by using a set of different du-ration values (Dif f V ). Moreover, we evaluate the time of the algorithm for answering M axCover of duration sequences, which is the maximal q-cover, for the rhythm queries [8] shown in Table III.
The parameters used in the generation of syn-thetic data are shown in Table IV. N means the number of events in the duration sequence. For example, N = 1000 means that there are 1000 duration events in the song. N D means the number of different duration values (DiffV) in the duration sequence. For example, N D = 3 means that the
TABLE IV
PARAMETERS USED IN THE EXPERIMENT
Parameters Meaning
N The number of events in the duration sequence M C The percentage of M axCover in the duration
sequence
N D The number of different duration values (DiffV) in the duration sequence
Rhy The rhythm query
duration sequence is created randomly from three
Dif f V ’s. Rhy means the sequence of the rhythm
query, for example, the Tango rhythm is represented by SSQQS. We choose nine of the most popular rhythms, listed in Table III and compare the running time of two algorithms by using each rhythm sepa-rately. MC means the percentage of M axCover in the duration sequence. According to the definition of M axCover, the correct rhythm query will be repeated through the music. Therefore, the value of MC is close to 100% with querying the rhythm correctly. Beside, how to choose the Dif f V ’s is also an important issue. We describe the details as follows:
• First, we define the duration of the Q rhythm, i.e., Q = 50.
• Then, the duration of the S rhythm is regarded
as 2Q, i.e., S = 100.
• Other Dif f V ’s must be combined as the
du-ration of one Q rhythm. For example, we can choose Dif f V = [25] (25 + 25 = 50) and
Dif f V = [30, 20] (30 + 20 = 50).
Some examples of Dif f V under different N D’s are shown in Table V. In the case of N D = 5, we first define Q= 50 and S = 100, and then we need
other three Dif f V ’s. Therefore, we choose Dif f V = [25] (25 + 25 = 50) and the set of Dif f V ’s = [30, 20] (30 + 20 = 50) to be the other three Dif f V ’s. Using Dif f V which is assigned by the user, if we also design an order to the duration sequence, we can control the value of M C.
Observing the form of the real music data, we set the default values of parameters to generate synthetic data that are similar to the real music data. In our simulation, we define a base case as shown in Table VI. According to the property of the duration events that two adjacent events can be combined
TABLE V
AN EXAMPLE OF THEDif f V (UNDER DIFFERENTN D) N D Dif f V
2 [50, 25] 3 [100, 50, 25] 4 [200, 100, 50, 25]
TABLE VI
BASE VALUES FOR PARAMETERS USED IN THE SIMULATION
Parameters Default values
N 10000
MC 100%
N D 3 ( Different duration values are 100, 50 and 25 )
Rhy [S, S, Q, Q, S]
to one large event, we need to generate the com-bination of events. Therefore, we assume that the duration of rhythm S is 100, and the duration of rhythm Q is 50. The combination case of duration events is shown in Table VII. Due to the property of
S that must be combined by two consecutive Q’s,
we do not consider the combination case of [25, 50, 25]. An example of the synthetic data generation with Dif f V = [100, 50, 25], Rhy = SSQQS, N = 17 and M C = 100% is shown in Table VIII.
TABLE VII
THE COMBINATION CASE OF DURATION EVENTS[100, 50, 25]
FORS =100 Rhythm Combination S [100] [50, 50] [50, 25, 25] [25, 25, 50] [25, 25, 25, 25] Q [50] [25, 25] TABLE VIII
AN EXAMPLE OF THE DATA GENERATION(N D = 3, Dif f V = [100, 50 ,25] , Rhy = SSQQS, N = 17ANDM C = 100%)
N S S Q Q S
1–8 [100] [25, 25, 50] [50] [25, 25] [100] 9–17 [50, 25, 25] [50, 50] [25, 25] [50] [100]
TABLE IX
ACOMPARISON OF THE RUNNING TIME(MILLISECONDS)OF THE
JMCALGORITHM AND THECIRSALGORITHM(UNDER THE BASE CASE)
Algorithm The running time
CIRS 44
JMC 8 (reduced 81.8%)
In order to control MC = 100%, we use the combination, as shown in Table VII, to be one element of the input. Moreover, we use the rhythm query as the order of data generation. For example, the first symbol of the rhythm query SQQSS is S, and we generate the combination of duration events from five cases of Rhythm S in Table VII randomly, and so on. In this way, we can generate the duration sequence that is covered by the rhythm query, and that is M axCover which we need.
B. Simulation Results of Synthetic Data
Now, we make a comparison of our JMC al-gorithm with the CIRS alal-gorithm by using the synthetic data. For the base case shown in Table VI, we make a comparison of the running time of our algorithms and the CIRS algorithm. The result is shown Table IX, which is the average of 20 dura-tion sequences. On the average, our algorithm can reduce about the 81.8% running time of the CIRS algorithm. The value of the reduced percentage can be calculated by using the formula described as follows:
reduced percentage= (1 − the running time of the J M C algorithm
the running time of the CIRS algorithm) × 100%.
In the first case, we vary the value of N , the num-ber of events in the duration sequence. The range of
N is set to 2000, 4000, 6000, ..., and 20000, while
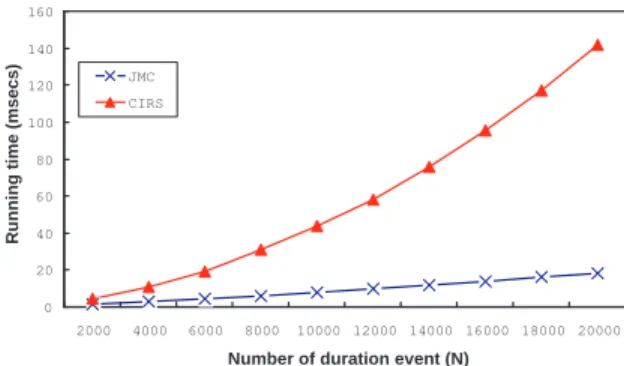
the other parameters are kept as their base values. Under changing the value of N , a comparison of the running time by using the JMC algorithm and the CIRS algorithm is shown in Figure 9. We can observe that when the value of N increases, the running time by using the JMC algorithm and the CIRS algorithm also increases. However, our algo-rithm needs shorter time to answer the same rhythm query than the CIRS algorithm. This is because that our algorithm can filter the false cut sequence (piece
0 20 40 60 80 100 120 140 160 2000 4000 6000 8000 10000 12000 14000 16000 18000 20000
Number of duration event (N)
Running time (msecs)
JMC CIRS
Fig. 9. A comparison of the running time of the JMC algorithm and the CIRS algorithm by using the different number of duration sequences(N )
of the duration sequence) in advance, whereas the CIRS algorithm does not use the pruning strategy. In this case, according to N D = 3, the CIRS algorithm needs to run the algorithm three times completely. In our algorithm, we get the result of M C = 100% for
q = 100 at the first round. Then, we can observe that
the length of M axCover is long enough to prune all cut sequences (the duration sequence of the second round for q = 50). Therefore, we do not need to run our algorithm in the second round. As compared to the CIRS algorithm, our JMC algorithm can reduce up to 66.7% of the running time.
In the second case, we vary the kinds of Rhy, the query rhythm. The nine kinds of Rhy are listed in Table III, and the base values are used for the other parameters. Under changing the different Rhy, a comparison of the running time by using the JMC algorithm and the CIRS algorithm is shown in Figure 10. We can observe that no matter what kind of Rhy is applied, the running time of the JMC algorithm is shorter than that of the CIRS algo-rithm. Moreover, our algorithm needs shorter time to answer the same rhythm query than the CIRS algorithm. This is because that our algorithm can filter the false cut sequence (piece of the duration sequence) in advance, whereas the CIRS algorithm does not use the pruning strategy. As compared to the CIRS algorithm, our JMC algorithm can reduce up to 78.7% of the running time.
IV. CONCLUSION
In this paper, we have presented the JMC (Jumping-By-M axCover) algorithm to locate the
0 10 20 30 40 50 60
Bolero Cha-Cha Foxtrot Jive Mambo QuickstepRumba Tango Waltz
The query rhythm
Running time (msecs)
JMC CIRS
Fig. 10. A comparison of the running time of the JMC algorithm and the CIRS algorithm by using different rhythm queries(Rhy)
maximum-length substring of the music duration sequence for rhythm queries, which can reduce the process cost of the CIRS algorithm [7]. Our proposed algorithm follows the definition of the CIRS algorithm and provides the pruning strategy to generate the result incrementally. From our simu-lation results, we have shown that our algorithm can reduce up to the 81.8% running time of the CIRS algorithm.
REFERENCES
[1] A. Ghias, J. Logan, D. Chamberlin, and B. C. Smith, “Query by Humming-musical Information Retrieval in an Audio Database,” in ACM Multimedia, 1995, pp. 231–236.
[2] D. Little, D. Raffensperger, and B. Pardo, “A Query by Humming System That Learns from Experiences,” in Proc. of the 8th
Int. Conf. on Music Information Retrieval, 2007, pp. 23–27.
[3] E. Unal, E. Chew, P. G. Georgiou, and S. S. Narayanan, “Challenging Uncertainty in Query by Humming Systems: A Fingerprinting Approach,” IEEE Trans. on Audio, Speech, and
Language Processing, vol. 16, no. 2, pp. 359–371, Feb. 2008.
[4] J. S. Downie, “Music Information Retrieval,” Annual Review of
Information Science and Technology, vol. 37, pp. 295–340, 2003.
[5] N. Orio, “Music Retrieval: A Tutorial and Review,” Foundations
and Trends in Information Retrieval, vol. 1, no. 1, pp. 1–96, Jan.
2006.
[6] H. C. Chen, Y. H. Wu, Y. C. Soo, and A. L. P. Chen, “Continuous Query Processing over Music Streams Based on Approximate Matching Mechanisms,” Multimedia Systems, vol. 14, no. 1, pp. 51–70, June 2008.
[7] M. Christodoulakis, C. S. Iliopoulos, and M. S. Rahman, “Iden-tifying Rhythms in Musical Texts,” Int. Journal of Foundations
of Computer Science, vol. 19, no. 1, pp. 37–51, Feb. 2008.
[8] A. L. P. Chen, C. S. Iliopoulos, S. Michalakopoulos, and M. S. Rahman, “Implementation of Algorithms to Classify Musical Texts According to Rhythms,” in Proc. 4th of Int. Sound and