A Pattern-Matching Scheme With High Throughput Performance and Low Memory Requirement

A Pattern-Matching Scheme With High Throughput

Performance and Low Memory Requirement

Tsern-Huei Lee, Senior Member, IEEE, and Nai-Lun Huang

Abstract—Pattern-matching techniques have recently been

ap-plied to network security applications such as intrusion detection, virus protection, and spam filters. The widely used Aho–Corasick (AC) algorithm can simultaneously match multiple patterns while providing a worst-case performance guarantee. However, as trans-mission technologies improve, the AC algorithm cannot keep up with transmission speeds in high-speed networks. Moreover, it may require a huge amount of space to store a two-dimensional state transition table when the total length of patterns is large. In this paper, we present a pattern-matching architecture consisting of a stateful pre-filter and an AC-based verification engine. The stateful pre-filter is optimal in the sense that it is equivalent to utilizing all previous query results. In addition, the filter can be easily realized with bitmaps and simple bitwise-AND and shift operations. The size of the two-dimensional state transition table in our proposed architecture is proportional to the number of patterns, as opposed to the total length of patterns in previous designs. Our proposed ar-chitecture achieves a significant improvement in both throughput performance and memory usage.

Index Terms—Aho–Corasick (AC) algorithm, Bloom filter, deep

packet inspection, pattern matching. I. INTRODUCTION

P

ATTERN matching has been an important technique in information retrieval and text editing for many years and has recently been applied to signature matching to help detect malicious attacks against networks. In a wider sense, pattern matching searches for occurrences of plain strings and/or reg-ular expressions in an input text string. This paper only con-siders the matching of plain strings.

Well-known pattern-matching algorithms include Knuth–Morris–Pratt (KMP) [1], Boyer–Moore (BM) [2], Wu–Manber (WM) [13], and Aho–Corasick (AC) [3]. The KMP and BM algorithms are efficient for single-pattern matching, but are not suitable for matching multiple patterns. The WM algorithm is an adaptation of the BM algorithm to multiple patterns. The AC algorithm preprocesses the patterns and builds a finite automaton that can match multiple patterns simultaneously, but may require a huge amount of memory space to do so. A straightforward implementation of the AC algorithm is to construct a two-dimensional state transition table for the finite automaton. Such an implementation requires

Manuscript received September 24, 2009; revised August 05, 2010; July 25, 2011; February 23, 2012; and July 12, 2012; accepted August 27, 2012; ap-proved by IEEE/ACM TRANSACTIONS ONNETWORKINGEditor I. Keslassy.

Date of publication November 20, 2012; date of current version August 14, 2013.

The authors are with the Institute of Communication Engineering, National Chiao Tung University, Hsinchu 300, Taiwan (e-mail: tlee@banyan.cm.nctu. edu.tw; nellen.cm93g@nctu.edu.tw).

Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.

Digital Object Identifier 10.1109/TNET.2012.2224881

a prohibitively huge amount of memory space when the total pattern length is large. Several schemes had been proposed to reduce the memory requirement. Some are incorporated in Snort [7], [8], an open-source intrusion detection/pre-vention application, and ClamAV [9], another open-source anti-virus/worm application. These compression schemes are related to our work and will be reviewed in Section II.

The AC algorithm guarantees linear-time deterministic per-formance under all circumstances and has thus been widely adopted in various systems. However, even with the linear-time worst-case performance guarantee, the throughput of the AC al-gorithm cannot keep up with transmission speeds in high-speed networks. Previous studies have exploited hardware capacity for massive parallel processing to proposed hardware accelerators for pattern-matching engines [4]–[6], [32], [33], but this lies out-side the scope of this paper.

This paper presents a pattern-matching architecture with high throughput performance and low memory requirements. Similar to the WM algorithm and the Hash-AV ClamAV scheme [30], our proposed architecture consists of a pre-filter and a verification engine. The function of the pre-filter is to query data structures built from patterns to find the starting positions of potential pattern occurrences. Once a suspicious starting position is found, the verification engine confirms true pattern occurrence. In the WM algorithm, the pre-filter was implemented as a shift table, and the verification engine checks all candidate patterns sequentially when a potential starting position is identified. In the Hash-AV ClamAV scheme, the pre-filter is a Bloom filter [14], [15], and the verification engine is a simplified version of the ClamAV implementation without the failure function. The proposed design, however, uses a bit vector, called master bitmap, with simple bitwise-AND and shift operations to accumulate query results. Consequently, our proposed pre-filter is stateful, as opposed to the statelessness in the WM algorithm and the Hash-AV ClamAV scheme. We prove in this paper that the proposed stateful pre-filter is optimal in the sense that it is equivalent to utilizing all previous query results. Our verification engine, which is a mod-ification of the AC automaton, checks all candidate patterns simultaneously rather than sequentially. Numerical results show that our design outperforms both the WM algorithm and the Hash-AV ClamAV scheme. Several other pre-filter designs have been previously proposed [16]–[28]. Similar to the hardware accelerators of pattern-matching engines, these designs used parallel processing to achieve high throughput performance and thus lie outside the scope of this paper.

It should be noted that our proposed stateful pre-filter is suitable for patterns of moderate or large lengths. For short pat-terns, its throughput performance degrades. This is a common disadvantage of schemes using pre-filters. The impact of short

Fig. 1. AC pattern-matching machine for [3]. (a) Goto function. (b) Failure function. (c) Output function.

patterns on our proposed architecture is studied in Section V. Nevertheless, the stateful concept improves throughput with little cost of master bitmap and simple bitwise-AND and shift operations.

The rest of this paper is organized as follows. Section II re-views some related work, including the original AC algorithm. Our proposed pattern-matching architecture is presented in Section III. In Section IV, we prove that our proposed architec-ture functions correctly and is an optimal design. Experimental results are provided in Section V, and conclusions are drawn in Section VI.

II. RELATEDWORK

In this section, we review the AC algorithm, previous com-pression designs for the AC algorithm, and the WM algorithm.

Throughout this paper, we shall use to

represent pattern set and to denote the input text string to be scanned.

A. Aho–Corasick Algorithm

The AC pattern-matching machine is dictated by three tions: a goto function , a failure function , and an output func-tion . Fig. 1 shows the AC pattern-matching machine for

[3].

One state, numbered 0, is designated as the start state. The goto function maps a pair (state, input symbol) into a state or the message . For example, in Fig. 1, we have

and if or . State 0 is a special state that never results in the message, i.e., for all , the alphabet. The failure function maps a state into a state and is consulted when the outcome of the goto function is the message. String is said to represent state if the shortest path on the goto graph from state 0 to state spells out . Let and be the strings that represent states and , respectively. We have if and only if (iff) is the longest proper suffix of that is also a prefix of some pat-tern. It is not difficult to verify that for our example. The output function maps a state into a set of patterns (which could be empty). The set contains pattern iff is

a suffix of the string representing state . As an example, we

have .

Note that there might be a self-loop on the start state of the goto graph. In the following definitions, we ignore the self-loop so that the goto graph can be considered as a tree. State is said to be a child state of state , and state the parent state of state , if there exists a symbol such that . State is said to be a branch state, a single-child state, or a leaf state if it has at least two child states, exactly one child state, or no child state, respectively. Moreover, state is said to be a final state if is not empty.

The operation of the AC pattern-matching machine is as follows. Let be the current state and be the current input symbol. An operation cycle is defined as follows.

1) If , the machine makes a state transition such that state becomes the current state and the next symbol of becomes the current input symbol. If

(empty set), the machine emits the set . The operation cycle is complete.

2) If , the machine makes a failure transition by consulting the failure function . Assume that

. The pattern-matching machine repeats the cycle with as the current state and as the current input symbol. Initially, the start state is assigned as the current state, and the first symbol of is the current input symbol. The property for all guarantees that one input symbol is processed by the pattern-matching machine in every operation cycle.

A straightforward implementation of the goto function uses a two-dimensional table to look up the next state. However, such an implementation requires a huge amount of memory space when the total length of patterns is large. Some compression schemes are reviewed in the following sections.

B. Bitmap Data Structure

In the bitmap data structure [10], each state has a -bit bitmap and a state array, where is the size of . The th bit of the bitmap is a 1 iff . The state array stores each non-fail , sorted by the value of . As a result, to find , one needs to count the total number of 1’s in the bitmap of state up to the th position if . To reduce the processing time, one can maintain running sums of every 32 bits in the bitmap, and we assume in this paper that run-ning sums are maintained for higher throughput performance. For convenience, this compression scheme is referred to as the bitmapped AC.

For certain applications such as anti-virus programs, it is highly likely that the state away from the start state is a single-child state. Therefore, path compression was introduced in [10] to squeeze four single-child states into one state. Memory requirements can be further reduced if the length of the compressed paths is not restricted. In the scheme proposed in [12], a state is eliminated if: 1) it is a single-child state; and 2) there is no incoming failure transition to it. Another effective compression technique proposed in [12], called leaf compression, eliminates leaf states with two modifications: 1) pushing the indication of the match to the penultimate state, and 2) copying the failure transitions of leaf states to the corresponding penultimate states as their new goto transitions.

The first modification is realized by adding one bit for each outgoing goto transition in a state, indicating whether or not it leads to a final state. The second modification reduces the number of transitions taken during the automaton traverse. If both path compression and leaf compression are adopted, then leaf compression adds a match indication bit to each symbol of the corresponding compressed path.

C. Banded-Row Format

In the banded-row format [11], which is used in Snort, the row elements are stored from the first nonzero value (or

non-fail value in the goto transition table) to the last nonzero

value, known as band values. For example, the banded-row format of the sparse vector (0 0 0 2 4 0 0 0 6 0 7 0 0 0 0 0) is (8 3 2 4 0 0 0 6 0 7), where the first element indicates the number of vector elements stored, referred to as bandwidth, and the second element represents the index (numbered from 0) of the first vector element stored, followed by the band values. The AC pattern-matching machine whose goto transition table is compressed with the banded-row format is referred to as the banded-row format AC.

D. AC-Bnfa

AC-bnfa is another alternative adopted by Snort for pattern matching. For each state, it stores a transition list that contains at least two words. The first word (in the current implementation, only the least significant 24 bits) stores the state number. The second word, called the control word, stores a control byte and the failure state, which takes 24 bits. The control byte contains one bit to indicate whether or not some patterns are matched in the state and another bit to show if the number of its child states, denoted by , is greater than or equal to 64. If , then the succeeding words are used to store the input symbols (1 B) and the corresponding next states (3 B). In case , a full array of 256 words is used to store all the possible input symbols and the corresponding next states. The (input symbol, corresponding next state) pairs are searched sequentially if

or, with binary search, if . A simple table lookup is sufficient if .

E. ClamAV Implementation

ClamAV [9] implementation limits the depth of the goto graph to two and partitions the patterns into groups so that two patterns are in the same group iff they have the same prefix of length two. All patterns in the same group are saved as a linked list associated with a leaf state. Whenever a leaf state is visited, all patterns on its linked list are checked sequentially.

The Hash-AV ClamAV scheme [30] adds a pre-filter to the ClamAV implementation. The pre-filter, called Hash-AV, is a Bloom filter built with hash functions. The input of the hash functions is a string of bytes. The authors analyzed the length distribution of ClamAV signatures and suggested choosing

and . The four hash functions selected are “mask” [30], “xor shift” [30], fast hash from hashlib.c [31], and sdbm [29]. A sliding window of bytes is used to move down the input text string during scanning. The hash functions are applied se-quentially to the bytes contained in the window. The ClamAV implementation is invoked for verification iff all query results are positive. Obviously, inserting all -byte substrings starting

at the first offsets of all signatures into the Bloom filter allows the sliding window to be moved bytes at a time. However, the false positive probability will be increased. Hash-AV ClamAV uses this strategy and chooses .

F. Wu–Manber Algorithm

The WM algorithm [13] consists of a pre-filter and a verifi-cation engine. To construct the pre-filter, only the first sym-bols of each pattern are considered, where is the length of

the shortest pattern. Let , represent the

-symbol prefix of pattern . A SHIFT table, a HASH table, a

PAT_POINT list, and a PREFIX table are required. The SHIFT

table is used to determine how many symbols in the text can be safely skipped during scanning. The HASH table, PREFIX table, and the PAT_POINT list are used when verification is needed. The SHIFT table is related to our pre-filter design and is de-scribed as follows.

Assume that the SHIFT table has entries. A hash func-tion, denoted by , is required for the construction of the

SHIFT table. The input of is a block of size symbols, and its output falls in . Initially, set

for all . Then, change

to if there exists , such that

, and

for all ,

and all .

A search window of length is used during scanning. Initially, the search window is aligned with the input text string, i.e., the substring contained in the search window is . During scanning, the last symbols of the text string contained in the search window are hashed. Let be the hash result. If , then the search window is

advanced by positions. In case ,

the verification engine is invoked and the candidate patterns are verified sequentially. After verification, the search window is advanced by one position.

III. PROPOSEDPATTERN-MATCHINGARCHITECTURE

As mentioned before, our proposed pattern-matching archi-tecture consists of a pre-filter and a verification engine. The pre-filter is designed based on Bloom filters, and the verifica-tion engine is modified from the AC algorithm.

A. Pre-Filter Design

As in the WM algorithm, only the first symbols of each pat-tern are considered in constructing the pre-filter, where has to be smaller than or equal to the length of the shortest pattern. To achieve a high degree of system performance, is normally chosen to be the length of the shortest pattern. Given a block size , our pre-filter design includes membership query

modules denoted as and . Every

membership query module has bits. Recall that is the -symbol prefix of pattern . The th bit of

, is set to 1 iff there exists a pattern such

that . Unlike the WM algorithm,

our pre-filter design uses membership query modules rather than the SHIFT table. As will be seen later, such a design allows pre-vious query results to be easily accumulated to improve system performance.

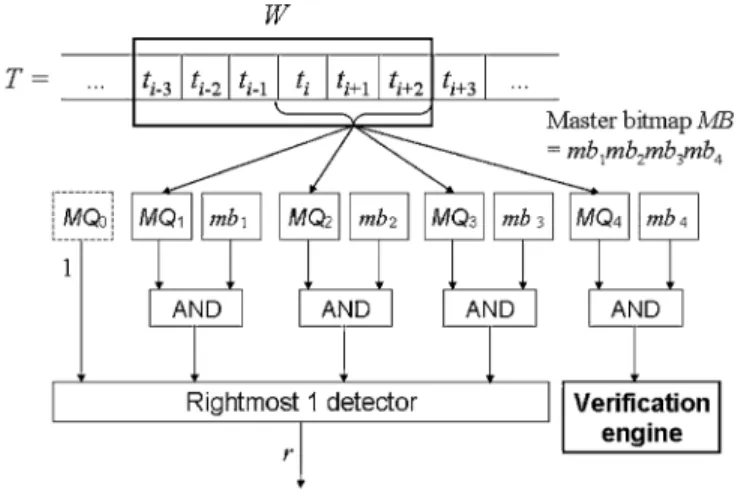
Fig. 2. Stateful pre-filter architecture for and .

As an example, assume that alphabet

and pattern set , where

, and . Since the length of the shortest

pat-tern is 5, we can choose . Assume that ,

and the hash function is the identity mapping. For such a set-ting, there are membership query modules. Let be the content of the th bit of the th membership query module. We have

iff , or 61; iff , or 46;

iff , or 69; and iff

, or 92.

Again, a search window of length is used during scanning. Initially, is aligned with the input text string so that the substring of contained in is . In general, assume that the substring of contained

in is . The -symbol suffix, i.e.,

, is used to query the

mem-bership query modules. Let , be the

report of and denote the

bitmap of the current query result. Note that iff

was set to 1, where .

We use a master bitmap of size bits to accu-mulate the previous query results and act as the state of the

pre-filter. Let represent the

master bitmap. Initially, we set , i.e.,

for all . After fetching a query result,

we perform , where & is the bitwise-AND operation. A suspicious substring starting from the first symbol contained in is found, and the verification engine is invoked

if . The search window is advanced by

positions if for all ,

or positions if and for

all . If is determined to be advanced

by positions, MB is right-shifted by bits and filled with 1’s for the holes left by the shift. Fig. 2 shows the pre-filter architecture for and . A virtual membership query module , which always reports a 1, is added to ensure the rightmost 1 detector functions correctly. The correctness of the stateful pre-filter is proved in Section IV.

The pre-filter is stateless without the master bitmap. In this case, only the current query result is used to determine window

advancement. It is not hard to see that, with the master bitmap, can be advanced by more positions. We provide analytical comparison of stateful and stateless designs in the Appendix. In fact, as shown in Section IV, the proposed implementation using master bitmap and simple bitwise-AND and shift operations is optimal in the sense that it is equivalent to utilizing all previous query results.

We use an example to explain the operation of the stateful pre-filter. Consider the membership query modules constructed above and assume that . Initially, contains 23764 and is 1111. The substring 64 is used for the first query, and the query result . Since

is advanced by one position, and becomes 1001. In the second iteration, the substring contained in is 37646,

and the query result is . Since ,

the search window is advanced by four positions, and is updated as 1111. In the third iteration, the substring 62 is used as the query, and the result is . Since

, a suspicious substring starting from the first symbol con-tained in is found. Therefore, the verification engine is in-voked, and the pattern is detected. After the veri-fication, the search window is advanced by four positions. Since the length of the remaining input text string, i.e., 21, is smaller than , the scanning process ends.

Note that, for the above example, the query result in the first iteration, i.e., , indicates that it is impossible to find a pattern occurrence starting from the third or the fourth symbol contained in because . In other words, after is advanced by one position, neither the second nor the third symbol contained in can be the starting symbol of a suspicious substring. Therefore, although the query result has

in the second iteration, it is safe to advance by four positions. We use the master bitmap to accumulate previous query results and carry them from previous iterations to the current one. Without (which becomes stateless), the search window can only advance by one position in the second iteration.

In general, performing multiple queries in each iteration can reduce false positive probability and increase window advancement. However, this requires more processing time than is needed to perform a single query. Assume that in each iteration queries are performed with different hash functions and independent sets of membership query mod-ules. Similar to the single-query case, the last symbols within are used for multiple queries during scanning. Let represent the bitmap reported from the th

query and . The master bitmap

is updated as . The window advancement

and the presence of a suspicious substring are determined according to the value of in the same way as in the single-query case. The optimal value of that maximizes throughput performance will be analyzed in the Appendix.

B. Verification Engine Design

The verification engine is designed based on the AC algorithm so that all candidate patterns can be verified simulta-neously. The use of the pre-filter requires modification to the AC algorithm. The first modification, which concerns the goto function, is to delete the self-loop, if exists, at the start state

because the task of consuming a symbol at the start state is taken over by the pre-filter. The second modification is to omit the failure function because once the goto function returns the message, we know that the suspicious substring found by the pre-filter is a false positive. The third modification is regarding the output function. Assume that patterns and satisfy , where is a nonempty string. Let be the state represented by string . In the original AC algorithm, includes pattern . In our proposed architecture, pattern is removed from . The reason is that if pattern occurs in , the pre-filter will notify the verification engine when the starting position of pattern is aligned with the search window. If includes pattern , then will be detected multiple times if is a substring of .

Since the failure function is not necessary, only the goto tion and the output function need to be stored. The output func-tion is simplified because at most one pattern is matched in each state. Similar to the scheme proposed in [12], we adopt the con-cept of variable-length path compression to reduce the memory requirements of the goto function. However, since there is no restriction caused by the failure function, our proposed architec-ture can yield better compression results than the scheme pro-posed in [12].

We call single-child state a first single-child state if its parent state is a branch state. State is said to be an explicit state if it is the start state, a branch state, a first single-child state, or a final state. We store all patterns and design data structures for explicit states. The patterns are stored con-tiguously in the Compacted_Patterns file. For example, if , then the Compacted_Patterns file

is .

For a branch state, we use the banded-row format, which al-lows fast random access without imposing a large memory re-quirement, to store its goto transition vector. As a result, we still have a two-dimensional state transition table. The resulting state transition table is named the Branch State Transition (BST) table. Note that the number of rows in the BST table is only equal to the number of branch states, which is at most for

patterns.

Assume that state is a single-child state and is represented by string . State is said to be a descendent state of state if it is represented by (the concatenation of and ), where is a nonempty string. Furthermore, state is said to be a descendent explicit state of state if, in addition to being a descendent state of state is an explicit state. State is said to be the nearest descendent explicit state (NDES) of state if state is a descendent explicit state of state and there is no other explicit state on the path from state to state .

Suppose that state is a first single-child state and state is its NDES. Let be the first pattern in the pat-tern set which contains as a prefix. The data structure for state includes .position and .distance, where .position and .distance respectively represent the position of the

th byte of in the Compacted_Patterns file and , where denotes the length of string . If the start state or a final state is a single-child state, its data structure is the same as that for state . Note that the data structure of state does not con-tain .NDES because one can always set the state number of

.NDES as one plus that of .

Fig. 3. Goto graph for and

. (a) Goto graph of the original AC algorithm. (b) Compressed goto graph in our proposed archi-tecture. (c) Path-compressed goto graph of the scheme proposed in [12].

Finally, for each leaf state, we store nothing but an identifier to indicate that all input symbols result in the message. Of course, every explicit state needs a flag to indicate whether or not it is a final state, and if it is, the identification of the matched pattern is stored. Similar to leaf compression [12], our design significantly reduces memory requirements for leaf states. Our design needs two bits for every explicit state to indicate its type (branch, single-child, or leaf) and another bit to indicate whether or not a match is found in the state. Except for the matched pat-tern (which is needed for all schemes), these three bits are the only information required for a leaf state. As for leaf compres-sion, one bit is added to every goto transition or to every symbol of the corresponding compressed path if path compression is adopted. For a large pattern set, we expect the number of ex-plicit states to be much smaller than the number of symbols of all patterns.

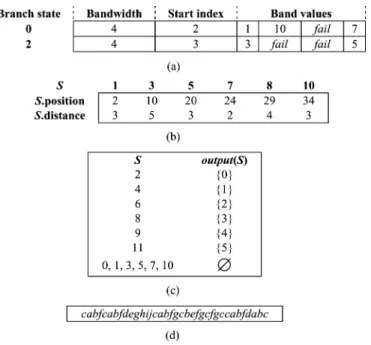
As an example, assume that alphabet and pattern set

. The corresponding goto graph of the original AC algorithm is shown in Fig. 3(a). Fig. 3(b) shows our compressed goto graph. Note that the states on the compressed goto graph are numbered so that the state number of .NDES for explicit single-child state is . Compared to Fig. 3(a), the number of states is reduced from 26 to 12. The single-child states 1, 3, 5, 7, and 10 are first single-child states and thus remain on the goto graph. Note that it is possible to eliminate those first single-child states if the label on each outgoing goto transition of a branch state is allowed to be a string. However, by doing so, the state transitions of a branch state become com-plicated, and system performance is degraded. Therefore, we do not adopt this strategy. Fig. 3(c) shows the path-compressed goto graph of the scheme proposed in [12]. Because of the

Fig. 4. Verification engine data structures for

and . (a) BST

table. (b) Data structure for first single-child states and single-child final states. (c) Output function. (d) Compacted_Patterns.

Fig. 5. Input text string and suspicious starting positions.

incoming failure transitions, the single-child states 1, 2, 3, 15, 16, 17, and 22 in Fig. 3(c) cannot be removed.

In Fig. 3(b), states 0 and 2 are branch states, while states 4, 6, 9, and 11 are leaf states. The remaining states are either first single-child states or single-child final states. Fig. 4 shows the data structures of our verification engine for this example. Assume the symbols in are sequentially encoded from 0 to 9. The vector representing goto transitions for state 0 is

( 1 10 7 ) and is stored as

(4 2 1 10 7). Similarly, the goto transition vector for state 2

is ( 3 5 ) and is stored

as (4 3 3 5). Let be state 7, a first single-child state. Since state 8, represented by , is the NDES of with distance 2 and is the first pattern that contains as a prefix, we store .position 24 and .distance . If is state 8, we store .position and .distance .

To explain the operation of the proposed veri-fication engine, let us consider the above

ex-ample with and

. The data structures are shown in Fig. 4. The input text string and the suspicious starting positions identified by the pre-filter are illustrated in Fig. 5. When the verification engine is invoked, the verification procedure starts to traverse the compressed goto graph from state 0. The verification procedures stops once the goto transition fails or the symbols of are exhausted.

Consider the suspicious starting position 1. Since state 0 is a branch state, the verification engine consults the BST table and knows that the first symbol in the suspicious substring, i.e., , is outside the band of state 0, which implies

. Therefore, the suspicious substring is a false positive and the verification procedure stops. Next, consider the suspicious starting position 2. Again, the verification procedure starts by consulting the BST table. This time, the engine finds that the first symbol in the suspicious substring, i.e., , is inside the band of state 0. However, the band values indicate that . Thus, this suspicious substring is also a false positive, and the verification procedure does not need to continue. Now, let us consider the suspicious starting position 3. The BST table indi-cates that the first symbol in the suspicious substring, i.e., , is inside the band of state 0 and . Consequently, the en-gine moves the current state from state 0 to state 7. Since state 7 is a first single-child state and its .position and .distance are respectively 24 and 2, the engine checks if the following sub-string in of length two is the same as the two-symbol sub-string starting from the 24th position of Compacted_Patterns. The checked result is true, therefore the engine updates the cur-rent state by increasing the state number by one to state 8. Since , Pattern 3, i.e., , is detected. The verifi-cation procedure does not stop here. State 8 is a single-child final state, and its .position and .distance are respectively 29 and 4. Thus, the engine compares the substring in , and the substring in Compacted_Patterns. The substrings are different, which implies the goto transition fails, therefore the verification procedure stops. Finally, consider the suspicious starting position 4. As in the previous case, the current state is moved from state 0 to state 10, and then from state 10 to state 11. State 11 is a leaf state, which implies: 1) some pattern is detected here; and 2) the goto transition will fail, and therefore the veri-fication procedure stops. Since we have , we know that Pattern 5, i.e., , is detected.

C. Time Complexity

The number of memory accesses required by each type of state is analyzed as follows. Assume that bytes are fetched in a memory access. For a branch state, to process one byte, we need memory access to obtain bandwidth (2 B), the index of the first vector element stored (1 B), state type (2 bits), and the final state indication (1 bit). In addition, memory access is required to get a band value (3 B) if the input symbol is within the band. If the state is a final state, another memory ac-cess is performed for the identification of the matched pattern (2 B). Therefore, a branch state requires at least and at

most memory accesses. For an

ex-plicit single-child state .distance bytes are processed with

at most memory accesses.

More specifically, we need to obtain .position (3 B), .distance (1 B), state type (2 bits), and the final state indication

(1 bit), up to to reach .NEDS, and for

the matched pattern if state is a final state. For a leaf state, we need memory access to obtain the state type and the iden-tification of the matched pattern. Since the operations are quite simple, the proposed architecture is also suitable for hardware implementation.

IV. CORRECTNESS ANDOPTIMALITYPROOFS OF THESTATEFUL

PRE-FILTER

In this section, we prove the correctness and optimality of the proposed stateful pre-filter.

A. Proof of Correctness

Consider the th iteration. Let

and respectively be the

contents of the search window and the master bitmap in the beginning of the considered iteration. Further let be the query result and be the updated master bitmap. We prove that the proposed stateful pre-filter does not miss any pattern occurrence by showing the following claim. Note that given an

and any , if

for all patterns , then there is no pattern occurrence starting from . Therefore, it is safe to advance the search

window by positions if for all

(without verification) or for

all and (after verification).

Claim: If then it

holds that there exists some , such that

for all patterns .

According to the operation of the proposed stateful pre-filter,

is always true, thus implies

. Therefore, the claim is true for

because meets the requirement. We prove the case by mathematical induction.

For , i.e., the first iteration, it is true that

iff . In other words, we have iff

for all patterns . Therefore, for the first iteration, the claim is true by choosing . Assume that it is true for and consider the th iteration.

The notation needs to be clarified since two iterations are con-sidered simultaneously. Let

, and respectively be the search window content, the master bitmap, the query results, and the updated master bitmap of the th iteration.

Similarly, let , and be

those of the th iteration. Assume that the search window is advanced by positions in the th iteration. If , we have , and the claim is true for the th iteration by choosing . Consider the case . After advancing the search window and updating

the master bitmap, we have and

.

Let and

assume that for some .

If , then it must hold that , and

there-fore the claim is true by choosing . Assume that

. Since , we have

or . The claim is true for the th

iteration by choosing if . Assume that

, which implies . Since ,

we know by hypothesis that there exists an , such that

for all patterns . Let and . We conclude that there exists an

, such that

for all patterns . Therefore, the claim is also true for the th iteration for . This completes the correctness proof of the proposed pre-filter.

B. Proof of Optimality

We now prove that the implementation with the master bitmap is optimal in the sense that it is equivalent to using all previous query results. For convenience, we call the scheme implemented with master bitmap Scheme A and the one using all previous query results Scheme B. We assume that Scheme B, as Scheme A, advances the search window for as many positions as possible in each iteration. The two schemes are equivalent if, in each iteration: 1) they advance the search window by the same number of positions; and 2) if one in-vokes the verification engine, the other as well. We prove the equivalence of Schemes A and B by mathematical induction on iteration number.

Consider the th iteration. Let

,

and respectively

be the search window content, the master bitmap, the query result, and the updated master bitmap of Scheme A. The symbol , is said to be a possible starting symbol of pattern occurrence for Scheme B in the beginning of the th it-eration iff it cannot be excluded based on the results of the first queries. We shall show that for Scheme A iff is a possible starting symbol of pattern occurrence of Scheme B in the beginning of the th iteration (Condition 1) and the condition for both schemes to invoke the verification engine is (Condition 2). Note that

(for Scheme A) iff (for Scheme A) and ,

and iff is considered a possible starting

symbol of pattern occurrence based solely on the th query result (for Scheme B). Therefore, Condition 1 implies both schemes advance the search window by the same number of positions (after verification, if needed) in the th iteration.

For , we have and .

Since no query was performed prior to the first iteration, every symbol contained in the search window is a pos-sible starting symbol of pattern occurrence of Scheme B in the beginning of the first iteration. Therefore, Condi-tion 1 is true. Moreover, Scheme A invokes the

verifica-tion engine iff . Since ,

the condition is identical to , which implies for some pattern , which in turn implies Scheme B has to invoke the verification engine to check for potential pattern occurrence starting from . Therefore, Condition 2 is also true and the two schemes are equivalent for the first iteration.

Assume that the two schemes are equivalent for the th iteration and consider the th iteration. Let

be the parameters of the th iteration and

, and be those of the th iteration for Scheme A. Assume that the search window is advanced by positions

in the th iteration. If , we have

. The last

symbols contained in , i.e., and

, can never be excluded as possible starting symbols of pattern occurrences based on the first queries, and the

symbols are newly contained

by the search window and cannot be excluded based on the first queries either. Thus, we conclude that all symbols contained in are possible starting symbols of pattern occurrences for Scheme B in the beginning of the th iteration.

Note that we also have for Scheme A.

Therefore, the th iteration is just like the first iteration. Consequently, the two schemes are equivalent for the th

iteration. Assume that . In this case, we

have

and . Again, the last

symbols contained in , i.e., and

, can never be excluded as possible starting symbols of pattern occurrences for Scheme B based on the first

queries, and the symbols

are newly contained by the search window and cannot be excluded based on the first queries either. Therefore, the

symbols and cannot

be excluded in the beginning of the th iteration.

In other words, , is a possible

starting symbol for pattern occurrence of Scheme B in the beginning of the th iteration. This corresponds

to for all . Consider the bit

. According to the proof of

the claim in Section IV-A, if , then the

symbol can be excluded

as a possible starting symbol of pattern occurrence for

Scheme B. Assume that . Since ,

we have . By hypothesis,

implies is a possible starting symbol of

pattern occurrence of Scheme B in the beginning of the th iteration. This fact, together with , implies that remains a possible starting symbol for pattern occurrence of Scheme B in the beginning of the th iteration. Therefore, Condition 1 is true for the th iteration.

Finally, assume that , which is the condition for Scheme A to invoke the verification engine. In this case, it holds that , which implies that Scheme B cannot exclude as a potential starting symbol of pattern occur-rence. Hence, it will invoke the verification engine to check pat-tern occurrence starting from . Consequently, Condition 2 is also true for the th iteration. This completes the proof of equivalence for Schemes A and B.

V. EXPERIMENTALRESULTS

In this section, we compare the performances of the investi-gated pattern-matching schemes. All schemes are implemented

Fig. 6. Throughput performance of the Pre-filter AC scheme for different values of block size .

in C++. For convenience, we name our proposed scheme Pre-filter AC. To study the impact of short patterns to Pre-filter AC, we conduct simulations for small values of .

A. Simulation Settings

The experiments are conducted on a PC with an Intel Pen-tium 4 CPU operating at 2.80 GHz with 512 MB of RAM, 8 kB L1 data cache, and 512 kB L2 cache. The entire ClamAV pat-tern set is used, containing 29 179 string signatures. The min-imum, maxmin-imum, average, and total lengths of the signatures are 10, 210, 66.43, and 1 938 433 B, respectively. The total number of states generated by the AC algorithm is 1 844 895. Since the shortest pattern is 10 B, we set the search window length . We concatenated executable files and script files to form the input text since malware can appear in the form of an executable or script.

B. Numerical Results

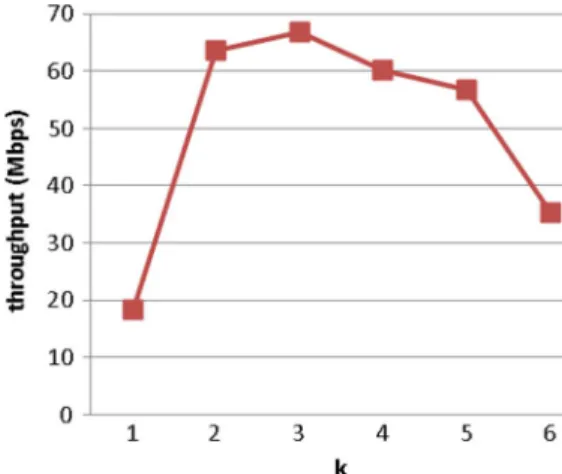
For the entire ClamAV pattern set, the time required to con-struct the data con-structure of the proposed Pre-filter AC scheme is 1812 ms. The construction is needed only in the beginning or when the pattern set is changed. Fig. 6 shows the throughput per-formance of Pre-filter AC for different values of block size . Note that for , the false positive probability of pre-filter is large, implying the verification engine is frequently invoked, reducing system throughput. The average window advancement tends to decrease for large values of . According to our exper-imental results , and 5 are good choices to achieve high system throughput, with being optimal. Thus, is used in the following experiments.

The size (in bits) of a membership query module in the proposed Pre-filter AC scheme (which is also the number of entries in the SHIFT table of the WM algorithm) is 2 . The resulting false positive probability is approximately 0.359. To ensure a fair comparison, we set the pre-filter size of the Hash-AV ClamAV scheme at 2 bits since it uses only one membership query module. Recall that to advance the search window by four positions each time to improve system per-formance, the Hash-AV ClamAV scheme inserts all -byte substrings starting at the first four offsets of all signatures into its membership query module. As a result, signatures

Fig. 7. Throughput comparison.

TABLE I

MEMORYREQUIREMENTCOMPARISON

shorter than bytes appearing in the input text may not be detected. For (the value suggested by the authors of [30]), the scheme requires a “two-scan” approach. That is, Hash-AV ClamAV is first performed for signatures longer than or equal to 12 B, and ClamAV is then executed for the rest of the signatures. We omit the second scan by removing signatures shorter than bytes for the Hash-AV ClamAV scheme in performance comparison.

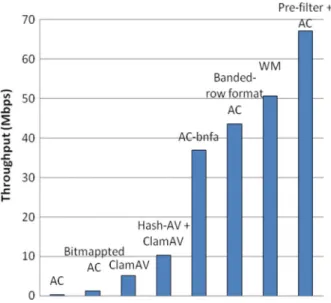
We compare the basic version of the proposed Pre-filter AC, i.e., one query per iteration, with various pattern-matching schemes from the literature. A simple hash function is adopted for our proposed pre-filter. Let be the data block to be hashed. The hash function generates as the hash result. Fig. 7 and Table I show the comparisons of throughput and memory requirements.

Our proposed Pre-filter AC scheme requires less than 4.6 MB, including 0.06 MB for pre-filter, 1.94 MB for patterns, and 2.58 MB for the data structures of the modified AC au-tomaton. In addition to low memory requirements, the proposed Pre-filter AC scheme yields higher throughput than all the other schemes. The comparisons are discussed in the following.

C. Comparison to AC-Based Implementations

The AC-based implementations include the original AC algo-rithm, bimapped AC, AC-bnfa, and banded-row format AC. As expected, the data structure of the original AC algorithm uses an extremely huge amount of memory space for the entire ClamAV pattern set. This results in low throughput because of cache misses. Among the other schemes, the bitmapped AC requires

the most memory space because every state needs a bitmap of 256 bits or 32 B. It was reported that the path compression tech-nique can achieve a 2.54:1 compression ratio [10], but even with path compression, its memory requirements are still larger than those of the other schemes. The bitmapped AC also yields lower throughput performance than the other schemes because it needs to compute the population count in a 32-bit bitmap.

The banded-row format AC and the AC-bnfa have relatively high throughput. Banded-row format AC actually outper-forms AC-bnfa because it allows fast random access, whereas AC-bnfa requires linear or binary search to perform state transition. The properties of fast random access and efficient memory reduction are the major reasons for us to adopt the banded-row format in our design.

Note that our proposed Pre-filter AC scheme requires much less memory space than the banded-row format AC because the size of the two-dimensional state transition table in Pre-filter AC is proportional to the number of patterns rather than the total length of patterns as in banded-row format AC.

D. Comparison to ClamAV-Based Implementations

The ClamAV implementation stores a partial AC trie of depth two. As a result, it requires the least amount of memory space among the investigated schemes. However, it has to sequentially check all patterns associated with a leaf state whenever it is visited, which could be time-consuming. In addition, no sym-bols in the input text are consumed during the checking pro-cedure if the checking fails. Thus, the throughput performance of ClamAV is unsatisfactory. With the use of a pre-filter, the Hash-AV ClamAV scheme improves throughput performance of the original ClamAV implementation.

E. Comparison to WM Algorithm

Experiments on the WM algorithm found the optimal block size is , which was used for the WM algorithm in perfor-mance comparison. As shown in Fig. 7 and Table I, the proposed Pre-filter AC scheme and the WM algorithm provide the best throughput performance, and the memory requirements of both are acceptable.

To evaluate performance under various fractions of malicious traffic, we replaced some content of a 2.2-MB Windows exe-cutable with 10, 100, or 1000 signatures. If the average size of a malicious program is 1 kB, then the respective fraction of malicious traffic for 10, 100, or 1000 signatures is about 0.45%, 4.5%, or 45%. Fig. 8 shows the experimental results. The throughput of the Pre-filter AC scheme is seen to decrease as the number of signatures in the input text increases. However, it still outperforms the WM algorithm.

Table II compares the memory requirements for different values of . Recall that is the size (in bits) of a membership query module in the Pre-filter AC scheme and is also the number of entries in the SHIFT table of the WM algorithm. As one can see, when is small, the WM algorithm requires less memory space than the Pre-filter AC scheme. However, the memory requirement of the WM algorithm grows rapidly as increases. By contrast, the growth for the Pre-filter AC scheme is relatively slow. When , the memory re-quirement of the Pre-filter AC scheme is 59.5% of that of the WM algorithm. The percentage decreases as increases. This

Fig. 8. Throughput for scanning files with different numbers of signatures.

TABLE II

MEMORYREQUIREMENTCOMPARISON FORDIFFERENTVALUES OF . INTHIS

TABLE, IS THESIZE(INBITS)OF AMEMBERSHIPQUERYMODULE IN THE

PRE-FILTER AC SCHEME AND ISALSO THENUMBER OFENTRIES IN THE

SHIFT TABLE OF THEWM ALGORITHM

is because the memory requirement of the verification engine in the Pre-filter AC scheme is not influenced by the value of , while that in the WM algorithm is. The size of the HASH table used in the verification engine of the WM algorithm increases as increases. Both schemes need to store the pattern set. The Pre-filter AC scheme uses the Compacted_Patterns file, which requires 1.94 MB. The WM algorithm needs slightly larger memory space because an ending symbol is required for each pattern. The pre-filters of both schemes take 0.06, 0.26,

1.04, and 4.19 MB of memory for and

, respectively. The verification engine of the Pre-filter AC scheme requires 2.58 MB, independent of . For the WM al-gorithm, the verification engines respectively takes 0.22, 0.61,

2.19, and 8.48 MB of memory for , and .

Fig. 9 shows the throughput comparison of the Pre-filter AC scheme and the WM algorithm for different values of . The input text is a 2.2-MB Windows executable. The Pre-filter AC scheme has higher throughput than the WM algorithm because: 1) the stateful concept allows the search window to be advanced more in comparison with the stateless design; and 2) the verifi-cation engine in the Pre-filter AC scheme checks all candidate patterns simultaneously, while that in the WM algorithm needs to check them one by one.

F. Impact of Short Patterns

To study the impact of short patterns on Pre-filter AC, we conduct simulations for small values of . The value of is chosen to be the optimal one for each . The input text is still a 2.2-MB Windows executable. As shown in Fig. 10, the throughput performance reduces as the value of decreases. In other words, pre-filtering does not help (and possibly even hurts)

Fig. 9. Throughput comparison for different values of .

Fig. 10. Impact of on the throughput performance of the Pre-filter AC scheme.

system performance if there are short patterns. This is a common drawback of schemes using pre-filters. One possible remedy is to utilize the verification result to help advance the pre-filter. How to efficiently combine the operations of the pre-filter and verification engines remains to be studied.

VI. CONCLUSION

In this paper, we propose a pattern-matching architecture that achieves high throughput with low memory requirements. In the architecture, we introduce the stateful pre-filter concept and present an AC-based verification engine that can check all can-didate patterns simultaneously. A master bitmap with simple bitwise-AND and shift operations is used to efficiently accu-mulate previous query results. Such a simple implementation is optimal because it is equivalent to utilizing all previous query results.

The performances of different pre-filter designs are evalu-ated both mathematically and numerically. The effect of mul-tiple queries in each iteration is also studied. Results show that the proposed pre-filter with the master bitmap (stateful) outper-forms both the proposed pre-filter without the master bitmap and the pre-filter of the widely used Wu-Manber algorithm (state-less). Moreover, our proposed schemes are compared to var-ious related works. The stateful architecture performs the best in

terms of both memory requirement and throughput among the schemes that yield satisfactory performance for both metrics. Therefore, for applications that require high throughput perfor-mance with memory space constraints, e.g., an embedded se-curity appliance in a high-speed network environment, our pro-posed stateful architecture is the preferred solution.

Clearly, a larger search window provides better throughput performance. However, the length of the search window is upper-bounded by the length of the shortest pattern. Conse-quently, to improve performance and reduce false positives, a virus expert should try to avoid short patterns in deriving signatures. Two interesting future research topics would be the implementation and performance comparison of various pat-tern-matching algorithms on multithread, multicore processors and the analysis of pre-filter performance for general cases.

APPENDIX

In this Appendix, we analytically compare the performances of stateful and stateless pre-filter designs. The stateless de-signs include the pre-filter presented in the WM algorithm and our proposed pre-filter without the master bitmap. The average window advancement per unit time, which deter-mines achievable throughput, is selected as the performance metric. For simplicity of analysis, we assume that symbols in patterns and input text string are independent and uniformly distributed over the alphabet. Good hash functions, together with (random) window advancement, can make this assump-tion acceptable to certain degree. Recall that the query result . Let

represent the probability of for any .

We have . Let denote the random

variable of window advancement for queries. The average window advancement, denoted by , can be evaluated by

(1) where is different for different algorithms.

A. Pre-Filter Performance

We use to represent the average time consumed in one query. As a consequence, the average time spent in queries is , and determines the pre-filter throughput. It is reasonable to assume that is the same for algorithms that use the same set of hash functions. Assuming that all investigated algorithms use the same set of hash functions, we can conclude that pre-filter throughput is proportional to . The optimal value of that maximizes throughput satisfies

(2) In the following, we separately derive for the pre-filter in the WM algorithm, the stateless version of the proposed pre-filter, and the stateful pre-filter.

1) Wu–Manber Pre-Filter: Conceptually, the window

ad-vancement decided by the SHIFT table in the WM algorithm is equivalent to that decided by the stateless version of our pro-posed pre-filter, except that the window is advanced by only one position if . Therefore, we have (3), shown at the bottom of the page, and can be obtained from (1) and (3).

2) Stateless Version of the Proposed Pre-Filter: For the

state-less version of our proposed pre-filter, the bit is not in-volved in determining window advancement. Consequently, we have (4), shown at the bottom of the page. Similarly, can be obtained from (1) and (4). Note that the average window ad-vancement of the stateless version of our pre-filter is greater than that of the WM algorithm. This is because when , the window advancement in the WM algorithm is always one, and it can be greater than one for our proposed pre-filter.

3) Stateful Pre-Filter: For the proposed stateful pre-filter, we

use a Markov chain to analyze the average window advance-ment. Again, the bit is not involved in determining window advancement. The states of the Markov chain corre-spond to the values of , the leftmost bits of after bitwise-ANDing with (but before the right shift). As a result, there are states on the Markov chain. Since the symbols in the patterns and input text string

if if if (3) if if (4)

are independent and uniformly distributed over the alphabet, the Markov chain is homogeneous.

Let be the state after the th iteration of queries. Furthermore, let

, denote state transition probabilities and represent the stationary proba-bility distribution. Given , one can compute and can then be obtained by

(5) where is the window advancement in state .

The derivation of is explained as follows. Let (binary representation), , and assume that, in state , the search window is to be advanced by positions. Furthermore, let be the leftmost bits of the right-shifted master bitmap in state . If , then

1 and . In this case, we have

, where is the number of 1’s in

. Assume that . We

have and .

The state transition probability if there exists ,

0 , such that and . Otherwise,

we have , where is the number

of 1’s in and is the number of 0’s in

.

B. Overall System Performance

Let be the average time spent on queries and ver-ification, if needed. determines achievable system throughput, and the optimal value of , which maximizes throughput, is given by

(6) Let represent the average time consumed in verification. In the WM algorithm, verification is required when the window advancement decided by the SHIFT table is 0. In the stateless version of Pre-filter AC scheme, verification is required when . Note that the two conditions are equivalent. For the proposed stateful Pfilter AC scheme, verification is re-quired if after bitwise-ANDing with . Since is always 1 before bitwise-ANDing with , the probability of after bitwise-ANDing with is equal to ). Therefore, we have

(7) for the WM algorithm and the stateless and stateful versions of the proposed Pre-filter AC scheme. Note that the value of depends on number of patterns and the verification algorithm. We numerically study the optimal value of next.

C. Numerical Results

The throughput performance depends on the values of , and . To find the optimal value of that maxi-mizes throughput, the other parameters are fixed as follows:

Fig. 11. Pre-filter performance comparison for various pattern numbers.

Fig. 12. Processing time comparison for scanning random texts of various sizes.

, and . For this scenario, satisfies (2) that maximizes throughput for the WM pre-filter and the stateless and stateful versions of the proposed pre-filter. Therefore, we choose as a basis for comparing pre-filter throughput, which, as mentioned before, is propor-tional to . Fig. 11 shows the results for various pattern numbers.

As noted in Appendix-A.2, the stateless version of the pro-posed pre-filter is seen to outperform the pre-filter of the WM algorithm, and the proposed stateful pre-filter provides the best performance because all previous query results, in addition to the current one, are used to determine window advancement in the stateful design.

The experiment shows that, given the abovementioned values

for , and ms and

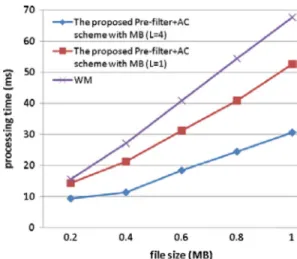
ms for our proposed Pre-filter AC scheme. From (6), optimally maximizes system performance of the pro-posed stateful Pre-filter AC scheme. To demonstrate the effect of multiple queries in each iteration, we conduct experiments to compare the processing times for the scheme with and . Fig. 12 shows the results for various file sizes. The implementation with requires about 1.7 times the pro-cessing time of that with . The processing time of the

WM algorithm is also provided in the figure for comparison, re-quiring about 1.3 and 2.2 times the processing time of our pro-posed stateful Pre-filter AC scheme with and , respectively.

REFERENCES

[1] D. E. Knuth, J. H. Morris, and V. R. Pratt, “Fast pattern matching in strings,” Stanford University, Stanford, CA, TR CS-74-440, 1974. [2] R. S. Boyer and J. S. Moore, “A fast string searching algorithm,”

Commun. ACM, vol. 20, pp. 762–772, Oct. 1977.

[3] A. V. Aho and M. J. Corasick, “Efficient string matching: An aid to bibliographic search,” Commun. ACM, vol. 18, pp. 333–340, Jun. 1975. [4] Y. Sugawara, M. Inaba, and K. Hiraki, “Over 10 Gbps string matching mechanism for multi-stream packet scanning systems,” Field Program.

Logic Appl., vol. 3203, pp. 484–493, Sep. 2004.

[5] L. Tan and T. Sherwood, “A high throughput string matching architec-ture for intrusion detection and prevention,” in Proc. 32nd Annu. Int.

Symp. Comput. Archit., 2005, pp. 112–122.

[6] T. H. Lee and C. C. Liang, “A high-performance memory-efficient pattern matching algorithm and its implementation,” in Proc. IEEE

TENCON, 2006, pp. 1–4.

[7] “Snort,” [Online]. Available: http://www.snort.org/

[8] M. Roesch, “Snort—Lightweight intrusion detection for networks,” in

Proc. 13th LISA, Nov. 1999, pp. s229–238.

[9] “Clam AntiVirus (ClamAV),” [Online]. Available: http://www.clamav. net/

[10] N. Tuck, T. Sherwood, B. Calder, and G. Varghese, “Deterministic memory-efficient string matching algorithms for intrusion detection,” in Proc. IEEE INFOCOM, 2004, vol. 4, pp. 2628–2639.

[11] M. Norton, “Optimizing pattern matching for intrusion detection,” Sourcefire, Inc., Columbia, MD, Sep. 2004.

[12] A. Bremler-Barr, Y. Harchol, and D. Hay, “Space-time tradeoffs in software-based deep packet inspection,” in Proc. IEEE HPSR, 2011, pp. 1–8.

[13] S. Wu and U. Manber, “A fast algorithm for multi-pattern searching,” TR-94-17, 1994.

[14] B. Bloom, “Space/time trade-offs in hash coding with allowable er-rors,” Commun. ACM, vol. 13, no. 7, pp. 422–426, May 1970. [15] A. Broder and M. Mitzenmacher, “Network applications of bloom

fil-ters: A survey,” Internet Math., vol. 1, no. 4, pp. 485–509, 2004. [16] S. Dharmapurikar, P. Krishnamurthy, T. Sproull, and J. Lockwood,

“Deep packet inspection using parallel bloom filters,” IEEE Micro, vol. 24, no. 1, pp. 52–61, Jan.–Feb. 2004.

[17] M. Attig, S. Dharmapurikar, and J. Lockwood, “Implementation results of bloom filters for string matching,” in Proc. Field-Program. Custom

Comput. Mach., Apr. 2004, pp. 322–323.

[18] S. Dharmapurikar and J. Lockwood, “Fast and scalable pattern matching for content filtering,” in Proc. ACM Symp. Archit. Netw.

Commun. Syst., 2005, pp. 183–192.

[19] S. Dharmapurikar and J. Lockwood, “Fast and scalable pattern matching for network intrusion detection systems,” IEEE J. Sel. Areas

Commun., vol. 24, no. 10, pp. 1781–1792, Oct. 2006.

[20] S. Dharmapurikar, P. Krishnamurthy, and D. E. Taylor, “Longest prefix matching using bloom filters,” in Proc. Conf. Appl., Technol., Archit.,

Protocols Comput. Commun., 2003, pp. 201–212.

[21] S. Dharmapurikar, P. Krishnamurthy, and D. E. Taylor, “Longest prefix matching using bloom filters,” IEEE/ACM Trans. Netw., vol. 14, no. 2, pp. 397–409, Apr. 2006.

[22] N. S. Artan and H. J. Chao, “Multi-packet signature detection using prefix bloom filters,” in Proc. IEEE GLOBECOM, 2005, vol. 3, pp. 1811–1816.

[23] N. S. Artan and H. J. Chao, “TriBiCa—Trie bitmap content analyzer for high-speed network intrusion detection,” in Proc. IEEE INFOCOM, May 2007, pp. 125–133.

[24] N. S. Artan, K. Sinkar, J. Patel, and H. J. Chao, “Aggregated bloom filters for intrusion detection and prevention hardware,” in Proc. IEEE

GLOBECOM, Nov. 2007, pp. 349–354.

[25] N. S. Artan, R. Ghosh, G. Yanchuan, and H. J. Chao, “A 10-Gbps high-speed single-chip network intrusion detection and prevention system,” in Proc. IEEE GLOBECOM, Nov. 2007, pp. 343–348.

[26] N. S. Artan, M. Bando, and H. J. Chao, “Boundary hash for memory-efficient deep packet inspection,” in Proc. IEEE ICC, May 2008, pp. 1732–1737.

[27] M. Bando, N. S. Artan, and H. J. Chao, “Highly memory-efficient loglog hash for deep packet inspection,” in Proc. IEEE GLOBECOM, 2008, pp. 1–6.

[28] N. S. Artan, Y. Haowei, and H. J. Chao, “A dynamic load-bal-anced hashing scheme for networking applications,” in Proc. IEEE

GLOBECOM, 2008, pp. 1–6.

[29] O. Yigit, “sdbm—substitute dbm,” 1990 [Online]. Available: http:// search.cpan.org/src/NWCLARK/perl-5.8.4/ext/SDBM_File/sdbm [30] O. Erdogan and P. Cao, “Hash-AV: Fast virus signature scanning by

cache-resident filters,” in Proc. IEEE GLOBECOM, 2005, vol. 3, pp. 1767–1772.

[31] GNU, “hashlib.c—Functions to manage and access hash tables for bash,” 1991 [Online]. Available: http://www.opensource.apple.com/ darwinsource/10.3/bash-29/bash/hashlib.c

[32] Y. E. Yang, H. Le, and V. K. Prasanna, “High performance dictio-nary-based string matching for deep packet inspection,” in Proc. IEEE

INFOCOM, 2010, pp. 1–5.

[33] J. Jiang, Y. Tang, B. Liu, X. Wang, and Y. Xu, “SPC-FA: Synergic parallel compact finite automaton to accelerate multi-string matching with low memory,” in Proc. ANCS, 2009, pp. 163–164.

Tsern-Huei Lee (S’86–M’87–SM’98) received the

B.S. degree from National Taiwan University, Taipei, Taiwan, in 1981, the M.S. degree from the University of California, Santa Barbara, in 1983, and the Ph.D. degree from the University of Southern California, Los Angeles, in 1987, all in electrical engineering.

Since 1987, he has been a member of the faculty with National Chiao Tung University, Hsinchu, Taiwan, where he is a Professor with the Department of Communication Engineering. During the past years, he served as a consultant of various companies to develop large-scale QoS-enabled frame-based switches/routers, integrated access devices, and unified threat management Internet appliances. His current research interests are in communication protocols, broadband switching systems, traffic management, wireless communications, and network security.

Prof. Lee received an Outstanding Paper Award from the Institute of Chinese Engineers in 1991.

Nai-Lun Huang received the B.S. and M.S. degrees

in communication engineering from National Chiao Tung University (NCTU), Hsinchu, Taiwan, in 2004 and 2006, respectively, and is currently pursuing the Ph.D. degree in communication engineering at NCTU.

Her current research interests include pattern matching, pre-filtering technique, and network security.

Ms. Huang is a recipient of the third prize in the contest of Embedded Software Design in SW/HW Codesign track held by the Ministry of Education of Taiwan Government in 2007. She received Academic Achievement Awards from NCTU in 2001 and 2005.