of fuzzy set theory into the support vector regression machine. The parameters to be estimated in the SVM regression, such as the components within the weight vector and the bias term, are set to be the fuzzy numbers. This integration preserves the benefits of SVM regression model and fuzzy regression model and has been attempted to treat fuzzy nonlinear regression analysis. In contrast to previous fuzzy nonlinear regression models, the proposed algorithm is a model-free method in the sense that we do not have to assume the underlying model function. By using different kernel functions, we can construct different learning machines with arbitrary types of nonlinear regression functions. Moreover, the proposed method can achieve automatic accuracy control in the fuzzy regression analysis task. The upper bound on number of errors is controlled by the user-predefined parameters. Experimental results are then presented that indicate the perfor-mance of the proposed approach.
Index Terms—Fuzzy modeling, fuzzy regression, quadratic
programming, support vector machines (SVMs), support vector regression machines.
I. INTRODUCTION
I
N many real-world applications, available information is often uncertain, imprecise, and incomplete and thus usually is represented by fuzzy sets or a generalization of interval data. For handling interval data, fuzzy regression analysis is an important tool and has been successfully applied in different applications such as market forecasting [19] and system identi-fication [24]. Fuzzy regression, first developed by Tanaka et al. [30] in a linear system, is based on the extension principle. In the experiments that followed this pioneering effort, Tanakaet al. [31] used fuzzy input experimental data to build fuzzy
regression models. The process was explained in more detail by Dubois and Prade in [16]. A technique for linear least squares fitting of fuzzy variables was developed by Diamond [11], [12] giving the solution to an analog of the normal equation of classical least squares. A collection of relevant papers dealing with several approaches to fuzzy regression analysis can be found in [23]. In contrast to the fuzzy linear regression, there Manuscript received July 24, 2006; revised October 19, 2006. This work was supported in part by the National Science Council, Taiwan under Grant NSC-95-2221-E-151-037.
P.-Y. Hao is with the Department of Information Management, National Kaohsiung University of Applied Sciences, Kaohsiung, Taiwan, R.O.C. (e-mail: haupy@cc.kuas.edu.tw).
J.-H. Chiang is with the Department of Computer Science and Information Engineering, National Cheng Kung University, Tainan, Taiwan, R.O.C. (e-mail: jchiang@mail.ncku.edu.tw).
Digital Object Identifier 10.1109/TFUZZ.2007.896359
such as linear, polynomial, exponential, and logarithmic. The support vector machines (SVMs), developed at AT&T Bell Laboratories by Vapnik et al. [9], [17], [35], have been very successful in pattern classification and function estima-tion problems for crisp data. They are based on the idea of structural risk minimization, which shows that the generaliza-tion error is bounded by the sum of the training error and a term depending on the Vapnik–Chervonenkis dimension. By minimizing this bound, high generalization performance can be achieved. A comprehensive tutorial on SVM classifier has been published by Burges [4]. Excellent performances were also ob-tained in the function estimation and time-series prediction ap-plications [14], [27], [36]. Hong et al. [20], [21] first introduced the use of SVM for multivariate fuzzy linear and nonlinear re-gression models. The fuzzy support vector rere-gression machine proposed by Hong [20] was achieved by solving a quadratic pro-gramming with box constraints. Jeng et al. [22] also applied the SVM to the interval regression analysis. They proposed a two-step approach for the interval regression by constructing two radial basis function (RBF) networks, each identified the lower side and upper side of data interval, respectively. The ini-tial structure of the RBF network is obtained by SVM learning approach. Consequently, a traditional backpropagation learning algorithm is used to adjust the network.
In this paper, we incorporate the concept of fuzzy set theory into the SVM regression model. The parameters to be identified in the SVM regression model, such as the components of weight vector and bias term, and the desired outputs in training sam-ples are set to be the fuzzy numbers. This integration preserves the benefits of SVM regression and fuzzy regression, where the Vapnik-Chervonenkis theory (also known as VC theory) [35] characterizes the properties of learning machines, which enable them to generalize well in the unseen data, whereas the fuzzy set theory might be very useful for finding a fuzzy structure in an evaluation system. The proposed fuzzy SVM regression analysis was achieved by solving a convex quadratic program-ming with linear constraints; in other words, it has a unique so-lution. In addition, the proposed algorithm here is model-free method in the sense that we do not have to assume the under-lying model function. By the choice of different kernel func-tions, we obtain different architectures of the nonlinear regres-sion functions, such as polynomial regresregres-sion functions, RBF regression functions. This model-free method turns out to be a promising method that has been attempted to treat fuzzy non-linear regression analysis. Moreover, the proposed method can 1063-6706/$25.00 © 2008 IEEE
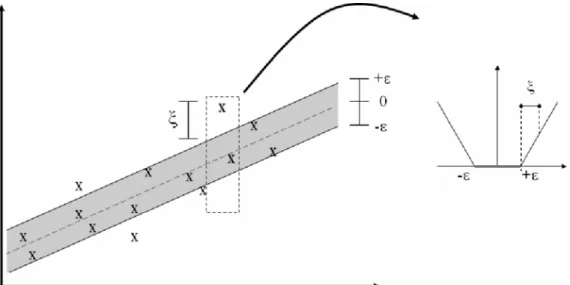
Fig. 1. The epsilon insensitive loss setting corresponding to a linear SV regression machine.
achieve automatic accuracy control in the fuzzy regression anal-ysis task. The number of errors in the obtained regression model is bounded by the user-predefined parameters.
The rest of this paper is organized as follows. A brief review of the theory of SVM regression is given in Section II. The fuzzy SVM regression is derived in Section III. Experiments are pre-sented in Section IV. Some concluding remarks are given in Section V.
II. SVM REGRESSIONMODEL
Suppose we are given a training data set , where denotes the space of input patterns, for instance, . In -SVM regression [14], [27], [35] the goal is to find a function that has at most deviation from the actually obtained targets
for all the training data. In other words, we do not care about errors as long as they are less than but will not accept any deviation larger than . An -insensitive loss function
if otherwise
is used so that the error is penalized only if it is outside the -tube. Fig. 1 depicts this situation graphically.
To make the SVM regression nonlinear, this could be achieved by simply mapping the training patterns by into some high-dimensional feature space . A best fitting function is estimated in that
feature space . To avoid overfitting, one should add a capacity control term, which in the SVM case results to be . Formally, we can write this problem as a convex optimization problem by requiring
minimize
subject to
(1) The constant determines the tradeoff between the com-plexity of and the amount up to which deviations larger than are tolerated. In short, minimizing the objective func-tion given in (1) captures the main insight of statistical learning theory, stating that in order to obtain a small risk, we need to control both training error and model complexity, by explaining the data with a simple model [35].
Using the Lagrange multiplier method, this quadratic pro-gramming problem can be formulated as the Wolfe dual form shown in (2) at the bottom of the page, where are the nonnegative Lagrange multipliers. Solving the above dual quadratic programming problem, we obtain the Lagrange mul-tipliers and , which give the weight vector as a linear combination of
maximize
. It is therefore convenient to introduce the so-called kernel function
The definition of kernel function prevents the direct compu-tation of inner production in the high-dimensional feature space, which is very time-consuming and makes the computation prac-tical. Using this quantity, the solution of a SVM has the form
To motivate the new algorithm that we shall propose, note that the parameter can be useful if the desired accuracy of the
ap-proximation can be specified beforehand. The selection of a pa-rameter may seriously affect the modeling performance. In ad-dition, the -insensitive zone in the SVM regression model has a tube (or slab) shape. Namely, all training data points are equally treated during the training of SVM regression model and are pe-nalized only if they are outside the -tube. In many real-world applications, however, the effects of the training points are dif-ferent. We would require a learning machine that must estimate the precise training points correctly and would allow more er-rors on the imprecise training points. In the next section, we incorporated the fuzzy set theory into the SVM regression task. The proposed fuzzy SVM regression takes the imprecision of training points into consideration. The vagueness (or insensi-tivity) of the obtained regression model depends on the vague-ness of the given training points.
III. FUZZYSVM REGRESSIONMODEL
In modeling some systems where available information is un-certain, we must deal with a fuzzy structure of the system con-sidered. This structure is represented as a fuzzy function whose parameters are given by fuzzy sets. The fuzzy functions are de-fined by Zadeh’s extension principle [15], [25], [37], [38]. Ba-sically, the fuzzy function provides an effective means of cap-turing the approximate, inexact natural of real world. In this section, we incorporate the concept of fuzzy set theory into the SVM regression model. The parameters to be identified in the SVM regression model, such as the components of weight vector and bias term, and the desired outputs in training samples are set to be the fuzzy numbers. For computational simplicity,
. Similarly, is the fuzzy bias term, which means “approximation ,” described by the center and the width . The fuzzy function
is defined by the following membership function [31]: if
if and
if and
(3)
where when .
Then, we deal with fuzzy desired output in the regression task. The given output data, denoted by , are also fuzzy numbers, where is a center and is the width. The membership function of is given by
To formulate a fuzzy linear regression model, the following are assumed to hold.
1) The data can be represented by a fuzzy linear model
Given can be obtained as
2) The degree of the fitting of the estimated fuzzy linear
model to the given data
is measured by the following index , which maximizes subject to , where
which are -level sets. The degree of fitting of the linear model to all data is defined by . 3) The vagueness of the fuzzy linear model is defined by
4) The capacity control term of the fuzzy linear model is de-fined by .
The regression problem is explained as obtaining the fuzzy weight vector and the fuzzy bias term
Fig. 2. Degree of fitting ofY to given fuzzy data ~Y .
and desired output is more than a given constant for all , where is chosen as the degree of the fitting of the fuzzy linear model by the decision-maker. The value can be obtained from
(4) which is equal to the early work by Tanaka [31] and is illustrated in Fig. 2.
Our regression task here is therefore to
subject to for all (5)
where is the term that characterizes the model complexity, the minimization of can be understood in the context of regularization operators [28] and is the term that characterizes the vagueness of the model. More vagueness in the fuzzy linear regression model means more inexactness in the regression result. is a tradeoff parameter chosen by the deci-sion-maker. The value of determines the low bound for the degree of fitting of the fuzzy linear model and is the degree of fitting of the estimated fuzzy linear model
to the given fuzzy desired output data .
are sets of surplus variables that measure the amount of variation of the constraints for each point where is a fixed penalty pa-rameter chosen by the user, a larger corresponds to assigning a higher penalty to errors. Fig. 3 depicts this situation graphically.
More specifically, according to (4), our problem is to find out the fuzzy weight vector and fuzzy bias term , which is the solution of the following quadratic programming problem:
(6)
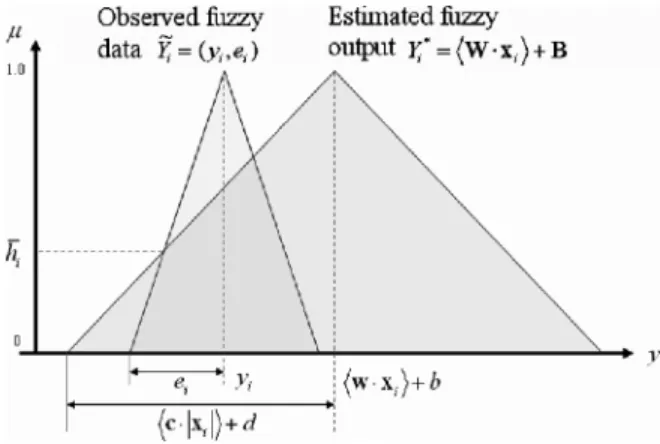
Fig. 3. Explanation of fuzzy linear regression model withY = hW 1 x i+ B .
subject to
and
for
Comparing Fig. 3 with Fig. 1, we can understand the differ-ence between SVM regression model and fuzzy SVM regression model. The SVM regression model seeks a linear function that has at most deviation from the actually obtained targets for all the training data, whereas the fuzzy SVM regression model seeks a fuzzy linear function with fuzzy parameters that has at least fitting degree from the fuzzy desired targets for all the training data.
We can find the solution of this optimization problem given by (6) in dual variables by finding the saddle point of the Lagrangian
(11)
and (12)
and (13)
Substituting (8)–(13) into (7), we obtain
Therefore, the dual problem is
While parameters and can be determined from the KKT conditions
(15)
(16) (17) (18)
For some , we have , and
more-over the second factor in (15) and (16) has to vanish. Hence, and can be computed as shown in (19) and (20) at the bottom
of the page, for some .
The fuzzy linear regression function is defined by the mem-bership function shown in (21) at the bottom of the page, where
when (19) (20) if if and if and (21)
TABLE V
COMPARISON RESULTSWITHVARIOUSKERNEL FUNCTION FORHOUSEPRICEDATA
sum of squared distances of given outputs and the estimation center decreases as the dimension of the feature space increases. It is reasonable since as the dimension of the feature space in-creases, the learning machine has more capacity to construct a complex regression model, and hence the accuracy of the re-gression result is improved. In addition, values of also show a decreasing trend on the order of Table V(a)–(d), which tells that the sum of squared spreads decreases as the dimension of the feature space increases. It is indicative of the fact that the vagueness of the obtained fuzzy regression model decreases as the capacity of the learning machine increases. On the contrary, the numbers of support vectors show an increasing trend on the order of Table V(a)–(d), which tells that we need more support vectors to construct a more complex regression model.
Fig. 7(a)–(d) illustrates the obtained fuzzy regression models with different kernel functions. It can be noticed that Fig. 7(d) has more central tendency than Fig. 7(a)–(c) because the ob-servations are all inside the estimated interval and the spreads of regression model in Fig. 7(d) are smaller than those in Fig. 7(a)–(c). It can also be noticed that the proposed algorithm is a model-free method. As described in Section III-C, we can actually use a larger class of kernels without destroying the mathematical formula of the quadratic programming problem given by (22). By choosing different kernels, we obtain dif-ferent architectures of the nonlinear regression models.
V. CONCLUSION
In this paper, we introduced fuzzy regression analysis by sup-port vector learning approach. The difference between the orig-inal SVM regression and the proposed fuzzy SVM regression is that the SVM approach seeks a linear function that has at most deviation from the actually obtained targets for all the training data, whereas the proposed fuzzy SVM approach seeks a fuzzy linear function with fuzzy parameters that has at least fitting degree from the fuzzy desired targets for all the training data. Incorporating the concept of fuzzy set theory into the SVM gression preserves the benefits of SVM regression and fuzzy re-gression, where the VC theory characterizes the properties of learning machines, which enable them to generalize well in the unseen data, whereas the fuzzy set theory might be very useful for finding a fuzzy structure in an evaluation system.
The main difference between our fuzzy SVM approach and the nonlinear fuzzy regression approaches by Buckley et al. [2], [3] and Celmins [6] is not crisp input-fuzzy output versus
fuzzy input-fuzzy output but model-free versus model-depen-dent. By the choice of different kernels, we can construct dif-ferent learning machines with arbitrary types of nonlinear re-gression functions in the input space. The model-free method turned out to be a promising method attempted to treat a fuzzy nonlinear regression task. Moreover, the proposed method can achieve automatic accuracy control in the fuzzy regression anal-ysis task. The upper bound on number of errors is controlled by the user-predefined parameters.
In this paper, we deal with estimating fuzzy nonlinear regres-sion model with crisp inputs and fuzzy output. In future work, we intend to devise algorithms for estimating fuzzy nonlinear regression model with fuzzy inputs and fuzzy output.
ACKNOWLEDGMENT
The authors would like to thank the anonymous reviewers for their constructive comments and suggestions.
REFERENCES
[1] A. Ben-Hur and W. S. Noble, “Kernel methods for predicting protein-protein interactions,” Bioinformatics, vol. 21, no. 1, pp. i38–i46, 2005. [2] J. Buckley, T. Feuring, and Y. Hayashi, “Multivariate non-linear fuzzy regression: An evolutionary algorithm approach,” Int. J. Uncertain.,
Fuzziness Knowl.-Based Syst., vol. 7, pp. 83–98, 1999.
[3] J. Buckley and T. Feuring, “Linear and non-linear fuzzy regression: Evolutionary algorithm solutions,” Fuzzy Sets Syst., vol. 112, pp. 381–394, 2000.
[4] C. J. C. Burges, “A tutorial on support vector machines for pattern recognition,” Data Mining Knowl. Discovery, vol. 2, no. 2, pp. 955–974, 1998.
[5] A. Celmins, “Least squares model fitting to fuzzy data vector,” Fuzzy
Sets Syst., vol. 22, no. 3, pp. 245–269, 1987.
[6] A. Celmins, “A practical approach to nonlinear fuzzy regression,”
SIAM J. Sci. Statist. Comput., vol. 12, no. 3, pp. 521–546, 1991.
[7] J.-H. Chiang and P.-Y. Hao, “A new kernel-based fuzzy clustering approach: Support vector clustering with cell growing,” IEEE Trans.
Fuzzy Syst., vol. 11, no. 4, pp. 518–527, 2003.
[8] J.-H. Chiang and P.-Y. Hao, “Support vector learning mechanism for fuzzy rule-based modeling: A new approach,” IEEE Trans. Fuzzy Syst., vol. 12, no. 1, pp. 1–12, 2004.
[9] C. Cortes and V. N. Vapnik, “Support vector network,” Mach. Learn., vol. 20, pp. 1–25, 1995.
[10] N. Cristianini and J. Shawe-Taylor, An Introduction to Support Vector
Machines. Cambridge, U.K.: Cambridge University Press, 2000. [11] P. Diamond, “Least squares fitting of several fuzzy variables,” in
Analysis of Fuzzy Information, J. C. Bezdek, Ed. Tokyo, Japan: CRC Press, 1987, pp. 329–331.
[12] P. Diamond, “Fuzzy least squares,” Inf. Sci., vol. 46, pp. 141–157, 1988.
[13] P. Diamond and H. Tanaka, “Fuzzy regression analysis,” in Fuzzy Sets
in Decision Analysis, Operations Research and Statistcs, R. Slowinski,
Ed. Boston, MA: Kluwer, 1998, pp. 349–387.
[14] H. Drucker, C. Burges, L. Kaufman, A. Smola, and V. N. Vapnik, “Sup-port vector regression machines,” in Advances in Neural Information
Processing Systems. Cambridge, MA: MIT Press, 1996, vol. 9, pp. 155–161.
[15] D. Dubois and H. Prade, “Operations on fuzzy number,” Int. J. Syst.
Sci., vol. 9, pp. 613–626, 1978.
[16] D. Dubois and H. Prade, Fuzzy Sets and Systems: Theory and
Applica-tions. New York: Academic, 1980.
[17] I. Guyon, B. Boser, and V. Vapnik, “Automatic capacity tuning of very large VC-dimension classifier,” Adv. Neural Inf. Process. Syst., vol. 5, pp. 147–155, 1993.
[18] P.-Y. Hao and J.-H. Chiang, “A fuzzy model of support vector ma-chine regression,” in IEEE Int. Conf. Fuzzy Syst. 2003, 2003, vol. 1, pp. 738–742.
[19] B. Heshmaty and A. Kandel, “Fuzzy linear regression and its applica-tions to forecasting in uncertain environment,” Fuzzy Sets Syst., vol. 15, pp. 159–191, 1985.
tection using string alignment kernels,” Bioinformatics, vol. 20, no. 11, pp. 1682–1689, 2004.
[27] A. J. Smola and B. Scholkopf, A tutorial on support vector regression NeuroCOLT2 Tech. Rep., 1998.
[28] A. J. Smola, B. Schölkopf, and K.-R. Müller, “The connection between regularization operations and support vector kernels,” Neural Netw., vol. 11, pp. 637–649, 1998b.
[29] B. Schölkopf, C. J. C. Burges, and A. J. Smola, Advances in Kernel
Method—Support Vector Learning. Cambridge, MA: MIT Press, 1999.
[30] H. Tankaka, S. Uejima, and K. Asai, “Fuzzy linear regression model,” in Proc. Int. Conf. Appl. Syst. Res. Cybern., Acapulco, Mexico, 1980, pp. 12–15.
[31] H. Tanaka, S. Uejima, and K. Asai, “Linear regression analysis with fuzzy model,” IEEE. Trans. Syst., Man, Cybern., vol. SMC-12, no. 6, pp. 903–907, 1982.
[32] H. Tanaka, “Fuzzy data analysis by possibilistic linear models,” Fuzzy
Sets Syst., vol. 24, pp. 363–375, 1987.
[33] H. Tanaka and J. Watada, “Possibilistic linear systems and their ap-plications to linear regression model,” Fuzzy Sets Syst., vol. 27, pp. 275–289, 1988.
[34] H. Tanaka and H. Lee, “Interval regression analysis by quadratic programming approach,” IEEE Trans. Fuzzy Syst., vol. 6, no. 4, pp. 473–481, 1998.
He is currently an Associate Professor in the Department of Information Management, National Kaohsiung University of Applied Sci-ences, Kaohsiung, Taiwan. His research interests include fuzzy theory, neural networks, pattern recognition, support vector machines, and modeling of bioinformatics problems.
Jung-Hsien Chiang (M’92–SM’05) received the
B.Sc. degree in electrical engineering from the National Taiwan Institute of Technology, Taiwan, R.O.C., and the M.S. and Ph.D. degrees in com-puter engineering from the University of Missouri, Columbia, in 1991 and 1995, respectively.
He is currently a Professor in the Department of Computer Science and Information Engineering, Na-tional Cheng Kung University, Taiwan. Previously, he was a Researcher in the Computer and Commu-nication Laboratory, Industrial Technology Research Institute, the largest information technology research institute in Taiwan. His current research interests include fuzzy modeling, neural networks, pattern clus-tering, and modeling of bioinformatics problems.