行政院國家科學委員會補助專題研究計畫成果報告
※※※※※※※※※※※※※※※※※※※※※※※※
※ ※
※ 奈米級三次元量測儀研製(3/3)-
※
※
子計畫一:奈米級三次元量測儀結構之設計與分析 ※
※ ※
※※※※※※※※※※※※※※※※※※※※※※※※
計畫類別:□個別型計畫 þ整合型計畫
計畫編號:NSC 89-2212-E-002-132-
執行期間:89 年 08 月 01 日至 90 年 07 月 31 日
計畫主持人:鍾 添 東
共同主持人:
本成果報告包括以下應繳交之附件:
□赴國外出差或研習心得報告一份
□赴大陸地區出差或研習心得報告一份
□出席國際學術會議心得報告及發表之論文各一份
□國際合作研究計畫國外研究報告書一份
執行單位:國立台灣大學 機械系
中 華 民 國 九十 年 十 月 八 日
行政院國家科學委員會專題研究計畫期末報告
奈米級三次元量測儀研製(3/3)-
子計畫一:奈米級三次元量測儀結構之設計與分析
Design and Analysis of A Nano-CMM Str uctur e
計畫編號:NSC 89-2212-E-002-132 執行期限:89 年 08 月 01 日至 90 年 07 月 31 日 主 持 人:鍾添東 國立台灣大學機械系 E –m a i l:ttchung@ccms.ntu.edu.tw 一、中文摘要 本計畫為整合型計畫『奈米級三次元量 測儀研製』之子計畫一:「奈米級三次元量 測儀結構之設計與分析」。本年為三年計畫 之第三年,主要目的為分析與量測奈米級三 次元量測儀之結構特性及其最佳化設計。首 先 建 立 最 終 設 計 的 量 測 儀 之 有 限 元 素 模 型,分析其靜態及動態特性,並進行最佳化 設計,接著以實驗量測其結構性能,與有限 元素分析的結果做比較。 本年度進行奈米級三次元量測儀之製 作及最佳化設計,並量測結構性能以驗證設 計及分析之正確性。 關鍵詞:奈米級三次元量測儀、有限元素 法、結構最佳化、 二、計畫緣由與目的 近年來我國半導體工業及微機械工程 快速發展,在微機械元件越做越小,晶片的 最小線寬越來越細的情況下,傳統的三次元 量 測 儀 [Coordinate Measuring Machines (CMM)] 已 不 敷 使 用 。 尤 其 在 半 導 體 製 程 中,對於平台的定位精度,通常需要量測到 奈米級(1 nm = 10-9 m)的精度,因此發展奈米 級的三次元量測儀技術,以應現今各種產業 之用,乃當務之急。Takamasu[1]研究傳統之 三次元量測儀與奈米級三次元量測儀之比 較,發現奈米級三次元量測儀的各種規格大 約是傳統三次元量測儀的 1/100 到 1/1000, 在此極為精密的規格下,各種元件的設計與 製造,都必須加以重新評估與考量。本研究 針對此需求,主要目的為設計與分析一奈米 級三次元量測儀結構。其量測範圍在 X 軸, Y 軸及 Z 軸方向分別為 20mm,20mm 及 10mm,量測解析度為 10nm。研究內容包含 結構設計、結構材料的選用、各方向滑動平 台的設計、滑軌的設計、結構靜態與動態特 最佳化、結構性能分析與量測等項目。 三、研究方法與研究進度 奈米級三次元量測儀經由設計初型之 數次修改後,目前已完成其最終設計,圖 1 為其最終設計圖。 圖1 Nano-CMM之最終設計圖 本年度計畫之主要目的為結構最佳化 及其特性分析與量測,各研究項目簡述如 下: 1. 建立最佳化問題: 建立結構最佳化問題包括了定義 設計變數、目標函數及限制條件等。其 設計變數可為模型尺寸,如結構之厚 度、寬度或高度等。目標函數可為結構 之質量或最大變形量等。將結構行為之 限制條件以處罰函數之形式加入目標 函數,由不同的目標函數建立各種最佳 化問題。 最 佳 化 方 法 可 從 非 線 性 程 式 法 (Nonlinear Programming)與遺傳演算法 (Genetic Algorithm)兩種分別進行,前者 為傳統最佳化方法,後者為一新興之全 域最佳化方法,各有其優缺點及適用領 域。
2. 建立最佳化設計之近似問題: 對 於 非 線 性 程 式 法 之 最 佳 化 問 題,需將非線性的限制條件加以近似, 使得最佳化在進行時可以加快速度,減 少運算的時間。 3. 建立靈敏度分析方法: 靈敏度分析(Sensitivity analysis)為 結構最佳化設計過程中必備的一道程 序,為建構最佳化數值問題時之重要資 訊,本研究採用有限差分法,建立各種 結構反應的靈敏度分析方法。 4. 結構靜態特性最佳化設計: 以有限元素軟體ANSYS建立結構 模型,包含基座、工作平台及CCD等部 分,如圖2所示。 圖2 Nano-CMM之有限元素模型 靜態特性最佳化問題以結構質量 為目標函數,設計變數如圖3所示為花 崗岩之ㄇ型樑寬度,並限制其CCD底端 之z方向自重位移量d,如3.1式所示,分 別以非線性程式法及遺傳演算法最佳 化,以求其結構輕量化。 m d m µ µ 1.00 80 . 0 ≤ ≤ (3.1) 圖3 Nano-CMM之有設計變數示意圖 比較非線性程式法及遺傳演算法 之最佳化結果,發現此問題以非線性程 式法所得之結果較佳,其ㄇ型樑結構初 始質量經由輕量化後降低了15.57 %,表 1為靜態特性之結構最佳化結果。 表1 Nano-CMM靜態特性結構最佳化結果 原設計值 最佳化值 設計變數X1(mm) 50.00 38.68 設計變數X2(mm) 50.00 45.40 設計變數X3(mm) 50.00 44.52 設計變數X4(mm) 50.00 47.69 CCD底端之z方向 自重位移量(μm) 0.90 1.00 ㄇ型樑結構質量 (Kg) 9.1687 7.7412 5. 結構動態特性最佳化設計: 動態特性最佳化問題亦以結構質 量為目標函數,設計變數為花崗岩之ㄇ 型樑寬度,並限制其結構之自然頻率w1 及w2,如3.2式所示,分別以非線性程式 法及遺傳演算法最佳化,以求其結構輕 量化。 HZ 314 Hz 257 Hz 204 Hz 167 2 1 < < < < ω ω (3.2) 比較非線性程式法及遺傳演算法 之最佳化結果,發現此問題以非線性程 式法所得之結果較佳,其ㄇ型樑結構初 始質量經由輕量化後降低了8.98 %,表2 為動態特性之結構最佳化結果。 表2 Nano-CMM動態特性以非線性程式法 最佳化設計之變數變化 原設計值 最佳化值 設計變數X1(mm) 50.00 43.49 設計變數X2(mm) 50.00 47.31 設計變數X3(mm) 50.00 46.82 設計變數X4(mm) 50.00 48.69 自然頻率1(Hz) 186.23 187.82 自然頻率2(Hz) 286.13 257.00 ㄇ型樑結構質量 (Kg) 9.1687 8.3452
6. 最佳化結果比較: 在靜態特性最佳化問題上,以非線 性程式法最佳化所得結果較佳,ㄇ型樑 結構質量可降低15.57 %,由9.1687 Kg 降至7.7412 Kg。 在動態特性最佳化問題上,以非線 性程式法最佳化所得結果較佳,ㄇ型樑 結構質量可降低8.98 %,由9.1687 Kg降 至8.3452 Kg。 本研究所進行之結構輕量化雖僅 對ㄇ型樑結構尺寸做更改,但由於其機 台底部高度對結構特性較無影響,因此 若能視實際情況降低高度,可再降低其 質量。 7. 結構性能量測: 將奈米級三次元量測儀以衝鎚法 ( Impulse Method )配合加速規的使用, 進行結構之自然頻率量測實驗。如圖 4~7所示將Nano-CMM分別以(基座)、(基 座+工作平台)、(基座+CCD)及(整部機 台)等四種情況進行量測: 圖4 Nano-CMM之基座簡圖 圖5 Nano-CMM之基座及工作平台簡圖 圖6 Nano-CMM之基座及CCD簡圖 圖7 Nano-CMM之整部機台簡圖 表3為實驗所得的自然頻率值,當 基座上加入工作平台或CCD部分後,將 使得整體之自然頻率降低,尤其在加入 CCD後會出現更低頻率的局部震動模 態,如圖8及圖9所示。 表3 Nano-CMM之自然頻率實驗值 自然頻率(Hz) 量測 編號 量測部分 Mode 1 Mode 2 Case1 基座 301.31 628.07 Case2 基座+工作平台 296.75 608.73 Case3 基座+CCD 201.56 286.68 Case4 整部機台 186.23 286.13 X Y Z # 1:201.56 Hz X Y Z # 1:201.56 Hz X Y Z # 1:201.56 Hz X Y Z # 1:201.56 Hz 圖8 Nano-CMM基座及CCD之自然振型1 X Y Z # 1:186.23 Hz X Y Z # 1:186.23 Hz X Y Z # 1:186.23 Hz X Y Z # 1:186.23 Hz 圖9 Nano-CMM整座機台之自然振型1 以有限元素軟體 ANSYS 建立之 模型,分析量測儀結構之自然頻率,並 與其實驗值做比較。表 4 為其自然頻率 之實驗值與分析值的比較,最大誤差為 8.99 %。
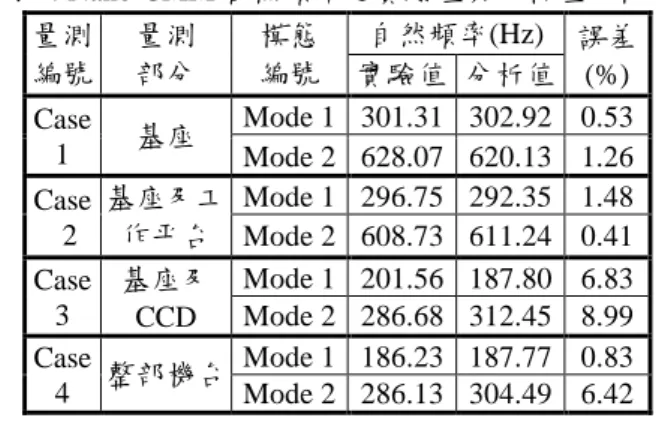
表 4 Nano-CMM 自然頻率之實驗值與分析值比較 自然頻率(Hz) 量測 編號 量測 部分 模態 編號 實驗值 分析值 誤差 (%) Mode 1 301.31 302.92 0.53 Case 1 基座 Mode 2 628.07 620.13 1.26 Mode 1 296.75 292.35 1.48 Case 2 基座及工 作平台 Mode 2 608.73 611.24 0.41 Mode 1 201.56 187.80 6.83 Case 3 基座及 CCD Mode 2 286.68 312.45 8.99 Mode 1 186.23 187.77 0.83 Case 4 整部機台 Mode 2 286.13 304.49 6.42 四、結果與結論 奈米級三次元量測儀已經完成結構最 佳化及性能量測,其實驗所得結果可驗證分 析結果之正確性。 在結構最佳化方面,包含靜態與動態特 性的質量輕量化:靜態特性最佳化是限制 CCD底端之z方向自重位移量,其非線性程 式法最佳化可將ㄇ型樑結構質量降低15.57 %;動態特性最佳化是限制整部機台之自然 頻率,其非線性程式法最佳化可將ㄇ型樑結 構質量降低8.98 %。 在結構性能分析與量測方面,以有限元 素軟體建立起結構模型,所分析之自然頻率 與實驗量測之誤差最大為8.99 %,在可接受 之範圍內。 本研究在奈米級三次元量測儀之結構 最佳化及性能量測上可提供確實而有用的 參考數據,對於將來的量測儀改良有相當的 幫助。 參考文獻
[1] K. Takamasu, S. Ozawa, T. Asano, A. Suzuki, R. Furutani and S. Ozono, “Basic Concepts of Nano-CMM (Coordinate Measuring Machine with Nanometer Resolution)”, The Japan-China Bilateral Symposium on Advanced Manufacturing Engineering, pp.155-158, 1996.
[2] Yang-Tai Lin, Tien-Tung Chung and Te-Chang Sun, “Weight Optimization of Nonlinear Truss Structure with Static Re-sponse”, J of CSME, no.4, vol.13, 1992. [3] Tien-Tung Chung and Te-Chang Sun,
“Weight Optimization of Reinforced Con-crete Beams with Static Nonlinear Re-sponse”, Structural Optimization, no.2/3, vol.18, pp.173-180, 1994.
[4] G. Taleb-Agha and R. b. Nelson, “Method for the Optimum Design of Truss-Type Structures”, AIAA J., V.14, N.4, pp.436-444, 1976.
[5] L. A. Schmit and B. arshi, “Some Ap-proximation Concepts for Structural Syn-thesis”, AIAA J., V.12, N.5 pp.692-699,1974.
[6] V. Braibant and C. Fleury, “An Approxi-mation Concepts Approach to Shape Op-timal Design”, Comp. Meth. In Appl. Mech. And Eng., V.53 pp.119-148, 1986. [7] W. M. Jenkins, “A genetic algorithm for
structural design optimization”, Emergent Computing Methods in Engineering de-sign, 1996.
[8] P. Hajela and E. Lee, “Genetic Algorithms in Topological Design of Grillage Struc-tures”, Discrete Structural Optimization, edited by W. Gutkowski and J. Bauer, Springer-Verlag, Berlin, pp. 30-39, 1994. [9] J. L. Marcelin and P.Tromprtte,
“Optimi-zation of composite beam structures using a genetic algorithm”, Structural Optimiza-tion 9, 236-244, 1995.
Design and Analysis of A Nano-CMM Str uctur e
Abstract
This project is the first sub-project of the integrated-project named “Design and Fabrication of a Nano-CMM (Coordinate Measuring Machine)” and is the third year of the whole three years project. The main object of this sub-project is to optimize the structure of a Nano-CMM and measure its responses. The finite element model is established to analyze the static and dynamic characteristics, and to do the optimum design of the structure. Then, the modal measurement of the structure is compared with the analysis results.
In this year, the fabrication and the opti-mization of a Nano-CMM have been accom-plished, and the validity and correctness of the whole design process are also verified from the experimental measurement.
Keywords:Nano-CMM, The Finite Element Method, Structural Optimization