三角形五心相關比例的探討

(1)

三角形五心相關比例的探討

蘇柏奇*游淑媛

苗栗縣立興華高級中學壹、前言 C A

UI/ 門， V

_I

/ 巧， W

_I

/ 門，們:

v

2 :

w

2

之函數 B 三角形上面的點和線之間的關條，一直都是中學幾何題材的重點所在，中學數學己論及五心的許多性質(未談及傍心) ，諸如:重心 G 與頂點的連線三等分三角形、外心到三頂點等距離、內心到三邊等距離、重心將中線分成 2: I 的兩段長度...等。其中，筆者關注的點在於五心各性質的類推，例如:外心到三頂點等距離，即 I

1:

J

'其餘四心到三頂點的距離雖然不一定相等，但是否成比例?同樣的，內心除外的四心到三邊的距離是否也成比例關條?從源頭可溯及古希臘的「孟氏定理」出發，本文推導出由三角形五心所得出的各相關臣離、長度和面積的比例關像。

如下圖 l 所示，我們考慮的三角形 MBC 之三邊長 BC=a ，

AC=b

,

AB=c ，且 P， Q， R

分別為直線 BC ，

AC

,

AB 上的點。當 AP ，

BQ

,

CR 三線相交於一點時，以 Z 點表示此交點。相關的長度、距離定義如下:令 Z 點到 A ，

B

,

C 三點的距離分別為 ZA= 叭， ZB= 片，

ZC=W

1;

Z 點到 P， Q ， R 三點的距離分別為 ZP= 門， ZQ= 門，

ZR =

W2 ;

Z 點到 BC ，

AC

,

AB

三邊的距離分別為d

"

吭

，

d)

再令 LA 、 ζB 及 LC 內的傍心分別為 A'， B'， C' 本文將於第二節介紹孟氏定理及推導後續討論所需的相關引、系理，並於第三節針對五心相關距離、長度、和面積的比例關像進行探討，在此先將第三節所得

的結果列表如表 I

a

,

b 及表 2

a

,

b 所示。

其中，因為直角三角形的外心在斜邊中點，童心為三角形的頂點，為方便起見，本文討論外心及童心的相關性質時，將排除直角三角形的情況。另外，表 2 。中外心的比僅限於銳角三角形。

_{國 l}

*為本文通訊作者

(2)

表 1

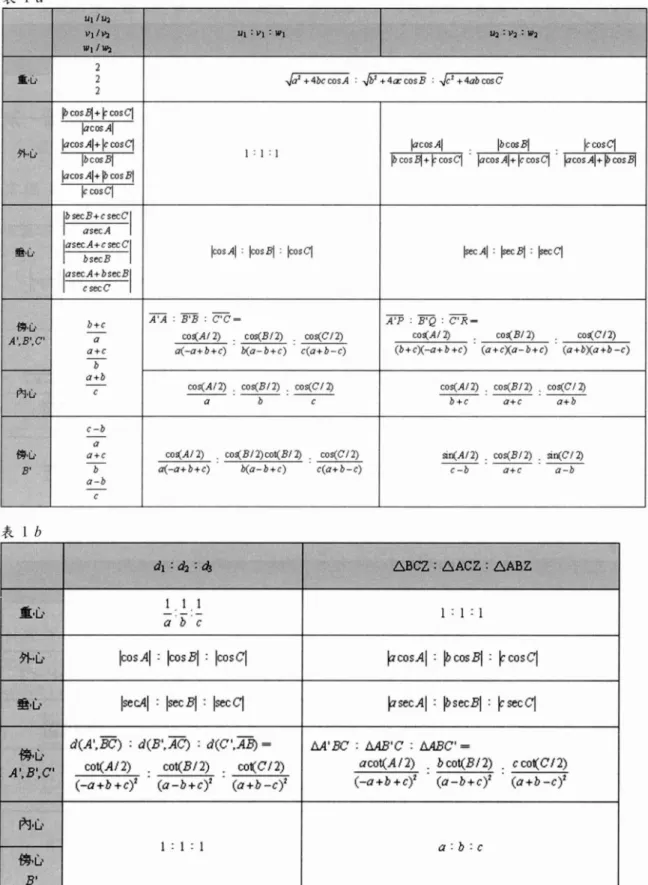
a

詢:1'2:的

.心

外心 UIfa句 vII 內 VIII 時 2 2 扣∞s 司+卡∞sCI lac自 4 伊∞sAI+ 卡∞sCI 仰自司伊∞sAI+~ ∞sBJ #∞sCI UI:VI:VII

4可4bccosA :.jb可石高高:、正I +4ab 間C

l l

l

IacosAI

~伽利卡 cos Cl

P ∞s 司+卡 cos Cl伊 cosAI+ 卡 cos Cl伊∞ sAI+ 伊∞s 司

童醫心

c-c-B-m-4

臨-Fm-7

巴拉一叫的一叫

蛇 -am-im-t b-a-a-PJsAI: 伽利: PJs

Cl

jsecAI:知司伊叫告辭b A'.B',C' 內心

b+c

A'A : B'B :

C'C-∞ s(AI2) .

c

os(Bl2) . ∞ s(CI2)

a(-a+b 刊)歧。-b 刊 )

c(a+b-c)

A'P : B'Q : C'R 圖

co s(AI 2)∞ s( BI2) ∞ s( CI2)

(b+cX-a+b

+e)

(a+cXa-b+c)

(a+bXa+b -c)

a

a+c

b

a+b

c ∞ s(AI2) . ∞ s(BI2) . ∞ s(CI:可

a b c

∞ s(AI2) . ∞ s(B I2) . co s(CI:力

b+c

a+c

a+b

c-b

傍心

a

a+c

∞ s(AI2) . ∞ s( BI2) ∞巾(BI:可 • cos(CI2)

a(

-a+b+c)

b(

a-b+c)

c(a+b-c)

sir(AI2) ∞s(B I2) . si r(CI 力

c-b

a+c

a-b

B

.

b

a-b

表 1

b

c dl:~:4 ~位:

AACZ: AABZ

虛心

_{a b c}

1 1 1

I

:.

I : I

外心扣。sAl: 卡os 司:

IcosCI

拉 eosAI

:

~

eos BI

:卡 eosCI

重心 |鉛叫I

:

Isee 司: I始eCI 伊鉛cAl: 特 seeBI

:

I':

seeCI

傍心

d(A'

,

BC) : d(B'.A

C) :

d(C'.A

S)

z M﹒砍了:

MEtC: MEC'=

A'.B'.C

.

∞t(AI2)

eo

t(

BI2)

. ∞'(C/2)

aeo

t(

AI2)

. beo

t(

BI2) . ceo'(C/2)

(-a+b+c)2

(a-b+c)l

(a+b-c)2

(-a+b+c)2

(a-b+c)2

(a+b-c)l

內心

1 : 1 : 1

a:b:c

傍心

B

.

(3)

科學教育月刊第 356 期中華民國 102 年 3 月

表 2

a

岫 f 旬

vII 均 UI:VI:"I 句:~﹒昀

"II 兩 2 盒·LJ 2 _{+-a' +2以+~，} _{J切， ν+~， dd +2b' -c'} 2 a'b'+de'+ 卦c'c'-b﹒ -c' _。'(-<I_{+b' H')} d ( J+b'+c'> db'+de'+2b'cg-b

.

-d a'b' +b'c'+2dc'-a' 呵C﹒ b'(d -b' H')

*LJ

b'(d-bz+e') 1: 1: 1 品，+b'cz+Mcg _a4_-c' a'c' +b'c'+ 泊、2_a•-b

.

c'(d +b' -c')

c'(d +b2-♂〉 a.1,1+b'c'+2a'b2-a• -b

.

(僅限銳角三角形) (僅限銳角三角形)

|甜(-0' 以~I

Ka'-b' +c'Xa' +b' -c')

S心苔，“'-川| 似-d+b'H可:似a'-b'H')I: 卡(d+b'-c')1

~Ar+cJ)|: 心，-L村，51 :↓以刊，51

K-a'+b' H'Xd'+b'-c ' ) 址'(川-向| K-a'+b'+e'Xd -b' H') ".心 b+c A'A: B'B:C'C • A'P: B'Q:C'R

.

.ra

d

.fC

A'.B',C

.

a

Jκ-a+b 刊)

抖。 -bH) 、肉。+b-c)

。H)J-a+bH

(a

+Cr!

a-bH

(a+b)Ja吋-c

a+c b a+b

_J

a(-a+b H) ...jb(a可言;J古古訂了內心 c

再三:拉宇:~平

b+c 。 +c 。+b c-b a 傍心 a+c

J平 J平:~平

J石3可3.~苟 .J(-o+b刊) B

.

b c-b a+c a-b a-b c 表 2

b

dl:為:‘ 企BCZ

:

6,

ACZ :

6,AB

Z

&心 l-c 'A-knu

--a

l

..

l

..

l 外·IJ

r<-d

+b2+ 叫:

/b(

a2_b2+ 叫:卡(d+b2_c2

)1

卡(-d +b2 + 叫: ~2(d_bl+ 叫:卡(a2+b2_叫

"IJ

~斗的I

:

ka!

-~!

+e2

)1:

(d

+~2

_c

2

)1

l

-d

+~l

+c 21 :

I計~I

: Id +;2 _c 21

傍心 dCA'，反~

:

d(B'.A仍:

d(C'.AI方--a+b+c a-b+c a+b-c

l'.A'Be :l'.AB

'C :

l'.AB

C'-a b c

-a+b+c a-b+c a+b-c

A'

,

B'

,

C

.

恥一恥

l l l a:b:c

B

.

(4)

大致而言，表 l 的關條式用到長度、角度量，但其式子較為簡潔;相對的，表 2 的關條式較為複雜，但僅用了長度量。其中，特別的是僅用長度量時，傍心的叫 :

d

_{2 :}d

₃

_及

M3

CZ: MCZ:

MBZ 反而得到較為簡潔、好用的表示。

貳、孟氏定理及相關引、系理

孟氏定理闡述三角形上三點共線的充要條件，如定理l 所示，證明從略。定理 1

:

ARxBPxCQ

如圖 2 所示，三點 P ， Q ， R 共線，若且唯若一一一=1 尺BxPCxQA A B 圖 2

P

Q

.

圖 3 Q 為後續各項比例的探討，引理 2 提供了所需的若干關條式。若引理 2 中的 H 、 AQ 、 AQ' 為中線或內、外角角平分線時，前述結論可進一步簡他(旦失理 3 )。利用餘弦定理、半角公式等，可將 MBC 之內角的三角函數比轉換成長度比(引理 4) ，並從而由表 1

a

,

b

得出表 2

a

,

b

。

引理 2: 如圖 3 ，在 MBC 中，直線 BC 上依序有 Q' ，

B

,

P

,

C

,

Q 五點，令(

BP

,

CP )

= (

m

,

n

),

(ζBAP ，

LCAP)

= 徊， β) ，

(

LCAQ

,

LBAQ')

= (

y

,

y')

，則

2.

3. BP

esinα

CP

bsinβ

--:-;;

_AP=

be

_---,--

sineα+的

_{, /}

_.AP

---=2

b

2

m

+ e

2

n

= 一一一一一一-mn

eS In α+bsinβ a

besin(α+β) 了云: besin(α+β)

AQ=

(5)

【證明】

設 AP=

x

,

AQ=

y

,

AQ'=

y'

MEP

BP

(αSLOα)/2 /I

"""'/O

R

BP

因一一一=-==

~~ ._，他簡得-==一一一

MCP

CP

(如此1 月 /2' .-.-, -

CP

bsin

j3

be

sineα+β)αSIOαbxsinβ

2.(

1) 由 MBC=MBP+MCP ，得 =一一一一+一一一一

2

化簡得 AP besin(α+β7 esinα+bsinβ

(2) 設 3日， LAPC= 叫，由餘弦定理，在 MBP 中，得∞sθ= m

2

于一 e

2 L.

mx

在 MCP 中，得 COS() =昕一n2-x2 ，得

4凡芷 2 2 .2ι2 2 2

m- +x--e

0-

-n--x

2mx

2月X

化簡得五2 坐立fE-mp7

G

eysin(α+β +y) besin(α+β) bysiny

3.

由 MEQ=MEC+MCQ ，得

=

. .

+一一一

2

一-besin(α+β) 他簡得 AQ=

esin(α+β +y)-bsiny

by'sin(α+β +y') besin(α+β) ey'siny'

同理 l=MCQ'=MEC+MEQ' ，得

=

. .

+一一一一一

2

一「 besin(α+β〕

1b 簡得 AQ'=. ---~-'-- ，，，'/證旱 bsin(α+β +y') 一 esiny'

*理 3: MBC 中:

一一

一-=

J2b

2

_+2e

2

_a

2

Ja

2

+

4becos A

若 AP 為中線，則 AP= w

=-2

2.

若 AP 為內角平分線，則 AP= 一-cos-.一-=

2be

A

b+e

2

3.

若 e

>

b ，則 ζA 的外角平分線與 BC 相交 Q ，且 AQ= 一-Sin 一， CQ= 一一-一一一--::::-

2be.

A 一一

e-b

2 -

-

e-b

【證明】一-2F2月↓ b2_月

_{G 勻}

_2e2

₊

_2b

2

_-a

2 由引理 2.2 '得 AP- =2:....一一二一一(一)"

=

2a

'2

(6)

-

.J

2c

2

+

2昕一。2

2

,

_2

_2 . ""

1_ _ _ __ , l

~ ~e ~

.J

a

2

+ 4bccos A

得 AP=v

2 又 b

2

+ c

2 = a

2 +

2bc ∞sA ，故得 AP= V~

2

2. 設 LBAP=L臼P= α= 芋，

一-=

bcsio

2α2bcsioαcosα 2bc

A

由引理 2.2 '得 AP=

---.._--

=

---一-cos-.

bsinα+csinα(b+c)sinα b+c

2 bcsin(

Jr

-2y)

3.(

I)將。 +2y= π 代人引理 2.3 '得 AQ=

csin(π -y)-bsioy

一-

2bc

sin y cos y2bc

2bc

.

A

t 簡得 AQ=----··· ，---' = 一---:-

cos

Y = - - .

Sin 一.

csiny-bsiny

c-b

2 BC

ABsinA

一一

2bc

. A

A

bc

(2) 如圓 3' 由引理 2.1 '得-==-=-一一其中 AQxsiny=一-SIl1 -XCOS- =一~sinA ，

CQ

AQsioy

-

c-b

2

2 c-b

故得高=坐了證畢

c-o

B

Q

圖 3 引理 4: 在 MBC 中:

1. cos A : cos B : cos C

=α(一。2

+b2+c2): b(a 2 _b 2+c 2): c(a 2

+b2 一 c2₎

2 cosf 斗:∞s;=JO(一。山作品可否:~叫一 c)

A B C

cot-: cot-:

cot 一 =-a+b+c

.

a-b+c:a+b-c

2 2 2

3. bsecB+csecC

2α2(一。2

+ b2 + c2)

bcosB

+ ccosC

。 secA

(a

2

_{_b}

2

_+c

2

_)(a

2

_{+ 昕一 c}

2

₎

_,

_acosA

。2b

2

_{+a2c2 +b2c2 _b}

4

_{_c}

4

2 ,

2

2 、 aLe一aL

+bL+c L)

bsecB

+csecC asecA +csecC asecA +bsecC

= cos

A :

cos

B :

cos C

a b c

(7)

科學教育月刊第 356 期中華民國 102 年 3 月【證明】由餘弦定理得: a

_a 2 +b2

+

C2

h

a 2 _b 2

+C 2

一。

2+b2_{_C}2

COSA =

‘

COS

lJ

=

‘

COSL

=一一一一一一一

2bc

2ac

2ab

得 cos

A :

cos

B :

cos C

=α(一。 2

+

b2

+

C2): 歧。2

_

b2

+

C2) : c(a 2

+ 昕一 c

2

)

2 因∞÷丹豆 =talt仁 JG+b+17+b叫

I(α +b+c)(一。 +b+c) 得 cot

'_' = .1

'J

(。一 b+c)( α +b-c) !(α +

b

+

c)(α -b+c) 同理∞Sγ =

,

I

L. V 峙。c

C

COS-=

2 (a

+

b

+

c)(a

+

b - c)

4ab

B

I

(α +

b

+

c)(α -b+c) __,

C

1(α +b+c)(a+b-c)

I '

"

, • cot 一 =

I

2

'J(一。 +b+c)(a+b-c)

-

2

'J(一。 +b+c)(a-b+c)

得∞sf:cos? 吋 =

.j

a(-a

+

且

_{cot 一: cot 一:}

ABC

_cot

_-=--

₌

_-a

₊

_b

₊

_c

_{:α -b+c:a+b-c.}

2 2 2

3.

由餘弦定理得secA

=

2bc

---

_. secB

_

=一一一一一， S自 C= 一一一

2ac

_

2ab

_a 2

+

b2

+

c2 '

--- -

a 2 _ b2

+

c2 '

--- -

a 2

+

b2 -

C尚依此方法，再根據一般的推演即可完成，過程省略。

參、五心的相關比例

我們在這一節裡，針對當交點 Z 為內心(1)、重心 (G) 、外心( 0) 、垂心( H) 、傍

心( A'， B'，C') 時，算出吼叫:

Wi

(i

=

1 ,

2)

,

d

j :

d

_{2 :}

d

3

等比例關條及

U

j

/門，門/吧，

W)

/w

2

之值以及相關三角形面積比。其中，例行性運算或中學階段熟悉的性質的證明過程從略。

~理 5 :如圖 4 ，令 Z=l 為 MBC 的內心'

2

3.

4. U)/u

_{2 =(b+c)/a}

,

v)/v

₂

=(α +c)/b ，

w)/w

_{2 =(a+b)/c.}

1 A l

B I

C I A

I

B

1 C

u.

:V

,:

w

,

=-cos-一 :-COS-: 一 cos 一-

_,

U" 2 · " 2 · ""2 -

,:

V

, :

W 一一一一-cos 一:一一一-cos 一一:一一一-COS-

.

a

2 b

2 c

2 -

•

• b+c

2 a+c

2 a+b

2

叫:

d

_{2 :}

d

₃

=

1 : 1 : 1 .

(8)

【單明】

2. BI .. QC .. AR

1

"s

VI ..

a

..

b

由孟氏定理 =x-=月三= 1 ，侍 ~x 一=--x'::"=l ，故得 VI

/

v

₂

=

(α +c)/b.

IQ

CA

RB

v2

a

+

c

a

~ 同理 U

_I

/u

₂

=

(b+c) 旬， WI /

w

₂

=

(a

+

b) /

c .

一-:::-

2ac

B

~ V 由系理 3.2 得 BQ

=

VI

+v

₂ = 一-cos 了且斗=--一，

a

+c

L

v

₂ tJ

A目

a+c

艾文

a+c

2ac

B

2ac

B

侍 V，.= 一一一一一-Jjυ= 一一一-一-x 一一-cos 一=一一一一一-cos 一，

a+b+c

~

a+b+c

a+c

2 a+b+c

2 .

b

~

b

2ac

B

2abc

B

仇=一一一-Jj U= 一一一-x 一一-cos 一= cos 一

ι a

+

b

+

c

~

a

+

b

+

c

a

+

c

2 (a

+

b

+

c)(a

+

c)

2 2bc

A

2abc

同理 U， - 一一一-cos-=- ，凡-

cos-=-

,

a+b+c

2 ι (a+b+c)(b+c)

2 .

2ab

C

2abc

C

W. =一一一一一一 -cos 一一. W吋= cos

一一-a+b+c

2'

"(a+b+c)(a+b)

2

1 A l B

1 C

t 簡後可得帆布:

W

,

=

-cos-=-:

-:-cos-=-:一 cos

a

2 b

2 c

2

1 A l B

1 C

札 : Vo :WO=一-cos-: 一-cos-: 一-cos- 證畢。

ιιι b+c

2 a+c

2 a+b

2

B A

C B

C 國 4 圖 5

*理 6: 如圖 5 '令 Z=G 為 MBC 的重心，

1. u

I /

u

2

=

VI /

v

2

=

WI /

w

₂

= 2 .

(9)

中華民國 102 年 3 月第 356 期科學教育月刊

MBG:

M3

CG:MBG =1:1: 1.

d

l :

d

2:

d

3

=

1/ α : 1/ b: 1/ c. 【證明】

3.

4. 得

故

x

l-2

x

v-v

BGQC AR

- - x

z;.- -

x ----

=

1

，得

GQ

CA

RB

由孟氏定理 VI

/v

₂

=

2.

' 一，一 . 一 . 一 . -

VI 寸地，叫 =:CR ， u2=jAP ， V2=;時，叫 =j 臼

U I /

u2

=

WI /

w

₂

=

2 .

-P

弋A

2-3

一-u 同理由系理 6.1 得

2. 又由金理 3.1 ，得芳:豆豆 :

CR

=

J

a

2

+

4bc

cos

A :

J

b

2

+

4ac

cos

B :

J

c

2

+

4ab

cos C

U I : VI : WI

= u

2 :

v

2 :

w

2

=

J

a

2

+

4bc∞sA:

J

b

2

+

4ac

cos

B :

~

c

2

+

4ab

c的 C 證畢。

故

是足理 7: 如圖 6 及圖 7 ，令 Z=H 為 MBC 的垂心，

B 一

的

-d

A 一吋 VI 一 | as自 A+csecC |

~

1

bsecB

I'

U I

I

bsecB

+ csecC|

U 2

lase心 A

I'

U 2 :

v

2

: 叫 =

d

l :

d

2 :

d

3

=

IsecAI: IsecBI: IsecCI

UI : VI : WI

=

IcosAI:

leo叫 :lcosCI

M3

CH : MCH : MBH

= αIsecAI :b

Isec

BI :

c Isec CI

2.

3.

4.

【誼明】

L.A

BQ

=

L.A

CR

=

r

,

BH

QCAR

1 一 λ--x

一-HQ

CA

RB

LBAP=LBCR=β ，設 LCAP=LCBQ=α ，當 MBC 為銳角三角形時，由孟氏定理 γ' 一

n- RY-n 一 γ' mm-n c 一 .mM +一 α RY-n n 一訂

“

-b

α 一

n-G 一

門

-h

得

簡

l巳

個 VI "。 smα

bsinr

1 一 x____=

,

V2 asm α +csmr asm β

*

c-

戶LV-ω-B

+一α

A-s

-LU C-戶 uv 03-G 一一-Ma 一門

r= 三 -LA ，故得

β=33 ，

因 α=2-4

MCH _

v2

_ b s e c B

MBC

VI

+

v

₂

asecA

+

bsecB

+csecC

再得

MBH

csecC

MBC

asecA +bsecB+csecC '

M3

CH

ase心 A

MBC

asecA+bse心 B+csecC'

M3

CH: MCH: MBH

=

asecA: bsecB:

csecC

同理

(10)

C d

_，

吼叫=在BCH la: μ CH Ib: μBH

1 c = sec

A :

sec

B :

sec C

.,.

(叫)

B

A

因此

C

B

國 7

BH.. QA.. CP

1 --x--x 一-

,

HQ

AC

BP

圖 6 當 MBC 為鈍角三角形時(設LA>

90° )

，由孟氏定理 Y' 一 β' 一

n-Y'

一一 α β' 一 n M

csm

y bsinα 一二-x

x - - - =

I V2 asmα-csiny csinβ {七簡得得

y=LA-ffI2

,

α=π 12-LC ， β=

ffI2-LB

,

也*

*

c- ma--

ρiw-的

-B

+一間

A-s

-FO piv 一 ρiw os-G 一 VI V₂ 因得

u

, :2 • "2 • "2V, :w 。 W

₂

來求

BP

=

csinβ ， V 2

,

接下來，透過計算吧， LBHP= π 12-LHBP= π 12 一 α ， 4三AHQ= π 12-LQAH= π 12 一 α ，們 =csinβ COt(ff

1

2 一 α)

...

Q)

由 V

₂

=HQ=AQcotLA 旬，又 AQ=

csiny

,

代人上式得 V

₂

=HQ=csinycot(ffI2α) ...@ 由 U

₂

=

HP

=

BP

cot

LBHP

，又

代人上式得

A~

csmy

又 AH= 一一之一=一一一一一

,

sin

LAHQ

sineπ12 一 α)

.

由 W

₂

=

HR

=

AH

cos

LAHR

=

ff 1

2 -

LHCP

=

ff 1

2 一 β ， W司 csin

YCOS(ff 1

2 一 β) 司 =HR= ,

sin(ff

1

2 一 α)

代人上式得

由Q) @@t旱

in

YCOS(ff 1

2 一 β) U2 : V2 : W 2

= c

sinβ COt(ff 12 α)

: c sin

Y

cot(

ff 1

2 一 α)

:

(11)

。:_..+__~.

smysmp _

~:_ D

sm

α s mα.

smysmp

= sm

fJ

tan

α:

smytan

α. 一一一一-一=sm fJ-一一一 :smy一一一一.一一一一一'

cos

αcosαcos αcos α

1

=于一一 --τ-一一=

-

sec

A :

sec

B :

sec C ... (

*

*叫)

smy smp

smα

c- pu-戶

LW-ω-B

+一前

A-s

了 O

P--戶 LW 03-G 一

門

-n

得

*

占*

*

/sz 、、

*

/sz 、、由一 | bsecB+csecC I

w

,

lasecA+bsec

Bl

同理之=

I

~ ~-- ~ ,~ ~-- ~

I

,

-.:..:L

=

1-

~--

••

, ~,

V__

~

1

U2 lase心 A

I'

W 2

1 csecC

I

由(料)(川*)得到:

V2

:叫=叫:

d

2 :

d

3

= Isec

AI :

Isec

BI :

Isec

CI 證畢。

2. 由

_u

1=1bsecB

+csecCIu"

V

,

=

I as叫 +csecCIv，

,

=

I IU, . V,

=

I IV司

I

asecA

IιιI

bsecB

I·

Z

-W

B- pu-

ρLV-的

-c

+一前

A-s

-PL PU 也戶LW nb-a 一 i

w

又 U

₂

:

v

2

:叫 =Is郎 AI:

IsecBI: Isec

Cl,

故得 U，

:

VI: 叫 =IbsecB

+ csecCI:lasecA+

cs閃 cl:las自 A+bs即 BI ( 引理 4.3

)

a b c

= Icos

AI :

Icos

BI :

Icos CI

證畢。

~理 8 :如圖 8 及圖 9 ，令 z=O 為 MBC 的外心，

1 叫:

d

2 :

d

3

= Icos AI :

I∞sBI:1∞sCI·

2. MCO: 在臼0:μBO= αIcosAI: bl伽利 :clcosCI

3 丘 -blωsBI +clcos 叫立 =αIcosAI +巾的 CI 丘 -alcos

AI

+ blcos BI

U2 一

αIcos AI

'

v2 -

blcos

BI

'

w2 -

clcos CI

4. u

I

:v

I

:w

I

=1:

1:

1 ,

u

2

:v

2

:w

2

=al∞sAl

b

Icos

BI

c Icos CI

,

" 2 ' · 2 ' ' ' 2 -

blcosBI +

~~osCIαIc的 AI+clc的 CI' al∞sAI+blcosBI

B

圖 8

A

C

(12)

【誼明】

圓 O 為 MBC 之外接圓，半徑為 R ，做 OD -l BC:

l

當叫的銳角三角形，得 3ω=jdOC=4

在 MOD 中，

_{d l}

=

Reos

L. BOD

=

ReosA ，同理 d

_{2 =}

ReosB 、 d

_{3 =}

ReosC

得證 d

_，

:

_{d 2 : d}

3

=

eosA: eosB:

eosC

...(吋

當 MBC 為鈍角三角形(L.A

>

90°) ，因 L.BOD = π - L.A ，在 M30D 中，

d l

=

Reos

L. BOD

=

-ReosA ，另 d

_{2 =}

ReosB 、 d

_{3 =}

ReosC

,

得證 d

_，

:

d

₂ :

d

₃

= - eos

A :

eos

B :

eos C ...

(* *)

由(* )(“)得叫 d

₂

:

d

₃

= leosAI: leosBI: leosCI

2.

3. AP

u，崎假設 BC 壇上的高為 d，當 MBC 為銳角三角形時:得-=-=斗」二乙=---:-，

OP

u2

d

l

又

d

_=AABC=

MOC+MOC+MOB

=

ad

,

+

bd2

+

cd)

f

目

U

I

+u2 =adl

+

bd2

+

cd)

d

_,

MOC

a

吭，守門

叫

一一

故此

ι -bd

--

司L. +cd

_、

于一土...們)

U2

aal

AP

u

_，

-u高當

MBC

為鈍角三角形 (

L

三

A>

90° )

:得===」一」

₌₇

_，

OP

u

₂

d

_l

又 d

=AABC=

-MOC+ MOC+ MOB

=叫 +bd

2 +c俏，

一一

d l

MOC

ad

,

扎 -u，

-ad,

+bd吋 +cd，

u.

bd兩 +cd、得二 1 ..乙= 1 _..L _..j ，故一上 =-L于斗...(叫)

U2

aal

U2

aa

,

bleos

BI

+ cleos CI

由們(叫)及叫:吭 :d

₃

=1∞sAl:

leos BI :

I∞sCI ，得丘=

U2

aleosAI

_ aleos

AI

+ cleos CI

wI _ aleos

AI

+ bleos

BI

同理二L 一

一一-V2

bleos訓

,

w2

巾的 CI

由 u， =al ∞sAl

u..

V,

=

bl∞sBI

V.

_

W 一

cl∞sci

2 -

bleosBI+cleos

C

I 門， '2αleosAI+cleosCI'I'

"2-

al∞sAI+bl∞sBI'"

αleosAI

bl∞sBI

cl∞sCI

又 u

_{I = VI = WI =}

R

，得叫 :V，: W 一

b

leos

BI

+ c leos

CIαleos AI

+ c leos

CIαleos

AI +

b

leos

BI

證畢 O

(13)

科學教育月刊第 356 期中箏民國 102 年 3 月

是足理 9:

如圖 10 ， MBC 中，

a>c>b

,

<乙 A ， L三 B， LC 內的傍心分別為 A' ， B' 及 C'

,

L三 A ， L三 B ，

LC

的內角平分線與對邊分別相交於P ，

Q

,

R 且外角平分線與對邊分別相交於 p' ，

Q'

,

R'

,

則:

l

對於三傍心 A' ， B' 及 C' 有，

AA'

b+c

BB'

a+c

CC' α +b

(I)

._--

=一一， -=-=一一， -==一一

PA'

a

QB'

b '

RC'

c

一一一一一τ- cos(A

1

2) . ∞s(BI2) ，

cos(C/2)

(2)

AA': β'B':CC 一一一一一一一一一一一一一一，

α(一α +b+c) b(α -b+c) c(α +b-c)

一一一一一「-

cos(AI2)

.

cos(B 12)

.

cos(C

12)

PA':QB':RC

一

(b+c)(一。 +

b

+

c) (

a

+

c

)(α -b+c) (α +b)(a+b-c)

acot(AI2)

,

bcot(BI2)

,

ccot(C/2)

(3) 叫 'BC:MB'C:MBC'= 一一一一一一一一

(一a+b+c)2'(α -b+C)2'

(a+b-c)2 '

P'

一一- cot(A

12)

,

cot(BI2)

,

cot(C/2)

(4)

d(A'

,

BC): d(B'

,

AC):

d(C'， AB) 一 -一一一一一一一一一一一一

(一。 +

b+C)2 '

(σ -b+C)2'

(a+b-c/ .

2.

對於傍心 B' 有，

(1)

丘=三二至

U 2

a

VI

a+c

WI

a-b

V 2

b '

w

2 C

(14)

cos(A/2) ∞s(B

/ 2)cot(B /

2)cos(C / 2)

u

,

:V

,

:W

,

=

,

a(-a

+

b

+

c)

b(α -b+

c)

c(α +b-c)

(2)

sin(A/2)

cos(B/2)

sin(C/2)

u句 :v句:

w

,.., ==一一-一一一-一.一-一一一-一一 -一一一-一一-~ ~ ~

c-b

a+c

a-b

(3)

咕:

d

₂:

d

₃

=

1:

1 汀，

(4)

M'BC: M'AC: M'AB

= α:

b:

c.

(5)

BB'

MBB'AB

x

AB'

x sin

LBAB'

QB'

MQB'

AQxAB'xsinLQAB"

ζA 外角為 2β。'

【證明】

1.(1)設 LA=2α。'

sin

LQAB'

=

sinβ ，又立豆_

_c

AC

= 主丘，

a+c

CC' α +b

RC'

c

AA'

b+c

PA' α

BB'

--一一一，同理

QB'

b

其中 sinLBAB'

=

sin(2π 一月=slnβ ，

AB

-==一一一一=一一，故得

AQ

bc/(α +c)

b '

4 目 ↑守

BB'

a+c

._ BB'

α+c 一一月牛 f 一一 (2) 由==一一二得-=-=一一一一，得BB'= 二千之-QB

QB'

b ' "" QB

a-b+c'

"~

--

a-b+c

其中豆豆為角平分線，由系理3.2 得豆豆=坐三cos手，代人上式

a+c

L

一-

a+c

2ac

B

2ac

BB'= 一一一一-x 一一三-cos- =一一一二-cos 一

a-b+c

a+c

2 a-b+c

2 c-2

-r

一--:-:

2bc

A

AA'= 一一一一-cos-.

-a+b+c

2

目守 dA'. 旬，，

一一一一一τ

cos(A/2)

. cos(B/2).

cos(C/2)

AA':BB':CC'=

---，--<-，一一一一一一一.一一一一一一 α(-a+

b+c)

b(α -b+c) c(α +b-c) 同理得化簡得一口 - -

. . - -

-PA': QB':R

C'

= 于二-AA':

- -

-BB':--γ CC'

o+c

a+c

a+o

cos(A /

2 ) .

cos(B /2)

.cos(C /2)

(b

+

c)(一。 +b+c)

(a+c)(a-b+c) (a+b)(a+b-c)

故得

AB'

c-b

由志理 9.2 (1)得斗-~=一一， U2 P'B' α

MB'C =.!.AB'CB'sinB'.

2 (3)

zζA :r -LC ζA+LC

:r

LB

又 ζAB'C= π 一一一一一一一一一一=一一一一=一一一一

2

一…

CB'

=

-=---:::一 CR' α -b+c 同理

(15)

4三B ，

B

LL.. / . ' " • • _ •~

1 c -

b

一-=-:

a-b

一一

得

sin B'

=

sin(一一一一)

=

COS

-=

，故得 MB'C=~x 一一一-AP'x 一一一-CR'xcos

2 2'

2 .

2 a-b+c

a-b+c

一-::-:

2bc.

A 一-=

2ab

. C

又由系理 3.3 得 AP'= 一--:-

Sill -::-

，侃'-一 -S Ill-::-

,

c-b

2'

a-b

2

1 c -

b

2bc . A

a - b

2ab .

C

B

MB'C=~x 一一一一一一一-S Ill-X

S

Ill-

X

cos-2

a-b+cc-b

2 a-b+ca-b

2

2 2ab

2

c

. A

B. C

=-一一一一一一一--=-

Sill

一-COS 一- S Ill-一

(a-b+cY

2

2 2a

2

_bc

_{A . B . C}

.. _ _.

2abc

2

•

A . B

C

M'BC=

-cos'="='sin'="'sin-=-.

MB

C'

= 一一一一一一-=-

S

Ill-

S

Ill-

cos-(-a+b+c)"

2

2 2 .

(a+b-cY

2

2 ,_

a cot( A I 2) . b cot( B I 2) . c cot( C I 2)

化簡得叫 'BC:

MB'C: MB

C'

=

v 一一一一.，

.一一一一-(一a+b+cY

(a-b+cY

(a+b-c)

故得同理 1

AB'

AB

' A

2. (1

)之--=--=-，由朱理 3.3 得 CP'

=

abl(c-b)

,

U2

B'P'

BP'

.~

u

,

AB

得 BP'

=

CP'+BC

=

abl(c-b)+ α = ac/(c-b) 故得斗= C

c-b

U2

BP'

。c/(c-b)

_。

BB'

同理主=旦二豆，又由系理9.1 (1)得之----一一

_W 2 c " _.. - . . . V2

QB'

b

(2)

AB': BB' : CB'

=

AA' cot B' : BB' : CC' cot B'

=

AA ' : BB' tan B' : C

C'

由系理 9.1(2)及 ζAB'C

=

Jr12-L三B12 ，

一一一一 I' n'

cos(A I 2)

cos(B 12)

. . . . f ' ' " ' n

',""

cos(C 12)

得 AB':

BB': CB'

=

---,'" -/

:一一一一一個n(Jr /2-BI2):一一一一一一

。(-a+b+c) b(α -b+c) c(α +b-c)

cos(A 12)

cos(B I 2)cot(B I 2)

COS(C 12)

。(一α +b+c) b(α -b

+c)

c(α +b-c)

AB'

c-b

一一-

a

一一一一-

c

一一一

(3)

由==一一一， t尋 P'B'= 一一一一-AP' ，同 f.l R'B'= 一一一一-CR' ，

P'B'

a

a-b+c

BB'

a+c

一一 h 一一一又由 9.1 (1)之--=一一，得仰'=-~-BB'，

QB'

b"

-

a+c

一一一一一一一一一=-:

a

一一- 0 一一一則 P'B':QB':R'B'= 一一一-AP': 一二一郎'.一一一一白，

a-b+c

a+c

a-b+c

。 2bc

. A

b

2ac

B

c

2ab.

C

一一一一-一一-Sill 一:一一一一一一一一一一-COS 一:一一一一一一一一一一-S

Ill-a-b+c c-b

2 a+c a-b+c

2 a-b+c a-b

2 畢

證

弓 h /了 O

C--叫一。可 h //-C B 一+ dM 「-G O 一尸UV 一句 h 一 /I 一'。 A 月一一昕一 C

(16)

肆、後記筆者曾從西瓦、孟氏定理推導出另一種判別三線共點的充要條件(載於參考文獻 1

) ,

並藉此探討重心、內心、外心及重心的部分性質。其後，偶然看到討論四心相關比例的文章(如參考文獻 2)' 因而促使筆者更深入思考。上述兩篇文章的討論僅限於銳角三角

形，本文則擴及鈍角三角形及傍心，先從角度、長度量併用的方式切人探討三角形五心

相關各距離、長度、和面積的比例關條(如表 1

a

,

b)

，再利用引理 4 將內角的三角函數比轉為長度比，從而得到僅有長度量的比例(如表2a，

b)

0

參考文獻

蘇柏奇(2 005) ，三角形上共點三線段分割圖形的比例，萬腦奔騰數學網(三)一數學科學與資訊科技共舞，交通大學。劉俊傑(

2006)

，換個觀點看三角形的四心，數學傳播，第30 卷第 2 期。

三角形五心相關比例的探討