A probability model for reconstructing secret sharing under the internet environment

(1)

I N F O R M A T I O N S C I E N C E S ELSEVIER Information Sciences 116 (1999) 109-127

A probability model for reconstructing secret

sharing under the internet environment

Ching-Yun Lee a,1, Yi-Shiung Yeh a,2, Deng-Jyi Chen a,.,

Kuo-Lung Ku b

a Institute of Computer Science and Information Engineering, National Chiao-Tung University, Hsinchu 30050, Taiwan, ROC

b Chung-Shan Institute of Science and Technology, Taoyuan, Taiwan, ROC

Received 17 January 1998; received in revised form 13 August 1998; accepted 24 October 1998

A b s t r a c t

Internet technologies have ushered in a new era for computer-related communications. Use of the Internet for commercial applications and resource sharing has accel- erated in recent years as well. Owing to such developments, Internet security has become a critical issue for both academic and commercial sectors. Several studies have focused on areas involving network security such as authentication, privacy, and integrity. In some applications, an important message can be divided into pieces and allocated at several different sites over the Internet for security access concern. For example, an important map that can be used to access a military base, a vital key that can be used to give a military order or command. To access such an important message, one must reconstruct the divided pieces from different sites under the given Internet environment. In this paper, we present a novel probability model for reconstructing secret sharing under the Internet. Also, how to assign the divided shares into different sites over the Internet is studied. Also proposed herein are algorithms to perform shares assignment and to evaluate the probability of reconstructing the divided pieces into the original secret. Illustrative examples and simulation results demonstrate the feasibility of the proposed approach. © 1999 Elsevier Science Inc. All rights reserved.

Keywords." Internet; Secret sharing; Graph theory; Spanning tree; Probability

"Corresponding author. Fax: +886 3 572 4176; e-mail: djchen@csie.nctu.edu.tw t E-mail: leecy@csie.nctu.edu.tw

2 E-mail: ysyeh@csie.nctu.edu.tw

(2)

110 C - Y . Lee et aL / htformation Sciences 116 (1999) 109-127 1. Introduction

The Internet has revolutionized computer-related communications. The Internet consists o f networks interconnected by a set o f routers which allow them to function as a single, large virtual network. The Internet functions as a global broadcasting medium, a mechanism for information dissemination, and a forum for collaboration and interaction between individuals and their computers regardless of geographical proximity. Such a capacity accounts for why use of the Internet has exploded in recent years. According to N e t w o r k Wizards 3, the n u m b e r of hosts on the Internet grew from 1,313,000 in J a n u a r y 1993 to 36,739,000 in July 1998. An added feature of the Internet is resource sharing a m o n g remote users, in which user can quickly access data from any site. Nevertheless, given its openness and easy access to the general public, the Internet is vulnerable to more attacks from intruders than any other network. A user can achieve a secure secret in Internet environments by adopting encryption/decryption algorithms [1,2] and secure key distribution protocols [3,4] as well as secret sharing schemes [5-7]. Sharing secrets a m o n g several individuals in a manner that no individual holds all the secrets is highly desired. Shamir [8] and Blakley [9] pioneered the notion o f secret sharing and provided the secret sharing schemes. An (m, 17) secret sharing scheme is a method which a secret, S, is divided into n shares (or shadows) in such a m a n n e r that the secret S cannot be reclaimed unless at least m shares are collected. This scheme is c o m m o n l y referred to as (117, n)-threshold scheme. Stinson [10] and Simmons [11] thoroughly review related developments on the secret sharing schemes.

A secret can be taken and divided it into pieces in several ways. To secure a secret, we can divide secret into shares and store shares at different sites over the Internet. The Internet provides resource sharing a m o n g remote users, thereby allowing quick access o f a message from any site. As generally known, a user can reconstruct a secret message by sending requests to the service. A service exports a set of commands. After executing a c o m m a n d , the service can transfer the requested shares to the user that invoked the c o m m a n d . Secret sharing schemes can be used for diverse applications, including i m p o r t a n t maps, secret recipes, and military c o m m a n d and control systems such as a fire controller. In addition, a general sharing scenario one can imagine can be modeled.

T w o types of shares, single-share and multiple-share, play a prominent role in the development of the share assignment method. Each participant could have only one share or a different n u m b e r o f shares (multiple-share). Single assignment secret sharing scheme assumes that each participant holds only one

3 This data is provided by Network Wizards and is available on the Internet at http:H www.nw.com/.

(3)

C.-Y. Lee et aL / h~formation Sciences 116 (1999) 109-127 111

share. Single-share protocol is limited in that if any share gets lost or can not be obtained, the secret message cannot be reconstructed. Typically, having two or more participants with the same share is desired owning to the availability. If the share is replicated, whether some of the replicas are down or unavailable is unimportant.

Among the promising applications of the Internet include high reliability/ availability and resource sharing. The reliability/availability improvement is owing to the redundant techniques used on the Internet. Some errors or other unexpected factors o f a network may disconnect the communication network, thereby influencing the performance and reliability of the Internet. Several network reliability measures have been defined in addition to the related evaluation methods [12-17]. The evaluation algorithm proposed in Ref. [16] with some modifications can be used to measure the SSRP (Secret Sharing Reconstruct Probability). The computational complexity of the reliability evaluation algorithm is NP-hard [18,19]. Probability generally refers to a system's ability to carry out a requested operation correctly and efficiently. However, allocating shares to appropriate locations for each user over the Internet enhances the secret sharing reconstruct probability. The distribution of shares heavily influences the SSRP. The share assignment problem involves finding a share distribution such that the SSRP measure is maximal. Exhaus- tive approach may be used to obtain the optimal solution with high compu- tation time. In this paper, we present a simple share assignment (SSA) algorithm based on priority search and some heuristics to achieve better share assignment.

The rest of this paper is organized as follows. Section 2 presents the notation, definitions, and problem statements used herein. Section 3 thoroughly describes the probability model and SSA algorithm to obtain the secret sharing reconstruct probability under the Internet. Section 4 presents some illustrative examples and simulation results to demonstrate the effectiveness of the proposed algorithm. The conclusion of the paper is finally summarized in Section 5.

2. Notation, definitions, and problem statements

Notation

G( V,E)

SAi

An undirected graph in which V represents the set of vertices (or nodes) and E represents the edges set of communication links for the network under consideration the set of shares such that any m of them can be used to reconstruct the secret, S

(4)

112 C-Y. Lee et al. / InJbrmation Sciences 116 (1999) 109-127

s~

M~

M E Pi(qi) Pr(E) G - e G + e SSA SSRP single-share, or share i in Ss multiple-share in Ss, such as Mi = {Sl tO $2}, M,_= { S3 tO S4 tO Ss}

a subset of E that represents the edges which merged together during the process o f finding all MSSTs probability o f node, edge, or link i works (fails) probability of event E

the graph G with edge e deleted

the graph G with edge e = (u, v) contracted such that node u and v

Simple Share Assignment algorithm Secret Sharing Reconstruct Probability Definitions

• SST: a share spanning tree that connects the user node (the node that recon-

struct the secret under consideration) to some other nodes such that its vertices hold all the required shares.

• MSST: a minimal SST such that there exists no other SST which is a subset o f it

• H P F - B F Search: The H P F - b r e a d t h first search uses the breadth-first search with high probability first, and keep track o f nodes visited. In H P F - B F Search, we start f r o m a node u (the user node) and first visit the node with the highest probability edge incident to u.

• SSRP: The probability that a user can successfully reconstruct a secret over the Internet, i.e., a user can access all the shares required f r o m remote sites despite the faults a m o n g the nodes and communication links. The MSSTs connect the user node to other nodes such that these nodes hold all the required shares for the user to reconstruct the secret. The SSRP can be determined by computing the probability that at least one o f the MSSTs is operational. Thus the secret sharing reconstruct probability for a user can be defined as the probability that at least one M S S T of the user is available. This can be written as

"ross[

where nmsst denotes the n u m b e r of MSSTs that reconstruct the secret.

• Shadows (Shares): We can take a secret and divide it into n pieces, called shadows or shares, such that any m o f them can be used to recover the secret.

• Multiple-share: a site with multiple-share (or multiple shares) suggests that it

contain more than one share.

• Allocation tree: An allocation tree is a tree that was reconstructed from a network and has allocated the share into it.

(5)

C - Y . Lee et al. I h~formation Sciences 116 (1999) 109-127 113

Problem statements

Informally, the Simple Share Assignment for secret sharing reconstruction is a scheme in which a distinguished host computer, user or client, secret and encrypts a secrets messages, S, and assigns all shares of S to other remote computers. F o r the share assignment problem, the following information is given:

(a) network topology,

(b) the shares required to reconstruct the secret, (c) user's location,

(d) the probability o f each node and communication link works. We also assume that the node and link failures are s-independent.

3. The system model and heuristic algorithm

In this section, we present a probability model of secret reconstruction and algorithms to perform shares assignment under the Internet environment. The Internet can be treated as a computer network that is represented by an undirected graph.

3.1. The system model

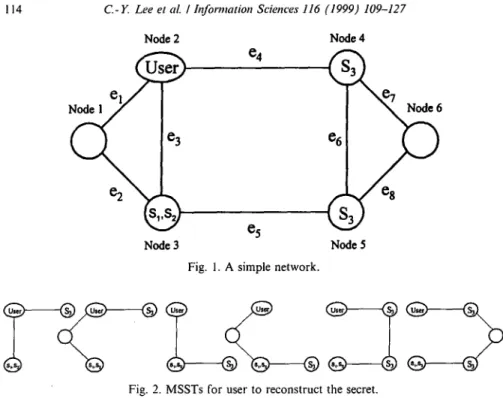
Informally, the model is a protocol in which a distinguished processor, or user, selects a secret message and divides it into n pieces, or shares. The divided shares o f the secret are then allocated into other processors. A user can access the secret by sending requests to other processors to return the needed shares for reconstruction. Therefore, the model is a probability measure for reconstructing the secret sharing. F o r example, assume that the commander with anyone o f the two vice-commanders is authorized to initiate an order. Herein, we divide a secret message into three shares, Sl, $2, $3, and give the commander multiple shares, {$1, $2} and the vice-commander one each, {$3}. Consider the network topology shown in Fig. 1 which consists o f six nodes with one multiple shares (node 3) and two replicated single-share (node 4, 5). A user can either recover the secret or initiate the order by sending a request message to nodes 3, 4, 5 to ask them to return shares S~, $2, $3. In general, the set of nodes and links involved in reconstructing the secret and access its required shares form a tree. A share spanning tree that connects the root node (the user that recreates the secret under consideration) to some other nodes such that its vertices hold all the required shares for reconstructing the secret. Fig. 2 depicts all MSSTs that represent the site which has shares required for a user to reconstruct the secret for the network application in Fig. 1.

(6)

114 C - Y . Lee et al. / Information Sciences 116 (1999) 109-127 Node 2

e 2 \

Node 3

e4

C5 Node 4

S3

I e 8 Node 5 Fig. 1. A simple network.

Fig. 2. MSSTs for user to reconstruct the secret.

Let the probability o f all nodes and links being operational be 0.9. By doing so, the SSRP o f secret S can be computed using conditional probability, as shown below.

SSRP(S) = PN2 PN3 PN4 P~3 Pe4 + qe3 Pm pN2 PN3 PN4 Pel p~2 Pe4 + (1 - Pe4 PN4)PN2 PN3 PNS Pe3 Pe5

+ qe3(1 -- Pe4 PN4) Pm PN2 P^'3 PN5 P~l PeZ P~5 + q~3 (1 -- Pel P~Z Pm )PN2 PU3 PN4 PN5 Pe4Pe5Pe6

+ qe3 q~6(1 -- Pel Pe2 P m ) PNZ PN3 PN4 PN5 PN6 Pe4 Pe5 Pe7 Pe8 = 0.59049 + 0.0478297 + 0. I 121931 + 0.00908764 + 0.0129618

+ 0.0010499 = 0.7736121,

where Pui denotes the probability of node i working and Pei represents the probability of edge i working, qui = (1 - Pu~), and q~,- = (1 - p~).

The probability o f reconstructing secret sharing on the Internet can be evaluated by the following two steps: finding all the MSSTs for that user and computing the probability o f the MSST to evaluate the SSRP. All disjoint MSSTs can be generated by the following minimal_sharespanning__tree algorithm with some modifications from the reliability algorithm in Ref. [16].

(7)

C-Y. Lee et aLI Information Sciences 116 (1999) 109-127 115 The MSST algorithm employs the graph expanding procedure and guarantees no replicated share spanning trees generated during the expansion of compu- tation tree. The MSST algorithm executes several reduction methods [20] to reduce the size of the problem and to simplify the probability evaluation. The complete MSST algorithm is given below.

Algorithm

M i n i m a l _ S h a r e _ S p a n n i n g _ T r e e (G, u);

Input:

G = (V, E, Ss) (the original network graph), and u (the user node)

Output:

the SSRP, Secret Sharing Reconstruct Probability

begin

repeat

/* reduce the original network graph G */

perform degree-1 reduction /* removes degree-1 nodes which contain no

required shares and removes their incident edges */

perform parallel reduction /* Suppose e,, = (u, v) and eb = (u, v) are two

parallel edges in G. We can reduce these redundant edges into a single

edge ec = (u, v) such that P,.c: = (1 - qea X qeb) "1

perform series reduction /* Let e, = (u, v) and eb : (v, w) be two series

edges in G such that degree(v) = 2 and node v contains no required shares. We can remove node v and replace edges e,, and eb by a single

edge ec = (u, w) such that Pec:= (P,,~ x p,, × Peh) */

perform degree-2 reduction /* Suppose node v, with node degree = 2, is a

reducible node. Then we can apply series reduction on node v and move the shares within node v to one of its adjacent nodes. */ until no reductions can be made

let G ~ be the network graph after reduction step F O U N D : = 0

M E : = 0

F I N D _ S S T ( G ~, ME) /* call F I N D _ S S T to find SSTs */

for

all s, t E F O U N D do /* remove the SSTs which are not MSSTs */ if (t N s) = s

then

remove from F O U N D

else if (t fq s) = t then remove S from F O U N D endif endif

repeat

nodes are introduced by the intermediary Of edged incident to them apply the reliability algorithm to all MSSTs in F O U N D to evaluate SSRP

output

the SSRP e n d M S S T

(8)

116 C.-Y. Lee et al. I hformation Sciences 116 (1999) 109-127 Function Find_SST( G, M E )

begin

if there are no SSTs in G then return(0) endif

if there exists one node v such that SAy _ Ss then FOUND: = F O U N D t3

{ME}

return endif

for all ei E {the set of edges incident to the node that contains the user} do

FIND_SST(G + el, M E U {ei})

G: = G - ei

remove the irrelevant components from G if there is no SSTs in G then return endif

repeat end F I N D _ S S T

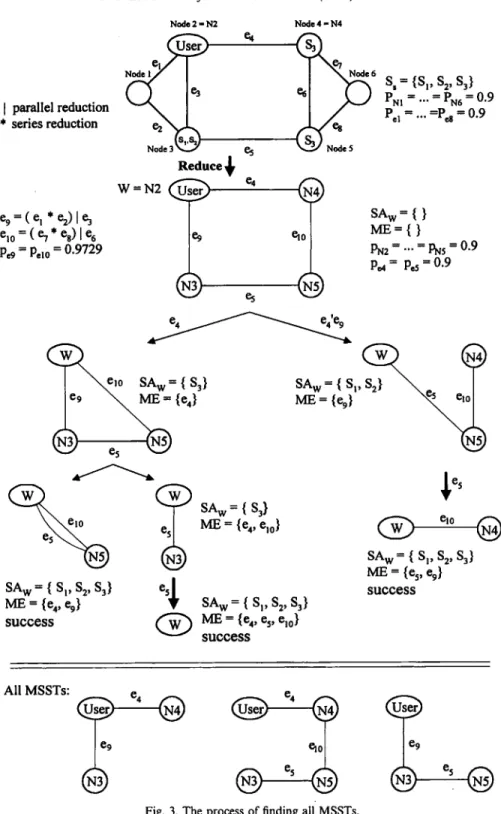
The previous example in Fig. 1 is used in the following to illustrate the MSST algorithm. Fig. 3 depicts the process of finding all MSSTs of MSST algorithm. The list of all MSSTs generated in F O U N D are {(e4, e9), (e4, e5, el0),

(es~ e9)}. The nodes are then introduced by the intermediary of edges incident to them. The set of all MSSTs of user to reconstruct the secret is {(e4, e9, N2, N3, N4), (e4, e5, elo, N2, N3, N4, N5), (es, e9, N2, N3, N5)}. Assume that the probability of all nodes and links working is 0.9. Applying the terminal reliability algorithm, e.g. [14,16], to the above MSSTs allows us to compute the SSRP of secret S, as shown below.

//msst /

SSRP(S) = Pr([,_JMSST

= PN2 PN3 PN4 Pe4 Pe9 + qe9 PN2 PN3 PN4 PN5 Pe4 Pe5 PelO + (1 -- Pe4 PNa)PN2PN3 PN5 Pe5 Pe9

= 0.6383197 + 0.0140117 + 0.1212807 = 0.7736121.

3.2. A simple example o f S S R P analys&

Example 1. Herein, a secret is divided into three shares: Sl, $2, and $3. Assume that one participant is more important than the others and give that participant multiple shares, {Sl, $2}. We allocate the shares into different sites over the Internet. To recreate the secret, the user must obtain the three shares together. Consider the network topology shown in Figs. 4 and 5 which consists of six nodes that allocated one multiple-share and three different single-share in redundant manner. Let the probabilities of all nodes and links being

(9)

C - Y . Lee et aL I Information Sciences 116 (1999) 109-127 [ parallel reduction * series reduction Node 2 - N2 e5 Reduce ¢ W=N2 ~ ~ e4 N o d e 4 = N 4 Node 5 e.to S, = {Sp S 2, S3} Pm = "'" = PN6 = 0.9 Pc1 = " ' " =Pd = 0.9 SA w = { } M E = { } 1~2 = -.. = l ~ s = 0 . 9 p,~ = p.~ = 0.9 % = ( % * % ) 1 % elo = ( e7 * %) 1% P~9 = Peto = 0.9729

SAw=I

e9 ~ M E = {e4} ~ e l o ~ e5 SAw = { s3} M E = {e 4, elo} SA w= { Sp S v S3} es[ ME = {Ca, e 9} ' ~ SA w = { SI, $2, $3}

SUCCESS ~ ME -- {e4, es, elo}

SUCCESS

SAw-- s,,

M E = {eg} "- ~ e 5 Q el 0 SA w = { Sp S 2, S 3} M E = {es, e9} SUCCESS 117

®

All MSSTs:

®

(10)

118

C-Y. Lee et aL / Information Sciences 116 (1999) 109-127

operational be 0.9. Fig. 4 depicts an optimal share assignment to this network topology and Fig. 5 displays a poor one. These allocations differ only in the share assignments, while the other parameters are identical.

This example demonstrates how share assignments affect the secret sharing reconstruct probability. Thus, the means of share assignment significantly af- fects the probability of secret sharing reconstruction. The following section presents a simple share assignment algorithm such that the probability o f secret sharing reconstruction can be maximized.

3.3. Prelim#~ary strategy of the simple share assignment 3.3.1. Underly#Tg concept

The concept of full set is introduced as follows. Full set is defined as a set containing all the required shares to reconstruct the secret under the Internet. F o r

an (m, n)- threshold secret sharing scheme, the full set of secret S is the set o f all

shares {St, Sz ... S,,} which is a unique case o f m = n . Full set is the basic

requirement of the SSRP. Recall the definition o f the minimal share spanning tree. The MSST for the secret must contain all the elements in the full set. This paper also concerns itself with the combination of the multiple-shares for the participants. By doing so, we attempt to obtain a larger number o f groups with the full set. Thus, the proposed approach is carried out to obtain an acceptable SSRP value. To prove this theorem, recall how SSRP is computed. SSRP is the probability that at least one of the MSSTs is working. The MSST spans one o f the full sets we just discovered. If more full sets are in the network, the number

Optimal (SSRP = 0.7691332)

Node 2

S3

e l

~

e3

e 2 x

Node 3 e 4

e5

Node 4

F e 8

Node 5

Fig. 4. The optimal share assignment of Example 1.

(11)

C.-Y. Lee et al. / hzformation Sciences 116 (1999) 109-127 119

Poor (SSRP = 0.7054569)

Node 2

e l

~

e3

e

2 -~

Node

3 e

4 e5

Node 4

®

e7 ~- c 8 Node 5 Fig. 5. The poor share assignment of Example 1.

of MSSTs is also larger. Hence, SSRP should be greater owing to P(A O B) >~ >~P(A) by the set theory.

Closely study the above example reveals the following:

(a) The transfer probability for a share is data link dependent. The fewer the data links capable of transferring the required data implies a higher transfer probability;

(b) The MSST with less nodes and links is more reliable; and

(c) The SSRP is the probability of the union o f the number o f MSSTs and can be enhanced by grouping the required shares as close to the.user node as possible.

Based on above observations, we propose a simple heuristic approach for share assignment. Underlying concepts of the heuristic approach are as follows:

1. Allocate the more influential shares first. (Share MI is more influential than share M2 if and only if the number o f shares o f Mj exceeds that of

M,_);

2. Complete the full set which occupies a minimum number o f nodes; 3. Allocate the shares to the more reliable sites; and

4. Allocate all shares as close to the user's location as deemed feasible. The above strategies are applied to develop our share assignment algorithm. The SSA algorithm is based on priority search and some heuristics, and is summarized in the following two parts.

Part 1: Classify and determine the allocation order of the shares.

Part 2: Use the H P F _ B F algorithm to reconstruct the network into a tree topology, then sequentially allocate these shares into the reconstructed tree according to the order obtained in Part 1.

(12)

120 C.-Y. Lee et al. I hTformation Sciences 116 (1999) 109-127

3.3.2. Reconstructing network into tree topology

Next, the network is reconstructed into a tree topology by using the H P F - BF search algorithm to travel all the edges. In H P F - B F search, we start from a node u (the user node) and visit the node from the highest to the lowest probability edge incident to u. Then all nodes adjacent to those nodes are visited, and so on. The H P F - B F algorithm uses the breadth-first search with high probability first to construct a H P F - B F tree by including only edges that lead to newly visited nodes. All those edges cumulatively form a tree with user node as its root.

. The complete H P F - B F search algorithm is given below.

Algorithm HPF-BF Search ( G, u);

Input: G = (V, E) (an undirected connected graph), and u (the user node). Output: T = (V, E'): a tree T with node set V and edge set E'.

begin

S: = {u}

L: = {ell Vei E E and 3v; E S, such that e i is incident to vi} E : = E - L V : = V - S E': = 0 S: = 0 repeat repeat

e: ={eil select an ei E L which has the maximum Pei} L: = L - {e}

f i E ' + {e} does not have cycle then E': = E ' + { e } endif S: = S + {vii Vvi f[ S and e is incident to vi }

until L = Q

L: = {e~ ] Vet E E, '~ei q[ E t, and 3vt E S, such that ei is incident to vi} V : = V - S

S: = 0 until V-- 0 end HPF-BF

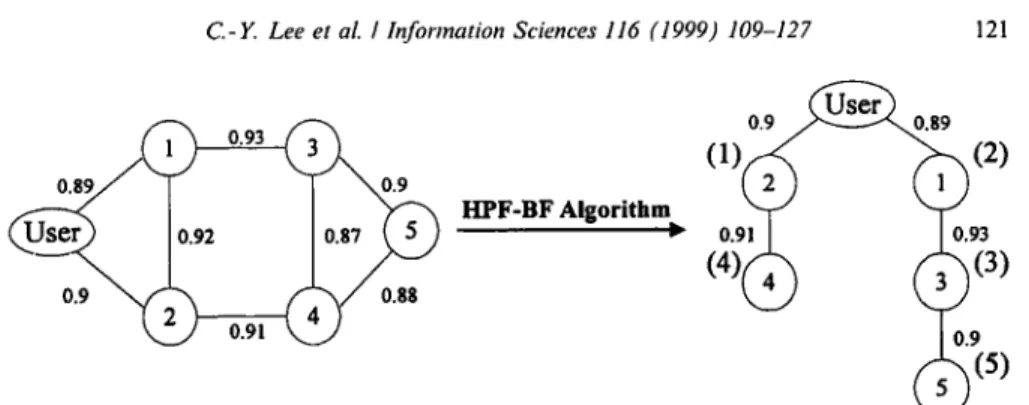
3.3.3. C. An example o f HPF-BF algorithm

Fig. 6 depicts a simple example o f using H P F - B F algorithm to construct the allocation tree. The parenthesized numbers associated with the nodes denote the order in which the nodes were searched by H P F - B F search algorithm.

3.4. The complete SSA algorithm

The SSA algorithm consists o f two steps. First, the algorithm determines the allocation order of the shares. Next, the algorithm executes the H P F - B F search

(13)

C-Y. Lee et al. I Information Sciences 116 (1999) 109-127 121

1o9 1o.87>

0.9 ~

0.88

0.9 ~ . 8 9 HPF-BF Algorithm 0.91 I 0.93 0.9

Fig. 6. A example of the HPF-BF Search algorithm.

and sequentially allocates the shares into the tree. The allocation order of the shares is determined by using the following procedures.

(a) Calculate the number o f shares o f each multiple-share. (b) Allocate the multiple-share with more unallocated shares first. (c) Calculate the number of unallocated shares o f each multiple-share. (d) Select and allocate the share which contains more unallocated shares to complete the full set. Select the multiple-share that contains more shares first to break the tie o f the number of unallocated shares.

(e) If all shares have been set to "allocated" then set all shares to "unallocated". A share assignment, which has the greatest number o f full set groups, is our preferred choice.

(f) Repeat steps c, d, and e until all the shares have been allocated.

Algorithm Simple_Share_Assignment;

Input: G = (V, E) (an undirected connected graph), u (the user node), and M (the set o f shares to be allocated).

Output: an allocation tree.

begin

S: = {v I v is the node that contains the user}

M': = I N _ O R D E R _ O F ( M ) / * M is the set of single and multiple shares */ V: = HPF-BF(S) repeat v: = F I R S T _ N O D E ( V ) v:= v -

{v}

m : = F I R S T _ S H A R E ( M ' ) M': = Air'- {m}

allocate multiple-share (or share) m into node v

until M ~ = O

(14)

122 C - Y . Lee et al. I Information Sciences 116 (1999) 109-127 Function

IN_ORDER_OF(M)

begin M': = 0 repeat for Vm ~ M do

count the number o f unallocated share in multiple-share (or share) m m: = {m'[ m' is in set M with the largest number o f unallocated share} M': = M'+{m}

M: = M - {m}

if all shares have been set to "allocated" then set all shares to "unallocated" endif

until M = O return(M')

end

IN_ORDER_OF

Function

FIRST_SHARE( Af);

begin

return the first multiple-share (or share) in an order set M ~

end

FIRST_SHARE

Function FIRST_NODE(V) begin

return the first node in an order set V

end

FIRST_NODE

3.5. Time complexity analysis

The computational complexity o f the SSA algorithm is the sum o f the run time o f determining the allocation order o f shares and finding the next location for share to be allocated. First, arranging the allocation order o f shares take

O((k+n)n)

comparisons in the worst case. Second, the H P F - B F search algorithm takes O((e + v)log v) to construct the H P F - B F tree in the worst case. Therefore, the time complexity o f algorithm SSA is O((k + n)n) + (e + v)log v), where v denotes the number o f nodes (vertices), e denotes the number o f edges, n denotes the number o f single-share, and k denotes the number o f multiple- share.

4. Illustrative examples and simulation results

In this Section, some examples and numerical results are employed to illustrate the effectiveness o f our approach.

(15)

c.-Y. Lee et al. / Information Sciences 116 (1999) 109-127 123 4.1. A n eight-node c o m m u n i c a t i o n n e t w o r k

Consider the network topology in Fig. 7 which consists of eight nodes and eleven communication links. N o d e 2 contains the user and the other nodes are regarded as share-storage locations. Assume that the probabilities of all nodes and links being operational are set to 0.9.

The secret sharing reconstruct probability of the secret S is evaluated by applying the algorithm presented in Section 3.1. In this example, the secret is divided into four shares. Assume that four single-share and two multiple-share are to be allocated. The multiple-share may contain more than one kind o f single-share. They are listed as follows.

The set of shares of secret S: S~ = {$1, $2, $3, 84} F o u r single-share: Sl, $2, $3, $4

Two multiple-share:Mi = {SI, $3}, M2 = {S2, 84}

T o reconstruct the secret message, the user must access all four divided shares (m = n) together. N o w we use H P F - B F search, starting from the user node, the root o f the tree, to construct the allocation tree. By doing so, we obtain the allocation order o f shares which is Ml, M2, SI, $2, $3, $4. A tree that is constructed from a network and allocated shares into it is called an allocation tree. Fig. 8 depicts an allocation tree and the SSRP value for this communication network.

Results obtained from our algorithm are compared to those o f a R a n d o m Allocation algorithm. We computed the SSRP of all r a n d o m distributions. Table 1 summarizes the maximum and minimum SSRP o f simulation results based on 5000 samples. Node 2 e 4 - e 2 e 5 Node 3 Node 4

%

Node 5 e 7 e$ Node 6 Node 7 Fig. 7. An eight-node communication network.

(16)

124 C - Y . Lee et al. I Information Sciences 116 (1999) 109-127 Node

3e5

~

1 ~

( ~ e 7 4

SSRP(S) = 0.8395743

7 S ~

Fig. 8. Allocation tree for the eight-node network. 4.2. The pacific basin network

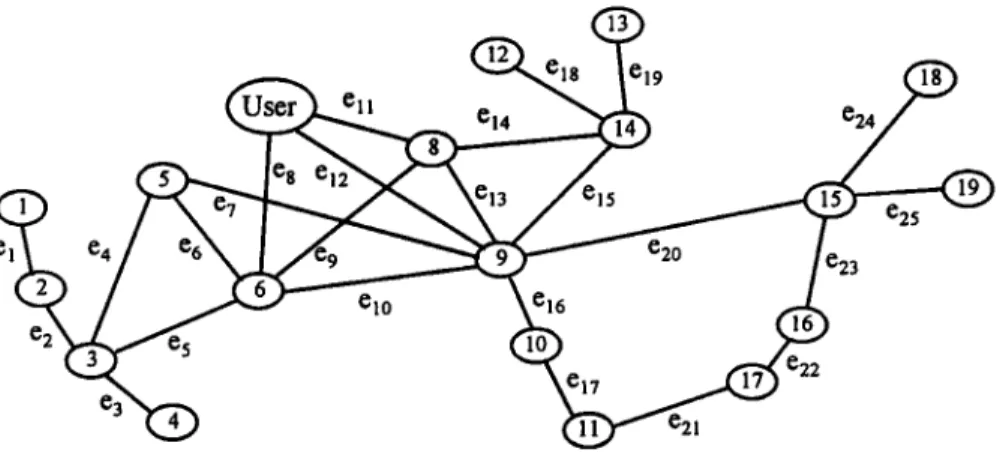
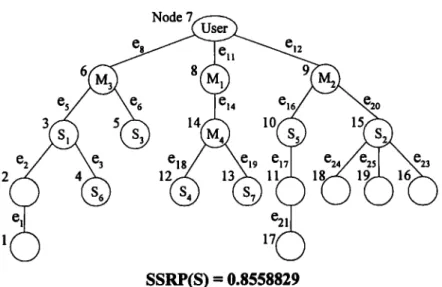
Fig. 9 displays the Pacific Basin network topology, which consists of nine-

teen sites and twenty-five communication links. Site 7 contains the user and the

other sites are considered share-storage locations. Let the probabilities of all

nodes and links being operational for the Pacific Basin network be 0.9.

In this example, we divide the secret into seven shares. Assume that seven

single-share and four multiple-share are to be allocated, and at least three

qualified multiple-share participants can recover the secret. They are listed

below.

The set of shares of secret S: Ss = {SI, $2, $3, $4, $5, $6, $7}

Seven single-share: Si, $2, $3, S4, S5, S6, 87

e3 e2 I

(17)

C - Y . Lee et al. I Information Sciences 116 (1999) 109-127 125

l!,

0211

1

SSl (S) - 0 . 8 5 5 8 8 2 9

Fig. 10. Allocation tree for the Pacific Basin network.

F o u r multiple-share: Mi = {$2, $4, $6, $7}, M2 = {Sl, $2, $3}, M3 = {$3, $4, $5, $6}, M4 = {SI, $5, $7}

The user must access all seven divided shares (m = n) together to recover the secret. We first use H P F - B F search, starting f r o m the user node, to reconstruct the network into a tree topology. Then we obtain the allocation order of shares which is MI, M3, M2, M4, SI, $3, $5, $2, $7, $4, $6. Fig. 10 depicts the allocation tree for the Pacific Basin network.

Results obtained f r o m our algorithm are c o m p a r e d to those of a R a n d o m Allocation algorithm. We c o m p u t e d the SSRP o f all r a n d o m distributions. Table 2 summarizes the m a x i m u m and m i n i m u m SSRP o f simulation results based on 5000 samples.

Tables 1 and 2 indicate that the proposed algorithm can obtain near optimal solutions. Result obtained from our algorithm in the Pacific Basin network indicates a slightly less than the optimal due to the use of the H P F - B F search algorithm. The H P F - B F algorithm can not guarantee that we will obtain the maximal n u m b e r of MSSTs. Exhaustive a p p r o a c h m a y be used to obtain the optimal solution with very expensive price. Previous investigations have demonstrated that exhaustive a p p r o a c h is an N P - h a r d problem [19,21]. Table 1

Simulation results of eight-node network

Network topology SSA algorithm Random algorithm

Eight-node network SSRP(S) = 0.8395743 Max. = 0.8395743

(18)

126 C-Y. Lee et al. / hformation Sciences 116 (1999) 109-127 Table 2

Simulation results of Pacific Basic network

Network topology SSA algorithm Random algorithm Pacific Basic network SSRP(S) = 0.8558829 Max. = 0.8669108

Min. = 0.3054878

5. Conclusion

Rapid expansion of the Internet is fueled by its ability to promote information sharing and to offer high availability. The Internet today is a wide- spread information infrastructure, reaching not only the technical fields of computer communications but throughout society. As the Internet has evolved, one of the major tasks is how to answer the request efficiently and reliably. Information on the Internet can be stored close to its normal point of use, thereby reducing both response times and communication costs. Effec- tively distributing shares to appropriate cites is the basic consideration for share assignment problem. In this paper, we present a probability model for secret sharing reconstruction and an algorithm for shares assignment and deal with two types of shares. Illustrative examples demonstrate the underlying concept of the model and the feasibility of our approach. According to simulation results, the proposed algorithm obtains approximate solutions efficiently. Particularly the (m, n)-threshold scheme is realized and evaluated based on the probability of secret sharing reconstruction.

References

[1] B. Schneier, Applied Cryptography: Protocols, Algorithms, and Source Code in C, 2nd Ed., Wiley, New York, 1996.

[2] R.L. Rivest, A. Shamir, L.M. Adleman, A method for obtaining digital signatures and public- key cryptosystems, Communication of the ACM 21 (2) (1978) 120-126.

[3] W.P. Lu, M.K. Sundareshan, Enhanced protocols for hierarchical encryption key manage- ment for secure communication in internet environments, IEEE Transaction on Communi- cations 40 (1992) 658-670.

[4] T. Hwang, W.C. Ku, Reparable key distribution protocols for internet environments, IEEE Transaction on Communications 43 (1995) 1947-1949.

[5] M. Ito, A. Saito, T. Nishizeki, Secret Sharing Scheme Realizing General Access Structure, Proc. IEEE Globecom'87, Tokyo, 1987, pp. 99-102.

[6] C.S. Laih, L. Harn, J.Y. Lee, T. Hwang, Dynamic threshold scheme based on the definition of cross-product in an N-dimensional linear space, Journal of Information Science and Engineering 7 (1991) 13-23.

[7] H.M. Sun, S.P. Shieh, On dynamic threshold schemes, Information Processing Letters 52 (1994) 201-206.

(19)

C - Y . Lee et al. I Information Sciences 116 (1999) 109-127 127 [9] G.R. Blakley, Safeguarding cryptographic keys, Proceedings of the AFIPS 1979 National

Computer Conference, vol. 48, New York, 1979, pp. 313-317.

[10] D.R. Stinson, An Explication of Secret Sharing Schemes Design, Codes and Cryptography, vol. 2, 1992, pp. 357-390.

[I 1] G.J. Simmons, An Introduction to Shared Secret and/or Shared Control Schemes and their Application, Contemporary Cryptology, IEEE Press, New York, 1991, pp. 441-497. [12] K.K. Aggarwal, S. Rai, Reliability evaluation in computer communication networks, IEEE

Transaction on Reliability R-30 (1981) 32-35.

[13] W.R. Kevin, Factoring algorithms for computing K-terminal network reliability, IEEE Transaction on Reliability R-35 (1986) 269-278.

[14] S. Hariri, C.S. Raghavendra, SYREL: A symbolic reliability algorithm based on path and cutset methods, IEEE Transaction Computers 36 (1987) 1224-1232.

[15] C.S. Raghavendra, V.K.P. Kumar, S. Hariri, Reliability analysis in distributed systems, IEEE Transaction Computers 37 (1988) 352-358.

[16] M.S. Lin, D.J. Chen, New reliability evaluation algorithms for distributed computing systems, Journal of Information Science and Engineering 8 (1992) 353-391.

[17] D.J. Chen, T.H. Huang, Reliability analysis of distributed systems based on a fast reliability algorithm, IEEE Transaction on Parallel and Distributed Systems 3 (2) (1992) 139-154. [18] A. Rosenthal, A computer scientist looks at reliability computations, in: Reliability and Fault

tree Analysis SLAM, 1975, pp. 133-152.

[19] L.G. Valiant, The complexity of enumeration and reliability problems, SIAM Journal of Computing 8 (1979) 410-421.

[20] O.R. Theologou, J.G. Carlier, Factoring and reductions for network with imperfect vertices, IEEE Transaction on Reliability 40 (1991) 210-217.

[21] M.O. Ball, Computational complexity of network reliability analysis: an overview, IEEE Transaction on Reliability R-35 (1986) 230-239.