A Secret-Sharing-Based Method for Authentication
of Grayscale Document Images via the Use of the
PNG Image With a Data Repair Capability
Che-Wei Lee, Student Member, IEEE, and Wen-Hsiang Tsai, Senior Member, IEEE
Abstract—A new blind authentication method based on the se-cret sharing technique with a data repair capability for grayscale document images via the use of the Portable Network Graphics (PNG) image is proposed. An authentication signal is generated for each block of a grayscale document image, which, together with the binarized block content, is transformed into several shares using the Shamir secret sharing scheme. The involved parameters are carefully chosen so that as many shares as possible are generated and embedded into an alpha channel plane. The alpha channel plane is then combined with the original grayscale image to form a PNG image. During the embedding process, the computed share values are mapped into a range of alpha channel values near their maximum value of 255 to yield a transparent stego-image with a disguise effect. In the process of image authentication, an image block is marked as tampered if the authentication signal computed from the current block content does not match that extracted from the shares embedded in the alpha channel plane. Data repairing is then applied to each tampered block by a reverse Shamir scheme after collecting two shares from unmarked blocks. Measures for protecting the security of the data hidden in the alpha channel are also proposed. Good experimental results prove the effectiveness of the proposed method for real applications.
Index Terms—Data hiding, data repair, grayscale document image, image authentication, Portable Network Graphics (PNG) image, secret sharing.
I. INTRODUCTION
D
IGITAL image is a form for preserving important infor-mation. However, with the fast advance of digital tech-nologies, it is easy to make visually imperceptible modifications to the contents of digital images. How to ensure the integrity and the authenticity of a digital image is thus a challenge. It is de-sirable to design effective methods to solve this kind of imageauthentication problem [1]–[3], particularly for images of
doc-uments whose security must be protected. It is also hoped that,
Manuscript received August 05, 2010; revised December 15, 2010 and April 07, 2011; accepted June 02, 2011. Date of publication June 20, 2011; date of current version December 16, 2011. This work was supported by the National Science Council under Project 99-2631-H-009-001. The associate editor coor-dinating the review of this manuscript and approving it for publication was Dr. Min Wu.
C. W. Lee is with the Department of Computer Science, National Chiao Tung University, Hsinchu 300, Taiwan (e-mail: paradiserlee@gmail.com).
W.-H. Tsai is with the Department of Computer Science, National Chiao Tung University, Hsinchu 300, Taiwan, and also with the Department of In-formation Communication, Asia University, Taichung 41354, Taiwan (e-mail: whtsai@cis.nctu.edu.tw).
Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Digital Object Identifier 10.1109/TIP.2011.2159984
Fig. 1. Binary-like grayscale document image with two major gray values.
if part of a document image is verified to have been illicitly al-tered, the destroyed content can be repaired. Such image content
authentication and self-repair capabilities are useful for the
se-curity protection of digital documents in many fields, such as important certificates, signed documents, scanned checks, cir-cuit diagrams, art drawings, design drafts, last will and testa-ments, and so on.
Document images, which include texts, tables, line arts, etc., as main contents, are often digitized into grayscale images with
two major gray values, one being of the background (including
mainly blank spaces) and the other of the foreground (including mainly texts). It is noted that such images, although gray valued in nature, look like binary. For example, the two major gray values in the document image shown in Fig. 1 are 174 and 236, respectively. It seems that such binary-like grayscale document images may be thresholded into binary ones for later processing, but such a thresholding operation often destroys the smooth-ness of the boundaries of text characters, resulting in visually unpleasant stroke appearances with zigzag contours. Therefore, in practical applications, text documents are often digitized and kept as grayscale images for later visual inspection.
In general, the image authentication problem is difficult for a binary document image because of its simple binary nature that leads to perceptible changes after authentication signals are em-bedded in the image pixels. Such changes will arouse possible suspicions from attackers. A good solution to such binary image authentication should thus take into account not only the secu-rity issue of preventing image tampering but also the necessity of keeping the visual quality of the resulting image. In this paper, we propose an authentication method that deals with binary-like grayscale document images instead of pure binary ones and si-multaneously solves the problems of image tampering detection and visual quality keeping.
Several methods for binary image authentication have been proposed in the past. Wu and Liu [4] manipulated the so-called flippable pixels to create specific relationships to embed data for authentication and annotation of binary images. Yang and Kot [5] proposed a two-layer binary image authentication method in which one layer is used for checking the image fidelity and the other for checking image integrity. In the method, a connec-tivity-preserving transition criterion for determining the flippa-bility of a pixel is used for embedding the cryptographic signa-ture and the block identifier. Later, Yang and Kot [6] proposed a pattern-based data hiding method for binary image authentica-tion in which three transiauthentica-tion criteria are used to determine the flippabilities of pixels in each block, and the watermark is adap-tively embedded into embeddable blocks to deal with the uneven embeddability condition in the host image. In the method pro-posed in [7], a set of pseudorandom pixels in a binary or halftone image are chosen and cleared, and authentication codes are ac-cordingly computed and inserted into selected random pixels. In Tzeng and Tsai’s method [8], randomly generated authenti-cation codes are embedded into image blocks for use in image authentication, and a so-called code holder is used to reduce image distortion resulting from data embedding. Lee et al. [9] proposed a Hamming-code-based data embedding method that flips one pixel in each binary image block for embedding a wa-termark, yielding small distortions and low false negative rates. Lee et al. [10] improved the method later by using an edge line similarity measure to select flippable pixels for the purpose of reducing the distortion.
In this paper, a method for the authentication of document images with an additional self-repair capability for fixing tam-pered image data is proposed. The input cover image is as-sumed to be a binary-like grayscale image with two major gray values like the one shown in Fig. 1. After the proposed method is applied, the cover image is transformed into a stego-image in the Portable Network Graphics (PNG) format with an addi-tional alpha channel for transmission on networks or archiving in databases. The stego-image, when received or retrieved, may be verified by the proposed method for its authenticity. Integrity modifications of the stego-image can be detected by the method at the block level and repaired at the pixel level. In case the alpha channel is totally removed from the stego-image, the entire re-sulting image is regarded as inauthentic, meaning that the fi-delity check of the image fails. The proposed method is based on the so-called -threshold secret sharing scheme proposed by Shamir [11] in which a secret message is transformed into
shares for keeping by participants, and when of the shares, not necessarily all of them, are collected, the secret message can be losslessly recovered. Such a secret sharing scheme is useful for reducing the risk of incidental partial data loss.
Conventionally, the concepts of “secret sharing” and “data hiding for image authentication” are two irrelevant issues in the domain of information security. However, in the proposed method, we combine them together to develop a new image au-thentication technique. The secret sharing scheme is used in the developed technique not only to carry authentication signals and image content data but also to help repair tampered data through the use of shares.
An issue in the self-repairing of tampered data at attacked image parts is that, after the original data of the cover image are embedded into the image itself for use in later data repairing, the cover image is destroyed in the first place and the original data are no longer available for data repairing, resulting in a con-tradiction. A solution to this problem is to embed the original image data somewhere else without altering the cover image it-self. The way proposed in this paper to implement this solution is to utilize the extra alpha channel in a PNG image to embed the original image data. However, the alpha channel of the PNG image is originally used for creating a desired degree of trans-parency for the image. Moreover, embedding of data into the alpha channel will create random transparency in the resulting PNG image, producing an undesirable opaque effect. One way out, as proposed in this paper, is to map the resulting alpha channel values into a small range near their extreme value of 255, yielding a nearly imperceptible transparency effect on the alpha channel plane.
Another problem encountered in the self-repairing of the original image data is that the data to be embedded in the
carrier are often large sized. For our case here with the alpha
channel as the carrier, this is not a problem because the cover image that we deal with is essentially binary-like, and thus, we may just embed into the carrier a binary version of the cover image, which includes much less data. Furthermore, through a careful design of authentication signals, a proper choice of the basic authentication unit (i.e., the unit of 2 3 image block) and a good adjustment of the parameters in the Shamir scheme, we can reduce the data volume of the generated shares effectively so that more shares can be em-bedded into the alpha channel plane. It is noted that, by the proposed method, the larger the number of shares is, the higher the resulting data repair capability becomes, as shown in the subsequent sections. Finally, we distribute the multiple shares
randomly into the alpha channel to allow the share data to have
large chances to survive attacks and to thus promote the data repair capability. To the best of our knowledge, this is the first
secret-sharing-based authentication method for binary-like
grayscale document images. It is also the first authentication method for such document images through the use of the PNG
image. Note that this method is not a secret-sharing technique but a document image authentication method.
The remainder of this paper is organized as follows: In Section II, the Shamir method on which the proposed method is based is first reviewed. In Section III, the details of the proposed method, including authentication signal generation, share data embedding, and tampered data repairing, are de-scribed. In Section IV, some discussions about the merits of the proposed method and the possible enhancements of security protection are given. Experimental results and a comparison of performances of the proposed method with others are shown in Section V, followed by conclusions in Section VI.
II. REVIEW OF THESHAMIRMETHOD FORSECRETSHARING
In the -threshold secret sharing method proposed by Shamir [11], secret in the form of an integer is transformed into shares, which then are distributed to participants for them
to keep; and as long as of the shares are collected, the orig-inal secret can be accordingly recovered, where . The detail of the method is reviewed in the following.
Algorithm 1: -threshold secret sharing.
Input: secret in the form of an integer, number of participants, and threshold .
Output: shares in the form of integers for the participants to keep.
Step 1. Choose randomly a prime number that is larger than . Step 2. Select integer values within the range of 0 through .
Step 3. Select distinct real values . Step 4. Use the following -degree polynomial to compute function values , called partial shares for
, i.e.,
(1)
Step 5. Deliver the two-tuple as a share to the th
participant where .
Since there are coefficients, namely, and through in (1) above, it is necessary to collect at least shares from the
participants to form equations of the form of (1) to solve these coefficients in order to recover secret . This explains the term threshold for and the name -threshold for the
Shamir method [11]. Below is a description of the just-men-tioned equation-solving process for secret recovery.
Algorithm 2: Secret recovery.
Input: shares collected from the participants and the prime number with both and being those used in Algorithm 1.
Output: secret hidden in the shares and coefficients used in (1) in Algorithm 1, where .
Steps.
Step 1. Use the shares
to set up
(2)
where .
Step 2. Solve the equations above by Lagrange’s interpolation to obtain as follows [12]:
Step 3. Compute through by expanding the following equality and comparing the result with (2) in Step 1 while regarding variable in the equality below to be in (2):
Step 3 in the above algorithm is additionally included for the purpose of computing the values of parameters in the pro-posed method. In other applications, if only the secret value need be recovered, this step may be eliminated.
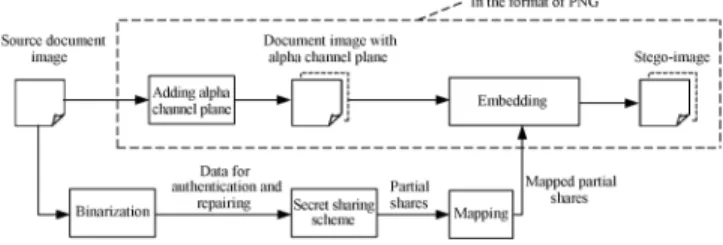
III. IMAGEAUTHENTICATION ANDDATAREPAIRING
In the proposed method, a PNG image is created from a bi-nary-type grayscale document image with an alpha channel plane. The original image may be thought as a grayscale
channel plane of the PNG image. An illustration of this process
of PNG image creation is shown in Fig. 2. Next, is bina-rized by moment-preserving thresholding [13], yielding a bi-nary version of , which we denote as . Data for authentica-tion and repairing are then computed from and taken as input to the Shamir secret sharing scheme to generate secret shares. The share values are subsequently mapped into a small range of alpha channel values near the maximum transparency value to create an imperceptibility effect. Finally, the mapped secret shares are randomly embedded into the alpha channel for the purpose of promoting the security protection and data repair ca-pabilities. Two block diagrams describing the proposed method are shown in Figs. 3 and 4.
Since the alpha channel plane is used for carrying data for authentication and repairing, no destruction will occur to the input image in the process of authentication. In contrast, con-ventional image authentication methods often sacrifice part of image contents, such as least significant bits (LSBs) or flippable pixels, to accommodate data used for authentication. In addi-tion, once a stego-image generated from a conventional method such as an LSB-based one is unintentionally compressed by a lossy compression method, the stego-image might cause false positive alarms in the authentication system. In contrast, the pro-posed method yields a stego-image in the PNG format, which, in normal cases, will not be further compressed, reducing the possibility of erroneous authentication caused by imposing un-desired compression operations on the stego-image.
A. Algorithm for Generation of a Stego-Image
A detailed algorithm for describing the generation of a stego-image in the PNG format of the proposed method is presented in the following.
Algorithm 3: Generation of a stego-image in the PNG format from a given grayscale image.
Fig. 2. Illustration of creation of a PNG image from a grayscale document image and an additional alpha channel plane.
Fig. 3. Illustration of creating a PNG image from a grayscale document image and an alpha channel.
Input: a grayscale document image with two major gray values and a secret key .
Output: stego-image in the PNG format with relevant data embedded, including the authentication signals and the data used for repairing.
Steps.
Stage I—generation of authentication signals.
Step 1. (Input image binarization) Apply moment-preserving thresholding [13] to to obtain two representative gray values
and , compute , and use as a threshold to binarize , yielding a binary version with “0” representing
and “1” representing .
Step 2. (Transforming the cover image into the PNG format) Transform into a PNG image with an alpha channel plane
by creating a new image layer with 100% opacity and no color as and combining it with using an image processing software package.
Step 3. (Beginning of looping) Take in an unprocessed raster-scan order a 2 3 block of with pixels
.
Step 4. (Creation of authentication signals) Generate a 2-bit
authentication signal with and
, where denotes the exclusive-or operation.
Stage II—creation and embedding of shares.
Step 5. (Creation of data for secret sharing) Concatenate the 8 bits of , , and through to form an 8-bit string, divide the string into two 4-bit segments, and transform the segments into two decimal numbers and , respectively.
Step 6. (Partial share generation) Set , , and in (1) of Algorithm 1 to be the following values: 1) (the smallest prime number larger than 15); 2) and ; and
3) , . Perform Algorithm 1 as a
(2, 6)-threshold secret sharing scheme to generate six partial shares through using the following equations:
(3)
where .
Step 7. (Mapping of the partial shares) Add 238 to each of through , resulting in the new values of through , respectively, which fall in the nearly total transparency range of 238 through 254 in the alpha channel plane .
Step 8. (Embedding two partial shares in the current block) Take block in corresponding to in , select the first two pixels in in the raster-scan order, and replace their values by and , respectively.
Step 9. (Embedding remaining partial shares at random pixels) Use key to select randomly four pixels in but outside
, which are unselected yet in this step, and not the first two pixels of any block; in the raster-scan order, replace the four pixels’ values by the remaining four partial shares through
generated above, respectively.
Step 10. (End of looping) If there exists any unprocessed block in , then go to Step 3; otherwise, take the final in the PNG format as the desired stego-image .
The possible values of through yielded by (3) above are between 0 and 16 because the prime number used there is 17. After performing Step 7 of the above algorithm, they become through , respectively, which all fall into a small interval of integers ranging from 238 to 254 with a width of 17 (the value of the prime number). The subsequent embedding of through
Fig. 4. Authentication process including verification and self-repairing of a stego-image in PNG format.
in such a narrow interval into the alpha channel plane means that very similar values will appear everywhere in the plane, resulting in a nearly uniform transparency effect, which will not arouse notice from an attacker.
The reason why we choose the prime number to be 17 in the above algorithm is explained here. If it was instead chosen to be larger than 17, then the aforementioned interval will be en-larged, and the values of through will become possibly smaller than 238, creating an undesired less transparent but
vi-sually whiter stego-image. On the other hand, the 8 bits
men-tioned in Steps 5 and 6 above are transformed into two decimal numbers and with their maximum values being 15 (see Step 5 above), which are constrained to lie in the range of 0 through (see Step 2 in Algorithm 1). Therefore, should
not be chosen to be smaller than 16. In short, is an
op-timal choice.
As to the choice of the block size, the use of a larger block size, such as 2 4 or 3 3, will reduce the precision of the resulting integrity authentication (i.e., the stego-image will be verified in a spatially coarser manner). On the other hand, it seems that a smaller block size such as 2 2 instead of 2 3 may be tried to increase the authentication precision. However, a block in the alpha channel with a size of 2 2 can be used to embed only four partial shares instead of six (see Steps 6–9 of Algorithm 3). This decreases the share multiplicity and thus reduces the data repair capability of the method. In short, there is a tradeoff between the authentication precision and the data repair capability, and our choice of the block size of 2 3 is a
balance in this aspect.
Finally, we use Fig. 5 to illustrate Steps 8 and 9 of Algo-rithm 3, where a core idea of the proposed method is presented, i.e., two shares of the generated six are embedded at the current block and the other four are embedded at four randomly selected pixels outside the block, with each selected pixel not being the first two ones in any block.
B. Algorithm for Stego-Image Authentication
A detailed algorithm describing the proposed stego-image authentication process, including both the verification and the self-repairing of the original image content, is presented in the following.
Fig. 5. Illustration of embedding six shares created for a block: Two shares embedded at the current block, and the other four in four randomly selected pixels outside the block, with each selected pixel not being the first two ones in any block.
Algorithm 4: Authentication of a given stego-image in the PNG format.
Input: stego-image , the representative gray values and , and the secret key used in Algorithm 3.
Output: image with tampered blocks marked and their data repaired if possible.
Stage I—extraction of the embedded two representative gray values.
Step 1. (Binarization of the stego-image) Compute , and use it as a threshold to binarize , yielding a binary version of with “0” representing and “1” representing .
Stage II—verification of the stego-image.
Step 2. (Beginning of looping) Take in a raster-scan order an unprocessed block from with pixel values through
, and find the six pixels’ values through of the corresponding block in the alpha channel plane of . Step 3. (Extraction of the hidden authentication signal) Perform the following steps to extract the hidden 2-bit authentication signal from :
(1) Subtract 238 from each of and to obtain two partial shares and of , respectively.
(2) With shares and as input, perform Algorithm 2 to extract the two values and (the secret and the first coefficient value, respectively) as output. (3) Transform and into two 4-bit binary values, concatenate them to form an 8-bit string , and take the first 2 bits and of to compose the hidden authentication
signal .
Step 4. (Computation of the authentication signal from the
current block content) Compute a 2-bit authentication signal
from values through of the six pixels of by
and .
Step 5. (Matching of the hidden and computed authentication
signals and marking of tampered blocks) Match and by checking if and , and if any mismatch occurs, mark , the corresponding block in , and all the partial shares embedded in as tampered.
Step 6. (End of looping) If there exists any unprocessed block in , then go to Step 2; otherwise, continue.
Stage III—self-repairing of the original image content
Step 7. (Extraction of the remaining partial shares) For each block in , perform the following steps to extract the remaining four partial shares through of the
corresponding block in from blocks in other than . (1) Use key to collect the four pixels in in the same order as they were randomly selected for in Step 9 of Algorithm 3, and take out the respective data , , , and
embedded in them.
(2) Subtract 238 from each of through to obtain through , respectively.
Step 8. (Repairing the tampered regions) For each block in marked as tampered previously, perform the following steps to repair it if possible.
(1) From the six partial shares through of block in corresponding to (two computed in Step 3(1) and four in Step 7(2) above), choose two of them, e.g., and , which are not marked as tampered, if possible.
(2) With shares and as input, perform Algorithm 2 to extract the values of and (the secret and the first coefficient value, respectively) as output.
(3) Transform and into two 4-bit binary values, and concatenate them to form an 8-bit string .
(4) Take the last 6 bits from , and check their binary values to repair the corresponding tampered pixel values of block by the following way:
if , set ; otherwise, set
where .
Step 9. Take the final as the desired self-repaired image .
IV. DISCUSSIONS
A. Merits of the Proposed Method
In addition to being capable of data repairing and being blind in nature (requiring no overhead other than the stego-image), the proposed method has several other merits, which are described in the following.
1) Providing pixel-level repairs of tampered image parts—As long as two untampered partial shares can be collected, a tampered block can be repaired at the pixel level by the proposed method. This yields a better repair effect for texts in images because text characters or letters are smaller in size with many curved strokes and need finer pixel-level repairs when tampered with.
2) Having higher possibility to survive image content
at-tacks—By skillfully combining the Shamir scheme, the
authentication signal generation, and the random embed-ding of multiple shares, the proposed method can survive malicious attacks of common content modifications, such as superimposition, painting, etc., as will be demonstrated by experimental results subsequently described.
3) Making use of a new type of image channel for data
hiding—Different from common types of images, a PNG
image has the extra alpha channel plane that is normally used to produce transparency to the image. It is differently utilized by the proposed method for the first time as a carrier with a large space for hiding share data. As a comparison, many other methods use LSBs as the carriers of hidden data.
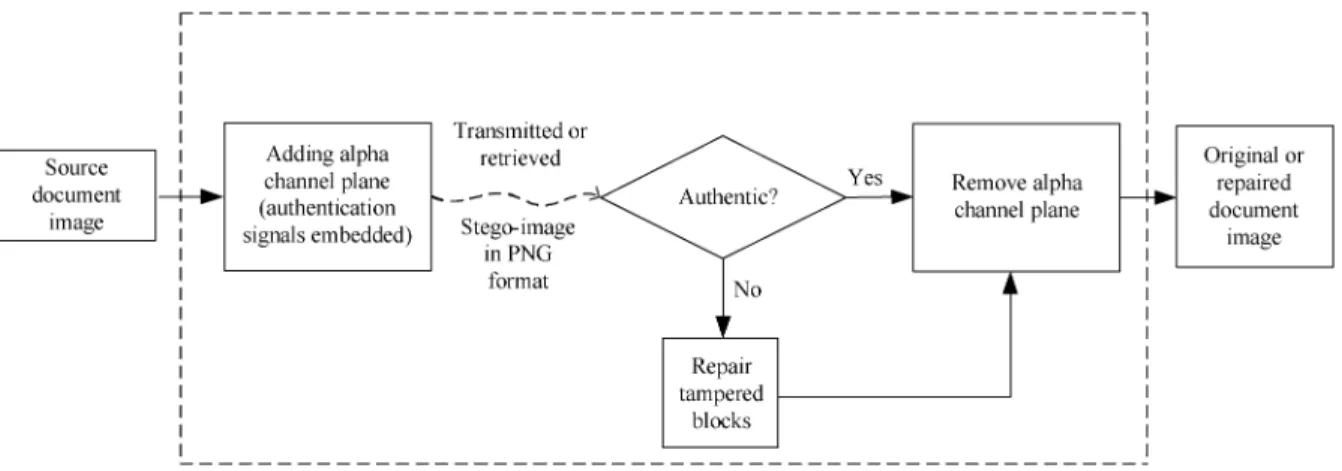
4) Causing no distortion to the input image—Conventional image authentication methods that usually embed authen-tication signals into the cover image itself will unavoidably cause destruction to the image content to a certain extent. Different from such methods, the proposed method utilizes the pixels’ values of the alpha channel for the purpose of image authentication and data repairing, leaving the orig-inal image (i.e., the grayscale channel) untouched and thus causing no distortion to it. The alpha channel plane may be removed after the authentication process to get the original image. Fig. 6 shows the framework of the proposed method in this aspect, and Fig. 7, shown for comparison, illustrates a conventional image authentication method.
5) Enhancing data security by secret sharing—Instead of hiding data directly into document image pixels, the pro-posed method embeds data in the form of shares into the alpha channel of the PNG image. The effect of this may be regarded as double-fold security protection, one fold con-tributed by the shares as a form of disguise of the original image data and the authentication signals and the other fold contributed by the use of the alpha channel plane,
Fig. 6. Framework of proposed document image authentication method.
Fig. 7. Framework of a conventional image authentication method.
which is created to be nearly transparent, as previously mentioned.
B. Measures for Security Enhancement
The secret key , which is used to randomize the pixel po-sitions for embedding the mapped partial shares through mentioned in Step 9 of Algorithm 3, provides a measure to pro-tect the shares. More specifically, as described in Algorithm 3, each block in the alpha channel plane may be regarded to con-sist of two parts, i.e., the first part including the first two pixels and the second including the remaining four. The first part of each block is used for keeping the first two partial shares and , and the second part for keeping the last four partial shares through of other blocks located at random posi-tions. Therefore, the probability of correctly guessing the lo-cations of all the embedded partial shares in a stego-image is , where is the size of the cover image, is the total number of blocks, each with
six pixels, and is the total number of
pixels in the blocks other than those in the first parts of all the blocks. This probability is obviously very small for common image sizes, meaning that a correct guess of the embedded par-tial shares is nearly impossible.
To enhance further the security of the data embedded in the stego-image, one additional measure is adopted in the proposed method (but not included in the previously proposed algorithms for clarity of algorithm descriptions). It is the randomization of the constant values of through used in Step 6 of Algorithm
3 and Step 3(2) in Algorithm 4. Specifically, in Step 3(2) in Al-gorithm 4, we can see that the input shares into AlAl-gorithm 2, i.e., and , can be easily forged, leading to the pos-sibility of creating fake authentication signals. To remedy this weakness, with the help of another secret key, we may choose these values of through for each block to be random within the allowed integer range of [11]. Then, the probability of correctly guessing all these values for all the blocks in a stego-image can be figured out to be
, which is also very small for common image sizes .
V. EXPERIMENTAL RESULTS ANDCOMPARISON
WITHOTHERMETHODS
A. Experimental Results Using a Document Image of a Signed Paper
The first results that we show here come from our experiments using a document image of a signed paper shown in Fig. 8(a). The result of applying Algorithm 3 to embed share data into Fig. 8(a) is shown in Fig. 8(b). As shown, the stego-image shown in the latter is visually almost identical to the cover image shown in the former, although the alpha channel content of the latter image includes the embedded data. As a comparison, Fig. 8(c) shows a result similarly created but without conducting Step 7 of Algorithm 3, which maps the original partial share values into the small interval of alpha channel values ranging from 238 through 254. An obvious opaque effect (nearly white) appears in Fig. 8(c).
We have also conducted image-modification attacks to the stego-images using two common image editing operations, namely, superimposing and painting. Tampered images yielded by the superimposing operation are presented in Figs. 7–10. It was observed from these experimental results that the superim-posing operation, such as that provided by the image editing software Adobe Photoshop or Corel PhotoImpact, destroys the content of the alpha channel values by replacing all the original alpha channel values at the attacked part with the new values of 255. Since the largest alpha channel values created by the proposed method is 254 (see Step 7 of Algorithm 3), all pixels with the unique values of 255 in the alpha channel plane may
Fig. 8. Experimental result of a document image of a signed paper. (a) Original cover image. (b) Stego-image with embedded data. (c) Another stego-image created without conducting partial share value mapping.
Fig. 9. Authentication result of a PNG document image of a signed paper at-tacked by superimposing a white rectangular shape on the signature in Fig. 6. (a) Tampered image yielded by the superimposing operation. (b) Result with tampered blocks detected and marked as gray. (c) Data repair result. (d) Data repair result with red dots indicating unrepaired tampered blocks. (e) Erroneous data repair result obtained with a wrong key.
be easily detected as tampered by a modified version of Step 3 of Algorithm 4, which we describe as follows:
Step 3 (Checking of superimposing attacks and extraction
of the hidden authentication signal) Check if both and are 255. If so, then regard the corresponding block in as attacked by superimposing, mark , , and all the partial shares embedded in as tampered, and go to Step 6; otherwise, perform the original operations of Step 3 of Algorithm 4.
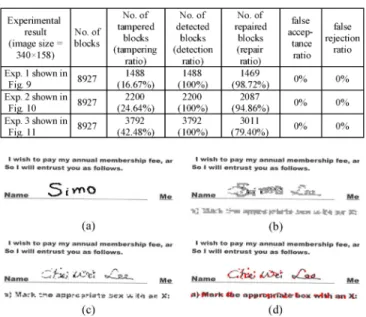
Fig. 9(a) shows the result of superimposing a white rectan-gular shape with a fake signature “Simo” on the genuine signa-ture “C. W. Lee” in the stego-image in Fig. 8(b). Fig. 9(b) shows the authentication result yielded by Algorithm 4, with the gray blocks indicating the detected tampered image parts. As shown, the superimposing rectangular part on the signature C. W. Lee has been completely detected. For each of the detected tampered blocks, if at least two untampered shares of it can be collected, its original content can be repaired, yielding the result shown in Fig. 9(c); otherwise, the tampered block is left unrepaired, as shown by the red dots in Fig. 9(d). Additionally, we show the data repair result obtained with a wrong key in Fig. 9(e). As
Fig. 10. Authentication result of the document image of a signed paper attacked by superimposing a white rectangular shape on a piece of text in Fig. 6(b). (a) Tampered image yielded by the superimposing operation. (b) Result with tam-pered blocks detected and marked as gray. (c) Data repair result. (d) Data repair result with red dots indicating unrepaired tampered blocks.
Fig. 11. Authentication result of the document image of a signed paper attacked by superimposing white raster rectangular shapes on the content in Fig. 6(b). (a) Tampered image yielded by the superimposing operation. (b) Result with tampered blocks detected and marked as gray. (c) Data repair result. (d) Data repair result with red dots indicating unrepaired tampered blocks.
shown, the repair work cannot be correctly accomplished; the result is just noise.
In Fig. 10(a), a text line under the signature in the signed paper disappeared after a white rectangular band was superim-posed on it. The results of image authentication and repairing are shown in Fig. 10(b) and (c), respectively. Although some blocks are not repaired, as indicated by the red dots in Fig. 10(d), the repair result of the text line is visually well recognizable. To test further the performance of the proposed method, we en-larged tampered areas during attacks, and a result is shown in Fig. 11. It is shown in the figure that the data repair result be-comes worse when the tampered area grows. This is reasonable because, when the tampered area becomes larger, fewer partial shares for data repairing will survive.
Table I includes the statistics of the performance of the pro-posed method shown by the above experimental results in terms of the five parameters, i.e., tampering, detection, repair,
false-acceptance, and false-rejection ratios, which are defined in the
following:
1) tampering ratio (the number of tampered blocks)/(the total number of blocks);
2) detection ratio (the number of detected blocks)/(the number of tampered blocks);
3) repair ratio (the number of repaired blocks)/(the number of detected blocks);
TABLE I
STATISTICS OFEXPERIMENTALRESULTS OFATTACKSUSINGSUPERIMPOSING
Fig. 12. Authentication result of the document image of a signed paper attacked by painting white color on the original signature and texts and replacing the signature by a fake one in Fig. 6(b). (a) Tampered image yielded by the painting operation. (b) Result with tampered blocks detected and marked as gray. (c) Data repair result. (d) Data repair result with red dots indicating unrepaired blocks.
4) false-acceptance ratio (the number of tampered blocks marked as untampered)/(the total number of tampered blocks);
5) false-rejection ratio (the number of untampered blocks marked as tampered)/(the total number of untampered blocks).
Note that the detection ratios are all 100% due to the ease in detection of the alpha channel values of 255 (using Step 3 described above) at image parts attacked by superimposing, as previously mentioned. Likewise, the alpha channel value corre-sponding to an intact block will not be 255 and can be easily checked to be so, yielding a false rejection rate of 0%. On the contrary, the alpha channel value corresponding to a tampered block is 255, which is easy to check as well, yielding a false ac-ceptance rate of 0%.
The content of a stego-image may be modified as well by the common operation of painting provided by well-known image editing software. Again, painting using Adobe Photoshop will replace the alpha channel values by 255, just like the superim-posing operation previously mentioned. However, it was found in this paper that the painting operation provided by Corel PhotoImpact does not change the alpha channel values. There-fore, we conducted experiments of stego-image attacks using this type of painting. Some results are given in Figs. 12–14. In Fig. 12, the painting operation was used to smear background gray values on the original signature “C. W. Lee” and write a fake signature “Simo” on it, as shown in Fig. 12(a). Fig. 12(b) shows the authentication result in which gray blocks were used again to indicate image parts where mismatching authentication signals were detected. Note that the smeared part (the signature C. W. Lee) and the added part (the signature “Simo”) have
Fig. 13. Authentication result of document image of a signed paper attacked by painting white color on the signature in Fig. 6(b). (a) Tampered image yielded by the painting operation. (b) Result with tampered blocks detected and marked as gray. (c) Data repair result. (d) Data repair result with red dots indicating unrepaired tampered blocks.
Fig. 14. Authentication result of the document image of a signed paper attacked by painting white color on the entire content of Fig. 6(b). (a) Tampered image yielded by the painting operation. (b) Result with tampered blocks detected and marked as gray. (c) Data repair result. (d) Data repair result with red dots indi-cating unrepaired tampered blocks.
been both revealed by the authentication process. In addition, it can be seen that some black parts exist within the gray region, meaning that these parts, although tampered, were not detected by the proposed method. This is due to the fact that there is actually a probability of 1/4 for an erroneous block authentication to occur because only two bits are created as the signal for block authentication (see Step 8 of Algorithm 3 or Step 5 of Algorithm 4). Although this probability seems large yet due to the use of the secret sharing technique for generating multiple shares, which are randomly embedded to survive attacks, correctly authenticated and repaired blocks still yield results with contents visually recognizable for image integrity judgment, as shown in Fig. 12(c) and (d).
In Fig. 13, the signature was removed by replacing it with the background gray value using painting. The results of image authentication and data repairing are shown in Figs. 13(b)–(d). Fig. 14 shows the results of removing the entire image content by painting. In both cases, the untouched content of the alpha channel values still yields repair results with their contents rec-ognizable to a certain degree.
It is noted here that, when a stego-image is tampered with by painting, which does not change the content of the alpha channel plane, the hidden authentication signals and data for re-pairing are not destroyed. Therefore, the computed authentica-tion signals from the alpha channel values are always true, and as long as the computed authentication signal is not identical to the extracted authentication signal for a block, the block will be
TABLE II
STATISTICS OFEXPERIMENTALRESULTS OFATTACKSUSINGPAINTING
OPERATIONS
Fig. 15. Authentication result of an image of a check in PNG format attacked by superimposing counterfeit number “750” located at the right side and text “Seven hundred fifty” located at the left side. (a) Original cover image. (b) Stego-image with embedded data. (c) Tampered image by the superimposing operation. (d) Result with tampered blocks detected and marked as gray. (e) Data repair result. (f) Unrepaired pixels shown in red (none for this example).
marked as having been tampered with. This explains why the false rejection rate is 0%. However, as previously mentioned, there is a probability of 1/4 for an erroneous block authentica-tion to occur because only 2 bits are created as the signal for block authentication, and this leads to a false acceptance ratio of at most 25%. These reasonings are verified by the performance statistics of Figs. 12–14 listed in Table II. The table also shows that the detection ratios are roughly around 75% as the attacked part becomes large (such as the case in Fig. 14), meeting the probabilistic expectation of 1/4 block authentication misses just mentioned. Also, the false acceptance ratios are smaller than 25%, as expected.
B. Experimental Results Using a Document Image of a Check
Experimental results yielded by the use of a document image of a check are shown in Figs. 15(a)–(f), where the cover doc-ument image and the stego-image generated by the proposed method are shown in Fig. 15(a) and (b), respectively. Both the amount-related text and numerals in the check image were mod-ified, as shown in Fig. 15(c). Fig. 15(d) shows that the tampering was successfully detected and marked as gray, and the result of data repairing is shown in Fig. 15(e). Finally, Fig. 15(f) shows the result of data repairing in which two unrepaired tampered
TABLE III
STATISTICS OFEXPERIMENTALRESULTS OFUSING ANIMAGE OF ACHECK
Fig. 16. Authentication result of a document image of a check in the form of PNG attacked by added noises. (a) Original cover image. (b) Stego-image with embedded data. (c) Tampered image with added noises. (d) Result with tam-pered blocks detected and marked as gray. (e) Data repair result. (f) Data repair result with red dots indicating unrepaired tampered blocks.
blocks are shown in red. Also, we show the statistics of this ex-periment in Table III.
At last, we put some noise onto the stego-image in Fig. 15(b) as an intended attack to the image, yielding the noisy image of Fig. 16(c), which was then authenticated by Algorithm 3 to get the result in Fig. 16(d) with detected tampered blocks marked in gray. The data repair result is shown in Fig. 16(e). As shown, some noise was not detected. The reason, as previously men-tioned, is again that there is a probability of 1/4 for an erroneous block authentication to occur. Fig. 16(f) shows the unrepaired pixels in red, and the statistics of this experiment is also included into Table III, where we can see that the false acceptance rate is about 17.12% resulting from the aforementioned undetected noise.
C. Comparison of Performances With Other Methods
A comparison of the capabilities of the proposed method with those of four existing methods is shown in Table IV. All but the proposed method will create distortion in the stego-image during the authentication process. More importantly, only the proposed method has the capability of repairing the tampered parts of an authenticated image.
Furthermore, among the methods with tampering localiza-tion capabilities at the block level such as [5], [8], and the pro-posed method, the propro-posed method provides a finer authenti-cation precision with the block size of 2 3. Specifically, the
TABLE IV
COMPARISON OFDOCUMENTIMAGEAUTHENTICATIONMETHODS
method in [5] needs larger macroblocks to yield pixel flippa-bilities for embedding authentication data. In the case of using smaller blocks, Tzeng and Tsai’s method [8] has a high pos-sibility to generate noise pixels, as mentioned in [6], and thus, they conducted experimental results with the larger block size of 64 64.
As to the distribution of authenticated image parts, because there exists no flippable pixel for use by the methods of [4]–[6] to embed data in all-white regions (such as marginal regions) of a document image, the distribution of authenticated image parts tends to be restricted to be on lines or strokes in the document, whereas the proposed method does not have this limitation. Nev-ertheless, in [4]–[6], the authenticity of an image part including such all-white regions can be still ensured by the use of crypto-graphic signatures embedded in other regions of the image. At last, the methods of [4]–[6] manipulate pixel flippability, and the method of [8] enforces pixel replacement for the aim of data embedding. The proposed method is the only one that makes use of the alpha channel plane instead of the bit plane.
VI. CONCLUSION
A new blind image authentication method with a data repair capability for binary-like grayscale document images based on secret sharing has been proposed. Both the generated authenti-cation signal and the content of a block have been transformed into partial shares by the Shamir method, which have been then distributed in a well-designed manner into an alpha channel plane to create a stego-image in the PNG format. The undesired opaque effect visible in the stego-image coming from embed-ding the partial shares has been eliminated by mapping the share values into a small range of alpha channel values near their max-imum transparency value of 255.
In the process of image block authentication, a block in the stego-image has been regarded as having been tampered with
if the computed authentication signal does not match that ex-tracted from corresponding partial shares in the alpha channel plane. For the self-repairing of the content of a tampered block, the reverse Shamir scheme has been used to compute the orig-inal content of the block from any two untampered shares. Mea-sures for enhancing the security of the data embedded in the alpha channel plane have been also proposed. Experimental re-sults have been shown to prove the effectiveness of the proposed method. Future studies may be directed to choices of other block sizes and related parameters (prime number, coefficients for se-cret sharing, number of authentication signal bits, etc.) to im-prove data repair effects. Applications of the proposed method to the authentication and the repairing of attacked color images may be also tried.
REFERENCES
[1] C. S. Lu and H. Y. M. Liao, “Multipurpose watermarking for image authentication and protection,” IEEE Trans. Image Process., vol. 10, no. 10, pp. 1579–1592, Oct. 2001.
[2] M. U. Celik, G. Sharma, E. Saber, and A. M. Tekalp, “Hierarchical watermarking for secure image authentication with localization,” IEEE
Trans. Image Process., vol. 11, no. 6, pp. 585–595, Jun. 2002.
[3] Z. M. Lu, D. G. Xu, and S. H. Sun, “Multipurpose image watermarking algorithm based on multistage vector quantization,” IEEE Trans. Image
Process., vol. 14, no. 6, pp. 822–831, Jun. 2005.
[4] M. Wu and B. Liu, “Data hiding in binary images for authentication and annotation,” IEEE Trans. Multimedia, vol. 6, no. 4, pp. 528–538, Aug. 2004.
[5] H. Yang and A. C. Kot, “Binary image authentication with tampering localization by embedding cryptographic signature and block identi-fier,” IEEE Signal Process. Lett., vol. 13, no. 12, pp. 741–744, Dec. 2006.
[6] H. Yang and A. C. Kot, “Pattern-based data hiding for binary images authentication by connectivity-preserving,” IEEE Trans. Multimedia, vol. 9, no. 3, pp. 475–486, Apr. 2007.
[7] H. Y. Kim and A. A?f, “Secure authentication watermarking for halftone and binary images,” Int. J. Imag. Syst. Technol., vol. 14, no. 4, pp. 147–152, 2004.
[8] C. H. Tzeng and W. H. Tsai, “A new approach to authentication of binary images for multimedia communication with distortion reduc-tion and security enhancement,” IEEE Commun. Lett., vol. 7, no. 9, pp. 443–445, Sep. 2003.
[9] Y. Lee, J. Hur, H. Kim, Y. Park, and H. Yoon, “A new binary image au-thentication scheme with small distortion and low false negative rates,”
IEICE Trans. Commun., vol. E90-B, no. 11, pp. 3259–3262, Nov. 2007.
[10] Y. Lee, H. Kim, and Y. Park, “A new data hiding scheme for binary image authentication with small image distortion,” Inf. Sci., vol. 179, no. 22, pp. 3866–3884, Nov. 2009.
[11] A. Shamir, “How to share a secret,” Commun. ACM, vol. 22, no. 11, pp. 612–613, Nov. 1979.
[12] C. C. Lin and W. H. Tsai, “Secret image sharing with steganography and authentication,” J. Syst. Softw., vol. 73, no. 3, pp. 405–414, Nov./ Dec. 2004.
[13] W. H. Tsai, “Moment-preserving thresholding: A new approach,”
Comput. Vis. Graph. Image Process., vol. 29, no. 3, pp. 377–393, Mar.
1985.
Che-Wei Lee (S’06) receives the B.S. degree in civil
engineering and the M.S. degree in electrical engi-neering in 2002 and 2005, respectively, from the Na-tional Cheng Kung University, Tainan, Taiwan. He has been working toward the Ph.D. degree in the De-partment of Computer Science from National Chiao Tung University.
His research interests include information hiding, image processing, and video technologies.
Wen-Hsiang Tsai (SM’84) received the B.S. degree
in electrical engineering from National Taiwan Uni-versity, Taipei, Taiwan, in 1973, the M.S. degree in electrical engineering from Brown University, Provi-dence, RI, in 1977, and the Ph.D. degree in electrical engineering from Purdue University, West Lafayette, IN, in 1979.
Since 1979, he has been with the National Chiao Tung University (NCTU), Hsinchu, Taiwan, where he is currently a Chair Professor of computer science. At the NCTU, he has served as the Head of the De-partment of Computer Science, the Dean of General Affairs, the Dean of Aca-demic Affairs, and a Vice President. From 1999 to 2000, he was the Chair of the Chinese Image Processing and Pattern Recognition Society of Taiwan and, from 2004 to 2008, the Chair of the Computer Society of the IEEE Taipei
Sec-tion in Taiwan. From 2004 to 2007, he was the President of Asia University, Taiwan. He has published 146 journal papers and 228 conference papers. His current research interests include computer vision, information security, video surveillance, and autonomous vehicle applications.
Dr. Tsai has been an Editor or the Editor-in-Chief of several international journals, including Pattern Recognition, the International Journal of Pattern
Recognition and Artificial Intelligence, and the Journal of Information Science and Engineering. He was a recipient of several awards, including the Annual
Paper Award from the Pattern Recognition Society of the USA; the Academic Award of the Ministry of Education, Taiwan; the Outstanding Research Award of the National Science Council, Taiwan; the ISI Citation Classic Award from Thomson Scientific; and more than 40 other academic paper awards from var-ious academic societies. He is a Life Member of the Chinese Pattern Recognition and Image Processing Society, Taiwan.