可公開驗證出價合法性的彌封式拍賣系統

全文

(1)國立交通大學資訊科學系碩士論文. 可公開驗證出價合法性的彌封式拍賣系統 A Sealed-Bid Auction with Publicly Verifiable Bid Validity. 研究生：黃佩琳指導教授：曾文貴. 中華民國. 教授. 九十三. 年六月.

(2) 可公開驗證出價合法性的彌封式拍賣系統 A Sealed-Bid Auction with Publicly Verifiable Bid Validity. 研究生：黃佩琳. Student：Pei-Lin Huang. 指導教授：曾文貴. Advisor：Wen-Guey Tzeng. 國立交通大學資訊科學系碩士論文. A Thesis Submitted to Department of Computer and Information Science College of Electrical Engineering and Computer Science National Chiao Tung University in partial Fulfillment of the Requirements for the Degree of Master in. Computer and Information Science June 2004 Hsinchu, Taiwan, Republic of China. 中華民國九十三年六月.

(3) 可公開驗證出價合法性的彌封式拍賣系統. 學生: 黃佩琳. 指導教授: 曾文貴博士. 資訊科學系國立交通大學. 摘要. 我們提出了一個具有可公開驗證出價合法性的拍賣系統。我們的想法結合了可驗證的加密知識簽章系統及公開金鑰之重新加密的證明。我們在對管理者的設計上，使用了兩種不同的管理者，註冊管理者及拍賣管理者，避免僅用一種管理者而使得管理者的權限過大。註冊管理者確認出價者的身分及其公開金鑰之間的對應關係，拍賣管理者則是管理拍賣時的一切活動。在我們的系統中，出價合法性不只包括了對出價價格的合法性更包括了出價者身分的合法性。我們最主要的設計便是使任何第三者都可以公開的驗證出價者出價的合法性卻又得不到與出價者身分及出價價格相關的任何訊息。如果任何人發現有不合法的出價都可以向拍賣管理者檢舉進而要求拍賣管理者撤銷該筆出價。因此我們的系統可以抵抗惡意的出價者提出不合法的出價干擾拍賣。除此之外，在我們的系統中，我們將出價者的簽章和出價價格結合當做出價內容。而我們系統中所使用的簽章簽名時需要出價者所記憶的密碼與儲存在出價者可攜式裝置中的部分私鑰一同配合使用，藉以增加安全性。關鍵字: 彌封式拍賣，可公開驗證，出價合法性. i.

(4) A Sealed-Bid Auction with Publicly Verifiable Bid Validity Student: Pei-Lin Huang. Advisor: Dr. Wen-Guey Tzeng. Department of Computer and Information Science National Chiao Tung University. Abstract. We proposed a sealed-bid auction with publicly verifiable bid validity, which is based on verifiable encryption of signature of knowledge and 1-out-of-P re-encryption proof of encryption keys. In our scheme, we have two semi-trusted managers, the registration manager RM and the auction manager AM. The registration manager RM guarantees the relationship between a bidder and his corresponding public key. The auction manager AM holds an auction and manages operations in an auction. Bid validity in our scheme contains the validity of both bidding price and the bidder. In our scheme, every one can verify the validity of the bid, but he can not get any information about the relation of the bidder’s identity and his bidding price. If there are invalid bids, anyone can ask the auction manager AM to revoke them. Hence, our scheme can prevent malicious bidders to disturb the auction. Besides, in our scheme, we combine the bidder’s signature and his bidding price as the bid. The signature we use here needs the bidder’s password memorized in his mind and the corresponding partial secret stored in his mobile device to increase the security. Keywords: Sealed-Bid Auction, Publicly Verifiable, Bid Validity. ii.

(5) 誌謝在此感謝我的指導老師曾文貴教授，在我碩士班兩年的學習過程中，不只讓我在學業上受益良多，更在生活上以及言行上給我許多教導。此外，我要感謝口試委員，交大資工系蔡錫鈞教授和清大資工系孫宏民教授，在論文上給予我許多良好的建議和指導，讓我的論文更加完善。除此之外我要感謝實驗室同學，尚宸、兆儀、振魁和坤杉的幫忙，實驗室學長成康、惠龍，學姊季穎的指導，以及實驗室學弟妹們在精神方面的鼓勵。最後，我要感謝我的家人，不論在精神或物質上都給予我極大的支持，讓我在無後顧之憂的情況下可以順利完成學業。在此，謹以此文獻給我所有我想要感謝的人。. iii.

(6) Table of Contents 摘要............................................................................................................. i Abstract ...................................................................................................... ii 誌謝........................................................................................................... iii Table of Contents ...................................................................................... iv Chapter 1 Introduction ................................................................................1 1.1 Auction Types ..................................................................................................2 1.2 The Properties of Sealed-Bid Auctions............................................................4 1.3 Thesis organization ..........................................................................................5. Chapter 2 Preliminaries ..............................................................................7 2.1 Interactive Zero-Knowledge Proof System of Knowledge..............................7 2.2 Signature of Knowledge ................................................................................ 11 2.3 Verifiable Encryption of Signature of Knowledge.........................................12 2.4 1-out-of-P Re-encryption Proof of Encryption Keys .....................................15 2.5 Previous Electronic Auction Schemes ...........................................................18. Chapter 3 A Sealed-Bid Auction with Publicly Verifiable Bid Validity ...22 3.1 Notations ........................................................................................................23 3.2 Our Basic Scheme..........................................................................................24. iv.

(7) 3.3 Analysis..........................................................................................................32 3.3.1 Security ...............................................................................................32 3.3.2 Properties ............................................................................................40. Chapter 4 Conclusion................................................................................43 Bibliography .............................................................................................45. v.

(8) Chapter 1 Introduction Electronic commerce has made a rapid progress in recent years. We can find out that more and more economic transactions are conducted through auctions. As we know, there are many famous auction websites, such as Yahoo!, eBay, and so on. In this thesis, we propose a sealed-bid auction with publicly verifiable bid validity. Our scheme is one of the first-price sealed-bid auctions. It has the properties of correctness, confidentiality, fairness, privacy, public verifiability, and robustness. Most important of all, our scheme can publicly verify the validity of the bids such that the invalid bids sent by malicious bidders can not disturb the auction. In our scheme, we combine the bidder’s signature and his bidding price as the bid using verifiable encryption of signature of knowledge, i.e. the bidder encrypts his signature using the encryption key corresponding to his bidding price, to let the others can verify the validity of the bidder, and then use 1-out-of-P re-encryption proof of encryption keys to make the others can not distinguish which encryption key the bidder uses. The signature we use here needs the bidder’s password memorized in his mind and the corresponding partial secret stored in his mobile device to increase the security. We use the idea proposed in [15] that use both password and partial secret to achieve strong security. It prevents the dictionary attack that if only the password is used. It also provides basic security that the attacker need guess the password if the mobile device is lost. Besides, similar to [6], in our scheme, we use two kinds of semi-trusted. 1.

(9) managers, the registration manager RM and the auction manager AM, to avoid concentration of all power in a single manager. The registration manager RM guarantees the relationship between a bidder and his corresponding public key. The auction manager AM holds auctions and manages operations in an auction. Bid validity in our scheme contains not only the validity of bidding price but also the validity of the bidder. In our scheme, every one can verify the bid validity but he can not get any information about the relation of the bidder’s identity and his bidding prices. If there exist some invalid bids, anyone can ask the auction manager AM to revoke those invalid bids. Hence, our protocol can prevent malicious bidders to disturb the auction.. 1.1Auction Types There are many different types of auctions. From [10], we can find out four basic types of auctions that are widely considered and analyzed: the increasing-price auction (also called English auction), the first-price sealed-bid auction, and the second-price sealed-bid auction (also called the Vickery auction), the decreasing-price auction (also called the Dutch auction). In the following, we describe their rules on the sale of a single item for simplicity. 1. The increasing-price auction In this type of auction, an item is offered at increasing prices. At the beginning, it may be offered at K tokens, and then at successive points of time i, it is bid at K + i * ∆ tokens (∆ may be a function of previous bids and other factors). At each time period, one or more bidders can bid for the item. At the end. 2.

(10) of the auction, the highest bidder takes the item and pays the price he bids. This type of auction has many disadvantages such as that the time needed to conduct the auction is potentially proportional to the price which the item is sold. Besides, this type of auction leaks a lot of information such that a careful observer will be able to conclude information about the price that each bidder is willing to pay for the auctioned item. However, the auction does have a very desirable feature: in economic terms, it allocates the item to the bidder with the highest valuation, since the bidder with the highest valuation will be willing to outbid all other bidders. 2.. The first-price sealed-bid auction In this type of auction, each bidder sends a sealed bid to an auctioneer who. opens all bids. The auctioneer determines the highest bid and sells the item to the highest bidder for his bidding price. Though, this type of auction can be executed in a single round of communication between the bidders and the auctioneer, it has some disadvantages. For example, the auctioneer will know the exact price that each bidder is willing to pay. Moreover, it does not support the optimal distribution of the item. In a sealed bid auction, bidders have beliefs about what others will bid. If a bidder believes that he has the highest bid and the second highest bid will substantially beneath that, then he has an incentive to lower his bid. For example, if he values an item at $1000, but he believes that the second highest bidder values the item at $500, then he is likely to place a bid slightly higher than $500. If the bidder is wrong about the distribution of other bids, then the final item will not be sold to him and the seller will be given a lower price than he would be. 3.

(11) given in the increasing-price auction. 3. The second-price sealed-bid auction It is a type of auction that combines the best features of the increasing-price bid and the sealed-bid auction. In this type of auction, each bidder submits a single bid to the auctioneer respectively, without seeing others’ bids, and the object is sold to the bidder who makes the highest bid. However, the price he pays is the second-highest bidder’s bid, or “second price”. This auction is sometimes called a Vickery auction after William Vickery, who wrote the seminal (1961) paper on auctions. 4. The decreasing-price auction This type of auction is similar to the increasing-price auction in which the bidding price varies over time. However, in this type of auction, the price decreases and at time i is K - i * ∆ tokens. The first bidder will take the item. This type of auction has the advantage of preserving maximum privacy, i.e. no information is revealed except the winning bid and bidder. However, like the increasing-price auction, it may be time consuming, and like the sealed-bid auction, it is not economically efficient.. 1.2 The Properties of Sealed-Bid Auctions After introducing the auction types, we present the properties of sealed-bid actions we concern. 1. Correctness If all parties act honestly, the winning price and the winner(s) are determined. 4.

(12) according to the auction rules correctly. 2. Confidentiality (of sealed bids) No bid information is revealed to any party (including the auctioneer) until the bid opening phase. 3. Fairness z. All bidders can look a proper polling on Internet.. z. After a bidder submits his bid, the bid cannot be modified. z. No bidder can deny his bid after he submits it. This is sometimes called non-deniability.. 4. Privacy (of losing bids) The losing bids remain confidential until the end of the auction even to the auctioneer. Differences between privacy and confidentiality of bids include z. Privacy only deals with losing bids;. z. Privacy is the confidentiality of the losing bids even after the bid opening phase.. 5. Public Verifiability The validity of the result of the auction can be publicly verified by every one. 6. Robustness Even if malicious bidders send invalid bids, the auction process is unaffected. In other words, the result of the auction is still correct even under the attack of malicious bidders.. 1.3 Thesis organization. 5.

(13) The remainder of his thesis is organized as follows: In Chapter 2, we shall briefly introduce the related theories and schemes. Then, we propose a sealed-bid auction with publicly verifiable bid validity and analyze its properties in Chapter 3. Finally, in Chapter 4, we conclude this thesis and indicate some future directions.. 6.

(14) Chapter 2 Preliminaries In this chapter, we will introduce some important theories and schemes that are involved in our scheme. In section 2.1, we will give the introduction about interactive zero-knowledge proof system of knowledge. In section 2.2, we will give basic idea of signature of knowledge. In section 2.3, we will introduce the definition of verifiable encryption of signature of knowledge. In section 2.4, we will state what 1-out-of-P re-encryption of encryption keys is and the difference between 1-out-of-P re-encryption proof and 1-out-of-P re-encryption proof of encryption keys. In section 2.5, we will introduce other auction schemes.. 2.1 Interactive Zero-Knowledge Proof System of Knowledge An interactive proof system. P, V. consists of two Turning machines P and V,. called “Prover” and “Verifier”, respectively. A typical interactive proof system has three rounds (commit-challenge-response). P first commits to a value. V then challenges on of two things: either the commitment has the right form or P knows the witness. P then responds to the challenge, while reveals no information about the witness. The real witness is randomized by the committed value in the first step. Consider the problem that the prover wants to prove that he knows the discrete. 7.

(15) logarithm x = log g y mod p of (p, q, y) where p = 2q+1, p, q are primes, g∈Gq-{1}, and g∈Gq. We want to show that P really know the value x. We call this type of proof “proof of knowledge”. In the setting of proof of knowledge, we require that the prover P be a polynomial-time probabilistic Turing machine (PTM) with a private input (witness). We consider the binary predicate Q such that for an input instance x of the right form, there is a corresponding secret ρ such that Q(x, ρ) = 1. The proof system of knowledge for Q is to show that the prover P knows a witness ρ for an input instance x. We use. P(ρ ),V ( x ) to denote the interactive proof system of P and V such that x. is the public common input and ρ is the prover P’s private input. If. P( ρ ),V (x ) = 1 ,. it means that the verifier V accepts that the prover P really knows the witness; otherwise, it means that the verifier rejects. Moreover, if we want to show that the interactive proof system of knowledge is zero-knowledge, we require that the interaction of the prover and the verifier can be simulated. Definition 2.1(Interactive Zero-Knowledge Proof System of Knowledge) Let P and V be both polynomial-time PTM’s. An interactive zero-knowledge proof system of knowledge. P,V. for the binary predicate Q satisfies the following. three conditions: 1. Completeness ∀x and ∀ρ with Q(x, ρ) = 1, Pr[ P( ρ ), V ( x ) = 1] = 1 . 2. Soundness. 8.

(16) There is a probabilistic (expected) polynomial-time knowledge extractor E such that ∀x∈Dom(Q), ∀P*. [. ] p(1x ) ⇒ Pr[E (P ,V , x ) = ρ , Q(x, ρ ) = 1] ≥ 1 − ε ( x ). Pr P * ( ρ ),V ( x ) = 1 ≥. *. *. *. where Dom(Q) means the domain of Q, p(⋅) is a polynomial, and ε(⋅) is negligible. 3. Zero-knowledge For each verifier V*, there is a simulator MV* such that the following two distributions are polynomially indistinguishable: z. { P(ρ ),V. z. {M (x )} V*. *. (x )}x∈Dom(Q ),Q ( x, ρ )=1 ;. x∈Dom (Q ). .. Notice in the definition 2.1, we have “for each verifier V*, there is a simulator”, while in reality, we usually use a stronger statement “there is a universal simulator M* for every verifier”. To be proof-oriented, the (universal) simulator simulates the “view” of the verifier V* interacting with P on common public input x and P’s private input is ρ. Here, “view” means the transcript (messages) exchanged by P and V*. Combining the universal simulator and the view concept, we have an alternative definition for zero-knowledge. Definition 2.2(Zero-Knowledge based on view and universal simulator) An interactive proof system of knowledge. P( ρ ),V (x ) is (computational). zero-knowledge if there is a universal simulator M* such that for every possible verifier V*, the following two distributions are polynomially indistinguishable, where. 9.

(17) M* runs in expected polynomial time depending on the run time of V*. z. {View(P(ρ ),V , x)}. z. {M (V , x )}. *. *. *. x∈Dom (Q ),Q ( x , ρ )=1. ;. .. x∈Dom(Q ). (. Furthermore, if the real transcript View P( ρ ),V * , x. (. ). and the simulated one. ). M * V * , x are identical, the system is called a perfect zero-knowledge interactive proof system of knowledge. From the above, we know that if we want to show that the interactive poof system of knowledge is zero-knowledge, we have to ensure the distributions of the simulated one and the real transcript are polynomially indistinguishable. For simplicity, we allow the simulator M* to output ⊥, denoting a failure round of simulation. We have another alternative definition for zero-knowledge. Definition 2.3(Zero-Knowledge failure). P( ρ ),V (x ) is (computational). An interactive proof system of knowledge. zero-knowledge if for every possible verifier V*, the following two distributions are polynomially indistinguishable: z. {View(P(ρ ),V , x)}. z. {m (V , x )}. *. *. (. where m* V * , x. *. ). x∈Dom(Q ). x∈Dom (Q ),Q ( x , ρ )=1. ;. .. (. ). (. ). the random valuable M * V * , x conditioned on M * V * , x ≠⊥ ,. [. ]. [. ]. that is, for all z, Pr m * (V * , x ) = z = Pr M * (V * , x ) = z M * (V * , x ) ≠⊥ and. [ (. ) ]. Pr M * V * , x ≠⊥ is non-negligible. In the following, we will give some basic idea of non-interactive proof system.. 10.

(18) In non-interactive proof system, the prover P produces a string of showing all the properties of an interactive proof system without interacting with the verifier. Hence, we need a random source to replace the verifier’s role in the interactive system. The more realistic is to use a secure (collision-resistant) hash function H in place of the verifier.. 2.2 Signature of Knowledge Signature of knowledge is a non-interactive zero-knowledge proof of knowledge, but being dependent on message m. For example, if the system’s public parameters are a large prime p where p=2q + 1, q is also a large prime, a generator g of Gq, and a secure (collision resistant) hash function H(⋅):{0,1}*→Zq. A user, said Bob, whose secret key is x and public key is y = g x mod p . Now, if Bob wants to sign for a message m, the pair (c, w) that. (. ). satisfies c = H m, p, g , y, g r mod p and w = r − cx where r∈RZq is the signature of knowledge x = log g y mod p on message m. By checking c = c’, we can verify the signature on m where. ( ). g w y c mod p = g r −cx g x. c. (. ). c'= H m, p, y, g w y c mod p . This is because. mod p = g r mod p .. Besides, in the above example, we can find out that we can also use the pair (a, w) to be the signature of knowledge x = log g y mod p for Bob on message m. The verifier can first compute c = H (m, p, g , y, a ) and then verify if a = g w y c mod p .. ( ). This is because g w y c mod p = g r −cx g x. c. mod p = g r mod p = a .. Similar to our scheme, the system’s public parameters are a large prime p where. 11.

(19) p = 2q + 1, q is a large prime, two generator g and h of Gq, and a collision resistant hash function H(⋅):{0,1}*→Zq. A user, said Bob, whose secret key contains the password π memorized in his mind and the corresponding partial secret α stored in his mobile device and public key is y = g α h π mod p . Now, if Bob wants to sign on message. m,. he. first. a = g r1 h r2 mod p ,. computes. c = H (m, p, g , h, y, a ) ,. w1 = r1 − cα , and w2 = r2 − cπ where r1,r2∈RZq, and then publishes (a, w1 , w2 ) as his signature of knowledge of α and π such that y = g α h π mod p on message m. The verifier can verify by first computing c = H (m, p, g , h, y, a ) and then verifying if a = g w1 h w2 y c mod p . This is because. (. g w1 h w2 y c mod p = g r1 −cα h r2 −cπ g α h π. ). c. mod p = g r1 h r2 mod p = a. 2.3 Verifiable Encryption of Signature of Knowledge Verifiable encryption is an encryption scheme where one can prove some property of data S, which is given in encrypted form. When the encryption scheme is secure, the encrypted data should reveal no information regard S. The setting of a verifiable encryption scheme is a two-party protocol between a prover P and a verifier V. Their common inputs are a public key Y, public value m, and a binary predicate Q. As a result of the protocol, V either rejects, or being convinced that the encryption of some value S under Y satisfies (m, S)∈Q. For example, Q is defined such that (m, S) ∈Q if and only if S is a signature of on message m with respect to some fixed public key Y. In other word, P convinces V that the encrypted data is a valid signature on m. The two-party protocol should ensure that V accepts an encryption of an invalid. 12.

(20) S with only negligible probability. Moreover, V should learn nothing except the fact that S is a valid signature with respect to m. The encryption key can belong to P, but typically belongs to a third party, and even in this case the third party should not need to take part in the protocol. In other words, P does not need to know the secret key (decryption key) X corresponding to public key (encryption key) Y. We find a definition of a secure verifiable scheme for a relation following [5]. Definition 2.4(Secure Verifiable Encryption) Let Q be a binary predicate and let LQ = {m ∃S : (m, S ) ∈ Q}. A secure verifiable encryption scheme for a binary predicate Q consists of a two party protocol and a recovery algorithm ℜ . We let VP (Y , m, k ) denote the output of V when interacting with P on input Y, m, and k, where k is a security parameter. We require that the following three properties hold: 1. Completeness ∀(Y, X)∈G(1k) and ∀m ∈ LQ , if P and V are honest then VP (Y , m, k ) ≠⊥ . 2. Validity For all prover P * and all (Y, X)∈G(1k), for every polynomials p(⋅) and all sufficiently large k, we have. [. ]. Pr (m, ℜ( X , b )) ∉ Q and b ≠⊥: b := VP* (Y , m, k ) <. 1 p(k ). 3. Computational Zero-Knowledge For every V* there exists a expected polynomial-time simulator MV* with black-box access to V* such that for all distinguishers A, all polynomials p,. 13.

(21) all m ∈ LQ , and all sufficiently large k, we have. [. ]. ( ). Pr A(Y , m, bi ) = i : (Y , X ) := G 1k ; b0 := M v* (Y , m, k ); b1 := VP* (Y , m, k ); i ∈ {0,1} <. 1 1 + 2 p(k ). In our scheme, P wants to convince the verifier V that he really knows the signature of knowledge, but V can not get any information about P’s secret. Hence, we give a modified definition of secure verifiable encryption of signature of knowledge in the version of interactive zero-knowledge proof system of knowledge introduced in section 2.1. Definition 2.5(Secure Verifiable Encryption of Signature of Knowledge). Let Q be the binary predicate such that for each instance x = (Y, m, EY(S)) of the right form, there is a corresponding secret ρ such that Q(x, ρ) = 1, where S is a valid signature with respect to m and EY(S) means the encryption of signature on message m with respect to some fixed public key Y. We require that the following three properties hold: 1. Completeness. ∀x and ∀ρ with Q(x, ρ) = 1, Pr[ P( ρ ), V ( x ) = 1] = 1 2. Validity. There is a probabilistic (expected) polynomial-time knowledge extractor E such that ∀x∈Dom(Q), ∀P*. [. ] p(1x ) ⇒ Pr[E(P*,V , x) = ρ , Q(x, ρ ) = 1] ≥ 1 − ε ( x ). Pr P * ( ρ ),V ( x ) = 1 ≥. *. *. where Dom(Q) means the domain of Q, p(⋅) is a polynomial, and ε(⋅) is negligible.. 14.

(22) 3. Computational Zero-Knowledge. If there is a universal simulator M* such that for every possible verifier V*, the following two distributions are polynomially indistinguishable: z. {View(P(ρ ),V , x)}. z. {m (V , x )}. *. *. where. *. x∈Dom(Q ),Q ( x , ρ )=1. x∈Dom(Q ). m* (V * , x ). ;. .. the. random. valuable. M * (V * , x ). conditioned. on. M * (V * , x ) ≠⊥ , that is, for all z,. [ (. ) ]. [ (. ). (. ) ]. Pr m * V * , x = z = Pr M * V * , x = z M * V * , x ≠⊥. [. and Pr M * (V * , x ) ≠⊥. ]. is. non-negligible.. 2.4 1-out-of-P Re-encryption Proof of Encryption Keys In order to have a witness indistinguishable protocol, we require an algorithm for random re-encryption of a bid, such as ElGamal encryption algorithm. Generally speaking, 1-out-of-P re-encryption proof defined in [11] means an efficient witness indistinguishable protocol, which a prover can prove that a given encrypted bid t, a encrypted list t1, .., tP, and a witness that tj is a re-encryption of t for j∈{1,…,P}, proves that indeed tj is a re-encryption of t without revealing index j. In most common electronic voting system, 1-out-of-P re-encryption proof is used for different messages. In our thesis, we use it for different encryption keys. We show the general 1-out-of-P re-encryption proof and the 1-out-of-P re-encryption proof of encryption keys in non-interactive form in the following.. 15.

(23) General 1-out-of-P re-encryption proof1 1. The prover generates a list {t1, …, tP} and publishes it. ( ) = (m Y. t1 = (T11 , T21 ) = m1Y r1 mod p, g r1 mod p. t 2 = (T12 , T22. r2. mod p, g r2 mod p. 2. #. ). ). (. t P = (T11 , T2 P ) = m P Y rP mod p, g rP mod p. ). (. 2. Suppose tj (1≤ j ≤P) is the re-encryption of t = (T1 , T2 ) = m j Y r mod p, g r mod p. (. ). ). i.e. (T1 j , T2 j ) = T1Y ε mod p, T2 g ε mod p .. 3. The prover computes ⎛⎛ T (1)(u i , vi ) = ⎜ ⎜⎜ 1i ⎜ ⎝ T1 ⎝. di. ⎞ ⎟⎟ Y ⎠. fi. di ⎞ ⎞ ⎟⎟ g f i mod p ⎟, ∀j , 1 ≤ i ≠ j ≤ P, d i , f i ∈R Z q ⎟ ⎠ ⎠ mod p , i = j , f i ∈R Z q. ⎛T mod p, ⎜⎜ 2i ⎝ T2. ) (ui , vi ) = (Y f mod p, g f (2) d = H ((T1 , T2 ), (T11 , T21 ),..., (T1P , T2 P ), (u1 , v1 ),..., (u P , v P )) (3) d j = d − ∑ d i mod q i. i. i≠ j. wi = f i − d i ε mod q, i = j wi = f i , ∀j , 1 ≤ i ≠ j ≤ P and publishes (d1 ,..., d P ), (w1 ,..., wP ) 4. The verifier verifies the proof as the follows (1) compute d = ∑ d i mod q = d1 + ...d P mod q i. (2) check if ⎛ (T1 , T2 ), (T11 , T21 ),..., (T1P , T2 P ), ⎜ d d1 ⎞ ⎛⎛ T d = H ⎜ ⎛⎜ ⎛ T11 ⎞ 1 w1 ⎛ T21 ⎞ w1 ⎟⎟ g mod p ⎟,..., ⎜ ⎜⎜ 1P ⎜ ⎜⎜ ⎟⎟ Y mod p, ⎜⎜ ⎟ ⎜ ⎝ T1 ⎜ ⎜ ⎝ T1 ⎠ ⎝ T2 ⎠ ⎠ ⎝ ⎝⎝ 1. The basic idea is log Y. T1 j T1. = ε = log g. T2 j T2. 16. dP. dP. ⎞ ⎛T ⎞ ⎟⎟ Y wP mod p, ⎜⎜ 2 P ⎟⎟ g wP ⎠ ⎝ T2 ⎠. ⎞ ⎟ ⎞⎟ mod p ⎟ ⎟ ⎟⎟ ⎠⎠.

(24) 1-out-of-P re-encryption proof of encryption keys2 1. The prover generates a list {t1, …, tP} and publishes it. ( ) = (mY. ) mod p ). t1 = (T11 , T21 ) = mY1r1 mod p, g r1 mod p t1 = (T12 , T22. r1 2. #. mod p, g r2. (. t1 = (T11 , T2 P ) = mYPrP mod p, g rP mod p. ). (. 2. Suppose tj (1≤ j ≤P) is the re-encryption of t = (T1 , T2 ) = mY jr mod p, g r mod p. (. i.e. (T1 j , T2 j ) = T1Y jε mod p, T2 g ε mod p. ). ). 3. The prover computes ⎛⎛ (1) (ui , vi ) = ⎜⎜ ⎜⎜ T1i T ⎝⎝ 1. di di ⎞ ⎞ ⎛ T2i ⎞ fi ⎟⎟ Yi mod p, ⎜⎜ ⎟⎟ g f i mod p ⎟, ∀j , 1 ≤ i ≠ j ≤ P, d i , f i ∈R Z q ⎟ ⎠ ⎝ T2 ⎠ ⎠ mod p, g f i mod p , i = j , f i ∈R Z q. ) (u i , vi ) = (Yi f (2) d = H ((T1 , T2 ), (T11 , T21 ),..., (T1P , T2 P ), (u1 , v1 ),..., (u P , v P )) (3) d j = d − ∑ d i mod q i. i≠ j. wi = f i − d i ε mod q, i = j wi = f i , ∀j , 1 ≤ i ≠ j ≤ P and publishes (d1 ,..., d P ), (w1 ,..., wP ) 4. The verifier verifies the proof as the follows (1) compute d = ∑ d i = d1 + ...d P mod q i. (2) check if ⎛ (T1 , T2 ), (T11 , T21 ),..., (T1P , T2 P ), ⎜ d d1 ⎞ ⎛⎛ T d = H ⎜ ⎛⎜ ⎛ T11 ⎞ 1 w1 ⎛ T21 ⎞ w1 ⎟⎟ g mod p ⎟,..., ⎜ ⎜⎜ 1P ⎜ ⎜⎜ ⎟⎟ Y1 mod p, ⎜⎜ ⎟ ⎜ ⎝ T1 ⎜ ⎜ ⎝ T1 ⎠ ⎝ T2 ⎠ ⎠ ⎝ ⎝⎝ 2. The basic idea is log Y j. T1 j T1. = ε = log g. T2 j T2. 17. dP. dP. ⎞ ⎛T ⎞ ⎟⎟ YPwP mod p, ⎜⎜ 2 P ⎟⎟ g wP ⎠ ⎝ T2 ⎠. ⎞ ⎟ ⎞⎟ mod p ⎟ ⎟ ⎟⎟ ⎠⎠.

(25) 2.5 Previous Electronic Auction Schemes We can find out that in most auctions, the validity of the bids is not verified or only verified by the auctioneer. z. The validity of the bids is not verified. Cachin [1] proposed a private bidding and auction scheme using the millionaire’s. protocol to determine who is richer without disclosing anything else about their wealth between two parties. This protocol employs two semi-trusted parties, T and V, as auction servers. All bidders and T are connected to V in secure channel. The server V chooses the random values for n instances of private bidding protocol. The bidders encrypt their bids, send them to the server V, but not involve further. The server V determines the highest bid through n successive queries to the server T who oblivious compares two bids, but who does not learn anything about the bids. At the end, V leans partial order of the bids, but not more. Noar[13] introduced a simple architecture for preserving the privacy of the bids of losing bidders while maintaining communication and computational efficiency. They employ an additional third party auction issuer that generate the programs for computing the auctions but does not take an active part in the protocol. Their protocol ensures that except collaboration of the auctioneer and the auction issuer, neither party gains any information about the bids, even after the auction is terminated. Moreover, bidders can verify the correctness of the auction. In [2], Kikuchi presented a new protocol for (M + 1)st-price auction, a style of auction in which the highest M bidders win and pay a uniform price, determined by (M + 1)st price. The scheme uses the verifiable secret sharing technique, where the. 18.

(26) bidding point is represented by the degree of a polynomial shared by the number of the auctioneers. In this scheme, there exist some drawbacks. For example, this scheme has an undesirable condition that the number of the auctioneers must be larger than the number of the bidding points, so it is difficult to set bidding points. Moreover, every one can anonymously disturb an auction by submitting an invalid bid. z. The validity of the bids is verified by the auctioneer before the opening phase. In this kind of auctions, the auctioneer often just verifies the bidding value (bidding format). Harkavy, Tygar and Kikuchi [10] described an auction service for secure. sealed-bid auctions, in which only the winning bid is disclosed. Both first-price and second-price auctions are supported. It is based on general techniques for secure ⎢ s − 1⎥ corrupted servers. multiparty computation and can tolerant up to t ≤ ⎢ ⎣ 3 ⎥⎦. However, the protocol is practical only for small value of s. In [9], Abe and Suzuli proposed the (M + 1)st-price auction using homomorphic encryption and mix and match technique. Their scheme realizes public verifiability of a winner and the wining bid. However, each bidder must compute K+1 zero-knowledge proofs in bidding, where K is the number of bidding points. Besides, in this protocol, the bidding price (bidding format) can be verified by every one. In [6], Omote and Miyaji proposed a second-price sealed-bid auction with public verifiability. In their scheme, they use the verifiable discriminant function of the p0-root to achieve public verifiability. z. The validity of the bids is verified by the auctioneer in the opening phase. In this kind of auctions, the auctioneer often just concern the validity of the. 19.

(27) winner. In [12], Franklin and Reiter use a set of distributed auctioneers and feature an innovative primitive called verifiable secret-sharing. Their protocol can also successfully prevent a single auctioneer altering a bid or throwing an auction to a single bidder. However, the confidentiality of bids of the bidders is not achieved, since the confidentiality is as essential as fairness. Besides, their protocol will result in all auctioneers knowing all bids after the auction is decided. The problem on privacy of losers is firstly point out by Kikuchi, Harkavy and Tyger[3]. The basic idea of the scheme is “secure addition”. However, the proposed scheme has a problem that the process of determining the winner does not work successfully when the winners with the same bidding price are multiple in the auction. In other words, this protocol can not work when two or more bidders bid at the same highest price. In [14], Liu, Wang and Wang, proposed a new multi-round sealed-bid auction scheme based on Shamir’s (t, n)-threshold secret sharing scheme. The protocol guarantees that no information about the losing bidders is leaked, and that the seller can collect the digital money from the winning bidder. In addition, the protocol support both first-price and second-price sealed-bid auction. In [4], Kikuchi, Hotta, Abe and Nakanishi modified [3] in which “mask” step are added to keep all bids private and only the winning bid and winner are determined by the collaboration of distributed servers. They improve the security of the protocol in [3] such that the second highest must be not known even by the winner. Watanabe and Imai [16] introduced a totally different trust third party, the off-line trusted third party (TTP), to achieve the universally verifiable auction scheme.. 20.

(28) They make use of a TTP in optimistic sense, i.e. the TTP takes part in the protocol only if one bidder cheats or simply crashes. However, this protocol has a disadvantage that all bidders have to participate in the auction at the beginning in the opening phase. In [8], Suzuki, Kobayashi and Morita presented the first sealed-bid auction scheme, which is only using multiple hash functions. This method drastically reduces the time taken for bidding and opening bids. However, it is not practical for opening all the bids if one of the auctioneers is distrust or can not release his secret seed. In [7], Peng, Boyd, Dawson and K. Viswanathan classified the published sealed-bid auction into four models according to how they deal with bid privacy and proposed a new model. Then give a comparison about the five models. In their model, they give another solution for bid privacy recovery, i.e. the registration authority an all the losing bidders cooperate to identify the dishonest winners by publishing their secrets, instead of a trust third party only being used. However, the drawback is that when the number of bidders involved is large, it is quite efficient to recover bid privacy. Hence, we propose a sealed-bid auction protocol with public verifiable bid validity. Every one in our protocol can verify the validity of the bid which contains the validity of the bidder and the validity of the bidding price. If anyone finds some invalid bids from malicious bidders, he can ask the auction manager AM to revoke them before the opening phase.. 21.

(29) Chapter 3 A Sealed-Bid Auction with Publicly Verifiable Bid Validity In this chapter, we propose a sealed-bid auction with publicly verifiable bid validity and analyze its security and properties. Here, bid validity contains not only the validity of the bidder but also the validity of the bidder’s bidding price. In our scheme, we combine the signature and the bidding price as the bid. The bidder generates his signature on message m using the signature of knowledge technique. The idea of our scheme is based on verifiable encryption of signature of knowledge and 1-out-of-P re-encryption proof of encryption keys. Our scheme uses two managers, the registration manager RM and the auction manager AM. RM is the registration manager who guarantees the relationship between a bidder and his corresponding public key. AM is the auction manager who holds auctions and manages operations in an auction. In our scheme, every one can verify the bidder’ s bid to check the bid validity, but can not get any information about the identities and bidding price of the bidders. If there exist some invalid bids, anyone can indicate them and ask the auction manager AM to revoke the invalid bids. The scheme can prevent some malicious bidders who send invalid bids to disturb the auction.. 22.

(30) 3.1 Notations Main notations used in our scheme are described as follows: RM. : the registration manager: z. handle the bidder’s registration;. z. manage RM’s bulletin board system (BBS) which publishes a list of public keys;. z. AM. declare the winner.. : the auction manager: z. manage the bidding phase;. z. manage AM’s bulletin board system (BBS) which publishes the computing process of bids;. z. declare the winning price.. m. : the unique message of the good; (e.q. the auction identity of the good). I. : the number of bidders;. i. : the index of bidders;. Bi. : a bidder whose index is i (i = 1,..,I );. p, q. : large primes such that p = 2q + 1;. g, h. : generators of Gq;. πi, αi. : Bi’s private key where πi is the password memorized in the bidder’s mind and αi is the corresponding partial secret stored in the bidder’s mobile device.. yi. : Bi’s public key where y i = g α i h π i mod p ;. P. : the number of prices;. 23.

(31) j. : the index of prices;. δj. : the j-th price (j = 1,…,P);. Xj. : the decryption key corresponding to the j-th price;. Yj. : the encryption key corresponding to the j-th price where Yj = g. xj. mod p for 1≤ j ≤P ;. Signk(). : a signature of knowledge signed by key k;. EY(). : ElGamal encryption with public key Y such that EY(W) = (G = gr mod p, M = WYr mod p) : ElGamal decryption with private key X such that. Dx(). DX(G, M) = M/Gx mod p H(). : a secure (collision-resistant) hash function : {0,1}*→Zq. (a ( ) , w( ) , w( ) ) : the signature of the bidder Bi on message m; (T ( ) , T ( ) ) : the bid of the bidder Bi; {(T ( ) , T ( ) ),..., (T ( ) , T ( ) )} : the bid list of the bidder Bi used for 1-out-of-P i. i. 1. i. 1. i 11. i 2. i. 2. i 21. i 1P. i 2P. re-encryption proof of encryption keys;. 3.2 Our Basic Scheme Our scheme has six main phases and their procedure is as follows: 1. Initialization. 2. Bidder registration. 3. Auction preparation. 4. Bidding. 5. Bid verification.. 24.

(32) 6. Opening. We describe them in detail in the following:. z Initialization The registration manager RM selects large primes p and q such that p = 2q + 1 and picks up g and h which are two generators of Gq. Besides, the registration. manager. RM. chooses. a. collision-resistant. hash. function. H(⋅):{0,1}*→Zq. Then the registration manager RM publishes p, g, h, and H on the RM’s BBS as system public parameters.. z Bidder registration When a bidder whose identity is Bob participates in an auction, he sends his identity and public key y with the signature Signα ,π ( y ) signed by signature of knowledge, using his password π memorized in his mind and the partial secret α stored in his mobile device, to the registration manager RM as a bidder registration. After all bidders finished their registrations, the registration manager RM publishes those public keys and their corresponding indexes on the RM’s bulletin boards system (BBS) but keeps the relation of the bidders’ identities and their public keys in secret. After the registration manager RM publishes the list of pairs of public keys and indexes, each bidder searches his corresponding index from the RM’s BBS using his public key.. z Auction preparation The auction manager AM publishes the price list {δ1,.. , δP} and the unique. 25.

(33) message m of the good on the AM’s BBS. Then the auction manager AM generates a pair of decryption key Xj and encryption key Yj corresponding to the price δj where X j ∈R Z q and Y j = g. xj. mod p for 1≤ j ≤P. Here, we have to. note that in order to stand for distinct price, so the decryption keys selected by the auction manager AM should be distinct. The auction manager AM holds the decryption keys and publishes the encryption keys on the AM’s BBS. After all those public keys are published, each bidder Bi (1≤ i ≤I) sends his index i and a list. {(T ( ) , T ( ) ),..., (T ( ) , T ( ) )} i 11. i 21. i 1P. i 2P. (. ). where (T1(ji ) , T2(ij) ) = EY j Signα i ,π i (m ). for 1≤ j ≤P to the AM’s BBS. In order to get the list. {(T ( ) , T ( ) ),..., (T ( ) , T ( ) )}, each bidder Bi has to follow i 11. i 21. i 1P. i 2P. the two steps described in Figure 3.1. First, each bidder has to make a signature on the unique message m of the good using signature of knowledge with his secrets which are the password πi memorized in his mind and the partial secret αi stored in his mobile device. After the generation of the signature, we can get. (a ( ) , w( ) , w( ) ) i. i. 1. i 2. to be the signature of knowledge of password πi and the partial. secret αi such that y i = g α i h π i mod p on message m for the bidder Bi. Second, he encrypts his signature using all the encryption keys published. Besides, it is worthy of remark that the generation of the signature of each bidder Bi only need to be done once. In other words, the signature of the bidder Bi used in an auction would be the same. Moreover, our encryption function only deals with the elements (w1(i ) , w2(i ) ) of the signature of the bidder Bi. We encrypt (w1(i ) , w2(i ) ) but let a (i ) be public. The bidder Bi will publish the element a (i ) of his signature in the bidding phase.. 26.

(34) Step 1: Each bidder Bi signs for the unique message m of the good to get a signature. Signα i ,π i (m ) :. 1. r1(i ) , r2(i ) ∈R Z q (i ) r (i ) a (i ) = g 1 1 h r2 mod p 2. c (i ) = H (m, p, g , h, y i , a (i ) ) 3. w1(i ) = r1(i ) − c (i )α i mod q w2(i ) = r2(i ) − c (i )π i mod q. Step 2: Each bidder Bi encrypts his signature P times using different encryption keys. (. ). EY j Signα i ,π i (m ) : ∀j , 1 ≤ j ≤ P 1. e (ji ) ∈R Z q T1(ji ) = g w1 h w2 (Y j ) j mod p (i ). T2(ij) = g. e (ji ). (i ). e(i ). mod p. Figure 3.1: Generation of the list of 1-out-of-P re-encryption proof of encryption keys. z Bidding Each bidder Bi selects his encryption key Y j corresponding to his bidding price δj. Bi then encrypts part of the signature (w1(i ) , w2(i ) ) generated in the auction preparation phase using the encryption key Y j described in Figure 3.2.. (. ). EY j w1(i ) , w2(i ) : 1 . e ( i ) ∈R Z q T1(i ) = g w1 h w2 (Y j ) (i ). (i ). e(i ). mod p. (i ). T2(i ) = g e mod p Figure 3.2: Generation of Bi’s bid. 27.

(35) After the encryption done, each bidder Bi sends his index i and (a (i ) , T1(i ) , T2(i ) ) to the AM’s BBS. Besides, Bi also has to provide two kinds of proofs (P+1 proofs) as showed in Figure 3.3. There are P proofs for the first kind proof and 1 proof for the second proof. The two kinds of proofs are described as follows: 1. P proofs for verifiable encryption of signature of knowledge of (i) r1(i ) , r2(i ) , αi, and πi such that w1(i ) = r1(i ) − c (i )α i (mod q ), w2(i ) = r2(i ) − c (i )π i (mod q ). to show that (a (i ) , w1(i ) , w2(i ) ) is valid signature.. (T ( ) , T ( ) ). (ii) e (ji ) such that. i 1j. i 2j. is the correct ciphertext of w1(i ) and w2(i ) .. (. ). The bidder Bi has to send c1(ij) , s1(ij) , s 2(i j) , s3(ij) , s 4(i j) , s5(ij) , ∀j , 1 ≤ j ≤ P , to AM’s BBS. 2. 1-out-of-P re-encryption proof of encryption keys such that no one except Bi can distinguish which encryption key is used. The bidder Bi has to show that for the encrypted bid. (T ( ) , T ( ) ) , i. 1. i. 2. there is a re-encryption in the. {(T ( ) , T ( ) ),..., (T ( ) , T ( ) )} i 11. i 21. i 1P. (T ( ) , T ( ) ) = (T ( )Y i 1j. i 2j. i. 1. i 2P. ε j. .. )(. i.e.. ). mod p, T2(i ) g ε mod p , T1(ji ) , T2(ij) is the re-encryption of. (T ( ) , T ( ) ). i. 1. i. 2. (i ) The bidder Bi has to send (c 21 ,..., c 2(iP) ), (z1(i ) ,..., z P(i ) ) to AM’s BBS.. 28.

(36) 1. verifiable encryption of signature of knowledge of r1(i ) , r2(i ) , αi, πi, and e (ji ) ∀j , 1 ≤ j ≤ P. (1). k1(ij) , k 2(ij) , k 3(ij) , k 4(ij) , k 5(ij) ∈R Z q d1(ij) = g. k1( ij ). d 2(ij) = g. k 2( ij). d 3(ij) = g. k 4( ij) k (i ). mod p, k3( ij). h. k5( ij). h. d 4(ij) = Y j 1 j g. mod p, mod p,. k 2( ij) − k 4( ij). (i ). h. k3( ij) − k 5( ij). mod p. (i ). (2). c1 j = H ( p, g , h, a , y i , T1(i ) , T2(i ) , d1(ij) , d 2(ij) , d 3(ij) , d 4(ij) ) (3). s1(ij) = k1(ij) − c1(ij)e (ji ) mod q, s 2(i j) = k 2(ij) − c1(ij) r1(i ) mod q, s3(ij) = k 3(ij) − c1(ij) r2(i ) mod q, s 4(i j) = k 4(ij) − c1(ij)c (i )α i mod q, s5(ij) = k 5(ij) − c1(ij)c (i )π i mod q. (. Sends c1(ij) , s1(ij) , s 2(i j) , s3(ij) , s 4(i j) , s5(ij). ). to AM’s BBS. 2. 1-out-of-P re-encryption proof of encryption keys. (1). ∀t ,1 ≤ t ≠ j ≤ P, c2(it) , f t (i ) ∈R Z q , (i ). (i ). c ⎞ ⎛ ⎛ T (i ) ⎞ c 2 t ⎛ T2(ti ) ⎞ 2 t f t(i ) f t( i ) ⎜ (i ) (i ) 1t ut , vt = ⎜ ⎜⎜ (i ) ⎟⎟ (Yt ) mod p, ⎜⎜ (i ) ⎟⎟ g mod p ⎟⎟ ; ⎟ ⎜ ⎝ T1 ⎠ ⎝ T2 ⎠ ⎠ ⎝ (i ) t = j , f t ∈R Z q ,. (. ). (u ( ), v( ) ) = ((Y ) mod p, g mod p ) (2). c ( ) = H ( p,q, g,h,T ( ) ,T ( ) ,(Y ,...,Y ),((T ( ) ,T ( ) ),...,(T ( ) ,T ( ) )),((u ( ) ,v ( ) ),...,(u ( ) ,v ( ) ))) i. f t( i ). i. t. t. f t( i ). j. i 2. i. 1. i. 2. P. 1. i 11. i 21. i 1P. i 2P. i. 1. i. 1. (3). c 2(i j) = c 2(i ) − ∑ c 2(it) mod q t≠ j. (i ). t = j , z t = f t (i ) − c 2(it)ε mod q; ∀t , 1 ≤ t ≠ j ≤ P, z t(i ) = f t (i ). (. )(. (i ) Sends c 21 ,..., c 2(iP) , z1(i ) ,..., z P(i ). ). to AM’s BBS. Figure 3.3: Two kinds of proofs for the bid of the bidder Bi. 29. i P. i P.

(37) z Bid verification This can be done by every one. If anyone finds invalid bids, then he can ask the auction manager AM to revoke them. If we want to verify the bid validity of the bidder Bi, we can do as follows: 1. Compute c (i ) = H ( m, p, g , h, y i , a (i ) ) 2. ∀j , 1 ≤ j ≤ P , compute ⎛ p, g , h, a (i ) , y i , T1(ji ) , T2(ij) , ⎞ ⎜ ⎟ (i ) (i ) s (i ) ⎜ (i ) c1(i ) s1(ij) ⎟ c s = H ⎜ T2 j g mod p, a (i ) 1 j g 2 j h 3 j mod p, ⎟ ⎜ (i ) c1(ij) s ( i ) s ( i ) ⎟ ( ( i) i) ( i ) ( i ) ( i ) i ( ) s 4 j s5 j (i ) c1 j (i ) s1 j s2 j s3 j 4j 5j ⎜ yc ⎟ g h p T Y g h g h p mod , / mod i 1 j j ⎝ ⎠. ( ). c~1(ji ). ( ) ( ) ( ). ( ). and verify if c~1(ji ) = c1(ij) . The idea of the verification is as Figure 3.4. (1) check e (ji ). (T ( ) ). c1( ij). i 2j. s1( ij). g. =g. c1( ij)e (ji ). g. k1( ij ) − c1( ij)e (ji ). =g. k1( ij ). = d1(ij) mod p. (2) check r1(i ) , r2(i ). (a ( ) ). c1( ij). i. g. s 2( i j). h. s3( ij). =g. c1( ij)r1( i ). h. c1( ij)r2( i ). g. k 2( ij) − c1( ij)r1( i ). h. k 3( ij) − c1( ij)r2( i ). =g. k 2( ij). h. k3( ij). = d 2(ij) mod p. (3) check α i and π i. (y ) c(i ) i. c1( ij). g. s 4( i j). h. s5( ij). =g. c1( ij)c ( i )αi. h. c1( ij)c ( i )π i. g. k 4( ij) − c1( ij)c ( i )αi. h. k5( ij) − c1( ij)c ( i )π i. =g. k 4( ij). h. k5( ij). = d 3(ij) mod p. (4) check w1(i ) = r1(i ) − c (i )α i , w2(i ) = r2(i ) − c (i )π i. (T ( ) ) (Y ) i 1j. =g. c1( ij). j. s1( ij). g. c1( ij)r1( i ) − c1( ij)c ( i )αi k (i ). = Yj 1j g. k 2( ij) − k 4( ij). h. h. s 2( i j). h. s3( ij). /g. s 4( i j). c1( ij)r2( i ) − c1( ij)c ( i )π i. h. s5( ij). c ( i )e. =g. c1( ij)w1( i ). k ( i ) − c1( ij)e (ji ). Yj 1j Yj 1j. h g. c1( ij)w2( i ). c ( i )e. k ( i ) − c1( ij)e (ji ). Yj 1j Yj 1j. k 2( ij) − c1( ij)r1( i ). h. k3( ij) − c1( ij)r2( i ). g. /g. k 2( ij) − c1( ij)r1( i ). k 4( ij) − c1( ij)c ( i )αi. h h. k 3( ij) − c1( ij)r2( i ). k5( ij) − c1( ij)c ( i )π i. k3( ij) − k5( ij). = d 4(ij) mod p. Figure 3.4: The idea of verifying the first proof in the bidding phase. 30. /g. k 4( ij) − c1( ij)c ( i )αi. h. k 5( ij) − c1( ij)c ( i )π i.

(38) (i ) 3. (1) Compute c 2(i ) = c 21 + ... + c 2(iP) mod q and. ⎞ ⎛ ⎟ ⎜ ⎟ ⎜ ⎜ p, g,h,T1(i ) ,T2(i ) ,(Y1 ,...,YP ), T11(i ) ,T21(i ) ,..., T1(Pi ) ,T2(Pi ) ,⎟ ⎟ ⎜ (i ) c (i ) ⎞ ⎟ (i ) c21 ⎜ ⎛⎜ ⎛ T11(i ) ⎞ 21 z (i ) i) ( ⎛ ⎞ T = H ⎜ ⎜ ⎜⎜ (i ) ⎟⎟ Y1 1 mod p, ⎜⎜ 21(i ) ⎟⎟ g z1 mod p ⎟⎟ ,...,⎟ ⎟ ⎟ ⎝ T2 ⎠ ⎜ ⎜⎝ ⎝ T1 ⎠ ⎠ ⎟ ⎜ (i ) (i ) c c ⎞ (i ) 2 P ⎟ ⎜ ⎛ ⎛ T (i ) ⎞ 2 P ( i ) (i ) ⎛T ⎞ ⎜ ⎜ ⎜ 1(Pi ) ⎟ YPz P mod p, ⎜ 2(Pi ) ⎟ g z P mod p ⎟ ⎟ ⎜T ⎟ ⎟⎟ ⎟ ⎜ ⎜⎜ ⎜⎝ T1 ⎟⎠ ⎝ 2 ⎠ ⎠ ⎠ ⎝⎝. ((. c~2(i ). ) (. )). (2) Verify if c~2(i ) = c2(i ). z Opening Starting from the highest price, the auction manager AM decrypts those ciphertexts starting on the downward prices as the follows: For X = XP, XP-1,… 1. ∀i, 1≤ i ≤ I , check if. (. )). (. a (i ) = D X EY (i ) Signα i ,π i (m ) ⋅ y ic j. (. ). = D X T1(i ) , T2(i ) ⋅ y ic =. T1(i ). (T ( ) ) i. X. ⋅ yic. (i ). (i ). (i ). (mod p ). 2. If the bid of the bidder Bi satisfies the equation, the auction manager AM publish the winning price is δ corresponding to the decryption key X and send the winner index i to the registration manager RM and then RM publishes the identity of the winner. 2. The AM publishes the decryption key X on AM’s BBS. If the winner’s identity is published, then the auction is terminated.. 31.

(39) 3.3 Analysis We shall analyze the security and the properties of our proposed scheme. We first describe the verifiable encryption of signature of knowledge is perfect zero knowledge and then state what properties our scheme has.. 3.3.1 Security In our scheme, we use verifiable encryption of signature of knowledge to confirm the validity of the bidders. Every one can verify the bids but can not get any information about the signature of knowledge of the bidders. Every one can be convinced that not only the signature of knowledge is of the right form but also the encrypted signature of knowledge is of the right form. We prove that the encryption used in our protocol is secure verifiable encryption of signature of knowledge in the following theorem.. Theorem 3.1. The verifiable encryption of signature of knowledge used in our scheme is secure with perfect zero-knowledge. Proof. We will prove that our protocol has the properties defined in definition 2.5 with perfect zero-knowledge. We first convert our verifiable encryption of signature of knowledge into interactive proof system instead of non-interactive proof system where V’s challenge is constant size. For simplicity, we remove the index i of the bidder and the index j for encryption keys. We describe the system as the follows and figure it out, then show the system IP-VESK is perfect zero-knowledge.. 32.

(40) Protocol IP-VESK. Input: (p, g, h, T1, T2, a, y); I.. P’s private input: (r1, r2, α, π, e); The following steps are run for q(n) times 1.. P→V : d1, d2, d3, d4 k1 , k 2 , k 3 , k 4 , k 5 ∈R Z q d1 = g k1 mod p d 2 = g k2 h k3 mod p d 3 = g k 4 h k5 mod p d 4 = Y k1 g k 2 − k 4 h k3 −k5 mod p. 2.. V→P : c1 c1∈{0,1}. 3.. P→V : s1, s2, s3, s4, s5 s1 = k1 − c1e mod q s 2 = k 2 − c1 r1 mod q s3 = k 3 − c1 r2 mod q s 4 = k 4 − c1cα mod q s5 = k 5 − c1cπ mod q. 4.. V verifies whether (1) check e ⇒ d1 = T2c1 g s1 mod p T2c1 g s1 = g c1e g k1 − c1e = g k1 = d1 (2) check r1, r2 ⇒ d 2 = a c1 g s 2 h s3 mod p a c1 g s 2 h s3 = g c1r1 hc1r2 g k 2 − c1r1 h k 3 − c1r2 = g k 2 h k 3 = d 2 (3) check α , π ⇒ d3 = (y c )c1 g s 4 h s5 mod p (y c )c1 g s 4 h s5 = g c1cα h c1cπ g k 4 − c1cα h k 5 − c1cπ = g k 4 h k 5 = d3 (4) check w1 = r1 − cα, w2 = r2 − cπ ⇒ d 4 = T1c1 Y s1 g s 2 h s3 /g s 4 h s5 mod p T1c1 Y s1 g s 2 h s3 /g s 4 h s5 = g c1 w1 h c1 w2 Y c1eY k1 − c1e g k 2 − c1r1 h k 3 − c1r2 /g k 4 − c1cα h k 5 − c1cπ = g c1r1 − c1cα h c1r2 − c1cπY c1eY k1 − c1e g k 2 − c1r1 h k 3 − c1r2 /g k 4 − c1cα h k 5 − c1cπ = Y k1 g k 2 − k 4 h k 3 − k 5 = d4. II.. V accepts if and only if all the above checks are correct. 33.

(41) P ( e, r1, r2, α, π ). p, g , h, T1 , T2 ,. V. a = g r1 h r2 mod p, y = g α h π mod p. I. The following steps are run for q(n) times k1 , k 2 , k 3 , k 4 , k 5 ∈R Z q d1 = g k1 mod p 1. d 2 = g k2 h k3 mod p d 3 = g k 4 h k5 mod p d 4 = Y k1 g k 2 − k 4 h k3 −k5 mod p d1 , d 2 , d 3 , d 4 2.c1∈{0,1} c1 s1 = k1 − c1e mod q s 2 = k 2 − c1 r1 mod q 3. s3 = k 3 − c1 r2 mod q s 4 = k 4 − c1cα mod q s5 = k 5 − c1cπ mod q s1 , s2 , s3 , s4 , s5 (1) check e ⇒ d1 = T2c1 g s1 mod p T2c1 g s1 = g c1e g k1 − c1e = g k1 = d1 (2) check r1, r2 ⇒ d 2 = a c1 g s 2 h s3 mod p a c1 g s 2 h s3 = g c1r1 hc1r2 g k 2 − c1r1 h k 3 − c1r2 = g k 2 h k 3 = d 2 (3) check α , π ⇒ d3 = (y c )c1 g s 4 h s5 mod p 4. (y c )c1 g s 4 h s5 = g c1cα h c1cπ g k 4 − c1cα h k 5 − c1cπ = g k 4 h k 5 = d3 (4) check w1 = r1 − cα, w2 = r2 − cπ ⇒ d 4 = T1c1 Y s1 g s 2 h s3 /g s 4 h s5 mod p T1c1 Y s1 g s 2 h s3 /g s 4 h s5 = g c1 w1 h c1 w2 Y c1eY k1 − c1e g k 2 − c1r1 h k 3 − c1r2 /g k 4 − c1cα h k 5 − c1cπ = g c1r1 − c1cα h c1r2 − c1cπY c1eY k1 − c1e g k 2 − c1r1 h k 3 − c1r2 /g k 4 − c1cα h k 5 − c1cπ = Y k1 g k 2 − k 4 h k 3 − k 5 = d4 II. V accepts if and only if all the above checks are correct.. 34.

(42) Completeness. If P has the knowledge of e, r1, r2, α, and π, then Pr [ P(e, r1 , r2 , α , π ), V ( p, g, h, a, y, T1 , T2 ) = 1] = 1. Validity. For any P*, the view of. P(e, r1 , r2 , α , π ), V ( p, g, h, a, y, T1 , T2 ) is. ⎛ D11 ,D 21 ,D31 ,D 41 ,C11 ,S11 ,S 21 ,S 31 ,S 41 ,S 51 ,..., ⎞ ⎜ ⎟ q(n) q(n) q(n) q(n) q(n) q(n) q(n) q(n) q(n) q(n) ⎟ ⎜ ,...,D ,D ,D ,D ,C ,S ,S ,S ,S ,S 1 2 3 4 1 1 2 3 4 5 ⎝ ⎠. (. where D1l ,D 2l ,D3l ,D 4l ,C1l ,S 1l ,S 2l ,S 3l ,S 4l ,S 5l. ). is the view of lth iteration.. Consider the extractor E ( P * (e, r1 , r2 , α , π ), V ( p, g, h, a, y, T1 , T2 )) to compute the secrets e, r1, r2, α, and π: 1. Run. P * (e, r1 , r2 , α , π ), V ( p, g, h, a, y, T1 , T2 ). to. get. an. instance. (d11 , d 21 , d 31 , d 41 , c11 , s11 , s 12 , s31 , s 14 , s51 ,..., d1i , d 2i , d 3i , d 4i , c1i , s1i , s 2i , s3i , s 4i , s5i , ..., d1q(n) , d 2q(n) , d 3q(n) , d 4q(n) , c1q(n) , s1q(n) , s 2q(n) , s3q(n) , s 4q(n) , s5q(n) ) 2. Randomly select l, 1≤ l ≤q(n) and rewind to the point (in lth iteration) where. d 11 , d 21 , d 31 , d 41 , c11 , s11 , s 12 , s 31 , s 14 , s 51 ,..., d 1i , d 2i , d 3i , d 4i is produced. Continue to run. P * (e, r1 , r2 , α , π ), V ( p, g, h, a, y, T1 , T2 ) from the rewinding point, set. c1l and obtain the rest s1i', s 2i ', s 3i', s 4i ', s 5i ',... Note that it is important to randomly select l in step 2, we describe the reason as follows. Let T be the computation tree of E ( P * (e, r1 , r2 , α , π ), V ( p, g, h, a, y, T1 , T2 )) and lth. 35.

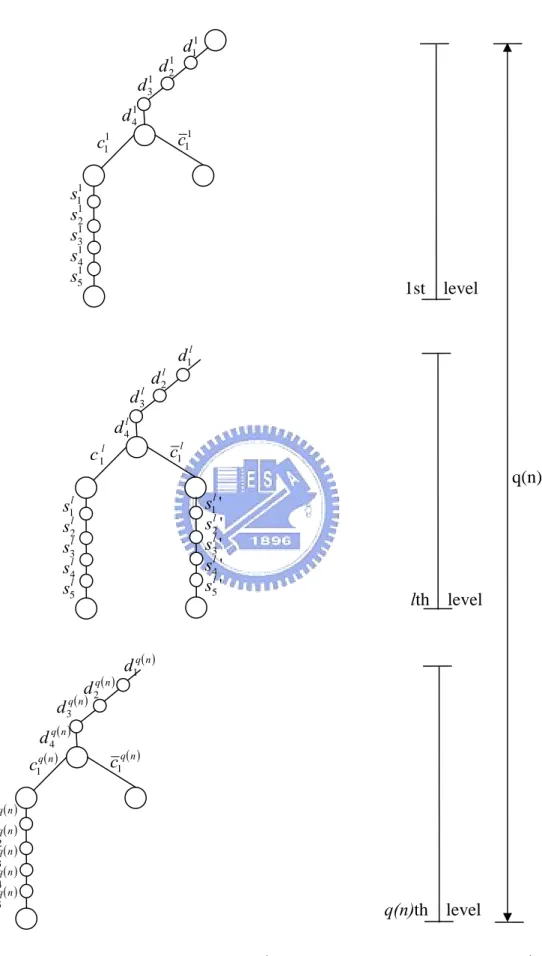
(43) level correspond to (D1l , D2l , D3l , D4l , C1l , S1l , S 2l , S 3l , S 4l , S 5l ) . There are total q(n) levels. Nodes in the q(n)th level are accepting nodes. Let Ni be the number of nodes in the ith level of T. There must be i such that Ni+1≥ probability of. 4 Ni since otherwise the accepting 3. P * (e, r1 , r2 , α , π ), V ( p, g, h, a, y, T1 , T2 ) is negligible. We call this. level heavy. For this i, at least a third of Ni nodes have two children, i.e. for each such node, c1i and c1i leads to acceptance. We figure out the computation tree T roughly as Figure 3.5. Now we consider the success probability of. (. ). E P * (e, r1 , r2 , α , π ), V ( p, g, h, a, y, T1 , T2 ) . The success probability of step 1 is 1/p(n).. The probability that l (in step 2) hits a heavy level is at least 1/q(n). The probability that we choose the rewinding point c1l (in step 2) is 1/3. Overall, the probability of getting the knowledge from (d11 , d 21 , d 31 , d 41 , c11 , s11 , s 12 , s31 , s 14 , s51 ,..., d1l , d 2l , d 3l , d 4l , 0 , s1l , s 2l , s3l , s 4l , s5l , ..., d1q(n) , d 2q(n) , d 3q(n) , d 4q(n) , c1q(n) , s1q(n) , s 2q(n) , s3q(n) , s 4q(n) , s5q(n) ). and (d11 , d 21 , d 31 , d 41 , c11 , s11 , s 12 , s31 , s 14 , s51 ,..., d1l , d 2l , d 3l , d 4l , 0, s1l ' , s 2l ' , s3l ' , s 4l ' , s5l ' ,...) is 1/(3p(n)q(n)). Thus, we can first compute c = H(m, p, g, h, y, a) and then compute e= s1l − s1l' , r1= s 2l − s 2l ' , r2= s 3l − s3l' , α=. 1 l 1 ( s 4 − s 4l ' ) , and π= (s5l − s5l ' ) with c c. probability 1/(3p(n)q(n)) for each execution E ( P * (e, r1 , r2 , α , π ), V ( p, g, h, a, y, T1 , T2 )) . If we repeated 3np(n)q(n) times, the success probability is at least 1-2-n.. 36.

(44) d. 1 3. d11. d 21. d 41 c11. c11 s11 s12 s31 s14 s51. 1st level. d. l 3. d 2l. d1l. d 4l c1l. c 1l. q(n) l 1 l 2 l 3 l 4 l 5. s s s s s. l 1 l 2 l 3 l 4 l 5. s s s s s. d d3q (n ) d 4q (n ). c1q (n ). q (n ) 2. ' ' ' ' '. lth level. d1q (n ). c1q (n ). s1q (n ) s2q (n ) s3q (n ) s4q (n ) s5q (n ). q(n)th level. Figure 3.5: The computation tree of E ( P * (e, r1 , r2 , α , π ), V ( p, g, h, a, y, T1 , T2 )). 37.

(45) Perfect Zero-knowledge. Let r be the q(n)-bit random string used by V*, V*’s view of interaction with P on. ( p, g, h, a, y, T1 , T2 ) is (r, d1, d2, d3, d4, c1, s1, s2, s3, s4, s5), where ( p, g, h, a, y, T1 , T2 ) is discarded for notational simplicity. We observe that c1 depends on ( p, g, h, a, y, T1 , T2 ) ,. ~ r, d1, d2, d3, and d4, that is, V * (( p, g, h, a, y, T1 , T2 ), r, d1 , d 2 , d 3 , d 4 ) = c1 . Therefore, for. any. ~ ~ ~ ~ ~ r , d 1 , d 2 , d 3 , d 4 , c~1 , ~ s1 , ~ s2 , ~ s3 , ~ s4 , ~ s5. fixed. ~ ~ ~ d1 = T2c1 g s1 mod p. ,. ~ ~ ~ ~ d 2 = a c1 g s2 h s3 mod p. with. constraints. ~ ~ ~ ~ d 3 = (y c )c1 g s4 h s5 mod p. ,. ,. and. ~ ~ ~ ~ ~ ~ ~ d 4 = T1c1 Y js1 g s2 h s3 /g s4 h s5 mod p , we have. [. (. ~ ~ ~ ~ r , d1 , d 2 , d 3 , d 4 , c~1 , ~ s1 , ~ s2 , ~ s3 , ~ s4 , ~ s5 Pr (R,D1 ,D2 ,D3 ,D4 ,C1 ,S1 ,S 2 ,S 3 ,S 4 ,S 5 ) = ~ =. )]. ~ ~ ~ ~ ~ ||V * ((p,g,h,a,y,T1 ,T2 ),~ r , d1 , d 2 , d 3 , d 4 ) = c~1|| 2 q(n) ⋅ q 3. The simulator M simulates the view. (( p, g, h, a, y, T , T ), ~r , d~ , d~ , d~ , d~ , c~ , ~s , ~s , ~s , ~s , ~s ) 1. 2. 1. 2. 3. 4. 1. 1. 2. 3. 4. 5. of. P (e, r1 , r2 , α , π ), V * ( p, g, h, a, y, T1, T2 ) as follows.. 1. Randomly select a bit string r’. 2. Randomly select a bit c1’’ and s1’, s2’, s3’, s4’, s5’∈Zq, and compute d1' = T2c1'' g s1' mod p, d 2' = a c1'' g s2' h s3' mod p, d 3' = (y c )c1'' g s4' h s5' mod p, d 4' = T1c1'' Y s1' g s2' h s3' /g s4' h s5' mod p. ~ 3. M runs V *((p, g, h, a, y, T1, T2 ), r', d1', d 2', d3', d 4') = c1' . If c1’ = c1’’, output. (r ' , d1 ' , d 2 ' , d3 ' , d 4 ' , c1 ' , s1 ' , s2 ' , s3 ' , s4 ' , s5 ') ; otherwise, output ⊥. In step 2, V* does not know M’s selection c1’’, which means. 38.

(46) ⎡ ~ * ⎛ ( p,g,h,a,y,T1 ,T2 ),r', ⎤ ⎞ ⎢V ⎜⎜ c1'' S1 C1'' S 2 S3 c C1'' S 4 S5 C1'' S1 S 2 S3 S 4 S5 ⎟⎟ = C1'' ⎥ C1'',S1,S 2 ,S 3 ,S 4 ,S 5 ⎢ ⎥⎦ ⎣ ⎝ T2 g ,a g h ,(y ) g h ,T1 Y g h /g h ⎠. Pr. =. = = =. ⎞ ⎛ ~ * ⎛ ( p,g,h,a,y,T1 ,T2 ),r', ⎞ ⎟ ⎜V ⎜ ⎟ 0 = ⎜ T 0 g s1' ,a 0 g s2' h s3' ,(y c )0 g s4' h s5' ,T 0Y s1' g s2' h s3' /g s4' h s5' ⎟ ⎟ ⎜ 1 ⎠ ⎝ 2 1 ⎟ ⎜ ⋅ ∑ 2 ⋅ q 5 s1',s2',s3',s4',s5' ⎜ ~ ⎛ ( p,g,h,a,y,T1 ,T2 ),r', ⎟ ⎞ ⎜ + V * ⎜⎜ 1 s1' 1 s2' s3' c 1 s4' s5' 1 s1' s2' s3' s4' s5' ⎟⎟ = 1 ⎟ ⎟ ⎜ ⎝ T2 g ,a g h ,(y ) g h ,T1 Y g h /g h ⎠ ⎠ ⎝ ~ ⎛ V * (( p,g,h,a,y,T1 ,T2 ),r',d1',d 2',d 3',d 4' ) = 0 ⎞ 1 ⎜ ⎟ 2 ⋅q ⋅ ∑ ⎜ ~ 5 ⎟ * 2⋅q d1',d 2',d 3',d 4' ⎜ + V (( p,g,h,a,y,T ,T ),r',d ',d ',d ',d ' ) = 1 ⎟ 1 2 1 2 3 4 ⎝ ⎠ 1 ⋅ q3 3 2⋅q 1 2. ~ ~ ~ ~ r , d1 , d 2 , d 3 , d 4 , c~1 , ~ s1 , ~ s2 , ~ s3 , ~ s4 , ~ s5 Hence, for ~ ⎡(R', D1', D2', D3' ,D4', C1', S1', S 2', S3', S 4', S5' ) ⎤ M (V*,( p, g, h, a, y, T1, T2 )) ≠⊥ ⎥ Pr ⎢ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ⎣⎢= r , d1 , d 2 , d 3 , d 4 , c1 , s1 , s2 , s3 , s4 , s5 ⎦⎥. (. ). ⎡(R', D1', D2', D3' ,D4', C1', S1', S 2', S3', S 4', S5' )⎤ ⎢ ⎥ ~ ~ ~ ~ r , d1 , d 2 , d 3 , d 4 , c~1 , ~ s1 , ~ s2 , ~ s3 , ~ s4 , ~ s5 Pr ⎢= ~ ⎥ ⎢and M (V*,( p, g, h, a, y, T , T )) ≠⊥ ⎥ 1 2 ⎣ ⎦. (. =. ). Pr[M (V*,( p, g, h, a, y, T1, T2 )) ≠⊥ ]. r , S1' = ~ s1 , S 2' = ~ s 2 , S 3' = ~ s3 , S 4' = ~ s 4 , S 5' = ~ s5 , C1'' = c1'' ] ⋅⎞ ⎛ Pr[R' = ~ ⎟ ⎜ ~ ~ ~ ~ ~ ~ ~ ⎟ ⎜ d1 = T2c1 g s1 mod p, d 2 = a c1 g s2 h s3 mod p, ⎟ ⎜ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ∑ c c1 s4 s5 mod p, d 4 = T1c1 Y s1 g s2 h s3 /g s4 h s5 mod p, ⎟ C1'' ⎜ d 3 = (y ) g h ⎟ ⎜ ~* ~ ~ ~ ~ ⎟ ⎜ V ( p,g,h,a,y,T1 ,T2 ),~ r , d1 , d 2 , d 3 , d 4 = c1'', c1'' = c~1 ⎠ ⎝ = ~ ~ ~ ~ ~* ~ ~ Pr V ( p,g,h,a,y,T1 ,T2 ),r , d1 , d 2 , d 3 , d 4 = c1'', c1'' = c1. (. [ (. ). 39. ). ].

(47) ~ ~ ~ ~ ~ ~ ~ d1 = T2c1 g s1 mod p, d 2 = a c1 g s2 h s3 mod p, ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ d 3 = (y c )c1 g s4 h s5 mod p, d 4 = T1c1Y s1 g s2 h s3 /g s4 h s5 mod p, ~ ~ ~ ~ ~ V * ( p,g,h,a,y,T1,T2 ),~ r , d1 , d 2 , d 3 , d 4 = c~1. (. 2 ⋅ 2 q(n) ⋅ q 3 1 2. =. =. ). (. ). ~ ~ ~ ~ ~ V * ( p,g,h,a,y,T1 ,T2 ),~ r , d 1 , d 2 , d 3 , d 4 = c~1. 2 q(n) ⋅ q 3 ~ ~ ~ ~ ~ ~ ~ for d1 = T2c1 g s1 mod p, d 2 = a c1 g s2 h s3 mod p, ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ d 3 = (y c ) c1 g s4 h s5 mod p, d 4 = T1c1 Y s1 g s2 h s3 /g s4 h s5 mod p. The expected run time of M (V*,( p, g, h, a, y, T1, T2 )) is 2⋅timeV*(p, g, h, a, y, T1, T2), which is polynomial bounded. Therefore, the protocol is secure with perfect zero-knowledge.. 3.3.2 Properties We can find out that our scheme has the properties of correctness, confidentiality, fairness, privacy, public verifiability, and robustness. And most important of all, our scheme has the property of publicly verifiable bid validity. We describe them more detail in the following. z. Correctness. If all parties act honestly, the winning price and the winner (s) are determined according to our auction rule correctly. z. Confidentiality. We use the registration manager RM to hold the relationship between the bidder’s identity and his public key and the auction manager AM to hold the. 40.

(48) decryption keys for all bidding prices. Hence, even every one can verify the validity of the bids, but no one can get any information about the bidder’s identity and his bidding price. z. Fairness. All bidders can look a proper polling on Internet and after each bidder submits his bid, he can not modify it. Besides, each bid contains the bidder’s signature and no bidder can deny. z. Privacy. In our scheme, even after the opening phase, the bidding prices of the losing bidders can be kept secret since the remainders of the decryption keys are not published by the auction manager AM. z. Public Verifiability. In the opening phase, the auction manager AM would publish the decryption keys corresponding to the bidding prices downwards until the winner is published. Every one can verify the result of the auction with those decryption keys published. Hence, the validity of the result in our auction can be publicly verified by every one. z. Robustness. In our scheme, every one can verify the validity of the bid. If there exist some invalid bids, anyone can ask the auction manager AM to revoke those invalid bids. Hence, our scheme can prevent malicious bidder sending invalid bids to disturb the auction. In other word, even there are invalid bids from malicious bidders, the result of our scheme is correct. z. Public Verifiable Bid Validity. 41.

(49) In our scheme, every one can verify the validity of the bidder and the validity of the bidder’s bidding price with the proofs for verifiable encryption of signature of knowledge.. 42.

(50) Chapter 4 Conclusion In this thesis, we have proposed a sealed-bid auction with publicly verifiable bid validity. Our scheme is one of the first-price sealed-bid auctions. It has the properties of correctness, confidentiality, fairness, privacy, public verifiability, and robustness. Most important of all, in our scheme, every one can publicly verify the validity of the bid such that malicious bidders can not send invalid bids to disturb the auction. In our scheme, we combine the bidder’s signature and his bidding price as the bids using verifiable encryption of signature of knowledge and then use 1-out-of-P re-encryption proof of encryption keys. The signature we use here needs the bidder’s password memorized in bidder’s mind and the corresponding partial secret stored in his mobile devices to increase the security. Bid-validity in our scheme contains not only the validity of bidding price but also the validity of the bidder. In our scheme, every one can verify the bid validity but he can not get any information about the bidder’s identity and his bidding price. If there exist some invalid bids, anyone can ask the auction manager AM to revoke those invalid bids. Hence, our protocol can prevent malicious bidder sending invalid bids to disturb the auction. In our scheme, if the registration manager RM is attacked, only the information about the relation of the bidder’s identity and his public key is leaked, no one can have the idea about the bidding price that the bidder bids. If the auction manager AM is attacked, only the information about the bidding price of the bidder is leaked, no. 43.

(51) one can get the idea about the relation between the bidder’s identity and his public key. In other words, in our scheme, if one manager is attacked, our scheme can achieve weak confidentiality. But if two managers collaborate, they can know the relation of the bidding price and the corresponding bidder’s identity. Besides, in the bidding phase of our scheme, each bidder has to send his bid with (P+1) proofs. The number of proofs needs to depend on the size of the price list. Hence, in future work, we hope to avoid the collaboration attack of the managers and reduce the number of proofs.. 44.

(52) Bibliography [1] C. Cachin, “Efficient private bidding and auctions with an oblivious third party,” In Proceedings of the 6th ACM conference on Computer and communications security, pages 120-127. ACM Press, 1999. [2] H. Kikuchi, “(M + 1)-st price auction,” In Paul F. Syverson, editor, Financial Cryptography, 5th International Conference, FC 2001, volume 2339 of Lecture Notes in Computer Science, pages 351-363. Springer-Verlag, 2002. [3] H. Kikuchi,M. Harkavy, and J. D. Tygar, “Multi-round anonymous auction protocols,” In Proceedings of the First IEEE Workshop on Dependable and Real-Time E-Commerce Systems, pages 62-69, 1998. [4] H. Kikuchi, S. Hotta, K.Abe, and S. Nakanishi, “Distributed auction servers resolving winner and winning bid without revealing privacy of bids,” In Proceedings of International Workshop on Next Generation Internet (NGITA 2000), pages 307-312, 2000. [5] J. Camenisch and I. Damgard, “Verifiable encryption, group encryption, and their Applications to separable group signatures and signature sharing schemes,” In Tatsuaki Okamoto, editor, Advances in Cryptology - ASIACRYPT 2000, volume 1976 of Lecture Notes in Computer Science, pages 331-345. Springer-Verlag, 2000. [6] K. Omote and A. Miyaji, “A second-price sealed-bid auction with verifiable discriminant of p0-th root,” In Matt Blaze, editor, Financial Cryptography, 6th. 45.

(53) International Conference, FC 2002, volume 2357 of Lecture Notes in Computer Science, pages 57-71. Springer-Verlag, 2003. [7] K. Peng, C. Boyd, E. Dawson, and K. Viswanathan, “Five sealed-bid auction models,” In Proceedings of the Australasian information security workshop conference on ACSW frontiers 2003, pages 77-86. Australian Computer Society, 2003. [8] K. Suzuki, K. Kobayashi, and H. Morita, “Efficient sealed-bid auction using hash chain,” In Dongho Won, editor, Information Security and Cryptology - ICISC 2000, volume 2015 of Lecture Notes in Computer Science, pages 183-191. Springer-Verlag, 2000. [9] M. Abe and K. , “M + 1-st price auction using homomorphic encryption,” In David Naccache and Pascal Paillier, editor, Public Key Cryptography, 5th International Workshop on Practice and Theory in Public Key Cryptosystems, PKC 2002, volume 2274 of Lecture Notes in Computer Science, pages 115-124. Springer-Verlag, 2002. [10] M. Harkavy and J. D. Tygar and H. Kikuchi, “Electronic auctions with private bids,” In Proceeding of 3rd USENIX Workshop on Electronic Commerce, 1998. [11] M. Hirt and K. Sako, “Efficient receipt-free voting based on homomorphic encryption,” In Bart Preneel, editor, Advances in Cryptology - EUROCRYPT 2000, volume 1807 of Lecture Notes in Computer Science, pages 539-556. Springer-Verlag, 2000. [12] M. K. Franklin and M. K. Reiter, “The design and implementation of a secure. 46.

(54) ,” In IEEE Transactions on Software Engineering, pages 302-312, IEEE Computer Society, 1996. [13] M. Naor, B. Pinkas and R. Sumner, “Privacy preserving auctions and mechanism design,” In Proceedings of the 1st ACM conference on Electronic commerce, pages 129-139. ACM Press, 1999. [14] S. Liu, C. Wang, and Y. Wang, “A secure multi-round electronic auction scheme,” In Proceedings of the EUROCOMM 2000, pages 330-334. Germany, May 2000. [15] S. Shin, K. kobara, and H. Imai, “Leakage-resilient authenticated key establishment protocols,” In Chi-Sung Laih, editor, Advances in Cryptology ASIACRYPT 2003, volume 2894 of Lecture Notes in Computer Science, pages 155-172. Springer-Verlag, 2000. [16] Y. Watanabe and H. Imai, “Reducing the round complexity of a sealed-bid auction protocol with an off-line TTP,” In Proceedings of the 7th ACM Conference on Computer and Communications Security, pages 80-86. ACM Press, 2000.. 47.

(55)