家族性病例對照資料之統計分析

(1)

國

立

交

通

大

學

統計學研究所

碩

士

論

文

家族性病例對照資料之統計分析

Statistical Analysis for Familial Case-Control Data

研究生：蘇筱嵐

指導教授：王維菁博士

(2)

家族性病例對照資料之統計分析

Statistical Analysis for Familial Case-Control Data

研究生：蘇筱嵐 Student：Hsiao-Lan Su

指導教授：王維菁博士 Advisor：Dr. Weijing Wang

國立交通大學

統計學研究所

碩士論文

A Thesis

Submitted to Institute of Statistics

College of Science

National Chiao Tung University

in Partial Fulfillment of the Requirements

for the Degree of

Master

in

Statistics June 2010

Hsinchu, Taiwan, Republic of China

(3)

家族性病例對照資料之統計分析

學生：蘇筱嵐指導教授：王維菁博士

國立交通大學統計學研究所

摘

要

家族性病例對照資料研究方法近年來常使用於探討疾病與致病因子之

關係。本論文回顧了分析家族資料的統計文獻方法：針對得病與否的反應

變數，考慮了邏輯斯迴歸模型; 針對得病時間的反應變數，考慮了 Cox 等

比風險模型。我們討論如何將建立在個別性資料上之研究方法推廣至家族

性資料，並探討如何將適用於前瞻性資料的方法修改為分析病例對照資料

所需做的假設與調整。此外，我們也透過模擬實驗來驗證推論過程中所需

要之條件與比較參數估計之表現。

關鍵字：家族性病例對照資料研究；前瞻性研究；邏輯斯迴歸模型；Cox PH

模型；Clayton 模型

(4)

Statistical Analysis for Familial Case-Control Data

Student: Hsiao-Lan Su

Advisor: Dr. Weijing Wang

Institute of Statistics

National Chiao Tung University

Hsinchu, Taiwan

Abstract

Familial case-control data are frequently used to study the relationship between disease

and risk factors. In the thesis, we review literature for analyzing familial data. The logistic

model is applied to model the probability of disease incidence. The Cox proportional hazards

model is applied to model the age at onset of the disease. For each model, we discuss how to

extend the method and model developed for individual data to familial data. In addition, we

discuss the criteria and modification from prospective data to case-control data. We also

propose simulation algorithms for generating case-control data and then, based on simulated

data, examine parameter estimates and crucial properties of the inference procedure.

Keywords: Familial case-control study; Prospective study; Logistic regression; Cox PH model;

(5)

誌

謝

碩士生涯的終點，也代表了十八年學生旅程的結束。這兩年能有所成果，

首先必須感謝我的指導老師─王維菁教授，我在理論的推導與邏輯思考

上，一直不是很敏感，反應也很慢，是老師像母親般不厭其煩的引導我從

大方向思考，也讓我學會了該如何去統整概念和如何論述的技巧，更幫助

我撐起整篇論文的架構，老師給予的訓練在我往後的人生中將會受用無窮。

再來要感謝所有交大統研 97 與悶騷的研究室同學們，因為有你們的一同

努力與分享，學習之路不至於乏味而無援。還有高中與大學的好友們，你

們的支持與鼓勵是我向前邁進的動力。

也必須感謝交大統計所所有的老師與郭姐，給予了我們良好的學習環

境，讓我在碩士這兩年學到了許多知識。還有我的口試委員徐南蓉教授、

黃信誠教授與洪慧念教授，謝謝你們的協助與討論，使論文更加完善。

最後，我要感謝我的母親，我知道我不是個貼心的好女兒，這幾年來讓

您辛苦了，您無條件的支持使我求學過程中完全無後顧之憂。最後，我想

將這篇論文獻給我們永遠懷念的父親，我會盡力達成您的期望。

感謝一路上曾幫助過我的貴人，希望大家未來的人生都順利而快樂。

蘇筱嵐謹誌于

國立交通大學統計學研究所

中華民國九十九年六月

(6)

List of Tables

Table 3.1 Joint probability for



Y Y given _p, _r





Z_p,Z_r



... 10

Table 4.1 Logistic regression analysis of case-control data ... 14

Table 4.2.A Checking reproducible properties of the population data (p=0.3) ... 17

Table 4.2.B Checking reproducible properties based on case-control data (p=0.3) ... 17

Table 4.2.C Checking reproducible properties based on case-control data (p=0.3) ... 18

Table 4.2.D Checking reproducible properties based on case-control data (p=0.3) ... 18

Table 4.5 The MLE of  based on case-control familial data ... 23

Table 5.1 Age-matched case-control data ... 25

Table 5.2 Age-matched case-control familial data ... 28

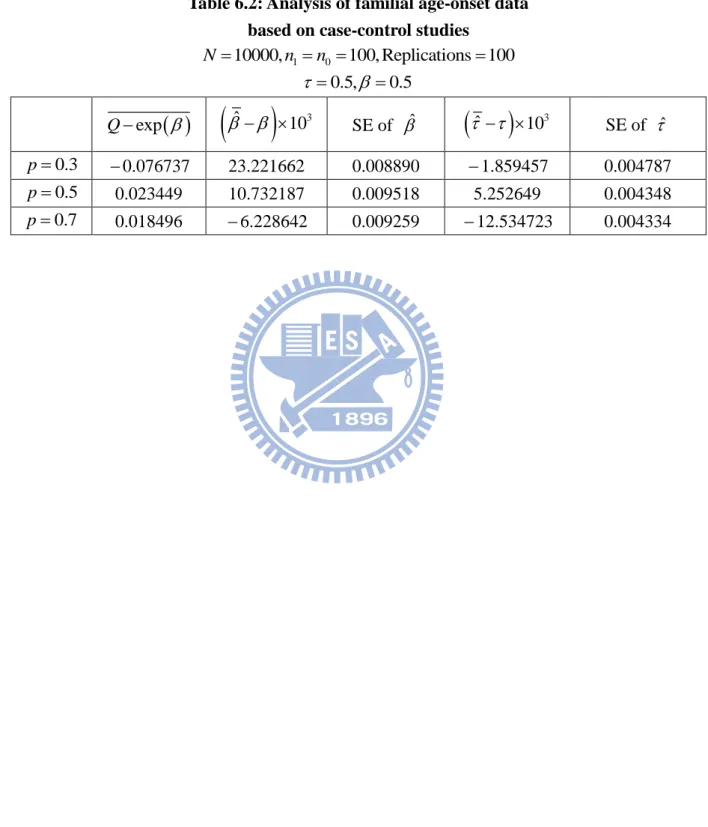
Table 6.1 Analysis of age-onset data based on case-control studies ... 35

(9)

List of Figures

(10)

Chapter 1 Introduction

1.1 Motivation

Scientists are interested in studying the roles of genetic and environmental factors on the

development of a disease. Besides the information about whether the disease is present or not,

age-at-onset has been viewed as a useful quantitative trait for some commonly-seen complex

diseases. For example, early onset of breast cancer has been viewed as an important hallmark

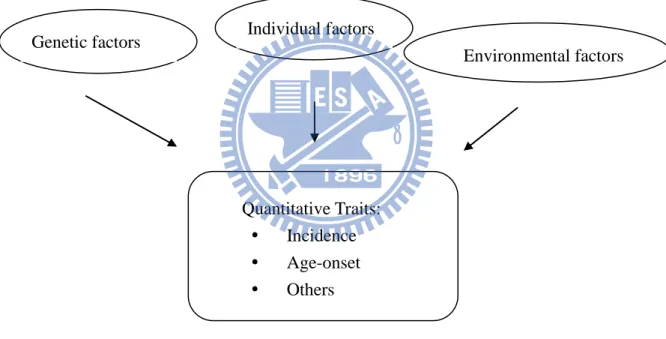
for genetic predisposition. Figure 1 highlights the scientific background which motivates this

thesis. For a quantitative trait, statisticians can perform regression analysis which the effects

of the explanatory variables on the response.

Figure 1: Scientific Background

We focus on two quantitative traits, namely disease incidence and age-at-onset. Disease

incidence can be coded as a binary variable. Age-onset variables are continuous but may be

censored due to termination of the study or loss to follow-up. Genetic, environmental and

individual factors are treated as observed covariates. Their influences on the chosen response

variable are of major interest. If disease incidence is the response variable, logistic regression

models can be adopted. If age-at-onset is studied, failure-time regression models such as Cox

proportional hazards models can be applied. When genetic information is not directly Environmental factors Individual factors Quantitative Traits:  Incidence  Age-onset  Others Genetic factors

(11)

measured, familial data can be used to detect its influence. Familial aggregation often

indicates that genetic or shared environmental factors play some role in the development of

the disease.

From the aspect of data design, the case-control sampling study is often applied to gather

the information of rare diseases. It has the advantage that sufficient number of cases can be

obtained and hence is cheaper and more convenient in comparison with a prospective study.

In recent years, familial case-control designs have become a popular choice in genetic

epidemiology. However statistical inference based on familial case-control data deserves

careful investigation since the underlying probability structure is not straightforward.

1.2 Outline

The purpose of the thesis is to review related literature under a unified framework and

examine some theoretical statements via simulations. In Chapter 2, we provide some

background for different types of case-control designs. In Chapter 3, we review literature on

logistic regression for familial prospective studies and case-control designs. Chapter 4

contains some simulation results which are conducted to verify crucial probability statements

for logistic regression analysis. In Chapter 5, we review literature on familial age-onset data

based on case-control designs. Chapter 6 contains simulation studies for checking the

assumptions that are required in analysis of age-onset data from case-control family studies.

(12)

Chapter 2 An Overview of Case-control Designs

Case-control designs are preferable because they are cheaper and more convenient. In

this chapter, we focus on two common case-control designs: namely the conventional and

familial designs.

2.1 Conventional Case-control Designs

Conventional case-control designs begin by recruiting a group of individuals with a specific

disease as “cases” and the other group of non-diseased individuals as “controls”. Cases and

controls are compared based on risk factors including familial history of the disease. Here

positive familial history is defined as presence of the disease in one or more first-degree

relatives. However potential bias may arise due to incorrect information of recall.

Furthermore individuals may differ in their family sizes so that positive family history is more

likely to occur in a larger family. The family sizes differ in cases and controls can lead to false

results. Liang (2000) discussed potential biases for conventional case-control designs in

details.

2.2 Familial Case-Control Designs

Familial data obtained from case-control designs are frequently used to detect disease

aggregation in families. This design begins by identifying a sample of diseased cases and an

independent sample of disease-free controls, and for each individual, hereafter called a

“proband”, determines his/her covariates, the family structure, and the disease status and covariates of relatives in the family. The disease status of relatives is treated as one part of the

responses in the model.

A major difference between the two designs lies in the sampling unit. The sampling unit in

familial case-control designs is a pre-defined set of family members. Compared to the

conventional design, familial case-control designs provide direct evaluations of the relatives

and can avoid misclassification of family history. It is also useful for genetic counseling.

(13)

2.3 The Issue of Matching in Case-Control Designs

In case-control designs, there are some confounding variables that may affect the

evaluation of the association between disease incidence and risk factors. So, sometimes we

must consider the necessity to match these confounding variables in the design stage. The

purpose of matching is to let the units between cases and controls have more comparability.

The matching method includes frequency matching and individual matching. In

conventional case-control design, if individual matching is part of the design, the conditional

logistic regression method mentioned in Breslow and Day (1980) may be adopted. When in a

familial case-control design, we note that the sampling units are families. So the matching

between case probands and control probands doesn’t guarantee the matching between case

relatives and control relatives. Thus the matching procedure in such studies should be subject

to some modification. First, the matching in design stage must be run under the condition that

the confounding variables are familial, for example: races. Second, correlations among

relatives have to be dealt with. Liang (1987) proposed a method for analyzing the matched

designs which accounts for the within-family correlation. For age-onset responses, Li et al.

(1998) also discussed situations under familial structure and matched procedure.

Finally, Sturmer and Brenner (2000) discussed the issue of the balance between power

(14)

Chapter 3 Logistic Regression on Different Designs

Logistic regression models are commonly adopted for modeling the relationship between

a binary response and covariates. We first discuss statistical inference based on prospective

studies which can be easily understood. Then we discuss how to construct the likelihood

function if the sample is obtained from a case-control design. Finally we will review the

literature on logistic regression analysis for familial case-control studies.

Denote Y as a binary indicator for disease status. Specifically Y 1 represents that the individual is diseased while Y 0 indicates that the individual is free of the disease. Denote

Z as a p1 vector of covariates. Consider the following logistic regression model:

exp( ) Pr( 1| ) 1 exp( ) T T Z Y Z Z          . (3.1)

Let {( ,Y Z_i _i) (i1,..., )}n denote the observed sample. If the data are collected from a

prospective design, the likelihood function can be written as

1 1 exp( ) 1 1 exp( ) 1 exp( ) i i Y Y T n i T T i i i Z Z Z               _ _   _ _     



. (3.2)

A case-control study, by contrast, identify a sample of diseased cases: Y 1 and another independent sample of non-diseased controls: Y 0 . The covariate Z is measured

afterwards. Notice that the distribution of data from a case-control study is based on





Pr Z Y instead of | Pr



Y Z as given in (3.1). However logistic regression analysis can |



still be applied to both sampling designs (Prentice and Pyke, 1979). In Sections 3.1 and 3.2,

we will review the results of Whittemore (1995) in which the probability structure under

conventional and familial case-control designs is well examined.

3.1 Conventional Case-Control Designs

Let  be the target population. The logistic regression model in (3.1) is equivalent to

Pr( 1| , ) log Pr( 0 | , ) T Y Z Z Y Z     _{ }   (3.3)

(15)

where  is the intercept that represents the log odds for developing the disease of the baseline group, and  is the log odds ratio between a subject with covariate Z and a subject of the baseline group. Since  reflects the effect of Z on Y , it is the parameter of

major interest.

As mention earlier, a sample based on a case-control design involves Pr



Z Y| ,



. Applying Baye’s rule, we obtain

Pr( | 1, ) Pr( 0 | ) exp( ) exp( ). Pr( | 0, ) Pr( 1| ) T Z Y Y Z Z Y Y     _       (3.4a)

Whittemore (1995) mentioned that one can imagine a hypothetical population denoted as * in which the covariate distribution is the same as in  such that

* * Pr( | 1, ) Pr( | 1, ) Pr( 0 | ) exp( ) exp( ) Pr( | 0, ) Pr( | 0, ) Pr( 1| ) T Z Y Z Y Y Z Z Y Z Y Y     _   _         . (3.4b) Define * * Pr( 0 | ) Pr( 1| ) exp( ) exp( ) Pr( 1| ) Pr( 0 | ) Y Y Y Y  _{ }    _         .

One can rewrite (3.4b) as

* * * * Pr( | 1, ) Pr( 0 | ) exp( ) exp( ) Pr( | 0, ) Pr( 1| ) T Z Y Y Z Z Y Y     _       . (3.5)

From (3.5), we can construct the following logistic model based on *:

* * Pr( 1| , ) log Pr( 0 | , ) T Y Z Z Y Z         . (3.6)

Now we discuss the implication of the above analysis. Comparing the two models in (3.3)

and (3.6), they differ in the intercept parameter but have the same slope parameter, which is of

major interest. In a case-control design, the sampling distribution is based on



*



Pr Z Y|  1, and Pr



Z Y|  0, *



, where



*





*



_



*



_

* Pr | Pr | 1, Pr 1| , Pr 1| Z Z Y Y Z Y          ;

(16)



*





*



_



*



_

* Pr | Pr | 0, Pr 0 | , Pr 0 | Z Z Y Y Z Y          . Notice that









* * Pr | Pr | Z Y 

 is independent with parameters. The likelihood function for

case-control data can be constructed based on model (3.6). Accordingly case-control data can

be treated as prospective data from * if the following condition holds:

* * Pr( | 1, ) Pr( | 1, ) Pr( | 0, ) Pr( | 0, ) Z Y Z Y Z Y Z Y          . (3.7)

As long as (3.7) is satisfied in collecting the case-control sample, one can proceed the

regression analysis, by pretending that the sample is from a prospective study, to obtain an

estimate of _{which is still reliable. We will examine the crucial condition in (3.7) via} simulations.

3.2 Familial Case-Control Designs

In analysis of familial data, some studies ignored probands’ information and only focus

on relatives’ data. Such an approach may lose efficiency by ignoring useful information in

probands’ data. Whittemore (1995) applied multivariate techniques to analyze familial

case-control data. Specifically she proposed a two-stage sampling procedure. Specifically in

the first stage, two types of probands (case and control) are sampled and then, in the second

stage, their relatives are sampled. To simplify the discussion, we focus on bivariate analysis

which means that only one relative is sampled based on each proband. The resulting

likelihood analysis contains two components. One involves the logistic model on probands as

introduced earlier. The other component is related to the model which measures the

dependence between a proband and his/her relatives.

Let (Y Z_p, _p) and ( ,Y Z_r _r) be the disease status and covariates for a proband and his/her

relative respectively. Denote Y (Y Yp, r) and Z (Zp,Zr). We will first discuss likelihood

(17)

design.

3.2.1 Likelihood analysis based on familial prospective data

A prospective study involves sampling from

Pr( ,Y Zr|Zp)Pr( | ) Pr(Y Z Zr|Zp). (3.8)

When only one relative is involved, Pr( | )Y Z Pr(Yp  y Yp, r yr|Z Zp, r) for y* 0,1 and

* = ,p r . Note that

Pr( | )Y Z =Pr(Yp|Z Zp, r) Pr(Y Y Zr| p, ).

Whittemore (1995) mentioned that a reasonable joint model should satisfy the so-called

“reproducible” assumption such that

1 0 Pr( , | , ) r r y p p r r p r y Y y Y y Z Z    



Pr(Y_p  y_p|Z_p); (3.9a) 1 0 Pr( , | , ) p p y p p r r p r y Y y Y y Z Z    



Pr(Yr  yr|Zr). (3.9b)

That is, the covariate of a person is sufficient to determine his/her disease status and hence the

relative’s covariate does not contribute extra information. The paper examines the plausibility

of the reproducible assumption. Suppose that the dependence between Y_p and Y within the r

same family may also be attributed to some un-measured latent variable denoted as U . If Pr(U Z| )Pr( )U , the reproducible assumption can be achieved. Whether this assumption makes sense depends on the scientific problem at hand.

When (3.9a) is true, it follows that

Pr( | )Y Z =Pr(Yp|Zp) Pr(Y Y Zr | p, ). (3.10)

(18)

log Pr( 1| ) Pr( 0 | ) p p T p p p Y Z Z Y Z       .

The second quantity Pr(Y Y Z_r | _p, )Pr(Y Y Z_r | _p, _p,Z_r) in (3.10) involves the dependence between a proband and his/her relative which is of major interest. Denote observed data

as{(Y Y Zpi, ri, pi,Zri) (i1,..., )}n . If the data is collected from a prospective sampling design,

the likelihood function can be written as









1 , , Pr , , | i i i i n p r r p i L    Y Y Z Z  











1 1 Pr | Pr | , i i i i n n p p r p i i i Y Z Y Y Z   











(1) (2) , , , L   L      , (3.11)

where L(1)



 ,



has the form as in (3.2) and  denotes additional parameter in

Pr(Y Y Z_r | _p, ) . Additional joint model assumption is required to specify the form of

Pr(Y Y Z_r | _p, ).

One model choice is the following model first proposed by Bahadur (1961):

1 1 Pr(( , ) | ( , )) ( ) (1yp ) yp( ) (1yr ) yr(1 ) p r p r p p r r p r Y Y Z Z  p p  p  p  t t (3.12) where





* * * * * * , 1 y p t p r p p     , and * * * * * exp( ) Pr( 1| ) * , 1 exp( ) T T Z p Y Z p r Z            .

The coefficient  satisfies the following constraint:





























1 1 1 1 min , min , . 1 1 1 1 p r r p p r p r p r r p p r p r p p p p p p p p p p p p p p  p p  _ _   _ _       _ _  _ _            

(19)

We will check whether this model satisfies the reproducible assumption via simulations. The

following table summarizes the joint probability of (Yp,Yr) given (Zp,Zr).

1 r Y  Y_r 0 1 p Y  1 ( p)( r) P  p p 1 1 (1 ) (1 ) (1 ) p r p p r r p p p p p p       3 ( p)(1 r) P  p p 1 (1 ) (1 ) (1 ) p r p p r r p p p p p p       0 p Y  2 (1 p)( r) P  p p 1 (1 ) (1 ) (1 ) p _r p p r r p p p p p p       4 (1 p)(1 r) P  p p (1 ) (1 ) (1 ) p _r p p r r p p p p p p      

Table 3.1 Joint probability for (Y Y_p, _r) given (Z_p,Z_r)

3.2.2 Likelihood analysis based on familial case-control data

A case-control study involves two independent samples from Pr( ,Y Z Y_r | _p 1) and

Pr( ,Y Z Y_r | _p 0). Notice that Pr( ,Y Z Y_r | _p)Pr(Y Z Y_r | , _p) Pr( |Z Y_p) and

Pr( |Z Y_p)Pr(Z Z Y_p, _r | _p)Pr(Z_p|Y_p) Pr(Z Y Z_r | _p, _p).

The reproducible assumption implies that, given Zp, Yp and Z are independent. Hence r

Pr( |Z Y_p)Pr(Z_p |Y_p) Pr(Z_r|Z_p). In summary we have







 



Pr Y Z Y_r, | _p Pr Y Z Y_r, | _p Pr Z_p|Y_p Pr Z_r|Z_p



Pr(Z_p|Y_p)



Pr(Y Z Y_r| , _p) Pr(Z_r |Z_p)



 . (3.13)

Recall that Pr(Z_p|Y_p) can be analyzed assuming that the data is from a prospective sample

(20)

* * Pr( 1| , ) log Pr( 0 | , ) p p T p p p Y Z Z Y Z         .

Accordingly the retrospective likelihood function is given by









* 1 , , , Pr , | i i n r i p i L     Y Z Y  











1 1 Pr | Pr | , i i i i n n p p r p i i i Z Y Y Y Z   











*(1) (2) , , , L   L      .

Notice that the information of  is also contained in familial case-control data when the reproducible assumption holds for the joint model.

(21)

Chapter 4 Simulations for Logistic Regression Analysis

In this chapter, we propose data generation algorithms to simulate case-control data for

logistic regression analysis. Some crucial probability statements will be examined to verify

whether the simulated data are reliable for statistical inference.

4.1 Data Generation for Individual Data 4.1.1 Prospective data of the true population

First of all, we generate population data from the model:





exp



_



_

Pr 1| , 1 exp Z Y Z Z           .

Then set the values of the parameters:  ,  and p. The algorithm is summarized below:  Step 1: Generate Z_i Bernoulli( )p

 Step 2: Given Z , generate _i









exp Bernoulli . 1 exp i i i Z Y Z           _ _   

The procedure is repeated for i1,...,N for very large N , say N10000. Denote

{( ,Y Z_i _i)(i 1,...,N)}

   .

4.1.2 Case-control data from the true population

Suppose that we generate nN observations from the population with n persons ₁

from the case group with Y 1 and n₀  n n₁ persons from the control group Y 0. The procedure is stated as follows.

 Step 1: Randomly select n subjects from the case group and record their values of 1 Zi;

 Step 2: Randomly select n subjects from the control group and record their values of 0

i

(22)

We briefly discuss how to implement Step 1 since Step 2 follows a similar procedure. First

identify the case population:  ₁ {(Y_i 1,Z_i) (i1,...,N₁)}where ₁

1 ( 1) N i i N I Y  



 . The

objective is to select n observations from ₁ N subjects. Label the subjects in ₁ ₁ from 1 to

1

N . At the first time, generate U U

 

0,1 and define s



N₁U



, where

 

is the Gauss function. A subject with label “s ” is selected into the case-control sample and removed

from ₁. The procedure is repeated n times. Specifically at the ₁ kth time, generate

 

0,1

U U and a subject with a re-defined label s



(N₁  k 1) U



is selected from the remaining case population containing N₁ k 1 subjects. Finally the case sample is formed and denoted as {(Y_k 1,Z_k) (k 1,..., )}n₁ . The control sample can be generated in a similar way.

4.2. Analysis on Individual Data

We examine whether the proposed case-control sampling procedure produces reliable

data. We let 1 1 * 1 1 ( *, 1) / ( 1) ( *, 0) / ( 0) N N i i i i i N N i i i i i I Z Y I Y R I Z Y I Y           





*0,1



and









1 1 * 1 1 *, 1 / *, 0 / n i i i n i i i I Z Y n r I Z Y n       





* 0 , 1



be the empirical estimates of









Pr * | 1, Pr * | 0, Z Y Z Y       and









* * Pr * | 1, Pr * | 0, Z Y Z Y       respectively.

The first criteria to evaluate the quality of data is checking whether r is close to * R . The *

(23)

the combined case-control data: {(Y_k 1,Z_k) (k 1,..., )}n₁ and {(Y_k 0,Z_k) (k 1,...,n₀)}. The MLE of ˆ and ˆ are obtained. By checking whether ˆ is close to the true value, we can examine whether the case-control data provide reliable information of . The results are summarized in Tables 4.1. We observe that the empirical estimate r is close to _* R *

obtained from the population data, the estimations of ˆ are also stable and close to the true value.

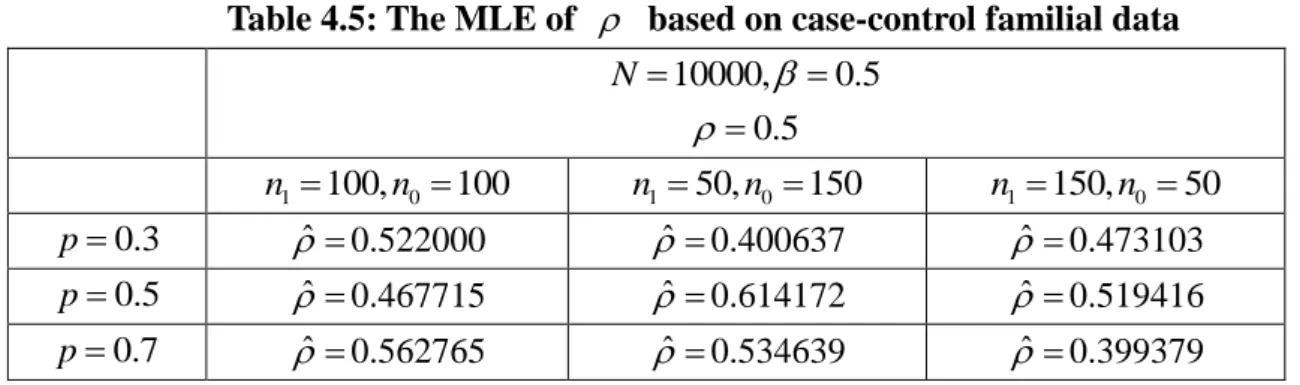
Table 4.1: Logistic regression analysis of case-control data

0.5,N 10000, Replications 100     1 100, 0 100 n  n  0 0 r R 1 1 r R

 

3 ˆ ₁₀    SE of ˆ 0.3 p 1.013132 1.018201 22.336209 0.034299 0.5 p 1.024408 0.992022 33.755393 0.027108 0.7 p 1.021804 1.003206 1.477217 0.028456 1 50, 0 150 n  n  0 0 r R 1 1 r R

 

3 ˆ ₁₀    SE of ˆ 0.3 p 0.991638 1.044951 31.116517 0.033287 0.5 p 0.978128 1.033878 56.818868 0.032211 0.7 p 1.013979 1.004441 20.400237 0.036247 1 150, 0 50 n  n  0 0 r R 1 1 r R

 

3 ˆ ₁₀    SE of ˆ 0.3 p 1.018330 1.038011 17.547938 0.036607 0.5 p 1.037552 1.021409 27.831059 0.038455 0.7 p 1.042732 1.009384 6.449529 0.038106

(24)

4.3 Data Generation for Familial Data

4.3.1 Familial prospective data of the true population

We first generate data following the model proposed by Bahadur (1961). First set the

values of the parameters:  , ,  and p. The algorithm is summarized below:  Step 1: Generate

i p

Z following Bernoulli

 

p and

i r

Z independently also following

Bernoulli

 

p ;  Step 2: Given i p Z and i r

Z , compute P P P P mentioned in Table 3.1; ₁, ₂, ₃, ₄  Step 3: Generate U_i Uniform 0,1

 

;

 Step 4: Set 1 1 1 2 1 2 1 2 3 1 2 3 1, 1 if 0 0, 1 if 1, 0 if 0, 0 if 1 i i i i i i i i p r i p r i p r i p r i Y Y U P Y Y P U P P Y Y P P U P P P Y Y P P P U       _ _ _ _{ }   _ _ _ _ _{  }   _ _ _{ } _ _  _.

The procedure is repeated for i1,...,N for N10000.

4.3.2 Familial case-control data from the true population

The procedure is stated as follows.

 Step 1: Randomly select n probands from the case families with 1 Yp_i 1 and record the

values of ( , , )

i i i

p r r

Z Y Z ;

 Step 2: Randomly select n probands from the control families with 0 Yp_i 0 and record

their values of ( , , )

i i i

p r r

Z Y Z .

4.4. Analysis on Familial Data

We first examine whether the algorithm for generating perspective data satisfies the

(25)

1 1 1 ( , , ) ( , , ) ( , ) N pi p pi p ri r i p p r N pi p ri r i I Y y Z z Z z q y z z I Z z Z z        



, and 1 1 1 ( , ) ( , ) ( ) N pi p pi p i p p N pi p i I Y y Z z q y z I Z z      



; 1 2 1 ( , , ) ( , , ) ( , ) N ri r pi p ri r i r p r N pi p ri r i I Y y Z z Z z q y z z I Z z Z z        



, and 2( r, r) q y z 1 1 ( , ) ( ) N ri r ri r i N ri r i I Y y Z z I Z z      



.

The reproducible condition should imply that q y z₁( _p, _p,z_r) q y z₁( _p, _p) and q y z₂( _r, _p,z_r) 2( r, r)

q y z

 . The results of these quantities based on prospective data and case-control data from the true population are recorded in Table 4.2 ~ 4.4. In analyzing the case-control familial

data, we assume  and  are known and then obtain the MLE of . By checking whether ˆ is close to the true value, we can examine whether the familial case-control data provide reliable information of the association in a family. This result is given in Table 4.5.

We observe that the performance of the reproducible properties is good in our population

data which means that the model is appropriate. But sometimes the reproducible properties do

not reflected in the simulated case-control data. Accordingly the estimations of ˆ will have worse results in these situations.

(26)

Table 4.2.A: Checking reproducible properties of the population data (p=0.3) 10000 N (y z_p, _p)(1,1) (y z_p, _p)(1, 0) (y z_p, _p)(0,1) (y z_p, _p)(0, 0) 1 r z  q₁ 0.734649 q₁0.630283 q₁ 0.265351 q₁0.369717 0 r z  q1 0.729743 q10.638770 q1 0.270257 q10.361230 1 q 0.731267 q₁0.636183 q₁ 0.268733 q₁0.363817 (y z_r, _r)(1,1) (y z_r, _r)(1, 0) (y z_r, _r)(0,1) (y z_r, _r)(0, 0) 1 p z  q₂ 0.718202 q2 0.607213 q2 0.281798 q2 0.392787 0 p z  q₂ 0.752438 q₂ 0.642232 q₂ 0.247562 q₂ 0.357768 2 q 0.742251 q₂ 0.632012 q₂ 0.257749 q₂ 0.367988

Table 4.2.B: Checking reproducible properties based on case-control data (p=0.3)

1 0 10000, 100, 100 N n  n  (y z_p, _p)(1,1) (y z_p, _p)(1, 0) (y z_p, _p)(0,1) (y z_p, _p)(0, 0) 1 r z  q₁ 0.545455 q₁0.547170 q₁ 0.454545 q₁0.452830 0 r z  q₁ 0.696970 q₁0.391304 q₁ 0.303030 q₁0.608696 1 q 0.636364 q10.448276 q1 0.363636 q10.551724 (y z_r, _r)(1,1) (y z_r, _r)(1, 0) (y z_r, _r)(0,1) (y z_r, _r)(0, 0) 1 p z  q₂ 0.590909 q₂ 0.575758 q₂ 0.409091 q₂ 0.424242 0 p z  q₂ 0.698113 q2 0.521739 q2 0.301887 q2 0.478261 2 q 0.666667 q₂ 0.536000 q₂ 0.333333 q₂ 0.464000

(27)

Table 4.2.C: Checking reproducible properties based on case-control data (p=0.3) 1 0 10000, 50, 150 N n  n  (y z_p, _p)(1,1) (y z_p, _p)(1, 0) (y z_p, _p)(0,1) (y z_p, _p)(0, 0) 1 r z  q₁ 0.363636 q₁0.282609 q₁ 0.636364 q₁0.717391 0 r z  q1 0.222222 q10.218750 q1 0.777778 q10.781250 1 q 0.275862 q₁0.239437 q₁ 0.724138 q₁0.760563 (y z_r, _r)(1,1) (y z_r, _r)(1, 0) (y z_r, _r)(0,1) (y z_r, _r)(0, 0) 1 p z  q₂ 0.590909 q2 0.222222 q2 0.409091 q2 0.777778 0 p z  q₂ 0.652174 q₂ 0.427083 q₂ 0.347826 q₂ 0.572917 2 q 0.632353 q₂ 0.371212 q₂ 0.367647 q₂ 0.628788

Table 4.2.D: Checking reproducible properties based on case-control data (p=0.3)

1 0 10000, 150, 50 N n  n  (y zp, p)(1,1) (y zp, p)(1, 0) (y zp, p)(0,1) (y zp, p)(0, 0) 1 r z  q₁ 0.782609 q₁0.763158 q₁ 0.217391 q₁0.236842 0 r z  q₁ 0.818182 q₁0.690476 q₁ 0.181818 q₁0.309524 1 q 0.807692 q1 0.713115 q1 0.192308 q10.286885 (y z_r, _r)(1,1) (y z_r, _r)(1, 0) (y z_r, _r)(0,1) (y z_r, _r)(0, 0) 1 p z  q₂ 0.695652 q₂ 0.527273 q₂ 0.304348 q₂ 0.472727 0 p z  q₂ 0.842105 q2 0.619048 q2 0.157895 q2 0.380952 q 0.786885 q 0.582734 q 0.213115 q 0.417266

(28)

(29)

1 0 10000, 150, 50 N n  n  (y zp, p)(1,1) (y zp, p)(1, 0) (y zp, p)(0,1) (y zp, p)(0, 0) 1 r z  q₁ 0.825397 q₁0.636364 q₁ 0.174603 q₁0.363636 0 r z  q₁ 0.733333 q₁0.787879 q₁ 0.266667 q₁0.212121 1 q 0.780488 q10.701299 q1 0.219512 q10.298701 (y z_r, _r)(1,1) (y z_r, _r)(1, 0) (y z_r, _r)(0,1) (y z_r, _r)(0, 0) 1 p z  q₂ 0.777778 q₂ 0.550000 q₂ 0.222222 q₂ 0.450000 0 p z  q₂ 0.727273 q2 0.727273 q2 0.272727 q2 0.272727 q 0.757009 q 0.612903 q 0.242991 q 0.387097

(30)

(31)

1 0 10000, 150, 50 N n  n  (y zp, p)(1,1) (y zp, p)(1, 0) (y zp, p)(0,1) (y zp, p)(0, 0) 1 r z  q₁ 0.724490 q₁0.575758 q₁ 0.275510 q₁0.424242 0 r z  q₁ 0.857143 q₁0.900000 q₁ 0.142857 q₁0.100000 1 q 0.768707 q1 0.698113 q1 0.231293 q10.301887 (y z_r, _r)(1,1) (y z_r, _r)(1, 0) (y z_r, _r)(0,1) (y z_r, _r)(0, 0) 1 p z  q₂ 0.734694 q₂ 0.755102 q₂ 0.265306 q₂ 0.244898 0 p z  q₂ 0.787879 q2 0.800000 q2 0.212121 q2 0.200000 q 0.748092 q 0.768116 q 0.251908 q 0.231884

(32)

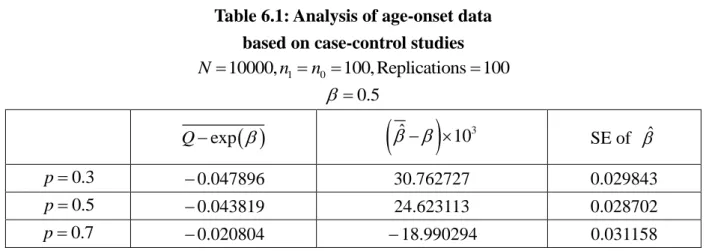
Table 4.5: The MLE of  based on case-control familial data 10000, 0.5 N   0.5   1 100, 0 100 n  n  n150,n0 150 n1 150,n0 50 0.3 p ˆ 0.522000 ˆ 0.400637 ˆ 0.473103 0.5 p ˆ 0.467715 ˆ 0.614172 ˆ 0.519416 0.7 p ˆ 0.562765 ˆ 0.534639 ˆ 0.399379

(33)

Chapter 5 Regression Analysis Based on Familial Data

For those who have developed the disease, the age at onset may be informative. As

mentioned in Li et al. (1998), early age of onset has been a hallmark for genetic predisposition

in most of diseases that aggregate in families. When age-at-onset is chosen as the primary

response, the effect of censoring has to be considered in the analysis.

In this chapter, we discuss several important issues on analyzing familial age-onset data.

Specifically denote T as the age-onset variable and Z as a p1 vector of covariates. The Cox proportional hazards model is the most well-known model for failure time variables

which can be written as



|



0

 

exp





,

T

t Z t Z

   (5.1) where ₀( )t is the baseline hazard function and  measures the effect of Z on the hazard and is of major interest. In familial failure-time analysis, the Cox model is imposed on

probands. For inference of ,_{we first review the analysis based on a prospective sample} and then extend the discussion to a valid case-control sample. Finally we will discuss the

modeling and inference frameworks when familial case-control data are collected.

5.1 Likelihood Analysis Based on Probands

Under right censoring, let C be the censoring variable. One observes that X  T C,

( )

I T C

   and covariates Z. In prospective studies, we identify a sample of individuals with specified covariates: Z and then determine their observed time and disease status: _i

(Xi, )i for i1,...,n. At time t , the risk set can be denoted as R t( ){ :i Xi t i, 1,..., }n .

Given the risk set information, a subject failing at time t with covariate Z_j given jR t( )

will contribute to the partial likelihood by









 





 













0 0 exp exp | . | exp exp T T j j j T T i i i t Z Z t Z t Z t Z Z          



(5.2)

(34)

Prentice and Breslow (1978) discussed the likelihood formulation based on case-control

age-onset data. It is important to first introduce the sampling procedure which involves how

to match a case subject with a control subject. Specifically at time t , m t observations are ( ) sampled from the case population containing those who develop the disease at time t and,

independently, n t( ) observations are sampled from the control population containing those

who have not developed the disease up to time t . Observed data can be summarized in Table

5.1.

Time:t _i Case:



X t_i, 1



Control:



X t_i, 0



1 t m t individuals ( )₁ n t individuals ( )₁ i t m t individuals ( )i n t individuals ( )i k t m t( )_k individuals n t( )_k individuals

Table 5.1 Age-matched case-control data

The case-control design for collecting age-onset data considers sampling from the

conditional distribution of Z based on ( , )X  . To establish the relationship between prospective and retrospective samples, Prentice and Breslow (1978) extended the result of

Cornfield (1951) to age-onset data and derived the following condition:

Pr( | , 1) / Pr( 0 | , 1) Pr( | , 0) / Pr( 0 | , 0) Pr( , 1| ) / Pr( , 1| 0) . Pr( , 0 | ) / Pr( , 0 | 0) Z X t Z X t Z X t Z X t X t Z X t Z X t Z X t Z                              (5.3)

Notice that when C is independent of both T and Z , we have

Pr( , 1| ) Pr( , | ) Pr( | ) Pr( ) ( ) ; Pr( , 0 | ) Pr( , | ) Pr( | ) Pr( ) C( ) X t Z T t C t Z T t Z C t t X t Z T t C t Z T t Z C t t                    Pr( , 1| 0) Pr( | 0) Pr( ) 0( ) . Pr( , 0 | 0) Pr( | 0) Pr( ) C( ) t X t Z T t Z C t X t Z T t Z C t t                  

(35)

Hence the right-hand side of (5.3) equals ( ) /t ₀( )t and, under the proportional hazard model, (5.3) becomes Pr( | , 1) / Pr( 0 | , 1) exp( ) Pr( | , 0) / Pr( 0 | , 0) T Z X t Z X t Z Z X t Z X t   _        _      . (5.4) Rearranging (5.4), we obtain Pr( 0 | , 1) Pr( | , 1) Pr( | , 0) exp( ) Pr( 0 | , 0) T Z X t Z X t Z X t Z Z X t                

which is equation (2) in Li et al. (1998). The left-hand side of (5.4) is identifiable based on

case-control data which implies that  is also identifiable based on such data.

Prentice and Breslow (1978) proposed a conditional likelihood approach for estimating

 based on case-control data. At time t , define R m t n t( ( ), ( )) as a set of all subsets of size ( )

m t from a total of m t( )n t( ) subjects. Given this risk set information, the first m t ( ) subjects with covariates Z₁,...,Z_{m t}_{( )} respectively actually belonging to the case group will contribute the probability









( ) 1 ( ) ( ( ), ( )) 1 | , | m t i i m t lj l R m t n t j t Z t Z     



 

(5.5)

where Z_lj denotes the covariate value for j th subject in the l th combinations. Notice that





( ) ( ) 0 1 ( ) 1 | { ( )} exp{ ( ... )} m t m t T i m t i t Z t Z Z       



and





( ) ( ) 0 1 ( ) 1 | { ( )} exp{ ( ... )}. m t m t T lj l lm t j t Z t Z Z       



It follows that









( ) 1 ( ) ( ( ), ( )) ( ( ), ( )) 1 | exp( ) , exp( ) | m t i T i m t T l lj l R m t n t l R m t n t j t Z s s t Z  _       





 

(5.6)

(36)

where sZ₁ ... Z_{m t}_{( )} and s_l Z_l₁ ... Z_{lm t}_{( )}. Finally the likelihood can be written as 1 ( ( ), ( )) exp( ) , exp( ) j j T k T j l l R m t n t s s    





(5.7)

where t₁ ... t_k denote observed failure times for the case group. It is important to note that

( ( ), ( ))

R m t n t only includes subjects who are sampled from the retrospective study at time t .

Hence it does not have the nested property of a regular risk set such as R t( )R t( ). It is important to mention that computation of (5.7) involves all possible permutations in the

denominator which is very time-consuming if m t( )n t( ) is not small. Several authors proposed algorithms to approximate the likelihood.

We provide a numerical example to illustrate construction of R m n( , ) in which the label

t is ignored to simply the presentation. Suppose the case-sample contains subjects with

covariates Z and ₁ Z respectively and the matched control-sample contains subjects with ₂

covariates Z and ₃ Z respectively. Hence ₄ R(2, 2) consists of 4 2

   

  combinations which

can be labeled by l1,..., 6 corresponding to

1 2 1 3 1 4 2 3 2 4 3 4

(Z Z, ), (Z Z, ), (Z Z, ), (Z Z, ), (Z Z, ), (Z Z, ) sets of covariates respectively. For example Z₂₂Z₃ corresponds to the second covariate with l2 . It follows that

1 2

sZ Z , s₁Z₁Z₂ , s₂ Z₁Z₃ , s₃ Z₁Z₄ , s₄ Z₂Z₃ , s₅ Z₂Z₄ and

6 3 4 s Z Z .

5.2 Likelihood Analysis Based on Familial Data

Table 5.2 summarizes observed case-control familial data in which probands’ times

(onset or censored) are matched. Specifically at time t , we sample _i m t case probands

 

_i

and their relatives and matched with n t control probands and their relatives. Denote

 

_i ( _p, _r)

X  X X as observed times and  ( _p, _r) as the corresponding indicators for a proband and his/her relative respectively.

(37)

Time Case family:



X_p t_i,_p 1



Control family:



X_p t_i,_p 0



1

t m t probands and their

 

1

relatives

 

1

n t probands and their

relatives

i

t m t probands and their

 

i

relatives

 

i

n t probands and their

relatives

k

t m t

 

k probands and their

relatives

 

k

n t probands and their relatives

Table 5.2 Age-matched case-control familial data

To simply the presentation, assume that there are two members in one family (one

proband and one relative). Observed information for a case subject includes

(Xp t,p 1,Zp,Xr,r,Zr) while the information for the corresponding age-matched control subject includes (Xp t,p 0,Zp,Xr,r,Zr) . Two samples from









Pr( Xr,r ,Z Zp, r | Xp t,p 1 ) and Pr(



Xr,r



,Z Zp, r |



Xp t,p 0 )



are drawn

independently.

Li et al. (1998) extended the discussions in Whittemore (1995) from binary data to

age-onset data. The model assumption consists of two stages. In the first stage, the model on

the proband namely Pr(Z_p|



X_p,_p



), is assumed to follow the Cox model. In the second stage, the model on Pr(



X_r,_r



|



X_p,_p



, )Z is constructed where Z (Z_p,Z_r). It should

家族性病例對照資料之統計分析

國

立

交

通

大

學

統計學研究所

碩

士

論

文