Evolution of the Second Lowest Extended State as a Function of the Effective Magnetic Field in the Fractional Quantum Hall Regime
Tse-Ming Chen,1 C.-T. Liang,1, ∗ M. Y. Simmons,2, 3 D. A. Ritchie,2 and M. Pepper2 1
Department of Physics, National Taiwan University, Taipei 106, Taiwan
2
Cavendish Laboratory, Madingley Road, Cambridge CB3 0HE, UK
3
School of Physics, University of New South Wales, Sydney 2052, Australia (Received December 15, 2003)
It has been shown that, at a Landau level filling factor ν=1/2, a two-dimensional electron system can be mathematically transformed into a composite fermion system interacting with a Chern-Simons gauge field. At ν=1/2, the average of this Chern-Simons gauge field cancels the external magnetic field Bext so that the effective magnetic field Beff acting on
the composite fermions is zero. Away from ν=1/2, the composite fermions experience a net effective magnetic field Beff. We present the first study of the evolution of the second lowest
extended state in a vanishing effective magnetic field in the fractional quantum Hall regime. Our result shows that the evolution of the second lowest extended state has a good linear dependence on the effective magnetic field Beff within the composite fermion picture.
PACS numbers: 73.43.-f, 73.40.-c
The fractional quantum Hall effect (FQHE) [1] observed in high-quality two-dimensional (2D) electron systems in the low-temperature, high-magnetic-field regime, arises from strong electron-electron interactions [2]. In the composite fermion (CF) pic-ture the FQHE can be understood as a manifestation of the integer quantum Hall effect (IQHE) of weakly interacting composite fermions [3]. It has been shown that at a Landau level filling factor ν=1/2, a 2D electron system can be mathematically transformed into a CF system interacting with a Chern-Simons gauge field. At ν=1/2 the average of this Chern-Simons gauge field cancels the external magnetic field Bext, so that the effective
mag-netic field Beff acting on the composite fermions is zero. Away from ν=1/2 the composite
fermions experience a net effective magnetic field Beff = (1−2ν)Bext. In this CF picture, we
can easily regard the FQHE of electrons in the external magnetic field Bext as the IQHE of
composite fermions in the effective magnetic field Beff. At ν=1/2 each composite fermion
is composed of an electron bound to two magnetic flux quanta, thus the density of the composite fermion system is equal to that of the electron system.
The existence of the extended (delocalized) states is an essential ingredient in the theory of the quantum Hall effect. It is now well established that the energy of an extended state in a quantum Hall system in the high-magnetic-field regime is centered around its Landau levels EN = (N + 1/2)¯hωc. When the magnetic field is decreased so as to push
the 2D electron system toward complete localization, the extended-state bands move down through the Fermi energy. However, it is believed [4, 5] that as B → 0 the extended states cannot disappear discontinuously below the Fermi level, but must “float up” in energy. With
http://PSROC.phys.ntu.edu.tw/cjp 307 2004 THE PHYSICAL SOCIETYc OF THE REPUBLIC OF CHINA
eff
this work we present the first experimental study of the evolution of the second lowest extended state as a function of the effective magnetic field in the fractional quantum Hall regime. Experimentally the evolution of the peaks in the longitudinal conductivity σxx (or
the longitudinal resistivity ρxx) can be used to map out the extended states in the density
(or energy)–magnetic field space. We performed the low-temperature measurements on a high-quality gated GaAs electron system. By changing the applied gate voltage, we were able to study the evolution of the second lowest extended state as a function of the electron density. In mapping out the diagram of the second lowest extended state of the FQHE within the composite fermion picture, we show that the evolution of the second lowest extended state conforms to the theoretical prediction in a finite effective magnetic field.
The sample investigated in this work was a modulation doped GaAs/AlGaAs het-erostructure grown by molecular beam epitaxy. The structure consists of a semi-insulating (SI) GaAs (001) substrate, followed by an undoped 20 nm GaAs quantum well, an 80 nm undoped Al0.33Ga0.67As spacer, a 210 nm Si-doped Al0.33Ga0.67As, and finally a 10 nm
GaAs cap layer. The Hall pattern was made by standard lithography and etching processes. At zero gate voltage, our sample has a carrier density of 9.12 × 1014 m−2 with a mobility of
300 m2/V s without illumination. Magneto-transport measurements were performed with
a top-loading He3 system and a superconducting magnet. The low-frequency AC lock-in
technique with a current of 10 nA applied to the sample was used in this work.
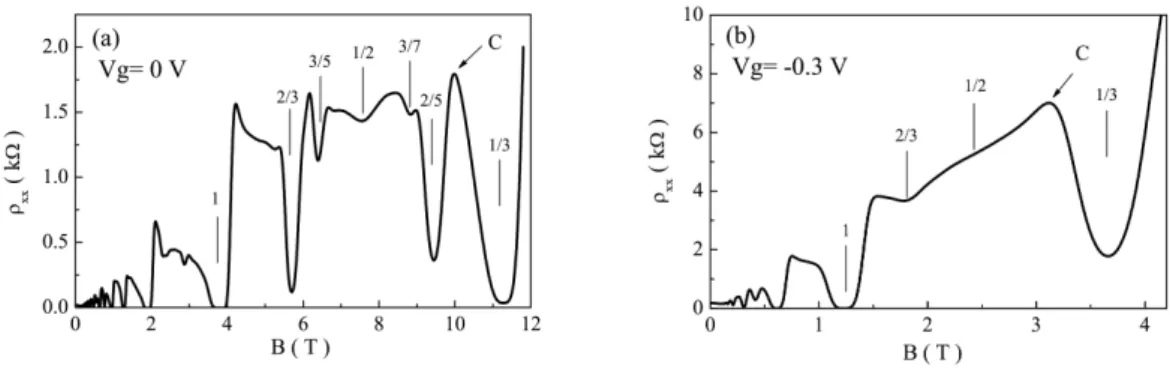
To identify the region for our study, we show in Fig. 1(a) and (b) the longitudinal magnetoresistivity traces ρxx(B) in the magnetic-field sweeps at two typical gate voltages.
Each peak in ρxxat a particular magnetic field and gate voltage represents the occupation of
an extended state energy band and yields one point for the ne–B phase diagram. A strong
localization at low density was expected, due to a reduction of the screening of a charged impurity potential in the dilute electron limit [12]. Therefore, by changing the applied gate voltage (electron density), we were able to change the localization of the 2DEG and study the evolution of the extended state in the ne–B phase diagram. What interests us most
in this paper is the second lowest extended state (labelled C in Fig. 1) in the fractional quantum Hall regime. From the measurement of the Hall and longitudinal resistance in the magnetic-field sweeps at fixed gate voltage, we can obtain the electron density, which shows a linear dependence on the applied gate voltage. By varying the applied gate voltage from 0 V to −0.34 V, we obtain an electron density from 9.12 × 1014 m−2 to 2.15 × 1014 m−2.
FIG. 1: ρxxas a function of the magnetic field for different gate voltages at T = 300 mK. The peaks
in ρxx (labelled C) for various gate voltages are used to map out the lowest extended state in the
n–B phase diagram.
FIG. 2: The ne–Bext phase diagram for the lowest extended state. The lowest extended state shows
a linear dependence on the external magnetic field.
As the applied gate voltage Vg is made more negative, the effective disorder increases (or
the magnetic field decreases) and the extended-state band moves down in energy. The energy of these extended states can be considered to be directly proportional to n in the data region. Our results also show that the evolution of the second lowest extended state in the FQHE shows a linear dependence on Bext in the ne–Bext phase diagram.
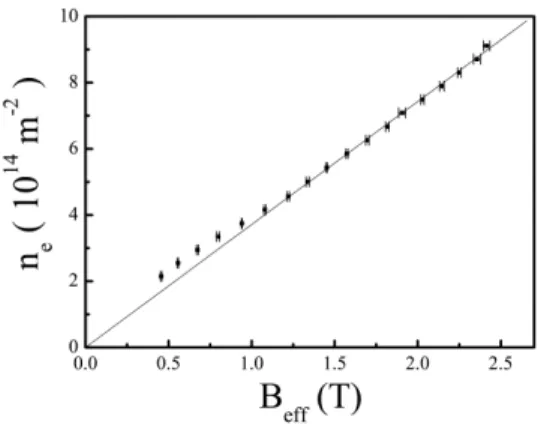
We now turn to our main experimental results. Within the composite fermion pic-ture, we studied the evolution of the second lowest extended state in the density-effective magnetic phase diagram, as shown in Fig. 3. We observed that the evolution shows a good linear dependence on the effective magnetic field Beffin the high Beffor low disorder region.
FIG. 3: The ne–Beff phase diagram for the extended state determined from the peaks in ρxx. The
dotted lines represent the conventional levels in the CF picture.
is given by EFCF = ¯h 2k2 F 2m? CF = (N +1 2)¯h eBeff m? CF , (1)
where kF = √4πne for a CF and ne is the carrier concentration. For the second lowest
extended state, with N = 1 and the cancellation of m?
CF in Eq. (1), we can derive the
relation ne
Beff
= 3e
2h, (2)
which is consistent with the relation νeffeBeff
h = ne, (3)
in the conventional Landau fan diagram in the composite fermion picture, while νeff= 1.5
for the second lowest extended state in the FQHE regime. Our experimental results show that the slope in Fig. 3 is 3.715 × 1014, close to the theoretical value, which is consistent
with Eq. (2). Moreover, we also found that, in the low effective magnetic field or high effective disorder limit, the second lowest extended state starts to show a deviation from the traditional Landau level within the CF picture.
In conclusion, we have performed the first study of the second lowest extended state as a function of the effective magnetic field Beff in the fractional quantum Hall regime. Our
experimental results show that the most pronounced resistance peak which corresponds to an effective filling factor νeff= 1.5 shows a linear dependence on Beff. In this device, we can
at a vanishing Beff. We hope that with better-quality samples, we will be able to study
whether floating-up can occur, which is a fundamentally important issue in the 2D field. This work was funded by the NSC, Taiwan and the EPSRC, United Kingdom. C. T. L. thanks T. Chin for her support.
References
∗ Electronic address: ctliang@phys.ntu.edu.tw
[1] T. Charkraborty and P. Pietilainen, The Fractional Quantum Hall Effect, (Springer-Verlag, New York, 1988).
[2] R. B. Laughlin, Phys. Rev. Lett. 50, 1395 (1983). [3] J. K. Jain, Phys. Rev. Lett. 63, 199 (1989). [4] D. E. Khmelnitskii, Phys. Lett. 106, 182 (1984). [5] R. B. Laughlin, Phys. Rev. Lett. 52, 2304 (1984).
[6] S. A. Kivelson, D. H. Lee, and S. C. Zhang, Phys. Rev. B 46, 2223 (1992).
[7] H. W. Jiang, C. E. Johnson, K. L. Wang, and S. T. Hannahs, Phys. Rev. Lett. 71. 1439 (1993). [8] A. A. Shashkin, G. V. Kravchenko, and V. T. Dogopolov, JETP Lett. 58, 220 (1993).
[9] T. Wang, K. P. Clark, G. F. Spencer, A. M. Mack, and W. P. Kirk, Phys. Rev. Lett. 72, 709 (1994).
[10] R. J. F. Hughes, J. T. Nicholls, J. E. F. Frost, E. H. Linfield, M. Pepper, C. J. B. Ford, D. A. Ritchie, G. A. C. Jones, E. Kogan, and M. Kaveh, J. Phys. Condens. Matter 6, 4763 (1994). [11] I. Glozman, C. E. Johnson, and H. W. Jiang, Phys. Rev. Lett. 74, 594 (1995).
[12] V. J. Goldman, J. K. Jain, and M. Shayegan, Phys. Rev. Lett. 65, 907 (1990). [13] A. L. Efros, Solid State Commun. 70, 253 (1989).