Joint weighted least squares estimation of frequency and timing offset for OFDM systems over fading channels

Joint Weighted Least Squares Estimation of

Frequency and Timing Offset

for

OFDM Systems over Fading Channels

Pei-Yun Tsai, Hsin-Yu

Kang and

Tzi-Dar Chiueh

...,.. ,. i , . and Graduate Institute of Electronics Engineering,

i Department

of

Electrical

Engineering

! , -

.

. . National Taiwan University, Taipei, Taiwan, 10617.

Absfracr-This paper presents an algorithm for joint ferences are then averaged among all pilot subcarriers or estimation of carrier frequency Offset and timing fre- over m w a l OFDM svmhok to =<timate the carrier fre-

~~~.

~~~~~~ ~ - . ..~~~~~~~~~~~~~. . near the Cram&-Rao bound in the variance of estimation

errors: Simulations of several estimation algorithms in a

estimation. Also the complex data of the pilot subcarriers, instead of their phases, are averaged. However, these multipath fading channel show'that this algorithm provides

the most accurate estimation in both the carrier frequency offset and the timing frequency offset.

. . ...

2 . I. INTRODUCTION

,'The OFDM modulation technique offers an attrac- tive solution to high-rate data access for its robust- ness against frequency-selective multipath fading and its simple equalization scheme. Moreover, it is also very efficient in spectrum utilization since the spectra of adjacentwbcarriers overlap. OFDM has therefore been adopted in several standards such as DVB-T, VDSL, and'IEEE'802.1 la. However, it is also well known that OFDM systems are veiy sensitive to synchronization ernjrs,. which can cause .inter-carrier interfejerence (ICI) and degrade system performance.

,,

All the OFDM standards mentioned above have ded- icated pilot subcarriers to facilitate the synchronization t&ks in the receivers. Various pilot-aided carrier fre- quency offset estimation and timing frequency offset estimation algorithms have been proposed [I], 121,

131,

141, 151, [ 6 ] , [71. Most of them utilized the detected phase of the received frequency-domain complex data in the pilot subcarriers. The phase shift in the received complex data due to carrier frequency offset is identical

in all subcarriers of an

OFDM symbol if IC1 is neglected. Classen[l], Kapoor[2] and Moose(3J have taken advan- tage of this fact to build their algorithms. The phases of the received pilot-subcarrier data are extracted and the

phase difference between two consecutive symbols in a pilot subcarrier is computed in [I] and

[Z].

The phase dif-

-

algorithms may produce biased estimation when there exists timing frequency offset, which occurs frequently in most communication systems.

Timing frequency offset, unlike carrier frequency off- set, causes phase shifts that are proportional to the subcarrier index as well as the offset itself. A very popular class of schemes estimate the timing offset by computing a slope from the plot of measured pilot sub- carrier phases versus pilot subcarrier index [41, 151, [61, [7]. In 141, the slope is obtained by averaging over phase differences between pairs of adjacent pilot subcarriers. On the other hand, both the phase and magnitude of the pilot subcarriers in a single OFDM symbol are used in the slope calculation in [51. In 161 and 171 linear regression is adopted in the estimation of the slope. All

of these four algorithms examine only the phases of the pilot subcarriers in one symbol, which are influenced by not only the timing offset but also frequency selective fading. Therefore, the estimated timing frequency offset can be severely degraded. One way to get around this problem is to first take the phase difference of the same pilot subcarrier in two adjacent

OFDM

symbols so that the frequency selective fading, being same in the two symbols, will he canceled.

Sliskovic[S] proposed to jointly estimate the carrier frequency offset and the timing frequency offset. In addition, a weight is assigned to each pilot subcarrier dur- ing averaging since the subcarriers suffer from different levels of fading and thus may have different

SNR.

The timing frequency offset is estimated by first computing the phase difference between a pair of adjacent pilot

suhcarriers, computing the. difference of that amount in two OFDM symbols, and then weighted averaging. The carrier frequency offset can he estimated by first calculating the pilot-suhcarrier phase difference between two OFDM symbols, removing the quantity contributed by the previously estimated timing frequency offset, and finally weighted averaging. Thus

in

this algorithm the accuracy of carrier frequency offset estimation depends on not only the noise contained in the measurements hut also the accuracy of timing frequency offset estimation. In this paper, a weighted least squares algorithm, also based on the pilot-aided scheme, is proposed. Both AWGN and multipath fading channels are considered and the optimal weight assignment that achieves the Cramtr- Rao bound is presented.

The rest of the paper is organized as follows. The OFDM signals with both carrier and timing synchro- nization errors are analyzed in Section 11. The proposed weighted least squares algorithm is presented in Sec- tion 111. In Section IV, the simulation results that demon- strate the potential of the proposed method comparing to others are shown. Finally, a conclusion is given in Section V.

11. OFDM SIGNALS W I T H SYNCHRONIZATION ERRORS

An OFDM baseband signal is given by modulating N complex data ( A h + ) using the inverse discrete F o u r i e r t r a n s f o r m (IDFI') on N subcarriers

as

shown in Fig. I . The suhcamiers spacing is 1/T, which is the inverse of the symbol duration. The n-th time-domain sample of the i-th symbol can be expressed as

N I 2 Ak,i&2n"k/N n =

_{-N ..}

_{0 :}

.

,,%,-I d , . = - k = - N / 2 + 1 ''

N

(1) Note that in order to combat inter-symbol interference

(1%). a cyclic prefix of

Ng

samples is inserted at the beginning of a symbol.

Assume that the received signal is influenced by a mul- tipath fading channel with a channel impulse response

h ( t ) =

Ch,(t).

6 ( t - r,(t)). (2)

The amplitude and delay of the r-th path

are

denoted by

h , ( t ) and

~ ~ ( t ) .

Consequently after convolving with the channel impulse response, the received signal takes the form of Z ( t ) =

Eh$)

' d ( t - r r ( t ) )

+

" ( t ) , (3) d-,,, I Fig. I. subcarrien.

System model of a OF'DM communication system with N

In addition to multipath channel fading, oscillator mismatch and Doppler effect inflict the received signal with carrier frequency offset and timing frequency offset.' If some carrier frequency offset A f and timing frequency offset 6.T, exist, where T, is the sampling interval in the transmitter, the m-th received sample of the 1-th symbol (counting from the end of the cyclic prefix) is given by

Zm,l = z ( t ) , P A f f It=lN,(l+6)T,+N,(l+6)T.+m(l+6)T. I

m = 0,1,.

.. ,

N

- 1,

(4)

where

NT

is equal to N

+

N o .

The receiver then drops the cyclic prefix and passes the

N

samples to an

N -

point discrete F o u r i e r rmnsfom (DFT) block. After DFT, the complex data on the

k-th

subcarrier consists of three components: signal term St,!, interference term I k , l and

noise term V k J . . ,

z k , l sk,L &,t

+

vh.1. ( 5 )

If I f k represents the channel complex response

on

subcamier

k,

then the signal term can he expressed as

sk,l

= H , . e j W i ( l N r + N . ) b t t

( 6 )

&k (1 f 6 ) ' (&P) - k (7)

.

e I n + h k ( l - + )

.

S ( n d k k ) ,

where

Note that f = Af

.

T is the normalized frequency

the distonion of the kth-subcarrier data in phase and magnitude, respectively. Moreover, the synchronization error destroys the orthogonality between subcarriers and the IC1 term, Z k , I 9 is induced and it is given by.

z k , l = A ~ , ~ , H,,

.

e j 2 n k ( l N r + i v g ) O p p

' p = - N / Z + l , p # k (9)

.

, p d p d - k )

.

S ( T $ p k )

Note

that in the case with small 6 and E , S(T$kk) is close to 1 and s(?iQpk) is near zero, and the IC1 term can he ignored. Consider the case when only the carrier frequency offset exists, Sk.1 will he rotated by (in addition to H k )

(10) 1

2 s ; ( l N r

+

N s )

+

m(1 - -)

N '

Note that this phase is independent of k and is identical in every subcarrier.

On

the contrary, in the case when only some timing frequency offset 6 exists, S k , l will be rotated by (in addition to H k )

6k 1

Za-(/Nr+

N g ) + r r 6 k ( l - -) (11)

N N ' .

which is proportional to the subcarrier index

k

as well as the symbol index 1.

111.

JOINT

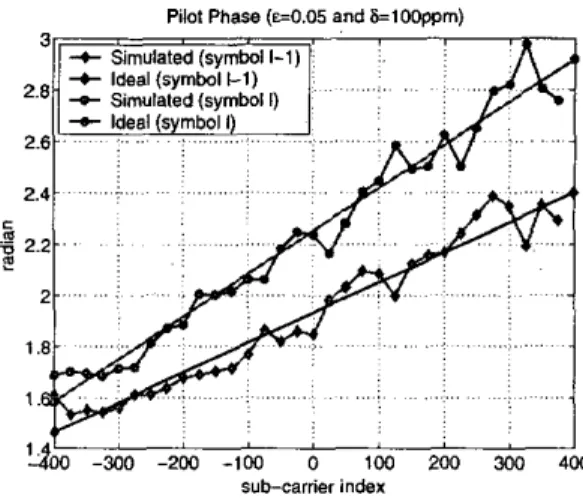
ESTIMATION ALGORITHMS In the AWGN channel, H k = 1 for all le and &,I

is distorted in phase and amplitude caused only by synchronization emors. This effect is clearly seen in Fig. 2, which illustrates the phases of suhcarrier data in two consecutive OFDM symbols when they are distorted by noise, carrier frequency offset, and timing frequency offset. The carrier frequency offset is 0.05 subcarrier

spacing

and

the timing frequency offset is 100 p,p.m. The received data contain IC1 and noise, therefore the extracted phases deviate from the two ideal straight lines. From the extracted subcarrier data phases, the least-

squares

(LS)

method can estimate the two straight lines,

from which the carrier frequency offset and the timing frequency offset can be derived. In the multipath fading channel, the complex channel response H k distorts the received data in magnitude and in phase. Moreover, signals on the deeply-faded subcarriers have low

S N R ,

while those on the subcarriers with little fading have high

SNR.

Obviously, the data phases of the subcarriers with higher SNR are much more reliable than those with lower

S N R

in

the estimation process.

We believe that the concept of weighting the data in each subcarrier is necessary because data of deeply- faded subcarriers should he assigned smaller weights to

Pilot Phase (~=0.05 and S = l w m )

sub-carrier index

Fig. 2. Phases of rubcarrier data in two OFDM symbols with 6 = 0.05. 6 = 100ppm. and Gaussian noise.

minimize their adverse effect on estimation accuracy. In addition, estimation based on the phase difference across two OFDM symbols has the advantage of removing the common channel phase. Finally, linear regression provides better estimation since it can find simultane- ously the best slope and intercept in terms of least. squared ermr. In light of all the'above considerations, we propose a weighted least squares (WLS) algorithm for joint estimation of the carrier frequency offset and timing frequency offset.

~ e t y = [yo y1

. . .

yJ- , I T represents J pilot Sukar- rier phase differences between two consecutive OFDM symbols and y, =

$(Z=i,iZ;i,,-l),

where

$0

is the phase of its argument and zj is the j-th pilot subcarrier index. Also let b = [m,d]' be an estimation of the slope m and the intercept d of the optimal straight line in the

y, versus pilot suhcrrier index plot, then y =

Xb

+

n,

where

The phase noise component

n

= [eo el

.

.

.

e ~ -rep- ~ ] ~ resents the errors in phase contributed by IC1 and AWGN

and e j = yj - $(Sz,,tS;2,1-,). The Gauss-Markov

solution for minimum-variance least-squares estimation, which achieves the Cram&-Rao bound [9], is given by

G

=

(XTWX)-lX*Wy,'

(13)

For simplicity, assume that the residual synchroniza- tion error is so small that IC1 can he neglected. The off- diagonal terms of E{nnT} are contributed by IC1 and can be ignored, hence the matrix inverse operation can he avoided and the j-th diagonal component of W, denoted

as wj, is given by

(14)

W . - o - 2

3 - e j : where

02;

is the variance of ej.

Assume that the channel response is almost static in the duration of two symbols, then y j is approximated by.

Y j =

$(ZZj,I

'

z:+l)

=

$(s,j,l

' s;j,l-l

+

SZjJ

'v;,,l-l

+ ~ ~ j , l ' ~ ; , , ~ ~ l + ~ ~ , , f ' ~ ~ j , l - l ~ = $(EsIHzj/ 3 ' 'S2(.4.,,.,)

+

SZj,l '

V&]

,+

V,,J '

s:&l

+

Vz;J ' V,:,f-l) z e j 2 9 r 3 + . . = . (15)

The first term in the right-hand side of the above equation is the desired output component with a phase related to the two synchronization errors L and

6

in &,,zj and

a

power equal to the squared received signal power. In high-SNR cases; the noise component in y j depends mainly on the two signal-noise product terms, whose power scales with

E,NoIH,,12.

Thus, assuming high SNR, wj can he approximated by [IO]

In the AWGN channel, wj is proportional to the inverse of !he Guassian

noise

power in the j-th pilot subcarrier. On the other h'and, in the multipath channel

w j scales with 'IHSjIz and'inversely with the Guassian noise power., In this case, the carrier frequency offset L

as: well as the timing frequency offset

6

can

be

derived

from'(l3) andwe have

and

IV. COMPARISON OF SIMULATED PERFORMANCE Assume that the carrier frequency offset and the timing frequency offset both exist, which is the typical d i e in communication systems. The root-mean-square

(RMS)

errors in the estimated offsets using different algorithms over a multipath fading channel are shown in Fig. 3 and Fig. 4. A carrier frequency error t = 0.05 and

a

timing frequency error

6

= 20 p.p.m. are introduced in the simulation. As can he seen from the two figures, the proposed WLS algorithm achieves, in most cases, the minimum RMS error in both carrier frequency offset estimation and timing frequency offset estimation. Note that even though a small-IC1 assumption 'is made in deriving the WLS joint estimation algorithm, the residual sydchronization error is so small in the tracking mode that the

IC1

can indeed he neglected.

V. CONCLUSION

In this paper, we proposed a joint estimation al- gorithm that can estimates both the carrier frequency offset and the timing frequency offset. With a weighted least squares technique, the proposed algorithm indeed generates offset estimates with minimum

R M S

errors. Therefore, we believe that this algorithm'can greatly en- hance the performance of OFDM-based communication receivers by reducing residual synchronization error and thus suppressing ICI.

Carrier frequency onset estimation ,... .

Ih

16 18 22 24 26 J8

SNR (dB) Fig. 3.

algorithms

Timing frequency oilset estimalion

Fig. 4 . algorithms.

.

I .

Simiilated timing frequency estimation ermn by different

R E F E R E N C E S

[I] F. Classen er al.. '.Frequency synchronization algonthmr for OFDM systems suitable for communication over frequency se- kclive fading ,channels:' in Pmc. oJ 1994 IEEE 44th Vrhindor Trchuology ConJennr.r. vol. 3. 1994. pp. 1655-1659. 121 S . K a p w r el al.. "Pilot assisted synchronization for wireless

OFDM systems over fast time varying fading channels:' in Pmr

of 19981EEE 48lh Vuhiwlor Trrh,!alogy Coq'cruncr. vol. 3. 1998.

pp. 2077-2080.

[3] P. H. Moose. "A Technique for onhogonal frequency division miiliiplexing frequency offset correnion," IEEE Trans. Commun..

vol. 42. pp. 2908-2914. Oct. 1994.

[4] D. K. Kim el 01.. "A new join1 algorithm of symbol timing

recovery and sampling clwk adjustment for OFDM systems:'

IEEE Trans. Consumer Electronics. vol. 44. Aug. 1998. pp. 1142-

1149.

IS] Y 1. Ryu CI ai.. 'Timing phase estimator overcoming Rayleigh fading for OFDM syslems." IEEE Tmm,zs. Consumer Electmdcs.

vo1:47;Aug. 2001. pp. 37&377

[6] 1. H. Ymh el 01.. "On synchronizing and deteding mulli-ramer CDMA nigna1s:'in Pmr. IEEE h t . CO,$ Universal Perroriol

Cornm,nicoIio,ls. 1995. pp. 512-516.

[7] A. 1. Coulson. 'Maximum likelihood synchronizalion for OFDM using a pilol: algori1hms:'IEEE J. S ~ l ~ c c c d Awm in Co!mnunico- iiow. vol. 19. Dec. 2001. pp. 2 4 8 6 2 4 9 4 .

[8] M. Sliskovie. "Carrier and Sampling frequency offset eslimalion and mrreclion in multicarrier systems." in P m r Globe",&.

"01. 1. 2W1. pp. 285-289.

[9] A. A. Giordano. Lean Spore Esti!ndriorl with Applicalions Io

Digirol Signal Pwrrfsing. John Wiley & sons. 1985.

[IO] Richardvan Nee and Ramjee Prasad. OFDM Wirrless Multirnedio