A novel nonsymmetric K_-Lanczos algorithm for the generalized nonsymmetric K_-eigenvalue problems

(1)

Nonsymmetric K _-Eigenvalue Problems

William R. Femg

Department of Applied Mathematics National Chiao Tung University

Hsin-Chu, Taiwan 30050, Republic of China an d

Kun-Yi Lin and Wen-Wei Lin lnstitute of Applied Mathematics National Tsing Hua University

Hsin-Chu, Taiwan 30043, Republic of China

Submitted by Richard A. Bnlaldi

ABSTRACT

In this article, we present a novel algorithm, named nonsymmetric K_-Lanczos algorithm, for computing a few extreme eigenvalues of the generalized eigenvalue problem Mx = AL%, where the matrices M and L have the so-called K +-structures. We demonstrate a K_-tridiagonalization procedure preserves the K *-structures. An error bound for the extreme K-Ritz value obtained from this new algorithm is presented. When compared with the class nonsymmetric Lanczos approach, this method has the same order of computational complexity and can be viewed as a special 2 X 2-block nonsymmetric Lanczos algorithm. Numerical experiments with randomly generated K--matrices show that our algorithm converges faster and more accurate than the nonsymmetric Lanczos algorithm. 0 Ekevier Science Inc., 1997

*This work was supported in part by the National Science Council of Taiwan, ROC, under Grant No. NSC-85-2121-M-009-009. E-mail: femg@helios.math.nctu.edu.tw.

+E-mail: d818102@am.nthu.edu.two.

‘This work was supported in part by the National Science Council of Taiwan, ROC. E-mail: wwlin@am.nthu.edu.t.

LINEAR ALGEBRA AND ITS APPLICATIONS 252:81-105 (1997)

0 Elsevier Science Inc., 1997 0024.3795/97/$17.00

(2)

82 WILLIAM R. FERNG ET AL. 1. INTRODUCTION

Many modeling problems in scientific computing require the develop- ment of efficient numerical methods for solving the associated eigenvalue problems. In quantum chemistry, for example, the time-independent Hartree-Fock model [l, 21 leads to the following generalized eigenvalue problem

Mx = ALx,

_(1.1)

where

M, L E

Rznx2*,

M = MT, L = LT,

h E C

is the eigenvalue of (1.11, and x E C2” is the corresponding eigenvector. Moreover,

M

is a so-called symmetric K+-matrix and can be represented in the block structure

&f=

A B

[

B A

1

(l-2)

with

A,

B E

R”‘“,

A = A',

B = B',

and

L

is a symmetric K--matrix

L=[-‘a _;I

(1.31

with C, A E R”lX”, C = CT, A = -AT. If we define the matrix K to be

(l-4)

where I, is the

n X n

identity matrix, then we have

and

(MK)'=MK=KM,

_(1.5)

(LK)“= -LK=KL.

_(1.6)

If matrix

L

is invertible, the generalized eigenvalue problem (1.1) can be transformed to the eigenvalue problem

(3)

That is, the generalized eigenvalue problem (1.1) is equivalent to the eigenvalue problem (1.5). Let

N s L-‘&f;

_(l-8)

one can verify that N is a 2n X 2n K--matrix [2].

In general, the matrices M and L can be very large (n = 106) and sparse, and only a few extreme eigenvalues are required. The nonsymmetric Lanczos algorithm [3] is one of the most widely used techniques for computing some extreme eigenvalues of a large sparse nonsymmetric matrix. In this approach, the matrix N is reduced to a tridiagonal matrix, which no longer has the K--structure, using a general similarity transformation. Information about N’s extreme eigenvalues tends to emerge long before the tridiagonalization process is complete. The Ritz values (eigenvalues of this tridiagonal submatrix) are used to approximate the extreme eigenvalues of N [4]. A convergence analysis for the nonsymmetric Lanczos method was recently presented by Ye in [5].

In [6], Flaschka considered the case when N is symmetric. The symmetric K--algorithm and KQR algorithm were proposed for solving problem (1.1).

In this article, we propose a new algorithm; we name it nonsymmetric K-Lanczos algorithm, for computing a few extreme eigenvalues of large sparse nonsymmetric K--matrices for problem (1.1). This new method utilizes the special properties of the K--structure, preserves the structure at each step, and reduces the K--matrix to a K_-tridiagonal matrix. The extreme eigenvalues are approximated by the K--Ritz values of the K_- tridiagonal matrix using nonsymmetric KQR or KQZ algorithm [7]. An error bound, which demonstrates the convergence behavior of this nonsymmetric K-Lanczos algorithm, is developed and analyzed for the K--Ritz values. This algorithm has the same order of computational complexity as the nonsymmetric Lanczos algorithm in terms of floating-point operations. A our numerical experiments with randomly generated nonsymmetric K--matrices show that the new algorithm converges faster than the classic nonsymmetric Lanczos algorithm. With minor modifications, the algorithm can be adapted for K+-matrices.

We organize this article as follows. In Section 2, we establish the existence of the nonsymmetric K_-tridiagonalization theorem. A new elimination procedure and the nonsymmetric KP-Lanczos algorithm is introduced in Sec- tion 3. Then we present an error bound for the extreme K--Ritz values and analyze the convergence behavior in Section 4. Numerical experiments and some remarks are summarized in Section 5 followed by the conclusion in Section 6.

(4)

84 WILLIAM R. FERNG ET AL.

2. NONSYMMETRIC K _-TRIDIAGONALIZATION

When the nonsymmetric Lanczos method is applied to a K-matrix, the algorithm treats this matrix as a general matrix and reduces it to a tridiagonal matrix which no longer has the K-structure. In this section, we shall prove that under certain conditions, if N E R 2nx2rr is a K--matrix, there exists a K+-similarity transformation X E R2” ’ 27’ such that X- ’ NX is an unreduced K_-tridiagonal matrix. That is,

where T,, T, E R”x” are tridiagonal, and

lCTl)t,t+l

I

+I(T2)i.t+l

I>

for i = 1,2,. . . , n - 1. Unlike the nonsymmetric Lanczos method, this similarity transformation preserves the K_-structure.

The following theorem can be proved immediately from theorems in [7].

THEOREM 2.1. Suppose N E R2nX2” is N K-matrix, K E R2nx2n is as

defined in (1.2) and the K_-Kylov mutm’x V = V[ N, x, n]

= x, Nx,..., _[ N”- ‘xl - Kx,

-KNx, .

. . , -Kh’-‘x] _(2.1)

for some x E R2”, has full rank.

(1) ZfX E R2nx2’r is a nonsingular K+-matrix such that R = XP ‘V is a

K _-upper triangular matrix, then H = XP ‘NX is an unreduced K--upper Hessenberg matrix.

(2) Let X E RenX2” be a K,-matrix with the first column x. If H = X-‘NX is an unreduced K--upper Hessenberg mutrix, then the K_-Kylov matrix V[ N, x, n] = XV[ H, e,,2,,, n], where V[ H, e1,2n, n] is a nonsingular K--upper triangular matrix and e,, 2n is the first column of I,,.

(3) Let H = X-l NX and H 2 Y-

’

m be K--upper Hessenberg matrices with X and Y both nonsingular K,-matrices. If H is unreduced and the first

(5)

columns of X and Y are linearly dependent, then l? is unreduced and X-‘Y is K-upper triangular.

Next we show that a K,-matrix can be factored into the product of a K-lower triangular matrix and a K-upper triangular matrix if the condi- tions are satisfied. This property is similar to the general LU-okcomposition theorem but in special K ,-structure.

THEOREM 2.2 (Real K+-LR Factorization). Let M E Rlnx2” be a K+-

matrix and be partitioned as follows:

MY

A B

[

B A’ 1

with A, B E R”’ “. Zf all the leading p rincipal subrcatrices of A •t B and

A - B are nonsingular, then there exists a K--lower triangular matrix L and a K--upper triangular matrix R such that M = LR.

Proof. Let

where I, is the n X n identity matrix. Then Z is nonsingular and

Since all leading principal submatrices of A + B and A - B are nonsingular,

A + B and A - B have the LR-decompositions, say, A + B = L, R, and

A - B = L,R,, where L,, L, are lower triangular and R, , R, are upper

triangular. Then

(6)

86 WILLIAM R. FERNG ET AL. It follows that 1 =- 2 L,R, + L,R, L,R, - L,R, L,R, - L,R, L,R, -I- L,R, = LR, where L= [

NJ, +

b?)

NJ, -

4)

G(L2 - L,) -d(L, _{+ L,) I} and R=

f<R, +

8,)

i(R, -

4)

-;(R, -R,) -;(R, + R,)

1

It is easy to check that L is 3 K-lower triangular matrix and R is a K_ upper triangular matrix. Now we prove the existence theorem for the nonsymmetric K~-Lanczos tridiagonalization.

THEOREM 2.3 (Existence Theorem). Let N be a K_-matrix. If V[iV, x, nl

and V[ NT, y, n] are nonsingular K_-Kylov matrices for some x, y E R’” such that B = V[N’l‘, y, n]“c[N, x, n] hay the real K,-LR decomposition, B = LR, then there exists a nonsingular K+-matrix X E R”’ such that T = X-‘NX is an unreduced K_-tridiagonal matrix.

Proof. Let

X = V[ N, x, n]R-‘.

Then X is a nonsingular K+-matrix. Since R is K--upper triangular, it follows from Theorem 1 that H = X-‘NX is an unreduced K--upper Hessenberg matrix. Also from the assumption B = V[ N ‘, y, nlTV[ N, x, n] = LR, we have V[NT, y, n] = XeTLT. L is K--lower triangular; hence LT is

(7)

K-upper triangular. Apply Theorem 1 once again; one obtains that G = XrNrX-r is unreduced K--upper Hessenberg. This implies that H = X-‘NX = G 7‘ is unreduced K-lower Hessenberg. Therefore

is an unreduced K_-tridiagonal matrix. ??

THEOREM 2.4. Let X and Y he nonsingular K+-matrices. Suppose that

(a) T = X-l NX and T = Y ’ NY are unreduced K _-tridiagonal matrices, (b) the first columns of X and Y are linearly dependent, and

(c) the first rows of X-’ and Y- ’ are linearly dependent; then X-

’

Y is a K.-diagonal matrix.

Proof. Since T and ? are unreduced K_-tridiagonal matrices, they can be viewed as unreduced K--upper Hessenberg matrices. By using Theorem 1, X-‘Y is a K+-upper triangular matrix. Apply the same argument once again. T’ = XTNTX-T and f’ = Y TYP T are unreduced K--upper Hessen- berg matrices; hence Y TX- T = (X-l Y jT is K+-upper triangular. It implies

that XP

'

Y

is a K+-diagonal matrix. W

We have proved that for a given K--matrix N and en-vectors x and y, if the product of K_-Krylov matrices V[NT, y, n]l‘V[N, x, n] has the real K+-LR decomposition, then there exists a nonsingular K+-matrix X such that X-‘NX is unreduced K_-tridiagonal. Similar results can be developed if the K--matrix N is replaced by a K+-matrix M.

In the next section, we introduce a new elimination procedure and derive the nonsymmetric K_-Lanczos algorithm for the unreduced K_-tridiagonal reduction on nonsymmetric K _-matrices.

3. NONSYMMETRIC K p-LANCZOS ALGORITHM

The nonsymmetric Lanczos method for extreme eigenvalue problems is to reduce matrix N E

Rznx2"

to tridiagonal form using a general similarity

(8)

88 WILLIAM R. FERNG ET AL. transformation X as [4]

ai

PI

X-‘NX = T = 0 Yzn-1 a2n

With the column partitionings, one denotes

x = [x,, . . .) Xan],

X-T=Y = [z&..., tj2J.

Upon comparing columns in NX = XT and N ?‘Y = YT T, one obtains that

and

Nx, = T~-,x~_~ + cxixj + Pjxj+l

NTyj = PI-1 yj-1 + ojyj + Yjy1/+i>

for j = l,..., 2n - 1, with yox, = 0 and /?,, y. = 0. These equations together with Y TX = I,, imply the three-term recurrence formulae for computing crj, pj, and 7,:

and

o, = yJTNxj, _(3.1)

Pj’,+ 1 = 7; = (N - ajl)xj - ‘Y~~~x,~_~, (3.2)

YjYj+l = pj = (N - aj’)Tyj - Pj-1 Yj-1. (3.3)

There is some flexibility in choosing pj and 7,. A canonical choice is to set Pj = llrjllz and yj = XT+ 1 pj*

In the previous section we proved that there exists a K+-similarity transformation such that a K--matrix can be reduced to an unreduced

(9)

K_-tridiagonal matrix. Suppose

T, =

X-‘NX=T= [ _;; _;I,

and

One wishes to be able to derive a set of formulae that are similar to the three- term recurrence formulae (3.1H3.3). H owever, there are more scalar factors oj, LSj, pj, p., yj, and qj to be determined than the identities at hand. Because of th. 1s difficulty, we develop a new elimination procedure to annihilate the lower subdiagonals fij‘s of T, so that we are able to derive the five-term recurrence formulae and propose the novel K_-Lanczos algorithm. First we prove the following lemma.

LEMMA 3.1. Suppose N is a 4 x 4 matrix with the following structure:

where

and la21l z Ibzll. Then th ere exists a 4 x 4 nonsingular K+-diagonal matrix D such that

DND-’ =

r

A *

-1

-B’ -A with

g=

(3.5)

Proof. The entry a2r is used as a “pivot” element. Depending on zero or nonzero of a21, we derive this lemma as follows.

(10)

90 WILLIAM R. FERNG ET AL. Case 1. If uzl = 0, let D be the K+-permutation matrix

then it is easy to check that DND-’ has the structure defined in (3.5).

Case II. _{If uzl + 0, ret}

D=

‘0

0 1 0 O&O 1 a!21 .+_ 10 0 0; 0 1 OL a21

then D is a K+-diagonal matrix. Since la,,l # Ib,,l, D is nonsingular and

D-1 =

One can verify that DND-’ has the structure in (3.5) ?? This elimination procedure can be generalized to the general 2n X 2n K_-tridiagonal cases. Suppose N is an unreduced K_-tridiagonal matrix with structure as defined in (3.4) but with

A= a1 c2 b, *. *. C” b,’ a,

I>

B=

(11)

and lbjl f lLjl for all j = 2,. . . , n. Without

bj #

0, for all j = 2,.

.

,

n.

Now

let

loss of generality, we assume

D, =

3 0

62

3 b,

0 0 1 0 D 1 1 1 1 0 0 1 1 1 0 0

g2

O

G

One can verify that

D,

is nonsingular and

with

--a1 * * 0 . (3.7) bz( g2h3*- b,b,) b,2 - 6,”

(12)

92

and

WILLIAM R. FERNG ET AL.

B(z) = -a’, * 0

**b2(g2b3*-**

b,&,) *

b; - 6;

-ii,

-c4 -z13 -6, -I& . _. . _. . _. . . . . . .

_.

.

_.

-z,

-6,

-z,

Here * denotes a component that has been modified. Note that the (2,l) entry of B has been eliminated.

Next we_ verify that NC’) is still unreduced by showing 16,&a - b,b,l f

Ibzb, - b,b,l. Suppose, otherwise, one has 6,6s - b,b, = &(b,b, -

b,6,). It implies (b, f b,Xb, f g3) = 0. However, this contradicts that the

assumption lb,1 z lb,1 and lb,1 f Ibnl. Th us, all corresponding lower subdiag- onal entries of Ac2) and B(‘) are unequal in absolute value. This means NC2) = D, ND,’ is maintained to be unreduced K_-tridiagonal.

This procedure can be repeated for i = 3, . . . , n, by defining D . g,‘o

b;“’

0 1 1 1 1 . &,!i)

b!“’

I 0 ith row (n + i)th row

(13)

where b,!‘) and bii) are the (i, i - 1) entries of A(‘) and I?(“), respectively. A(‘) and B(‘) denote the matrices after (i - 1) modifications. Note that whenever the “pivot” element bi’) equals zero, one can choose Di to be a proper K+-permutation matrix. By letting D = D,, D,_1 1.. D,, we proved the following theorem.

THEOREM 3.1. Suppose

is a 2n X 2n unreduced K _-trtdiagonal matrix; then there exists a nonsingu- lar K,-matrix D such that the lower subdiagonals of B are annihilated. That is,

DND-’ = A(“) B(n)

1

-B’“’ -A’“’

’

where A’“) remains tridiagonal and B’“’ is upper bidiagonal.

With this elimination procedure and the result of Theorem 3, we have the following theorem.

THEOREM 3.2

(

K-Lanczos Reduction Theorem). Let N be a K_-matrix.

Zf

V [ N, x, n] and V [ N T, y, n] are nonsingular K_-Krylov matrices for some x, y E R2” such that V[NT, y, nITVIN, x, n] has the real K+-LR decompo- sition, then there exists a nonsingular K,-matrix X E R’” such that

X-‘NX=T= [ _;I $1,

where T, is trtdiagonal and T, is upper bidiagonal.

(3.8)

With this theorem, we derive a set of five-term recurrence formulae, hence the novel approach: the K_-Lanczos algorithm. These formulae are similar to the three-term formulae (3.1)~(3.3) for nonsymmetric Lanczos algorithm.

(14)

94 WILLIAM R. FERNG ET AL. With column partitionings, we denote

x=[v-,

,...‘~,IKZJ$

,.*.>

a,],

(3.9)

x-T=y=[yl>y2

,...>

ynIKy1Jy2

>..., KY,],

(3.10)

and

P2 ff2

T,= . T2 =

Upon comparing columns in NX = XT and N r Y = YT ‘, we obtain

Nxj = yjxj_l + ajxj + ~j,lxj+l - $‘Gcj_, - tijZCxj, (3.12) and

NTYj

=

Pjyj-1 +

Cyjyj + T+lyj+l +

‘j&/j + Yj+l&/y+l, (3.13)

forj = l,...,n - l,withx, = y,, = 0. These identities together with Y TX = 12” imply

oj = y,rNxj, (3.14)

Gj = y,rNICrj, (3.15)

and

~j,lxj,l = rj+l = Nxi - ‘Y~x~-~ - ojxj + qj&j_l + GjKxj, (3.16)

(3j+lz2n + ?j+lK)Yj+l =Pj+l = NTyj - /3jyj_l - ojyj - GjKyj. (3.17) There is some flexibility in choosing the scalar factor fij+ 1. An intuitive choice is to set pj+, = l(rj+llls; then one can derive Y,+~ = xi’,,~,+~, and r;.+, =

(15)

C&j+

l)*Pj+

1’ If I~j+ll z I?j+ll, one obtains yj+l = (T+lz2n + Tj+IK)-lpj+l Yj+l = 2 Z (3.18) Yj+ 1 - Yj:1

We now summarize these mathematical formulations in the following,

which we call nonsymmetric K_-Lanczos algorithm.

Algorithm: Nonsymmetric K_-Lanczos

Given nonzero vectors x1 and y1 such that x:y, = 1 and

II412 = II yJl2 = 1. Set PI = y1 = 1, q1 = 0. Set x,, = y, = 0, and p, = yl. Set j = 1. Gj = y,?N’ocj; j=j+1; rj=Nx. 1- _Yj-l*j-2 _{- aj-lxj+lYj-l} pi = NTl;j_l - Pj_lyj_2 - - ‘ocj-2 + ~j-l”j-l Pj = Ilrjlle; aj-lYj-l - Gj_,Qj-l; xj = rj/Pj; T Yj = xjPj; jJ. = (Kxj)pj; End while End Algorithm Let Xj= [X1,X2,...,XjIKrl,~2,...,~j],

(16)

96 WILLIAM R. FERNG ET AL. and

?;=

CTl)j CT2)j

-(T,)j

-(Tl)j

₁

’

where (Tl)j and (T,)j are the leading j-by-j principal submatrices of T, and T,, respectively. It can be verified that

and

where ej, 2n is the jth column of I,,. Thus, whenever pJ = ll~jll~, the columns of Xj define an invariant subspace for N. Termination in this regard is therefore a welcome event. However, if l-y,1 = +;I, then the iteration terminates without any invariant subspace information. This problem is one of the difficulties associated with Lanczos-type algorithms.

Eigenvalues of 2; are called the K-Ritz values and used for the approxi- mations of N’s eigenvalues. Note that K is of the form defined in (1.2), and the computations fij and Kyj are free and can be viewed as permutations. It should not be counted as matrix-vector multiplications. Therefore, this nonsymmetric K_-Lanczos algorithm has the same order of computational complexity as the nonsymmetric Lanczos algorithm in terms of floating point operations.

4. ERROR BOUND ANALYSIS

An error bound for the K--Ritz values obtained from the nonsymmetric K_-Lanczos algorithm is presented in this section. Hereinafter 9”k is the set of polynomials of degree less than or equal to k. The next theorem estab- lishes a relation between a 2 X e-block tridiagonal matrix and its leading principal submatrices.

THEOREM 4.1. Let i;, E R2”x2n

2 x 2 blocks and fin E R2mx2m

be a block tridiagonal mutr$ with be a leading principal submatrix of T,,. Then [e 1,2n9

e2,2nlHf(~)[e1,2~~e2.2nl

(17)

for all

f EL@‘- ‘,

where ei,2n and ei,2m are the ith columns of I,, and I,,, respectively.

Proof. The proof follows from Theorem 3.3 in [51.

Suppose T,, is the K_-tridiagonal matrix obtained from applying rr iterations of the nonsymmetric K_-Lanczos algorithm to a nonsymmetric K_-matrix N and T, is a K-principal submatrix of Tn. One can find permutations matrices fIsn E R2”x2n and II,, E R2mx2m such that GA~2” and GmT,,nIBm, are block tridiagonal matrices with 2 X 2 blocks. Following from the previous theorem, we have

[e

1,2nr e2,2”lHn2Hnf(Tn)n2n[e1.2n. e2.2J

= [e 1,2rn~ e2,2mlHn,“,f(T,)n2,[e,,2,7 e2,2J (4.2)

for all f ~9~“‘~~. Since 112” and f12,,, are permutation matrices, (4.2) becomes

b

1,2npe n+~,2nlHf(~n)[el,2n~en+l,2nl

= [e 1,2m> e,+l.2,1Hf(~m)[el,2,~ %+1,2A (4.3) for all fCYzm-l.

For simplicity, our error-bound analysis focuses on the case where T,, and

T, are both diagonalizable. Suppose T, = XHAY and T,,, = P “00, where A=diag(A, ,..., &I-A, ,..., -A,)=

1

Al o -A 0

1

,

1

and

0

=diag(fI, ,..., 0,l -8, . . . . -0,) =

[

0,

o _.

0 1 ,

1

(18)

98 WILLIAM R. FERNG ET AL.

for all f E.c?~~-‘. This implies

XT

f(A,>

[

I[

0 XH

_n+l 0 _f(

_-*I)

1

Yl*

Yn+J

P,H

f(@J

=

[

I[

0

PH n+l 0

f( -@J

_I

[41>

4.+11*

(4.5)

Here xi, yi,

pi,

and

qi

are the ith column of X, Y, P, and Q, respectively. Denote (1) Xl x1 =

1

(2) ’

1

Xl

where x$‘), xf’ E R”. Using the similar notation for xnfl, yl, Y”+~, p,,

P n+l, 411 and qn + 1, we obtain the identity from (4.5),

(XII) +

P)"(f(W +f(

-A,))(

Y'l"

+

Y!2')

=

₍

_P'll'

₊

_Pi2')H(f(@,) _{+f(-@,))(q(,')}

₊

_d2’)

_(4.6)

for all

fE.Pyazmel.

Let

g(nl)

=f(A,>

+f(-A,>,

g ~9""~~.

Then

(4.6)

can be rewritten as

2

g(hi)(fi,l +

ii!

n+i.l)(Yi,l + Yn+i,l) i=l (4.7) Define and (k) = El inf m=l p(x)l, pE.@,p(hl)=l XES (4.8)

(19)

where S and s are two disjoint sets. An error bound for the extreme K-Ritz values obtained from the nonsymmetric K_-Lanczos algorithm is derived in the following theorem.

THEOREM 4.2. Suppose T,and T,,, are diagonalizable so that ACT,) =

{A,, . . . . A” ) -A, ,..., -A,} and ACT,) = {O,, . . . , 0, 1 - 8,, . . . , - 0,). As-

sume that A, is the largest eigenvalue in magnitude of T,, and ( A, - 13~1 =

minj(Al - 8.1. Let (TV = (A,,. .., A,} and ~9~ = IO,, . . . , 19,). Zf crl U tF1 =

S, U S, wzt 42 S, and S, disjoint, and s = lS,I < 2m - 3, then

14 -

a

G

&(12m-3-s)(s1)S1(s2,s1)

lxll +

xn+l,lllly

+ y

11 n+l,l

I

x

l

klxi,l +

‘n+i,lJ

IYi,l +

Yn+i,ll

i=2

+ ClPi,l + Pn+i,lIl9i,l +

9m+i,ll .

i=2 1

(4.10)

Proof. Substituting g(x) = (r - B,)h(xKI,,,Jx - A) for any h E

L?~“‘-~-~ with h(A,) = 1 into (4.7), one obtains

The error bound (4.10) follows immediately.

In [5], Ye presented a convergence analysis for the nonsymmetric Lanczos algorithm. Error bounds for Ritz values and Ritz vectors were established. In [6], Flaschka discussed the error bound from applying Lanczos-type algorithm to symmetric K--matrices. If we apply the nonsymmetric Lanczos algorithm on K-matrix N to obtain a tridiagonal matrix T,,, after m iterations and

(20)

loo WILLIAM R. FERNG ET AL.

THEOREM 4.3. Suppose that N and T, are diagonalizable with u(N) =

IA 1,...,A,,-Al,..., -A,,} and a(T,,,) = (O,, . . . , 0,). Assume that 1 A, -

8,) = minj]h, - $1, and let a, = (A,, . . . , A,, -A,, . . . , -A,}, 3s = (es,. . . , 0,). Zf us U G2 = fl U tfz with ffl and $ disjoint, and s = l&l <

2m - 2, then

IA, -

8,l <

E~“‘-“-“)($)(~

s,)

x (Xff2/Yi,112 + C:‘i21qi,112)1’2

]Yi,i] (4.11)

Following from the discussion in [5] we analyze the magnitude of #)(Si)

as follows. Suppose S, lies inside an ellipse E and A, lies on the major axis of E but outside S,. Let 1 Ai ] = d and the length of foci and semimajor axis of E

are c and a, respectively. Then 0 < c Q a < d. Let T,(x) be the Chebyshev polynomial of degree k on [ - 1, I] (see [S, 91). Then

min _max]?+-)] _{= mEa$pk(r)I} ₌

Tk(U/C)

pE9k,p(A*)=l xeE T (d/c) ) k where p,(x) = Tk((d - x)/c)/Tk(d/c) [8l. Hence

&I”‘(

S,)

=G Tk(

a/c>

Tk(d/c) *

(4.12)

Since 1 Q a/c < d/c, we have T,(a/c) < Tk(d/c). Furthermore, if a +Z d,

that is, Ai is well separated from the ellipse E, then .sik)(S1) is small. The

bigger the difference between a/c and d/c, the smaller the bound of (4.12). Note that d/c is a measure of separation of A, from E, and a/c is a

measure of flatness of the ellipse E.

On the other hand, if s = ] S, 1 is small, 6,( S,, S,) is a bound number. If s is large and, in addition, ]x - Al < 1 A, - A] for most A E S, and any x E S,, then S,(S,, S,) is a product of s numbers (see (4.9)), most of which are less than one. Hence it is a small number.

(21)

Thus, for an extreme eigenvalue h,, we can partition (+i U G1 into a union of S, and S, so that s is small and S, lies in a flat ellipse, which is well separated from A,. Then Theorem 4.2 says that we can expect a good approximation bo_und for A,. By comparing Theorems 4.2 and 4.3, since the

(

S, 1 is less than

(

S, 1, (4.10) is a tighter error bound.

5. NUMERICAL EXPERIMENTS AND REMARKS

In this section, we use several numerical experiments to access the viability of the proposed nonsymmetric K_-Lanczos algorithms to extract the eigenpairs for the K_-eigenvalue problem (1.5). In the experiments, we focused on finding the eigenvalues with maximal absolute values and the corresponding eigenvectors. Based on the numerical results, we compare the convergence behavior and numerical efficiency of this novel structure- preserving algorithm with the conventional nonsymmetric Lanczos algorithm. The results reported herein were obtained using Pro-Matlab 3.x. Random K-matrices with known exact eigenvalues are generated. The spectral distri- butions of these random K-matrices are manipulated to be clustered along the real axis and imaginary axis to match the typical phenomena arising in the time-independent Hartree-Fock model. The ratios of the largest eigenvalue in magnitude to the second largest, lh,(/Jh,l, are all less than LO2 in order to test the robustness of the algorithms. Many experiments have been conducted and we report here only a few of them in Table 1, which shows the number of iterations required for the K-Ritz value and Ritz value to converge to the largest eigenvalue in magnitude for matrices of different sizes. Figures l-3 illustrate the convergent behavior of these two algorithms for the first three testings. We note that the results in Table 1 are typical among all testings.

TABLE 1

COMPARISON OF NUMBER OF ITERATIONS REQUIRED TO CONVERGE TO THE LARGEST EICENVALUE IN MAGNITUDE

Size of matrix N Nonsytn. K_-Lanczos Nonsyrn. Lanczos

500 21 35

1000 31 51

5ooo 82 113

loo00 84 126

(22)

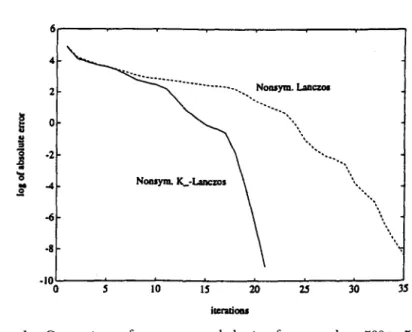
102 WILLIAM R. FERNG ET AL FIG. 1. matrix. 4- -8 - ': -10 0 5 10 15 20 25 30 3s iuxatiau

Comparison of convergence behavior for a random 500 X 500 K-

FIG. 2. Comparison of convergence behavior for a random 1000 X 1000 matrix.

(23)

40’ J

0 20 40 60 80 100 120

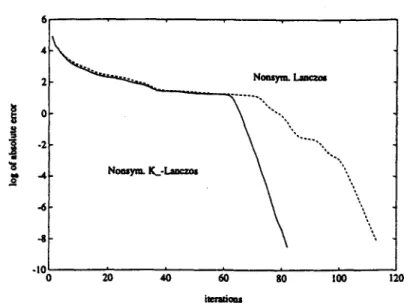
FIG. 3. Comparison of convergence behavior for a random 5000 X 5000 K_- matrix.

On the basis of these results, we observe that the proposed nonsymmetric K_-Lanczos algorithm converges faster in terms of the number of iterations

to converge than the classic nonsymmetric Lanczos approach in all experi-

ments we conducted. Some remarks are in order.

1. After j iterations, nonsymmetric K_-Lanczos algorithm produces a

2j X 2j k _-tridiagonal matrix, while nonsymmetric Lanczos algorithm pro-

duces a j x j tridiagonal matrix. The computational complexities for the

nonsymmetric K_-Lanczos reduction and the nonsymmetric Lanczos reduc-

tion are approximately even.

2. The KQR algorithm [6] or KQZ algorithm [7] should be applied to

compute the K-Ritz values from the K_-tridiagonal matrix. On the other

hand, the QR algorithm [lo, 11, 121 or QZ algorithm 1131 can be applied for computing the Ritz values from the tridiagonal matrix. The computational

cost for obtaining the same number of K-Ritz values via KQZ algorithm and

Ritz values via QZ algorithm are equal [7].

3. If the extreme eigenvalue in mag@ude A, of a K-matrix N is

complex, it follows that A,, A,, -hi, -A, are all extreme eigenvalues in

magnitude of N. There will be four K-Ritz values obtained at one time from

(24)

104 WILLIAM R. FERNG ET AL.

ues at the same time. However, the Ritz values produced by the nonsymmetric Lanczos algorithm cannot attain this behavior.

4. If q is the 2j X 2j K_-tridiagonal matrix produced by the nonsymmetric K_-Lanczos_ algorithm, there exists a permutation matrix IIZj such that IIzj?;IIi; = I; is a 2 X 2-block tridiagonal matrix. Indeed, nonsymmetric K_-Lanczos algorithm can be viewed as a special 2 X 2-block nonsymmetric Lanczos algorithm. Hence better convergent rate can be expected.

5. Neither the nonsymmetric Lanczos algorithm nor the 2 X 2-block nonsymmetric Lanczos algorithm can maintain the K_-structure like the nonsymmetric K_-Lanczos algorithm does.

6. One may construct counterexamples to make the algorithm break down. However, the breakdown situation has not been observed in our numerical experiments with randomly generated K_-matrices.

6. CONCLUSION

In this article, we propose a novel method, the nonsymmetric K_- Lanczos algorithm, for solving the K_-eigenvalue problems, Nx = Ax, hence the generalized eigenvalue problems Mx = ALx. We proved the existence of K_-tridiagonalization theorem, developed a new elimination procedure, and derived an error bound for the extreme K--Ritz value. Numerical experiments show that nonsymmetric K_-Lanczos algorithm converges faster than the classic nonsymmetric Lanczos algorithm in all randomly generated test K--matrices. We remark that the error bound is not intended to provide a practical computable estimation of the number of iterations required, but rather to illustrate the convergence behavior of the nonsymmetric K_-Lanczo algorithm.

REFERENCES

1. J. Olsen, H. J. A. Jensen, and P. Jorgensen, Solution of the large matrix equations

which occur in response theory, ]. Cornput. t’hys. 74:265-282 (1973).

2. J. Olsen and P. Jorgensen, Linear and nonlinear response functions for an exact

state and for an MCSCF state, J. Chem. Phys. 82:3235 (1985).

3. B. N. Parlett; D. R. Taylor, and Z. A. Liu, A look-ahead Lanczos-algorithm for

unsymmetric matrices, Math. Comput. 44:105-124 (1985).

4. G. H. Golub and C. Van Loan, Matrix Computations, 2nd ed., Johns Hopkins

Press, Baltimore, 1989.

5. Q. Ye, A convergence analysis for nonsymmetric Lanczos algorithms, Math.

(25)

6. U. Flaschka, Eine variante des Lanczos-algorithmus fuer grosse, duenn besetzte symmetrische Matrizen mit Blockstruktur, Doctoral Dissertation, Bielefeld Uni- versitaet, 1992.

7. U. Flaschka, W. W. Lin, and J. L. Wu, A KQZ algorithm for solving linear- response eigenvalue equations, Linear AZgebra Appl. 165:93-123 (1992). 8. T. A. Manteuffel, The Tchebychev iteration for nonsymmetric linear systems,

NUWUX Math. 28:307-327 (1977).

9. T. A. Manteuffel, Adaptive procedure for estimating parameters for the nonsymmetric Tchebychev iteration, Numer. Math. 31:183-208 (1978).

10. J. G. F. Francis, The QR transformation: A unitary for the solution of the LR transformation, Cornput. J. 4:332-334 (1961).

11. V. N. Kublanovskaya, On some algorithms for the solution of the complete

eigenvalue problem, USSR. Comp. Math. Phys. 3637-657 (1961).

12. H. Rutishaueser, Solution of eigenvalue problems with the LR transformation, Nat. Bur. Stand. App. Math. Ser. 49:47-81 (1958).

13. J. Olsen, H. J. A. Jensen, and P. Jorgensen, Solution of the large matrix equations which occur in response theory, J. Comput. Phys. 74:265-282 (1988).