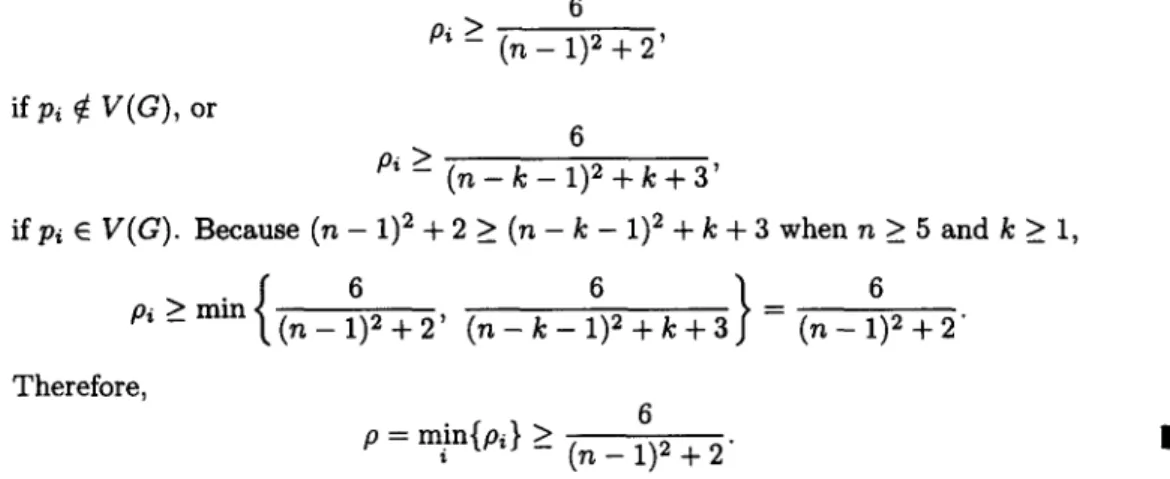Recursive constructions for perfect secret sharing schemes

P E R G A M O N Computers and Mathematics with Applications 37 (1999) 87-96 An Intqm'~llonal ,Journal

computers &

msthemati

R e c u r s i v e C o n s t r u c t i o n s for P e r f e c t

S e c r e t S h a r i n g S c h e m e s

H U N G - M I N SUN

Department of Information Management Chaoyang University of Technology

Wufeng, Taichung County Taiwan 413, R.O.C. hmsunQma±l, cyut. edu. tw S H I U H - P Y N G S H I E H

Department of Computer Science and Information Engineering National Chiao T u n g University

Hsinchu, Taiwan 30050, R.O.C. sspQcs£e, nctu. edu. tw

(Received May 1997; revised and accepted March 1998)

A b s t r a c t - - A secret sharing scheme is a method which allows a secret to be shared among a set of participants in such a way that only qualified subsets of participants can recover the secret. A secret sharing scheme is called perfect if unqualified subsets of participants obtain no information regarding the secret. The information rate of a secret sharing scheme is defined to be the ratio between the size of secret and the m a x i m u m size of the shares. In this paper, we propose some recursive constructions for perfect secret sharing schemes with access structures of constant rank. Compared with the best previous constructions, our constructions have some improved lower bounds on the information rate. © 1999 Elsevier Science Ltd. All rights reserved.

Keywords--Cryptography, Secret sharing scheme, Information theory, Access structures.

1. I N T R O D U C T I O N

A secret sharing s c h e m e is a m e t h o d which allows a secret K to be shared a m o n g a set of participants P in such a w a y that only qualified subsets of participants can recover the secret [1,2]. T h e information kept by each participant is called share. T h e collection of subsets of participants that can reconstruct the secret in this w a y is called access structure, denoted b y r. It is natural to require r to be monotone, t h a t is, if X E r and X C X ' C_ P , then X ' E r . A minimal qualified subset Y E r is a subset of participants such t h a t Y' ~ F, for all y t c Y. The basis of F, denoted by r0, is the family of all minimal qualified subsets. For any r o C_ 2 P, the closure of Fo is defined to be cl(F0) = {X ~ : 3 X • r 0 , x c X ~ c_ p } . Therefore, an access structure F is the same as the closure of its basis r0, cl(Fo). In the special case where F = {A [ A C_ P and IAI > m}, the secret sharing scheme is called an (m, n)-threshold scheme [3,4], where IPI = n. A secret sharing scheme is called perfect if unqualified subsets of participants obtain no information regarding the This work was supported in part by the National Science Council, T~iwan, under Contract NSC-87-2213-E-324-003. 0898-1221/99/$ - see front matter (~) 1999 Elsevier Science Ltd. All rights reserved

PII: S0898-1221(99)00049.8

secret [5,6]. It means t h a t the prior probability

p(K

= K0) equals the conditional probability

p(K = Ko I

given any shares of an unqualified set). The information theoretic models for threshold schemes and secret sharing schemes were defined by Karnin et

al.

[7] and Capocelli

et al.

[8], respectively. We refer to Gallager [9] and Hamming [10] for a treatment of information theory. Following the approach of [8], we can state the requirements for a secret sharing scheme by using the entropy function H as follows:

(1) any qualified subset can reconstruct the secret

V x e r H ( K

] X) = 0, and (2) any unqualified subset has no information on the secret

V x ~ r H ( K I X ) =

g ( g ) .

An important issue in the implementation of perfect secret sharing schemes is the size of shares. Let K be the secret space and S be the maximum share space. The information rate for a secret sharing scheme is defined as p = log 2

]K]/log

2 ]S] (see [5]). The information rate for share Si is defined as p, = log 2 ]KI/log 2 ]S~], where S5 is the share space for Si. We will use the notation

PS(F, p, q)

to denote a perfect secret sharing scheme with access structure F and information rate p for a set of q keys. Given any access structure F, Ito

et aL

[2,11] showed that there exists a perfect secret sharing scheme to realize the structure. Benaloh and Leichter [1] proposed a different algorithm to realize secret sharing schemes for any given monotone access structures. In both constructions, the information rate decreases exponentially as a function of n, the number of participants. After that, many researchers focused on studying the perfect secret sharing scheme for graph-based access structure F having basis F0, where F0 is the collection of the pairs of participants corresponding to edges [5,6,8,12-16]. Among these constructions, Stinson [16] proposed the idea of decomposition construction which is more general t h a n previous constructions [5,8,12-15]. In addition, he proved that, for any graph G with n vertices having maximum degree d, there exists a perfect secret sharing scheme for the access structure based on G in which the information rate is at least

2/(d +

1). Recently, Blundo

et aL

[17] showed that Stinson's lower bound is tight.

The rank of an access structure F is the maximum cardinality of a minimal qualified subset. An access structure is uniform if every minimal qualified subset has the same cardinality. Therefore, the graph-based access structure is the case of access structure with rank two. Perfect secret sharing schemes with access structures of constant rank were studied by Stinson [15]. He applied Steiner systems to construct perfect secret sharing schemes with access structures of rank three. The constructed secret sharing scheme has the information rate

4 ( n - 1 ) ( n - 2)' if F is nonuniform and n - 2, 4 (mod 6) or

6 p_>

(n- l)(n- 2)'

if F is uniform and n -- 2,4 (rood6), where n is the number of participants. Note t h a t if n doesn't satisfy the condition: n - 2,4 (mod6), it is necessary to find an n' > n such that n' = 2, 4 (rood 6). The degree of a participant in a secret sharing scheme with access structure cl(F0) is defined to be the number of subsets in F0 which contain the participant. Based on the edge-colourings of bipartite graphs, Stinson [15] also studied the construction of secret sharing schemes with access structures of rank m. The constructed secret sharing schemes have the information rate

m

( 2 m - 1 ) . m - 2 + d

Perfect Secret Sharing Schemes 89 In this paper, we propose some recursive constructions for perfect secret sharing schemes with access structures of constant rank. If F is an access structure (either uniform or nonuniform) of rank three on n participants, we show t h a t there exists a secret sharing scheme with information

rate 6

p>

(n - 1) 2 + 2'

for n > 5. If F is a uniform access structure of rank m on n participants, we show t h a t there exists a secret sharing scheme with information rate

n - m + l >

(:)

Compared with the best previous constructions [15], our constructions have some improved lower bounds on the information rate.

2. P R E L I M I N A R I E S

Suppose F is an access structure having basis F0. A A-decomposition of F0 consists of a collection { F 1 , . . . , Ft} such t h a t the following requirements are satisfied.

(1) Fh C_ F0 for 1 < h < t.

(2) For each X E F0, there exist at least A indices il < . . . < ix such t h a t X E Fij for

I < j < A .

Let P h be the set of participants in a scheme with access structure cl(I"h). Stinson [16] proposed the Decomposition Construction (DC) for secret sharing schemes. T h e proposed construction is more general t h a n other well-known constructions [5,8,12-14].

THEOREM 2.1. DECOMPOSITION

CONSTRUCTION,

DC. (See [16].) Let F be an access structure on n participants, having basis F0, and suppose that { F 1 , . . . , Ft} is a A-decomposition of F0. A s s u m e that for each access structure cl(Fh), there exists a perfect secret sharing scheme with information r a t e Pih for each Pi E P h , and a set of q keys. Then there exists a P S ( F , p, q~ ), where

p = m i n ~ (1/pih) : l < i < n . {h:p~EPh}

Let's consider the case when the basis of an access structure is a graph and l"i's are complete multipartite graphs. Because there exists a P S ( c I ( G ) , p = 1, q) for any complete multipartite graph [5], we can obtain the following theorem.

THEOREM 2.2. (See [6,16].) Suppose access structure G is a graph with vertex set V and edge set E for which a complete multipartite covering exists, say I-I = { G 1 , . . . , Gt}. For each vertex v E V define P~ = [{i : v E V~}[, where V~ denotes the vertex set of Gi. For each edge e E E defineTe = t{i : e E Ei}[, w h e r e E i denotes the edge set of Gi. Let R = max{P~ : v E V} and T = min{Te : e E E}. Then there exists a P S ( c l ( G ) , p , qT), where q is a prime power and p >_ T / R .

B y decomposing graph into stars, Stinson [16] showed t h a t for any graph G with n vertices having m a x i m u m degree d, there exists a perfect secret sharing scheme for the access structure in which the information rate is at least 2 / ( d + 1). In the following, we propose a construction which is similar to the one proposed by Stinson [16].

We assume t h a t P = { P l , P 2 , . . . P n } is the set of participants corresponding to the vertices of the graph G, and the secret/iF -- (K1, K2) is taken randomly from GF(q) x G F ( q ) , where q is a prime and q > n. Let f ( x ) = K2x + K1 (rood q). yl is computed from f ( x ) as follows:

Obviously, given yi and yj, for i ~ j, f ( x ) can be determined uniquely. Therefore, one who gets two or more yi's can recover the secret K . However, one without knowledge of any yi obtains no information on the secret. Note t h a t one who gets one Yi can obtain partial information on the secret.

T h e dealer selects n r a n d o m numbers, r l , . . . , rn over GF(q). The share of participant p, is given by

Si = (ai,1, • • • ,ai,t,. • • ,aS,n), where 1 < t < n, ai,t = ri(mod q), ai,t = rt + y t ( m o d q ) , a,,t is empty, i f t = i, if ~ is an edge of G, and if t ~ i and ~ - ; is not an edge of G.

Thus the constructed secret sharing scheme is a perfect secret sharing scheme with access struc- ture G and information rate 2 / ( d + 1).

THEOREM 2.3. f f F is a uniform access structure of rank two and degree d, then there exists a P S ( r , p, q2), where p > 2 / ( d + 1).

PROOF.

(I) First, we show t h a t the above constructed secret sharing scheme for g r a p h G is perfect. (a) Let X be a subset of participants and X E F. So, there exists p i , p j • X ( i ~ j ) such

t h a t PiPj is an edge of G. Therefore, participant pi owns ai# = ri and ai,j = rj + yj, and participant pj owns a j j = rj and aj,i = ri + Yi. Thus, participant Pi and participant pj can recover yi and yj, and t h e n recover the f ( x ) and the secret K . (b) Let X be a subset of participants and X ~ F. Therefore, for any pair of participants

p i , p j • X ( i ~ j),~=(~ is not an edge of G. We assume t h a t X can recover yi. Therefore, there exists participant Pi who owns ai,~ = ri and participant pj who owns aj,i = ri + yi . Thus ~-pj is an edge of G. This is a contradiction to t h a t pipj is not an edge of G. Hence, X cannot recover any yi. T h a t is, X obtains no information on t h e secret K .

(II) Second, we show t h a t the above constructed secret sharing scheme has information rate 2/(d + 1).

T h e share of participant pi is an n-dimeusional vector. Except t h a t ai,j's (for all j, ~ ~ E ( G ) ) are empty, every a i j is over GF(q). Therefore, the size of share S~ is log(qd'+l), where di is the degree of vertex Pi of G. T h e m a x i m a l size of the shares is log(qd+l), where d is the m a x i m u m degree of G. T h e size of the secret is log(q2). Thus, the information rate of the secret sharing scheme is

2 • log q 2

P = (d + 1) • logq d + l |

3. S E C R E T S H A R I N G

S C H E M E S W I T H

A C C E S S S T R U C T U R E S OF R A N K

T H R E E

In this section, we propose a decomposition construction of perfect secret sharing schemes with access structures of r a n k three, and evaluate the information rate of the constructed scheme. For an access structure of r a n k three, with basis Fo, we can decompose Fo into {F1, F2} such t h a t r0 = F1 U F2 where cl(F1) is a uniform access structure of rank two and cl(F2) is a uniform access structure of r a n k three.

Assume t h a t P = (Pl, P2, • • •, Pn } is the set of participants and the secret K = (K1, K2, K3, K4, K s , K s ) is taken r a n d o m l y from (GF(q)) 8, where q is a prime and q > 2n + 2. Let f ( x ) = K6x 5 + K s x 4 + Kax 3 + K3x 2 + K2x I + K1 (modq). y~ is c o m p u t e d from f ( x ) as follows:

Perfect Secret Sharing Schemes 91 Thus one who gets six or more yi's can recover f(x) and then the secret K . However, one without knowledge of any yi obtains no information on the secret.

We use G to denote the access structure cl(F1) whose rank is two. From Section 2, we know t h a t there exists a graph-based secret sharing scheme realizing cl(Fl) in which the secret is

(Y2n+l, Y2n+2)

and the share of participant p~ is Si(G).

In addition, we define Gi, for 1 < i < n, is the graph with vertices V(Gi) and edges E(Gi),

where

V(GO = {p~ [ for all p3,where {p~,p~,p~} ~ F2} and

E(Gi) = { ~ [ for all p - - ~ , w h e r e {pi,pj,p~} • F2}.

T h e dealer selects 2n random numbers, r l , . . . , r2n, over GF(q). As the construction in Section 2, there exists a secret sharing scheme realizing Gi in which the secret is (ri + yi, rn+i + yn+i) and

the share of participant p1 is S~(Gi) for p~ • V(Gi).

T h e share of participant pi is given by

Si = <ri, rn+i, ai,1,..., ai,t,..., ai,n, S~(G)),

where 1 < t < n,

a~,t = & ( V d ,

ai,t = (rt + yt,rn+t + Yn+t), ai,t is empty,

if p~ • V(Gt),

if ~ • E(G),

otherwise.

and

Thus the constructed secret sharing scheme is a perfect secret sharing scheme realizing the access structure with basis F0.

THEOREM 3.1. / [ r ~ an access structure (either uniform or nonurdform) of rank three on n participants, then there exists a PS(F, p, q6), where

6 p >

( n - 1) 2 + 2' PROOF.

PART I. First, we show t h a t the above constructed secret sharing scheme is perfect.

(a) Let X e cl(F2) be a subset of participants. So, there exists P~,Pj,Pk E X ( i # j # k) such t h a t {Pi,pj,pk} E F=. Participant p~ owns r~, rn+~, S~(Gj), and Si(Gk). Participant pj owns rj, r,~+j, Sj(G~), and Sj(Gk). Participant Pk owns rk, r,~+k, Sk(Gi), and Sk(Gj).

From Sj(G~) and Sk(G~), they can recover ri + yi,rn+i + Yn+~ because PjPk is an edge of G~. From S~(Gj) and Sk(Gj), t h e y can recover rj + yj,rn+j + Yn+j because P~Pk is an edge of Gj. From S~(Gk) and Sj(Gk), they can recover rk + yk,r,t+k + Yn+k because p~pj

is an edge of Gk. Thus, participants p~, pj, and Pk can recover y~, Yn+~, Yj, Y,~+j, Y~,

and Yn+k, and t h e n recover the f(x) and the secret K .

Now, we consider the case of X ~ cl(P2) but X • cl(F1). Let X be a subset of participants which satisfies X ~ cl(F2) but X • cl(F1). So, there exists Pi,pj • X ( i # j) such that

{p~,pj} • F1. Participant p~ owns r~, rn+~, a~,j = (rj + yj,rn+j + y,~+j), and S~(G).

Participant pj owns r j , rn+j, aj,~ = (r~ + y~,rn+~ + yn+~), and Sj(G). T h e y can recover

Yi, Yn+i, yj, Yn+j, Y2,~+1, and yo.n+2, and then recover f(x) and the secret K .

(b) Let X ~ F be a subset of participants. Therefore, there do not exist three participants p~, pi, and p~ in X such t h a t {p~,pl,p~} • Fo., or two participants p~ and p~ in X such t h a t {p~,pj} • F1. We assume t h a t X can recover the value y~ for some i • { 1 , . . . ,2n}.

Hence, there exist participant p~ who owns ri, and participants pj and Pk who can recover ri + Yi (or participant pj who owns ri + y~). Thus PjPk is an edge of Gi (or PiPj is an edge of G). Thus {P~,Pj,Pk} 6 F2 or {Pi,Pj} 6 F1. This is a contradiction. Hence X obtains no information on y~ for 1 < i < 2n. In addition, X obtains no information on Y2n+l, Y2n+2 because it does not contain two participants Pi and pj in X such that PiPj is an edge of G. Therefore, X obtains no information on Yi, for 1 < i < 2n + 2, and hence the secret K .

PART II. Second, we show t h a t the information rate of the above constructed secret sharing scheme is at least

6

(n - 1)2 + 2"

The share of participant Pi is

Si = (ri, rn+i, ai,1, . . . , ai,t, . . . , ai,n, Si( G) ) .

or log(q 2) if ~ 6 E(G). log(q d'(v)+l) if p~ 6 V(G),

share Si is equal to

Let di(Gt) be t h e degree of vertex pi in Gt. T h e size of a~,t is equal to log(q d'(a')+l) ifpi 6 V(Gt)

T h e the size of S~(G) is equal to 0 if p~ ~ V(G), or is equal to where di(G) is the degree of vertex pi in G. Hence, the size of

i f p i ¢ V ( a ) , or

log (q~t:P~eat (ddG*)+l)+2) ,

log (qE~:p~e~

(d,(Gt)+l)+d,(G)+3),

if Pi 6 V(G). Because the size of the secret is equal to log(q6), the information rate of the share Si, Pi is equal to 6 E (d,(a,) + 1) + 2 '

t:pl EGt

if pi ~ V(G), or is equal to if Pi 6 V(G). (a)

(d~(at) + 1) + d~(G) +

3'

t:p~6Gt

F is uniform: if F is a uniform access structure of rank three, then p~ is equal to

6

(di(Gt) + 1) + 2"

t:p~EGt

Because p = mini{p~}, the information rate of the proposed secret sharing scheme is equal to

6

{

}

max E (d~(Gt) + l) + 2

i

t:p~EGt

where G~ is the graph with vertices

V(G~) = {pj for all p j , w h e r e {p~,pj,pk} 6 F0} and edges

Perfect Secret Sharing Schemes 93

(b)

I n t h e w o r s t c a s e w h e n

di(Gt)

= n - 2 for all i a n d t, t h e lower b o u n d o f t h e i n f o r m a t i o n

r a t e 6 (n - 1)5 + 2 c a n b e a c h i e v e d , w h e r e n is t h e n u m b e r o f p a r t i c i p a n t s . F is n o n u n i f o r m : b y t h e s a m e w a y in (a), we c a n p r o v e t h a t 6 Pi >_ (n - 1) 2 + 2 ' i f p i

q~ V(G).

I f p ~ E

V(G)

a n d ~ E E ( G ) , t h e n

d~(Gt)

= 0. I f p i e

V(G)

a n d

PiPt q~ E(G),

t h e n

di(Gt)

<_ n - k - 2, w h e r e

k = dr(G),

1 < k < n - 2. T h e r e f o r e ,

6

Pi >-

_{(n - 1) 2 + 2 '} if

Pi q~ V(G),

o r 6 Pi _>

_{( n - k - 1 ) 2}

_{+ k + 3 '}

i f p i E V ( G ) . B e c a u s e ( n - I ) 2 + 2 > ( n - k - I ) 2 + k + 3 w h e n n E 5 a n d k > l ,

{

°

°

)

°

p i > _ m i n ( n - l ) 2 + 2 ' ( n - k - l ) 2 + k + 3 = ( n - l ) 2 + 2 ' T h e r e f o r e , 6 p = m i n { p i } _> ( n - 1) 2 + 2"

C o m p a r e d w i t h t h e lower b o u n d p r o v i d e d b y S t i n s o n [15] in s o m e cases, o u r lower b o u n d is b e t t e r t h a n S t i n s o n ' s lower b o u n d . T h e c o m p a r i s o n c a n b e seen in T a b l e 1 a n d T a b l e 2.

Table i. B o u n d s on the information rate for uniform access structures of rank three on n participants for n )_ 5, where • denotes the m e t h o d providing the better bound.

n Stinson's M e t h o d O u r M e t h o d n ~ 0 ( m o d 6 ) n-~ 1,3 ( m o d 6 ) n - - 2,4 (rood6) n -- 5 (rood6) 6 p > _ w

n(n +

1) 6 p > w n ( n - 1) 6 p ~ * (n - 1)(n - 2) 6 p_> (n --k 1)(n + 2) 6 P>- ( n _ 1)2 + 2 " 6 p>_ (n -- 1) 2 + 2" 6 p > (n -- i)2@2 6 p > • (n - 1) 2 + 2

Table 2. B o u n d s on the information rate for nonuniform access structures of rank three on n participants for n > 5, where • denotes the m e t h o d providing the better bound. n Stinson's M e t h o d O u r M e t h o d n -= 0 (mod6) n ~ 1 , 3 (mod6) n - - 2 , 4 (mod6) n - 5 (mod6) 4 p _ > ~ n(n -}- 1) 4 p > _ w

n ( n -

1) 4 p > ( n - 1 ) ( n - 2) 4 p ~ (n + 1)(n + 23 6 > P _{(n + 1) 2 -{- 2*}

4 . S E C R E T S H A R I N G S C H E M E S W I T H

U N I F O R M A C C E S S S T R U C T U R E S O F R A N K m

In this section, we propose a decomposition construction of secret sharing schemes with uniform access structures of r a n k m. We construct secret sharing schemes with uniform access structures of r a n k m by using the secret sharing schemes with uniform access structures of r a n k m - 1. Let F be a uniform access structure of rank m on n participants. Assume t h a t P = { P l , P 2 , . . . ,Pn} is the set of participants and the basis of F is Fo. We can decompose Fo into the union of F~'s, for 1 < i < n, where F~ = {X : X E Fo and X contains participant Pi}. Thus F = cl(Fo) = cl(F1) U . . . U cl(Fn). We define F* = {X : X U {Pi) E Fi}, i.e., F* is the set of Fi which participant Pi is removed from each element in Fi. Therefore, each cl(F*) is a uniform access structure of rank m - 1. Here we define h(i) to be a function which indicates the secret space of the secret sharing schemes with uniform access structures of rank i to be ( G F ( q ) ) h(i). We assume t h a t the secret K = (K1, K 2 , . . . , Kin), where each Ki, for 1 < i < m, is taken r a n d o m l y from ( G F ( q ) ) h(m-1). T h e dealer selects a polynomial f ( x ) of degree m . h ( m - 1) - 1 with coefficients K and computes y~ as follows:

Yi = f ( i ) ( m o d q ) , for i = 1,. . . , n . h ( m - 1).

T h u s one who gets m . h(rn - 1) or more y~'s can recover f ( x ) and t h e n the secret K . However, one without knowledge of a n y y~ obtains no information on the secret. We use Y 1 , Y 2 , . . . , Y,~ over ( G F ( q ) ) h('n-1) to denote these n . h(ra - 1) yi's. T h e dealer selects n r a n d o m numbers R1, R 2 , . . . , Rn over ( G F ( q ) ) h(m-1). We assume t h a t there exists a secret sharing scheme realizing cl(F~) in which the secret is P~ + Yi and the share of participant P1 is Sj(F*).

T h e share of participant p~ is given by

I ~ $ • $ • •

s, = s , (

,),.., s,(r,_,),

Thus, the constructed secret sharing scheme is a perfect secret sharing scheme with access struc- ture F.

THEOREM 4.1. L e t F be a uniform access s t r u c t u r e o f r a n k m on n participants. T h e n there e ~ s t s a

for q > n . ( m - 1)!. PROOF.

(i)

First we show t h a t the above constructed secret sharing scheme is a perfect secret sharing scheme realizing the uniform access structure F of rank m.

(a) Let X be a subset of participants and X E F. W i t h o u t loss of generalization, we assume t h a t X = { P l , P 2 , . . . ,Pro}. Because X \ { p i } E F~, X can recover P~ + Y i , for 1 _< i < rn. In addition, each participant Pi owns P~. Therefore, t h e y can recover Y~, for 1 < i < m, and t h e n recover the f ( x ) and the secret K .

(b) Let X be a subset of participants and X ~ F. We assume t h a t X can recover y~. T h e n X m u s t be able to recover r~ and r~ + y~. Thus, p~ E X and there exists a subset X ~ of X such t h a t X ~ E F~. Therefore, X ~ U {p~} E F~. T h a t is, X ~ U {pi} is a qualified subset. Because X ~ U {Pi} C_ X, X is also a qualified subset. This is a contradiction. Hence X cannot recover any y~. Thus X obtains no information on the secret K .

Perfect Secret Sharing Schemes 95

(II) Second, we show t h a t the information rate of the above constructed secret sharing scheme is at least

n - m + l

(:)

T h e secret space (GF(q)) h(m), of the constructed secret sharing scheme is equal to ( G F (q))m.h(m-1). Therefore, h(re) = re. h(m - 1). From Section 2, we know t h a t there exist secret sharing schemes with access structure of rank two in which h(2) is equal to 2. Therefore, we can obtain h(re) = re!. T h a t is, the secret space of the constructed secret sharing scheme is equal to (GF(q)) m!. We define p(re, n) to be the lower bound of the information rate of secret sharing schemes with uniform access structures of rank re on n participants. Therefore,

p('Tn,, n)

Because 0 <_ p ( r e - 1 , n - 1) < 1, We can obtain

m

( n - l ) . ( 1 / p ( m - l , n - 1 ) ) + l "

p(re, )

p(m - 1, n - 1) m m ( n - 1 ) + p ( m - 1, n - 1) - n m p(m,n) k n " P(m-- l ' n - - 1 ) k

From Section 2, we know t h a t

Therefore,

m. ( m - 1 ) . . . . - 3

n . ( n - 1 ) . . . ( n - k + 3 ) p ( 2 , n - k + 2 ) n - k + 2 " • p ( 2 , n - k + 2 ) . m ! . ( n - r e + l)! n - m + l p(m, n) > = |

o,

(:)

Compared with the best previous lower bound of p(m, n), studied by Stinson [15], which is

m

( 2 m - l ) . m - 2 + d

where d is t h e m a x i m u m degree of any participant, our lower bound is b e t t e r t h a n Stinson's lower bound when

3+ 8v - 1

m >

4

5. C O N C L U S I O N S

Based on the secret sharing schemes with graph-based access structures, we propose a decom- position construction to realize the perfect secret sharing schemes with uniform access structures of rank 3. In addition, we give a recursive construction for perfect secret sharing schemes with uniform access structures of constant rank. If F is an access structure (either uniform or nonuni- form) of rank three on n participants, we show t h a t there exists a secret sharing scheme with information rate

6

p >

(n - 1) 5 + 2'

for n _> 5. If F is a uniform access structure of rank m on n participants, we show t h a t there exists a secret sharing scheme with information rate

n - m + l

Compared with the best previous constructions, our constructions have some improved lower bounds on the information rate.

R E F E R E N C E S

1. J. Benaloh and J. Leichter, Generalized secret sharing and monotone functions, In Advances in Cryptology- Crypto'88 Proceedings, Lecture Notes in Computer Science, Volume 403, pp. 27-35, Springer-Verlag, Berlin,

(1990).

2. M. Ito, A. Saito and T. Nishizeki, Secret sharing scheme realizing general access structure, In Proc. IEEE

Globecom'87, Tokyo, pp. 99-102, (1987).

3. G.R. Blakley, Safeguarding cryptographic keys, In Proc. AFIPS 1979 National Computer Conference, New

York, Volume 48, pp. 313-317, (1979).

4. A. Shamir, How to share a secret, Commun. of the ACM 22 (11), 612--613, (1979).

5. E.F. Brickell and D.R. Stinson, Some improved bounds on the information rate of perfect secret sharing schemes, Journal of Cryptology 5, 153-166, (1992).

6. M. wan Dijk, On the information rate of perfect secret sharing schemes, Designs, Codes and Cryptography 6,

143-169, (1995).

7. E.D. Karnin, J.W. Greene and M.E. Hellman, On secret sharing systems, IEEE Trans. on Inform. Theory

29, 35--41, (1983).

8. R.M. Capocelli, A. De Santis, L. Gargano and U. Vaccaro, On the size of shares for secret sharing schemes,

Journal of Cryptology 6, 157-167, (1993).

9. R.G. Gallager, Information Theory and Rehable Communications, John Wiley ~ Sons, New York, (1968).

10. R.W. Hamming, Coding and Information Theory, Prentice-Hall, Englewood Cliffs, N J, (1986).

11. M. Ito, A. Saito and T. Nishizeki, Multiple assignment scheme for sharing secret, Journal of Cryptology 6,

15-20, (1993).

12. C. Blundo, A. De Santis, L. Gargano and U. Vaccaro, On the information rate of secret sharing schemes, In

Advance in Cryptolog~-CRYPTO'9~, Lecture Notes in Comput. Sci., Volume 740, pp. 148-167, (1993).

13. C. Blundo, A. De Santis, D.R. Stinson and U. Vaccaro, Graph decompositions and secret sharing schemes, In

Advance in Cryptology-Proceedings of Eurocrypt'9~, Lecture Notes in Comput. Sci., Volume 658, pp. 1-24,

(1993).

14. C. Blundo, A. D e Santis, D.R. Stinson and U. Vaccaro, Graph decompositions and secret sharing schemes,

Journal o] Cryptology 8, 39-63, (1995).

15. D.R. Stinson, N e w general lower bounds on the information rate of secret sharing schemes, In Advance in Cryptology-CRYPTO'gP, Lecture Notes in Comput. Sci., Volume 740, pp. 168-182, (1993).

16. D.R. Stinson, Decomposition constructions for secret sharing schemes, I E E E Trans. Inform. Theory 40,

118-125, (1994).

17. C. Blundo, A. De Santis, R. De Simone and U. Vaccaro, Tight bounds on the information rate of secret sharing schemes, Designs, Codes and Cryptography 11 (1), 1-25, (1997).