Analyses of mode coupling in joined parallel phononic crystal waveguides
Jia-Hong Sun and Tsung-Tsong WuUltrasonics Laboratory, Institute of Applied Mechanics, National Taiwan University, Taipei 106, Taiwan 共Received 1 September 2004; revised manuscript received 25 February 2005; published 24 May 2005兲 In this paper, we present an analysis of coupling effects in joined parallel phononic crystal waveguides. The finite difference time domain共FDTD兲 method with periodic boundary condition is adopted to analyze the band gaps and dispersion relation of phononic waveguides. The defect modes of a single phononic waveguide are analyzed and first discussed to serve as a basis for a joined waveguides system. Then, the dispersion relation and displacement field of supermodes of joined waveguides are calculated and discussed. Both displacement pattern and transmission coefficient of the defect modes are calculated. To transfer the power from one waveguide to another, the coupling lengths are evaluated by numerical experiments and can be understood by the concept of beat length. Finally, we analyze an elastic waveguide coupler and demonstrate that the coupler can potentially be employed as a power switch of the acoustic wave.
DOI: 10.1103/PhysRevB.71.174303 PACS number共s兲: 63.20.⫺e, 43.20.⫹g, 43.40.⫹s, 46.40.Cd
I. INTRODUCTION
In recent years, much research has been devoted to pho-tonic crystals that demonstrate the band gaps of electromag-netic 共EM兲 wave propagation in periodic dielectric media. Due to the analogy between elastic waves and electromag-netic waves, inhomogeneous media consisting of different elastic materials have also become a topic of academic inter-est. Such inhomogeneous structures, named “phononic crys-tals,” typically consist of two or more materials with a peri-odic arrangement. The acoustic band gap共ABG兲 is similar to the optic band gap in photonic crystals in that the acoustic wave propagation in a certain frequency range is forbidden.1–3In addition to bulk acoustic waves, band gaps
for surface acoustic waves have also been demonstrated.4–6 The existence of large acoustic band gaps has been revealed by several phononic crystal examples made of solid or fluid constituents.7–11
The total band gap of elastic wave propagation toward any direction in the phononic crystals has been predicted and observed.12 The localization of elastic waves with the
ar-rangement of defects in phononic crystals as a linear wave-guide was also studied through the calculation of the trans-mission coefficient.13 The research of waveguide structures such as linear straight waveguides with resonant cavities or with a vertical stub was reported.14–17Alternative inclusions
of phononic crystals were also discussed, and a narrow pass band was designed in a liquid-based phononic crystal structure.18,19These studies inspired the research of coupling behavior of joined parallel linear phononic crystal waveguides in this paper.
When one linear waveguide is close enough to another in a phononic crystal structure, the coupling effect between the two waveguides is so strong that they are bounded as a single system. Each eigenvalue corresponding to an eigenstate of the single waveguide splits into two values in the case of the joined waveguides system. This exciting phenomenon is similar to what appeared in photonic crystals.20–22
The calculations in our work are based on the finite dif-ference time domain 共FDTD兲 method. The defect mode of elastic wave propagation is analyzed with the periodic
boundary condition by applying the Bloch theorem. The su-permodes of joined parallel phononic crystal waveguides are studied so that the beat phenomenon is revealed to evaluate the coupling lengths of the system of joined waveguides. Therefore, an elastic wave coupler is demonstrated and, fur-ther, an enhanced coupler is presented. Due to a stronger coupling effect, the enhanced coupler shortens the coupling length and reduces the size of the coupler.
To make our arguments clear, the method of calculation and defect modes of a single waveguide in the phononic crystals are introduced in Sec. II. The coupling effect of joined parallel waveguides is reported in Sec. III. Later, the dispersion relation and displacement field of supermodes for the coupling waveguides are discussed. The coupling length in a system of two joined waveguides is also introduced. The analysis of an elastic coupler in the system of two waveguides is in Sec. IV. Lastly, a summary of the results is presented in Sec. V.
II. DEFECT MODES OF A PHONONIC CRYSTAL WAVEGUIDE
In previous research, the acoustic band gap of elastic wave propagation in phononic crystals was identified by cal-culating the dispersion curves or the transmission coefficient. The most popular technique employed to analyze the disper-sion relation of elastic waves in phononic crystals is the plane wave expansion 共PWE兲 method. The PWE method transforms the elastic wave equation into Fourier space and solves the simplified eigenvalue problem. With the arrange-ment of defects, the straight linear waveguide can still be analyzed by the PWE method with the concept of a super-cell. However, to solve the eigenvalue problem of PWE with the supercell condition, it takes a great number of wave vec-tors in the reciprocal space to guarantee an accurate value of modes and limits the efficiency of calculation.
Generally, the three-dimensional heterogeneous finite dif-ference formulation with staggered grids is adopted to study the wave propagation in phononic crystals. The composite structures of phononic crystals can be easily calculated by
replacing the material constant of the corresponding location. Tanaka et al.23first introduced the Bloch theorem to treat the periodic boundary condition of the unit cell of phononic crystals. By recording the displacement inside the unit cell and taking the Fourier transformation, the eigenfrequencies of a given wave vector k are indicated by selecting the reso-nance peaks of the spectrum. The advantages of adopting the FDTD method to calculate dispersion curves include less calculation time, more material-selecting flexibility, and in-clusion shape variation. Due to the discrete grids, one pos-sible error is the approximate shape of inclusions. In this paper, the FDTD method is employed to solve the supercell problem for obtaining dispersion relations of single wave-guide defect modes and joined wavewave-guides supermodes. To be more efficient, the parallelism computation program with a message passing interface共MPI兲 is realized and the calcu-lations are executed on a PC cluster system with 16 CPUs.
The phononic crystal, which we take into consideration, is a solid/solid two-dimensional phononic crystal consisting of epoxy as the base and steel as the cylinders. The lattice con-stant a of the phononic crystal structure is 8 mm, and the radius of the cylinder is 3 mm. In this case, the filling ratio f is equal to 0.442. To simulate the wave propagation in the structure using the FDTD method, each unit cell is divided into 24⫻24 grids, with a time step interval of 20 ns. The density and elastic constant C11and C44of steel are assumed
as 7900 kg/ m3, 280.2 GPa, and 82.9 GPa, respectively, and
those for epoxy are 1180 kg/ m3, 7.61 GPa, and 1.59 GPa. In
the two-dimensional phononic crystal cases, as shown in Fig. 1, the elastic wave propagates within the X-Y plane perpen-dicular to the cylinders and the phononic structure is infinite along the Z direction. Thus, the polarization modes of elastic waves can be decoupled into the in-plane mode and the anti-plane mode共X-Y plane兲. The present work is to study phe-nomena of waveguides, and therefore we consider the in-plane mode wave propagation, which includes longitudinal and transverse waves.
Dispersion curves of steel/epoxy phononic crystal are cal-culated first. The displacement is recorded within 200 000 time steps and the Fourier transform is applied to find the resonance frequencies. Our result shows that the total band gap of this phononic crystal is located between 86 kHz and 197 kHz. By applying the concept of a supercell, dispersion curves of a linear straight waveguide in phononic crystals can be calculated by combining several basic unit cells. The
elastic wave mostly propagates within the waveguide, but also leaks slightly to the neighboring area. The allowed modes inside the waveguide include the extended modes, which fall outside the total band gap, and defect modes, which fall in the range of total band gaps. The results are consistent with those reported by Khelif et al.15
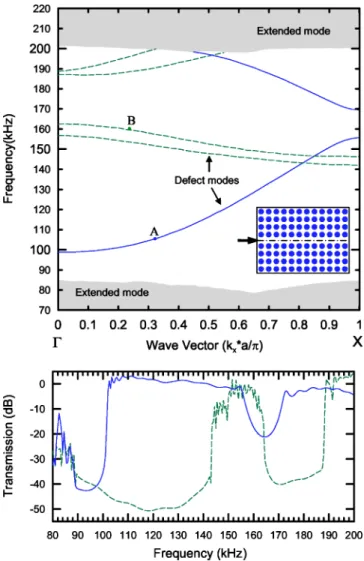
To investigate the coupling effect of waveguides, we con-sider a supercell consisting of 8.5⫻1 unit cells and a wave-guide with a 6 mm width共the distance between two neigh-boring cylinders on both sides兲. The inset of Fig. 2共a兲 shows the cross section of the single waveguide, and a dashed-dotted line denotes the mirror plane of the structure. Similar to the conventional acoustic waveguides, the defect modes in Fig. 2共a兲 can be classified as symmetric modes 共solid lines兲 and antisymmetric modes共dashed lines兲, with respect to the mirror plane of the waveguide. In the range of total band gap, the symmetric modes extend in the frequency intervals 99–156 and 169– 198 kHz, and the antisymmetric modes ex-tend in intervals 142–163 and 187– 198 kHz.
The defect modes of the waveguide are identified by the transmission coefficients and the displacement fields. First, we launch a Gaussian weighted plane-wave package with a FIG. 1. The oblique view of a two-dimensional phononic crystal
waveguide. The lattice constant a and the width of waveguide d are marked in the figure.
FIG. 2. 共Color online兲 Defect modes of the elastic wave inside the phononic crystal waveguide. 共a兲 Dispersion curves of defect modes.共b兲 The transmission coefficient through the waveguide.
central frequency of 140 kHz and with a duration of 100s. The transmission coefficient is obtained by taking a Fourier transform of the average of elastic wave displacements re-corded across the waveguide and comparing the spectra with those without phononic crystals. Since the polarization of a longitudinal wave is along the X direction, the longitudinal wave excites the symmetric modes. Likewise, polarization of the transverse wave is along the Y direction, therefore induc-ing antisymmetric modes inside the sinduc-ingle waveguide. Figure 2共b兲 shows that the transmission coefficient of the elastic wave propagating inside the waveguide is a function of fre-quency. In our example, the studied waveguide is 15 lattice constants in length, which, accordingly, lets the transmission coefficient fully reflect the properties of the band gap. For the symmetric modes, a gap exists below 102 kHz and an-other gap is in the interval 155– 172 kHz, while the pass bands for antisymmetric modes are between 144 and 164 kHz and those higher than 188 kHz. Indeed, the defect modes are clearly identified by the transmission coefficients. Next, we apply the FDTD approach to calculate the dis-placement fields of elastic waves. We consider the phononic crystal structure containing 8.5⫻10 unit cells. The periodic condition is used along the boundaries in the Z direction for the two-dimensional structure. In addition, the perfectly matched layer共PML兲24,25is adopted as the absorbing
bound-ary condition for the boundaries in the X and Y directions. The longitudinal wave, with a specific central frequency f, is generated to excite symmetric defect modes, while the trans-verse wave is stimulated for antisymmetric defect modes.
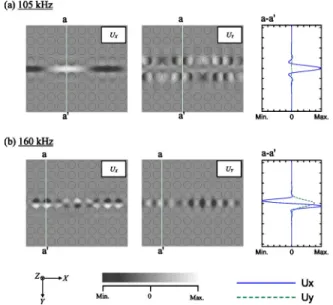
In Fig. 3共a兲, we show the displacement fields of point A marked in Fig. 2共a兲. The symmetric mode is excited by the longitudinal wave with 105 kHz. UX and UY represent the displacement components along the X and Y directions; their values of the cross section are shown in the gray scale. The white color and black color represent the maximum value
and minimum value, respectively. For better understanding, we also plot the displacement components along a-a
⬘
to identify the modes with a solid line representing UX and a dashed line representing UY. Obviously, the displacement components in both directions are symmetric to the mirror plane of the waveguide. Meanwhile, Fig. 3共b兲 shows the re-sult of point B in Fig. 2共a兲 with the 160 kHz transverse wave, which belongs to the antisymmetric modes. We note that the displacement fields of the chosen points A and B in Fig. 2共a兲 demonstrate the symmetric and antisymmetric modes, thereby coinciding with the transmission analyses shown in this section.III. COUPLINGS OF PHONONIC CRYSTAL WAVEGUIDES The manipulation of defects in photonic crystals induced several optic communication applications, including the low loss transmission bending structures and wavelength division multiplexing 共WDM兲 devices.20 The analogy of photonic
crystals and phononic crystals inspires the research of cou-pling phononic crystal waveguides. In the following, we present analyses of joined parallel phononic crystal waveguides.
A. Coupling effect and supermodes of coupling phononic waveguides
Waveguide in a phononic crystal structure can be consid-ered as a composition of adjacent point defects. Thus, the individual modes of point-defect unit cells will couple as the defect modes of a waveguide. Similarly, two waveguides will join together as a single system when one linear waveguide is close enough to another. The eigenvalue corresponding to eigenstates of the single waveguide will split into different modes, which results in a coupling effect between these two joined waveguides. Dispersion curves of coupling modes of the system can be calculated as those in the single waveguide using the FDTD method. We consider a system of two linear straight waveguides with the width of each waveguide being 6 mm, coincidentally the same as the previous case in Sec. II. In this case, there is one row of phononic unit cells be-tween the two waveguides, as shown in the inset of Fig. 4共a兲. The two nearby waveguides can be considered as one joined system which supports the supermodes, i.e., the allowed de-fect modes of the system. They can also be obtained by the dispersion relation.
The supermodes of the system of joined waveguides are calculated with a supercell consisting of 10⫻1 unit cells. Figure 4共a兲 demonstrates the results of dispersion curves. The solid lines are the supermodes of the coupling waveguides system and the dashed lines are the defect modes of a single waveguide system, as shown in Fig. 2共a兲. The dispersion curves of the system of two waveguides appear in pairs due to the coupling effects. Thus, it seems that the supermodes are split from defect modes of the single wave-guide. In this phononic crystal structure, if the number of rows of phononic unit cells between two waveguides is larger than two, then the coupling effect is hard to detect. Apparently, the coupling effect of waveguides depends on the distance between two waveguides.
FIG. 3. Elastic wave displacement fields inside the phononic crystal waveguide.共a兲 The displacement fields of the 105 kHz lon-gitudinal wave which belongs to the symmetric mode.共b兲 The dis-placement fields of the 160 kHz transverse wave which belongs to the antisymmetric mode.
It can be understood that for two identical waveguides, the lowest-order modes include even 共symmetric兲 and odd 共antisymmetric兲 polarity with respect to the mirror plane be-tween the waveguides. In this case, the cross section of the two joined waveguides is shown in the inset of Fig. 4共a兲, with a dashed-dotted line representing the mirror plane.
Symmetric and antisymmetric types of supermodes are marked in Fig. 4共a兲. Solid arrows indicate symmetric modes and dashed arrows indicate antisymmetric super-modes. Similarly, the types of supermodes are examined in two ways: the analysis of transmission coefficients and dis-placement fields.
Transmission coefficient is calculated by comparing the spectra of penetrating waves, as we mentioned in Sec. II. To examine the mode type of a system of two joined waveguides, the incident waves include both the longitudinal wave and the transverse wave. Unlike the symmetric mode, which is only excited by longitudinal waves in a single waveguide, both symmetric and antisymmetric modes can be excited by longitudinal waves in the system of joined waveguides. Symmetric and antisymmetric cases are con-trolled by modulating the phase of incident waves. The sym-metric共antisymmetric兲 case of longitudinal waves means the incident longitudinal wave is symmetric 共antisymmetric兲 with respect to the mirror plane. The transmissions are shown in Fig. 4共b兲. A solid line shows the symmetric super-mode while a dashed line shows the result of the antisym-metric supermode. In comparison with the joined parallel waveguides, the result of the longitudinal wave inside a single waveguide in Fig. 2共b兲 is also plotted as a dotted line. We find that the frequency range of the symmetric super-mode shifts toward lower frequency while the range of the antisymmetric supermode shifts toward higher frequency. This phenomenon helps make the supermodes clear in Fig. 4共a兲. Symmetric and antisymmetric cases of transverse waves are also calculated, and transmissions of both cases are shown in Fig. 4共c兲. The definition of the lines is the same as those of Fig. 4共b兲. The frequency ranges of the super-modes also have a similar tendency to that of the longitudi-nal wave.
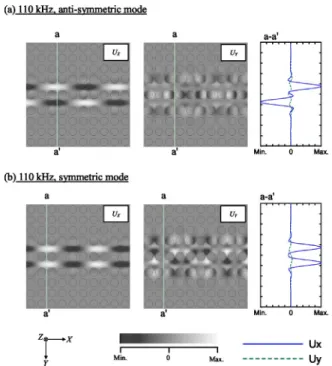
The chosen displacement fields in Fig. 5 show propaga-tion modes of the elastic wave. The setup of the numerical calculation is similar to the examples of Fig. 3, except that the structure is composed of 10⫻10 unit cells. In this ex-ample, elastic waves of the central frequency f = 110 kHz propagating inside the system of two joined waveguides are demonstrated. The longitudinal waves are excited at these two waveguide entrances with the symmetric supermode in the synchronous phase and the antisymmetric supermode in the inverse phase, both with respect to the mirror plane. The displacement fields are shown in Figs. 5共a兲 and 5共b兲. The definition of the color and lines in Fig. 5 is the same as that in Fig. 3. Since the incident waves are polarized along the X direction, the displacement component UX is significantly larger than UY. The results in Fig. 5共a兲 clearly demonstrate the symmetry of both UX and UY. On the other hand, the results in Fig. 5共b兲 show the antisymmetric property. The wavelength is evaluated by lattice constant a, and the values are 5.9a and 4.7a in Figs. 5共a兲 and 5共b兲, respectively. It re-veals that wave vector k of the symmetric supermode is larger than that of the antisymmetric supermode for waves with the same central frequency. This result is also in good agreement with the modes indicated in Fig. 4共a兲.
B. Coupling length of coupling waveguides
Supermode dispersion of a system of joined parallel waveguides implies that if there is a constant frequency FIG. 4.共Color online兲 The supermodes of the system of joined
phononic crystal waveguides.共a兲 The dispersion curves of the su-permodes. Solid arrows indicate the symmetric supermode and dashed arrows indicate the antisymmetric supermodes.共b兲 Trans-mission coefficients of symmetric and antisymmetric longitudinal wave cases. 共c兲 Transmission coefficients of symmetric and anti-symmetric transverse wave cases.
source inside the waveguide, then it is possible that there are more than two allowed modes with different wave vectors k. Hence, the beat phenomenon performs in the system of joined parallel waveguides if both symmetric and antisym-metric supermodes arise. The following study reveals the beat phenomenon due to the coupling effect of joined waveguides.
Numerical experiments of wave propagation in the system of two joined waveguides are conducted by using the FDTD method. To investigate the mode coupling effect, we employ a simple linear two-waveguide structure which has one row of unit cells between the waveguides as shown in Fig. 6共a兲. In Fig. 6共b兲, an elastic wave with f =110 kHz propagating into the upper waveguide from the left entrance will transfer back and forth between the lower and upper waveguides. A similar result is also observed for the elastic wave with f = 140 kHz in Fig. 6共c兲. The necessary distance for the elastic wave to transfer from one waveguide to another is called the
coupling length. It can be observed that the coupling length
of the elastic wave of f = 110 kHz is smaller than the one of
f = 140 kHz, whose values are 11.7a and 22.5a, respectively.
In Fig. 6共d兲, the elastic wave of f =155 kHz also transfers between the two waveguides with the coupling length being about 25.1a. However, since there are more than two allowed modes of the elastic wave, the energy transformation pattern between the two waveguides is more complicated than the cases of f = 110 and 140 kHz. We choose the frequency range of 105– 145 kHz for later calculations because of the simple split-modes condition. FDTD numerical experiments con-clude the correlation curve of coupling length and elastic wave frequency as the solid line in Fig. 7, where the cou-pling length varies from 7.9a to 22.5a in the range 105– 145 kHz.
We note that the coupling length can be analyzed with the knowledge of beat frequency in traditional optics.26 Beat
phenomena between the symmetric and antisymmetric modes arise when excitation is neither symmetric nor anti-symmetric. Since the corresponding wave vectors k of the symmetric and antisymmetric supermodes are different when the elastic wave has the same frequency, the relative phase of these modes will shift when the wave propagates. Therefore, the coupling length is estimated as half a beat length of the two supermodes and can be derived from the dispersion curves. Beat length LB is computed as LB= 2/兩kS− kA兩, where kS and kA are the corresponding symmetric and anti-symmetric wave vectors of the chosen frequency and can be decided from supermode dispersion curves. For example, the corresponding normalized wave vectors are 0.446 and 0.379 for the elastic wave of f = 110 kHz in Fig. 4. Thus, the beat length can be evaluated as LB= 2a /兩0.446−0.379兩⬇29.85a and the coupling length is approximately 14.9a. The pre-FIG. 5. Displacement fields of the elastic wave propagation
in-side the phononic crystal waveguide.共a兲 The 110 kHz antisymmet-ric supermode elastic wave.共b兲 The 110 kHz symmetric supermode elastic wave.
FIG. 6. Amplitude fields which show power transfer between joined parallel phononic crystal waveguides.共a兲 The cross section of the system of joined waveguides.共b兲 The amplitude field for the 110 kHz incident wave. 共c兲 The amplitude field for the 140 kHz incident wave. 共d兲 The amplitude field for the 155 kHz incident wave.
FIG. 7. 共Color online兲 The relationship between the coupling lengths and frequency of elastic waves. The dashed line is the cal-culated half a beat length and the solid line is the result of FDTD numerical experiments.
dicted coupling length by the calculation of half a beat length is represented by the dashed line in Fig. 7.
Thus, the coupling length is a function of frequency de-pending on the difference of the wave vectors of super-modes. The larger the difference is, the shorter the coupling length will be. The coupling length relations obtained from calculation of the beat length and FDTD numerical experi-ments show the same tendency. The mismatch may be caused by the input of the longitudinal wave source. Hence, the power of the symmetric and antisymmetric supermodes is not equal. The power transfer between two waveguides requires that both the symmetric and antisymmetric super-modes can propagate in the structure. In the present case, the power transfer does not occur below 100 kHz since antisym-metric supermodes do not exist. Our analysis mainly focuses on the range 105– 145 kHz, or the coupling length cannot be evaluated by the beat frequency analysis because there are too many allowed modes of the elastic wave. For example, with f = 155 kHz, it causes a larger mismatch of coupling lengths in Fig. 7 for frequencies higher than 145 kHz.
IV. ANALYSIS OF AN ELASTIC WAVE COUPLER The beat phenomenon of the two-waveguide system proves the elastic wave power transfer between two joined waveguides is feasible with a necessary coupling length, which varies with different frequencies. The similar coupling effect of photonic crystals has been adopted to serve as the wavelength division multiplexing 共WDM兲 in optic commu-nication devices.20 In phononic crystal structure, joined
waveguides can potentially be employed as a power switch of the acoustic wave, which can also control the mechanical power. The concept is realized by patterning the coupler length to switch the elastic wave with a specific frequency. In the system of joined waveguides, a cross state appears when incident elastic waves switch from one waveguide into an-other and the coupler length is an odd multiple of the cou-pling length. However, the bar state20appears when the
elas-tic wave propagates in and out through the input waveguide, causing the coupler length to be an even multiple of the coupling length.
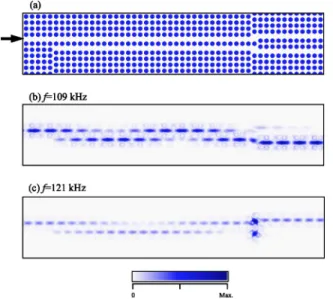
In Fig. 8共a兲, we show an elastic wave coupler with an interactive length of 33a with one entrance on the left side and two exits on the right side. From the relationship shown in Fig. 7, we estimate that the coupler will perform the cross state at 109 kHz for the elastic wave and at 121 kHz for the bar state. Numerical experiments are shown in Figs. 8共b兲 and 8共c兲, respectively. The displacement field of the propagating wave with f = 109 kHz shows that the coupler demonstrates a cross state while the coupler with f = 121 kHz acts as a bar state. It is worth noting that although the elastic wave reso-nates in the joint area of outlets in Fig. 8共c兲, the power leaves the coupler remaining in the bar state, as we predicted. To quantify the efficiency of power transfer, we analyze the dis-placement of each exit. Power exchange ratios between two outputs are 26 dB for the cross state and 28 dB for the bar state. Therefore, the system of two waveguides consisting of solid/solid phononic crystal can potentially be treated as an elastic wave coupler for the elastic wave in the solid media,
and the selection of waves with different central frequencies is controlled by the coupling length of the coupler.
Obviously, a coupler with a shorter coupling length is more flexible for the purpose of application. The previous analysis shows that the greater the coupling effect, the larger the difference of supermodes. Therefore, an enhanced system of joined parallel waveguides is proposed. The inset of Fig. 9 shows the design of the cross section of enhanced joined waveguides. The structure is similar to the waveguides in Fig. 4 except that the diameter of unit cells between the waveguides I and II, i.e., the separation of the joined parallel FIG. 8. An elastic wave coupler and displacement fields of propagating waves.共a兲 The cross section of the elastic wave coupler with a coupler length of 33a. 共b兲 The amplitude of the 109 kHz elastic wave which shows a cross state.共c兲 The amplitude of the 121 kHz elastic wave which shows a bar state.
FIG. 9. 共Color online兲 The dispersion relation of the enhanced joined parallel waveguides.
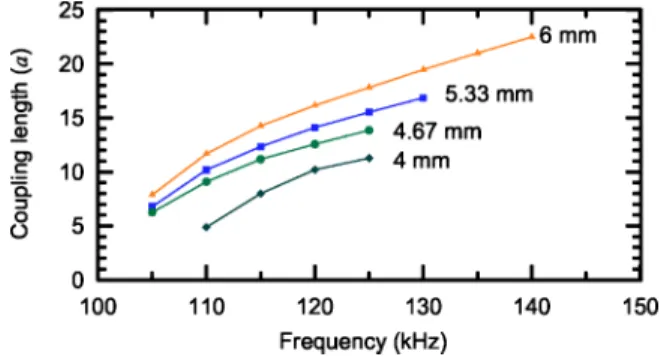
waveguides, is smaller 共4 mm in this case兲. Dispersion curves shown in Fig. 9 validate our enhanced design in which the variation of wave vectors for different supermodes is larger than that of the previous structure. Further, relation between the coupling length and separation 共6 mm, 5.33 mm, 4.67 mm, and 4 mm兲 of the joined parallel waveguides is studied and shown in Fig. 10. The result shows that the smaller the separation, the shorter the cou-pling length.
To design an enhanced coupler, the enhanced joined waveguides with a separation of 4 mm are chosen. The length of the enhanced coupler is 20a, which is smaller than the standard coupler of 33a with a separation of 6 mm. The enhanced coupler performs a cross state at 112.8 kHz and a bar state at both 119.5 and 110.2 kHz. Table I shows the comparison of the two mentioned couplers. The result shows that power exchange ratios of the enhanced coupler are smaller than those of the standard one, but still larger than 12 dB. Obviously, with the enhanced joined waveguides, the size of the enhanced elastic wave coupler can be reduced and multiselection in the same coupler is possible.
Although the above analyses show that the bulk wave coupler proposed is promising, we note that the big diffrac-tion loss of bulk waves has to be faced. One interesting al-ternative is to use surface wave propagation in a two-dimensional phononic crystal.6 Detailed analysis of such a
surface wave coupler awaits further study. It is worth noting that in the study of a surface wave coupler, the existing im-age technique27,28can be employed to check the validity of
computation results.
V. SUMMARY
In this paper, we have investigated the coupling phenom-enon of joined parallel phononic crystal waveguides. Two-dimensional steel/epoxy phononic crystal and the FDTD method are employed to study the coupling effects of joined phononic waveguides. The supermodes resulting from the coupling effect between the joined waveguides can be treated as split modes of the defect modes. We demonstrated that supermodes are indeed symmetric and antisymmetric modes which split from defect modes of a single waveguide. The result shows that the symmetric supermode shifts toward a lower frequency while the antisymmetric mode veers toward a higher frequency. A beat phenomenon between symmetric and antisymmetric modes arises when both modes are ex-cited. The coupling lengths needed to transfer the power from one waveguide to another are evaluated by numerical experiments, and results can be interpreted by the concept of beat length. Finally, an enhanced elastic waveguide coupler is proposed and demonstrated that the coupling length can obviously be reduced.
ACKNOWLEDGMENTS
The authors acknowledge the financial support of this re-search by the National Science Council of ROC 共NSC 92-2212-E-002-058兲 and NTU-ITRI center.
1M. S. Kushwaha, P. Halevi, L. Dobrzynski, and B. Djafari-Rouhani, Phys. Rev. Lett. 71, 2022共1993兲.
2M. S. Kushwaha, P. Halevi, G. Martinez, L. Dobrzynski, and B. Djafari-Rouhani, Phys. Rev. B 49, 2313共1994兲.
3M. S. Kushwaha and P. Halevi, Appl. Phys. Lett. 64, 1085 共1994兲.
4Y. Tanaka and S. I. Tamura, Phys. Rev. B 58, 7958共1998兲. 5Y. Tanaka and S. I. Tamura, Phys. Rev. B 60, 13 294共1999兲. 6Tsung-Tsong Wu, Zi-Gui Huang, and S. Lin, Phys. Rev. B 69,
094301共2004兲.
7F. R. Montero de Espinosa, E. Jimenez, and M. Torres, Phys. Rev. Lett. 80, 1208共1998兲.
8M. Torres, F. R. Montero de Espinosa, D. Garcia-Pablos, and N. Garcia, Phys. Rev. Lett. 82, 3054共1999兲.
9M. Torres, F. R. Montero de Espinosa, and J. L. Aragon, Phys. Rev. Lett. 86, 4282共2001兲.
10R. E. Vines J. P. Wolfe, and A. V. Every, Phys. Rev. B 60, 11 871 共1999兲.
11R. E. Vines and J. P. Wolfe, Physica B 263–264, 567共1999兲. 12J. O. Vasseur, P. A. Deymier, B. Chenni, B. Djafari-Rouhani, L.
Dobrzynski, and D. Prevost, Phys. Rev. Lett. 86, 3012共2001兲. 13M. Kafesaki, M. M. Sigalas, and N. García, Phys. Rev. Lett. 85,
4044共2000兲.
14A. Khelif, B. Djafari-Rouhani, J. O. Vasseur, P. A. Deymier, Ph. Lambin, and L. Dobrzynski, Phys. Rev. B 65, 174308共2002兲. 15A. Khelif, B. Djafari-Rouhani, J. O. Vasseur, and P. A. Deymier,
Phys. Rev. B 68, 024302共2003兲.
16A. Khelif, A. Choujaa, B. Djafari-Rouhani, M. Wilm, S. Ballan-FIG. 10.共Color online兲 The coupling lengths of joined parallel
waveguides with different separations.
TABLE I. Comparison of the two couplers.
Coupler separation/length
Cross state Bar state Frequency 共kHz兲 Power ratios 共dB兲 Frequency 共kHz兲 Power ratios 共dB兲 6 mm/ 33a 109 26 121 28 4 mm/ 20a 112.8 19 119.5 110.2 18 12
dras, and V. Laude, Phys. Rev. B 68, 214301共2003兲.
17A. Khelif, B. Djafari-Rouhani, V. Laude, and M. Solal, J. Appl. Phys. 94, 12共2003兲.
18J. O. Vasseur, P. A. Deymier, A. Khelif, Ph. Lambin, B. Djafari-Rouhani, A. Akjouj, L. Dobrzynski, N. Fettouhi, and J. Zem-mouri, Phys. Rev. E 65, 056608共2002兲.
19Y. Pennec, B. Djafari-Rouhani, J. O. Vasseur, A. Khelif, and P. A. Deymier, Phys. Rev. E 69, 046608共2004兲.
20Stefano Boscolo, Michele Midrio, and Carlo G. Someda, IEEE J. Quantum Electron. 38, 1共2002兲.
21Sergey Kuchinsky, Vladislav Y. Golyatin, Alexander Y. Kutikov, Thomas P. Pearsall, and Dusan Nedeljkovic, IEEE J. Quantum Electron. 38, 10共2002兲.
22F. S.-S. Chien, Y.-J. Hsu, W.-F. Hsieh, and S.-C. Cheng, Opt. Express 12, 1119共2004兲.
23Y. Tanaka, Y. Tomoyasu, and S. I. Tamura, Phys. Rev. B 62, 7387 共2000兲.
24J. Berenger, J. Comput. Phys. 144, 185共1994兲.
25W. C. Chew and Q. H. Liu, J. Comput. Acoust. 4, 341共1996兲. 26E. Hecht, Optics, 4th ed.共Addison-Wesley, San Francisco, 2002兲. 27R. E. Vines, Shin-ichiro Tamura, and J. P. Wolfe, Phys. Rev. Lett.
74, 2729共1995兲.
28Y. Sugawara, O. B. Wright, O. Matsuda, M. Takigahira, Y. Tanaka, S. Tamura, and V. E. Gusev, Phys. Rev. Lett. 88, 185504共2002兲.