Applications of conflict-free Petri nets to parallel programs and asynchronous circuits

APPLICATIONS OF CONFLICT-FREE PETRI NETS TO

PARALLEL PROGRAMS AND ASYNCHRONOUS CIRCUITS*

HSU-CHUN

YEN

Dept. of Electrical Engineering, National Taiwan University

Taipei, Taiwan

10764,

R.O.C.

ABSTRACT We propose a unified approach for dealing with the race detection problem for two entirely different models, namely, parallel programs and asynchronous circuits. We first show that the problem of determining whether two transitions in a l-bounded conflict-free Petri net call become enabled simultaneously is solv- able in polynomial time. (This will be referred to as the pairwise concurrency problem.) We then show that the race detection problem for parallel programs (asynchronous circuits) and the pairwise concurrency problem for Petri nets are closely related to each other. As a result, race conditions can be detected efficiently (i.e., in polynomial time) for those parallel programs and asynchronous circuits that can be modeled by l-bounded conflict-free Petri nets. Since most problems concerning Petri nets are very difficult to solve, our polynomial time result is of interest and significance in its own right.

1

Introduction

Petri nets provide an elegant and useful tool for model- ing concurrent systems. In many applications, however, modeling by itself is of little practical use if one can- not analyze the modeled system. Unfortunately, Petri nets remain one of the least understood models, despite the broad attention they have been receiving over the p a d two decades. In fact, most Petri net problems are extremely difficult, t o solve, if not impossible. For ex- ample, for general Petri nets, the bouiidedness problem is EXPSPA CE (exponential space)-complete [ 13,181, the reachability problem is decidable [11,15] (although the only known algorithin is not even primitive recursive) and is EXPSPACE-hard [13], and the contadnment and equivalence problems are unclecidable [ 11.

* ~ l & supported in part by the National Science Council the Republic China under Grant

A natural approach t o ease the high degree of dif- ficulty associated with Petri net analysis is to restrict our attention to 'restricted' classes of Petri nets, hoping for such restricted ones to have easier solutions. Of all the restricted classes of Petri nets studied in the liter- ature, most notable is that of conflict-free Petri nets [5,6,7,S,10,12]. In particular, the boundedness prob- lem has been shown to be PTIME (polynomial time)- complete [SI, the reachability problem has been proved to be NP (nondeterministic polynomial time)-complete [6], whereas the containment and equivalence problems have been shown t o be

I

I

;

(the second level of the poly- nomial time hierarchy) complete [6]. If we further re- strict ourselves to bounded conflict-free Petri nets, the upper bound of reachability can be improved to PTIME [71.

In a recent article 191, it was indicated that the ex- pressive power of conflict-free Petri nets is somewhat limited. Specifically, it was show that conflict-free Petri nets cannot b e used to model the well-known mutual exclusion problem. In view of that, a natural ques- tion arises: H o w useful a r e conflict-free P e t r i n e t s in m o d e l i n g real-world problems? In this paper. we will provide evidence to demonstrate that, despite their limited expressive power, coIiflict-free Petri nets can still be very useful in modeling and analyzing real- world problems. To that end, we first define the so-called pazrwcse concurrency problem for Petri nets. The pair- wise concurrency problem is that of, given a Petri net

P and two transitions t and t', determining where there exists a reachable marking in P in which t and t' are en- abled simultaneously. We then prove that the pairwise concurrency problem for 1-bounded conflict-free Petri nets is solvable in polynomial time. (In contract, the problem is EXPSPACE-complete for geneial Petri nets.)

Finally, we show that the pairwise concurrency problem, coupled with its polynomial time algorithm, provides an efficient tool for detecting race conditions in parallel problems and asynchronous circuits.

A race condition in a parallel program refers to the situation in which two statements try to access the same memory location simultaneously, and at least one of them attempts t o alter the content of the location. The existence of race conditions will result in the outcome of the execution of a parallel program to be speed-dependent. As a result, different runs of the same program on the same data may result in different outcomes- which is clearly undesirable in program design. In the study of asynchronous circuits, a fundamental issue is to iden- tify the situation in which the raising of a signal by one circuit element is in conflict with the lowering of the sa.me signal by another element. (Such a conflict con- stitutes a race.) In this paper, we will show that our derived polynomial time algorithm for the pairwise con- currency problem for 1-bounded conflict-free Petri nets can be applied to answering the race detection problem for parallel programs as well as for asynchronous cir- cuits. In fact, it was posed as an open question in [19] as to whether an efficient algorithm exists in the case of asynchronous circuits. We provide an answer to the question in the affirmative.

The contributions of this paper include the following:

1. From the analytical aspect of Petri nets, we show that the pairwise concurrency problem for 1-bounded conflict-free Petri nets is solvable in polynomial time. Since few Petri net problems have polyno- mial time solutions, our result is important in its own right. Furthermore, in solving the problem, we adopt a novel technique which may have other applications to the analysis of Petri nets.

2. By demonstrating the relations between the pair- wise concurrency problem for Petri nets and the race detection problem for parallel programs and asynchronous circuits, we illustrate that conflict- free Petri nets are not just theoretically nice, they

have real-world applications as well.

2

Definitions

Let Z (N) denote the set of (nonnegative) integers, and

Zk

(Nk) the set of vectors of

k

(nonnegative) integers. For a k-dimensional vector v, let v(i), 1

5

i

5

k, denote the ith component of v. For a given value of

k,

let 0

denote the vector of k zeros (i.e., O(i) = 0 fori = 1

,...,

k).

A Petri Net (PN, for short) is a 4-tuple (P,T,cp,po), where P is a finite set of places, T is a finite set of tran- sitions, ‘p is a flow function cp : ( P x T) U ( T x P )

-+ { O , l } , and pa is the initial marking pa : P + N.

A

marking is a mapping p : P + N. A transition t E T is enabled at a marking p iff for every p E P, cp(p,t)

5

p(p).

A transition t may fire at a marking p if t is enabled at p . We then write p

f

p ‘ , where p’(p) = p(p) - cp(p,t)

+

cp(t,p) for all p E P. A sequence of transitions u = tl...t, is a firing sequence from pa (or a firing sequence of ( ~ , ~ , ‘ p , p o ) ) iff po

3

p1

4

...

41

p, for some se-

quence of markings p1,

..+,.

(We also write ‘ p o

5

p n 7 . )

We write ‘ p o

5’

t o denote that U is enabled and can

be fired from po, i.e., p o

5

iff there exists a marking p

such that pa I; p .

to be

a mapping : T -+ N such that

#,,(t)

= the number of occurrences of t in u. Let p

5

p’. The value of 6 ,

denoted by A(u), is defined to be p’

-

p (E

Zk,

where

k

is the number of places in the Petri net). We let

S(a)

denote the set of transitions occurring in 0, i.e.,

Let P = (P,T,cp, p o ) be a PN. The reachability set of

P

is the set

R(P)

= { p

1

po

5

p for some U}.

P

is said to be

k

- bounded (for some

k

E N ) iff V p E R ( P ) , Vp E

P , p ( p )

5

k.

Given a place s, we let s*={tlcp(s,t) =

l , t E T} and * s = { t l p ( t , s ) = 1,t E T}. A place s and a transition t are on a self-loop iff t E S* and

t

E *s,

i.e., s is both an input and output place o f t .

P

is said t o be conflict-free iff for every place s, either

Given a sequence of transitions u, we define

S(u) =

{tlt

E T , # u ( t )

> 0 ) .

1. 1S.J

5

1,

In words, a Petri net is conflict-free if every place which is an input of more than one transition is on a self-loop with each such transition ([10,12]). In a conflict-free Petri net, once a transition becomes enabled, the only way t o disable the transition is to fire the transition itself. (That is, Vt,t’ E T , t

#

t’, p

A

p’ and p

5

implies p’

2.)

Notice that marked graphs are conflict- free, although the converse need not be true. (See [17] for more about Petri nets.)

The pairwise concurrency problem for Petri nets is that of, given a Petri net P=(P, T, (p, p o ) and two

transitions U and U , determining whether there

exists a reachable marking p (i.e., p E R(P)) such

that both U and U are enabled in p.

In the following section, we will show the problem t o be solvable in polynomial time.

3

The

complexity bound

We first show that, given two transitions U and U , if a

path simultaneously enabling U and U exists, then there must exist a short ‘witness’ which can be partitioned into ‘segments’. We then use a lemma from [8] to con- struct those segments one by one in polynomial time to answer the pairwise concurrency problem. First, we present some lemmas to set the stage for our polynomial time algorithm.

Lemma 3.1: Let po

5 p

be a computation enabling transitions U and U simultaneously. Then there exist ul and 0 2 such that (1) = #u1,,2, ( 2 ) p o

up

p , (3)

S(a2)

C

S ( a l ) , and (4) V r , # o l ( r )

5

1. (In words, 01u2

is a rearrangement of o such that if a transition occurs in o, it can also be found in gI; in addition, no transition

in g1 appears more than one time in 01.)

Proof. First, we claim that if p o 6*t p’ (where 61,b2 are sequences of transitions and 1 is a transition) and

v

transition r , s(62)

c

S(&),

0

5

# & ( T )

5

1, and t

$

S(&),

then p o

‘9

,U‘.

To prove the above claim, assume that t is not en- abled in p”, where p o

%

p”. This implies one of t’s

input places, say p , must be empty in p”. However, t is

enabled in p”’, where po

‘3

p”’, indicating the existence of a transition, say t’ in S2, which deposits a token to p .

Since S(6,) S(S,), t’ must be in S1. Since the Petri net is conflict-free and t @

S(&,),

p’‘(p)

# 0

- a contra- diction. So t must be enabled in p”. Since the Petri net is conflict-free and t @ S(6,) (because S(6,)

C

S(&)

and

t S(6,)), the firing of t in p” will not affect the en- abledness of the subsequent transition sequence 52. This

completes the proof of the claim.

To prove the statement of the lemma, we repeat- edly apply the above procedure to o by examining one transition at a time, starting from the leftmost one.

(6, =

S2

= A, initially.) If the examined transition has not yet been encountered, add that transition to 61; oth-

erwise, add t o 5 2 . 0

The next lemma indicates that if U and v can be- come enabled simultaneously, then there exists a short witness satisfying certain properties. More precisely, we have:

Lemma 3.2: If po

5

p is the shortest (or one of the shortest) computation enabling transitions U and v si-

multaneously, then D can be rearranged into o l 0 2 . . t Dk

such that (1) po

u’‘T’k

p , (2)

Vl

5

i

5

k , V transitions r , # o , ( r )

I

1, (3) V1

I

i

5

b - 1, S(0itl)

c

S ( d :

and (4) b

5

n and lo1

5

n 2 , where n is the number of transitions of the Petri net.

Proof. Conditions (1)-(3) can be derived easily by re- peatedly applying Lemma 3.1. In what follows, we prove

(4).

We first show that IC I n. Suppose this is not the case. Then there must exist a j , 1

5

j

5

IC- 1 such that S ( a j ) = S ( O , + ~ ) (since S(al), S ( D ~ ) , . . .

,

S(Q) forms a ‘shrinking’ sequence of nonempty sets (i.e., S(o1)

2

S(o2)

2

. . ’

2

S ( o k ) ) ; furthermore, there are at most n transitions in the Petri net). Consider the following three cases:

1. A(D,) contains a negative component: Since the Petri net is 1-bound and conflict-free, uJtl could never be fired.

many times will render the Petri net unbounded a contradiction.

3. A(a,) = 0: In this case, U~ can be removed with-

out affecting the simultaneous enabledness of U

and W . This contradicts the assumption that U

be the shortest.

la1

5

n2 follows immediately from

k

5

n and the fact that o l r V i , does not contain any transition more than once.

Even though Lemma 3.2 allows us to put a polyno- mial upper bound on the length of the shortest path enabling U and U , a polynomial time algorithm for the

pairwise concurrency problem does not follow immedi- ately. However, we can use the 'maximum' sequence of transitions enabled in the starting marking of that seg- ment, rather than the exact o, stated in Lemma 3.2. It

is then possible to construct a path (even though it may no longer be the shortest; it is still polynomial in length) in polynomial time to enable U and 'U, if any such path exists.

Lemma 3.3: Let po

"s*

p be a computation enabling transitions U and w simultaneously. If a; is a sequence

satisfying (1) po

4,

(2) V transitions T , #ol(r)

5

6 1

5

1, (3) S ( 4

c

S(o1), (4) U , ' U

Sl

S ( o ; ) - S ( 4 , then a( a2

po % p r , for some p', and U and v are enabled in p'. Proof. According to conditions (2) and (3)

,

S ( a ; ) -

S(a1) does not contain any transition belonging to u2.

This, in conjunction with the conflict-freedom property, ensures that no transition in u2 will become disabled as a result of firing transitions in S ( U ~ ) -

S(al).

Hence,

/io 4 p', for some p'. In addition, (4) implies that U

and v are enabled in p'. CI

4 0 2

The following lemma indicates the existence of a polynomial time algorithm to construct the maximum sequence of transitions in a given marking. In addition, the sequence consists of each of the enabled transitions exactly once.

Lemma 3.4: (from [SI) Given a conflict-free Petri net

P=( P, T , 9, p o ) , we can construct in polynomial time a path a enabled in po in which no transition in U is used

more than once, such that if some transition t is not used in o, then there is no path (emanating from p o ) in which t is used.

Lemma 3.5: Given a l-bounded conflict-free Petri net

P = ( P , T , y , p o ) , let po ula%'uL p , 1

5

IC

5

n, be the

shortest computation guaranteed by Lemma 3.2. Let Ti

be T

-

( { u , v } - S ( o i ) ) , and (p; be the restriction of 'p on T,. Suppose uia;. . . U; is a sequence of transitions

defined recursively as follows: V1

5

i

5

k,

U: is the sequence of transitions guaranteed by Lemma 3.4 with

respect to ( P , Ti, y i , ~ ~ - ~ ) , where po -it-' Then po -+ p' is a computation enabling U and v simul-

taneously (i.e., U and 'U are enabled in p').

Proof. First consider a;. It is easy to see the following:

a'a' ...a'

12 k

1. V r , # a l ( ~ ) I 51.

5

1 and

5

1 are due to Lemmas

3.2 and 3.4, respectively. (That is, no transition

occurs more than once in crl and o;.) According to Lemma 3.4, if a transition is not in ai, then there is no path in which the transition is used. Hence, v r , #a1 ( r )

I

#a;

2. S ( a 2...ak) 5

S(al)

- Lemma 3.2.

3. U , w

6

S(oi)

-

S(U1).

Recall that TI = T - ( { u , w } - S(al)) and o; is with respect to (P,Tl,yl,po). Hence, if U ( v ) is not in ul, then it is not in U; either.

U'

Using Lemma 3.3, we immediately have that po f p1 uz'"uk +

p", for some pr', and U and v are enabled in p". Start- ing in p1 and repeatedly applying the above argument, we can easily show that po

5

li p r is a computation

enabling U and v simultaneously. 0

a'o' ...a'

The above lemma suggests an iterative way of con- structing a path to enable U and w simultaneously, if

such a path exists. In each stage, we construct a se- quence of maximum length which is enabled in the re- sulting marking of the previous stage. The only problem with this approach is that for each

i,

the presence or ab- sence of U (or v) in a:, 1

<

i

5

IC, must coincide with

that in ot. Since we have no knowledge of the transitions ,

used in ut, how do we know whether we should include or exclude U and v in constructing the maximum se-

quence? At first glance, it seems that nondeterministic steps (for guessing the presence of absence of U and v in all k1 1

5

5

5

n, segments) were inevitable. A careful examination, however, reveals that such nondetermin- ism can be avoided by taking advantage of the ‘shrink- ing property’ of the sequence cr1, u21

...,

g k mentioned in

Lemma 3.2. More precisely, if’ U (or v) does not appear in, say aj, then U (or v ) will never occur in subsequent segments crj+1,

...,

u k . This is exactly the key property upon which our polynomial time algorithm relies.

Theorem 3.6: The pairwise concurrency problem for 1-bounded conflict-free Petri nets is solvable in polyno- mial time.

Proof. We let Find-Max-Seq(P, T,p, po) (where (P, T , p, p o )

is a conflict-free Petri net) be a procedure that outputs a sequence of transitions cr in which no transition in cr is used more than once, and if some transition

t

is not used in cr, then there is no path in ( P , T , p , p o ) in which t is used. The existence of a such procedure is guaranteed by Lemma 3.4.

We construct the sequence c;cri. . .o; stated in Lemma 3.5. In our procedure, we use two variables, namely i and j , to represent the indices of the segments in which U

and U , respectively, are b u s e d for the first time. (More

precisely, U ( U ) is assumed to be used in u;, 1

5

1 5 i - 1

(cr;, 1

5

1 <_ j - l ) , but not in a:, i

5

T <_

k

(u:,

j

5

T

5

5 ) . ) Since we do not know in advance the

exact values of i and j in the path enabling U and v , we consider all possibilities of i and j , each of which ranges from 1 t o n

+

1. (For example, i = 1 indicates that U

was never used; i = n

+

1 indicates that U is used in

every segment.) The algorithm is as follows.

Procedure Concurrent-Pair(P, T , p, po, U , U )

/*

U , v E T ; This procedure is to determine whether transitions U and v can become enabled simultaneously in a 1-bounded conflict-free Petri net (P, T, p, p o ) .

*/

for i := 1 to n

+

1 do for j := 1 to n

+

1 do begin T‘ :=

T;

/ I := /Lo; for 1 := 1 to n do begin if i = 1 then T’ := T’ - { U } ; if j = 1 then T’ :=

T’

- { U } ; a:=Find - M a x - Seq(P, T’, 9’. / I ) ;

let {I’ be the marking such that p

5

p’;

if U and v are enabled in p’

then

EXIT

and return ‘YES’

else p := p’ end

end return ‘NO’

The procedure should be quite easy to understand. We thus have a polynomial time algorithm for the pairwise concurrency problem. 0

4

Two

applications

In this section, we demonstrate how the polynomial time result obtained in the previous section (concerning the pairwise concurrency problem for 1-bounded conflict- free Petri nets) can be applied t o the detection of race conditions in parallel programs and asynchronous cir- cuits.

4.1

Parallel Programs

As defined in

121,

a parallel program consists of several tasks running simultaneously (i.e., in parallel). Tasks can be thought of as independently executing sequen- tial processes except at points where they communi- cate. Synchronization between tasks is by means of the so-called event variables. Two kinds of operations can be applied to an event variable, namely post and waif.

Upon reaching a wuit var statement, the normal ex- ecution of a ta.sk will be suspended if the associated event variable var has not been posted; the task will resume its normal execution only when var becomes posted by anot,her task. A ‘race condition can be de- fined as the situation in which two statements try to

access the same memory location siniultaneously, and at least one of them attempts to alter the content of the location. The existence of race conditions will result in the outcome of the execution of a parallel program to be speed-dependent. As a result, different runs of the same program on the same data may result in differ- ent outcomes- which is clearly undesirable in program design.

In what follows, we use a simple example to motivate the idea of using the pairwise concurrency problem for Petri nets to capture the essence of race conditions in parallel programs.

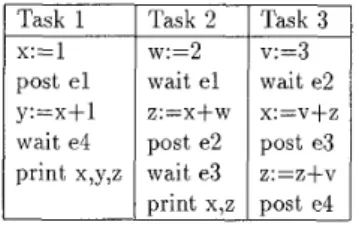
Example 1: Consider a simple parallel program P con- sisting of three tasks T,,TZ and T3 in Table 1. (The program was given in

[a]

as an illustrating example.)

Task 1

I

Task 2

I

Task 3

x:=l

I

w:=2

I

v:=3

Table 1: A simple parallel program.

The use of Petri nets to model parallel programs is not new. (See e.g. [14,16] for using Petri nets to model Ada programs.) Using the similar idea (as that in [14, 16]), P can easily be modeled by the Petri net depicted in Figure 1. (Notice that places el,e2,e3 and e4 are used for representing the four event variables in P ; in each of these places, the presence of a token indicates that its associated event variable has been posted.)

Now consider a possible race between statements y :=

z + 1 (of Task 1) and z := v + z (of Task 3) in the parallel program P given in Example 1. (Note that variable z is written by Task 3 and is read by Task 1; by definition,

this constitutes a possible race.) By tracing the first few steps of the execution of P , it is not hard to see that a race indeed could happen between these two statements. Hence, the program is not race-free. A careful examina-

tion of Petri net N will also reveal the same fact. More

precisely, there is a firing sequence which enables the two transitions labeled y := z

+

1 (of Task 1) and z := U

+

z

(of Task 3) simultaneously.

In view of the above, detecting whether a parallel program is race-free is closely related to the pairwise concurrency problem for Petri nets. Given a parallel program P , we define P R ( P ) = { ( t , t ’ )

I

statements t,t’ belong to two different tasks in P , t and t’ have certain variables in common, and at least one of t and t’ tries t o write to one of their shared variables.} (In words,

PR(P) defines the set of all possible pairs of conflict statements in P . ) Given a Petri net N = ( P , T , f , p o ) , let C o n ( N ) = { ( t , t ‘ )

I

there exists a reachable marking in

N such that transitions t,t‘ are enabled simultaneously

}. We have the following easily shown result:

Theorem 4.1: Given a parallel program P , P is race- free iff PR(P)

n

C o n ( N ) =

0,

where N is a Petri net

modeling P .

Suppose we let class C to be the class of parallel programs satisfying the following constraints:

1. No if-then-else statements.

2. Do loops are allowed; but post statements are dis- allowed inside a do loop.

3. No two tasks can post the same event variable.

It is not hard t o see that for each class C parallel pro- gram, its associated Petri net is 1-bounded and conflict- free. Using the complexity result obtained in the previ- ous section, we have the following theorem:

Theorem 4.2: The race detection problem for class C parallel programs can be solved in polynomial time.

4.2

Asynchronous circuits

In [3,4,19], Petri nets were used to model the behaviors of asynchronous circuits. Consider the so-called Muller C-element (see [3]) whose diagram is depicted in Fig-

ure 2. Such element has been modeled by a Petri net displayed in Figure 3 [3]. The labels a+ and a- repre- sent the raising and lowering, respectively, of input a’s signal. (b+, b-, e+, and c- are defined likewise.) By

raising (lowering) a signal we mean the change of the sig- nal from 0 t o 1 (1 t o 0). In the study of an asynchronous circuit, a fundamental issue is to identify the situation in which the raising of a signal by one element i s in conflict with the lowering of the same signal by another element. (This kind of conflict can be thought of as a mace in the circuit.) In the modeling Petri net, this sort of conflict corresponds t o the situation in which two designated transitions (modeling the raising and the lowering of a

signal in the modeled circuit) become enabled simulta- neously - which is exactly what the pairwise concur- rency problem is about. Furthermore, it was suggested in [3,4,19] that the class of 1-bounded conflict,-free Petri nets is exactly the one needed to model asynchronous circuits. As a result, our polynoinial time algorithm de- rived in the previous section provides a tool for analyzing whether a circuit suffers from the kind of race described above. In fact, it was posed as an open problem in [19] as to whether a such polynomial time algorithm exists.

In this paper, we answer the question in the affirmative.

5

Conclusion

In this paper, we have used the pairwise concurrency problem for (1-bounded conflict-free) Petri nets to cap- ture the notion of a race condition for a class of parallel programs (and asynchronous circuits). We have also demonstrated the pairwise concurrency problem for 1- bounded conflict-free Petri nets to be solvable i n poly- nomial time. As a result, the race detection problem for parallel programs (and asynchronous circuits) can be solved in polynomial time as well. Several questions remain t o be answered. They include:

1. Can we extend our work to more complicated par- allel programs?

2. Can other problems concerning parallel programs (or asynchronous circuits) be modeled and ana- lyzed by Petri nets?

3. Does the pairwise concurreiicy problem defined in

this paper have other applications?

References

H. Baker. Rabin’s Proof of the Undecidability of the Reachability Set Inclusion Problem of Vector Addi- tion Systems. Memo 79. MIT Project M.4C, Computer Structure Group, Cambridge, MA, 1973.

V. Balasundaram and K. Kennedy. Compile-time De- tection of Race Conditions in a Parallel Program. Pmc. of the International Conference on Supercomputing, Crete, Greece, June 1989, pp. 175-185.

J . Brzozowski and C. Seger. Advances in Asynchronous Circuit Theory (Part 11). EATCS Bulletin 43:199-263, 1991.

T. Chu. Synthesis of Self-Timed VLSI Circuits from Graph-Theoretical Specifications. Ph.D. Thesis? MIT, 1987.

S . Crespi-Reghizzi and D. Mandrioli. A Decidability Theorem for a Class of Vector -4ddition Systems. In- fornaation Processing Letters, 3(3):78-80, 197.5.

R. Howell and L. Rosier. Completeness Results for Conflict-Free Vector Replacement Systems. J . of Com- puter and System Sciences, 37:349-366, 1988. R. Howell and L. Rosier. On Questions of Fairness and Temporal Logic for Conflict-Free Petri Nets. In G. Rozenberg, editor, Advances in Petri Nets 1988, pages 200-226, Springer-Verlag, Berlin, 1988. LNCS 340.

R. Howell, L. Rosier, and H. Yen. An O ( d 5 ) Algo- rithm to Decide Boundedness for Conflict-Free Vector Replacement Systems. Information Processing Letters. 25:27-33, 1989.

R. Howell, L. Rosier and H. Yen. Normal and Sinkless Petri Nets. Proc. of 7th International Conference on

the Fundamentals of Computing Theory, Szeged, Hun- gary, August 1989, pp. 234243. To appear in Journal

of Computer and System Sciences.

N. Jones, L. Landweber, and Y. Lien. Complexity of Some Problems in Petri Nets. Theoret. Comp. Sci.. 4 : 2 77-299, 1977.

R. Kosaraju. Decidability of Reachability in Vector Ad- dition Systems. Proc. 14th Ann. AChISymp. on Theory

of Computing, 267-280, 1982.

L. Landweber and E. Robertson. Properties of Conflict- Free and Persistent Petri Nets. JACM, 25(3):352-364. 1978.

R. Lipton. The Reachability Problem Requires Expo- nential Space. Technical Report 62. Yale University, Dept. of CS., New Haven, Conn., January 1976.

[14] D. Mandrioli, R. Zicari, C. Ghezzi and F. Tisato. Mod- eling the Ada Task System by Petri Nets. Comput. Lang. 10 (1): 43-61, 1985.

[15] E. Mayr. An Algorithm for the General Petri Net Reachability Problem. SIAM J. Comput. 13 (3): 441- 460, 1984.

[ l G ] T . Murata, B. Shenker and S. Shatz. Detection of Ada Static Deadlocks Using Petri Net Invariants. IEEE Transactions on Software Engineering 15(3): 314-325, March 1989.

[17] J. Peterson. Petri Net Theory and the Modeling of Sys- tems. Prentice-Hall, Englewood Cliffs, N.J., 1981. [18] C. Rackoff. The Covering and Boundedness Problems

Theoret. Comp. Sci., for Vector Addition Systems.

6~223-231, 1978.

[19] M. Tiusanen. Some Unsolved Problems in Modeling Self-Timed Circuits Using Petri Nets. EATCS Bulletin 361152- 160, 1988. 8- b-

is

+

e2

c,

+=v+z

j p o s t e4

Figure 1. Petri net N modeling program P in Table 1.

b a