第四章 四邊形

注意：

允許學生個人、非營利性的圖書館或公立學校合理使用

本基金會網站所提供之各項試題及其解答。可直接下載

而不須申請。

重版、系統地複製或大量重製這些資料的任何部分，必

須獲得財團法人臺北市九章數學教育基金會的授權許

可。

申請此項授權請電郵

ccmp@seed.net.tw

Notice:

Individual students, nonprofit libraries, or schools are

permitted to make fair use of the papers and its

solutions. Republication, systematic copying, or

multiple reproduction of any part of this material is

permitted only under license from the Chiuchang

Mathematics Foundation.

Requests for such permission should be made by

e-mailing Mr. Wen-Hsien SUN ccmp@seed.net.tw

第

第

四

四

章

章

四

四

邊

邊

形

形

一、多邊形

4.1 多邊形

籬笆的格子、六角螺帽外圍的各個面(圖 4-1)、門、窗等，都 是多邊形的形象。 如圖 4-2 那樣，由一些線段首尾順次連結組成的圖形，叫做 多邊形。組成多邊形的各條線段叫做多邊形的邊，每相鄰兩條邊 的公共端點叫做多邊形的頂點。連結多邊形不相鄰的兩個頂點之 線段叫做多邊形的對角線，多邊形各邊的長度之總和叫做多邊形 的周長。例如圖 4-2 甲中，AB、BC、CD、DE、EA 是多邊形的 邊，A、B、C、D、E 是多邊形的頂點，AC、AD、BD、BE、CE 是多邊形的對角線，AB、BC、CD、DE、EA 的長度之總和是多 邊形的周長。 多邊形用表示它的各個頂點之字母來表示。如圖 4-2 甲的多 邊形記作多邊形 ABCDE。 一個多邊形至少要有三條邊，有三條邊的是三角形，有四條 邊的叫做四邊形，有五條邊的叫做五邊形，有 n 條邊的叫做 n 邊 形。 圖 4-1 圖 4-2 C B D A 甲 E 乙 C B D A E G F

把多邊形的任何一條邊向兩方延長，如果多邊形的其它各邊 都在延長所得直線的同側，這樣的多邊形叫做凸多邊形(另一定義 為：多邊形內部任意二點所連結的線段都落在此多邊形內部，則 稱此多邊形為凸多邊形)。例如，圖 4-2 甲、圖 4-3 甲中的多邊形 是凸多邊形，圖 4-2 乙、圖 4-3 乙中的多邊形不是凸多邊形(稱之 為凹多邊形)。以後，本書中所說的多邊形都是指凸多邊形。 多邊形相鄰兩邊所組成的角叫做多邊形的內角，簡稱多邊形 的角。多邊形的角之一邊與另一邊的反向延長線所組成之角叫做 多邊形的外角，多邊形的外角也就是與它有公共頂點的內角之鄰 補角。例如，在圖 4-3 甲中， DAB∠ 、 ABC∠ 、 BCD∠ 、 CDA∠ 是多邊形的角， DAE∠ 、 BAN∠ 、 ABG∠ 等式多邊形的外角。與 多邊形每一內角相鄰有兩個外角，這兩個外角是相等的。(為什 麼？)

練 習

1. (口答) 在圖 4-3 甲中，如果 AB = 20 mm、 BC =30 mm、 13 CD = mm、DA= 21mm、∠ABC = °60 ，那麼四邊形 ABCD 的周長等於多少？在頂點 B 處有幾個外角？是哪幾個？各等 於多少度？ 2. (口答) 從四邊形的一個定點出發，可以作幾條對角線？每條 對角線把四邊形分成幾個三角形？ D C B A E M H G F K L N C B D A E F 圖 4-3 甲 乙

4.2 多邊形的內角和

我們知道，三角形的內角和等於180°，怎樣計算邊數為 n 的 多邊形之內角和呢？如果能將多邊形分割成一些三角形，問題就 解決了。 在已知 n 邊形 A A A_{1 2 3⋯}A_n內任取一點 O (圖 4-4)，連結OA 、₁ OA 、₂ OA 、…、₃ OA ，_n 這些線段將 n 邊形分成以 O 為公共頂點的 n 個三角形。由此可得，n 邊形的內角和等 於這 n 個三角形的內角和減去以 O 為頂點 的 n 個角之和。因為 n 個三角形內角的和 是n_i180°，以 O 為頂點的 n 個角之和是一 個周角，等於 360°，所以 n 邊形的內角和是 180 360 ( 2) 180 n_i ° − ° = −n _i ° 由此得到下面的定理： 多邊形內角和定理 n 邊形的內角之和等於 (n−2) 180_i °。 取多邊形每一個內角的一個鄰補角，它們相加的和叫做多邊 形的外角和。因為多邊形每一個內角與它的一個鄰補角的和等於 180°，應用上面的定理，可以推算，n 邊形 n 個外角的和等於 180 ( 2) 180 360 n_i ° − −n _i ° = ° 於是得到 推論 1 任意多邊形的外角和等於 360°。 在第二章，我們學過兩邊分別平行的 兩個角的關係，現在，我們應用多邊形內 角和定理來研究兩邊分別垂直的兩個角的 大小有什麼關係。 如圖 4-5， 1∠ 的兩邊分別垂直於 A∠ 的兩邊，那麼，因為 1∠ 與 A∠ 是一個四邊 形的兩個內角，而這個四邊形的另外兩個 內角都等於 90°，所以 圖 4-4 O 1 A 6 A 5 A 4 A 3 A 2 A n A 圖 4-5 A D C B 1 E 2 3 4

1 A (4 2) 180 2 90 180 ∠ + ∠ = − i ° − × ° = ° 即 1∠ 與 A∠ 互補。 又∠2、 3∠ 、 4∠ 的兩邊也分別垂直於 A∠ 的兩邊。 因為 3∠ = ∠1，所以 3∠ 與 A∠ 也互補。 又因為∠2與 A∠ 都是 1∠ 的補角，所以 2∠ = ∠A。 同理∠ = ∠4 A。由此得到： 推論 2 如果一個角的兩邊分別垂直於另一個角的兩邊，那 麼這兩個角相等或互補。 當兩個角都是銳角或都是鈍角時，這兩個角相等；當兩個角 中一個角是銳角一個是鈍角時，這兩個角互補。 【例 1】 已知一個多邊形，它的內角和等於外角和的兩倍，求這 個多邊形的邊數。

□

解 設多邊形的邊數為 n，因它的內角和等於 (n−2) 180_i °、 外角和等於 360°，所以； (n−2) 180_i ° =2 360_i °。 解得n = 6。 答：這個多邊形的邊數是 6。 【例 2】 測斜坡的傾斜角可以用坡度板。坡度板上有半圓形的角 度刻度，0°線垂直於板邊，在圓心處掛一自然下垂的金 屬指針，把板邊放在斜坡上，看指針所指的度數，就是 斜坡傾斜角α 的度數。說明它的道理。

□

解 按題意，畫出坡度板測斜坡傾斜角的幾何圖形，如圖 4-7。 圖 4-6 α α A D C B E O 圖 4-7

∵ DO ⊥ AC 、 DE ⊥ AB且∠ < °D 90 、∠ < °α 90 ∴ ∠ = ∠α D (兩邊分別垂直的銳角相等) 所以，指針所指的度數就是斜坡的傾斜角

α

的度數。

練 習

1. 幾邊形的內角和等於它的外角和？ 2. 一個多邊形的每一個外角都是 72°，這個多邊形的內角和是 多少度？ 3. 已知兩組對應邊互相垂直的兩個角之差為 35°，求這兩個角 的度數。

習 題 十 二

1. 畫一個四邊形並連結它的各條對角線，作一條線段等於： (1) 它的各條對角線的和； (2) 四邊形的周長。並且比較它與各條對角線的和之大小。 2. 五邊形有幾個頂點？經過五邊形的一個頂點有幾條對角線？ 五邊形共有幾條對角線？ 3. 過 n 邊形的一個頂點有幾條對角線？這些對角線把 n 邊形分 成幾個三角形？用這種分法證明多邊形內角和定理。 4. 在四邊形 ABCD 中，已知： A∠ = ∠D 、 B∠ = ∠C。 求證： AD// BC 。 5. 六角螺母正面成六邊形，六個內角相等，求每一個內角的度 數。 6. (1) 一個多邊形的內角和等於1080°，求它的邊數； (2) 一個多邊形的每一個內角都等於144°，求它的邊數； (3) 一個多邊形的每一個外角都等於 30°，求它的邊數。 7. 銳角△ABC 的高 BE 與 CF 的交點是 H， EHF∠ 與 A∠ 有什麼

二、平行四邊形

4.3 平行四邊形及其性質

兩組對邊分別平行的四邊形叫做 平行四邊形。如圖 4-8 四邊形 ABCD 中，AB//DC 、AD// BC ，那麼四邊形 ABCD 是平行四邊形。平行四邊形利用 符號「

_▱

」表示，平行四邊形 ABCD 記作「

_▱

ABCD」，讀作「平行四邊形 ABCD」。 下面研究平行四邊形的一些性質。我們已經學過了三角形， 如果畫出平行四邊形的一條對角線，就把平行四邊形分成兩個三 角形，可以利用三角形的性質來研究平行四邊形。 首先研究平行四邊形的兩組對邊、兩組對角的關係。 作

_▱

ABCD的對角線 AC，將它分 成△ABC 與△CDA(圖 4-9)。 ∵ AB CD 、// AD//BC ∴ ∠ = ∠1 3、∠ = ∠2 4 又 ∵ AC =CA ∴ △ABC ≅ △CDA ∴ AB =CD、 CB = AD、∠ = ∠B D 又 ∵ ∠ + ∠ = ∠ + ∠1 4 2 3 ∴ ∠ = ∠A C 由此得到： 平行四邊形性質定理 1 平行四邊形的對角相等。 平行四邊形性質定理 2 平行四邊形的對邊相等。 如圖 4-10，l₁ //l ，AB、CD 是 ₂ l 、₁ l 之間的任意兩條平行線₂ 段，顯然，ABCD 是平行四邊形。因為平行四邊形的對邊相等， 所以 AB CD= 。由此得到： 推論 夾在兩條平行線間的平行線段相等。 A _D C B 圖 4-8 A _D C B 圖 4-9 1 2 3 4

從推論可以知道，如果兩條直線平行，那麼一條直線上所有 個點，到另一條直線的距離都相等。兩條平行線中，一條直線上 任意一點到另一條直線的距離，叫做這兩條平行線的距離。如圖 4-11，l₁ //l ，₂ A 是l 上的任意一點，₁ AB ⊥ l₂，B 是垂足，線段 AB 的長就是l 、₁ l 的距離。 ₂ 平行四邊形還有下面性質： 平行四邊形性質定理 3 平行四邊形的對角線互相平分。

已知：

_▱

ABCD，對角線 AC、BD 相交於點 O(圖 4-12) 求證： OA OC= 、 OB OD= 證明： ∵

_▱

ABCD中， AB CD // ∴ ∠ = ∠1 4、∠ = ∠2 3 又 ∵ AB =CD (平行四邊形的對邊相等) ∴ △OAB ≅△OCD ∴ OA OC= 、 OB OD= 我們知道，三角形具有穩定性，而四邊形就沒有穩定性。可 以利用四邊形的不穩定性製成活動的平行四邊形框(圖 4-13)、汽 車的防護鏈(圖 4-14)等。 圖 4-10 A D C B 1 l 2 l 圖 4-11 A B 1 l 2 l O A _D C B 圖 4-12 1 2 4 3 圖 4-13 圖 4-14

【例 1】 過△ABC 的頂點 A、B、C，分別引對邊的平行線，它們 兩兩相交於 A′、 B′、 C′。求證：△ABC 的三條高是 △A B C′ ′ ′三邊的垂直平分線。 已知： 如圖 4-15，C B′ ′// BC、 C A′ ′// AC、B A′ ′// AB、 AD ⊥ BC 、 BE ⊥CA、 CF ⊥ AB。 求證： AD、BE、CF 分別是 C B′ ′、 C A′ ′、 B A′ ′的垂 直平分線。 證明： ∵ C B′ ′//BC 、 C A′ ′// AC 、B A′ ′// AB AB CD // ∴ BC =C A′ (夾在兩條平行線間的平行線段相等) 同理 BC = AB′ ∴ C A′ = AB′ 又 ∵ AD ⊥ BC ∴ AD ⊥C B′ ′ 所以 AD 是 C B′ ′的垂直平分線。 同理 BE、CF 分別是 C A′ ′、B A′ ′的垂直平分線。 在前一章裡，我們已經證明過三角形三邊的垂直平分線交於 一點，由於例 1 中的△A B C′ ′ ′三邊的垂直平分線就是△ABC 的三 條高，可見，三角形的三條高也相交於一點。 【例 2】 已知：

_▱

ABCD中，對角線 AC 與 BD 相交於點 O， M、N 分別是 OA、OC 的中點 (圖 4-16) 求證： BM = DN 、 BM //DN 。 證明： ∵ 四邊形 ABCD 是平行四邊形 E A D C B 圖 4-15 F A′ C′ B′ M A D C B N O

∴ OB OD= 、 OA OC= (平行四邊形的對角線互相平分) ∵ 1 2 OM = OA、 1 2 ON = OC ∴ OM =ON 又 ∵ ∠MOB = ∠NOD ∴ △MOB ≅ △NOD ∴ BM = DN 、 BMO∠ = ∠DNO ∴ BM //DN

練 習

1. 舉出日常生活中常見的平行四邊形的一些例子。 2. 已知：在

_▱

ABCD中， AE ⊥ BC 、 CF ⊥ AD，E、F 是垂足 求證：△ABE ≅△CDF 3. 如 圖 4-12 ， 已 知 O 是

_▱

ABCD 的 對 角 線 交 點 ， 如 果 24 AC = mm、BD = 38mm、AD = 28mm，求△OBC 的周長。

4.4 平行四邊形的判定

判定一個四邊形是不是平行四邊形，除了根據定義來判斷以 外，還有以下判定定理： 平行四邊形判定定理 1 一組對邊平行且相等的四邊形 是平行四邊形。 已知： 四邊形 ABCD， AB CD 、 AB// =CD (圖 4-17) 求證： 四邊形 ABCD 是平行四邊形。 證明： 連結 AC。 ∵ AB CD // ∴ ∠ = ∠1 2 又 ∵ AB =CD、 AC =CA ∴ △ABC ≅ △CDA A _D C B 圖 4-17 1 3 2 4

∴ ∠ = ∠3 4 ∴ BC // AD 所以四邊形 ABCD 是平行四邊形。 「平行且等於」用符號「 」表示。如圖 4-17， AB = DC、 // AB DC ，可以記作 AB DC，讀作「AB 平行且等於 DC」。 與定理 1 相類似，利用全等三角形，容易證明平行四邊形判 定定理 2、3。 平行四邊形判定定理 2 兩組對邊分別相等的四邊形 是平行四邊形。 平行四邊形判定定理 3 對角線互相平分的四邊形是 平行四邊形。

【例 1】 已知：

_▱

ABCD中，E、F 分別是邊 AD、BC 的中點

(圖 4-18)。 求證： EB = DF 。 證明： ∵ 四邊形 ABCD 是平行四邊形 ∴ AD BC (平行四邊形對邊平行且相等) ∵ 1 2 ED = AD、 1 2 BF = BC ∴ ED BF ∴ 四邊形 EBFD 是平行四邊形 (一組對邊平行並且相等的四邊形是平行 四邊形) ∴ EB = DF (平行四邊形的對邊相等) 圖 4-18 E A _D C B _F 圖 4-19 E A D C B

【例 2】 已知： 線段 BC 與直線 BC 外一點 A (圖 4-19)。 求作： 以 A 為一頂點，以線段 BC 為一邊的平行四邊 形。 作法： 1. 連結 AB。 2. 分別以 A、C 為圓心，以 BC、AB 為半徑 作弧，兩弧相交於點 D。 3. 連結 AD、CD。 四邊形 ABCD 就是所求的平行四邊形。 證明： ∵ AD= BC、 DC = AB ∴ 四邊形 ABCD 是平行四邊形 (兩組對邊分別相等的四邊形是平行四邊形) ∵

_▱

ABCD的一邊是 BC、一個頂點是 A ∴ 四邊形 ABCD 就是所求的平行四邊形 討論： 如果連結 AC，同理可作四邊形 AEBC，它也是 所求的平行四邊形。此題有兩個解。

練 習

1. 求證：兩組對角分別相等的四邊形是平行四邊形。 2. 把兩個全等的三角形，按不同的方法拼成四邊形，可以拼成 幾個不同的四邊形，它們都是平行四邊形嗎？為什麼？ 3. 已知：

_▱

ABCD，E 是 AB 的中點、F 是 CD 的中點 求證： EF = BC 4. 延長△ABC 的中線 AD 至 E，使 DE = AD。 求證：四邊形 ABEC 是平行四邊形。

習 題 十 三

1. 在

_▱

ABCD中： (1) 已知周長為 28 cm、 3 4 AB = BC ，求各邊的長； (2) 已知∠ + ∠ =A C 200°，求各角的度數。

2. 已知

_▱

ABCD與

_▱

AEFD如圖。 求證：△ABE ≅△DCF 。 3. 求證：平行四邊形對角線的交點到 一組對邊的距離相等。 4. 已知： E、F 是

_▱

ABCD對角線 AC 上的兩點，並且 AE =CF。 求證： BE = DF 。 5. 求證：平行四邊形一條對角線的兩個端點到另一條對角線的 距離相等。 6. 如圖，

_▱

ABCD 中， AE ⊥ BC 、 AF ⊥CD ，垂足分別是 E、F， 1 60 ∠ = °、BE = 2cm、DF =3cm， 求各內角的度數與各邊的長。 7. (1) 畫一條直線與已知直線平 行，並且距離為 20 mm。這樣的直線可以畫幾條？ (2) 求作一條直線與已知兩條平行直線平行且距離相等。 8. 求證：一組對邊平行、一組對角相等的四邊形是平行四邊形。 9. (1) 已知 A、C 是直線 l 同側的兩點， AB ⊥l 、 CD ⊥l，垂 足分別是 B、D，且 AB CD= 。 求證： AC //l (圖甲)。 (2) 如果一塊木板兩邊是直線，把兩把曲尺的一邊靠緊木板 邊緣，再看木板另一邊緣對曲尺另一邊上刻度是否相 等，就能判斷木板的兩個邊緣是否平行。為什麼？(圖乙) (第 2 題) A F E D C B (第 6 題) A F E D C B 1 甲 (第 9 題) A B C D l 乙

10. 已知： E、F、G、H 分別是

_▱

ABCD的邊 AB、BC、CD、 DA 上的點，並且 AE =CG、 BF = DH 。 求證： 四邊形 EFGH 是平行四邊形。 11. 已知： AC 是

_▱

ABCD的一條 對角線， BM ⊥ AC 、 DN ⊥ AC，垂足分別是 M、N。 求證： 四邊形 BMDN 是平行四 邊形。 12. 已知：

_▱

ABCD的對角線 AC 上兩點 E、F，且 AE =CF。 求證： 四邊形 BFDE 是平行四邊形。 13. 求證：平行四邊形一組對角的平分線如果不在同一條直線 上，那麼它們互相平行。 14. 求作平行四邊形，使： (1) 以已知點 A、B、C 為頂點，這樣的平行四邊形可以作 幾個？寫出其中一個的作法。 (2) AB = a、 BC =b、 ABC∠ =α 。

4.5 矩形

根據四邊形的不穩定性，我們可以把一個平行四邊形的形狀 改變成有一個直角的平行四邊形(圖 4-20)。有一個角是直角的平 行四邊形叫做矩形(通常也叫做長方形)。矩形是人們日常生活與 生產中最常見的四邊形，如課本、黑板、門、窗等都呈矩形。 (第 11 題) A M N D C B A _D C B 圖 4-20 A D C B

因為矩形是一種特殊的平行四邊形，所以它除具有平行四邊 形的所有性質外，還具有一些特殊的性質。 如圖 4-21，

_▱

ABCD中， A∠ 是直角。因為 C∠ = ∠A(平行四 邊形的對角相等)，所以 C∠ 也是直角。又因 B∠ 、 D∠ 都與 A∠ 互 補，所以 B∠ 、 D∠ 也都是直角，由此得到： 矩形性質定理 1 矩形的四角都是直角。 矩形還有下面的性質： 矩形性質定理 2 矩形的對角線相等。 已知： 矩形 ABCD (圖 4-22) 求證： AC = DB 證明： 在矩形 ABCD 中， ∠ABC = ∠DCB = ∠Rt (矩形的四個角都是直角) AB =CD (平行四邊形的對邊相等) BC =CB ∴ △ABC ≅ △DCB ∴ AC = DB 要判定一個四邊形是矩形，除了根據定義外，還可以根據下 面的定理： 矩形判定定理 1 有三個角是直角的四邊形是矩形。 矩形判定定理 2 對角線相等的平行四邊形是矩形。 已知：

_▱

ABCD中， AC = DB (圖 4-22) 求證：

_▱

ABCD是矩形 證明： ∵ AC = DB、 BC = CB AB = DC (平行四邊形的對邊相等) ∴ △ABC ≅ △DCB 圖 4-21 A D C B 圖 4-22 A D C B

∴ ∠ABC = ∠DCB 又 ∵ AB//DC ∴ ∠ABC+ ∠DCB = 2Rt∠ ∴ ∠ABC = ∠Rt ∴

_▱

ABCD是矩形 在生產中，工人在製作門框或矩形零件時，常用測量兩條對 角線是否相等來檢查直角的精度，就是根據這個定理。 【例】 已知：如圖 4-23，矩形 ABCD 的兩條對角線相交於點 O， ∠AOD =120°， AB = 4cm。求矩形對角線長。

□

解 ∵ 四邊形 ABCD 是矩形 ∴ AC = BD (矩形的對角線相等) 又 ∵ 1 2 OA=OC = AC 1 2 OB =OD = BD (平行四邊形的對角線互相平分) ∴ OA OD= ∵ ∠AOD =120° ∴ 180 120 30 2 ODA OAD ° − ° ∠ = ∠ = = ° 又 ∵ ∠DAB = ∠Rt (矩形的四個角都是直角) ∴ BD = 2AB = ×2 4 cm =8 cm

練 習

1. 求證：四個角都相等的四邊形是矩形。 2. 求證：對角線互相平分並且相等的四邊形是矩形。 3. 用刻度尺怎樣檢查一個四邊形零件是不是矩形？ 4. 利用矩形性質，證明直角三角形斜邊上的中線等於斜邊的一 半。 圖 4-23 A B C D O

4.6 菱形

有一組鄰邊相等的平行四邊形叫做菱形。 菱形也是一種特殊的平行四邊形，所以它除具有平行四邊形 的所有性質外，也具有一些特殊的性質。 如圖 4-24，

_▱

ABCD中，AB = AD。因為 CD = AB、BC = AD (平行四邊形的對邊相等)，所以四條邊都相等。因此得到： 菱形性質定理 1 菱形的四條邊都相等。 菱形還有下面的性質： 菱形性質定理 2 菱形的對角線互相垂直，並且每一條對角 線平分一組對角。 已知： 菱形 ABCD 中，對角線 AC 與 BD 相交於點 O (圖 4-25)。 求證： AC ⊥ BD；AC 平分 BAD∠ 與 BCD∠ ；BD 平分 ∠ABC 與 ADC∠ 。 證明： ∵ 四邊形 ABCD 是菱形 ∴ AB = AD BO =OD (菱形是平行四邊形) ∴ 在等腰三角形 ABD 中， AC ⊥ BD，AC 平分 ∠BAD。同理 AC 平分 BCD∠ ；BD 平分 ABC∠ 與 ADC∠ 。 要判定一個四邊形是菱形，除了根據定義外，還可以根據下 面的定理： 菱形判定定理 1 四邊都相等的四邊形是菱形。 菱形判定定理 2 對角線互相垂直的平行四邊形是菱形。 圖 4-24 A D C B 圖 4-25 A D C B O

【例】 已知： 矩形 ABCD 的對角線 AC 的垂直平分線與邊 AD、BC 分別交於 E、F(圖 4-26) 求證： 四邊形 AFCE 是菱形 證明： ∵ 四邊形 ABCD 是 矩形 ∴ AE //FC ∴ ∠ = ∠1 2 又 ∵ ∠AOE = ∠COF AO =CO ∴ △AOE ≅ △COF ∴ EO = FO ∴ 四邊形 AFCE 是平行四邊形 (對角線互相平分的四邊形是平行四邊形) 又 ∵ EF ⊥ AC ∴

_▱

AFCE是菱形 (對角線互相垂直的平行四邊形是菱形)

練 習

1. 證明菱形的兩個判定定理。 2. 從菱形的鈍角之頂點向對邊作垂線，如果垂線平分對邊，求 菱形各角的度數。 3. 求證：有一條對角線平分一個內角的平行四邊形是菱形。

4.7 正方形

有一組鄰邊相等並且有一個角是直角的平行四邊形叫做正 方形。 由正方形的定義可以得知，正方形 既是有一組鄰邊相等的矩形，又是有一 個角是直角的菱形。所以，正方形同時 具有矩形與菱形的所有性質。這些圖形 的包含關係如圖 4-27。 圖 4-26 A D C B O F E 1 2 圖 4-27 矩形 集合 菱形 集合 正方形 集合

容易知道，正方形有下面的性質： 正方形性質定理 1 正方形的四個角都是直角，四條邊都 相等。 正方形性質定理 2 正方形的兩條對角線相等，並且互相 垂直平分，每條對角線平分一組對角 反過來，如果一個圖形既是矩形又是菱形，那麼根據定義就 可以斷定它是正方形。 【例】 已知： 如圖 4-28，四邊形 ABCD 是正方形， AA′= BB′= CC′ = DD′。 求證： 四邊形 A B C D′ ′ ′ ′是正方形 證明： ∵ 四邊形 ABCD 是 正方形 ∴ AB = BC =CD = DA (正方形的四條邊都相等) 又 ∵ AA′ = BB′ =CC′ = DD′ ∴ D A′ = A B′ = B C′ = C D′ ∵ ∠ = ∠ = ∠ = ∠ = °A B C D 90 (正方形的四個角都是直角) ∴ △AA D′ ′ ≅△BB A′ ′ ≅△CC B′ ′≅△DD C′ ′ ∴ D A′ ′= A B′ ′= B C′ ′= C D′ ′ ∴ 四邊形 A B C D′ ′ ′ ′是菱形 (四邊都相等的四邊形是菱形) ∴ △AA D′ ′ ≅ △BB A′ ′ 又 ∵ ∠ = ∠2 3、 1∠ + ∠ = °2 90 ∴ ∠ + ∠ = °1 3 90 ∵ ∠D A B′ ′ ′=180° − ∠ − ∠ =1 3 180° − ° = °90 90 ∴ 四邊形 A B C D′ ′ ′ ′是正方形 (有一個角是直角的菱形是正方形) 圖 4-28 A _D C B 1 2 3 A′ B′ C′ D′

練 習

1. 兩條對角線互相垂直平分且相等的四邊形是哪種四邊形？ 為什麼？ 2. 正方形的一條對角線與一邊所成的角是多少度的角？為什 麼？ 3. 如果一個菱形的兩條對角線相等，那麼它一定是正方形。為 什麼？ 4. 如果一個矩形的兩條對角線互相垂直，那麼它一定是正方 形。為什麼？

4.8 中心對稱、中心對稱圖形

在前一章，我們學過關於直線對稱的圖形。在日常生活與工 農業生產中，還會遇到關於點對稱的圖形，例如，飛機的螺旋槳、 風車的風輪等，就是關於一點對稱的圖形的實例(圖 4-29)。它們 的每個葉片旋轉180°後，都轉到與它相對的葉片的位置。 如果把一個圖形繞著一個點旋轉180°後，它與另一個圖形重 合，那麼我們說這兩個圖形關於這個點對稱。這個點叫做對稱中 心。這兩個圖形中的對應點，叫做關於中心的對稱點。例如，圖 4-30 的△ABC 繞點 O 旋轉180°後，它就與△A B C′ ′ ′重合，因此， △ABC 與△A B C′ ′ ′關於點 O 對稱，點 O 是對稱中心，點 A 與 A′、 點 B 與 B′、點 C 與 C′是關於中心 O 的對稱點。 根據定義，關於中心對稱的兩個圖形可以重合，因此，這兩 個圖形全等。 圖 4-29 圖 4-30 A O C B A′ B′ C′

如圖 4-30，在中心對稱的兩個圖形中，對應點 A、A′、B、B′、 C、 C′ 都分別與對稱中心 O 在一條直線上，並且 OA OA= ′、 OB =OB′、 OC =OC′。由此得到下面性質： 性質 1 關於中心對稱的兩個圖形，對稱點連線都經過對稱 中心，並且被對稱中心平分。 又因為點 O 是線段 AA′與 BB′的中點，容易證得 AB A B′ ′， 同理 BC B C′ ′、CA C A′ ′，由此得到 性質 2 關於中心對稱的兩個圖形，對應線段平行(或在同一 條直線上)且相等。 性質 1 的逆命題：「如果兩個圖形的對應點連線都經過某一 點，並且被這一點平分，那麼這兩個圖形關於這一點對稱」也成 立。我們有時用它來判定兩個圖形是否關於一點對稱。 【例】 作四邊形 ABCD 關於點 O 的對稱圖形。 已知： 四邊形 ABCD 與一點 O (圖 4-31)。 求作： 四邊形 ABCD 關於中心 O 的對稱圖形。 分析： 要作四邊形 ABCD 關於點 O 的對稱圖形，只要 作 A、B、C、D 四點關於點 O 的對稱點，再順次連結各 點即可。 作法： 1. 連結 AO 並延長到 A′，使 OA′ =OA，得到 點 A 的對稱點 A′。 2. 同樣作 B、C、D 的對稱點 B′、 C′、 D′。 3. 順次連結 A′、 B′、 C′、 D′各點。 四邊形 A B C D′ ′ ′ ′就是所求的四邊形。 圖 4-31 A O C B A′ B′ C′ D D′ 圖 4-32 O A (C) D (A) C (A) B (A)

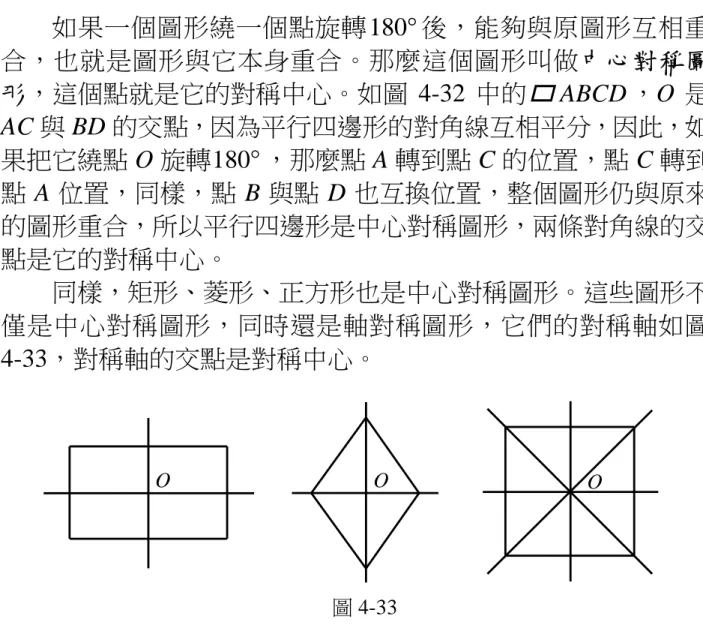
圖 4-34 圖 4-35 如果一個圖形繞一個點旋轉180°後，能夠與原圖形互相重 合，也就是圖形與它本身重合。那麼這個圖形叫做中心對稱圖 形，這個點就是它的對稱中心。如圖 4-32 中的

_▱

ABCD，O 是 AC 與 BD 的交點，因為平行四邊形的對角線互相平分，因此，如 果把它繞點 O 旋轉180°，那麼點 A 轉到點 C 的位置，點 C 轉到 點 A 位置，同樣，點 B 與點 D 也互換位置，整個圖形仍與原來 的圖形重合，所以平行四邊形是中心對稱圖形，兩條對角線的交 點是它的對稱中心。 同樣，矩形、菱形、正方形也是中心對稱圖形。這些圖形不 僅是中心對稱圖形，同時還是軸對稱圖形，它們的對稱軸如圖 4-33，對稱軸的交點是對稱中心。 在我們的周圍，中心對稱圖形是很多的。例如，具有中心對 稱圖形形狀的物體能夠在所在平面繞對稱中心平穩地旋轉，所以 在生產中旋轉的零件之形狀常設計成中心對稱圖形。如電風扇葉 片(圖 4-34)。因為中心對稱圖形形狀勻稱美觀，所以建築物上常 用這種圖形作裝飾圖案(圖 4-35) 圖 4-33 O O O

練 習

1. 舉出幾個中心對稱圖形的實例。 2. 線段、射線、兩條相交直線，是不是中心對稱圖形？如果是， 指出對稱中心位置。 3. 正三角形、五角星是不是中心對稱圖形，為什麼？

習 題 十 四

1. 已知： 矩形 ABCD，M 是 BC 的中點，BC = 2AB。 求證： MA⊥ MD。 2. 矩形對角線組成的對頂角中，有一組是 60°，對角線與各邊 組成的角是多少度？ 3. 已知： O 是矩形 ABCD 對角線的交點，E、F、G、H 分別 是 AO、BO、CO、DO 上的一點，並且 AE = BF = CG = DH 。 求證： 四邊形 EFGH 是矩形。 4. 求證：兩條平行線與第三條直線相交，兩組內錯角的平分線 相交所成的四邊形是矩形。 5. 求作矩形 ABCD，使 AB = a、 BC = b。 6. 求證：如果菱形的一個角是120°，那麼從這個角的頂點向對 角的兩邊所引兩條垂線分別平分這兩邊。 a b (第 5 題) E D C B A F G (第 7 題) H M

7. 已知： △ABC 中，AB = AC，M 為 BC 的中點，MG ⊥ AB、

MD ⊥ AC、GF ⊥ AC、DE ⊥ AB，垂足分別為 G、

D、F、E，GF、DE 相交於 H。 求證： 四邊形 HGMD 是菱形。

8. O 是矩形 ABCD 對角線的交點，作DE// AC、CE//BD，DE、 CE 交於 E。求證：四邊形 OCED 是菱形。 9. 畫菱形 ABCD，使 AC =50mm、∠BAD = °60 。 10. 已知： △ABC 中，∠ = °C 90 ，角 C 的平分線交 AB 於點 D， 作 DE ⊥ BC 、 DF ⊥ AC ，垂足分別是 E、F。 求證： 四邊形 CFDE 是正方形。 11. 已知正方形 ABCD，AB = 24mm，對 邊中點的連線將正方形分成四個小 正方形，再同樣分下去，分三次所得 的正方形的周長是多少？ 12. 求證：正方形的兩條對角線把正方形 分成四個全等的等腰直角三角形。 13. 求證：矩形的各內角平分線組成的四 邊形是正方形。 14. 求證：依次連結正方形各邊的中點所成四邊形為正方形。 15. 以一條已知線段為對角線，求作正方形。 16. 填充下列定理中所缺的詞： (1) 兩條對角線 的平行四邊形是矩形； (2) 兩條對角線 的四邊形是矩形； (3) 兩條對角線 的平行四邊形是菱形； (4) 兩條對角線 的四邊形是菱形； (5) 兩條對角線 的矩形是正方形； (6) 兩條對角線 的菱形是正方形； (7) 兩條對角線 的平行四邊形是正方形； (8) 兩條對角線 的四邊形是正方形。 (第 11 題) C B D A

17. 求作： (1) 已知點 A 關於點 O 的對稱點； (2) 已知線段 AB 關於點 O 的對稱線段； (3) 已知△ABC 關於點 O 的對稱三角形。 18. 作一個與已知四邊形 ABCD 中心對稱的四邊形。 (1) 以頂點 A 為對稱中心； (2) 以 BC 邊的中點 O 為對稱中心。 19. 作已知線段 AB 關於點 O(不在 AB 上)的對稱線段 A B′ ′。再作 A B′ ′ 關於點 O′ (不在 A B′ ′ 上)的對稱線段 A B′′ ′′ 。並證明： // A B′′ ′′ AB。 20. 求證：任何一個具有對稱中心的四邊形是平行四邊形。(用中 心對稱證明) 21. 已知：直線 x、y 互相垂直，垂足為 O。作線段 AB 關於軸 x 的對稱線段 A B′ ′。再作關於 A B′ ′關於 y 軸的對稱線段 A B′′ ′′。 線段 AB 與 A B′′ ′′是否關於點 O 對稱？

三、梯形

4.9 梯形

前面，我們研究的平行四邊形是兩組對邊分別平行的特殊四 邊形。現在，我們研究只有一組對邊平行的另一種特殊四邊形。 一組對邊平行而另一組對邊不平 行的四邊形叫做梯形(圖 4-36)。平行的 兩邊叫做梯形的底(通常把較短的底叫 做上底，較長的底叫做下底)，不平行 的兩邊叫做梯形的腰，兩底的距離叫 做梯形的高。 圖 4-36 C D B A E F

一腰垂直於底的梯形叫做直角梯形(圖 4-37)，兩腰相等的梯 形叫做等腰梯形(圖 4-38)。 直角梯形與等腰梯形都是特殊的梯形。 下面研究等腰梯形的性質： 等腰梯形性質定理 等腰梯形在同一底上的兩個角相等。 已知： 如圖 4-39，在梯形 ABCD 中，AD//BC、AB = DC。 求證： ∠ = ∠B C。 分析： 我們學過「等腰三角形兩底角相等」。如果能將等 腰梯形在同一底上的兩個角，轉化成等腰三角形的兩個底角，定 理就容易證明了。 證明： 過 D 點作DE// AB ，交 BC 於點 E，得到△DEC ∵ AD//BC 、DE // AB ∴ AB = DE (夾在兩平行線間的平行線段相等) ∵ AB = DC ∴ DE = DC ∴ ∠ = ∠1 C ∵ ∠ = ∠1 B ∴ ∠ = ∠B C 反過來，如果梯形在同一底上的兩個 角相等，兩腰是否相等呢？ 如 圖 4-40 ， 在 梯 形 ABCD 中 ， B C ∠ = ∠ ，如果延長 BA、CD 交於點 E，那 麼由 B∠ = ∠C、AD// BC 可以推出△BCE 與 △ADE 都是等腰三角形，得 E∠ 的平分線 EF 垂直平分 AD 與 BC，所以梯形 ABCD 是以 EF 為軸的對稱圖形，因此 AB = DC，由此 圖 4-37 C D B A 圖 4-38 C D B A 圖 4-39 C D B A E 1 圖 4-40 C D B A E F

得到： 等腰梯形判定定理 在同一底上的兩個角相等的梯形是 等腰梯形。 由定理的推導過程可知，等腰梯形是軸對稱圖形，經過兩底 中點的直線是它的對稱軸。 【例】 已知梯形的兩底與兩腰，作梯形。 已知： 線段 a、b、c、d，其中 a b> (圖 4-41)。 求作： 梯形 ABCD，使 AB// DC ， AB = a、 DC =b、 DA= c、 CB = d。 分析： 假定梯形 ABCD 已經作出。作DE//CB 交 AB 於點 E，可得平行四邊形 EBCD，於是 DE =CB = d 、 EB = DC =b、 AE = −a b。又 DA c= ，已知三邊可以作 出△AED，再作平行四邊形 DEBC，就可以得到所求的 梯形，問題就解決了。

作法： 1. 作△AED，使 AE = −a b、DA c= 、DE = d

2. 延長 AE 到點 B，使 EB b= 。 3. 分別過點 B、D 作BC// DE 、DC// AB ， BC、DC 相交於點 C。 四邊形 ABCD 就是所求的梯形。 證明： 根據作法， AB = − + =(a b) b a、 DC = c。 又因四邊形 EBCD 是平行四邊形(對邊平行)， 所以 CD = EB = b、 CB = DE = d。 所以，四邊形 ABCD 是所求的梯形。 討論： 三條線段 (a b− )、c、d 符合三角形三邊的關係 定理時，作圖題才有解。 圖 4-41 C D B A E a b c d a b c _d

練 習

1. (口答)一個四邊形有一組對邊平行但不相等，它是梯形嗎？ 為什麼？ 2. 求證： (1) 等腰梯形的對角線相等； (2) 對角線相等的梯形是等腰梯形。 3. 求證：等腰梯形上底的中點與下底兩端點距離相等。

習 題 十 五

1. 在梯形 ABCD 中，已知 AD//BC 、 AD = AB 、 BC = BD 、 120 A ∠ = °，求其它三個角的度數。 2. 已知直角梯形的一腰長 10 cm，這條腰與一個底所成的角是 30°，求另一腰的長。 3. 梯形的上底長為 4 cm，過它的一個端點引一腰的平行線與下 底相交，所得三角形的周長是 12 cm。求這個梯形的周長。 4. (1) 已知： 梯形 ABCD 中，AD//BC，DC > AB、BC > AD 求證： ∠ > ∠B C。 (2) 已知： 梯形 ABCD 中，AD// BC， B∠ > ∠C、BC > AD 求證： DC > AB。 5. 畫梯形 ABCD，使底 AD =3cm、BC =6cm，腰 AB = 4cm、 60 B ∠ = °。 6. 依照下圖，用兩種不同的方法證明等腰梯形的判定定理。 (第 6 題) C D B A E C D B A E F

7. 已知等腰梯形的銳角等於 60°，它的上下兩底分別為 15 cm、 49 cm。求它的腰長。 8. 作等腰梯形，使高為 a、上底為 b、下底為 c。

4.10 平行線等分線段

為了進一步研究梯形的性質，我們來證明下面的定理： 平行線等分線段定理 如果一組平行現在一條直線上截得 的線段相等，那麼在其它直線上截得 的線段也相等。 我們僅對三條平行線的情形進行證明。 已知： 如圖 4-42， AB CD// //EF 、 AC =CE 。 求證： BD = DF 。 證明： 過點 B、D 分別作 GH 的平 行線 BM、DN，分別交 CD、 EF 於點 M、N，便可得

_▱

ACMB 、

_▱

CEND。 ∴ BM = AC、 DN =CE 、 BM //DN ∵ AC =CE ∴ BM = DN 又 ∵ BM //DN 、MD// NF ∴ ∠ = ∠1 2、 3∠ = ∠4 ∴ △BMD ≅ △DNF ∴ BD = DF (第 8 題) a b c 4 2 圖 4-42 1 G F K H L M N C D B A E 3

從這個定理，可以推出下面結推： 推論 1 經過梯形一個腰的中點與底平行的直線，必平分另 一腰。 如圖 4-43，在梯形 ABCD 中，如果 E 是腰 AB 的中點， // EF AD ，交 DC 於點 F，那麼 DF = FC 。 如圖 4-44，E 是△ABC 的 AB 邊之中點，EF // BC ，交 AC 於點 F，過頂點引直線MN //BC。由上面的定理可知：AF = FC， 由此得到下面的推論： 推論 2 經過三角形一邊的中點與另一邊平行的直線必平 分第三邊。 應用平行線等分線段定理，我們可以任意等分一條線段。 【例】 已知： 線段 AB (圖 4-45)。 求作： 線段 AB 的五等分點 作法： 1. 作射線 AC。 2. 在射線 AC 上以 任 意 長 順 次 截 取 AD = DE = EF = FG =GH 3. 連結 HB。 4. 過點 G、F、E、D 分別作 HB 的平行線 GL、FK、EJ、DI，分別交 AB 於點 L、K、 J、I。 L、K、J、I 就是所求的五等分點。 圖 4-43 B F E D C A 圖 4-44 B F E N C A M 圖 4-45 C D B A E M L K J F H G I N

證明： 過點 A 作MN //HB 。 ∵ MN // DI // EJ // FK //GL//HB AD = DE = EF = FG =GH ∴ AI = IJ = JK = KL = LB (平行線等分線段定理)

練 習

1. 練習本上的橫格是平行且等距的，用橫格將 10 cm 長的線繩 五等份、七等份、九等份，分別用不同色筆在繩上劃上等分 點。 2. 畫一條線段，用直尺、圓規將它 分成三等份。 3. 如圖，已知：l₁// l 、 AC₂ =CB。 求證： DC =CE。

4.11 三角形、梯形的中位線

連結三角形兩邊中點的線段叫做三角形的中位線。 注意：三角形的中位線與三角形的中線不同。 三角形中位線定理 三角形的中位線平行於第三邊，並且 等於它的一半。 已知： △ABC 中， AD = DB、 AE = EC (圖 4-46)。 求證： DE// BC、 1 2 DE = BC。 證明： 延長 DE 至點 F，使 EF = DE，連結 CF。 ∵ AE = EC 、 DE = EF ∴ 點 A 與 C、D 與 F 關於點 E 對稱。 (第 3 題) A B D C E 1 l 2 l 圖 4-46 F C D B A E

∴ AD FC (中心對稱的性質) 又 ∵ AD = DB ∴ DB FC ∴ 四邊形 BCFD 是平行四邊形 ∴ DF = BC 、 DE//BC (平行四邊形的對邊平行且相等) ∵ 1 2 DE = DF ∴ 1 2 DE = BC 連結梯形兩腰中點的線段叫做梯形的中位線。 梯形中位線定理 梯形的中位線平行於兩底，並且等於兩底 和的一半。 已知： 梯形 ABCD 中， AD//BC 、AM = MB、 DN = NC (圖 4-47)。 求證： MN // BC 、 1( ) 2 MN = AD+ BC 。 分析： 我們設法利用三角形中 位線定理。連結 AN 並延長，可得△ABE，如果能 證明 N 是 AE 的中點， 那麼就容易證明這個定理。 證明： 連結 AN 並延長，交 BC 的延長線於點 E。 ∵ DN = NC 、 AD CE// ∴ AN = NE (平行線等分線段定理) 在△ABE 中 ∵ AM = MB、 AN = NE ∴ MN // BC 、 1( ) 2 MN = BC+CE (三角形中位線定理) 圖 4-47 M C D B A E N

又 ∵ 點 D 與點 C，點 A 與點 E 關於點 N 對稱 ∴ AD CE= ∴ 1( ) 2 MN = AD+ BC 【例】 求證順次連結四邊形四條邊的中點，所得的四邊形是平 行四邊形。 已知： 如圖 4-48，在四邊形 ABCD 中，E、F、G、 H 分別是 AB、BC、CD、 DA 的中點。 求證： 四邊形 EFGH 是平行四 邊形。 證明： 連結 AC。 又因四邊形 EBCD 是平 ∵ AH = HD、 CG GD= ∴ HG// AC 、 1 2 HG = AC (三角形中位線定理) 同理EF // AC 、 1 2 EF = AC ∴ HG EF 所以四邊形 EFGH 是平行四邊形。

練 習

1. (口答) A、B 兩點被池塘隔開，在 AB 外選一點 C，連結 AC 與 BC，並分 別找出 AC 與 BC 的中點 M、N。如 果測得MN = 20m，那麼 A、B 兩點 間的距離是多少？為什麼？ 2. 已知：三角形的各邊分別為 6 cm、 8 cm 與 10 cm，求連結各邊中點所 成三角形各邊的長。 圖 4-48 F C D B A E G H (第 1 題) A B M C N

練 習

3. 已知： 梯形 ABCD， AD//BC ，對角線 AC、BD 相交於 點 O， A′、 B′、 C′、 D′分別是 AO、BO、CO、 DO 的中點。 求證： (1) 四邊形 A B C D′ ′ ′ ′是梯形； (2) 梯形 ABCD 的周長等於梯形 A B C D′ ′ ′ ′周長的 2 倍。 4. (1) 梯形的上底長 8 cm，下底長 9 cm，求中位線長； (2) 梯形的上底長 8 cm，中位線長 9 cm，求下底長。

習 題 十 六

1. 作一條線段，再把它 7 等份。 2. 求證：直角梯形的兩個直角頂點到對腰中點的距離相等。 3. 已知： M、N 分別是

_▱

ABCD的邊 AB、CD 的中點，CM 交 BD 於點 E、AN 交 BD 於點 F。 求證： BE = EF = FD

4. 已知： 在△ABC 中，D、E、F 分別是 BC、CA、AB 邊的

中點。 求證： (1) ∠FDE = ∠A； (2) 四邊形 AFDE 的周長等於 AB+ AC。 5. 求證：三角形的一條中位線與第三邊上的中線互相平分。 6. 已知： 四邊形 ABCD 中，E 是 AB 的中點、F 是 CD 的中 點、G 是 AC 的中點、H 是 BD 的中點，並且 E、F、 G、H 不在同一條直線上。 求證： EF 與 GH 互相平分。 7. 求證：順次連結矩形四邊中點所得的四邊形是菱形。 8. 求證：順次連結菱形四邊中點所得的四邊形是矩形。

9. 如圖，已知：AA′// EE′、 AB = BC =CD = DE 、 A B′ ′= B C′ ′=C D′ ′ = D E′ ′、 28 AA′ = mm、EE′ = 36mm， 求 BB′、 CC′、 DD′的長。 10. 已知： 梯形 ABCD 中，AD//BC 、 AB = AD+BC ，M 為 CD 中點。

求證： AM、BM 分別平分 DAB∠ 與 CBA∠ 。

11. 在等腰梯形中，已知一角是 45°、高是 h m、中位線長 m m， 求兩底的長。 12. 已知： 如圖，在梯形 ABCD 中，AD//BC ，E、F 分別是 AB、DC 的中點。 求證： 1( ) 2 GH = BC− AD 13. 已知△ABC 的三邊長為 a、b、c，三條中位線組成一個新三 角形，新三角形的三條中位線又組成一個三角形，以此類推， 求第四次組成的三角形之邊長。 (第 12 題) (第 13 題) C B A A B D C E _F G H (第 9 題) A B D C E A′ B′ C′ D′ E′

小 結

一、本章主要內容是多邊形、平行四邊形(包括矩形、菱形、 正方形)與梯形的有關知識。 二 、 多 邊 形 的 一 些 有 關 概 念 ， 多 邊 形 的 內 角 和 等 於 (n−2) 180_i °、外角和等於 360°，這些知識是研究多邊形的邊、 角關係之基礎。 三、幾種特殊的四邊形：平行四邊形(包括矩形、菱形、正方 形)與梯形，是常見的四邊形。 1. 幾種特殊四邊形的關係如圖 4-49： 2. 幾種特殊四邊形的性質： 邊 角 對角線 平行 四邊形 對邊平行且相等 對角相等 兩條對角線互相平分 矩形 對邊平行且相等 四個角都 是直角 兩條對角 線互相平 分 且相 等 菱形 對邊平行、四條 邊都相等 對角相等 兩條對角 線互相垂 直 且平 分，每條對角線平分一組對 角 兩組對邊 分別平行 四邊形 平行 四邊形 矩形 菱形 梯形 正方形 直角 梯形 等腰 梯形 有一個角 是直角 有一組 鄰邊相等 有一個角 是直角 有一組 鄰邊相等 有且僅有一組 對邊平行 兩腰相等 有一個角是 直角 圖 4-49

正方形 對邊平行、四條 邊都相等 四個角都 是直角 兩條對角 線互相垂 直 平分 且相等，每條對角線平分一 組對角 等腰 梯形 兩底平行、兩腰 相等 同一底上 的兩個角 相等 兩條對角線相等 3. 幾種特殊四邊形的常用判定方法： 平行 四邊形 (1) 兩組對邊分別平行； (2) 兩組對邊分別相等； (3) 一組對邊平行且相等； (4) 兩組對角線互相平分。 矩形 (1) 有三個角是直角； (2) 是平行四邊形，並且有一個角是直角； (3) 是平行四邊形，並且兩條對角線相等。 菱形 (1) 四條邊都相等； (2) 是平行四邊形，並且有一組鄰邊相等； (3) 是平行四邊形，並且兩條對角線互相垂直。 正方形 (1) 是矩形，並且有一組鄰邊相等； (2) 是菱形，並且有一個角是直角。 等腰 梯形 是梯形，並且同一底上的兩個角相等。 四、中心對稱與軸對稱是兩種對稱，它們有一個共同的性 質：即對稱的兩個圖形全等。有一個明顯區別是：關於中心對稱 的兩個圖形中，對應線段平行；而關於軸對稱的兩個圖形中，對 應線段不一定平行。如果一個軸對稱圖形有兩條互相垂直的對稱 軸(例如，矩形、菱形、正方形)，那麼它必是中心對稱圖形，這 兩條對稱軸的交點就是它的對稱中心。 五、以平行四邊形為基礎，推出平行線等分線段定理。這個 定理的兩個推論分別是梯形、三角形的中位線之判定定理。 三角形中位線定理：三角形的中位線平行於第三邊並且等於 它的一半，是梯形中位線定理的基礎，由它很容易推出梯形中位 線定理：梯形的中位線平行於兩底並且等於兩底和的一半。

複習參考題四

1. 求證：四邊形的兩條對角線之和大於周長的一半而小於周長。 2. 一個四邊形的內角都是銳角嗎？能都是直角嗎？能都是鈍角

嗎？為什麼？

3. 四邊形四個內角的比是 1：2：3：4，求各角的度數。 4. 已知：

_▱

ABCD中， BAC∠ > ∠CAD。

求證： ∠BDC > ∠ADB。

5. 已知：

_▱

ABCD中，E、F 分別是 AD 與 BC 的中點，AF 與 BE 交於點 G、CE 與 DF 交於點 H。

求證： EF 與 GH 互相平分。

6. 已知：

_▱

ABCD的對角線相交於點 O，EF 經過點 O，與

AB 交於點 E、與 CD 交於點 F，G、H 分別是 AO 與 CO 的中點。 求證： 四邊形 EHFG 是平行四邊形。 7. 求證： (1) 等腰三角形底邊上任一點與兩腰的距離之和 等於腰上的高； (2) 等腰三角形底邊延長線上任一點與兩腰的距 離之差等於腰上的高。 8. 求證：如果平行四邊形四個內角的平分線能夠圍成一個四邊 形，那麼這個四邊形是矩形。 9. 已知： 矩形的對角線長 d、一邊長 s ( d > s)。 求作： 矩形。 10.已知： 菱形的周長為 p、一條對角線長 d ( 1 2 d < p)。 求作： 菱形。 11.已知：菱形之周長它的高之 8 倍。求它的各角。 12.從菱形的兩條對角線之交點分別向各邊引垂線。求證：連結 各垂足的四邊形是矩形。

13.菱形周長為 20 cm，兩鄰角的比為 1：2，求較短的對角線長。 14.菱形周長為 10 cm，一條對角線長為 2.5 cm，求菱形各角的度 數。 15.在已知銳角三角形 ABC 的外面作正方形 ABDE 與正方形 ACFG。求證：(1) BG =CE； (2) BG ⊥CE 。 16.在正方形 ABCD 的邊 BC 之延長線上取一點 E，使 CE = AC ， 連結 AE，交 CD 於 F。求 AFC∠ 的度數。 17.已知： E 是正方形 ABCD 內一點， EA= AB = BE。 求證： ∠ECD = ∠EDC = °15 。

18.已知： △ABC 中， ACB∠ = ∠Rt ，四邊形 ACDE 與 CBFG 是在△ABC 外的正方形，△ABC 的高 CH 之反向延

長線交 DG 於點 M。

求證： (1) DG = AB； (2) 1

2

CM = DG。

19.已知： O 是

_▱

ABCD的對稱中心，EF 與 GH 經過點 O，

EF 分別交 AB、CD 於點 E、F，GH 分別交 AD、

BC 於點 G、H。

求證： 四邊形 EHFG 是平行四邊形。

20.已知： △BEC 與△DFA 是

_▱

ABCD外的等邊三角形。 求證： △BEC 與△DFA 是中心對稱圖形。 21.(1) 已知： 四邊形 ABCD 中， AB = DC、 AC = BD、 AD ≠ BC 。 求證： 四邊形 ABCD 是等腰梯形。 (第 20 題) A B D _C F E

(2) 如果(1)的題設中沒有 AD ≠ BC，那麼四邊形一定是等腰 梯形嗎？為什麼？ 22.畫梯形 ABCD，使底 AD = 2cm、底BC = 4cm、∠ = °B 45 、 60 C ∠ = °。 23.如圖，在 AD 的兩側作 ADC∠ = ∠DAB，以 A 與 D 為起點， 分別在 AB 與 DC 上截取 4 條線段，所有線段的長相等，那麼 相應分點的連線把 AD 五等份。為什麼？

24.已知： △ABC 中，∠ = °A 90 ，D、E、F 分別是 BC、CA、 AB 邊的中點。 求證： AD = FE 。 25.已知： E 與 F 分別是

_▱

ABCD的邊 AD 與 BC 上的點，並 且 AE = BF ，G 是 AF 與 BE 的交點，H 是 CE 與 DF 的交點。 求證： GH // BC 、 1 2 GH = BC。 26.已知： AD 是△ABC 的中線、E 是 AD 的中點，F 是 BE 的 延長線與 AC 的交點。 求證： 1 2 AF = FC 。 27.已知等腰梯形的中位線長 6 cm、腰長 5 cm，求它的周長。 28.從

_▱

ABCD的頂點 A、B、C、D 向形外的任意直線 MN 引垂 線 AA′、 BB′、CC′、 DD′，垂足是 A′、 B′、C′、 D′。求證： AA′+CC′ = BB′+ DD′。 C B A (第 23 題) D 1 A A₂ A₃ A₄ 1 B B₂ B₃ B₄

29.求證：梯形對角線中點的連線平行於底，並且等於兩底差的 一半。 30.在△ABC 中，如果 AB =30cm、 BC = 24cm、CA= 27 cm、 AE = EF = FB 、 EG// FD// BC 、FM //EN // AC 。求陰影部 分三個三角形周長的和。 17 世紀初，幾何原本傳入中國。義大利傳教士利瑪竇(Matteo Ricci; 1552 − 1610)來到中國後，與徐光啟(1562 − 1633)於 1606 年將幾何原本前 6 卷的內容譯成中文，1607 年在北平 出版。 Elements 原意是指學科中具有廣泛應用基礎而又重要的定 理，譯成原本甚為恰當。至於幾何二字，有人認為是拉丁文 geometria(即英文中 geometry )的音譯。由於前 6 卷的內容主 要都涉及現今所謂幾何學的內容，而幾何學在此之前，並沒 有在中國出現過，所以利瑪竇與徐光啟就在原本的書名前面 加上幾何二字，以顯示該書的主題。 又有人認為，幾何在漢語中有多少或若干的意思(中國的古算 經中，就常出現問物幾何之類的字眼，即問一共有多少件物 品的意思)，所以在這裏，幾何二字是用來表示這書與數學有 關。無論如何，幾何原本四字，就由當時一直流傳，沿用至 今。 (第 30 題) A B D C F E N M G