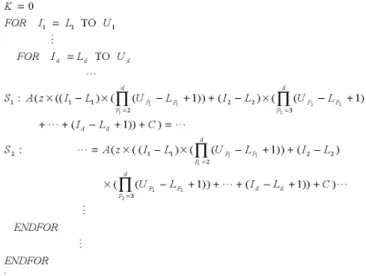One-dimensional I test and direction vector I test with array references by induction variable

(1)

Int. J. High Performance Computing and Networking, Vol. 3, No. 4, 2005 219

One-dimensional I test

and direction vector I test

with array references by

induction variable

Minyi Guo

School of Computer Science and Engineering, University of Aizu, Aizu-Wakamatsu City, 965 8580 Fukushima, Japan

State Key Lab for Novel Software Technology, Nanjing University, PRC

Fax: +81 242 37 2744 E-mail: minyi@u-aizu.ac.jp

Weng-Long Chang*

Department of Computer Science and Information Engineering, National Kaohsiung University of Applied Sciences,

415 Chien Kung Road, 807 Kaohsiung, Taiwan E-mail: changwl@ mail.stut.edu.tw

*Corresponding author

Jian Lu

State Key Lab for Novel Software Technology, Nanjing University, PRC

E-mail: lj@nju.edu.cn

Minglu Li

Department of Computer Science and Engineering, Shanghai JiaoTong University,

Shanghai, China

E-mail: li-ml@cs.stut.edu.cn

Abstract: In this paper, theoretical aspects to demonstrate the accuracy of the Interval Test

(the I test and the direction vector I test) to be applied for resolving the problem stated above is presented. Also, it is proved from the proposed theoretical aspects that under a specific direction vector θ = =( , ,1…=d) there are integer-valued solutions

for one-dimensional arrays with subscripts formed by induction variable and under other specific direction vectors there are no integer-valued solutions. Experiments with benchmarks, cited from Parallel loop, Vector loop and TRFD (Perfect benchmark), reveal that our framework can properly enhance the precision of data dependence analysis for one-dimensional arrays with subscripts mentioned above.

Keywords: parallelising/vectorising compilers; data dependence analysis; loop parallelisation; loop vectorisation; automatic loop transformation.

Reference to this paper should be made as follows: Guo, M., Chang, W-L., Lu, J. and Li, M. (2005) ‘One-dimensional I test and direction vector I test with array references by induction variable’, Int. J. High Performance Computing and Networking, Vol. 3, No. 4, pp.219–226.

(2)

220 M. GUO, W-L. CHANG, J. LU AND M. LI

Biographical notes: Minyi Guo is currently an Associate Professor at the Department of Computer Software, at the University of Aizu, Japan. Guo has served as programme committee or organising committee member for many international conferences. He is the Editor-in-Chief of the Journal of Embedded Systems. He is also on the editorial board of the

International Journal of High Performance Computing and Networking, the Journal of

Embedded Computing, the Journal of Parallel and Distributed Scientific and Engineering

Computing and the International Journal of Computer and Applications. Guo’s research

interests include parallel and distributed processing, parallelising compilers, data parallel languages, data mining, molecular computing and software engineering. He is a member of the ACM, IEEE, and IEICE.

Weng-Long Chang received his PhD degree in computer science and information engineering from the National Cheng Kung University, Taiwan, Republic of China, in 1999. He is currently an Assistant Professor at the Southern Taiwan University of Technology. His research interests include molecular computing and languages and compilers for parallel computing.

Jian Lu received his BS degree, MS degree, and PhD degree from Nanjing University of PR China in 1982, 1984, 1988, respectively. Currently, he is a Professor at Department of Computer Science and Technology, Vice Director of the Institute of Computer Software at Nanjing University and Director of State Key Laboratory of Novel Software Technology of P.R. China. His research interests include formal methods, mobile agent technology and software architecture.

Dr. Minglu Li is a Full Professor and Vice Char of Department of Computer Science and Engineering of Shanghai Jiao Tong University (SJTU). Now, he is also Director of Grid Computing Center of SJTU, a member of Expert Committee of ChinaGrid Program of Ministry of Education of China, PI of ShanghaiGrid of Science and Technology Commission of Shanghai Municipality(STCSM), an Associate Editor of International

Journal of Grid and Utility Computing, an member of editorial board of International

Journal of Web Services Research, a member of executive committee of Technical

Committee on Services Computing of IEEE.

1 INTRODUCTION

Achieving a good data dependence analysis is a critical, issue in order to reduce the communication overhead and to exploit parallelism of applications as much as possible. This task becomes even more important in distributed memory systems where, in addition to accomplishing a high parallelism of computation and low communication overhead among the processors, it is essential to develop a new analysis technique for data dependence.

There are several well-known data dependence analysis algorithms applicable for one-dimensional arrays under constant bounds or variable bounds: the GCD test (Banerjee, 1988, 1993, 1997), Banerjee’s method (Banerjee, 1988, 1993, 1997), the I test and the direction vector I test (Kong et al., 1991; Niedzielski and Psarris, 1999; Psarris et al., 1991, 1993; Psarris and Kyriakopoulos, 1999), the extended I test (Chang and Chu, 1998), the generalised direction vector I test (Chang and Chu, 2001) and the interval reduction test (Huang and Yang, 2000). There are also several well-known data dependence analysis algorithms applicable for multi-dimensional coupled arrays under constant bounds or variable bounds: the generalised GCD test (Banerjee, 1988, 1993, 1997), the Lambda test (Li et al., 1990), the generalised Lambda test (Chang et al., 1999), the multi-dimensional I test

(Chang et al., 2001), the multi-dimensional direction vector I test (Chang et al., 2002), the Power test (Wolfe and Tseng, 1992) and the Omega test (Pugh, 1992). There are several well-known data dependence analysis algorithms applicable for arrays with linear subscripts with symbolic coefficients, or with non-linear subscripts under symbolic bounds: the infinity Banerjee test (Petersen, 1993), the Range test (Blume and Eigenmann, 1998), the infinity Lambda test (Chang and Chu, 2000), the access range test (Paek, 1997; Hoeflinger, 1998) and one analysis method for pointers and induction variables (Wu, 2001).

In this paper, we propose a sophisticated technique of data dependence analysis. This approach is to test dependence if there are integer-valued solutions for one-dimensional arrays with subscripts formed by induction variable. Without direction vectors, there are integer-valued solutions for one-dimensional arrays with subscripts formed by induction variable. Furthermore, it is also shown that under a specific direction vector θ = =( , ,₁… =_d) there are integer-valued solutions for one-dimensional arrays with subscripts formed by induction variable.

Shen et al. (1992) had indicated that in real programmes one-dimensional arrays with subscripts formed by induction variable occur quite frequently. A d-nested loop accessing a one-dimensional array with subscripts formed by induction variable is shown in Figure 1.

(3)

ONE-DIMENSIONAL I TEST AND DIRECTION VECTOR I TEST WITH ARRAY REFERENCES BY INDUCTION VARIABLE 221

Figure 1 An example of a nested loop with induction variable

Induction variable is a one scalar integer variable, which is used in a loop, to simulate loop’s index variables: it is incremented or decremented by a constant amount in each iteration. Every induction variable can be replaced by a linear function in loop’s index variables. The transformation, which does so, is called induction variable substitution. Since the variable K in Figure 1 is one induction variable, it can be replaced z ×

1 2 1 1 2 3 2 2 1 1 2 2 (( ) ( d ( 1)) ( ) ( d ( p p p p p p I −L × ∏ = U −L + + I −L × ∏ = U −L 1) (i_d L_d 1))

+ + + − + where d is the number of common loops and z is one integer variable (Banerjee, 1988, 1993, 1997; Paek, 1997; Hoeflinger, 1998). Therefore, the code in Figure 1 is transformed into the code in Figure 2, after finishing the processing of induction variable substitution for the variable K.

Figure 2 The transformed loop after induction variable

substitution for the induction variable K

Because dependence between S1 and S2 in Figure 2 may arise in different iterations of the common loops, we deal with the loop iteration variables referenced in S1 as being different variables from those referenced in S2 subject to common loop bounds. Therefore, when analysing dependence arising from a statement pair nested in d common loops, the problem will involve n unique variable

(where n = 2d). Furthermore, variables X2k–1 and X2k (1 ≤ k ≤ d) are different instances of the same loop iteration variable, Ik. Assume that L2k–1, L2k, U2k–1 and U2k are, respectively, lower bounds and upper bounds for X2k–1 and X2k. Because variables X2k–1 and X2k(1 ≤ k ≤ d) are different instances of the same loop iteration variable, Ik, lower

bounds for X2k–1 and X2k are the same and upper bounds for X2k–1 and X2k also are the same.

The problem of determining whether there exists dependence for the array A between S1 and S2 in Figure 2 can be reduced to that of checking whether one system of a linear equation with n unknown variables has a simultaneous integer solution, which satisfies the constraints for each variable in the system. It is assumed that one linear equation in a system is written as:

1 2 2 2 3 4 3 3 2 1 2 1 1 2 3 2 2 2 1 2 (( ) (( 1) ( 1)) ( ) (( 1) ( 1)) ( ) (( 1) ( 1)) ( ) ( 1) ( )) 0, d d d d j j j j d d d d d d d d z X X U L U L X X U L U L X X U L U L X X U L X X − + + − − − × − × − + × × − + + − × − + × × − + + + − × − + × × − + + + − × − + + − = (1)

where each Lk and each Uk are an integer variable and are,

respectively, one lower bound and one upper bound for the k-the loop for (1 ≤ k ≤ d). Because z is the greatest common divisor for all the coefficients in the left-hand side of equation (1), all the coefficients in equation (1) are divided by z and equation (1) is rewritten as

1 2 2 2 3 4 3 3 2 1 2 1 1 2 3 2 2 2 1 2 ( ) (( 1) ( 1)) ( ) (( 1) ( 1)) ( ) (( 1) ( 1)) ( ) ( 1) ( ) 0. d d d d j j j j d d d d d d d d X X U L U L X X U L U L X X U L U L X X U L X X − + + − − − − × − + × × − + + − × − + × × − + + + − × − + × × − + + + − × − + + − = (2) It is postulated that the constraints to each variable in

equation (2) are represented as

2 1 and ,2

k k k k

L ≤ X ₋ X ≤U (3)

where (1 ≤ k ≤ d). Let us use an example to make clear the illustrations stated above. Consider the nested do-loop in Figure 3. The variable K in Figure 3(a) is incremented by one in each iteration in the nested loop. So it is a one induction variable. After finishing the processing of induction variable substitution for the induction variable K, the result is shown in Figure 3(b). In Figure 3(b), the lower and upper bounds of the first (outer) loop and the second (inner) loop are, respectively, 1 and 10. Therefore, the bounds of the do-loop are constants. This do-loop executes 100 iterations by consecutively assigning the values 1, 2, …, 10 to J and I and executing the body (the main statement S) exactly once in each iteration. The net effect of the do-loop execution is then the ordered execution of the statements:

(4)

226 M. GUO, W-L. CHANG, J. LU AND M. LI

the Interval Test (the I test and the direction vector I test) to be applied for resolving the problem stated above. Also, it is proved from the proposed theoretical aspects that under a specific direction vector θ = =( , ,1… =d) there are

integer-valued solutions for one-dimensional arrays with subscripts formed by induction variable and under other specific direction vectors there are no integer-valued solutions. Experiments with benchmarks, cited from Parallel loop, Vector loop and TRFD (Perfect benchmark), reveal that this framework can properly enhance the precision of data dependence analysis for one-dimensional arrays with subscripts mentioned above. The proposed theorems can improve the precision of data dependence analysis for one-dimensional arrays with references formed by induction variable. Depending on the application domains, it is suggested that the proposed theorems be applied together with the front-end of a parallelising compiler to provide data dependence analysis for one-dimensional arrays with references formed by induction variable.

ACKNOWLEDGEMENT

This work was partially supported by the 973 Program of China under Grant 2002CB312002 and NSFC of Jiangsu Province under Grant BK2002203.

REFERENCES

Banerjee, U. (1988) Dependence Analysis for Supercomputing, Kluwer Academic Publishers, Norwell, Massachusetts.

Banerjee, U. (1993) Loop Transformations for Restructuring

Compilers: The Foundations, Kluwer Academic Publishers,

Norwell, Massachusetts.

Banerjee, U. (1997) Dependence Analysis, Kluwer Academic Publishers, Norwell, Massachusetts.

Blume, W. and Eigenmann, R. (1998) ‘Nonlinear and symbolic data dependence testing’, IEEE Transaction on Parallel and

Distributed Systems, Vol. 9, No. 12, pp.1180−1194.

Chang, Chu and Wu, J. (1999) ‘The generalized lambda test: a multi-dimensional version of banerjee’s algorithm’,

International Journal of Parallel and Distributed Systems and Networks, Vol. 2, No. 2, pp.69–78.

Chang, W-L. and Chu, C-P. (1998) ‘The extension of the I test’,

Parallel Computing, Vol. 24, pp.2101–2127.

Chang, W-L. and Chu, C-P. (2000) ‘The infinity lambda test: a multi-dimensional version of Banerjee’s infinity test’, Parallel

Computing, Vol. 26, No. 10, August, pp.1275–1295.

Chang, W-L. and Chu, C-P. (2001) ‘The generalized direction vector I test’, Parallel Computing, Vol. 27, No. 8, July, pp.1117–1144.

Chang, W-L., Chu, C-P. and Wu, J-H. (2001a) ‘A multi-dimensional version of the I test’, Parallel Computing, Vol. 27, No. 13, September, pp.1783–1799.

Chang, W-L., Chu, C-P. and Wu, J-H. (2002) ‘A precise dependence analysis for multi-dimensional arrays under specific dependence direction’, Journal of System and

Software, Vol. 63, No. 2, pp.99–112.

Dongarra, J., Reinhardt, M.F. and Russell, S.J. (1991) ‘Parallel loops − a test suite for parallelizing compilers: description and example results’, Parallel Computing, Vol. 17, pp.1247−1255. Eigenman, R., Hoeflinger, J. and Padua, D. (1998) ‘On the

automatic parallelization of the perfect benchmarks’, IEEE

Transactions on Parallel and Distributed Systems, Vol. 9,

No. 1, January, pp.5–23.

Hoeflinger, J.P. (1998) Inter-procedural Parallelization using

Memory Classification Analysis, PhD Thesis, University of

Illinois at Urbana-Champaign.

Huang, T-C. and Yang, C-M. (2000) ‘Data dependence analysis for array references’, The Journal of System and Software, Vol. 52, pp.55–65.

Kong, X., Klappholz, D. and Psarris, K. (1991) ‘The I test’, IEEE

Transaction on Parallel and Distributed Systems, Vol. 2,

No. 3, July, pp.342−359.

Levine, D., Callahan, D. and Dongarra, J. (1991) ‘A comparative study of automatic vectorizing compilers’, Parallel

Computing, Vol. 17, pp.1223–1244.

Li, Z., Yew, P-C. and Zhu, C-Q. (1990) ‘An efficient data dependence analysis for parallelizing compilers’, IEEE

No. 1, January, pp.26−34.

Niedzielski, D. and Psarris, K. (1999) ‘An analytical comparison of the I-test and Omega test’, LCPC’99: Twelfth

International Workshop on Languages and Compilers for Parallel Computing, pp.251–270.

Paek, Y. (1997) Compiling for Distributed Memory

Multiprocessors based on Access Region Analysis, PhD

Thesis, University of Illinois at Urbana-Champaign.

Petersen, P.M. (1993) Evaluation of Programs and Parallelizing

Compilers Using Dynamic Analysis Techniques, PhD Thesis,

University of Illinois at Urbana-Champaign, January.

Psarris, K. and Kyriakopoulos, K. (1999) ‘Data dependence testing in practice’, Proceedings of the 1999 International Conference

on Parallel Architectures and Compilation Techniques,

pp.264–273.

Psarris, K., Klappholz, D. and Kong, X. (1991) ‘On the accuracy of the banerjee test’, Journal of Parallel and Distributed

Computing, Vol. 12, No. 2, June, pp.152–158.

Psarris, K., Kong, X. and Klappholz, D. (1993) ‘The direction vector I test’, IEEE Transaction on Parallel and Distributed

Systems, Vol. 4, No. 11, pp.1280−1290.

Pugh, W. (1992) ‘A practical algorithm for exact array dependence analysis’, Communication of the ACM, Vol. 35, No. 8, August, pp.102−114.

Shen, Z., Li, Z. and Yew, P-C. (1992) ‘An empirical study of Fortran programs for parallelizing compilers’, IEEE

No. 3, July, pp.356−364.

Wolfe, M. and Tseng, C-W. (1992) ‘The power test for data dependence’, IEEE Transaction on Parallel and Distributed

Systems, Vol. 3, No. 5, September, pp.591−601.

Wu, P. (2001) Analysis of Pointers and Induction Variable

and Container Objects for Dependence Tests, PhD

Thesis, University of Illinois at Urbana-Champaign, UIUCDCS-R-2001-2209.