MIMO-OFDM系統之偵測與低密度同位檢查碼解碼

國 立 交 通 大 學

電信工程學系碩士班

碩士論文

MIMO-OFDM 系統之偵測與低密度同位檢查碼

解碼

Detection and LDPC Codes Decoding for

MIMO-OFDM Systems

研 究 生：黃冠榮

黃冠榮

指導教授：吳文榕 博士

MIMO-OFDM 系統之偵測與低密度同位檢查碼解碼

Detection and LDPC Codes Decoding for MIMO-OFDM

Systems

研 究 生：黃冠榮 Student：Kuan-Jung Huang

指導教授：吳文榕 博士 Advisor：Dr. Wen-Rong Wu

國 立 交 通 大 學

電信工程學系碩士班

碩 士 論 文

A Thesis

Submitted to Department of Communication Engineering

College of Electrical Engineering

National Chiao-Tung University

in Partial Fulfillment of the Requirements

for the Degree of

Master of Science

In

Communication Engineering

July 2006

Hsinchu, Taiwan, Republic of China

MIMO-OFDM 系統之偵測與低密度同位檢查碼解碼

研究生：黃冠榮 指導教授：吳文榕 博士

國立交通大學電信工程學系碩士班

中文摘要

本篇論文主要為研究多輸入多輸出（MIMO）正交分頻多工（OFDM）系統 上之訊號偵測與低密度同位檢查碼之解碼。在低密度同位檢查碼的解碼上，我們 使用了三種解碼演算法，包括 Normalized belief propagation（BP）based 演算法、 Normalized a-posteriori probability（APP）based 演算法、和 Layer normalized BP based 演算法。這三種不同的解碼演算法，皆比低密度同位檢查碼標準的解碼演 算法─ Sum-product 演算法有更高的可實現性，同時在運算複雜度與效能的取捨 上，都有不錯的表現。而在 MIMO 訊號的偵測上，我們使用了最小均方誤差 （MMSE）與最大事後機率（MAP）偵測。其中，我們將 MMSE 偵測與軟性反 對映結合以獲得軟性輸出（soft outputs），而 MAP 偵測則可直接由所接收到的訊 號來求得軟性輸出。另外，為了降低 MAP 偵測本身龐大的計算量，我們在 MAP 偵測前預先使用了 list sphere decoding 演算法，以降低在 MIMO 訊號偵測上的運 算複雜度。最後，我們在 IEEE 802.11n 與 IEEE 802.16e 系統上模擬，以驗證低 密度同位檢查碼對系統效能上的改善，特別是使用 MAP 偵測 MIMO 訊號時，使 用低密度同位檢查碼對系統效能會有相當大的改進。

Detection and LDPC Codes Decoding for MIMO-OFDM

Systems

Student: Kuan-Jung Huang

Advisor: Dr. Wen-Rong Wu

Department of Communication Engineering

National Chiao-Tung University

Abstract

In this thesis, we study signal detection and decoding of low-density parity-check (LDPC) codes for multi-input-multi-output (MIMO) orthogonal-frequency- division-multiplexing (OFDM) systems. Three types of LDPC codes decoders are investigated, the Normalized belief-propagation (BP) based algorithm, the

Normalized a-posteriori probability (APP) based algorithm, and the Layered normalized BP based algorithms. These decoding algorithms are much simpler to implement than the standard LDPC codes decoding algorithm, namely the

sum-product algorithm, and can achieve good tradeoff between decoding complexity and performance. For MIMO signal detection, we consider the

minimum-mean-squared error (MMSE) and a maximum a-posteriori probability (MAP) detector. The MMSE detector is combined with a soft-bit demapper to obtain soft outputs, while the MAP detector is designed to have soft outputs directly. To redue the high computational inherent in the MAP detector, we apply an efficiency algorithm called the list sphere decoding. Simulations with IEEE 802.11n and IEEE 802.16e systems show that the LDPC codes decoder can effectively improve the system performance, particularly when it combined with the MAP detector.

誌謝

本篇論文得以完成，首先要感謝的就是我的指導老師 吳文榕教授，我至今 仍記得：兩年前，老師在學生名額已滿的情況下，仍然不吝增加自己的負擔，加 收了我這樣的一個學生，讓我有幸在老師的實驗室內完成我兩年的學業與論文研 究。在我研究所求學期間，老師亦給我論文研究詳盡的指導，使我論文研究之研 究方向不會偏離正軌，而老師細心、嚴謹的求學態度更使我受益匪淺。這裡，真 的是非常的感謝老師。 其次，我要感謝李俊芳學長、楊華龍學長、李彥文學長、許兆元學長和李峰 宇學長，在我的研究及課業學習上所提供的的指導與協助，且同時感謝寬頻通訊 與訊號處理實驗室所有同學與學弟妹們的幫忙。其中，特別感謝士琦、星宇、宛 儀和坤浩，以及我大學的摯友明哲，本篇論文可以說是由大家所完成的，在我的 論文中：11n 的系統是士琦所提供的，16e 的介面則是由星宇整合的，而 11n 和 16e 模擬所需的通道模型則是宛儀所建立的，甚至我在 LDPC Codes 上的疑惑， 都是明哲不厭其煩的解釋，我才得以明白，如果沒有大家的協助，我是不可能完 成本篇論文的。最後致上我最深的感謝給我的父母和姊姊，他們給予我精神上的 鼓勵和經濟上的支持，使我無後顧之憂順利完成研究所的碩士學位，謝謝你們。 民國九十五年七月 研究生黃冠榮謹識於交通大學

內容目錄

第 1 章 簡介 ...1 第 2 章 低密度同位檢查碼 ...4 2.1 編碼器...4 2.2 圖形解碼...5 2.2.1 Tanner Graph ...6 2.2.2 圖形解碼概念...7 2.3 Sum-Product演算法 ...8

2.3.1 Bit node至Check node機率資訊...8

2.3.2 Check node至Bit node機率資訊...9

2.3.3 Bit node事後機率資訊...12 2.3.4 Sum-Product演算法解碼流程 ...13 2.4 Normalized BP-based演算法 ...14 2.4.1 UMP BP-based演算法...14 2.4.2 正規化參數...16 2.4.3 正規化參數之推導...18 2.4.4 Normalized BP-based演算法解碼流程 ...21 2.5 Normalized APP-based演算法 ...22 2.5.1 APP-based演算法...22 2.5.2 Normalized APP-based演算法 ...22 2.5.3 Normalized APP-based演算法解碼流程 ...23 2.6 Layered BP演算法...24 2.6.1 Layered BP演算法...24 2.6.2 Layered BP演算法修正...25

2.6.3 Layered Normalized BP-based演算法解碼流程 ...27

2.7 模擬結果...28 第 3 章 MIMO-OFDM系統...32 3.1 MIMO-OFDM系統 ...32 3.2 MIMO MMSE偵測 ...33 3.3 軟性反對映...35 3.4 軟性輸入軟性輸出之MIMO MMSE接收機 ...41 3.5 低密度同位檢查碼在 802.11n之應用...42 3.6 低密度同位檢查碼在 802.16e之應用...43 3.7 通道模型...45 3.7.1 802.11n通道模型...45 3.7.2 802.16e通道模型...46

3.8 模擬結果...47

3.8.1 802.11n系統模擬結果...47

3.8.2 802.16e系統模擬結果...62

第 4 章 最佳MIMO系統偵測 ...69

4.1 MAP位元偵測...70

4.2 List Sphere Decoding演算法...73

4.2.1 搜尋半徑與搜尋中心...73

4.2.2 實數List Sphere decoding演算法...75

4.2.3 實數List Sphere decoding演算法運算流程...80

4.2.4 實數List Sphere decoding演算法修正...82

4.3 Max-Log-MAP List Sphere偵測器 ...88

4.4 802.11n系統模擬結果...89 第 5 章 結論與未來研究目標 ...105 5.1 結論...105 5.2 未來研究目標...106 附錄A 802.11n基礎矩陣 ...107 附錄B 802.16e基礎模型矩陣...109 參考文獻 ... 112

表目錄

表 3-1 LDPC CODES之區塊大小和碼率表...45

表 3-2 通道模型LOS/NLOS參數 ...46

表 3-3 通道模型路徑損失參數 ...46

圖目錄

圖 2-1 TANNER GRAPH...6

圖 2-2 解碼器架構圖 ...7

圖 2-3 BIT NODE至CHECK NODE機率資訊 ...8

圖 2-4 CHECK NODE至BIT NODE機率資訊 ...9

圖 2-5 事後機率資訊 ...12

圖 2-6y=sgn x× Ψ

( )

x 函數圖...15

圖 2-7 NORMALIZED BP-BASED演算法模擬結果 ...29

圖 2-8 NORMALIZED APP-BASED演算法模擬結果 ...29

圖 2-9 LAYERED BP演算法模擬結果 ...30

圖 2-10 LAYERED NORMALIZED BP-BASED演算法模擬結果 ...31

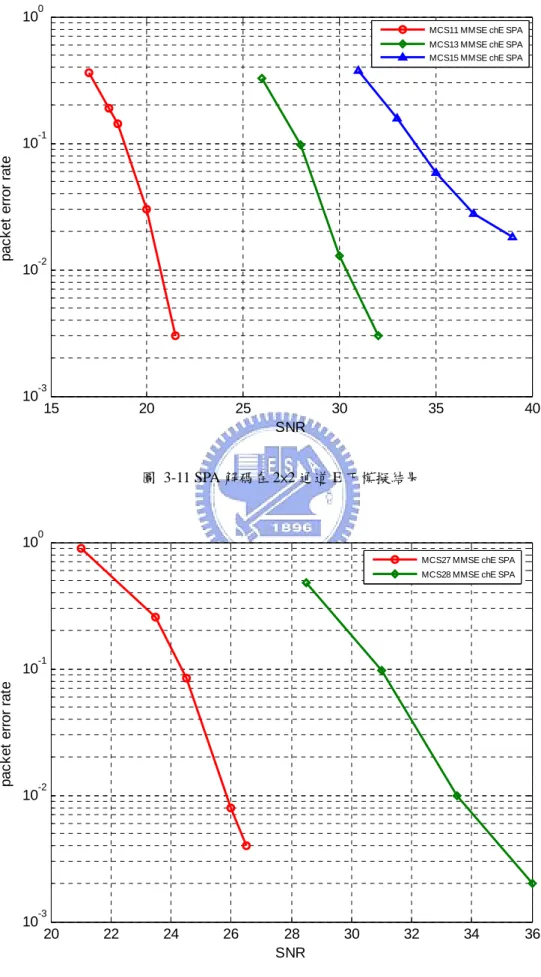
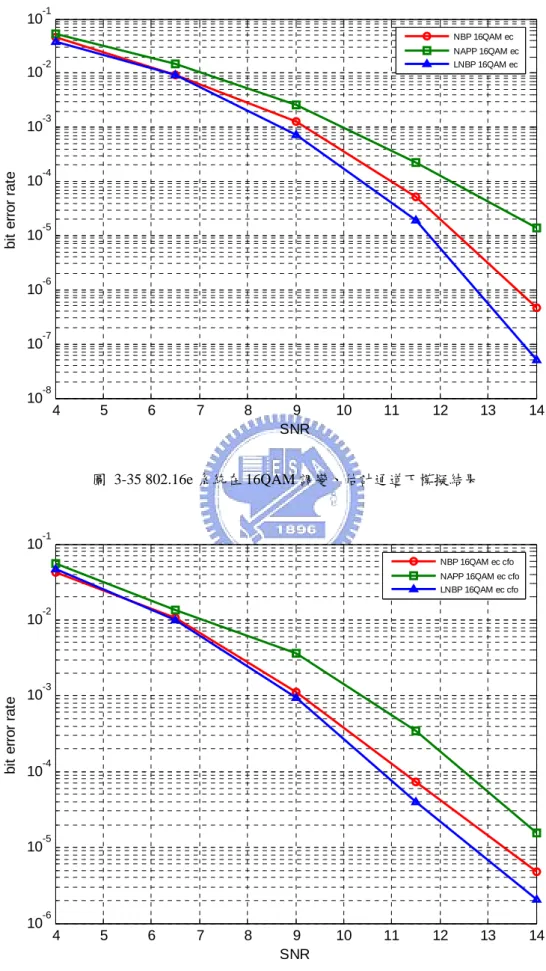
圖 3-1 MIMO-OFDM系統傳送端方塊圖 ...32 圖 3-2 單天線傳送接收器 ...35 圖 3-3 16QAM星狀圖的分割示意圖...38 圖 3-4 IN-PHASE位元中，16QAM之簡化對精確LLR計算方法比較圖 ...39 圖 3-5 IN-PHASE位元中，64QAM之簡化對精確LLR計算方法比較圖 ...40 圖 3-6 2×2 之軟性輸入軟性輸出MMSE接收器 ...41 圖 3-7 SPA解碼在 2×2 通道B下模擬結果 ...50 圖 3-8 SPA解碼在 4×4 通道B下模擬結果 ...50 圖 3-9 SPA解碼在 2×2 通道D下模擬結果 ...51 圖 3-10 SPA解碼在 4×4 通道D下模擬結果 ...51 圖 3-11 SPA解碼在 2×2 通道E下模擬結果...52 圖 3-12 SPA解碼在 4×4 通道E下模擬結果...52 圖 3-13 NBP解碼在 2×2 通道B下模擬結果 ...53 圖 3-14 NBP解碼在 4×4 通道B下模擬結果 ...53 圖 3-15 NBP解碼在 2×2 通道D下模擬結果 ...54 圖 3-16 NBP解碼在 4×4 通道D下模擬結果 ...54 圖 3-17 NBP解碼在 2×2 通道E下模擬結果...55 圖 3-18 NBP解碼在 4×4 通道E下模擬結果...55 圖 3-19 NAPP解碼在 2×2 通道B下模擬結果 ...56 圖 3-20 NAPP解碼在 4×4 通道B下模擬結果 ...56 圖 3-21 NAPP解碼在 2×2 通道D下模擬結果...57 圖 3-22 NAPP解碼在 4×4 通道D下模擬結果...57 圖 3-23 NAPP解碼在 2×2 通道E下模擬結果 ...58 圖 3-24 NAPP解碼在 4×4 通道E下模擬結果 ...58 圖 3-25 LNBP解碼在 2×2 通道B下模擬結果 ...59

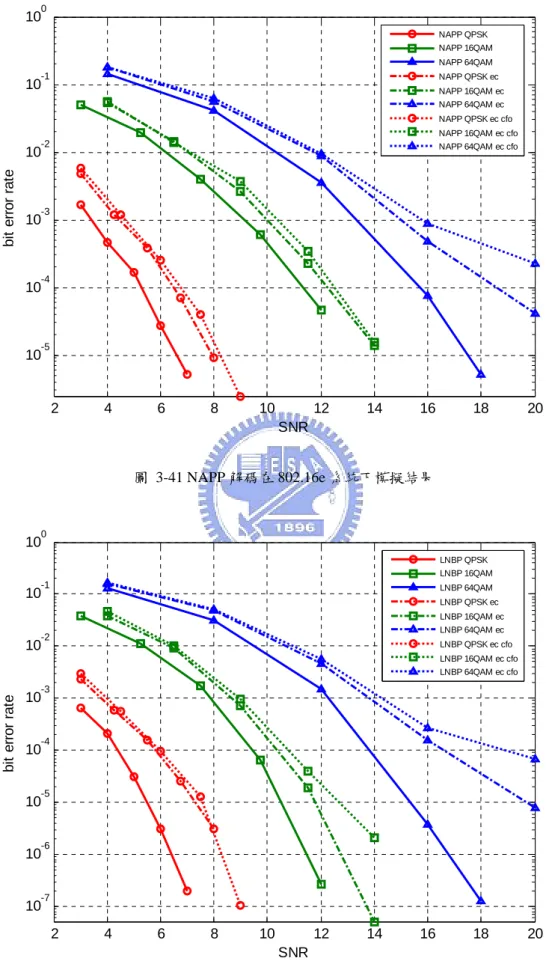
圖 3-26 LNBP解碼在 4×4 通道B下模擬結果 ...59 圖 3-27 LNBP解碼在 2×2 通道D下模擬結果...60 圖 3-28 LNBP解碼在 4×4 通道D下模擬結果...60 圖 3-29 LNBP解碼在 2×2 通道E下模擬結果 ...61 圖 3-30 LNBP解碼在 4×4 通道E下模擬結果 ...61 圖 3-31 802.16E系統在QPSK調變、理想通道下模擬結果...63 圖 3-32 802.16E系統在QPSK調變、估計通道下模擬結果...63 圖 3-33 802.16E系統在QPSK調變、估計通道、加入CFO效應下模擬結果...64 圖 3-34 802.16E系統在 16QAM調變、理想通道下模擬結果 ...64 圖 3-35 802.16E系統在 16QAM調變、估計通道下模擬結果 ...65 圖 3-36 802.16E系統在 16QAM調變、估計通道、加入CFO效應下模擬結果....65 圖 3-37 802.16E系統在 64QAM調變、理想通道下模擬結果 ...66 圖 3-38 802.16E系統在 64QAM調變、估計通道下模擬結果 ...66 圖 3-39 802.16E系統在 64QAM調變、估計通道、加入CFO效應下模擬結果....67 圖 3-40 NBP解碼在 802.16E系統下模擬結果 ...67 圖 3-41 NAPP解碼在 802.16E系統下模擬結果...68 圖 3-42 LNBP解碼在 802.16E系統下模擬結果...68 圖 4-1 2×2 MAP偵測之接收機 ...70 圖 4-2 搜尋候選列表示意圖 ...73

圖 4-3 實數LIST SPHERE DECODING演算法運算流程圖 ...80

圖 4-4N_t =2實數LIST SPHERE DECODING演算法搜尋圖...82

圖 4-5 LSE搜尋中心在 64QAM 2×2 通道下測試結果 ...85

圖 4-6 LSE搜尋中心在 16QAM 4×4 通道下測試結果 ...85

圖 4-7 MMSE搜尋中心在 64QAM 2×2 通道下測試結果...86

圖 4-8 MMSE搜尋中心在 16QAM 4×4 通道下測試結果...86

圖 4-9 2×2 之MAX-LOG MAP LIST SPHERE偵測器 ...88

圖 4-10 SPA解碼在 2×2 通道B下模擬結果 ...90 圖 4-11 SPA解碼在 4×4 通道B下模擬結果 ...90 圖 4-12 SPA解碼在 2×2 通道D下模擬結果 ...91 圖 4-13 SPA解碼在 4×4 通道D下模擬結果 ...91 圖 4-14 SPA解碼在 2×2 通道E下模擬結果...92 圖 4-15 SPA解碼在 4×4 通道E下模擬結果...92 圖 4-16 MCS11 在 2×2 通道B下模擬結果 ...93 圖 4-17 MCS27 在 4×4 通道B下模擬結果...93 圖 4-18 MCS11 在 2×2 通道D下模擬結果...94 圖 4-19 MCS27 在 4×4 通道D下模擬結果...94 圖 4-20 MCS11 在 2×2 通道E下模擬結果 ...95 圖 4-21 MCS27 在 4×4 通道E下模擬結果 ...95

圖 4-22 NBP解碼在 2×2 通道B下模擬結果 ...96 圖 4-23 NBP解碼在 4×4 通道B下模擬結果 ...96 圖 4-24 NBP解碼在 2×2 通道D下模擬結果 ...97 圖 4-25 NBP解碼在 4×4 通道D下模擬結果 ...97 圖 4-26 NBP解碼在 2×2 通道E下模擬結果...98 圖 4-27 NBP解碼在 4×4 通道E下模擬結果...98 圖 4-28 NAPP解碼在 2×2 通道B下模擬結果 ...99 圖 4-29 NAPP解碼在 4×4 通道B下模擬結果 ...99 圖 4-30 NAPP解碼在 2×2 通道D下模擬結果...100 圖 4-31 NAPP解碼在 4×4 通道D下模擬結果...100 圖 4-32 NAPP解碼在 2×2 通道E下模擬結果 ...101 圖 4-33 NAPP解碼在 4×4 通道E下模擬結果 ...101 圖 4-34 LNBP解碼在 2×2 通道B下模擬結果 ...102 圖 4-35 LNBP解碼在 4×4 通道B下模擬結果 ...102 圖 4-36 LNBP解碼在 2×2 通道D下模擬結果...103 圖 4-37 LNBP解碼在 4×4 通道D下模擬結果...103 圖 4-38 LNBP解碼在 2×2 通道E下模擬結果 ...104 圖 4-39 LNBP解碼在 4×4 通道E下模擬結果 ...104

第1章 簡介

1948 年Shannon發表了現代通訊理論最重要的論文“A Mathematical Theory of Communication [1]”，精準地預測所有通訊系統的基本極限，並開創了一個全 新的數學領域：消息理論（Information Theory）。他提出對於任何傳輸速率小於 或等於通道容量（capacity）的情況下，必定存在一種編碼方式，可以達成任意 小的錯誤率。雖然他並未具體指出如何設計此種錯誤更正碼（error correction

code），但卻提供了相當寶貴的依循法則，也為通訊工程指引了一個明確的目標。

目前較為熟知的錯誤更正碼包括線性區段碼（Linear Block Codes）[2]、漢明碼 （Hamming Codes）[3]、摺積碼（Convolutional Codes）[4]，以及里德所羅門碼 （Reed-Solomon Codes）[5]。近 10 年來，則以渦輪碼（Turbo Codes）[6]和低密 度同位檢查碼（LDPC Codes）[7]最受重視。LDPC Codes在 1962 年由MIT的Robert Gallager發明，當時卻因被認為複雜度過高而被遺忘將近 30 年，直至近年來被重 新研究後才發現其優越的性能。

LDPC Codes是一種特殊的線性區段碼，藉著定義一個同位檢查矩陣（parity check matrix），我們得以有系統地產生碼字（codeword），並規範訊息位元（message bits）之間的關係。在LDPC Codes中的同位檢查矩陣為一稀疏矩陣（sparse matrix），因此稱之為低密度（Low Density）。每一個LDPC Codes的同位檢查矩 陣皆可以Tanner Graph[8]表示。而LDPC Codes的解碼方式則是在Tanner Graph上 利用Sum-product演算法 [9]進行check node和bit node的訊息可靠度交換。

LDPC Codes 運作原理相似於 Turbo Codes，藉由重複遞迴（iterative）的處 理方式來逼近沈農極限（Shannon limit）。然而 Turbo Codes 的碼尺寸（code size） 過大，因此在解碼過程經歷數次遞迴後會造成延遲時間過長，因此無法適用於 WLAN、即時語音通訊或需要即時數據處理等應用。相較之下，由於 LDPC Codes 的行為容易分析、error floor 較低、硬體實現度高以及較高的解碼速度（在 LDPC Codes 中主要是記憶體處理，而 Turbo Codes 則完全由運算處理實現）。此外，

LDPC Codes 專利已經過期，所以很多公司都可以使用而不必付費。

目前 LDPC Codes 在 IEEE 802.11n、IEEE 802.15.3a 以及 IEEE 802.16e 的技 術提案中皆被熱烈討論，而下一代衛星數位視訊廣播標準（DVB-S2）也決議以 LDPC Codes 取代 Turbo Codes。在未來，以 LDPC Codes 取代 Turbo Codes 的後 勢相當看好。

多輸入多輸出(Multiple-input Multiple-output：MIMO)系統，該技術最早是由 Marconi 於 1908 年提出的，它利用多天線來抑制通道衰落。根據收發兩端天線 數量，相對於普通的 SISO（Single-Input Single-Output）系統，MIMO 還可以包 括 SIMO（Single-Input Multiple-Output）系統和 MISO（Multiple-Input

Single-Output）系統。原則上，通道容量隨著天線數量的增大而線性增大。也就 是說可以利用 MIMO 系統倍數地提高無線通道容量，在不增加頻寬和天線發送 功率的情況下，頻譜利用率可以倍數地提高。

MIMO的核心概念為利用多根發射天線與多根接收天線所提供之空間自由 度提升傳輸速率與改善通訊品質；它主要有兩種功能形式：一為空間多工（spatial multiplex），另一為空間分集（spatial diversity）。前者是在發射端利用多根天線 傳送不同資料序列，並在接收端利用多根天線的空間自由度將該組資料序列分別 解出。經由此一程序，在發射端與接收端之間彷彿形成一組虛擬的平行空間通 道，可在同一時間、同一頻段，以同一功率傳送多個資料序列。如此一來，整體 系統的有效資料傳輸率便可以在不增加任何通訊資源的前題下提升數倍。而後者 是利用發射或接收端的多根天線所提供的多重傳輸途徑來對抗通道衰落（fading） 的影響；所謂分集意即多重選擇性，它可由多個獨立的傳輸途徑中選擇或組合出 衰落現象較輕微的接收訊號，以維持穩定的鏈路品質。空間多工接收機的演算法 主要有貝爾實驗室的BLAST演算法、ZF演算法、MMSE演算法 [13]、ML演算法 等 [20]。而空間分集主要代表便是空時區塊編碼(Space-Time Block Coding, STBC)，它於發射端將待傳送之資料符元（data symbol）在空間與時間上作預前 編碼，產生適當的冗餘（redundancy），並在接收端經由簡易的處理將此冗餘轉

化為「分集增益」（diversity gain）。 本篇論文主要是在討論LDPC Codes的解碼器設計，與MIMO系統的偵測 （detection）。在LDPC Codes的解碼器設計上，由於Sum-product演算法的複雜性 過高，不利於硬體的設計與實現，在此我們使用了三種以Sum-product演算法為 基礎而簡化的LDPC Codes解碼演算法，並在 802.11n與 802.16e的系統上，模擬 比較此三種LDPC Codes解碼演算法的效能。而在MIMO系統的偵測上，則討論 現存MIMO偵測上較常見的MMSE演算法，與以ML演算法為基礎的MAP偵測 [20]，再結合上述三種以Sum-product演算法為基礎而簡化的LDPC Codes解碼演 算法，並在 802.11n的系統上模擬比較此兩種MIMO偵測演算法的效能。 本篇論文的結構如下: 第二章將介紹LDPC Codes，包括編碼的原理，與解 碼演算法，其中包含Sum-product演算法，與以Sum-product演算法為基礎而簡化 的Normalized belief propagation based（Normalized BP-based）演算法 [10]、 Normalized a-posteriori probability based（Normalized APP-based）演算法 [11]、 Layered belief propagation（Layered BP）演算法 [12]。第三章則簡介MIMO-OFDM 系統，包括此系統的數學模型建立、MIMO MMSE偵測演算法 [13]，軟式反對映 （soft demapping）[14]，和LDPC Codes在 802.11n[15][16]與 802.16e[18][19]的系 統上的應用。第四章則討論以MAP演算法為基礎的偵測，並將之與List Sphere decoding演算法 [22]結合，以降低MAP偵測的運算複雜度。最後總結在第五章中。

第2章 低密度同位檢查碼（LDPC Codes）

低密度同位檢查碼LDPC Codes（Low-Density Parity-Check Codes）[7]原本是 由Robert Gallager在 1962 年所發明的，這是一種使用長段的線性區段碼（Linear Block Codes）。由於當時電腦能力不足以處理複雜性運算，因此使人們淡忘許 久，直到 1995 年由Mackey與Neal重新發展出Tanner Graph[8]，在解碼時使用兩 個狀態的同位檢查格（parity check trellis），使得解碼器容易實現，並使其效能接 近沈農極限（Shannon limit），加上近幾年來VLSI技術的快速發展，亦使得LDPC Codes又逐漸被人們所廣為討論。

2.1 編碼器（Encoder）

LDPC Codes 的編碼方式為由產生矩陣（generator matrix）G乘上訊息向量 （information vector）U 而產生碼字向量（codeword vector）V ，即UG V= 。由 於 LDPC Codes 亦為線性區段碼（Linear Block Codes），故須符合碼字向量V 乘 上同位檢查矩陣（parity check matrix）H 後等於零的規則，亦即_p H Vp T =0，所 以可由下列方法得到產生矩陣G和碼字向量V 。假設一 LDPC Codes 以

(

N K,

)

的 線性區段碼表示，則其中有M =N−K個檢查位元（parity check bits）， K 個訊息 位元（message bits）與訊息向量U 相同。則：

( )

T 0 T p p H V =H UG = (2.1) 0 T p H G ⇒ = (2.2) 。由於將同位檢查矩陣H 中的任意兩列交換或進行 MOD2 運算，所得之新同位_p 檢查矩陣仍可滿足

( )

2.2 式，故可將原來的同位檢查矩陣H 使用高斯消去法_p

（Gaussian elimination）推導至

( )

2.3 式：

[

]

'

p M K M M

H = P _× I _× (2.3)

其中P_{M K×} 為同位檢查部（parity check part），I_{M M×} 為 M M× 的單位矩陣（identity matrix）。而其所對應的產生矩陣G為： T K K K M G= ⎣⎡I _× P_× ⎤_{⎦ (2.4)} ，將

( )

2.3 式與

( )

2.4 式代入

( )

2.2 式中驗證：

[

]

' 0 M K T p M M M K M K M K K K P H G I P P P I × × × × × × ⎡ ⎤ ⎢ ⎥ = _{⎢ ⎥}= ⊕ = ⎢ ⎥ ⎣ ⎦ (2.5) 。一般說來，產生矩陣G通常不為稀疏矩陣（sparse matrix），故編碼時的運算複 雜度，會隨碼字長度（codeword length）N呈 2 N 級數增加。

2.2 圖形解碼

目前LDPC Codes有多種解碼的演算法，其中包括：Majority-logic（MLG） 解碼、Bit-flipping（BF）解碼、Sum-product演算法（SPA）[9]，而Sum-product 演算法又有其它別名：Belief propagation演算法（BPA）、Message Passing algorithm （MPA）。在上述LDPC Codes的解碼演算法中，以Sum-product演算法的效能最 好，有最低的位元錯誤率（bit error rate），然而其運算複雜度亦最高，硬體實現 上也最困難。因此，吾人使用了三種以Sum-product演算法為基礎而修正的演算 法：Normalized belief propagation based（Normalized BP-based）演算法 [10]、 Normalized a-posteriori probability based（Normalized APP-based）演算法 [11]、 Layered belief propagation（Layered BP）演算法 [12]，以降低運算複雜度，增加 硬體的可實現性。

2.2.1 Tanner Graph

在 LDPC Codes 中，可將一M×N的同位檢查矩陣H 分成兩個部份，這兩_p

個部份分別包含 check node 和 bit node。第一個部份是把同位檢查矩陣H 的每一_p

列（row）看成一個 check node，故總共有 M 個 check node。第二個部份是把每 一行（column）看成一個 bit node，也就是碼字的長度，相當於有N 個 bit node。 由於 LDPC Codes 解碼的過程要符合H V_p T =0，所以連結到同一個 check node 的所有 bit node 均要滿足H V_p T =0的關係式，也就是說只有在該列上元素 （element）為“1”的 bit，其 bit node 才有連結到該列所代表的 check node。舉例

來說，若 1 1 0 1 0 1 0 0 1 0 0 1 1 0 1 0 1 1 0 0 1 0 0 0 1 1 0 0 1 1 0 1 1 1 0 1 1 0 0 0 1 0 1 0 1 0 0 1 0 1 0 0 0 1 0 0 1 1 1 1 p H ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ，則 Tanner Graph 可表示為下圖： 圖 2-1 Tanner Graph check node 1 B 2 B 3 B 5 B 6 B 7 B 8 B 9 B 10 B 4 C 5 C 6 C 1 C 4 B 2 C 3 C bit node

2.2.2 圖形解碼概念

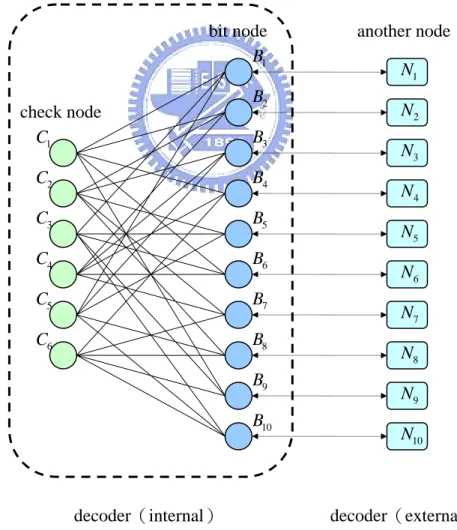
由圖 2-2 的解碼器架構圖可知 LDPC Codes 的解碼過程是應用到 Message Passing 的概念，由 bit node 及 check node 這兩端互相算出機率再傳送給另一端。 在計算由一特定 bit node 到某一 check node 的機率，是由其它連結到該 bit node 所有 check node，及連結到此 bit node 的 another node 所決定的。同樣的，要計 算由一特定的 check node 到某一 bit node 的機率時，亦是由其它連結到該 check node 所有 bit node 來求出。而在最後要求某一 bit 的機率，則是由所有連結到該 bit node 的 check node 及 another node 決定的。下節將討論的其解碼演算過程。

圖 2-2 解碼器架構圖 check node 1 B 2 B 3 B 5 B 6 B 7 B 8 B 9 B 10 B 2 N 3 N 4 N 5 N 6 N 7 N 8 N 9 N 10 N 1 N 4 C 5 C 6 C 1 C 4 B 2 C 3 C

bit node another node

2.3 Sum-Product 演算法

2.3.1 Bit node 至 Check node 機率資訊

圖 2-3 bit node 至 check node 機率資訊

如圖 2-3 所示，其中p 表示由 another node_i N 傳送至 bit node_i B 的機率資訊，_i

ij

r 表示由 check noteC 傳送至 bit node_j B 的機率資訊，_i q 表示由 bit node_ij B 傳送_i

至 check noteC 的機率資訊。若 bit node_j B 與 K 個 check node 及 another node_i N 相_i

連結，且彼此獨立（independent），則：

(

)

(

)

(

)

( ) { } ' ' \ ij i ij j M i j P q ξ P p ξ P r ξ ∈ = = =

∏

= (2.6) ，其中ξ等於1或0，M i

( )

表示同位檢查矩陣H 之第 i 行為“_p 1”之列的集合，而

( ) { }

\ M i j 則表示在集合M i

( )

中，不包含第 j 個元素之子集合。 為了簡化運算，我們使用Log-Likelihood ratio（LLR），則依據LLR之定義：

( )

log

₍

(

1

)

₎

0 P a LLR a P a = = = (2.7)

check node bit node another node

i B i N ij r j C ij q i p

，可求得LLR r

( )

_ij 、LLR p

( )

_i 與LLR q

( )

_ij ，並將之代入

( )

2.6 式可得：

( )

( )

( )

( ) { } ' ' \ ij i ij j M i j LLR q LLR p LLR r ∈ = +

∑

(2.8)

，

( )

2.8 式即為以 LLR 形式所表示之 bit node 至 check node 機率資訊之計算式。

2.3.2 Check node 至 Bit node 機率資訊

圖 2-4 check node 至 bit node 機率資訊

如圖 2-4 所示，check nodeC 與 K 個 bit node 相連結且彼此獨立。由於解碼_j

的過程需符合H Vp T =0的關係式，所以連結到同一個 check node 的所有 bit node 要滿足： 1 2 3 i 1 i i 1 K 0 B ⊕B ⊕B ⊕B₋ ⊕ ⊕B B₊ ⊕B = (2.9) ，則由

( )

2.9 式，可推得：

(

)

(

)

(

)

(

)

1 2 3 1 1 1 2 3 1 1 1 1 0 0 ij i i K ij i i K P r P B B B B B B P r P B B B B B B − + − + = = ⊕ ⊕ ⊕ ⊕ ⊕ = = = ⊕ ⊕ ⊕ ⊕ ⊕ = (2.10) 。為了求出

(

2.10

)

式的通式，將K = 代入，並假設2 P B

(

1= =1

)

a1、P B

(

2 = =1

)

a2 check node bit node

j C i B ij q ij r

可求得下式：

(

)

(

)

(

)

(

)

(

)(

)

1 2 1 2 2 1 1 2 1 2 1 2 1 1 1 0 1 1 P B B a a a a P B B a a a a ⊕ = = − + − ⊕ = = + − − (2.11) ，我們將

(

2.11

)

式進一步化簡成下式：

(

)

(

)(

)

(

)

(

)

(

)(

)

(

)

2 2 1 1 1 2 2 2 1 1 1 2 1 1 2 1 1 2 1 2 1 2 2 1 1 2 1 1 2 1 2 0 2 2 i i i i a a a P B B a a a P B B = = − − − − − ⊕ = = = + − + − − ⊕ = = =

∏

∏

(2.12) ，若K =n時亦成立，可推得：

(

)

(

)

(

)

(

)

1 1 1 2 3 1 1 1 1 1 2 3 1 1 1 1 2 1 2 1 1 2 0 1 2 n i i n n n i i n n a P B B B B M a P B B B B M − = − − − = − − − − ⊕ ⊕ ⊕ = = = + − ⊕ ⊕ ⊕ = = = −

∏

∏

(2.13) ，則：

(

)

1 1 1 2 1 1 2 n n i i M a − − = + =

∏

− (2.14) ，假設在K = +n 1時，P B

(

n = =1

)

an：

(

)

(

)

(

)

(

)

(

)(

)

1 2 3 1 1 1 1 2 3 1 1 1 1 1 1 0 1 1 n n n n n n n n n n n n P B B B B B a M M a P B B B B B a M a M − − − − − − ⊕ ⊕ ⊕ ⊕ = = − + − ⊕ ⊕ ⊕ ⊕ = = + − − (2.15) ，由

(

2.12

)

式及

(

2.14

)

式，可將

(

2.15

)

式推導至下式：

(

)

(

)(

)

(

)

(

)

(

)(

)

(

)

1 1 1 2 1 1 1 2 1 1 2 1 1 2 1 2 1 2 2 1 1 2 1 1 2 1 2 0 2 2 n i n n i n n i n n i n a a M P B B B a a M P B B B − = − = − − − − − ⊕ ⊕ = = = + − + − − ⊕ ⊕ = = =

∏

∏

(2.16) ，經由歸納法證明，我們由

(

2.16

)

式之結果，來推得

(

2.10

)

式之通式：

(

)

(

)

( ) { }

(

)

(

)

(

)

( ) { }

(

)

' ' \ 1 2 1 1 ' ' \ 1 2 1 1 1 1 2 1 1 2 1 1 2 0 0 2 i j i L j i ij i i K i j i L j i ij i i K Q P r P B B B B B Q P r P B B B B B ∈ − + ∈ − + − − = = ⊕ ⊕ ⊕ ⊕ = = + − = = ⊕ ⊕ ⊕ ⊕ = =

∏

∏

(2.17) ，其中Q_{i j'} =P q

(

_{i j'} = ，1

)

L j

( )

表示同位檢查矩陣H 之第 j 列為“1”之行的集合，_p 而L j

( ) { }

\ i 則表示在集合L j

( )

中，不包含第 i 個元素之子集合。 依據

( )

2.7 式 LLR 之定義，

(

2.17

)

式可進一步簡化為：

( )

₍

(

)

₎

( ) { }

(

)

(

)

( ) { } ' ' \ ' ' \ 1 1 2 1 log log 0 1 1 2 i j ij i L j i ij ij i j i L j i Q P r LLR r P r Q ∈ ∈ − − = = = = + −

∏

∏

(2.18) ，接著，我們求出下兩式：

( )

' ( )' ' ' ' ' log 1 1 i j LLR q i j i j i j i j i j Q Q LLR q e Q Q = ⇒ = − − (2.19)

( )

1 tanh tanh 2 1 x x x x x x e e x e x e e e − − − ⎛ ⎞ − = ⇒ _{⎜ ⎟}= + ⎝ ⎠ + (2.20) ，並將x=LLR q

( )

i j' 代入

(

2.20

)

式中：

( )

' ' ' ' ' ' 1 1 1 2 1 tanh 2 1 1 i j i j i j i j i j i j Q Q Q LLR q Q Q − − _{⎛ ⎞} = − = _{⎜ ⎟} ⎝ ⎠ + − (2.21) ，再把

(

2.21

)

式之結果代入

(

2.18

)

式內：

( )

( )

( )

_{( )}

( ) { }

( )

( )

_{( )}

( ) { } 1 ' ' \ 1 ' ' \ 1 1 1 tanh 2 log 1 1 1 tanh 2 L j i j i L j i ij L j i j i L j i LLR q LLR r LLR q − ∈ − ∈ ⎛ ⎞ − − _{⎜ ⎟} ⎝ ⎠ = ⎛ ⎞ + − _{⎜ ⎟} ⎝ ⎠

∏

∏

(2.22) ，其中 L j 表示同位檢查矩陣

( )

H 之第 j 列為“1”之行的個數。

( )

( )

1 1 1 1 1

tanh log 2 tanh log

2 1 1 y y y y y y − ₌ + _{⇒ −} − ₌ − − + (2.23)

最後，我們將

( )

( )

( )

( ) { } 1 ' ' \ 1 1 tanh 2 L j i j i L j i y − LLR q ∈ ⎛ ⎞ = − _{⎜ ⎟} ⎝ ⎠

∏

代入

(

2.23

)

式中，可求得：

( )

( )

( )

_{( )}

( ) { } 1 ' ' \ 1 2 1 tanh tanh 2 L j ij i j i L j i LLR r − LLR q ∈ ⎛ _{⎛ ⎞}⎞ = × − × ⎜_{⎜ ⎜ ⎟}⎟_⎟ ⎝ ⎠ ⎝

∏

⎠ (2.24)

，

(

2.24

)

式即為以 LLR 形式所表示之 check node 至 bit node 機率資訊之計算式。

2.3.3 Bit node 事後（a-posteriori）機率資訊

圖 2-5 事後機率資訊

如圖 2-5 所示，由於碼字中的位元B 其“_i 0”與“1”的機率，是由所有與 bit

nodeB 連結的 check node 及 another node_i N 所決定，所以我們可推得： _i

(

)

(

)

(

)

( ) i i ij j M i P B ξ P p ξ P r ξ ∈ = = =

∏

= (2.25) ，再依照

( )

2.7 式，將

(

2.25

)

式以 LLR 的形式表示：

( )

( )

( )

( ) i i ij j M i LLR B LLR p LLR r ∈ = +

∑

(2.26) ，

(

2.26

)

式即為以 LLR 形式所表示之 bit nodeB 事後機率資訊之計算式。 _i

check node bit node another node

j C i B i N ij r i p

最後再由

(

2.26

)

式所得之結果進行判決（decision），若LLR B

( )

_i ≥0，則表 示經過解碼後位元B 判決為“_i 1”，反之若LLR B

( )

_i <0，則表示經過解碼後位元B_i 判決為“0”，我們可用下式表示：

( )

( )

0 1 0 0 i i i LLR B B LLR B ⎧ ≥ ⎪ = ⎨ _< ⎪⎩ (2.27)

2.3.4 Sum-Product 演算法解碼流程

第一步：初始化（initialize），設定最大遞迴次數“k_Max”，並令一開始的 check node 至 bit node 之“1”與“0”的機率資訊是相等的： ( )0

( )

0.5 log 0 0.5 ij LLR r = = (2.28) ，其中，上標“

( )

k ”內的數字“k”，表示為第k次遞迴所得之結果。 第二步：計算 bit node 至 check node 之機率資訊：

( )

( )

_{( )}

( )

( )

( ) { } 1 ' ' \ k k ij i ij j M i j LLR q LLR p LLR − r ∈ = +

∑

(2.29)

第三步：計算 check node 至 bit node 之機率資訊：

( )

( )

_{( )}

( ) ( )

( )

( ) { } 1 ' ' \ 1 2 1 tanh tanh 2 L j k k ij i j i L j i LLR r − LLR q ∈ ⎛ _{⎛ ⎞}⎞ = × − × ⎜_{⎜ ⎜ ⎟}⎟_⎟ ⎝ ⎠ ⎝

∏

⎠ (2.30) 第四步：計算 bit nodeB 事後機率資訊，並進行判決： _i ( )

_{( )}

_{( )}

( )

( )

( ) k k i i ij j M i LLR B LLR p LLR r ∈ = +

∑

(2.31) ( ) ( )

( )

( )

_{( )}

0 1 0 ₀ k i k i _k i LLR B B LLR B ⎧ ≥ ⎪ = ⎨ < ⎪⎩ (2.32) 第五步：重複遞迴，直到解出的碼字符合H Vp T =0，或k =kMax。

2.4 Normalized BP-based 演算法

2.4.1 UMP（Uniformly Most Powerful）BP-based 演算法

由於

(

2.24

)

式，check node 至 bit node 之機率資訊的計算式中，內含tanh及 1 tanh− 的函式，故在硬體的設計上極為困難，為了降低硬體的複雜度，我們使用 了其它的函式來逼近

(

2.24

)

式，以方便電路的實現。 首先我們引進兩個式子：

( )

( )

sgn exp log i i i i i i a = ⎜⎛ a ⎞_⎟ ⎛_⎜ a ⎞_⎟ ⎝ ⎠ ⎝ ⎠

∑

∏

∏

(2.33)

( )

log tanh , 0 2 x x ⎛ ⎛ ⎞⎞ x Ψ = − _{⎜ ⎜ ⎟⎟} > ⎝ ⎠ ⎝ ⎠ (2.34) 。將

(

2.33

)

式及

(

2.34

)

式代入

(

2.24

)

式中，可推導出：

( )

( )

( )

( )

( ) { }

( )

( )

( )

( ) { }

( )

( ) { }

( )

( )

(

( )

)

(

( )

)

' 1 ' \ ' 1 ' \ ' ' \ ' ' 2 1 tanh tanh 2 2 1 tanh sgn tanh 2

exp log tanh

2 1 sgn L j i j ij i L j i L j i j i L j i i j i L j i L j i j i j i LLR q LLR r LLR q LLR q LLR q LLR q − ∈ − ∈ ∈ ⎛ ⎛ ⎞⎞ ⎜ ⎜ ⎟⎟ = − ⎜ ⎟ ⎜ _{⎝ ⎠}⎟ ⎝ ⎠ ⎛⎛ ⎛ ⎛ ⎞⎞⎞ ⎜⎜ ⎜ ⎜ ⎟⎟⎟ = − ⎜⎜ ⎜ ⎜_⎝ ⎟_⎠⎟⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎞ ⎛ ⎛ _{⎛ ⎞}⎞⎞ ⎟ ⎜ ⎜ _{⎜ ⎟}⎟⎟ × _⎟ ⎜ ⎜ ⎜_⎝ ⎟_{⎠⎟ ⎟}⎟ ⎝ ⎠ ⎝ ⎠⎠ = − × × Ψ Ψ

∏

∏

∑

( ) { } ( ) { } ' \ ' \ L j i i∈L j i ∈ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝

∑

⎠

∏

(2.35) 由於函數 sgn

( )

sgn log tanh 2 x y= x × Ψ x = − x× ⎛⎜_⎜ ⎛⎜ ⎞⎟⎞⎟_⎟ ⎝ ⎠ ⎝ ⎠有兩個特性： 第一個特性為當 x 值越小，對應的 y 值會越大，反之亦然，如圖 2-6 之曲線圖。 第二個特性為Ψ

( )

x 即為自己本身的反函數，如下式所示：

( )

(

x

)

x, x 0 sgn

( )

x

(

sgn

( )

x

( )

x

)

x Ψ Ψ = > ⇒ × Ψ × Ψ = (2.36)

-4 -3 -2 -1 0 1 2 3 4 -10 -8 -6 -4 -2 0 2 4 6 8 10 x y 圖 2-6y=sgn x× Ψ

( )

x 函數圖 由函數Ψ

( )

x 的第一個特性，可知在

(

2.35 式中的

)

(

( )

)

( ) { } ' ' \ i j i L j i LLR q ∈ Ψ

∑

之值 會與最大的Ψ

(

LLR q

( )

_{i j'}

)

之值近似，而最大的Ψ

(

LLR q

( )

_{i j'}

)

又會被最小的

( )

i j' LLR q 所決定，故我們可推得下式：

( )

(

)

( ) { } ' ' ( ) { }\

(

( )

'

)

' ( ) { }\

( )

' ' \ max min i j i j i j i L j i i L j i i L j i LLR q LLR q LLR q ∈ ∈ ∈ ⎛ ⎞ Ψ ≈ Ψ _{= Ψ ⎜ ⎟} ⎝ ⎠

∑

(2.37) ，又因為函數Ψ

( )

x 的第二個特性，我們可將

(

2.37 式之結果代入

)

( )

(

)

( ) { } ' ' \ i j i L j i LLR q ∈ ⎛ ⎞ Ψ⎜_⎜ Ψ ⎟_⎟ ⎝

∑

⎠中，並近似為

(

2.38 式：

)

( )

(

)

( ) { } ( ) { }

( )

( ) { }

( )

' ' \ ' ' 'min\ 'min\ i j i L j i i j i j i L j i i L j i LLR q LLR q LLR q ∈ ∈ ∈ ⎛ ⎞ Ψ⎜_⎜ Ψ ⎟_⎟ ⎝ ⎠ ⎛ ⎛ ⎞⎞ ≈ Ψ Ψ_{⎜ ⎜ ⎟⎟}= ⎝ ⎠ ⎝ ⎠

∑

(2.38)

因此

(

2.24

)

式，check node 至 bit node 之機率資訊的計算式可再做進一步的化簡， 並以

(

2.39

)

式近似之：

( )

( )

( )

( )

(

_{( )}

)

( ) { }

( )

( ) { } ' ' \ ' ' \ ' 1 sgn min ij L j ij i j i j i L j i i L j i LLR r LLR r LLR q LLR q ∈ ∈ ≈ = − ×

∏

× (2.39) ，藉由

(

2.39

)

式的結果，我們可把原本

(

2.24

)

式複雜的tanh及 1 tanh− 函數簡化為 min 函數，以利硬體電路的實現。

2.4.2 正規化參數（Normalization factor）

若列權重（row weight（列之元素為“1”的個數））等於ρ，在比較

(

2.24

)

式 與

(

2.39

)

式後，我們可發現，在

(

2.24

)

式的

(

( )

)

( ) { } ' ' \ i j i L j i LLR q ∈ Ψ

∑

的項次為1，而

(

2.39

)

式的 ( ) { }

(

( )

'

)

'max\ i j i∈L j i Ψ LLR q 的項次為ρ− ，兩式之間相差1 ρ− 個項。故當2

LDPC Codes 同位檢查矩陣H 其碼字長度短，列權重小時，UMP BP-based 演算_p

法之效能與 Sum-product 演算法並不會有太大的間距（gap），但隨著碼字長度 變長，列權重亦增加時，兩者之間將會有 1dB 以上的間距。 藉由

(

2.35

)

式與

(

2.39

)

式，可觀察到LLR r

( )

_ij 與LLR r 之間有兩樣特性： '

( )

_ij 特性一、LLR r

( )

_ij 與LLR r 恆同時為正或同時為負： '

( )

_ij

( )

(

)

(

( )

)

sgn LLR r_ij =sgn LLR r' _ij (2.40) 証明：由圖 2-6 與

(

2.35

)

式可知：

( )

(

( )

)

(

( )

)

( ) { } ' ' ' ' \ 0 0 0 i j i j i j i L j i LLR q LLR q LLR q ∈ > ⇒ Ψ > ⇒

∑

Ψ > ∵ (2.41)

( )

(

)

( ) { } ' ' \ 0 i j i L j i LLR q ∈ ⎛ ⎞ ∴Ψ⎜_⎜ Ψ ⎟_⎟> ⎝

∑

⎠ (2.42) 。亦可由

(

2.39

)

式中得知：

( )

' _{( ) { }}

( )

' ' \ 0 min 0 i j i j i L j i LLR q LLR q ∈ > ⇒ ∴ > ∵ (2.43) ，因為

(

( )

)

( ) { } ' ' \ 0 i j i L j i LLR q ∈ ⎛ ⎞ Ψ⎜_⎜ Ψ ⎟_⎟> ⎝

∑

⎠ ，i'∈minL j( ) { }\i LLR q

( )

i j' > ，且兩者最後皆乘上0

( )

( )

(

_{( )}

)

( ) { } ' ' \ 1 L j sgn i j i L j i LLR q ∈ − ×

∏

之式，故sgn

(

LLR r

( )

_ij

)

=sgn

(

LLR r'

( )

_ij

)

。 特性二、LLR r

( )

ij 之絕對值恆小於LLR r 之絕對值： '

( )

ij

( )

_ij '

( )

_ij LLR r < LLR r (2.44) 証明：

( )

(

( )

)

( ) { }

( )

_{( ) { }}

( )

' ' \ ' ' \ ' min ij i j i L j i ij i j i L j i LLR r LLR q LLR r LLR q ∈ ∈ ⎛ ⎞ = Ψ⎜_⎜ Ψ ⎟_⎟ ⎝ ⎠ =

∑

(2.45)

( )

(

)

( ) { } ' ' ( ) { }\

(

( )

'

)

' ( ) { }\

( )

' ' \ max min i j i j i j i L j i i L j i i L j i LLR q LLR q LLR q ∈ ∈ ∈ ⎛ ⎞ Ψ > Ψ _{= Ψ ⎜ ⎟} ⎝ ⎠

∑

(2.46) 。由圖 2-6 可知：

( )

( )

1 2 1 2 x > x ⇒ Ψ x < Ψ x (2.47) ，由

(

2.46

)

式之結果，可推得：

( )

(

)

( ) { } ( ) { }

( )

( )

(

)

( ) { } ( ) { }

( )

( )

( )

' ' ' \ ' \ ' _{' \} ' ' \ min min ' i j i j i L j i i L j i i j i j i L j i i L j i ij ij LLR q LLR q LLR q LLR q LLR r LLR r ∈ ∈ ∈ ∈ ⎛ ⎞ _{⎛ ⎛ ⎞⎞} Ψ⎜_⎜ Ψ ⎟_⎟> Ψ Ψ⎜_⎝ ⎜_⎝ ⎟_⎠⎟_⎠ ⎝ ⎠ ⎛ ⎞ ⇒ Ψ⎜_⎜ Ψ ⎟_⎟< ⎝ ⎠ ⇒ <

∑

∑

(2.48)

。藉由此兩項特性，我們可對LLR r 乘上一個正規化參數“'

( )

_ij α ”：

( )

( )

( )

( )

(

_{( )}

)

( ) { }

( )

( ) { } ' ' \ ' ' \ " ' 1 sgn min ij ij L j i j i j i L j i i L j i LLR r LLR r LLR q LLR q α α ∈ ∈ = × = × − ×

∏

× (2.49) ，使LLR"

( )

r 能比_ij LLR r 更近似'

( )

_ij LLR r ，而有較好的效能。而正規化參數“

( )

_ij α ” 可由

(

2.50

)

式求得：

( )

{

}

( )

{

'

}

ij ij E LLR r E LLR r α = (2.50)

2.4.3 正規化參數之推導

由於在 BPSK 和 AWGN 之狀態下所求出來的正規化參數，仍可適用於 MIMO-OFDM 系統與多重路徑通道（Multipath channel），故為了簡化運算我們 假設系統使用 BPSK 調變與 AWGN 通道，並只考慮第一次遞迴所產生的效應， 忽略在第二次遞迴後所造成的影響。若定義接收端所接收到的訊號為y ，雜訊_R 機率分佈之變異數（variance）為N ，列權重為₀ ρ，則在第一次遞迴內， ( )1

( )

ij LLR q 會被初始化為 0 4 R y N ，我們可設定

{

Xi:i=1, 2,…,W

}

=

{

qi j' : 'i ∈L j

( ) { }

\ i

}

，其中 i X 為 i.i.d.隨機變數，而W = − 。 ρ 1 我們可由

(

2.22

)

式、

(

2.39

)

式與上段所得之結果，得到：

( )

{

}

( )

( )

1 1 1 1 tanh 2 log 1 1 tanh 2 W W _i i ij W W _i i X E LLR r E X = = ⎧ _{⎛ ⎞}⎫ − − ⎪ ⎜ ⎟⎪ ⎪ ⎝ ⎠⎪ = ⎨ _{⎛ ⎞}⎬ ⎪ _{+ − ⎜ ⎟}⎪ ⎪ _{⎝ ⎠}⎪ ⎩ ⎭

∏

∏

(2.51)

( )

{

' ij

}

{

min

(

1 , 2 , W

)

}

E LLR r =E X X …X (2.52) ，並將結果代入

(

2.50

)

，以計算正規化參數α 。

為了計算E LLR r

{

'

( )

_ij

}

，令Y_i = X_i , i=1, 2,…W ，則Y 的機率密度分佈函數_i

（probability density function）為：

( )

(

( )

( )

)

( )

2

( ) ( )

i i i i Y X X X f y = f y + f −y ×u y = f y ×u y (2.53) ，其中

( )

i X f i 為X 之機率密度分佈函數，_i u i

( )

則為 unit-step 函式。因為X 為 i.i.d._i 隨機變數，所以Y 亦為 i.i.d.隨機變數，故我們可由_i

(

2.53

)

式推得：

( )

(

)

(

(

)

)

{

}

(

)

1 2 1 2 1 ' min , , , , , ij W W W P LLR r y P Y Y Y y P Y y Y y Y y P Y y > = > = > > > =⎡_⎣ > ⎤_⎦ … … (2.54) ，由於 LLR r'

( )

_ij > ，所以： 0

( )

{

' ij

}

0

(

'

( )

ij

)

E LLR r =

∫

∞P LLR r > y dy (2.55) ，接著我們將

(

2.54

)

式代入

(

2.55

)

式可得：

( )

{

}

(

)

( )

1 0 1 1 0 0 ' 1 i W ij Y y W W E LLR r P Y y dy f y dy dy y y Q Q dy y y Q Q dy μ μ μ μ σ σ μ μ σ σ ∞ ∞ ∞ ∞ = ⎡_⎣ > ⎤_⎦ ⎡ ⎤ = _{⎢ ⎥} ⎣ ⎦ ⎡ ⎛ − ⎞ ⎛ + ⎞⎤ = _⎢ − _{⎜ ⎟}+ _{⎜ ⎟⎥} ⎝ ⎠ ⎝ ⎠ ⎣ ⎦ ⎡ ⎛ − ⎞ ⎛ + ⎞⎤ + _{⎢ ⎜ ⎟}+ _{⎜ ⎟⎥} ⎝ ⎠ ⎝ ⎠ ⎣ ⎦

∫

∫ ∫

∫

∫

(2.56) ，其中 0 4 N μ = ， 2 0 8 N σ = ，（ ( )1

( )

0 4 ij R LLR q y N = ∵ ），

( )

2 2 1 2 x x Q x e dx π ∞ − =

∫

， 又因為

(

2.56

)

式之第二項之值極小，故可忽略，所以

(

2.56

)

式可再簡化為：

( )

{

'

}

0 1 W ij y y E LLR r μ Q μ Q μ dy σ σ ⎡ ⎛ − ⎞ ⎛ + ⎞⎤ ≈ _⎢ − _{⎜ ⎟}+ _{⎜ ⎟⎥} ⎝ ⎠ ⎝ ⎠ ⎣ ⎦

∫

(2.57)

為了進一歩推導

(

2.51

)

式，我們定義：

( )

1 1 1 1 tanh 2 1 i i X W W W _i X i i X e e β = = − ⎛ ⎞ = − _{⎜ ⎟}= + ⎝ ⎠

∏

∏

(2.58) ，則依據泰勒展開式（Taylor’s series），可得到： 3 5 7 1 log 2 1 3 5 7 β _β β β β β ⎛ ⎞ − _{= − + + + +} ⎜ ⎟ + _{⎝ ⎠} (2.59) ，由於：

( )

( )

3

( )

5

( )

7

sign β =sign β =sign β =sign β = (2.60)

，所以：

( )

{

}

{ }

2 1 1 1 log 2 1 2 1 k ij k E E LLR r E k β β β − ∞ = ⎧ − ⎫ = _{⎨ ⎬}= + − ⎩ ⎭

∑

(2.61) ，令m_k = ⎣ ⎦E⎡β k⎤，則因為X 為 i.i.d.隨機變數，故： _i

( )

1 1 1 tanh 2 tanh 2 tanh 2 tanh 2 tanh 2 W W _i k i W i i W i W i W i X m E X E X E X E Y E = = ⎧ ⎛ ⎞⎫ = _⎨ − _{⎜ ⎟⎬} ⎝ ⎠ ⎩ ⎭ ⎧ ⎛ ⎞⎫ = ⎨ ⎜_⎝ ⎟_⎠⎬ ⎩ ⎭ ⎧ _{⎛ ⎞}⎫ = ⎨ ⎜_⎝ ⎟_⎠⎬ ⎩ ⎭ ⎧ ⎛ ⎞⎫ ⎪ ⎪ = ⎨ ⎜ ⎟⎬ ⎪ ⎝ ⎠⎪ ⎩ ⎭ ⎧ ⎛ ⎞⎫ = ⎨ ⎜ ⎟_{⎝ ⎠}⎬ ⎩ ⎭

∏

∏

(2.62) ，由

(

2.62

)

式之結果，可求得：

( )

{

}

3 5 7 2 3 5 7 k k k ij k m m m E LLR r = ⎛_⎜m + + + + ⎞_⎟ ⎝ ⎠ (2.63) ，最後，我們將

(

2.57

)

式與

(

2.63

)

式代入

(

2.50

)

式中，即可求得正規化參數α 。

由上述推導的關係式中，我們可發現，正規化參數α 之值的大小，會與當時 的 SNR（訊雜比，signal to noise ratio）之值有關，但實際上，由於正規化參數α 對 SNR 的靈敏度（sensitive）並不高，我們只需尋找使位元錯誤率（bit error rate） 介於 3

10− 到 4

10− 之間的某個 SNR 之值，並用此 SNR 之值來求得正規化參數α ， 此正規化參數α 即可操作在任何 SNR 之值上。

2.4.4 Normalized BP-based 演算法解碼流程

第一步：初始化，設定最大遞迴次數“k_Max”，並令一開始的 check node 至 bit node 之“1”與“0”的機率資訊是相等的： ( )0

( )

0.5 " log 0 0.5 ij LLR r = = (2.64)

第二步：計算 bit node 至 check node 之機率資訊：

( )

( )

_{( )}

( )

( )

( ) { } 1 ' ' \ " k k ij i ij j M i j LLR q LLR p LLR − r ∈ = +

∑

(2.65)

第三步：計算 check node 至 bit node 之機率資訊： ( )

( )

_{( )}

( )

(

( )

( )

)

( ) { } ( )

( )

( ) { } ' ' \ ' ' \ ''k ij 1 L j sgn k i j min k i j i L j i i L j i LLR r α LLR q LLR q ∈ ∈ = −

∏

× (2.66) 第四步：計算 bit nodeB 事後機率資訊，並進行判決： _i ( )

_{( )}

_{( )}

( )

( )

( ) " k k i i ij j M i LLR B LLR p LLR r ∈ = +

∑

(2.67) ( ) ( )

( )

( )

_{( )}

0 1 0 ₀ k i k i _k i LLR B B LLR B ⎧ _≥ ⎪ = ⎨ < ⎪⎩ (2.68) 第五步：重複遞迴，直到解出的碼字符合H Vp T =0，或k =kMax。

Normalized BP-based 演算法解碼流程，除了在第三步：計算 check node 至 bit node 之機率資訊外，其它步驟大致上與 Sum-Product 演算法解碼流程相同。

2.5 Normalized APP-based 演算法

2.5.1 APP-based 演算法

觀察 Sum-product 演算法中，bit node 至 check node 機率資訊之計算式

( )

2.8：

( )

( )

( )

( ) { } ' ' \ ij i ij j M i j LLR q LLR p LLR r ∈ = +

∑

與 bit nodeB 機率資訊之計算式_i

(

2.26

)

：

( )

( )

( )

( ) ' ' i i ij j M i LLR B LLR p LLR r ∈ = +

∑

，我們可發現兩式之形式非常接近，只相差一個 check node 至 bit node 機率資訊

( )

ij

LLR r ，所以只要同位檢查矩陣 H 之行權重（column weight（行之元素為“1”

的個數））夠大，則LLR q

( )

ij 與LLR B

( )

i 會非常近似。在此情況下，我們可將所

有的 bit node 至 check node 機率資訊，以 bit node 機率資訊來近似，也就是說， 我們可省略掉 Sum-Product 演算法解碼流程中的第二步。透過此一化簡，我們可 大幅的降低解碼時的運算量，也由於省略了 bit node 至 check node 機率資訊的計 算，在硬體設計上更可節省掉將近一半的記憶體空間。

2.5.2 Normalized APP-based 演算法

我們可將 APP 演算法與 Normalized BP-based 演算法結合，做進一歩的簡 化，也就是把 APP 演算法中 check node 至 bit node 機率資訊計算式以

(

2.49

)

式取 代。由於我們在計算正規化參數α 時，只考慮第一次遞迴所產生的效應，忽略了

第二次遞迴後所造成的影響，而在第一次遞迴內，APP 演算法的LLR B

( )

_i （bit

機率資訊）相同，皆會被初始化為LLR p

( )

_i （another nodeN 至 bit node_i B 機率資_i

訊），即：

( )0

_{( )}

( )1

( )

_{( )}

i APP base ij BP base i LLR B ₋ LLR q LLR p

−

= = (2.69)

，故 Normalized APP-based 演算法與 Normalized BP-based 演算法之正規化參數α 皆可用相同的計算式求得。而 Normalized APP-based 演算法之正規化參數α 也只

需尋找使位元錯誤率介於 3

10− 到 4

10− 之間的某個 SNR 之值，求得正規化參數α 。

2.5.3 Normalized APP-based 演算法解碼流程

第一步：初始化，設定最大遞迴次數“k_Max”，並令一開始的 bit nodeB 之機率資_i

訊為 another nodeN 至 bit node_i B_i之機率資訊：

( )0

_{( )}

_{( )}

i i

LLR B =LLR p (2.70)

第二步：計算 check node 至 bit node 之機率資訊： ( )

( )

_{( )}

( )

(

( )

_{( )}

)

( ) { } ( )

_{( )}

( ) { } 1 1 ' \ ' \ ''k ij 1 L j sgn k i' min k i' i L j i i L j i LLR r α LLR − B LLR − B ∈ ∈ = −

∏

× (2.71) 第三步：計算 bit nodeB 事後機率資訊，並進行判決： _i ( )

_{( )}

_{( )}

( )

( )

( ) " k k i i ij j M i LLR B LLR p LLR r ∈ = +

∑

(2.72) ( ) ( )

( )

( )

_{( )}

0 1 0 ₀ k i k i _k i LLR B B LLR B ⎧ ≥ ⎪ = ⎨ < ⎪⎩ (2.73) 第四步：重複遞迴，直到解出的碼字符合H Vp T =0，或k =kMax。

在 Normalized APP-based 演算法解碼流程中，我們並不需要初始化 check node 至 bit node 之機率資訊，取而代之的，是對 bit node 之機率資訊進行初始化 的動作。而最大的不同點，則是完全省略掉了 bit node 至 check node 機率資訊的 計算，使得 Normalized APP-based 演算法解碼流程只有四個步驟，這亦是 Normalized APP-based 演算法能大幅降低運算量的原因。

2.6 Layered BP 演算法

2.6.1 Layered BP 演算法

整個 Layered BP 演算法的概念，就是將同位檢查矩陣H 從水平（horizontal）_p 方向分割成數個不同的層（layer），每一層稱為一個子矩陣（sub-matrix），並 將每一個子矩陣視作一個單位的同位檢查矩陣來處理，進行解碼的運算。在同一 次遞迴內，處理完一個子矩陣的解碼，若其解出的碼字符合H V_p T =0，則停止； 如果沒有，才再進行下一層的運算。一直到所有的子矩陣皆完成解碼的運算後， 才算完成一次遞迴。 而其分割的原則：在同一個子矩陣內的任兩列，其為“1”的元素之位置不得 重疊（non-overlaping），即其為“1”的元素之位置不得在同一行上，換言之，一 子矩陣其行權重之值不能大於1。依據上述之特性，我們可發現；在一個子矩陣 內，一個 check node 仍會與多個 bit node 連結，但一個 bit node 就只會連結到一 個 check node，故我們必須對 Sum-product 演算法做部分的修正，才能對一個子 矩陣進行解碼的運算。在此，我們先對單一個子矩陣做解碼的分析：

計算 bit node 至 check node 之機率資訊：

( )

( )

( )

_{( )}

( 1)

( )

"

k k k

ij i ij

LLR q =LLR B +LLR − r (2.74)

計算 check node 至 bit node 之機率資訊：

( )

( )

_{( )}

( ) ( )

( )

( ) { } 1 1 ' \ 1 " 2 1 tanh tanh 2 L j k k ij ij i L j i LLR − r − LLR q ∈ ⎛ _{⎛ ⎞}⎞ = × − × ⎜_{⎜ ⎜ ⎟}⎟_⎟ ⎝ ⎠ ⎝

∏

⎠ (2.75) 計算 bit nodeB 事後機率資訊： _i ( )

_{( )}

( )

( )

( )

( )

" k k k i ij ij LLR B =LLR q +LLR r (2.76) 。其中

(

2.76

)

式中的LLR r

( )

ij 是由

(

2.75

)

式計算更新（update）所得之值。

觀察

(

2.74

)

式與

(

2.75

)

式，我們可發現，在

(

2.74

)

式中所更新的LLR q （bit

( )

_ij

nodeB 至 check node_i C 機率資訊）_j ，會立即被使用於LLR r

( )

_ij （check nodeC 至_j

bit nodeB 機率資訊）的計算上，而 Layered BP 演算法也因為此項特性，可以只_i

用較少的遞迴次數，便達到和 Sum-product 演算法相同的位元錯誤率；另外，因 為我們是將一個子矩陣視為一個同位檢查矩陣來處理，而一個子矩陣的解碼運算 中，最多只會有和碼字長度一樣多的 bit node 至 check node 之機率資訊要儲存， 所以在此一架構下，硬體設計可節省掉將近一半的記憶體空間；這是 Layered BP 演算法的兩個優點。但 Layered BP 演算法仍有其缺點存在，其中一個是

(

2.75

)

式 （check node 至 bit node 之機率資訊計算式），此計算式中的tanh及 1

tanh− 函式太 過複雜，並不適合硬體設計；另一個則是其將同位檢查矩陣H 分層處理的架構，_p 需處理完一個子矩陣，才能進行下一個子矩陣的運算，而原本 Sum-product 演算 法在解碼時，是以平行化運算的結構來進行解碼運算，但 Layered BP 演算法分 層處理的架構卻破壞了其平行化處理的優點，降低了解碼的速度。

2.6.2 Layered BP 演算法修正

為了解決上述的兩個缺點，吾人提出兩個方法，對 Layered BP 演算法作些 微的修正，以處理這兩個缺點。其中第一個缺點，我們可將 Layered BP 演算法 與 Normalized BP-based 演算法結合（可稱之為 Layered Normalized BP-based 演 算法），把

(

2.75

)

式以

(

2.49

)

式取代。同樣地，我們在計算正規化參數α 時，也 只考慮在第一次遞迴內第一個子矩陣所造成的影響，而不去考慮第二個子矩陣之 後的效應，而在第一次遞迴的第一個子矩陣內，Layered BP 演算法的LLR q （bit

( )

_ij

皆會被初始化為LLR p

( )

_i （another nodeN 至 bit node_i B 機率資訊）_i ，即： ( )1

( )

( )1

( )

_{( )}

_ ij _{Layer BP} ij _{BP base} i LLR q LLR q LLR p − = = (2.77)

，故 Layered Normalized BP-based 之正規化參數α 之值與 Normalized BP-based 演算法之正規化參數α 之值相同，可用相同的計算式求得。 而第二個缺點，由於將同位檢查矩陣H 任意兩列向量進行置換，並不會影_p 響到碼字的結構，亦不會改變解碼器的架構，仍滿足H V_p T =0的關係式。故我 們可透過將同位檢查矩陣H 的列向量做交換的運作，來增加其可平行化處理的_p 部份。原來的 Layered BP 演算法對同位檢查矩陣H 進行子矩陣的分割時，某一_p 子矩陣“ A ”之下一層子矩陣“ B ”的第一個列“b ”，必然與子矩陣₁ A 的某列，其為 “1”的元素之位置有重疊；但在子矩陣B 的列b 之後的所有列（含下一層之後之₁ 所有子矩陣的所有列），卻有可能符合「其為“1”的元素之位置不得重疊」之限 制，也就是說這些能符合此限制的列，皆可於子矩陣 A 同屬於同一個子矩陣。所 以我們可藉由列交換的運作，讓同位檢查矩陣H 分割出來的子矩陣數目較使用_p 方法原本分割出來的子矩陣數目少，增加 Layered BP 演算法可平行化處理的部 份。 我們就此一分割方法舉例說明： 若同位檢查矩陣： 1 0 1 1 0 0 1 0 0 1 0 0 1 0 0 1 1 1 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 0 0 0 1 0 0 1 0 0 1 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 p H ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ (2.78) ，依照原本的方式進行分割，可分為6層：

1 0 1 1 0 0 1 0 0 1 0 0 1 0 0 1 1 1 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 0 0 0 1 0 0 1 0 0 1 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 p H ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ (2.79) ，若使用修正後的方式進行分割，則會分為3層： 1 0 1 1 0 0 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 0 1 0 0 1 1 1 0 1 1 1 0 1 1 0 0 0 1 0 0 1 1 0 1 0 0 1 1 0 1 0 0 1 0 1 1 0 0 1 p H ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ (2.80)

2.6.3 Layered Normalized BP-based 演算法解碼流程

若同位檢查矩陣 H 被分割成 M 層子矩陣：

第一步：初始化，設定最大遞迴次數“k_Max”，並令一開始的 check node 至 bit node 之“1”與“0”的機率資訊是相等的： ( )0

( )

0.5 " log 0 0.5 ij LLR r = = (2.81)

，而 bit nodeB 之機率資訊則為 another node_i N 至 bit node_i B_i之機率資訊：

( )0,1

_{( )}

_{( )}

i i

LLR B =LLR p (2.82)

則表示為第m層子矩陣內之計算。

第二步：計算 bit node 至 check node 之機率資訊：

( )

( )

( , )

_{( )}

( 1)

( )

"

k k m k

ij i ij

LLR q =LLR B +LLR − r (2.83)

第三步：計算 check node 至 bit node 之機率資訊： ( )

( )

_{( )}

( )

(

( )

( )

)

( ) { } ( )

( )

( ) { } ' ' \ ' ' \ ''k _ij 1 L j sgn k _{i j} min k _{i j} i L j i i L j i LLR r α LLR q LLR q ∈ ∈ = −

∏

× (2.84) 第四步：計算 bit nodeB 事後機率資訊，並進行判決： _i ( , 1)

_{( )}

( )

( )

( )

( )

" k m k k i ij ij LLR + B =LLR q +LLR r (2.85) ( ) ( )

( )

( )

_{( )}

0 1 0 ₀ k i k i _k i LLR B B LLR B ⎧ _≥ ⎪ = ⎨ < ⎪⎩ (2.86) 第五步：若解出的碼字符合H V_p T =0，停止解碼之運算；若不是，則移往下一 層子矩陣，重複遞迴，直到解出的碼字符合H V_p T =0，或

(

k =k_Max&m=M

)

。

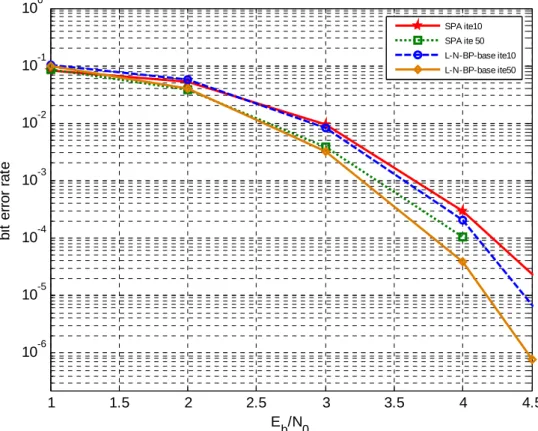
2.7 模擬結果

我們將上述所提到的 LDPC Codes 解碼演算法，使用

(

273,191

)

Gallager Codes，在 BPSK 系統、AWGN 通道環境下進行測試，並將這些 LDPC Codes 之 解碼演算法的效能和 Sum-product 演算法的效能做比較。

由圖 2-7 與圖 2-8 之模擬結果，可知經由正規化參數修正後的演算法，有較 低的位元錯誤率，其效能更接近 Sum-product 演算法的模擬結果，而其中的 df （dynamic factor，依照其所在之 SNR 來計算其正規化參數之值）與 cf（constant factor，正規化參數之值固定由介於10−3到 4 10− 之間的某個 SNR 所求得）兩者之 模擬結果機乎是相同的，由介於 3 10− 到 4 10− 之間的 SNR 之值所計算之正規化參 數確實可操作在任何 SNR 上。