On the time complexity of minimum and maximum global snapshot problems

(1)

Information

Pry;t4zeing

Information Processing Letters 67 (1998) 151-156

On the time complexity of minimum and maximum

global snapshot problems

Loon-Been Chen I, I-Chen Wu *

Department of Computer Science and Information Engineering, National Chiao Tung University, 1001 Ta-Hsueh Road, Hsinchu, Taiwan Received 1 June 1997; received in revised form 28 April 1998

Communicated by T. Asano

Abstract

Deriving the minimum and maximum global snapshots is very useful for some error detection problems in distributed programs. Several researchers, e.g., Groselj, Chen and Wu, have shown that the minimum and maximum global snapshot problems are linear-time reducible to the maximum constant-ratio network flow (MCNF) problem, here defined as the well- known maximum network flow problem with m = O(n), where m is the number of edges and n is the number of vertices in the given flow network. In this paper we show in a reverse way that the MCNF problem is also linear-time reducible to these global snapshot problems. Thus, we can conclude that the global snapshot problems are “as difficult as” the MCNF problem in terms of time complexity. 0 1998 Elsevier Science B.V. All rights reserved.

Keywords: Distributed systems; Computational complexity; Error detection; Global snapshot

1. Introduction

Error detection and debugging are critical tasks in developing distributed programs. Many research results [3,4,8] suggest that a distributed program usu- ally adheres to certain invariant conditions to func- tion properly. For example, in a distributed program, several tokens may be distributed over the processors (e.g., the token may represent the number of resources and critical sections), and the number of these tokens is bounded in a range at any snapshot, regardless of how tokens are moved over different processors. The conventional means of detecting whether or not the above condition holds are to derive the minimum or maximum number of tokens for all possible snapshots.

* Corresponding author. Email: icwu@csie.nctu.edu.tw. ’ Email: lbchen@csie.nctu.edu.tw.

This problem is referred to as the minimum or maximum global snapshot problem [6].

Groselj [6] recently proposed an interesting method to derive the minimum global snapshot. In this method, he reduced this snapshot problem to a maximum constant-ratio network flow (MCNF) problem. The MCNF problem is defined herein as the well-known maximum network flow problem with m = o(n), where rn is the number of edges and n is the number of vertices in the given flow network. Chase and Garg [l] independently obtained similar results. Later, Chen and Wu [2] proposed a general technique, called normalization, for deriving both minimum and maximum global snapshots. According to their results, these snapshot problems are linear-time reducible to the MCNF problem.

Above investigations only point out that the time complexities of the minimum and maximum global

(2)

1.52 L.-B. Chen, I-C. Wu/Infornmtion Processing Leners 67 (1998) 151-156

snapshot problems will not be higher than those of the MCNF problem. However, whether or not the time complexities for the above snapshot problems can be lower than those of the MCNF problem remains unknown. To resolve this question, this paper shows in a reverse manner that the MCNF problem is also linear-time reducible to these global snapshot problems. Thus, we can conclude that the above global snapshot problems are “as difficult as” the MCNF problem in terms of time complexity.

The rest of this paper is organized as follows. Section 2 describes our model and the notations used in this paper. Sections 3 and 4 discuss the time complexities of the minimum and maximum global snapshot problems, respectively. Concluding remarks are finally made in Section 5.

2. Model and notations

A distributed program consists of processes com- municating via a network. These processes share no memory and no global clock. Pairs of processes must communicate via network channe2s. In addition, the state of such a program is distributed over these processes and channels in each snapshot.

Events

The states of processes change only when events [7] (atomic actions) are executed. Three kinds of events on each process are of relevant concerned:

(1) internal event: performs a local computation; (2) send event: sends a message to another process via

the channel; and

(3) receive event: receives a message from another process via the channel.

Note that each process should start with an initial internal event and end with a$nal internal event.

Next, the chronological order of events is defined by assuming that the event ei happens before event ej ,

denoted by ei + ej , if and only if one of the following conditions holds [7]:

(1) (2)

(3)

events ei and ej occur in the same process and ei occurs before ej ;

event ei is the sent event of a message and event ej is the receive event of the same message; and another event f?k exists such that ei + ek and ek --f ej.

Internal event Send event Receive event Initial internal event Final internal event Internal arc of message arc

sink part

Fig. 1. Event graph of a run for a distributed program

Global snapshot

Consider a possible run for a distributed program. The system can proceed from one state to another by executing events. A set EC of events are said to be

consistent if event e E EC and event e’ -+ e imply that e’ E EC. A global snapshot is a collection of states, one from each process and channel, immediately after executing a consistent set of events. Herein, of relevant concern is the total number of tokens. Therefore, a

state value can actually be represented by its token number. In addition, the minimum (maximum) global snapshot is the global snapshot with the minimum (maximum) number of tokens among all possible snapshots.

Event graph

An event graph is used to represent a run for a distributed program under the following conditions: (1) a vertex denotes an event, and (2) if event ei + ej and no event ek exists such that ei + f?k and ek + e there is a corresponding arc, denoted by (ei , ej ), ‘2

from ei ‘s vertex to ej ‘s. For example, Fig. 1 illustrates an event graph. An arc (ei, ej) is referred to as a

message arc if it corresponds to an in-transit message from event ei to ej. Otherwise, the arc is referred to as an internal arc because it corresponds to an internal state transition inside a process. For each message arc a, S, denotes the number of message tokens; for each internal arc a = (ei, ej), S, denotes the token number of the corresponding process after execution of the event ei and before the event ej. In addition, * In this paper, we use (u, v) to represent ordered pairs and use (u, V) to represent unordered pairs.

(3)

u = source

CN

w = sink

L.-B. Chen, I-C. Wu /Information Processing Lxtters 67 (1998) 151-156 source part

PU P(u,v) Pv P(v.w) Pw

(4 @)

cut corresponding

t0 CN

Fig. 2. (a) A common graph. (b) The event graph translated from the graph in (a).

153

the vertex corresponding to an initial (final) internal event is called an i-vertex (f-vertex). Moreover, the arc incident to i-vertex (f-vertex) is called an i-arc (f-arc). Clearly, each process has an internalpath from its i-vertex to its f-vertex without going through any message arcs.

cuts

A cut in an event graph H partitions the vertex set U into two disjoint sets such that one, called the source

part and denoted by US, contains all the i-vertices. Meanwhile, the other, called the sink part and denoted by U,, contains all the f-vertices. The cost of a cut C is

cost(C) = _c s a. VQJa: a=(u,u),

UEU.7. VEU,

For example, in Fig. 1, the costs of cuts Ct , C2 and C3 are 14, 12 and 16, respectively.

A cut of the event graph is consistent if and only if the set of all events in the source part are consistent. From this definition, we can infer that each consistent cut corresponds to a global snapshot and the cut cost is actually the number of tokens of the global snapshot. Obviously, for each consistent cut C, each arc in C must be from the source part to the sink part.

The minimum (maximum) consistent cut is the consistent cut with the least (largest) cost among all consistent cuts. Also, the minimum (maximum) consistent cut cost is the cost of the minimum (maximum)

consistent cut. Clearly, the minimum (maximum) consistent cut corresponds to the minimum (maximum) global snapshot.

Global snapshot model

In the proposed model, the event graph with arc costs is assumed to be given in advance. Garg and Waldecker 141 suggested that in practice, for each event in each process Pi, Pi sends its token number to a process, called the checker process. This process runs an algorithm for deriving the minimum or maximum global snapshot.

3. Minimum global snapshot

This section shows that the MCNF problem is linear-time reducible to the minimum global snapshot problem. Given a flow network N (see Definition 1 below), the linear-time reduction algorithm given below constructs an event graph H such that the mm-cut capacity of N equals the minimum consistent cut cost of H. Fig. 2 presents an example of the reduction.

Definition 1. A flow network N = (V, E) is a di- rected graph in which each edge (u, v) E E has a non- negative capacity c(u, u) > 0. One node s is designated as the source and another node t is designated as the sink. A cut is a set of arcs all incident to two disjoint vertex sets partitioned from V, where one set

(4)

154 L.-B. Ghen. I-C. Wu/Infomation Processing Letters 67 (1998) 151-156

with node s is referred to as the source set, and the other with node t is referred to as the sink set. The capacity of a cut C, denoted by capacity(C), is the total capacity of all arcs (on C) from the source set to the sink set. A minimum cut of the flow network is the cut with the least capacity. The least capacity is also called the mm-cut capacity.

Reduction Algorithm. 1. 2. 3. 4. 5. 6.

For each vertex u in N, create the corresponding internal path Pu. This operation takes 0 (n) time. For each pair of vertices (u, u), if (u, V) or (v, U) is in N, create the corresponding internal path

P(u,u) (or, equivalently, P(,,,)). This operation takes O(m) time.

For each internal path, add two internal events such that the path is divided into three parts: the i-arc, the middle part, and the f-arc. All message arcs added below must have their vertices incident to the middle parts. This operation takes 0 (m + n) time. For each internal path P(u,v), create a message arc a(,,,) from Pc~,~) to Pu and a message arc a(,,,) from Pc~,~) to Pu. This operation takes O(m) time.

Set the cost of f-arc of Ps and i-arc of Pt to oo, where s is the source and t is the sink of N. Set the costs of other i-arcs and f-arcs to 0. Set the costs of all other internal arcs (in the middle parts) to oo. This operation takes O(m + n) time.

For each message arc a(,,,), if (u, V) is in N, set s aW) = c(u, v); otherwise, set &(,,,) = 0. This operation takes 0 (m) time.

[n the above reduction algorithm, each consistent cut CH in H is said to correspond to a cut CN in N, denoted by CH I+ CN, if and only if the following property holds:

Al. For each vertex u in N, 2) is in the source (sink) part of cut CN if and only if CH cuts across the i-arc (f-arc) of the internal path P,, .

For example, in Fig. 2, CH I+ CN. Note that since the source s (the sink t) is always in the source (sink) part, CH ImiSt dWayS CUtS aCrOSS the i-aIT Of P, (the f-arc of Pt). Theorem 2 proves that the minimum consistent cut cost of H equals the mm-cut capacity in N.

Theorem 2. For a given jlow network, its min-cut

capacity equals the minimum consistent cut cost in the event graph constructed from the above reduction algorithm.

Proof. Let N be the given flow network and H be the reduced event graph. In addition, let KH be the set of all the consistent cuts in H, K,++N be the set of all cu_ts in KH, that correspond to some cut in N, and KH-N be KH - KH++N. In this proof, it obviously suffices to prove that the following two properties hold:

Bl. For each consistent cut CH in KUH++N.

COSt(c’l-r) = 00.

B2. Among all consistent cuts CH in KH-N,

vcHF&iTIN (COSt(CH)) = E

(c~pucity(CN))*

This holds if the following two properties hold. B21. For each cut CN, there exists at least one CH in

KHAN such that CH t+ CN. B22. For each cut CN ,

Properties B21 and B22 imply Property B2 owing to the following reason:

$n (CUpUCig(CN)) N = min VCN Inin (COSt(CH))) VCH,CH+'cN = vcH$HnN (c&CH)).

Initially, Property Bl must be proven. From Property Al, for each consistent cut in KH++N, the cut must cut across i-arcs or f-arcs except for the f-arc of PS and the i-arc of Pt (s and t are the source and sink vertices of N). On the other hand, for each consistent cut CH in gH+,N, the Cut CH must Cut across Some internal arc in the middle parts or the f-arc of P, or the i-arc of

Pr. Since these arcs have costs oo (see the Reduction Algorithm), we obtain COSt(CH) = 00.

Second, both Properties B21 and B22 must be proven. Given a cut CN that partitions the vertices

(5)

L.-B. Cht ?n, I-C. Wu /Information Processing Letters 67 (1998) 151-l 56 PU P(u,v) Pv PU P(u,v) Pv -9,

\

0 0 I WI

w

w aa, I

::--’

I a.zv,u 03 I \ ‘-__ _- 0 0 0 PU P(u,v) Pv PU P(u,v) Pv 0 0 0 0) W co a%v -i; a+ co --S -0 0‘ _ - o’

W

(a>

@I

(4

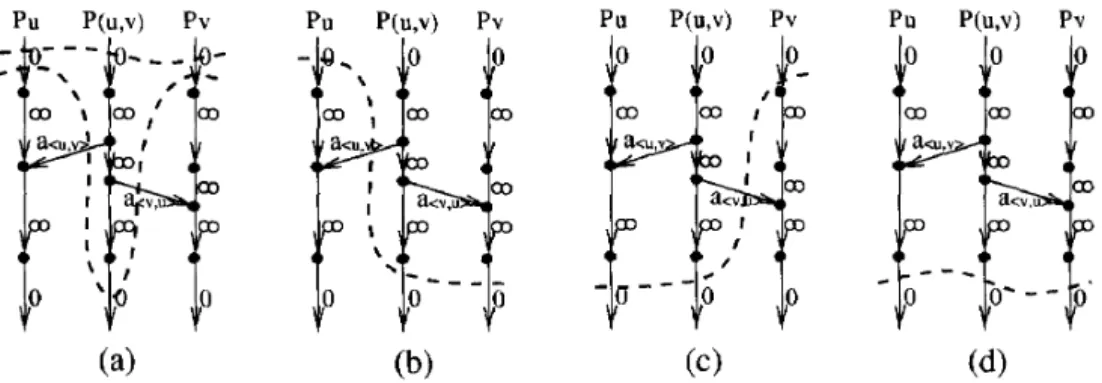
Fig. 3. Four cases of a consistent cut cuts across internal paths Pu , Pv, and P(,.,).

of N into V, and V,, a consistent cut CH (in H) can be constructed, having the minimum cost among all consistent cuts in KH,.+N, as follows. First, to let CH I-+ CN, CH must cut across each Pu as in property Al. Then, we need to verify the consistency and examine the minimum cost among each set of P(U.v), PU and Pv:

(1)

(2)

(3)

(4)

If CH cuts across i-arc of both P,, and Pv (u E V, and u E V,), as shown in Fig. 3(a), a consistent Cut in KHHN Can Cut aCrOSS either i-aK Or f-~C

of P(u,u). we let CH cut across the i-arc because the arc will have a smaller cost. In this case, no edge contributes cost to CN and no message arc contributes cost to CH .

If CH cuts across i-arc of Pu and f-arc of Pv (u E

V, and u E V,), as shown in Fig. 3(b), CH must cut

across f-arc of P(,,,). Otherwise, the cut will be inconsistent. In this case, edge (u, v) contributes c(u, u) to CN. Corresponding message arc a(,,,) contributes Sac,, “) to CH.

If C,y cuts across f-arc of Pu and i-arc of Pv

(u E Vt and u E V,), CH must cut across f-arc of P(u.v). This case is similar to case (2).

If CH cuts across f-arc of both Pu and Pu

(u E Vr and u E V,), as shown in Fig. 3(d), CH

must cut across f-arc of P(u,u)_ In this case, no edge contributes cost to CN and, no message arc contributes COSt t0 CH.

From above discussion, cut CH is consistent for the following reason. For each pair of Pu and Pu , there are no message arcs between them. For each PC,,,>, all the message arcs incident to P(,,,) are from P(,,,) to the corresponding Pu and Pu . From the above discussion,

1.55

CH is consistent due to the consistency among each set of P(,,,), Pu, and Pv. In addition, it is obvious from above that

capacity(C’lv) = cosf( CH ) = min (cost( CL)). VC;I,C;lt+CN

Thus, both Properties B21 and B22 hold. 0

4. Maximum global snapshot

Herein, both minimum and maximum global snapshot problems can be reduced to each other in the following manner: (1) based on the normulization technique 121, reset the cost of each message arc to zero, while not changing any consistent cut cost; and (2) change the cost S of each internal arc to M - S, where M is the maximum cost among all arcs. Thus, we can conclude that the maximum global snapshot problem is also “as difficult as” the maximum network flow problem in terms of time complexity.

5. Conclusion

From the investigations of Chase and Garg [l], Chen and Wu [2], and Groselj [6], the minimum and maximum global snapshot problems are linear-time reducible to the MCNF problem. In this paper, we show in a reverse manner that the MCNF problem is also linear-time reducible to these global snapshot problems. Thus, we can conclude that the global snapshot problems are “as difficult as” the MCNF problem in terms of time complexity. The fact that

(6)

156 L.-B. Chen, I-C. Wu /Information Processing Letters 67 (1998) 151-156

0(n2 logn) has been the optimal time complexity for the MCNF problem for many years [5] implies the difficulty in improving the 0(n2 logn) global snapshot algorithms (as well as that for the MCNF problem).

Acknowledgments

The authors would like to thank the National Sci- ence Council of the Republic of China for financially supporting this research under Contract No. NSC-86- 2213-E-009-32.

References

[l] CM. Chase, V.K. Garg, Efficient detection of restricted classes of global predicates, in: 9th Intemat. Workshop on Distributed Algorithms, 1995.

[2] L.B. Chen, LC. Wu, On detection of bounded global predicates, in: Proc. Intemat. Conference on Distributed Systems, Software Engineering, and Database Systems, Taipei, 1996.

[3] R. Cooper, K. Marzullo, Consistent detection of global predicates, in: Proc. ACM/ONR Workshop on Parallel and Distrib- uted Debugging, 199 1, pp. 167-I 74.

[4] V.K. Garg, B. Waldecker, Detection of weak unstable predicates in distributed programs, IEEE Trans. Parallel Distrib. Systems 5 (3) (1994) 299-307.

[5] A.V. Goldberg, R.E. Tarjan, A new approach to the maximum- flow problem, I. ACM 35 (4) (1988) 921-940.

[6] B. Groselj, Bounded and minimum global snapshots, IJZEE Parallel Distrib. Technol. (1993) 72-83.

[7] L. Lamport, Time, clocks and the ordering of events in a distributed system, Comm. ACM 21 (7) (1979) 558-565. [8] LC. Wu, Multilist scheduling: a new parallel programming

model, Ph.D. Thesis, School of Computer Science, Carnegie Mellon University, 1993.