118 IEEE COMMUNICATIONS LETTERS, VOL. 7, NO. 3, MARCH 2003
A Robust Timing Synchronization Scheme
in Multiple Antenna Systems With Doppler
Frequency Shifts
Shan-An Yang and Jingshown Wu, Senior Member, IEEE
Abstract—In this letter, we propose a timing synchronization
scheme for a dual antenna system in Rayleigh-fading environ-ments. Instead of assuming the channel gain to be constant during the training duration, we consider the time-variant nature of the multiplicative distortions and formulate them with linear combinations of eigenfunctions. Then, we derive a formula to find the maximum-likelihood estimation of the channel timing and simulate the performance with both ideal and nonideal channel state information. The results show that this approach outperforms the conventional ones especially when the Doppler spread is severe.
Index Terms—Antenna arrays, fading channels, MIMO, timing
synchronization.
I. INTRODUCTION
I
N A MULTIPLE antenna system, timing error can cause severer degradation than the single antenna case since intersymbol interference affects all antennas at the same time. Traditionally, symbol timing recovery can be obtained based on the maximum-likelihood (ML) criterion and implemented in the open-loop or closed-loop form. For example, the well-known early-late gate method and the wave different method (WDM) are closed-loop timing synchronizers [1]. On the other hand, the timing estimator developed in [2] is an open-loop timing estimator for a dual antenna system. However, these estimators are obtained under the assumption of quasi-static channel in the training duration. When the Doppler frequency shift is severe, the quasi-static assumption may result in significant error such that the performance deteriorates with broadened Doppler bandwidth. In this paper, we take the time variation of the channel gains into consideration and formulate the multiplicative distortions with linear combinations of their eigenfunctions. Based on this scheme, we derive the ML esti-mate of the symbol timing. The performance of this scheme is numerically simulated and tested under nonideal channel state information (CSI) and channel model mismatch. The results show that the proposed scheme outperforms the conventional one.Manuscript received October 9, 2002. The associate editor coordinating the review of this letter and approving it for publication was Dr. N. Al-Dhahir. This work was supported in part by National Science Council and Ministry of Educa-tion Taiwan, under Grant NSC 90-2213-E-002-041 and Grant 89E-FA 06-2-4-7. The authors are with the Department of Electrical Engineering and Graduate Institute of Communication Engineering, National Taiwan University, Taipei 10617, Taiwan, R.O.C. (email: wujsh@cc.ee.ntu.edu.tw).
Digital Object Identifier 10.1109/LCOMM.2003.809989
II. SYSTEMDESCRIPTION AND THEEIGENFUNCTION
DECOMPOSITIONAPPROACH
The communication system under consideration has two transmitting antennas and two receiving antennas. The trans-mitting antennas send the training signals as
(1) where denotes the length of the training sequence, is the index number of transmitting antenna, is the symbol time du-ration, is the training sequence, and is the square-root raised cosine pulse shaping function with roll-off factor . The received signal at receiving antenna is modeled as
(2) where is multiplicative distortion, is the additive noise and is channel delay. is modeled as zero mean cyclic symmetric complex Gaussian random process having identical autocorrelation function [2] as
(3) where denotes the expectation over the ensembles, means complex conjugate, represents the zero order Bessel func-tion of the first kind, is the maximum Doppler frequency, and is cyclic symmetric white Gaussian random processes with autocorrelation function . In addi-tion, all of these random processes are assumed to be indepen-dent. As in [3], it is possible to find the eigenfunctions, , which satisfy
(4) where are the corresponding nonnegative real eigenvalues. and are the initial time and final time of the observation duration, respectively. and are obtained numerically by approximating (4) with a discrete one with sufficient resolution. Then, we transform it into the matrix form and find the eigen-vectors and eigenvalues of the autocorrelation matrix [4], [5].
Assuming , can be expressed as
(5) where
(6)
1089-7798/03$17.00 © 2003 IEEE
YANG AND WU: A ROBUST TIMING SYNCHRONIZATION SCHEME 119
and is complex Gaussian random variable with variance . If for some , the limiting operation in (5) is removed and is taken as the maximum integer that renders positive. Now, our objective is to estimate the channel delay given the received signal, , . By an extension to the deriva-tion in [6] and that and are independent, we can get the joint probability density function of and , conditioned on and . By taking logarithm of the probability den-sity function and neglecting irrelevant constants and scaling, we obtain the likelihood function as
(7) Now, we can apply (2)(5)(6) and rewrite the last term of (7) in matrix form to obtain
(8)
(9) where and are a column vector and a diagonal
ma-trix given by and
. The superscripts and denote the transpose and Hermitian transpose, respectively. Here, we have used the fact that a shift in does not change its statistical property. To maximize , we obtain the ML channel estimate as
(10)
where and
. is a matrix with elements
given by (11) where , , , . is defined as (12) where (13) Based on (5) through (13), we find the ML estimate of in (14), shown at the bottom of the page.
Note that the last term in (14) is independent of for proper choices of and . As a result, (14) is simplified as
(15)
III. SIMULATIONRESULTS ANDDISCUSSION
Depending on the bandwidth of the random process, it is suf-ficient to well approximate with a small [3]. There-fore, with an appropriate value of , the limit operation in (15) can be removed with only negligible degradation in per-formance. We find that for normalized maximum Doppler fre-quency, , less than 0.05, the first two eigenvalues consist of more than 85% of the total energy. In the following simulations, we show that with , the estimation error is greatly reduced compared with the conventional ML based on quasi-static assumption for normalized maximal Doppler fre-quency as large as 0.06.
A. Comparison With the Conventional Approach
The conventional scheme uses simple correlation to acquire the estimate of [2]. This is equivalent to have and ap-proximate as a constant function in (6) without the limit operation in (5). In Fig. 1, we compare the proposed scheme with to the conventional correlation approach. The pa-rameters of the simulation are given as follows. The roll-off factor is 0.3, and the pulse shaping function is truncated to around . The continuous waveform is represented by 32 samples per symbol. The acquisition interval is assumed to be around the correct timing delay. The orthogonal training sequence pair is
and . We can see that
the conventional approach deteriorates seriously as the max-imum Doppler frequency shift increases, while the proposed method retains reasonable performance. We can see that for nor-malized frequency as large as 0.05, the proposed method with dB has the same performance as the conventional method with dB. The improvement is more sig-nificant at high SNR.
B. Sensitivity to Non-Ideal CSI and Channel Model Mismatch As suggested in (15), the timing synchronization requires the knowledge of signal to noise ratio and the maximum Doppler frequency shift. Thus, we investigate sensitivity of the proposed method to the nonideal CSI. In Fig. 1, we plot the performance of the proposed method with nonideal information of SNR. The systems are designed with 8 dB or 20 dB larger than
(14)
120 IEEE COMMUNICATIONS LETTERS, VOL. 7, NO. 3, MARCH 2003
Fig. 1. Performance comparison with the conventional scheme for various inaccurate SNR values.
Fig. 2. Performance for various designed value off .
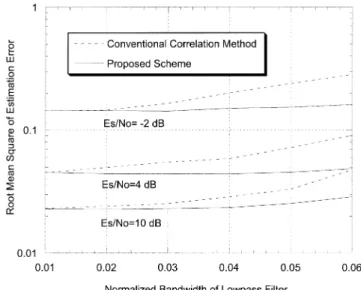
or lower than the actual . Fig. 2 depicted the perfor-mance of the estimators with a fixed design value of in var-ious Doppler frequency spread environments. In addition, we also investigate the effect of model mismatch. We feed white noise into ideal lowpass filters to obtain the multiplicative dis-tortion while the system is designed under assumption of Jakes Doppler spectrum with . The results are com-pared to the conventional correlation approach and illustrated in Fig. 3. It shows that the proposed method is also insensitive to model mismatch. The reason for the insensitivity of model mis-match is explained as follows. The first eigenfunction is very close to a constant and the second eigenfunction is similar to a straight line. The mismatched model just changes the corre-sponding eigenvalues so that the importance of each component is slightly mis-weighted.
C. Implementation Complexity
Since this scheme is insensitive to model mismatch and CSI, we can choose the average value of the SNR and for the
Fig. 3. Performance comparison with channel model mismatch.
target operating environment. Thus, we can find and com-pute beforehand and store them in ROM. Spe-cial care can be taken to make nondiagonal elements of
negligibly small to reduce the computation. must be calculated via (12) and (13) in real time, which dom-inate the computational complexity of this scheme. Compared to the conventional correlation method with the same oversam-pling ratio, it takes approximately twofold multiplications and additions for .
IV. CONCLUSION
We have proposed a timing synchronization scheme using eigenfunction decomposition of the multiplicative channel dis-tortions. The results show that the proposed scheme performs much better than the conventional approach. In addition, it is quite robust with nonideal channel state information and channel model mismatch. The derivation and discussion in this letter can be easily extended to multiple-input multiple-output systems. This scheme can be applied in burst-based transmis-sion in multiple-input multiple-output systems in high Doppler bandwidth environments.
REFERENCES
[1] G. O. Y. S. F. Hau and C. Y. Chan, “The use of WDM for timing syn-chronization in Rayleigh fading channel,” in Proc. ICSP, Seattle, WA, May 1998, pp. 1640–1645.
[2] A. F. Naguib, V. Tarokh, N. Seshadri, and A. R. Calderbank, “A space-time coding modem for high-data-rate wireless communica-tions,” IEEE J. Select. Areas Commun., vol. 16, pp. 1459–1478, Oct. 1998.
[3] H. J. Landau and H. O. Pollak, “Prolate spheroidal wave functions, fourier analysis and uncertainty. II,” Bell Syst. Tech. J., vol. 40, pp. 65–84, 1961.
[4] G. F. Alberto, “Eigenvectors of a toeplitz matrix: Discrete version of the prolate spheroidal wave functions,” SIAM J. Alg. Discrete Meth., vol. 2, no. 2, pp. 136–141, 1981.
[5] , “Toeplitz matrices commuting with tridiagonal matrices,” Linear
Alg. Applicat., vol. 40, pp. 25–36, 1981.
[6] J. G. Proakis, Digital Communications. New York: McGraw Hill, 1995, ch. 6.