A Linear Space Algorithm for Haplotype Blocks Partitioning
Using Limited Number of Tag SNPs
Yaw-Ling Lin
∗Wen-Pei Chen
Hsiang-Sheng Shin
Dept. of Comput. Sci. and Info. Management,
College of Computing and Informatics, Providence University,
200 Chung Chi Road, Shalu, Taichung, Taiwan 433.
yllin@pu.edu.tw, wenpei.keynes@gmail.com, g9571065@pu.edu.tw
Abstract
The pattern of linkage disequilibrium (LD) plays a cen-tral role in genome-wide association studies of identi-fying genetic variation responsible of common human diseases. A Single Nucleotide Polymorphism or SNP is a DNA sequence variation occurring when a sin-gle nucleotide in the genome differs between members of species. Recent studies show that the patterns of linkage disequilibrium observed in human chromosome reveal a block-like structure; the high LD regions are called haplotype blocks, and furthermore, a small sub-set of SNPs, called tag SNPs, is sufficient to capture the haplotype patterns in each haplotype block. Both Patil [18] and Zhang et al. [24] have proposed algo-rithms to partition haplotype sample into blocks fully under the circumstances of requiring minimal number of tag SNPs. However, when resources are limited, in-vestigators and biologists may not be able to genotype all the tag SNPs and instead must restrict the num-ber of tag SNPs used in their studies. In this paper, we examine several haplotype block diversity evalua-tion funcevalua-tions and propose dynamic programming al-gorithms for haplotype block partitioning with using ∗This work is supported by grants from the Taichung
Veterans General Hospital and Providence University (TCVGH-PU-968110) and in part by the National Science Council (NSC-96-2221-E-126-002) Taichung, Taiwan, Re-public of China.
the limited number of tag SNPs. We implement these algorithms and analyze the chromosome 21 haplotype data given by Patil et al. [18]. When the sample is par-titioned into blocks fully, we identify a total of 2,266 blocks and 3,260 tag SNPs which is smaller than those identified by Zhang et al. [24]. We demonstrate that Zhang’s algorithm does not find the optimal solution due to ignoring the non-monotonic property of com-mon haplotype evaluation function. The algorithms described have been implemented in the web-based system as the analysis tools for bioinformaticists and geneticists.
Keywords:SNP, Diversity, haplotype block, tag SNP, dynamic programming.
1
Introduction
A Single Nucleotide Polymorphism, or SNP, is a small genetic variation, that occur within a per-son’s DNA sequence. It occurs when a single nu-cleotide is replaced by others. Mutation in DNA is the principle factor resulted in the phenotypic dif-ferences among human beings, and SNPs are the most common mutations. They are useful poly-morphic markers to investigate genes susceptible to diseases or those related to drug responsiveness.
Furthermore, a small subset of SNPs directly in-fluences the quality or quantity of the gene prod-uct, and increase a risk to certain diseases and to severe side effect by drugs. Alleles of SNPs that are close together tend to be inherited to-gether. A haplotype refers to a set of SNPs found to be statistically associated on a single chromo-some. Haplotypes defined by common SNPs have important implications for identifying disease as-sociation and human traits [3, 19]. Recent studies have shown that the patterns of linkage disequilib-rium (LD) observed in human chromosome reveal a block-like structure [3, 4, 18], and therefore the entire chromosome can be partitioned into high LD regions interspersed by low LD regions. The high LD regions are called haplotype blocks and the low LD ones are referred to as recombination hotspots. Within a haplotype block, there is little or no recombination that occurs and the SNPs are highly correlated. There are only a few common haplotypes, that account for most of the varia-tion from person to person, in a haplotype blocks. Furthermore, each haplotype block, in which the genome is largely made up of regions of low di-versity, can be characterized by a small number of SNPs, which are referred to as tag SNPs [13]. Tag SNPs are aimed at characterizing candidate genes avoiding redundancies in genotyping. Most of the tag SNP selection strategies are haplotype based. The aim is to identify a minimal subset of SNPs that can characterize the most common haplotypes [18, 24]. The characteristics of hap-lotype blocks and tag SNPs are very important and useful for medicine and therapy. Studying on haplotype blocks and tag SNPs not only decrease the cost for detecting inherited diseases but also
has many contributions for classifying the race of human and researching on species evolution. Diversity functions
Several operational definitions have been used to identify haplotype-block structures, includ-ing LD-based [4, 22], recombination-based [12, 23], information-complexity-based [1, 14, 6] and diversity-based [2, 18, 25] methods. The result of block partition and the meaning of each haplotype block may be different by using different measur-ing formula. For simplicity, haplotype samples can be converted into haplotype matrices by assigned major alleles to 0 and minor alleles to 1.
Definition 1 (haplotype block diversity) Given an interval [i, j] of a haplotype matrix A, a diversity function, δ : [i, j] → δ(i, j) ∈ R is an evaluation function measuring the diversity of the submatrix A(i, j).
Haplotype blocks are the genome regions with high LD, thus it implies that no matter what kinds of haplotype block definition we used, the patterns of haplotype within the block will be small, and the diversity of the block will be low. In terms of diversity functions, the block selection prob-lem can be viewed as finding a segmentation of given haplotype matrix such that the diversities of chosen blocks satisfy certain value constraint. Following we examine several haplotype block di-versity evaluation functions. Given an m × n hap-lotype matrix A, a block S(i, j) (i, j are the block boundaries) of matrix A is viewed as m haplo-type strings; they are partitioned into groups by merging identical haplotype strings into the same group. The probability pi of each haplotype
pat-tern si, is defined accordingly such that
P pi= 1.
As an example, Li [15] proposes a diversity for-mula defined by δD(S) = 1 − X si∈S p2i. (1)
Note that δD(S) is the probability that two
hap-lotype strings chosen at random from S are dif-ferent from each other. Other measurements of diversity can be obtained by choosing different diversity function; for example, to measure the information-complexity one can choose the infor-mation entropy (negative-log) function [1, 14, 6]:
δE(S) = −
X
si∈S
pilog pi. (2)
In the literatures [18, 24, 25], Patil and Zhang et al. define a haplotype block as a region where at least 80% of observed haplotypes within a block must be common haplotype. As the same defini-tion of common haplotype in the literatures, the coverage of common haplotype of the block can be formulated as a form of diversity:
δC(S) = 1 − P si∈C pi P si∈U pi = P si∈M 1 m P si∈U pi . (3)
Here U denotes the unambiguous haplotypes, C denotes the common haplotypes, and M denotes the singleton haplotypes. In other words, Patil et al. require that δC(S) ≤ 20%.
Some studies [4, 28, 26] propose the haplotype block definition based on LD measure D0; however,
there is no consensus definition for it so far. Zhang and Jin [28] define a haplotype block as a region in which all pair-wise |D0| values are not lower than
a threshold α. Let S denote a haplotype interval [i, j]. We define the diversity as the complement of minimal |D0| of S. By the definition, S is a
haplotype block if its diversity is lower than 1 − α. δL1(S) = 1 − min{(|D0i0j0|)|i ≤ i0< j0≤ j}. (4)
Zhang et al. [26] also propose the other definition for haplotype block; they require at least α pro-portion of SNP pairs having strong LD (the pair-wise |D0| greater than a threshold) in each block.
Similarly, we can use the diversity to redefine the function. We define the diversity as the proportion of SNP pairs that do not have strong LD. There-fore, haplotype interval S is a feasible haplotype block if its diversity is smaller than a threshold. We can use the following diversity function to cal-culate the diversity of S. Here N (i, j) denotes the number of SNP pairs that do not have strong LD in the interval [i, j].
δL2(S) = ¡N (i, j)(j−i)+1
2
¢ = 1 N (i, j) 2[(j − i)2+ j − i]
. (5) Diversity measurement usually reflects the activ-ity of recombination events occurred during the evolutionary process. Generally, haplotype blocks with low diversity indicates conserved regions of genome.
Definition 2 (monotonic diversity) A diver-sity function δ is said to be monotonic if, for any haplotype block (interval) I = [i, j] of A, it follows that δ(i0, j0) ≤ δ(i, j) whenever [i0, j0] ⊂ [i, j]; that
is, the diversity of any subinterval of I is always no larger than the diversity of I.
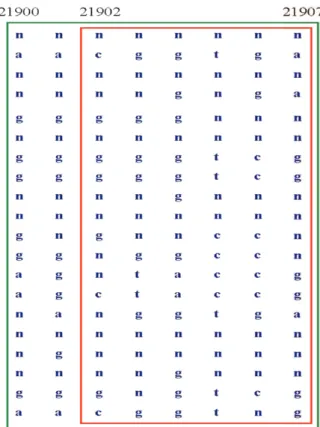
It is easily verified that many diversity functions, including the diversity functions (1) and (2), are monotonic. However, the evaluative function of common haplotype proposed by Patil et al. [18] does not satisfy the monotonic property when the haplotype sample has missing data. For example, in Figure 1, it is a small portion of human chro-mosome 21 haplotype sample provided by Patil, here n denotes the missing data. We can observe
that the coverage of common haplotype of interval [21900,21907] is 9/10, more than 80%. Therefore, according to the definition proposed by Patil et al., it is a feasible haplotype block. On the other hand, the coverage of common haplotype of inter-val [21902,21907] is 3/7, less than 80%, so it is not a feasible haplotype block. Note that interval [21900,21907] and interval [21902,21907] are two intervals terminated at the same SNP locus, and interval [21900,21907] which has more SNPs is a feasible haplotype block but interval [21902,21907] is not.
Figure 1: The evaluative function of common hap-lotype does not satisfy the monotomic property when the haplotype sample has missing data.
Tag SNPs can capture most of the haplotype diversity in the blocks, and therefore could poten-tially capture most of the information for associ-ation between a trait and the SNP marker loci.
We can figure out the diversity and features of each haplotype block easily and economically by using tag SNPs. For these reasons, we want to define the haplotype structure by using tag SNPs as fewer as possible. In previous studies, Patil et al. [18] defined a haplotype block as a region in which a fraction of percent or more of all the ob-served haplotypes are represented at least n times or at a given threshold in the sample. They ap-plied the optimization criteria outlined by Zhang et al. [24, 25] and describe a general algorithm that defines block boundaries in a way that mini-mizes the number of tag SNPs that are required to uniquely distinguish a certain percentage of all the haplotypes in a region. Patil et al. have developed a greedy algorithm and identified a total of 4,563 tag SNPs and a total of 4,135 blocks to define the haplotype structure of human chromosome 21. In each block they required at least 80% of haplo-type must be represented more than once in the block. In addition, Zhang et al. [24] used a dy-namic programming approach to reduce the num-bers of blocks and tag SNPs to 2,575 and 3,582, respectively.
Patil and Zhang’s algorithms both partition the haplotype sample in to blocks fully under the cir-cumstances of requiring minimal number of tag SNPs. However, when resources are limited, in-vestigators and biologists may not be able to geno-type all the tag SNPs and instead must restrict the number of tag SNPs used in their studies. In this paper, we propose several dynamic programming algorithms concerning haplotype block partition problems.
Problem 1 (longest-blocks-t-tags) Given
limit D, we wish to find a list of feasible blocks whose total tag SNP numbers is less than t such that the total length is maximized. That is, output the set S = {B1, B2, . . . , B|S|} such
that (∀Bi ∈ S)(δ(Bi) ≤ D) and
P
tag(Bi) ≤ t;
tag(Bi) denote the number of tag SNPs required
for block Bi, so that |B1| + |B2| + · · · + |B|S|| is
maximized.
In our previous study [16], we show that assum-ing all of the feasible blocks and tag SNPs required for each block have been preprocessed, the longest-blocks-t-tags problem can be solved in O(tL) time and O(tn) space, here L denotes the total number of feasible blocks and n represents the total num-ber of SNPs. In this paper, we propose a linear space algorithm for the same problem.
2
Method
In this section, we show dynamic programming algorithms to partition haplotype blocks with con-straints on diversity and tag SNP number. That is, we want to find the longest segmentation S con-sist of some blocks with the diversity of each block is less than an upper limit D and the total number of tag SNPs required for these blocks does not ex-ceed a specific number t. This problem had been discussed by Zhang et al. [27], but here we propose a more time-efficiency and linear space algorithm to solve the problem. The problem definition is shown in Problem 1.
Our algorithm begin with the preprocessing of the farthest site (good partner) [17] for each SNP marker. According to the haplotype block defi-nition in Patil [18] and the discussion in previous section, we know that the common haplotypes
cov-erage evaluation function is not monotonic. That is, for each SNP marker j there will be a left far-thest marker i so that [i, j] is the longest haplo-type block among all feasible blocks that termi-nated at site j, but some interval [i0, j] ⊂ [i, j]
are not feasible blocks. Thus, before the compu-tation of finding the longest segmencompu-tation using limited tag SNPs, we need to preprocess the set of left good partners Li for each SNP marker i,
Li = {x|[x, i] is a feasible haplotype block}. We
can use the event list [17, 20] which is computed by techniques of suffix tree [7, 21] and lowest common ancestor (LCA) [9] to find the Lifor each SNP
lo-cus i in O(mn), linear proportional to the input size of haplotype matrix, time. Furthermore, we also need to pre-compute the number of tag SNPs required for each feasible haplotype block. This problem can be solve by using the algorithm de-scribed in section 2.1. The time complexity of the algorithm is O(2t0L); here L is the number of all
feasible blocks, and t0is the maximum number of tag SNPs required among all feasible blocks. In our experience, the preprocessing will need much time, however, we just need to compute it once.
2.1
Tag SNP Selection Algorithms
According to the haplotype block definition de-fined by Patil et al. [18], they require that at least ρ = 80% of unambiguous haplotypes are repre-sented more than once. Using the same criteria as in Patil [18], for each block, we want to minimize the number of SNPs that distinguish uniquely at least ρ percentage of the unambiguous haplotypes in the block. Those SNPs can be thought of as a signature of the haplotype block partition.
num-Figure 2: An example of a longer block but re-quired few tag SNPs.
ber of tag SNPs required increases as the length of haplotype block increases in general, there are exceptions to the case. As an example shown in Figure 2, the block a which consisted of 3 SNP markers needs 3 tag SNPs to distinguish each hap-lotype uniquely, but the block b which consisted of 4 SNP markers just needs 2 tag SNPs (i.e. column 2 and column 4.)
The problem of finding the minimum number of tag SNPs within a block to uniquely distinguish all the haplotypes is known as the MINIMUM TEST SET problem, which has been proven to be NP-Complete [5]. Thus, there are no polynomial time algorithms that guarantees to find the optimal so-lution for any input. Although, some approxima-tion algorithms such as the greedy algorithm have been proposed but may fail to find the optimal solution [11, 30, 29]. In order to find the opti-mal solution, we adopt the brute force method to find tag SNPs within a block. Our strategy for selecting the tag SNPs in haplotype blocks is as the following. First, the common haplotypes are grouped into k distinct patterns by merging the compatible haplotypes in each block. After the missing data are assigned in each group, we decide the least number of tag SNPs required based on the least number of haplotype groups needed to be
distinguished such that haplotypes in these groups contain at least ρ percentage of the unambiguous haplotypes in the block. Finally, we select a loci set consisted of minimum number of SNPs on the haplotypes such that at least ρ percentage of the unambiguous haplotypes can be uniquely distin-guished; the exhaustive searching method can be used very efficiently since the number of tag SNPs needed for each block is usually modest in the situ-ation. The exhaustive searching algorithm shown in Figure 3 enumerates next t-combination in lexi-cographic order to generate the next candidate tag SNP loci set until each pattern can be uniquely distinguish.
2.2
Longest Blocks Partition Using
Limited Number of Tag SNPs
In our previous study [16], given an m×n haplo-type matrix, after the preprocessing of left farthest site for each SNP marker and tag SNPs required for each feasible blocks, we show that finding the longest blocks covered by t tag SNPs can be found in O(tL)(or O(tnl)) time; here t denotes the num-ber of tag SNPs used, and L =Pni=1|Li| denotes
the total number of feasible blocks. The results are summarized as following.
Let f (i, t) define the length of the longest seg-mentation of haplotype matrix A(1, i) covered by
t tag SNPs, and tag(i, j) denote the number of tag
SNPs required for block which is bounded by sites
i and j. It is interesting to note that f (i, t) can be
computed by the following recurrence relation:
f (1, 0) = ½ 0 if tag(1, 1) > 0 1 if tag(1, 1) = 0 f (1, t) = 1 if t ≥ 1 f (i, t) = −∞ if t < 0 f (i, t) =
FindTag(B, ρ) . Find the number of tag SNPs required for haplotype block B such that ρ percentage of unambiguous haplotypes in B can be distinguished uniquely.
Input: A percentage ρ and haplotype block B with unambiguous haplotype pattern P = {p1, p2, . . . , pk}; the haplotypes number in each pattern is n1, n2, . . . , nk.
Output: The tag SNPs required for haplotype block B. 1 Sort k haplotype patterns in P = hp1, p2, . . . , pki.
. pi’s are listed in decreasing order of the number of haplotype strings.
2 U = ρ · (Pki=1ni) . U is the number of ρ percentage of unambiguous haplotypes.
3 Find the minimum number g such thatPgi=1ni≥ U
4 t ← dlog2ge . t is the minimum number of tag SNPs required.
5 for i ← 1 to t − 1 do . initiate the tag SNP loci set {a[1], a[2], . . . , a[t]}. 6 a[i] ← i
7 a[t] ← a[t − 1]; h ← 0
8 while h < U do . h is the total haplotype strings that can be distinguished. 9 i ← t . generate the next t-combination in lexicographic order. 10 while a[i] = l − t + i do . l is the length of haplotype string .
11 i ← i − 1 12 if i = 0 13 t ← t + 1 14 for i ← 1 to t do 15 a[i] ← i 16 else 17 a[i] ← a[i] + 1 18 for j ← i + 1 to t do 19 a[j] ← a[i] + j − i
20 h ←Pnx, x ∈ {x|px is the haplotype that can be distinguished by tag SNP.}
21 return t
Figure 3: The exhaustive searching algorithm for tag SNPs selection.
max f (i − 1, t) maxk∈Li ½ (i − k + 1)+ f (k − 1, t − tag(k, i)) ¾ (6)
The maximized segmentation S between sites 1 and i will have two cases, either the site i is included in the last block of S or not. If site i is not included in the last block of S, it will find S between sites 1 and i−1, otherwise there will exist a site k ∈ Li such that [k, i] is the last block of S.
In the latter case, the tag SNPs required for the bock [k, i] is tag(k, i) which has been calculated in preprocessing, so we can find other blocks which are covered by other t−tag(k, i) tag SNPs between sites 1 and k − 1.
Note that if l is the average number of |Li| for
each SNP marker i, f (i, t) will be able to be deter-mined in O(l) time suppose f (1..(i − 1), t)’s and f (·, 1..(t−1))’s being ready. It follows that f (·, t)’s can be calculated from f (·, 1..(t − 1))’s totally in O(nl) time. Thus a computation ordering from f (·, 1)’s, f (·, 2)’s, . . . , to f (·, t)’s leads to the fol-lowing result.
Theorem 1 (longest-blocks-t-tags) Given a haplotype matrix A, a diversity upper limit D and the number of tag SNP t, find a segmen-tation S consisted of k feasible blocks such that (∀i)(δ(Bi) ≤ D) and
P
tag(Bi) ≤ t, so that the
total length of S is maximized can be done in O(tnl) time after the preprocessing of Li and
tag(k, i)’s, k ∈ Li, for each SNP marker i.
The recurrence relation has been used to de-velop a dynamic programming algorithm, the al-gorithm also can be viewed in [16]. We must point out that the algorithm also can be used to parti-tion haplotypes into blocks with a fixed genome coverage, that has been discussed by Zhang et al. [27]. We can define the length of block B = [i, j] as the actual length of the genome span-ning form the i-th SNP to the j-th SNP. Given an m × n haplotype matrix of a chromosome of length G and a percentage α ≤ 1, find a segmenta-tion S = {B1, B2, . . . , B|S|} with the total length
`(S) ≥ αG such that the total tag SNPs required is minimized; the recurrence relation f (1, n, t) is a block length evaluation function, given n, we can increase the value of f (1, n, t) by increasing the value of t until f (1, n, t) ≥ αG. After finding the t such that f (1, n, t) ≥ αG, we can get the bound-aries of each block by tracing back.
2.3
Linear Space Algorithms
In section 2.2, given an m × n haplotype ma-trix A, a diversity upper limit D, and a specific number of tag SNPs t, we propose an O(tnl) (or O(tL)) time algorithm for finding the longest seg-mentation S containing blocks with the diversity of each block is no greater than D and the total tag SNPs number required for these blocks does not exceed t. We apply the dynamic programming technique to general case and obtain the following recurrence relation. Note that f (i, j, t) define the length of the longest segmentation of haplotype
matrix A(i, j) covered by t tag SNPs. f (i, i, 0) = ½ 0 if tag(i, i) > 0 1 if tag(i, i) = 0 f (i, i, t) = 1 if t ≥ 1 f (i, j, t) = −∞ if t < 0 f (i, j, t) = −∞ if j < i f (i, j, t) = max f (i, j − 1, t) maxk∈Lj ½ (j − k + 1)+ f (i, k − 1, t − tag(k, j)) ¾ (7)
Lemma 1 Given an m × n haplotype matrix A, a diversity upper limit D, and the number of tag SNPs t, for an any constrained interval [i, j], 1 ≤ i ≤ j ≤ n, find a segmentation consisted of k feasible blocks such that (∀i)(δ(Bi) ≤ D) and
P
tag(Bi) ≤ t, so that the total length of S is
maximized can be done in O(|j − i|lt) time after the preprocessing of Li and tag(k, i)’s, k ∈ Li, for
each SNP marker i.
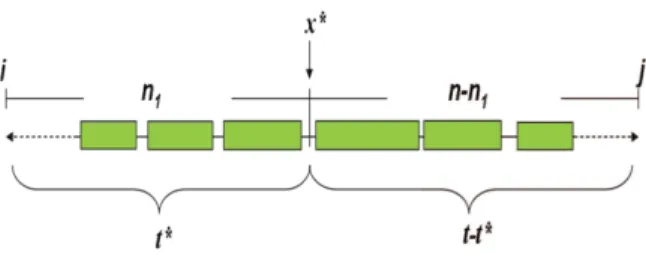
Clearly, the space complexity of our algorithm shown in [16] is O(tn) for the retrieval of the boundaries of each block by tracking back. Such space requirement results in practiced difficulties in cases where t and n become too large. For the reason, we need to have a space-efficiency algo-rithm to solve the problem. Using the similar con-cept as in [10], we find a cut-point x∗ to divide n
SNP sites into two parts, n1 and n2, and use t∗ tag SNPs for n1and the other t − t∗ tag SNPs for
n2 such that the total size of blocks covered by t∗ tags in n1 and blocks covered by t − t∗ tags in n2 is maximized. We obtain the following recurrence relation.
Figure 4: Illustration of the idea of recurrence
f (i, j, t).
The idea behind the recurrence relation is illus-trated at Figure 4. Note that in order to make the total size of blocks tagged by t∗ SNPs and t − t∗
SNPs maximized, we can not assign a half of t to t∗ directly, because in some case, the bt
2c-th
and the (bt
2c + 1)-th SNP will be used to tag the
same block which is the member of the longest seg-mentation. If we use the first to the bt
2c-th SNPs
to tag the blocks in n1, and use the (b2tc + 1)-th
to the t-th SNPs to tag the blocks in n2, we will
not get the longest segmentation on n SNPs. In general case, there will be many pairs of t∗ and x∗ solutions which fit our request. For the
pur-pose of time efficiency, we want to make x∗ and t∗ to approach the half of n and t as far as
pos-sible. Let t0 denote the maximum number of tag
SNPs required among all feasible blocks. In or-der to find the appropriate value of t∗ and x∗, we
can examine t∗ in t
0 continuous possible values,
bt 2c − b t0 2c ≤ t∗≤ b2tc + d t0 2e, and examine x∗ in
all SNPs loci for each selection of t∗. Since t
0 is
small in general case, we can find the t∗ and the x∗quickly. After finding the appropriate values of t∗ and x∗, we can execute the steps recursively to
partition the original problem to two subproblems repeatedly. Until t ≤ t0, we just use the dynamic
programming algorithm shown in [16] to solve each subproblem. Here we can trace back to output the boundaries of each block. The algorithm is shown in Figure 5.
Theorem 2 (longest-blocks-t-tags) Assume
the maximum number of tag SNPs required among all feasible blocks, t0, is a fixed constant.
Given a haplotype matrix A, a diversity upper limit D, and the number of tag SNPs t, find a segmentation S consisted of k feasible blocks such that (∀i)(δ(Bi) ≤ D) and
P
tag(Bi) ≤ t, so that the total length of S is maximized can be done in O(tnl) time and using linear space after the preprocessing of Ri, Li and tag(k, i)’s, k ∈ Li, for each SNP marker i.
Proof. We propose an O(tnl) time algorithm,
LisTag(i, j, T ), shown in Figure 5. The correct-ness of the algorithm can be shown as follow. When T ≤ t0, the algorithm uses the dynamic
programming algorithm shown in [16] to compute
f (i, j, T ) and output the boundaries of each blocks
by tracing back. If T > t0, we must find a x∗
be-tween sites i and j, and find a t∗ between 0 and T . Subsequently, we can find a maximum
seg-mentation S1 tagged by t∗ SNPs between sites i
and x∗ and a maximum segmentation S
2 tagged
by T − t∗ SNPs between sites x∗+ 1 and j so that
the total size of S1 and S2 is equal to S which is
the maximum segmentation tagged by T SNPs be-tween sites i and j. In general case, there will be many pairs of t∗ and x∗solutions which fit our
re-quest. For the purpose of time efficiency, we want to make x∗ and t∗ to approach the half of n and t
as far as possible. In order to find the appropriate values of t∗and x∗, we can examine t∗in t
0
contin-uous possible values, bt
2c − bt20c ≤ t∗≤ b2tc + dt20e,
and examine x∗in all SNPs loci for each selection
of t∗. In the case of T > t
0, we first compute
f (i, x, t)’s and f (x + 1, j, T − t)’s, i ≤ x ≤ j − 1, bt
2c − dt20e ≤ t ≤ b2tc + dt20e, and put the result
into two two dimensional arrays A and B. Note that the computation of f (x+1, j, T −t)’s uses the similar idea with opposite direction as the compu-tation of f (i, x, t)’s; we use the right good partners
Ri, Ri = {x|[i, x] is a feasible haplotype block},
to compute f (x + 1, j, T − t)’s from x = j − 1 down to x = i. Then we can find x∗ and t∗ such
that the total length of blocks tagged by t∗ tag
SNPs between sites i and x∗ and blocks tagged by T − t∗tag SNPs between sites x∗+ 1 and j is
max-imized. That is, we can find x∗ and t∗ such that f (i, x∗, t∗)+f (x∗+1, j, T −t∗) is maximized. Next
steps we use recursive algorithm LisTag(i, x∗, t∗)
and LisTag(x∗+ 1, j, T − t∗) to list blocks tagged
by t∗ SNPs in [i, x∗] and blocks tagged by T − t∗
SNPs in [x∗+ 1, j].
In the algorithm, we use five global data struc-tures involving arrays E, F , S, A, and B. Arrays
E and F are used to store the good partner points Li and Ri for each SNP marker i, and array S
is used to store the tag SNPs required for each feasible blocks. The data in E, F and S arrays were calculated in preprocessing, and the space of each array is L, the number of all feasible blocks. In addition, we use two dimensional array A for computing f (i, x, 0..bT
2c + dt20e)’s and B for
com-puting f (x + 1, j, 0..bT
2c + dt20e)’s. Note that the
computation of f (i, j, t) will compare the values of
LisTag(i, j, T ) . List blocks covered by T tag SNPs in [i, j] with maximized total length. Input: Interval [i, j] and number of tag SNPs T .
Output: The boundaries of blocks covered by T tag SNPs.
Global variable: E, F , S, A, B. . E and F are used to store the good partner pointers Li and
Riwhich have been preprocessed dependent on diversity constraints D,
S is used to store the tag SNPs required for each feasible blocks, two dimensional arrays A and B are global temporary working storages. 1 if T ≤ t0 then
2 for t ← 0 to T do 3 for x ← i to j do
4 Directly compute A[t, x] = f (i, x, t) according to recurrence relation 7. 5 Trace back on A array to output the boundaries of blocks covered by T tag SNPs. 6 return
7 for t ← 0 to bT
2c + dt20e do
. Compute A[t mod (t0+ 1), x] = f (i, x, t), ∀x ∈ [i..j − 1], t ∈ [bT2c − bt20c..bT2c + dt20e]. 8 for x ← i to j − 1 do
9 Compute A[t mod (t0+ 1), x] = f (i, x, t) by formula 7. 10 for t ← 0 to bT
2c + dt20e do
. Compute B[t mod (t0+ 1), x] = f (x + 1, j, t), ∀x ∈ [i..j − 1], t ∈ [bT2c − bt20c..bT2c + dt20e]. 11 for x ← j down to i + 1 do
12 Compute B[t mod (t0+ 1), x] = f (x, j, t) by formula 7 with opposite direction. 13 Find (x∗, t∗) = arg max
i≤x≤j,bT
2c−bt02c≤t≤bT2c+dt02e{A[t, x] + B[T − t, x]}.
. Pointer back tracking to find the x∗, and t∗
14 LisTag(i, x∗, t∗) . recursive call to report blocks in interval [i, x∗] with t∗ tags.
15 LisTag(x∗+ 1, j, T − t∗) . recursive call to report blocks in interval [x∗, j] with T − t∗ tags.
Figure 5: The O(nlt) time and linear space algorithm for haplotype blocking with constraints on diversity and the number of tag SNPs.
Therefore, if t0 denotes the maximum tag(k, j), the maximum number of tag SNPs required among all feasible blocks, we at most need to store the val-ues of f (·, ·, (t − t0)..(t − 1)) and f (i, j − 1, t) while compute the value of f (i, j, t). In our experience, we know that the t0 will be equal to 8 at most as an example of Patil’s haplotype data. It means that the space of two dimensional arrays A and B is t0×n, so the space complexity for the algorithm is O(L + t0n). Since t0is generally a constant and
L > n in most practical cases, we can prove the space used by the algorithm is O(L + n).
The time complexity of the algorithm is O(nlt) as shown in the following by induction. Let T (n, t) denotes the time needed for LisTag(1, n, t). As-sume that T (n0, t0) ≤ c
2n0lt0 for all n0< n, t0< t. According to the algorithm, we have:
T (n, t) = c| {z }1nlt line 7-13 + T (n1, t∗) | {z } line 14 + T (n − n1, t − t∗) | {z } line 15 By induction, T (n, t) ≤ c1nlt + c2n1lt∗+ c2(n − n1)l(t − t∗) ≤ l(c2nt + c1nt + 2c2n1t∗− c2n1t − c2nt∗) ≤ l[c2nt + (53c2n1t∗− c2n1t) +(c1nt +13c2n1t∗− c2nt∗)] ≤ l[inc2nt + c2n1(53t∗− t) + (c1nt +13c2nt − c2nt∗)] ≤ l{c2nt + c2n1[35(b2tc + dt20e) − t] +(c1+13c2)nt − c2n(bt2c − dt20e)} ≤ l{c2nt + c2n1[35(2t+t20 + 1) − t] +(c1+13c2)nt − c2n(2t−t20 − 1)} ≤ l[c2nt + c2n1(56t0+53−16t) + (c1+13c2)nt −1 2c2nt + c2n(t20 + 1)] ≤ l[c2nt + c2n1(56t0+53−16t) +104c2nt −12c2nt +c2n(t20 + 1)](Let c1= 151c2) ≤ l[c2nt + c2n1(56t0+35−16t) + c2n(t20+ 1 − 10t)] ≤ c2nlt
Let t ≥ 5t0+ 10, the above inequality will come into existence, so we can prove the time complexity
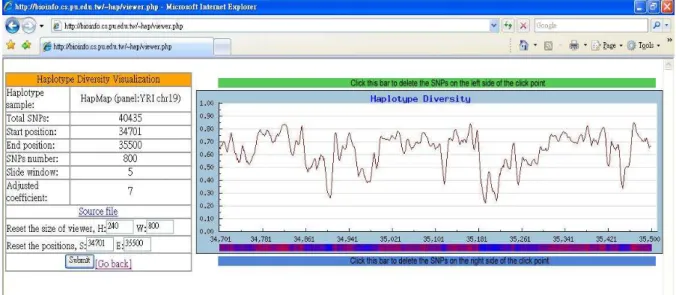
Figure 6: A view of the haplotype sample – HapMap phase II haplotypes, chr19 in the YRI panel – by diversity visualization tool.
3
Experimental Results and
Diver-sity Visualizations
In response to needs for analysis and obser-vation of human genome variation, we have es-tablished a website and apply the algorithms de-scribed in this paper to provide several analy-sis tools for bioinformatic and genetic researchers. The web-based system consists of a list of PHP and PERL CGI-scripts together with several C programs for selecting haplotype blocks and an-alyzing the haplotype diversity. We also collect the haplotype data of human chromosome 21 from Patil et al. [18] and download haplotypes for all the autosomes from phase II data of HapMap [8] so that the bioinformatic researchers can use the data to evaluate the performance of the tools. On the other hand, researchers also can input their own haplotype data by pasting the haplotype sample or uploading the file of haplotype sample, or in-put the address of other websites’ haplotype data. The website provides tools to examine the di-versity of haplotypes and partition haplotypes into blocks by using different diversity functions. By using the diversity visualization tool, researchers can observe the diversity of haplotypes in the form of the diagram of curves. The tool uses the di-versity function (1), δD, to calculate the
diversi-ties of all intervals. Figure 6 shows an example of the diversity visualization of the haplotype sample downloaded from HapMap.
The website also provides the tools for
re-searchers to partition haplotypes into blocks with constraints on diversity and tag SNP number; by using the tool, researchers can find the longest seg-mentation consists of non-overlapping blocks with limited number of tag SNPs. Researchers can up-load a haplotype sample or select a sample from our database, and then input a number of tag SNPs to partition the sample. As an example; we pick the shortest contig of Patil’s haplotype sam-ple (contig number: NT 001035, 69 SNPs) and paste to the system; applying the diversity func-tion (3), δC, and requiring the diversity must not
be greater than 0.2 (at least 80% of common haplo-type) in each block; using 10 tag SNPs, the sample can be partitioned into 19 haplotype blocks, and there are total of 61 SNPs in these blocks.
In order to test our program, we also apply our block partition tools which can be used to find the longest segmentation covered by the minimum number of tag SNPs to the haplotype data of hu-man chromosome 21 from Patil et al. [18]. Using the tool with the diversity function (3), δC, and
the same criteria as in Patil (80% of common hap-lotype coverage), when the haphap-lotype sample is partitioned into blocks fully, a total of 3,260 tag SNPs and a total of 2,266 haplotype blocks are identified. In contrast, Patil et al. [18] identified a total of 4,563 tag SNPs and a total of 4,135 blocks, and Zhang et al. [24] identified a total of 3,582 tag SNPs and a total of 2,575 blocks. Our program reduces the number of tag SNPs and blocks by 28.6% and 45.2% comparing to Patil et al.. We
No. of blocks Average no.
Common No. of requiring ≥ 1 common All Common
Method SNPs/block blocks SNPs haplotype/block blocks(%) SNP(%)
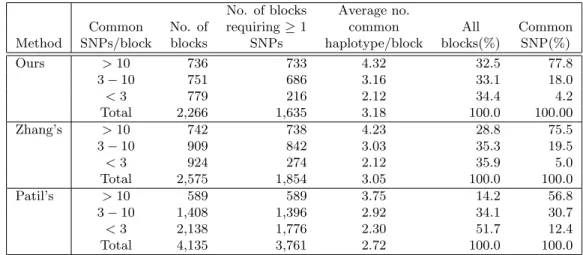
Ours > 10 736 733 4.32 32.5 77.8 3 − 10 751 686 3.16 33.1 18.0 < 3 779 216 2.12 34.4 4.2 Total 2,266 1,635 3.18 100.0 100.00 Zhang’s > 10 742 738 4.23 28.8 75.5 3 − 10 909 842 3.03 35.3 19.5 < 3 924 274 2.12 35.9 5.0 Total 2,575 1,854 3.05 100.0 100.0 Patil’s > 10 589 589 3.75 14.2 56.8 3 − 10 1,408 1,396 2.92 34.1 30.7 < 3 2,138 1,776 2.30 51.7 12.4 Total 4,135 3,761 2.72 100.0 100.0
Table 1: The comparison of properties of haplotype blocks defined by Zhang, Patil and us with 80% of common haplotype coverage.
also demonstrate that the results of Zhang et al. are not optimum.
Table 1 shows the comparison of properties of haplotype blocks defined by Zhang, Patil and us with 80% coverage of common haplotype. Our program discovers a total of 736 blocks containing more than 10 SNPs per block. The blocks with more than 10 SNPs account for 32.48% of all of blocks. The average number of SNPs for all of the blocks is 10.61. The largest block contains 128 common SNPs, which is longer than the largest block (containing 114 SNPs) identified by Patil et al. and the same as in Zhang et al.. Figure 7 shows the partition results of the Patil’s haplotype sample; each block boundaries and the summaries of the analysis are shown in the frame on the left, and the contents of each block are shown in the frame on the right.
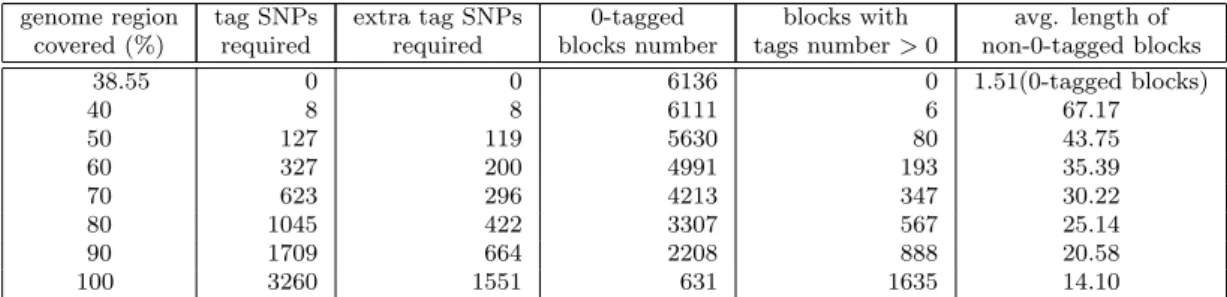
Furthermore, Tables 2 and 3 show more anal-ysis data of our experimental results. According to the results, we can partition 38.55% of genome region into blocks where does not require any tag SNPs. This is because that most of these blocks just contain few common SNPs, and there are 80% of unambiguous haplotypes have the same hap-lotype pattern (compatible) in these blocks. We term these SNP loci as non-informative markers because they are the same among most (80%) of population. These data also show that as the genome region covered increases, we need to in-crease more and more extra tag SNPs to cap-ture the haplotype information of the blocks, and the number of zero-tagged blocks becomes fewer. Note that, although the average length of non-zero-tagged blocks becomes shorter as the
chromo-some region covered increase, the average length of total blocks becomes longer.
Both Zhang et al. and we have proposed a dy-namic programming algorithm to solve the prob-lem of finding the longest segmentation with lim-ited tag SNPs. However, it is observed that our algorithm obtains better results than theirs on the same haplotype sample. One of the main reasons is that their algorithm presumes that the common haplotypes evaluation function proposed by Patil et al. satisfy the monotonic property. However, when the haplotype sample has missing data, the diversity function does not satisfy the monotonic property. For example, Figure 8 shows the anal-ysis results of Zhang’s and our algorithms on the same haplotype sample; this sample just has 69 SNPs, which is a small part of Pail’s haplotype data, its contig number is NT 001035. Using the sample criteria (80% of common haplotype), our method can partition the sample into 20 blocks and identify 18 tag SNPs, on the other hand, Zhang’s algorithm partitions the sample into 23 blocks and used 22 tag SNPs. The results are similar in interval [21840,21875], but in interval [21876,21899], our method discovers 3 blocks and 3 tag SNPs, which is better than Zhang’s (6 blocks and 6 tag SNPs). In interval [21900,21908], both Zhang’s and our methods find 2 blocks, but our method just needs 3 tag SNPs rather than 4 that is found by Zhang’s method. These cases demon-strate that Zhang’s algorithm does not find the optimal solution due to the non-monotonic prop-erty of common haplotype evaluation function.
Our web system is freely accessible at http://bioinfo.cs.pu.edu.tw/∼hap/index.php.
Figure 7: Use diversity function δC and require the diversity of blocks must not be greater than 0.2 to
partition Patil’s haplotype data into blocks fully.
tag SNPs genome region extra genome 0-tagged blocks with avg. length of used covered (%) region increased (%) blocks tags number > 0 non-0-tagged blocks
0% (0) 38.55 38.55 6136 0 1.51(0-tagged blocks) 10% (326) 59.99 21.44 4991 192 35.52 20% (652) 70.85 10.86 4145 367 29.37 30% (978) 78.62 7.77 3387 516 26.79 40% (1304) 84.61 5.99 2897 712 22.38 50% (1630) 89.02 4.41 2250 844 21.29 60% (1956) 92.59 3.57 1814 1002 19.41 70% (2282) 95.30 2.71 1478 1159 17.79 80% (2608) 97.29 1.99 1014 1289 16.90 90% (2934) 98.64 1.35 719 1421 15.89 100% (3260) 100.00 1.36 631 1635 14.10
Table 2: The analysis data based on the number of tag SNPs required. genome region tag SNPs extra tag SNPs 0-tagged blocks with avg. length of
covered (%) required required blocks number tags number > 0 non-0-tagged blocks
38.55 0 0 6136 0 1.51(0-tagged blocks) 40 8 8 6111 6 67.17 50 127 119 5630 80 43.75 60 327 200 4991 193 35.39 70 623 296 4213 347 30.22 80 1045 422 3307 567 25.14 90 1709 664 2208 888 20.58 100 3260 1551 631 1635 14.10
Figure 8: The experimental results of Zhang’s and our algorithms on a small part of Patil’s data. Some preliminary results, including the selection of different diversity functions as well as choosing meaningful diversity constraints, in using our tools can also be found in the web system.
4
Conclusion
In this paper, we examine several haplotype di-versity evaluation functions; by using appropriate diversity functions, the block selection problem can be viewed as finding a segmentation of given haplotype matrix such that the diversities of cho-sen blocks satisfy certain value constraint. Tag SNPs can capture most of the haplotype diversity in the blocks, and therefore could potentially cap-ture most of the information for association be-tween a trait and the SNP marker loci. Instead of genotyping all of the SNP markers on the chro-mosome, one may wish to use only the genotype information on the tag SNP. We can figure out the haplotype features of most population by just checking a few SNP markers. Thus, studying the tag SNPs can dramatically reduce the time and effort for genotyping, without losing much haplo-type information.
We present dynamic programming algorithms for haplotype blocks partitioning with constraints on diversity and tag SNP number. In Theorem 1, we show that finding a maximum segmentation with limited tag SNPs number can be done in
O(tnl) time; furthermore, we reduce the space
complexity into O(L + n) by using the algorithm LisTag(i, j, T ). We need to point out that these efficiency results of our algorithms can be applied in many different definition of diversity functions only if we can pre-compute boundaries of all of feasible blocks and tag SNPs required for these blocks.
We also show that the results discovered by our method is superior to Zhang et al.’s [24]. Due to the non-monotonic property of common haplotype evaluation function, we demonstrate that Zhang’s algorithm will not find the optimal solution when the haplotype samples have missing data.
References
[1] Eric C. Anderson and John Novembre. Find-ing Haplotype Block Boundaries by UsFind-ing the Minimum-Description-Length Principle. Am.
J. of Human Genetics, 73:336–354, 2003.
[2] D. Clayton. Choosing a set of haplotype tag-ging SNPs from a larger set of diallelic loci.
Nature Genetics, 29(2), 2001.
[3] M. J. Daly, J. D. Rioux, S. F. Schafiner, T. J. Hudson, and E. S. Lander. High-resolution haplotype structure in the human genome.
Nature Genetics, 29:229–232, 2001.
[4] S. B. Gabriel, S. F. Schaffner, H. Nguyen, et al. The structure of haplotype blocks in the human genome. Science, 296(5576):2225– 2229, 2002.
[5] M.R. Garey and D.S. Johnson. Computers
and Intractability – A Guide to the Theory of NP-Completeness. Freeman, New York, 1979.
[6] G. Greenspan and D. Geiger.
Model-based inference of haplotype block variation. In Seventh Annual International Conference
on Computational Molecular Biology (RE-COMB), 2003.
[7] D. Gusfield. Algorithms on Strings, Trees and
Sequences: Computer Science and Computa-tional Biology. Cambridge University Press,
[8] International HapMap Project. http://www.hapmap.org/index.html.en. [9] D. Harel and R. E. Tarjan. Fast algorithms
for finding nearest common ancestors. SIAM Journal on Computing, 13(2):338–355, 1984. [10] D. S. Hirschberg. A linear space algorithm for
computing maximal common subsequences. Commun. ACM, 18(6):341–343, 1975. [11] Yao-Ting Huang, Kui Zhang, Ting Chen,
and Kun-Mao Chao. Selecting additional tag SNPs for tolerating missing data in genotyp-ing . BMC Bioinformatics, 6(263), 2005. [12] R. R. Hudson and N. L. Kaplan.
Statisti-cal properties of the number of recombination events in the history of a sample of DNA se-quences. Genetics, 111:147–164, 1985. [13] G. C. Johnson, L. Esposito, B. J. Barratt,
et al. Haplotype tagging for the identifica-tion of common disease genes. Nat Genet., 29(2):233 – 7, Oct 2001.
[14] M. Koivisto, M. Perola, R. Varilo, W. Hen-nah, J. Ekelund, M. Lukk, L. Peltonen, E. Ukkonen, and H. Mannila. An MDL method for finding haplotype blocks and for estimating the strength of haplotype block boundaries. In 8th Pacific Symposium on Biocomputing (PSB), pages 502–513, 2003. [15] W.H. Li and D. Graur. Fundamentals of
Molecular Evolution. Sinauer Associates, Inc, 1991.
[16] Yaw-Ling Lin, Tso-Ching Lee, and Wen-Pei Chen. Dynamic programming algo-rithms for haplotype blocks partitioning with tagSNPs minimization. In Proceedings of the 24rd Workshop on Combinatorial Mathemat-ics and Computation Theory, pages 148–157, Nantou, Taiwan, April 28-29, 2007.
[17] Yaw-Ling Lin and Wei-Shun Su. Identifying long haplotype blocks with low diversity. In Proceedings of the 23rd Workshop on Combi-natorial Mathematics and Computation The-ory, pages 151–159, Changhua,Taiwan, Apr 28-29, 2006.
[18] N. Patil, A. J. Berno, D. A. Hinds, et al. Blocks of limited haplotype diversity revealed by high resolution scanning of human chro-mosome 21. Science, 294:1719–1723, 2001.
[19] J. D. Rioux, M. J. Daly, M. S. Silverberg, K. Lindblad, H. Steinhart, Z. Cohen, et al. Genetic variation in the 5q31 cytokine gene cluster confers susceptibility to Crohn dis-ease. Nature Genetics, 29:223–228, 2001. [20] Wei-Shun Su. A Study on SNP Haplotype
Blocks. Master’s thesis, Providence Univer-sity, Jun 2006.
[21] Esko Ukkonen. On-Line Construction of Suf-fix Trees. Algorithmica, 14(3):249–260, 1995. [22] J.D. Wall and J.K Pritchard. Haplotype blocks and linkage disequilibrium in the hu-man genome. Nature Reviews Genetics, 4(8):587–597, 2003.
[23] N. Wang, J.M. Akey, K. Zhang,
R. Chakraborty, and L. Jin. Distribution of recombination crossovers and the origin of haplotype blocks: the interplay of population history, recombination, and mutation. Am. J. Human Genetics, 71:1227–1234, 2002. [24] K. Zhang, M. Deng, T. Chen, M.S.
Water-man, and F. Sun. A dynamic programming algorithm for haplotype block partitioning. In The National Academy of Sciences, vol-ume 99, pages 7335–7339, 2002.
[25] K. Zhang, Z.S. Qin, J.S. Liu, T. Chen T, M.S. Waterman, and F. Sun. Haplotype block par-titioning and tag SNP selection using geno-type data and their applications to associ-ation studies. Genome Res., 14(5):908–916, 2004.
[26] Kui Zhang, Zhaohui Qin, Ting Chen, Jun S. Liu, Michael S. Waterman, and Fengzhu Sun. HapBlock: haplotype block partitioning and tag SNP selection software using a set of dy-namic programming algorithms. Bioinfor-matics, 21(1):131–134, 2005.
[27] Kui Zhang, Fengzhu Sun, Michael S. Water-man, and Ting Chen. Dynamic programming algorithms for haplotype block partitioning: applications to human chromosome 21 haplo-type data. In RECOMB ’03: Proceedings of the seventh annual international conference on Research in computational molecular bi-ology, pages 332–340, New York, NY, USA, 2003. ACM Press.
[28] Kun Zhang and Li Jin. HaploBlockFinder: haplotype block analyses. Bioinformatics, 19(10):1300–1301, 2003.
[29] Peisen Zhang, Huitao Sheng, and Ryuhei Ue-hara. A double classification tree search algo-rithm for index SNP selection. BMC Bioin-formatics, 5(89), Jul 2004.
[30] W. Zhao, M. L. Fanning, and T. Lane. Effi-cient RNAi-based gene family knockdown via set cover optimization. Artif. Intell. Med., 35(1):61–73, Sep 2005.