Printed in Great Britain. All rights reserved Copyright@ 1993 Pergamon Press Ltd
A Systolic Algorithm
for Dynamic Programming
CHAU- JY LIN
Department of Applied Mathematics, National Chiao Tmrg University Hsinchu, 30050, Taiwan, R.O.C.
(Received and accepted May 1993)
Abstract-we present a formal systolic algorithm to solve the dynamic programming problem for an optimal binary search tree. For a fixed integer j such that 2 5 j 5 n, first we derive a linear systolic array to evaluate the minimal cost Q,j for 1 5 i < j. Then we combine these (n - 1) linear systolic arrays to form a two-dimensional systolic array. The computational model consists of [(n2 + 2n - 4)/4] processing elements. The algorithm requires (2n - 3) time steps to solve this problem. The elapsed time within a time step is independent of the problem size n. It is suitable for the VLSI implementation due to the identical and simple structure of processing elements. We also prove the correctness of this algorithm by induction.
1. INTRODUCTION
In recent years, computer science has devoted much attention to problems related to highly structured computer systems, and their potential applications. Current very large scale integrated (VLSI) technology requires uniformity and regularity in both the processing elements (PEs for short) and their integration on a given chip. These requirements naturally lead one to conceive of a multiprocessor system with a large number of relatively simple and uniform processors interconnected in a regular pattern. A simple computational model of such a system is the systolic array [ 11. A systolic array is a model of parallel computer consisting of rudimentary PEs, each capable of performing some simple operation. Many systolic arrays have been designed to solve some problems [2-51. A parallel algorithm which can be executed on a systolic array is called a systolic algorithm.
The dynamic programming for an optimal binary search tree can be solved sequentially in 0(n3) running time steps for n its problem size [6]. In this paper, we present a formal parallel algorithm, which is executed on a computational model of two-dimensional systolic array, to solve this problem. The operations of each individual PE are designed explicitly. The design procedure to obtain the systolic algorithm is considered in detail. We hope that this concept can be applied to obtain systolic algorithms for solving some other problems.
4 systolic array can be considered as a network which consists of a few types of computational PEs. Since there is no shared memory in our systolic array and the data broadcasting behavior is not allowed, the data transformation between PEs should be handled by some explicit com- munication links. A communication link with a name e-link which joins PEl to PE2 is called an input link of PE2 and an output link of PEl. The data being sent out from PEl via e-link is denoted by eout. The data being received by PE2 via e-link is denoted by ei,. Each PE performs This work was supported partially by the National Science Council in Taiwan, R.O.C. under the contract number NSC 82-0208-M009-22.
“j-lj
WJ wj-2j ‘J-25"j-5j
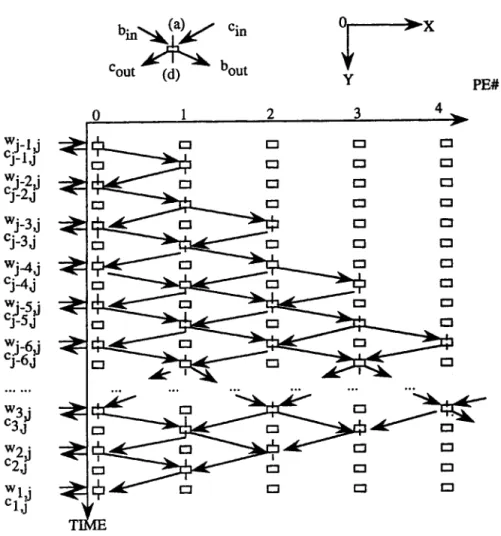
‘J-55 “j-6j ‘J-6J X Y PE#Figure 1. The graph for the dynamic programrm ‘ng problem. the following three tasks:
(1) to receive data from its input links;
(2) to execute one loop of the designed systolic algorithm; (3) to send data to its output links.
The maximal time unit (all PEs are considered) to do these three tasks is called a time step. In our algorithm the elapsed time unit within a time step is constant. Moreover, if the e-link is labeled with 7 delays (denoted by 7D) for 7 a positive integer, it means that when PEl sends out its eout at the time step t, then such eout is the ein of PE2 at the time step t + 7. Our systolic array requires five communication links. Only one of them has 7 = 2; the remaining links have only one delay. The symbol 7D on a link will be omitted when 7 = 1.
2. THE DESIGN PROCEDURE
FOR SOLVING
DYNAMIC
PROGRAMMING
Without loss of generality, the dynamic programming problem for an optimal binary search tree can be stated as follows.
“For 1 5 i < q < j 5 n, find ci,j = wi,j + iyj~j{ci,g + ce,j} where wi,j are the given values; the
initial cost value ci,i+i are considered as the value of w;,i+i for 1 5 i 5 n - 1.”
For any fixed integers i, j with 1 5 i < j 5 n, the process to evaluate the value of the ci,j is considered as follows.
(2)
(3)
(4
Group
the above known cost values into the form ci,q + cq,j. Then two forms of themare Set aS a pair. These pail3 are denoted by Pk = {ci,j-k + cj_k,j, Ci,i+k + ci+k,j} for
1 5 Ic I: [(j - i)/2J.
During the evaluation of ci,j, the above pairs Pk will be referred in the decreasing order of
k.
That is, suppose that Pk is used at the time step i!k, thenk’ < k”
if and only if tkl > tkll.When
PI
is used to evaluate ci,j at a time step tl, the given value wi,j is involved at the time step tl + 1. This tl + 1 is also the time step that ci,j has produced.0 1 2 3
) PE#
Gy I* I, I*
le I*[
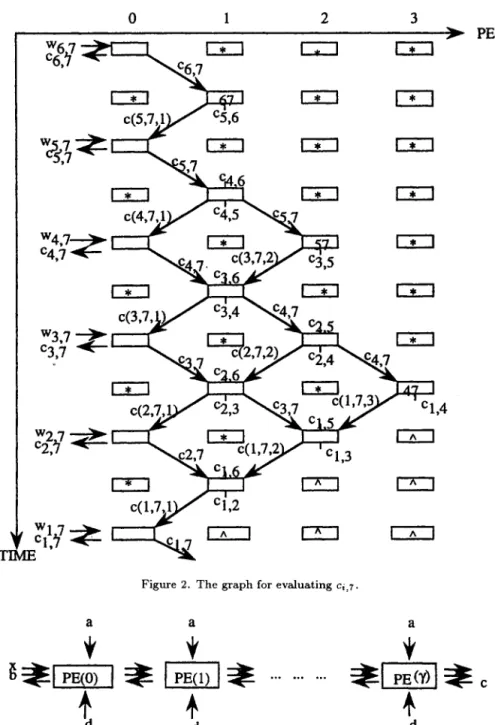
Figure 2. The graph for evaluating c;,~
a
a
aLet 1 = [(j - i)/2J. W e k now that
Pl
is the first pair to be used in order to evaluate the ci,j. Suppose that to is the time step to evaluate the minimal value in4.
We define c(i, j, I) = minPI
and call this c(i,j, I) the P,-partial result of ci,j. Following (I - 1) time steps, the pairs Pk for 1 5 Ic < 1 will be referred within the time interval (tc,tc + I- l] respectively. That is, the Pk- partial result of ci,j which is defined as ~(i,j,k) = min{c(i,j,k+l), ci,j-k+cj_k,j, ci,i+k+Ci+k,j} will be evaluated at the time step to + I- Ic. If we let
c(i, j,
I+ 1) be a large enough number “00,” then the c(i, j, I) can be redefined as the min{c(i,j,l + l), ci,j-l + cj-l,j, ci,i+r + ci+,,j}. Since we have ci,j = c(i,j, 1) + wi,j, this ci,j will be evaluated at the time step to + 1. We define c(i, j, 0) = c(i, j, 1) + wi,j as our desired result ci,j.Let j be a fixed integer such that 2 5 j < n. Under the preceding description to evaluate the ci,j, we design a linear systolic array to produce the value of ci,j for 1 < i < j. First, an ly-plane with integer coordinates is chosen. The z-axis is the index of PE and the y-axis the time step (see Figure l), where each PE will be referred to as PE(c, t) for z 2 0 and t 2 1. The solving strategy of evaluating ci,j is described as follows.
(1) From the description of the dynamic programming problem and the order of Pk to be referred, we know that the computation of ci,j requires the value of cu,j for i < u. Thus, when cu,j coming from a PE( 0, t), we need one communication link (say b-link) to transmit such cu,j p assing through PE(0, t), PE(l, t + l), . . . , to PE(r, t + r) for r = j - u. Then this cu,j will be stored in a register, say E, of PE(r, t + r) in order to evaluate the follow- ing Cvf for 15 21 < u.
(2) Since the value of c, ,j is propagating on the b-link for (j-u) time steps, and then this cu,j will be stored in a register of a PE, we need a control link (say z-link) to indicate that at what time step this cu,j will be stored in the register E.
(3) The &partial results c(i, j, k) of ci,j for 1 5 k: 5 [(j - i)/2] are transmitted on a link (say c-link) from PE(t,t) to PE(k - 1, t + l), in order to be used to evaluate the following Pk-i-partial results c(i, j, /c - 1) of the Ci,j.
The diagram of our designed consideration is shown in Figure 1, where b-link, z-link (not shown) and c-link have one delay of time step. The symbols (u) and (d) appearing in Figure 1 mean that these two corresponding input values are received from the output links of other linear arrays which are evaluating the c,,, for 1 5 CY < u < j. An illustrative example with j = 7 is shown in Figure 2, where the numbers 67, 57, 47 appearing respectively in three PEs mean that at the time steps 2, 5, 8, these PEs have stored cs,r, cg,r, c4,7 in their registers, respectively. The symbols “*” and “^” mean that PEs are in waiting and stopping states, respectively.
Figure 1 is projected along the time axis (y-axis) to obtain a linear systolic array as shown in Figure 3, where the cij comes out from PE(0) at the time step t = 2(j - i) - 1 for 1 5 i < j. There are y + 1 PEs to be used with y = [j/2] - 1. In Figure 3, once the ci,j comes out, it is transmitted along the b-link for (j - ;) time steps and finally it is stored in the register E of PE(j - i) provided that this PE exists. Since the control link x-link (having the same direction of b-link) is used to indicate that this ci,j will be stored in the register E of PE(j - i) at the time step t = 3(j - i) - 1, we let the zin = (j - i) in PE(0) at the time step t = 2(j - i) - 1. When the ci,j is propagating on the b-link, the value on the z-link is decreased by one at each time step. This implies that if zin = 1 is recognized by the PE(j - i) then this PE stores its bin into its register E.
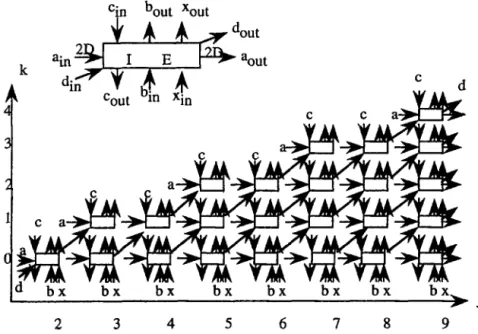
From the above design with 2 5 j 5 n, we obtain (n - 1) linear systolic arrays each consisting of [j/2] PEs. We combine these (n - 1) linear systolic arrays to form a two-dimensional array as shown in Figure 4, where ci,j comes out from the c-link of PE( j, 0) at the time step t = 2( j - i) - 1. In order to let these data ci,j in time arrive at the PEs which require such data ci,j, we introduce two communication links (the u-link and the d-link) between the PEs in Figure 4. The d-link goes from PE(j, k) to PE(j+ l,lc+ 1) and the u-link from PE(j, Ic) to PE(j + 1, Ic). Moreover, the d-link has one time step delay but the u-link has two delays. The ci,j is first transmitted along the d-link for (j - i) time steps then it is transmitted along the u-link after this time step. That is, once the ci,j has been computed at PE(j, 0), it passes through PE(j + 1, l), PE(j + 2,2), . . . ,
PE(2j - i, j - i) along the d-link, then passing through PE(2j - i, j - i + l), PE(2j - i, j - i +
2),
. . . . PE(2j -
i, n) along the a-link. The choice of d-link or a-link for propagating the ci,j is controlled by a new control link (say y-link). Having a similar consideration on the c-link, the y-link indicates whether the ci,j being on the d-link should be redirected to the a-link or not. Note that the work of the y-link can be replaced by that of the z-link, because any ci,j is propagating on d-link and on b-link for the same (j - i) time steps. Thus, the x-link and y-link have the same indicator in a PE at any time step. So we do not show the y-link in our systolic array.Note that there are two types of PEs in our computational model. One type contains the PE(j,O). The other type contains the PE(j, k) for iE > 0. We use an index I in each PE to distinguish these two types. When we consider the behavior of each PE as a finite state machine, the diagram of its states is shown in Figure 5, where SO, ~1, sg, and s3 are the initial, executing, stopping and waiting states, respectively; “^, *” are two special symbols; “-*, -*” denote the logical complements of “^, *” respectively; II = {din} d enotes that the input data d;, of a PE is used as a signal to control the states of PEs. When din = ^ is recognized by a PE, then this PE stops its execution after this time step.
2
3
4
5
6
7
8
9
Figure 4. The systolic array for the dynamic programming.
Figure 5. The states of PEs.
3. THE SYSTOLIC
ALGORITHM
To design the systolic algorithm, we define the corresponding five procedures as follows:
signal-stop G begin bout = ^; aout = ^; coUt = ^; dout = ^;z,,~ := ^ end.
waiting G begin bout = *; aout = co; coUt = co; dout = *; xoUt := *
end.
adding-w-value E
storing-c-value G begin E := bin; aoUt := din; b,,t := *; dout := *; x,,t := * end.
decreasing-x-value G begin bout := bin; xout := tin - 1; aout := oin; d,,t := din end.
Algorithm: DYNAMIC-PROGRAM E
[Initial state].
Set tin = 0 in PE(j,O) for 2 5 j 5 n. Set tin = 00 for PE(j,k) with k > 0. Set E = * in all PEs. Set oin = oo in PE(2m + 1, m) for m positive integer. Set I = 0 in PE(j, 0) and I = 1 in PE(j, k) for k > 0. The input data for the d-link in PE(j, 0) are (0, *, 0, *, . . . ,O, “}, where the 0 appears exactly (j - 1) times. The input data for the b-link and the x-link in PE(j,O) are the sequences {wj-i,j, *, wj_z,j, *, . . . , wl,j, *} and (1, *, 2, *, . . . , j - 1, *}, respectively. That is, the components of links are interspaced within stars which provide the delay needed so the components can meet PE(j, 0) correctly.
[Execution state].
repeat /* do parallel for all PEs */ if din = ^ then signal-stop;
if din = * then waiting; if din # n and din # * then
begin case I of 0: adding-w-value;
1: begin
if Zin = 1 then storing-c-value else decreasing-x-value;
Gout :=
min{ci,
,
ain + bin, din + E} endend until din = ^.
4. THE CORRECTNESS
PROOF
We use the notation PE(j, k)[din = 1, coUt = 2, . . .]t = to to denote the statement that PE(j, k) has din = 1, c,,t = 2, and so on at the time step t = to. The symbol “A +- B” means that the statement A implies the statement B. From the initial state of our systolic algorithm, two lemmas are obtained.
LEMMA 1. For 0 5 k < [j/2] < j 2 n, we have PE(j, k)[din = ^, dout = ^]t = 2j - k - 2.
PROOF. The input data for the d-link of PE(j - k, 0) are (0, *, 0, *, . . . ,O, “} with zeros appearing (j - k - 1) times. The procedure of signal-stop implies that
PE(j - k, O)[din = ^) dout = ^]t = 2(j - k - 1).
+PE(j - k + 1, l)[din = ^, dout = ^]t = 2(j - k - 1) + 1.
+PE(j, k)[& = ^) dout = ^]t = 2(j - k - 1) + k = 2j - k - 2. I
LEMMA 2. For 1 2 k < j 5 n, we have PE(j, k)[xin = 1, z,,,,~ = *]t = 3k - 1.
PROOF. From the initial values on the z-link, we have PE(j, O)[Zi, = 5, zoUt = 6]t = 26 - 1 for 1 5 6 5 j - 1. The procedure decreasing-x-vahe executes the statement: “if xin > 1 then 2out = %I - 1 else xoUt = *” in all the PE(j, k) with k # 0. Thus, we have
PE(j, O)[xin =
6,
xout = k]t = 2k - 1. *PE(j, l)[Xi, = k, x,,t = k - l]t = 2k.LEMMA 3. For 1 5 k < [j/2] < j < n, PE(j,k) assigns its bin into its register E and PE(j, k)
assigns its din to aout at the time step t = 3k - 1.
PROOF. By Lemma 2 and the execution of procedure storing-c-value which performs the as-
signments E := bi, and a,,t := din. I
The major part of the correctness verification in our algorithm is the following proposition. (**) “The value of ci,j is produced in PE(j, 0) at the time step t = 2(j -i) - 1 for 1 <_ i < j 5 n.”
That is, we will show PE(j, 0)[ c,,t = ci,j]t = 2(j - i) - 1. This proposition (**) will be proved by mathematical induction on the variable N = (j - i).
LEMMA 4. The proposition (**) is true for N = 1.
PROOF. When N = 1, this proposition (**) is shown by the initial state and the execution of
adding-w-value. That is, we have PE(j,O)[bi, = wj_l,j,ci, = 0, c,“t = bin + ci,]t = 1. Thus, cj_l,j = wj_l,j is produced in PE(j, 0) at the time step t = 2(j - j + 1) - 1 = 1. I
Now we assume that the proposition (**) is true for all N 5 m with m a given positive integer. We want to show that the proposition (**) is true for N = m + 1. The following three lemmas are considered under this induction hypothesis.
LEMMA 5. For 1 5 i < j 5 n, N = m + 1 and 1 5 k 5 [(j - i)/2J, we have (a) PE(j, k)[E = cj-k,j]t = 3k - 1.
(b) PE(j, k)[din = cd,j_k]t = 2j - k - 2i - 1. (c) PE(j, k)[bin = Ci+k,j]2 = 2j - k - 2i - 1. (d) PE(j, k)[ai, = ci,i+k]t = 2j - k - 2i - 1. PROOF.
(a) Following Lemma 3, we have PE(j, k)[si, = l]t = 3k - 1. By the induction assumption with j - (j - k) = k 5 m, we have
PE(j,O)[b,,t = tout = cj-k,j]t = 26 - 1. *PE(j, k)[bin = cj-k,j]t = 3k - 1.
Hence, we obtain PE(j, k)[E = cj_k,j]t = 3k - 1 by the procedure stating-c-value.
(b) By (j - k) - i 2 m, PE(j - k, O)[d,,t = c,,t = ci,j-k]t = 2(j - k - i) - 1 and this ci,j_k is transferring on the d-link for k time steps. We obtain
PE(j, k)[din = ci,j_k]t = 2(j - k - i) - 1 + k = 2j - k - 2i - 1.
(c)
BY j - (i + k) I m, PE(j,O)[Lt
= tout = ci+k,j
]t = 2(j - i - k) - 1 and this ci+k,j is transferring on the b-link for k time steps. We havePE(j, k)[bin = ci+k,j]t = 2j - k - 2i - 1.
(d) By (i+k)-i 5 m,PE(i+k,O)[d OUt = tout = ci,;+k]t = 2k- 1 and this ci,i+k is propagating on the d-link for k time steps. We have
PE(i + 2k, k)[din = ci,i+k]t = 3k - 1. From Lemma 2 together with k < [(i + 2k)/2], we have
PE(i + 2k, k)[Zin = l]t = 3k - 1.
+PE(i + 2ky k)[a,“t = din = ci,i+k]t = 3k - 1.
Then this ci,i+k is transferring on the a-link for 2(j - i - 2k) time steps. Therefore, we have
From the value of k with the constraint 1 5 k 5 [(j - i)/2], we obtain 2j - k - 2i - 1 > 3k - 1.
Thus, the two values of ci,j-k + Cj-k,j and ci,i+k -I- ci+k,j for evaluating the c(i,j, k) will be retrieved and performed by PE(j, k) in time. The evaluation of the &partial result of ci,j is at the time step t = 2j - k - 2i - 1 for 1 < k 5 [(j - i)/2]. F or an illustrative example of the evaluation of c1,7, we have i = 1, j = 7 and k 5 3. The evaluations of c(1,7,3), c(1,7,2) and c(1,7,1) are at the time step 8, 9, 10 respectively. The value cl,7 = w1,7 + c(l,7, 1) is obtained at t = 11 (see Figure 2).
Let I = [(j - i)/2]. The following two lemmas show that the first q-partial result c(i,j, I) of ci,j is evaluated at the time steps t = 31- 1 or t = 31+ 1 depending on whether (j - i) is an even or an odd integer.
LEMMA 6. For 1 5 i < j 5 n, N = m + 1, let 1 = [(j - i)/2j. If m + 1 is an even integer, then
we have
(a) The q-p ar la result c(i,j, 1) of ci,j t’ 1 is evaluated in PE(j, l) at the time step t = 31 - 1,
(b) The value of ci,j is coming out from PE(j, 0) at the time step t = 2(j - ;) + 1. PROOF.
(a) Following the description in Section 2, we have P, = {ci,j_, + cj_l,j, ci,i+l + ci+l,j} with 1 = l(j - i)/2] and
c(i, j,
l) = min 9. By (j-i) = N = m+l is even, we have 1 = (j-i)/2 and j - 1 = i + 1. Hence, the two terms appearing in P, are identical. That is, we haveC(i,j, 1) = Ci,j-1 + Cj-l,j. By the induction assumption with (j - 1) - i = 21- 1 = 1 5 m,
we have
PE(_i
- l,O)[cout
=
ci,j-l, dout = ci,j-Jt = 2(j - 1 - i) - 1 = 2(i + I- i) - 1 = 21- 1. +PE(j, l)[di, = ci,j_,]t = 31 - 1.Similarly, we have
PE(j, O)[c,“t = Cj_l,j) bout = Cj-,,j]t = 2l- 1. +PE(j, l)[bi” = cj_l,j]t = 31 - I.
From Lemma 2 we have
PE(j, l)[Zin = l]t = 31 - 1.
aPE(j, l)[E = bin = cj_l,j]t = 31 - 1.
Note that PE(j,f)[ai, = CO,C~~ = m]t = 31 - 1 f rom the initial state. Thus, we obtain PE(j, l)[c,“t = C(i,j, 1) = din f E = Ci,j-l + Cj-,,j]t = 31 - 1.
(b) From Lemma 5, the remaining &partial results c(i,j, k) of ci,j with 1 5 k < 1 are
evaluated in the time interval [31,41- 21. That is, we have
PE(j, k)[cin = ~(i, j, k + l), c,,t = ~(i, j, k)]t = 31- 1 + (1 - k) for 1 5 k 2 1.
*PE(j, O)[ci, = ( C i,j, l),bi, = Wi,j,C,,t = Gin + bin = Cij]t = 41 - 1.
Since j - i = m + 1 = 21, we have 41 - 1 = 2(m + 1) - 1 = 2(j - i) - 1. Hence, ci,j is
coming out from PE(j, 0) at the time step t = 2(j - i) - 1 for j - i = m + 1. Therefore,
the proposition (w) is true for N = m + 1 which is an even integer. I LEMMA 7. For 1 5 i < j 5 n, N = m + 1, let l = [(j - i)/2]. If m + 1 is an odd integer, then
we have
(a) The PI-partial result c(i, j, 1) of ci,j is evaluated in PE(j, 1) at the time step t = 31+ 1.
PROOF.
(a) Since j - i = m + 1 is an odd integer, we have 1 = m/2 and j - i = 21+ 1. As we have mentioned, the first q-partial result of Ci,j is c(i, j, I) = min{ci,j_, + cj_r,j, ci,i+, + ci+r,j}; here we assume that j - 1 > i + 1. We claim that these four cost values will appear in PE(j, 1) at t = 31+ 1.
(1) By (j - 1) - i 5 m, PE(j - l,O)[ Gout = Ci,j-l, dout = Ci,j-,]t = 2(j- I- i)- 1 = 21+ 1. + PE(j,l)[di, = ci,j-l]t = 31+ 1.
(2) BY j - (j - 1) < m, PE(j, O)kout = Cj-l,j, b out = cj-l,j ]t = 2(j - j + 1) -
+ PE(j, l)[bin = cj-,,j]t = 31 - 1.
1=21- 1.
By Lemma 2 we have PE(j, l)[Zin = l]t = 31- 1. Hence, PE(j, I)[E = cj_i,j]t = 31- 1. This implies PE(j, l)[E = cj-l,j]t = 31+ 1.
(3) By (i + 1) - i < m, we have
PE(i + l,O)[Cout = Ci,i+lr Clout = Cj,i+l]t = 2(i + I- i) - 1 = 21- 1. By I< [(i + 21)/2] and Lemma 2, we have
PE(i + 21,1)[xici, = l]t = 31- 1.
+PE(i + 21,l)[di” = ci,i+/, 2in = 1, aout = ci,i+l]t = 31 - 1. *PE(j, l)[ai, = Ci,i+/]t = 31- 1 + 2(j - i - 21) = 31+ 1.
(4) By j - (i + 1) 5 m, PE(j, O)[C,,~ = Ci.+l,j, bout = ci+,,j]t = 2(j - i - 1) - 1 = 21+ 1. + PE(j, l)[bin = ci+,,j]t = 31+ 1.
Therefore, these four cost values are already in PE(j, 1) at t = 31 + 1. Hence, the q-partial result
c(i, j,
1) of Ci,j is evaluated in PE(j, 1) at t = 31+ 1.(b) From PE(j, l)[ c,,t = c(i, j, l)]t = 31+ 1 and the result of Lemma 5, the following &partial results c(i, j, k) with 1 5 L < 1 are evaluated in the following (I- 1) time steps. That is, we have
PE(j, l)[~,,,~ = c(i, j, l)]t = 31+ 1.
+PE(j, k)[Cin = C(i, j, k f l), Gout = c(i,j,k)]t=31+1+1-k=41-k+l forl<k<l.
+PE(j,l)[Ci” = C(i,j,Z), Co"t = C(i,j,l)]t = 41.
+PE(j, O)[Ci, = C(i,j, I), bin = wi,j, c,"t = tin + bin = ci,j]t = 41+ 1. +PE(j, O)[C,“~ = Ci,j]t = 41+ 1.
Since I= m/2 and m + 1 = j - i, we have 41+ 1 = 2(m + 1) - 1 = 2(j - i) - 1. Therefore,
the proposition (**) is true when N = m + 1 is an odd integer. I
THEOREM. For 1 5 i < j 5 n, the systolic algorithm DYNAMIC-PROGRAM is correct to
produce ci,j in PE(j, 0) at the time step t = 2(j - i) - 1.
PROOF. Under the mathematical induction, this theorem is proved by the results of Lemmas 4, 6
5. CONCLUSION
In this article, we present a formal systolic algorithm to solve the dynamic programming problem of an optimal binary search tree. For a fixed integer j such that 2 5 j 5 n, first we derive a linear systolic array with [j/Z] PEs to evaluate the minimal cost q,j for 1 _< i < j. Then we combine these (n - 1) linear systolic arrays to form a two-dimensional systolic array. Hence, this computational model consists of [(n’ + 2n - 4)/4] PEs. The systolic algorithm requires (2n - 3) time steps to solve this problem. The elapsed time within a time step is independent of the problem size n. It is very suitable for the VLSI implementation due to the identical and simple structure of PEs. We also prove the correctness of this algorithm. In general, the verification of a parallel algorithm is difficult for the concurrent executions of many PEs. However, the mathematical induction is a suitable method to be used for verifying the correctness of a systolic algorithm. This designed consideration of our systolic algorithm can be applied to solve other problems, such as the combinatorial enumeration, the computational geometry and the graph theory problems. Furthermore, for developing the systolic algorithms, we are interested in the study of systolic algorithms such that the storage in any PE and the elapsed time of a time step are considered to be independent of the problem size.
REFERENCES
1. H.T. Kung, Why systolic architecture ?, IEEE Trans. CornpuLlers 15, 37-46 (1982).
2. C.Y. Chang and K. Ya.o, Systolic array processing of the sequential decoding algorithms, Intern. J. it High Speed Camptiling 1, 465-480 (1989).
3. F.C. Lin and I.C. Wu, Broadcast normalization in systolic design, IEEE Trans. on Comprt. C-37, 1121-1126 (1988).
4. J.A. Mchugh, Algorithmic Graph Theory, Prentic-Hall, Inc. Englewood Cliffs, NJ, (1990).
5. S.Y. Kung, On supercomputing with systolic/wavefront array processors, Proc. of IEEE 72,867-884 (1984). 6. E. Horowitz and S. Sahni, Fundamenlals of Computer Algorithms, Computer Science Press, Inc., (1978). 7. C.A. Mead and L.A. Conway, InboducGn to VLSI Systems, Addison-Wesley, Reading, MA, (1980).