Quantum transport in the presence of a finite-range time-modulated potential
C. S. Tang and C. S. ChuDepartment of Electrophysics, National Chiao Tung University, Hsinchu 300, Taiwan, Republic of China ~Received 6 September 1995; revised manuscript received 26 October 1995!
Quantum transport in a narrow constriction and in the presence of a finite-range time-modulated potential is studied. The potential takes the form V(x,t)5V0u(x)u(a2x)cos(vt), with a the range of the potential and x the transmission direction. Intrasubband transitions for the electrons and for arbitraryv are made possible by the finiteness in the potential range. Our results show that, as the chemical potential m increases, the dc conductance G exhibits dip structures when m is at n\v above the threshold energy of a subband. These structures in G are found in both the small a (a;l) and the large a (a@l) regime. These dips are associated with the formation of quasi-bound-states. Our results can be reduced to the limiting case of a d-profile oscillating potential when both a!l and V0a!1 are satisfied. The assumed form of the time-modulated potential is expected to be realized in a gate-induced potential configuration.
I. INTRODUCTION
Inelastic scattering processes in quantum transport have drawn continuous attention in the recent past. One of the common models used is to invoke a time-modulated poten-tial, with a certain spatial profile, to the system.1–9 The model has also been extended to incorporate the inelastic effects due to phonons by introducing a time-modulated po-tential involving the phonon operators.10–13 These studies have demonstrated, among others, the interesting feedback effect of the inelastic scattering on the elastic channel. Even though the above model is appropriate only for inelastic pro-cesses that preserve the phase coherence of the transmitting particles, the model has practical importance because the co-herent inelastic scattering can be realized, at least, in the case when the time-modulated potential is well specified.
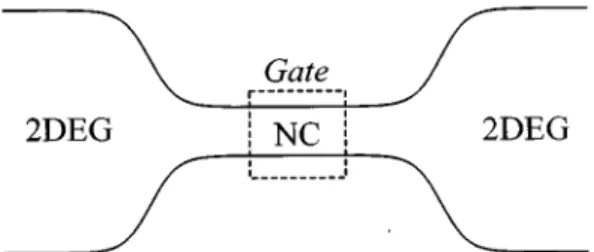
A possible realization of the coherent inelastic scattering processes in nanostructures is expected to be found in gate-controlled quantum point contacts~QPC’s!, as shown in Fig. 1. A similar gate-induced potential configuration has been suggested by Gorelik et al.,9 who considered microwave-induced effects on the Josephson current through a narrow constriction ~NC!. Their focus is on the resonance of the microwave frequency with the energy levels of the Andreev bound states formed in the NC, which has both ends con-nected to superconducting electrodes. For our purposes here, a simple exhibition of the coherent inelastic scattering is ex-pected to be found readily in a normal state gate-controlled QPC. Recent development in the split-gate technology has made possible the fabrication of such gate-controlled QPC’s.14,15 The split gates, when negatively biased, define electrostatically a NC on a two-dimensional electron gas
~2DEG!. The dc quantum transport properties of these QPC
systems has been studied intensively.16,17 More recently, there is growing interest in the time-dependent properties, such as the effects of photons, in these QPC systems.18 –23It is thus legitimate to consider the quantum transport in a NC that is acted upon by an additional, ac biased gate, as shown in Fig. 1. This ac biased gate, which is different from the split gates that define the NC, induces on the NC a time-modulated potential. The scattering of the conduction
elec-trons by this time-modulated potential is both coherent and inelastic.
There is another reason why quantum transport in a NC in the presence of a time-modulated, gate-induced potential is interesting. This is closely related to the density of state
~DOS! structures in the NC. The energy levels in the NC are
quantized into one-dimensional subbands so that the DOS is singular at the subband bottoms. In the presence of attractive impurities, such singularities in the DOS lead to dip struc-tures in the dc conductance G, as the chemical potentialm increases.24 –32The dip structures occur whenmis just below a subband edge. According to Bagwell,25these dip structures are associated with the formation of impurity-induced quasi-bound-states.25The wave function at this energymand in this subband is evanescent along the longitudinal direc-tion. Hence, for the case of an attractive impurity, a quasi-bound-state splits off from each subband.25An electron origi-nally in a propagating state in other subband can thus be scattered elastically into and be trapped by this quasi-bound-state. This gives rise to dip structures in G.
The quasi-bound-state features in G are found also when a point barrier oscillates in a NC.5In this case, for a not-too-large oscillation amplitude, the dc conductance G exhibits dip or peak structures when m is at n\v above a subband edge. These structures correspond to the situation when the electrons can make transitions, via inelastic processes, to the quasi-bound-state just below the subband edge. That there is
FIG. 1. Sketch of the gated QPC in which a narrow channel is connected adiabatically at each end to a 2DEG electrode. The gate induces a finite-range time-modulated potential in the narrow con-striction.
53
quasi-bound-state, induced by the point oscillating barrier, below each subband edge is demonstrated by Bagwell and Lake5 from the energy poles in the current transmission co-efficients. The existence of these quasi-bound-states is again due to the singular DOS near a subband edge. It is important to ask whether such quasi-bound-state features in G persist in the case of a finite-range time-modulated potential. This question has not been addressed before and if the quasi-bound-state features did persist in a finite-range time-modulated potential it will have important implications to time-dependent properties of QPC systems. Furthermore, since the potential is expected to be gate induced, the prob-lem is within reach of the recent experimental capability.
In this paper, we simplify the problem by assuming the gate-induced potential in the NC to be represented by the form V0u(x)u(a2x)cos(vt), where a is the range of the potential and x is the transmission direction. Our simplifica-tion is in replacing the smooth longitudinal potential profile, of which the potential builts up within a longitudinal distance of orderl, by an abrupt profile. The abruptness of the profile is expected to do nothing but introduce additional multiple scatterings between the two abrupt edges of the potential. This results in additional harmonics in G. Thus, for the case when the magnitude of these harmonics is small, our results are expected to resemble qualitatively the features in a smooth profile potential. An explicit smooth-profile consid-eration, however, is left to the further study. Using this small-harmonic-magnitude criterion, we find the quasi-bound-state features in G in both the small a (a;l) and the large a (a@l) regime.
Our results show that intrasubband transitions for the electrons and for arbitraryv are made possible by the finite-ness in the range of the time-modulated potential, which breaks the longitudinal translation invariance in the narrow channel. With this understanding, we expect the quasi-bound-state features found in this paper to appear also in the case of a time-dependent electric field, longitudinally or transversely polarized, as long as the field has a finite range. The transversely polarized electric field gives rise to inter-subband transitions, whereas the longitudinally polarized electric field gives rise to intrasubband transitions. There are two important features associated with this finite-range con-sideration. First, the range a of the potential or the electric field is assumed to be less than the phase-breaking length lfso that the entire transmission process is coherent and can be described by a time-dependent Schro¨dinger equation. Sec-ond, the two reservoirs at both ends of the narrow channel can be taken to be free from the time-modulation effects so that the distribution of the incident electrons is well deter-mined. Thus the quantum transport in the presence of a finite-range time-modulated potential or electric field can be cast into a Landauer-Bu¨ttiker-type formalism. The conditions imposed by the above two features are within recent experi-mental capabilities because the phase-breaking length lfcan be made sufficiently long by lowering the temperature.
The conditions are different, however, for the case when the time-dependent potential or the electric field is of infinite range and covers the entire system.19,22The major difference between the finite-range and the infinite-range situations is that the reservoirs are affected by the time-dependent fields
in the latter situation. The adiabatic turning on of the time-dependent electric field is utilized to make a connection with the distribution of the electrons in the remote past. The infinite-range situation is different from the finite-range situ-ation, both in the theoretical treatment and in the experimen-tal setting, but together they provide a complementary under-standing to the time-dependent properties in QPC systems.
In this work, the inelastic scattering is solved nonpertur-batively and we find that even within the small-harmonic-magnitude criterion the inelastic scattering has to be treated beyond one sideband approximation. The sideband index n labels those electrons whose net energy change is n\v. Fur-thermore, our results can be reduced to the limiting case of a
d-profile oscillating potential when both a!l and V0a!1 are satisfied.
In Sec. II we present the formulation for the inelastic scattering and the connection of the current transmission co-efficients with the conductance G. In Sec. III we present numerical examples illustrating the quasi-bound-state fea-tures in a finite-range time-modulated potential. Finally, Sec. IV presents a conclusion.
II. THEORY
In this section, the inelastic scattering problem is formu-lated and the equations for the current transmission and re-flection coefficients are obtained. The conductance G is then expressed in terms of these coefficients.
The QPC is modeled by a NC connected adiabatically at each end to a 2DEG. Hence the transmission of the electrons into or out of the NC region is adiabatic.33The gate-induced potential is assumed to affect only the NC region of the QPC. Therefore we need only to formulate the inelastic scattering in the NC region. The NC is taken to have a quadratic trans-verse confinement potential vy2y2. The gate-induced poten-tial takes the finite-range time-modulated form
V~x,t!5V0u~x!u~a2x!cos~vt!, ~1! whose connection with a smooth-profile potential has been discussed in the preceding section.
Choosing the energy unit E*5\2k
F
2/2m*, the length unit a*51/kF, the time unit t*5\/E*, and V0 in units of E*, the dimensionless Schro¨dinger equation becomes
@2¹21v
y
2
y21V~x,t!#C~xW,t!5i ]
]tC~xW,t!. ~2! Here kF is a typical Fermi wave vector of the reservoir and m* is the effective mass. The transverse energy levels are quantized, with «n5(2n11)vy and fn(y ) the wave func-tion. The finite-range time-modulated potential is uniform in the transverse direction and does not induce intersubband transitions, leaving the subband index n unchanged. Thus for a nth subband electron incident along xˆ and with energy
m, the scattering wave function can be written in the form
Cn1(xW,t)5fn(y )c(x,t), where
c~x,t!5
5
eikn~m!xe2imt1
(
mrn~m!e2ikn~m1mv!xe2i~m1mv!t if x,0
(
p @Jp~V0/v!e2ipvt#
E
de@A˜n~e!eikn~e!x1B˜n~e!e2ikn~e!x#e2iet if 0,x,a
(
mtn~m!eikn~m1mv!xe2i~m1mv!t if x.a
~3!
and n,m are the final subband and sideband indices, respec-tively. The effective wave vector for an electron with energy
« and in the nth subband is given by
kn(«)5
A
«2(2n11)vy. The sideband index m corresponds to the net energy change of m\vfor the outgoing electrons. It is very important to note that had the length of the NC been infinite and the range of the potential V(x,t) extended to cover the entire NC, the longitudinal wave vector knwould be a good quantum number so that no real transition could have occurred. However, as long as V(x,t) has a finite range, kn is no longer conserved and real transitions from
kn(«) to kn(«6mv) are permitted for electrons traversing
the potential. Thus the finiteness in the range of the time-modulated potential alone makes possible the absorption of energy by the electrons for arbitrary v. This picture holds regardless of the range, long or short, and the profile, abrupt or smooth, of the potential. The mathematical statement of the above physical picture turns out naturally and is given by Eq. ~4! in the following.
The expressions for the reflection and the transmission coefficients can be obtained from matching the wave func-tions and their derivatives at the two ends of the finite-range time-modulated potential. For the above matching to hold in all time, the integration variablee in Eq. ~3! has to take on discrete values m6mv. Hence we can write A˜n(e) and
B˜n(e) in the form
F˜n~e!5
(
mFn~m!d~e2m2mv!, ~4!
where F˜n(e) refers to either A˜n(e) or B˜n(e). After
perform-ing the matchperform-ing and eliminatperform-ing the current reflection coef-ficients rn(m), we obtain the equations relating An(m),
Bn(m), and the current transmission coefficients tn(m),
tn~m!5
(
m8 @An~m8
!e2iKn 2~m,m8!a 1Bn~m8
!e2iKn 1~m,m8!a #Jm2m8~V0/v!, ~5! kn~m1mv!tn~m!5(
m8 kn~m1m8
v!@An~m8
!e2iKn 2~m,m8!a 2Bn~m8
!e2iKn 1~m,m8!a # 3Jm2m8~V0/v!, ~6! and 2kn~m!dm05(
m8 @An~m8
!Kn1~m,m8
! 1Bn~m8
!Kn2~m,m8
!#Jm2m8~V0/v!, ~7! where Kn6(m,m8
)5kn(m1mv)6kn(m1m8
v). Equations~5!–~7! can be shown explicitly to reduce to the
correspond-ing equations for the d-profile time-modulated potential in the a→0 limit.35
The zero-temperature conductance is given by
G5~2e2/h!
(
n50 N
Gn, ~8!
where N11 is the number of propagating subbands in NC for the chemical potentialm. Here Gn5(m
8
Gnm
and the sum-mation is over all m such that kn(m1mv) is real. The
con-tribution to G from electrons incident in subband n and transmitted into sideband m is denoted by Gnm and is given by
Gnm5@kn~m1mv!/kn~m!#utn~m!u2. ~9!
Solving Eqs. ~5!–~7!, we obtain tn(m), An(m), and
Bn(m), from which the current reflection coefficient rn(m) can be calculated,
rn~m!5
(
m8@An~m
8
!1Bn~m8
!#Jm2m8~V0/v!2dm0. ~10!We solve the coefficients rn(m) and tn(m) exactly, in the
numerical sense, by imposing a large enough cutoff to the sideband index. The correctness of our procedure is checked against the conservation of current condition, given by
(
m8
kn~m1mv!kn~m! @utn~m!u
21ur
n~m!u2#51. ~11!
III. NUMERICAL RESULTS
We calculate, in the following, the conductance G of a NC acted upon by a finite-range time-modulated potential. The finite-range time-modulated potential does not induce intersubband transitions and so each occupied subband con-tributes independently to the total conductance. Thus it suf-fices for our purposes here to present the conductance of only one subband, which we take to be the lowest one.
In this section, the behavior of G with respect to the chemical potentialm is studied. Since G depends also on the potential range a and the oscillating amplitude V0, we
present the behavior of G in four situations. First, this G behavior is shown for a fixed while varying V0. Second, the G behavior for V0 fixed while a varying is presented. The third situation is to compare the G behavior for different
v. Finally, we present the time-averaged spatial distribution for the scattering state whose incident energy is very close to the quasi-bound-state structure.
In our numerical examples, the NC is taken to be that in a high-mobility GaAs-AlxGa12xAs with a typical electron density n;2.531011cm22and m*50.067me.
Correspond-ingly, we choose an energy unit E*5\2k
F
2/(2m*)59 meV, a length unit a*51/kF579.6 Å, and a frequency unit v*5E*/\513.6 THz. We also take vy50.035, such that
the effective NC width is of the order of 103 Å. In the fol-lowing, in presenting the dependence of G onm, it is more convenient to plot G as a function of X instead, where X5@(m/vy)11#/2. The integral value of X is the number of
propagating channels.
In Fig. 2 G is plotted against X for a5150, while V0 is varying. The frequencyvis taken to be 0.014, whose energy intervalv corresponds to an intervalDX5v/(2vy)50.2 on
the ordinate. The threshold, or the subband edge, is at X51. We note that a major dip structure occurs at X51.2, which corresponds to X2DX51. This is the
quasi-bound-state features because the electron with energy at X can make a transition to the subband edge by giving up an energy v. We note also that, in general, for larger V0, the structure at X5112DX are more evident. This is the situation when the electron can emit an energy of 2vand makes a transition to the subband edge. The wavelength of the electron decreases
as X increases. The relation is given by
l52p/
A
2vy(X21). At the location of the first dip, whenX51.2, we have l553. Thus, near the first dip, the potential range is reasonably long, with a.2.8l.
Besides the quasi-bound-state features, there are harmonic structures. These structures are smaller for the lower V0. That these harmonics are associated with the multiple scat-tering between the abrupt edges of the potential can be iden-tified from a resonance relation l52a/n, with n a positive integer. Correspondingly, the harmonic peaks are at Xn511DXn, withDXn5(np/a)2/(2vy). According to the
above estimate, the first five harmonic peaks are at Xn.1.006, 1.025, 1.056, 1.1, and 1.16, which correspond
quite reasonably to those in Fig. 2. However, for X.1.2, the harmonic peaks correspond more closely to X51.21DXn. This can be explained as follows. The harmonics for X.1.2 are contributed mostly from those electrons that give away an energy of v so that the harmonics at X are at 1.21DXn. We also see that the harmonic amplitudes are
essentially smaller than the dip structure at X51.2, thus sat-isfying our small-harmonic-amplitude criterion. From this re-sult, we expect the quasi-bound-state features to be evident in a smooth-profile time-modulated potential.
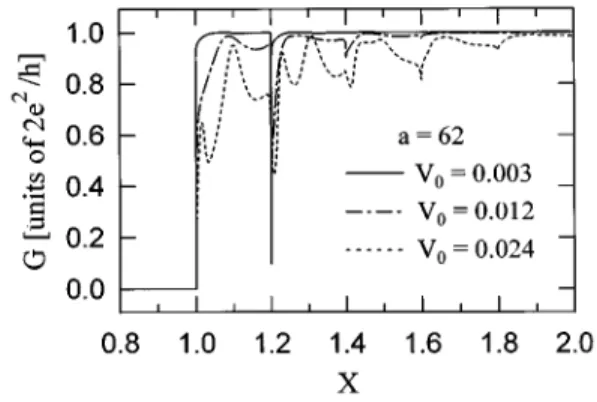
In Fig. 3, G is plotted against X when a562. The wave-length of the electron at the occurrence of the first dip is
l553 so that a.1.2l and the case corresponds to that of a
small potential range. The harmonics are essentially sup-pressed for V050.003, with a very narrow dip at X51.2. But at V050.012, when the harmonics are barely emerging, a new dip structure is developed at X51.4 while the first dip structure is widened. Both dip structures are quite evident. At V050.024, the harmonic amplitudes become very large. Similar arguments used for Fig. 2 can be applied here to identify the harmonic peak locations, but we do not repeat the details here.
In Fig. 4, we fix V0 at 0.012 while varying a. We note FIG. 2. Conductance G as a function of X for potential range
a5150 and frequencyv50.014. The potential oscillating ampli-tudes are a, V050.016; b, V050.012; and c, V050.008. The curves are vertically offset for clarity. The dip structures at X51.2 are due to the quasi-bound-state when the electrons, after giving away an energyv, make transitions to a subband edge. We note that, for larger V0, the quasi-bound-state features at X5112DX, with DX50.2, are more evident.
FIG. 3. Conductance G as a function of X for the case of a small potential range a562, while the potential oscillating amplitudes are V050.003, 0.012, and 0.024, respectively. The frequencyv is the same as in Fig. 2. The harmonic features become significant for V050.024.
that the a550 result, which corresponds to the case a.l, exhibits the emerging effects of the harmonics and the dip structures are very shallow. Interestingly, for larger a, the dip structures become more pronounced while the widths of the dips are narrower. The oscillation amplitudes of the harmon-ics remain essentially of the same order. From the results of Figs. 2– 4, we conclude also that the harmonic amplitude in G is very sensitive to V0 but much less so to the potential range a.
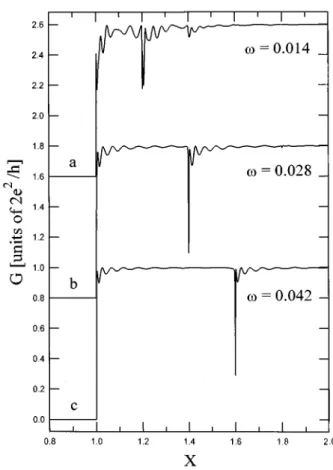
In Fig. 5, we present the case for a5200, V050.012, and different v values. In curve a, the dip structures are sub-jected to the effect of the harmonics, since at the dip location the harmonic amplitude is not that small. However, for curves b and c, the harmonic amplitudes are very small near the location of the dip. We point out also that the electron wavelengthsl near the dip structure in the curves b and c, are 37.6 and 30.7, respectively. Thus, for example, in curve c, a.6.5l and we are in the very long potential range re-gime. The quasi-bound-state features are still very clear.
In Fig. 6, we plot the time average of the scattering state spatial probability density for a5200, V050.012,
v50.028, and X51.399. The dip location is at X51.4. Our
choice of the parameters is near the occurrence condition of the quasi-bound-state. The probability density shows the eva-nescent nature of the trapped electron. This is demonstrated by the exponential tails, at both edges of the potential, which decay into the regions away from the potential. The electron
is assumed to be incident from the left-hand side of the time-modulated potential so that the charge density has a spatial oscillation in the incoming ~source! region but not in the transmitted~drain! region. Furthermore, the higher probabil-ity densprobabil-ity near the two edges of the finite-range time-modulated potential shows that the quasi-bound-state pro-cesses take place more frequently within a distance of order
l from the edges of the profile or at which the spatial
varia-tion in the potential occurs. Using this result, the spatial pro-file of the time-modulated potential in Fig. 2, curve c, can be taken to be adiabatic. This is because the V050.008 is much less than the transverse energy level spacing 2vy, which is
equal to 0.07. The dip structure is quite evident even in this situation. This demonstrates that dip structures are expected to be evident even in a time-modulated potential with an adiabatic spatial profile.
IV. CONCLUSION
We have solved nonperturbatively the quantum transport in a NC and in the presence of an abrupt-profile time-modulated potential. The scattering process is both inelastic and coherent. We find quasi-bound-state features in all po-tential ranges, including both the long- and the short-range regimes. The dip structures associated with the quasi-bound-state occur when m is at m\v above the threshold of a FIG. 4. Conductance G as a function of X for V050.012 and
v50.014. The interaction ranges are a, a5150; b, a5100; and c, a550. The curves are vertically offset for clarity. For larger a, the dip structures become more pronounced, while the widths of the dips are narrower.
FIG. 5. Conductance G as a function of X for long potential range a5200 and V050.012. The frequencies are a, v50.014; b, v50.028; and c, v50.042. The curves are vertically offset for clarity. We can see that the quasi-bound-state features are still very clear for a.6.5l, at X51.6, as shown in curve c, when the small-harmonic-magnitude criterion is satisfied.
subband edge. We find also that the inelastic processes occur more likely in the region when the potential profile varies spatially. In addition, from the results we have not shown here, we find that a one-sideband approximation, in general, violates the conservation of current requirement. Our results show that the violation of the current conservation is serious not only near the first dip structure (X511DX) but also in all the lower incident energy region (1<X<11DX).
We have presented arguments for the implications of our abrupt-profile time-modulated potential results to that of a smooth-profile time-modulated potential. We summarize and
supplement our arguments in light of the similarity and the difference between the two potential profiles. The abrupt-profile time-modulated potential and the smooth-abrupt-profile time-modulated potential are similar in that they both break the longitudinal translational invariance. This allows the electrons to absorb or emit energy in units of \v, for arbi-trary v. Consequently, the electrons can make transitions, via inelastic processes, to the quasi-bound-state just beneath a subband edge, giving rise in G to dip structures. A conclu-sion drawn from this similarity between the two profiles is that inelastic processes leading to quasi-bound-state features are permitted in both of the profiles.
These two potential profiles are different, however, in that the abrupt-profile potential introduces additional multiple scatterings between the two abrupt edges of the potential and gives rise to harmonics in G. Due to these additional mul-tiple scatterings, the electrons effectively stay longer within the abrupt-profile time-modulated potential region than within the smooth-profile time-modulated potential region. As a result, the quasi-bound-state features in the former po-tential profile might be perturbed, being either enhanced or suppressed. By proposing a small-harmonic-magnitude crite-rion, we attempt to look at cases where the perturbation from the harmonics to the quasi-bound-state features is small. In these cases, when the features of the two profiles are ex-pected to be similar qualitatively, the quasi-bound-state fea-tures are found.
In conclusion, the coherent inelastic scattering and the quasi-bound-state features are found in a NC, acted upon by an abrupt-profile time-modulated potential. The features are argued to appear in the case of a smooth-profile time-modulated potential, in particular, and are expected to affect the time-dependent properties of NC, in general.
ACKNOWLEDGMENT
This work was partially supported by the National Sci-ence Council of the Republic of China through Contract No. NSC85-2112-M-009-015.
1M. Bu¨ttiker and R. Landauer, Phys. Rev. Lett. 49, 1739~1982!. 2D. D. Coon and H. C. Liu, J. Appl. Phys. 58, 2230~1985!. 3X. P. Jiang, J. Phys. Condens. Matter 2, 6553~1990!. 4M. Y. Azbel, Phys. Rev. B 43, 6847~1991!.
5P. F. Bagwell and R. K. Lake, Phys. Rev. B 46, 15 329~1992!. 6F. Rojas and E. Cota, J. Phys. Condens. Matter 5, 5159~1993!. 7M. Wagner, Phys. Rev. B 49, 16 544~1994!.
8V. A. Chitta, C. Kutter, R. E. M. de Bekker, J. C. Maan, S. J. Hawksworth, J. M. Chamberlain, M. Henin, and G. Hill, J. Phys. Condens. Matter 6, 3945~1994!.
9
L. Y. Gorelik, V. S. Shumeiko, R. I. Shekhter, G. Wendin, and M. Jonson, Phys. Rev. Lett. 75, 1162~1995!.
10B. Y. Gelfand, S. Schmitt-Rink, and A. F. J. Levi, Phys. Rev. Lett.
62, 1683~1989!.
11W. Cai, T. F. Zheng, P. Hu, B. Yudanin, and M. Lax, Phys. Rev. Lett. 63, 418~1989!.
12W. Cai, P. Hu, T. F. Zheng, B. Yudanin, and M. Lax, Phys. Rev. B
41, 3513~1990!.
13J. M. Mohaidat, K. Shum, and R. R. Alfano, Phys. Rev. B 48, 8809~1993!.
14B. J. van Wees, H. van Houton, C. W. J. Beenakker, J. G. Wil-liamson, L. P. Kouwenhoven, D. van der Marel, and C. T. Foxon, Phys. Rev. Lett. 60, 848~1988!.
15D. A. Wharam, T. J. Thornton, R. Newbury, M. Pepper, H. Ahmed, J. E. F. Frost, D. G. Hasko, D. C. Peacock, D. A. Ritchie, and G. A. C. Jones, J. Phys. C 21, L209~1988!. 16S. Washburn and R. A. Webb, Rep. Prog. Phys. 55, 1311~1992!. 17F. A. Buot, Phys. Rep. 234, 73~1993!.
18
S. Feng and Q. Hu, Phys. Rev. B 48, 5354~1993!. 19
A. Grincwajg, M. Jonson, and R. I. Shekhter, Phys. Rev. B 49, 7557~1994!.
20Q. Hu, Appl. Phys. Lett. 62, 837~1993!.
21R. A. Wyss, C. C. Eugster, J. A. del Alamo, and Q. Hu, Appl. Phys. Lett. 63, 1522~1993!.
22L. Y. Gorelik, A. Grincwajg, V. Z. Kleiner, R. I. Shekhter, and M. Jonson, Phys. Rev. Lett. 73, 2260~1994!.
FIG. 6. Time-averaged probability^uc(x,t)u2& as a function of the longitudinal position x. The parameters are a5200, V050.012, v50.028, and X51.399. The probability density peaks near the two edges of the time-modulated potential, at x50 and 200, which shows that the quasi-bound-state processes take place more frequently within a distance of order l from the edges of the profile or at which the potential has spatial variations.
23T. J. B. M. Janssen, J. C. Maan, J. Singleton, N. K. Patel, M. Pepper, J. E. F. Frost, D. A. Ritchie, and G. A. C. Jones, J. Phys. Condens. Matter 6, L163~1994!.
24
C. S. Chu and R. S. Sorbello, Phys. Rev. B 40, 5941~1989!. 25P. Bagwell, Phys. Rev. B 41, 10 354~1990!.
26E. Tekman and S. Ciraci, Phys. Rev. B 43, 7145~1991!. 27J. A. Nixon, J. H. Davies, and H. U. Baranger, Phys. Rev. B 43,
12 638~1991!.
28Y. B. Levinson, M. I. Lubin, and E. V. Sukhorukov, Phys. Rev. B
45, 11 936~1992!.
29Y. Takagaki and D. K. Ferry, Phys. Rev. B 46, 15 218~1992!. 30J. Faist, P. Gue´ret, and H. Rothuizen, Phys. Rev. B 42, 3217
~1990!.
31C. C. Eugster, J. A. del Alamo, M. R. Melloch, and M. J. Rooks, Phys. Rev. B 46, 10 146~1992!.
32C. S. Chu and Ming-Hui Chou, Phys. Rev. B 50, 14 212~1994!. 33
L. I. Glazman, G. B. Lesorik, D. E. Khmelnitskii, and R. I. Shekhter, Pis’ma Zh. E´ ksp. Teor. Fiz. 48, 218 ~1988! @JETP Lett.
48, 238~1988!#; A. Yacoby and Y. Imry, Phys. Rev. B 41, 5341
~1990!.
34The wave function in the region 0,x,a is, by construct, a so-lution of the time-dependent Schro¨dinger equation and has been proposed by Coon and Liu in Ref. 2, in their study of the time-dependent quantum-well tunneling.
35C. S. Chu and C. S. Tang ~unpublished!. The d-profile time-modulated potential results, however, are given in Ref. 5.