風險值之估計風險解決方式---條件異質形式未知下自體抽樣的應用

行政院國家科學委員會專題研究計畫 成果報告

風險值之估計風險解決方式--條件異質形式未知下自體抽

樣的應用

研究成果報告(精簡版)

計 畫 類 別 ： 個別型 計 畫 編 號 ： NSC 95-2415-H-151-001- 執 行 期 間 ： 95 年 08 月 01 日至 96 年 07 月 31 日 執 行 單 位 ： 國立高雄應用科技大學企業管理系 計 畫 主 持 人 ： 李政峰 計畫參與人員： 碩士班研究生-兼任助理：張伊渟、阮于真 處 理 方 式 ： 本計畫涉及專利或其他智慧財產權，2 年後可公開查詢

中 華 民 國 96 年 09 月 29 日

行政院國家科學委員會專題研究計畫成果報告 計畫編號：NSC 95-2415-H-151-001- 執行期限：95 年 8 月 1 日至 96 年 7 月 31 日 主持人：李政峰 高雄應用科技大學企業管理系 中文摘要 風險值估計的準確性對於風險管理至 為重要 ，低估/高估資產損失的風險值將會 不當的膨脹/縮小尾部事件的發生機率。造 成風險值估計不確定的來源有許多，其中 之一是小樣本模型參數之估計誤差。此一 問題直到最近才得到文獻的重視 ，但解決 方式尚不夠完備。本文提出 wild 自體抽樣 (wild bootstrap)的程序，以估計未知形式的 條件異質變異數 ，並依此建立有限樣本下 風險值的機率分配。透過此估計的機率分 配，可得到平滑後 (bootstrap smoothing)的 風險值，可將之視為考慮參數估計不確定 性的修正風險值。此外，亦可經由風險值 的自體抽樣分配，建立風險值的信賴區 間，以呈現參數估計誤差對風險值估計的 影響。模擬結果顯示，平滑後的修正風險 值所形成的預測區間，較原先的風險值所 形成的預測區間，具有較正確的實際覆蓋 率。 關鍵詞：風險值、自體抽樣、wild 自體抽 樣 Abstract

Value-at-Risk (VaR) is increasingly used in the field of risk management recently. VaR is a number that tells the risk manager how much the maximum potential loss on a portfolio could be over a certain horizon and for a given probability. Hence, both obtaining the precise point estimates for the VaR and measuring the uncertainty from estimation of VaR turn out to be important for empirical applicants.

The variability in VaR estimates can have

three sources. The first one is due to the model misspecifications on the mean and volatility functions. Second, the wrong assumptions on the return distributions could make the VaR estimates misleading. Third, the estimation errors of parameters at finite samples may be incorparated in the calculation of VaR. All of these sources could affect the precision on VaR , and cause the risks in applying the VaR empirically.

The literature suggests to compute the uncertainty in the VaR estimates in the form of confidence intervals. For reaching these goals, many authors, under strict assumptions on the returns, had derived the analytical formulas for the VaR confidence intervals and the VaR distributions. These assumptions they used exclude the important feature of many financial time series, which are called the volatility clustering and fat tail, and reduce the usefulness in empirical studies. In addition, some authors used boostrap methods to deal with the same issues maintaining the assumption that GARCH model is the true model, which is not fit to the data.

distribution using wild bootstrap skills in the environments of GARCH and SV models. Based on the bootstrap distribution of VaR, we’re going to construct the confidence intervals for the VaR point estimates, and increase the precision of VaR estimates using the bootstrap smoothing method. The bootstrap smoothing is a way that reduces the estimation errors by smoothing the bootstrapped VaRs. Wild bootstrap is proved to be useful in approximating the conditional heteroskedasticity of unknown form. Hence,

the proposed method is expected to be highly useful in empirical applications. 一、前言 近十年來， VaR(風險值)廣泛應用於 資產風險管理領域。根據 Basle 銀行監理 委員會 1995 年的建議，當銀行在從事風險 性資產交易時 ，要求銀行根據風險值的概 念 ，計算風險交易的資本需求，以因應市 場可能的不利變動。換句話說 ，在大部分 的情況下 (例如 ，99%或 95%)，銀行保 留的風險性資產需足以應付交易資產組合 於持有期間 (例如 ，10 天)的最大損失。 當實際損失大於預測的風險值時，風險管 理者將需重新調整資產組合，以控制損失 的大小。因此，在實際應用時，VaR 估計 值的準確性 ，便顯得相當重要。目前有許 多研究致力於提供準確的 VaR 點估計值， 但是，估計難免產生誤差，因此，風險管 理者除了需要點估計值外，亦需要衡量準 確性的測度。 VaR 的正式定義是，在未來既定的期 間 (horizon)(一天或一星期 )與名目覆蓋 率 (coverage rate)(1%或 5%)下，資產組合 損失率 (負的報酬率)的條件機率分配之右 尾分位數 (quantile)。由於條件機率分配未 知，VaR 值亦未知，文獻上提出不同的方 法(例如，參數化的方法或非參數化的方法) 來估計風險值。這使得 VaR 的估計面臨三 種不確定(或稱風險)，(1)模型設定錯誤的 風險、(2)條件機率分配假設錯誤的風險， 與(3)參數估計誤差的風險。這些不確定會 影響 VaR 值的計算，造成應用上的風險， 故稱為「風險值的風險」。 為衡量 VaR 的風險，現有的文獻建 議，應以 VaR 信賴區間的形式來量化不確 定性。而信賴區間的建立方式，多採用蒙 地卡羅模擬法或針對利潤/損失分配做假 設。Jorion(1996)首先在報酬率為「獨立且 相同分配」(iid)的常態與 t 分配下，導出 VaR 的 信 賴 區 間 的 解 析 式 (analytical formulas);Dowd(2000)在 iid 的常態分配假 設下，導出 VaR 的機率分配;但報酬率為 iid 的假設排除實証常見的波動聚集與厚尾情 形 ， 而 降 低 其 實 用 性 。 Dowd(2001) 使用 order statistics 理論來估計 VaR 的信賴區 間。Christoffersen et. al.(2005)假設正確模 型 為 GARCH(1,1) ， 利 用 自 體 抽 樣 法 (bootstrap)建立 VaR 等相關統計量的自體 抽樣分配，以此建立 VaR 值的信賴區間， 並以區間長度來衡量估計的不確定程度。 Miazhynskaia and Aussenegg(2005) 在 GARCH 的環境下，使用貝氏統計量，建立 VaR 的分配，以利信賴區間的計算，並與 許多方法做比較。 由以上討論知道，衡量 VaR 的應用風 險須先估計 VaR 的機率分配。然而，若報 酬率分配不為 iid 與特定分配，就作者目前 的了解，則 VaR 的條件機率分配為未知， 致使建立信賴區間成為不可行。有鑒於 此，本文擬由幾個方面來延伸既有的文 獻。首先，本文使用自體抽樣法來估計 VaR 的條件機率分配，使用自體抽樣困難之處 在於資料的產生過程(DGP)未知，特別是未 知 形 式 的 異 質 變 異 數 。 Christoffersen et. al.(2005)的作法是假設資料的條件變異數 為 GARCH(1,1)，並視為正確的模型設定。 嚴格來說，此作法是值得商榷的，這等於 又引進另一種不確定性進入自體抽樣的程 序中，可能會使最後的結果產生偏誤。本 文擬以 wild bootstrap(以下稱為 WB)來處理 條件異質性未知的問題。此方法經許多文 獻證實，其近似未知形式之異質變異數的 能力頗佳，例如，Killian(2002)等人證實，

當真實 DGP 為 GARCH 或 SV(stochastic volatility)類型的模型時，WB 可以一致性 估 計 自 我 相 關 係 數 的 分 配 。 相 較 於 Christoffersen 的作法，WB 的方法似乎更 一般化。一旦估計出 VaR 的機率分配，即 可取得相對應的分位數，建立信賴區間。 在某一時點，我們想要知道，使用當 時所有的訊息，損失率的條件機率分配的 尾部情形，這表示尾部極端事件發生的可 能性。在此，我們僅考慮風險值(VaR)測 度。簡單來說，風險值為損失率條件機率 分配的右尾分位數。其定義為，基於 T 期 的 所 有 訊 息 ， 在 名 目 機 率 為 p ( 例 如 ， 05 . 0 , 01 . 0 = p k T VaR ₊ 與一定的期間 下，最大的損 失 (正值)為， k 其次，文獻對於風險值不確定性的另 一發現是，VaR 的點估計值常有「低估」 的現象(例如，Pascual, L., J. Romo，and E. Ruiz(2001);Christoffersen et. al.(2005))。上 述的文獻大多著重在風險值信賴區間的建 立，尚未提出完備的解決方法。以銀行為 例，因 VaR 值低估，銀行從事風險性資產 交易所需提供的資產要求數量也跟著降 低，一旦極端事件真的發生，將面臨緩衝 不足的情形。為此，本文擬以 Bootstrap smoothing 方式(Kitamura，1999)來降低 VaR 估計的變異，以得到較正確的 VaR 估計 值。實際的作法是，根據 WB 所估計的分 配，取自體抽樣分配的平均值，作為修正 後的 VaR 值。

(

yT+k >VaRT+k |IT

)

= p Pr (3) 在(1)式與(2)式下，風險值可寫成， k T p T k T c VaR _{+ |} =μ + ₁₋ ⋅σ ₊ (4) 此 處 ， 為 的 第 個 分 位 數。 為標準化後的干擾項 p c1₋ F(.) p − 1 (.) F t t t y σ μ ε = − 的 累積機率分配。若假設 為標準常態分 配，在 (.) F 05 . 0 = p _，c0.95 =1.645。 實証文獻上常用來描述波動性的模型 首推 GARCH，此模型在描述財務資料的波 動聚集(volatility clustering)與厚尾(fat tail) 性質時，有不錯的表現。其設定如下， 文章的結構如下，第二節為模型設定 與風險值，我們在此節介紹風險值的模型 設定;第三節為風險值的估計與估計誤差; 第四節模擬分析與自體抽樣。 GARCH(1，1): (5) 2 1 2 1 2 − − + + = t t t ω αe βσ σ 為 了 保 證 波 動 性 為 恒 定 ， 須 要 求 1 < +β α 與φ <1。 二、模型設定與風險值 假設資產組合的損失率(將報酬率乘 以 負 號 ) 為 一 恆 定 的 數 列 ， 令 代表 期所有的訊息，更進一 步假設其動態過程如下， t y

{

, ₋₁,...

}

= t t t y y I _t 三、風險值的估計與不確定性 以下介紹 GARCH(1,1)模型下，風險 值的計算。 1.先將資料去除平均數後，以最大概似 法 估 計 之 ， 得 到 估 計 的 波 動 性 數 列

{ }

T t t 1 2 ˆ ₌ σ _{， 與 標 準 化 後 的 殘 差 數 列} t t t y σ t t e y =μ+ (1) 此 處 ， 干 擾 項 為 一 martingale difference sequence(m.d.s.) ， i.e. ，此假設並未要求條件同 質變異數，因此涵蓋許多條件異質變異數 模型，例如 ARCH，GARCH，SV 等。 t e

(

et|It−1

)

=0 E μ ε ˆ ˆ = − ˆ。 2.根據估計的結果，形成往前多期( ) 的波動預測值，如下， k

(

ˆ ˆ

)

ˆ , 2 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ | 1 2 | 2 2 2 | 1 2 ≥ + + = + + = − + + + k e T k T T k T T T T T σ β α ω σ σ β α ω σ (6) 為了描述損失率的波動性，將干擾項 寫成， t t t e =σε (2) 3.由標準化殘差的實際分配中取得第 p − 1 _{的分位數，用來估計}c1−p_，如下， 此處，εt_為一iid_{數列，具有平均數為} 0，變異數為 1，且分配函數為 ，而 為形式未知的條件變異數。 (.) F σt2

(

{ }

T

)

t t p p F cˆ₁₋ = ˆ−11− εˆ ₌₁ (7) 最後計算估計的風險值，

T k T p T k T c VaR | _{1 |} ^ ˆ ˆ ˆ _{− +} + =μ+ σ (8) 四、模擬分析與自體抽樣 在本節，擬以模擬分析來研究 wild 自 體抽樣近似 GARCH 模型的實際表現。我 們讓資料分別由 GARCH 模型產生，再將 每組資料分別配適 GARCH 模型。須注意 的是，在進行自體抽樣程序時，我們以 wild 自體抽樣來產生自體抽樣樣本，而非假設 DGP 為 GARCH。 在 GARCH 下，自體抽樣程序如下， 1. 將原始資料 扣掉平均數，得到序 列不相關的殘差

{ }

1 T t t y ₌

{ }

_{=1 ，根據 wild 自體} 抽樣產生樣本 T t t e

{ }

* 1 t _t y T = _如下， * * * ˆ , ( t t iid t t _{t t} y e e e z z N μ = + = ⋅ ∼ 0,1) (9) 2. 將自體抽樣樣本去掉平均數後，估計 GARCH(1,1) 模 型 ， 得 到 參 數 估 計 值

(

* * *

)

* * , , , θ = μ ω α β 2* ˆ_t ， 估 計 的 波 動 性 σ _{，與標準化後的殘差數列 ˆ}* t ε _。 3. 條件在T 期的訊息，根據下列式子，反 覆產生往前k_{期的波動性預測值，}

(

)

2* 2 * * * 2 1| 2 * * * * 2* | 1| ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ , 2 T T T T T k T T k T e k σ ω α βσ σ ω α β σ + + + − = + + = + + ≥ (10) 需注意的是，波動性的預測需條件在最後 一期的觀察值 而非自體抽樣殘差上，以 及根據原始殘差所計算的最後一期波動性 2 ˆ_T e 2* T σ _。 4. 由自體抽樣標準化殘差的實際分配中 取得第1 p− 的分位數 ，並計算自體 抽 樣 的 VaR 值 ， 1 p T k T| _。 * 1 p c− * ˆ ₊ * ^ * * ˆ ˆ VaRT k T+ | =μ +c₋ σ 5. 重複步驟 1 至 4 許多次（例如，B 次） 後 ， 進 行 Bootstrap smoothing ， * _* | RT k T i+ | , ，並形成自體抽 樣 ( 1 1 B T k T i VaR + Va = =

∑

p − _{)% 單 邊 的 預 測 區 間} * VaR + | , T k T ⎛_−∞ ⎤ ⎜ ⎥ ⎝ _{⎦ ，再計算}yT k+ 落入此區間 的次數。 6. 形成VaRT k T+ | _之(1−α _{)%自體抽樣信賴} 區間(c ,c )，此二分位數來自於風險值2 的自體抽樣分配，如下， * * 1

{

}

* * 1 1 / * * 1 2 1 α α − −

{

}

* 2 * / 2 T k T t T k T c G VaR c G VaR + = − + = = | 1 | 1 T T t= ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ ₍₁₁₎ * (.) G 此處， 為風險值的自體抽樣分配 的 CDF，接著再計算真實風險值VaRT k+|_落 入此信賴區間的比率。 接著，我們介紹本計劃的模擬分析設 計。損失率的 DGP 如下， t t y =μ+σε_t 此處， 。GARCH 設定如 下， ) 1 , 0 ( ~N iid t ε , 0 μ = 2 t σ 2 − t βσ ₁ 2 1 − + + =ω αe_t 此處，

(

α β

)

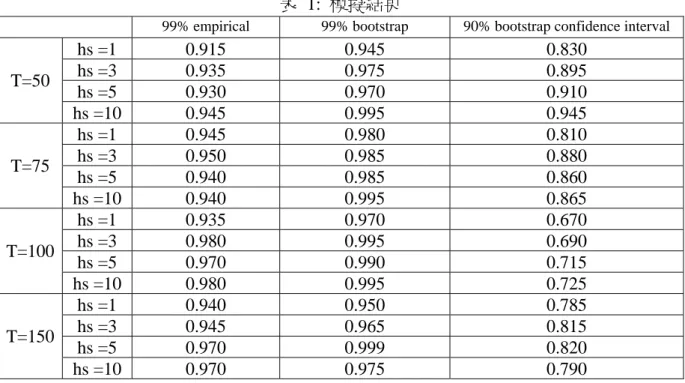
ω 。 β α =0.1, = 8, =(400/252)⋅ 1− − 75 , 50 = 10 , 5 . 0 此外，樣本長度設定為T ， 往前預測的期數為 150 , 100 , , 3 , 1 = k ，模擬次數為 2000 次，每次抽樣進行 500 次自體抽樣。 模擬結果如表 1 所示。 表 1 的第一欄代表信心水準 99%的 VaR 實際覆蓋率，而第二欄代表則代表經 過 bootstrap smoothing 後的風險值的覆蓋 率。比較不同樣本與預測期數可以發現， VaR 估計值確實有低估的情形，以 T=50 為例，在不同的預測期數下，覆蓋率介於 91.5%至 94.5%間，普遍低於名目的覆蓋水 準 99%；但隨樣本數增加，VaR 估計值的 準確度增加，但實際覆蓋率仍普遍低於名 目覆蓋率。而第二欄的數字則顯示，經平 滑後的 VaR 值，其準確度確實增加許多， 因此，實際的覆蓋率相當接近於名目值， 而且，即使在 T=50 的情形下，亦表現相當 穩健。因此，比較第一欄與第二欄的數字， 我們得到初步的結論，bootstrap smoothing

確實可以提高風險值估計的準確度，在實 證上應該是比較可信的方法。 另外，第三欄數字呈現 wild bootstrap 方式建立風險值 90%信賴區間的結果；若 信賴區間估計準確，實際上的覆蓋率將相 當接近於名目的信賴水準 90%。模擬結果 顯示，在大部份的情形，實際的覆蓋率約 低於名目值有 10%左右，顯示實際估計的 信賴區間過窄，導致區間的覆蓋率過低。 至於詳細的原因，可能需要進一步仔細研 究。 五、計劃結果自評： 本文的模擬結果發現，估計誤差對風 險值有相當程度的影響。經應用本文的抽 樣程序，平滑化後的風險值，其實際覆蓋 率有顯著的改善，顯示 wild 自體抽樣程序 可以有效的近似 GARCH。此一結果符合 計畫原先的預期，同時，此結果對於實證 應用者有很高的參考價值；此外，模擬結 果亦發現，估計 VaR 值的信賴區間，包 含真實風險值的情況，在 GARCH 模型 時，覆蓋率相對較低，此點與原先預期有 些許出入，至於詳細的原因，有待未來繼 續研究。整體而言，本文的方法適用於實 証研究建立可信賴風險值之用。 六、參考文獻：

[1].Chappell, D. and Dowd, K. (1999) `` Confidence Intervals for VaR .`` Financial Engineering News 9: 1-2.

[2]. Christofersen, P. and S., Goncalves (2005), ``Estimation Risk in Financial Risk Management'', Journal of Risk, vol. 7, No. 3, pp: 1-28.

[3]. Dowd, K. (2001), `` Estimating VaR with Order Statistics, `` The Journal of Derivatives. pp. 23-30.

[4]. Goncalves S. and L., Kilian (2002), ``Bootstrapping Autoregressions with Conditional Heteroskedasticity of Unknown Form `` ECB working paper No. 196.

[5]. Harvey, A., Ruiz, E. and N. Shephard (1994), ``Multivariate Stochastic Variance Models'', Review of Economic Studies, 61， 247-264.

[5]. Jorion, P. (1996), ``Risk2: Measuring the Risk in Value-at-Risk'', Financial Analysis Journal, 52, 47-56.

[6]. Kitamura, Y. (1999), ``Predictive Inference and Bootstrap ``, working paper. [7]. Miazhynskaia T. and W.， Aussenegg (2005), ``Uncertainty in Value-at-Risk Estimates under Parametric and Non-parametric Modeling `` working paper. [8]. Pascual, L., J. Romo, and E. Ruiz (2001), ``Forecasting Returns and Volatilities in GARCH Processes Using the Bootstrap. `` working paper.

6

表 1: 模擬結果

99% empirical 99% bootstrap 90% bootstrap confidence interval

hs =1 0.915 0.945 0.830 hs =3 0.935 0.975 0.895 hs =5 0.930 0.970 0.910 T=50 hs =10 0.945 0.995 0.945 hs =1 0.945 0.980 0.810 hs =3 0.950 0.985 0.880 hs =5 0.940 0.985 0.860 T=75 hs =10 0.940 0.995 0.865 hs =1 0.935 0.970 0.670 hs =3 0.980 0.995 0.690 hs =5 0.970 0.990 0.715 T=100 hs =10 0.980 0.995 0.725 hs =1 0.940 0.950 0.785 hs =3 0.945 0.965 0.815 hs =5 0.970 0.999 0.820 T=150 hs =10 0.970 0.975 0.790